فرق توقع الرياضيات. من أجل تحقيق نتائج إيجابية ، فإنه لا يقل أهمية
مهمة 1.احتمال إنبات بذور القمح 0.9. ما هو احتمال أن تنبت ثلاث بذور على الأقل من بين أربع بذور؟
حل. دع الحدث أ- من أصل 4 بذور ، تنبت 3 بذور على الأقل ؛ حدث في- من أصل 4 بذور ، تنبت 3 بذور ؛ حدث مع 4 بذور تنبت من 4 بذور. وفقا لنظرية الجمع الاحتمالية
الاحتمالات  و
و  التي تحددها صيغة برنولي المستخدمة في الحالة التالية. دع السلسلة تعمل ص
اختبارات مستقلة، لكل منها احتمال وقوع الحدث ثابتًا ومتساويًا ص، واحتمال عدم وقوع هذا الحدث يساوي
التي تحددها صيغة برنولي المستخدمة في الحالة التالية. دع السلسلة تعمل ص
اختبارات مستقلة، لكل منها احتمال وقوع الحدث ثابتًا ومتساويًا ص، واحتمال عدم وقوع هذا الحدث يساوي  . ثم احتمالية أن يكون الحدث أالخامس صستظهر الاختبارات بالضبط
. ثم احتمالية أن يكون الحدث أالخامس صستظهر الاختبارات بالضبط  مرات ، محسوبة بواسطة صيغة برنولي
مرات ، محسوبة بواسطة صيغة برنولي
 ,
,
أين  - عدد التوليفات من صعناصر بواسطة
- عدد التوليفات من صعناصر بواسطة  . ثم
. ثم

الاحتمال المطلوب
المهمة 2.احتمال إنبات بذور القمح 0.9. أوجد احتمال أن تنبت 350 بذرة من أصل 400 بذرة.
حل. احسب الاحتمال المطلوب  وفقًا لصيغة برنولي ، يكون صعبًا بسبب إرهاق الحسابات. لذلك ، نطبق صيغة تقريبية تعبر عن نظرية لابلاس المحلية:
وفقًا لصيغة برنولي ، يكون صعبًا بسبب إرهاق الحسابات. لذلك ، نطبق صيغة تقريبية تعبر عن نظرية لابلاس المحلية:
 ,
,
أين  و
و  .
.
من بيان المشكلة. ثم
 .
.
من الجدول 1 من التطبيقات نجد. الاحتمال المطلوب يساوي
المهمة 3.بين بذور القمح 0.02٪ من الحشائش. ما هو احتمال أن يكشف الاختيار العشوائي لـ 10000 بذرة عن 6 بذور أعشاب؟
حل. تطبيق نظرية لابلاس المحلية بسبب الاحتمالية المنخفضة  يؤدي إلى انحراف كبير في الاحتمال عن القيمة الدقيقة
يؤدي إلى انحراف كبير في الاحتمال عن القيمة الدقيقة  . لذلك ، للقيم الصغيرة صلكي يحسب
. لذلك ، للقيم الصغيرة صلكي يحسب  قم بتطبيق صيغة Poisson المقاربة
قم بتطبيق صيغة Poisson المقاربة
 ، أين .
، أين .
يتم استخدام هذه الصيغة عندما  ، وأقل صو اكثر ص، كلما كانت النتيجة أكثر دقة.
، وأقل صو اكثر ص، كلما كانت النتيجة أكثر دقة.
حسب المهمة  ;
;
 . ثم
. ثم
المهمة 4.نسبة إنبات بذور القمح 90٪. أوجد احتمال أن ينبت من 500 بذرة مزروعة ، 400 إلى 440 بذرة.
حل. إذا كان احتمال وقوع حدث أفي كل من صالاختبارات ثابتة ومتساوية صثم الاحتمال  هذا الحدث أفي مثل هذه الاختبارات سيكون هناك على الأقل
هذا الحدث أفي مثل هذه الاختبارات سيكون هناك على الأقل  مرة ولا أكثر
مرة ولا أكثر  يتم تحديد الأوقات بواسطة نظرية لابلاس المتكاملة بالصيغة التالية:
يتم تحديد الأوقات بواسطة نظرية لابلاس المتكاملة بالصيغة التالية:
 ، أين
، أين
 ,
,  .
.
وظيفة  تسمى وظيفة لابلاس. الملاحق (الجدول 2) تعطي قيم هذه الوظيفة لـ
تسمى وظيفة لابلاس. الملاحق (الجدول 2) تعطي قيم هذه الوظيفة لـ  . في
. في  وظيفة
وظيفة  . في القيم السالبة Xبسبب غرابة وظيفة لابلاس
. في القيم السالبة Xبسبب غرابة وظيفة لابلاس  . باستخدام وظيفة لابلاس ، لدينا:
. باستخدام وظيفة لابلاس ، لدينا:
حسب المهمة. باستخدام الصيغ أعلاه ، نجد  و
و  :
:
المهمة 5.يتم إعطاء قانون توزيع المتغير العشوائي المنفصل X:
البحث: 1) التوقع الرياضي. 2) التشتت. 3) الانحراف المعياري.
حل. 1) إذا كان قانون التوزيع منفصلاً متغير عشوائيمعطى بالجدول
|
| ||||||
حيث يتم إعطاء قيم المتغير العشوائي x في السطر الأول ، ويتم إعطاء احتمالات هذه القيم في السطر الثاني ، ثم يتم حساب التوقع الرياضي بواسطة الصيغة
2) التشتت  المتغير العشوائي المنفصل Xيسمى التوقع الرياضي للانحراف التربيعي لمتغير عشوائي عن متغيره توقع رياضي، أي.
المتغير العشوائي المنفصل Xيسمى التوقع الرياضي للانحراف التربيعي لمتغير عشوائي عن متغيره توقع رياضي، أي.
تميز هذه القيمة متوسط القيمة المتوقعة للانحراف التربيعي Xمن  . من الصيغة الأخيرة لدينا
. من الصيغة الأخيرة لدينا
تشتت  يمكن العثور عليها بطريقة أخرى ، بناءً على خاصيتها التالية: variance
يمكن العثور عليها بطريقة أخرى ، بناءً على خاصيتها التالية: variance  يساوي الفرق بين التوقع الرياضي لمربع المتغير العشوائي Xومربع توقعاتها الرياضية
يساوي الفرق بين التوقع الرياضي لمربع المتغير العشوائي Xومربع توقعاتها الرياضية  ، إنه
، إنه
لكي يحسب  نؤلف القانون التالي لتوزيع الكمية
نؤلف القانون التالي لتوزيع الكمية  :
:
3) لتوصيف تشتت القيم المحتملة لمتغير عشوائي حول متوسط قيمته ، يتم تقديم الانحراف المعياري  متغير عشوائي X، يساوي الجذر التربيعي للتباين
متغير عشوائي X، يساوي الجذر التربيعي للتباين  ، إنه
، إنه
 .
.
من هذه الصيغة لدينا: 
المهمة 6.متغير عشوائي مستمر Xتعطى من خلال دالة التوزيع المتكاملة

البحث عن: 1) دالة التوزيع التفاضلي  ؛ 2) التوقع الرياضي
؛ 2) التوقع الرياضي  ؛ 3) التشتت
؛ 3) التشتت  .
.
حل. 1) دالة التوزيع التفاضلي  متغير عشوائي مستمر Xيسمى مشتق دالة التوزيع المتكاملة
متغير عشوائي مستمر Xيسمى مشتق دالة التوزيع المتكاملة  ، إنه
، إنه
 .
.
الوظيفة التفاضلية المطلوبة لها الشكل التالي:

2) إذا كان متغير عشوائي مستمر Xمن خلال الوظيفة  ، ثم يتم تحديد توقعه الرياضي من خلال الصيغة
، ثم يتم تحديد توقعه الرياضي من خلال الصيغة

منذ الوظيفة  في
في  وعلى
وعلى  يساوي صفرًا ، إذن من الصيغة الأخيرة لدينا
يساوي صفرًا ، إذن من الصيغة الأخيرة لدينا
 .
.
3) التشتت  حدد بالصيغة
حدد بالصيغة


المهمة 7.طول الجزء هو متغير عشوائي موزع بشكل طبيعي مع توقع رياضي يبلغ 40 مم وانحراف معياري قدره 3 مم. البحث: 1) احتمال أن يكون طول الجزء التعسفي أكثر من 34 مم وأقل من 43 مم ؛ 2) احتمال انحراف طول الجزء عن توقعه الرياضي بما لا يزيد عن 1.5 مم.
حل. 1) دع X- طول الجزء. إذا كان المتغير العشوائي Xمنح دالة تفاضلية  ، ثم احتمال ذلك Xسيأخذ القيم التي تنتمي إلى المقطع
، ثم احتمال ذلك Xسيأخذ القيم التي تنتمي إلى المقطع  ، من خلال الصيغة
، من خلال الصيغة
 .
.
احتمال تحقيق التفاوتات الصارمة  تحددها نفس الصيغة. إذا كان المتغير العشوائي Xموزع من قبل القانون العادي، الذي - التي
تحددها نفس الصيغة. إذا كان المتغير العشوائي Xموزع من قبل القانون العادي، الذي - التي
 , (1)
, (1)
أين  هي وظيفة لابلاس ،
هي وظيفة لابلاس ،  .
.
في المهمة. ثم

2) حسب حالة المشكلة ، أين  . بالتعويض عن (1) ، لدينا
. بالتعويض عن (1) ، لدينا

 . (2)
. (2)
من الصيغة (2) لدينا.
يمكن النظر في مفهوم التوقع الرياضي باستخدام مثال رمي النرد. مع كل رمية ، يتم تسجيل النقاط التي تم إسقاطها. يتم استخدام القيم الطبيعية في النطاق من 1 إلى 6 للتعبير عنها.
بعد عدد معين من الرميات ، بمساعدة العمليات الحسابية البسيطة ، يمكنك إيجاد المتوسط قيمة حسابيةالنقاط المتساقطة.
بالإضافة إلى إسقاط أي من قيم النطاق ، ستكون هذه القيمة عشوائية.
وإذا قمت بزيادة عدد الرميات عدة مرات؟ في كميات كبيرةرميات ، سوف يقترب المتوسط الحسابي للنقاط رقم محدد، والتي تسمى في نظرية الاحتمالات التوقع الرياضي.
لذلك ، يُفهم التوقع الرياضي على أنه متوسط قيمة متغير عشوائي. يمكن أيضًا تقديم هذا المؤشر كمجموع مرجح للقيم المحتملة.
هذا المفهوم له عدة مرادفات:
- متوسط القيمة؛
- متوسط القيمة؛
- مؤشر الاتجاه المركزي
- اللحظة الأولى.
بمعنى آخر ، إنه ليس أكثر من رقم يتم توزيع قيم المتغير العشوائي حوله.
في مجالات متنوعة النشاط البشريستكون مناهج فهم التوقع الرياضي مختلفة إلى حد ما.
يمكن أن ينظر إليه على أنه:
- متوسط الفائدة المتلقاة من اتخاذ قرار ، في حالة النظر في مثل هذا القرار من وجهة نظر نظرية الأعداد الكبيرة ؛
- المبلغ المحتمل للربح أو الخسارة (نظرية القمار) ، محسوبة في المتوسط لكل من المعدلات. في العامية ، تبدو مثل "ميزة اللاعب" (إيجابية للاعب) أو "ميزة الكازينو" (سلبية للاعب) ؛
- نسبة الربح المحصل من المكاسب.
التوقع الرياضي ليس إلزاميًا على الإطلاق لجميع المتغيرات العشوائية. إنه غائب بالنسبة لأولئك الذين لديهم تباين في المجموع المقابل أو التكامل.
خصائص التوقع
مثل أي معلمة إحصائية ، فإن التوقع الرياضي له الخصائص التالية:

الصيغ الأساسية للتوقعات الرياضية
يمكن إجراء حساب التوقع الرياضي لكل من المتغيرات العشوائية التي تتميز بكل من الاستمرارية (الصيغة أ) والتمييز (الصيغة ب):
- M (X) = ∑i = 1nxi⋅pi ، حيث x هي قيم المتغير العشوائي ، و pi هي الاحتمالات:
- M (X) = ∫ + ∞ − ∞f (x) ⋅xdx ، حيث f (x) كثافة احتمالية معينة.
أمثلة على حساب التوقع الرياضي
مثال أ.
هل من الممكن معرفة متوسط ارتفاع التماثيل في القصة الخيالية حول بياض الثلج. من المعروف أن كل من التماثيل السبعة لها ارتفاع معين: 1.25 ؛ 0.98 ؛ 1.05 ؛ 0.71 ؛ 0.56 ؛ 0.95 و 0.81 م.
خوارزمية الحساب بسيطة للغاية:
- أوجد مجموع كل قيم مؤشر النمو (متغير عشوائي):
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31; - المبلغ الناتج مقسومًا على عدد التماثيل:
6,31:7=0,90.
وهكذا ، فإن متوسط ارتفاع التماثيل في القصة الخيالية هو 90 سم ، وبعبارة أخرى ، هذا هو التوقع الرياضي لنمو التماثيل.
صيغة العمل - M (x) \ u003d 4 0.2 + 6 0.3 + 10 0.5 \ u003d 6
التنفيذ العملي للتوقعات الرياضية
يتم استخدام حساب المؤشر الإحصائي للتوقع الرياضي في مختلف المجالات الأنشطة العملية. أولاً نحن نتكلمعن المنطقة التجارية. في الواقع ، يرتبط تقديم Huygens لهذا المؤشر بتحديد الفرص التي يمكن أن تكون مواتية ، أو على العكس من ذلك ، غير مواتية لبعض الأحداث.
 تستخدم هذه المعلمة على نطاق واسع لتقييم المخاطر ، خاصة عندما يتعلق الأمر بالاستثمارات المالية.
تستخدم هذه المعلمة على نطاق واسع لتقييم المخاطر ، خاصة عندما يتعلق الأمر بالاستثمارات المالية.
لذلك ، في الأعمال التجارية ، يعمل حساب التوقع الرياضي كطريقة لتقييم المخاطر عند حساب الأسعار.
أيضًا ، يمكن استخدام هذا المؤشر عند حساب فعالية تدابير معينة ، على سبيل المثال ، بشأن حماية العمال. بفضله ، يمكنك حساب احتمال وقوع حدث.
مجال آخر لتطبيق هذه المعلمة هو الإدارة. يمكن أيضًا حسابها أثناء مراقبة جودة المنتج. على سبيل المثال ، باستخدام حصيرة. يمكن حساب التوقعات عدد ممكنإنتاج الأجزاء المعيبة.
تبين أيضًا أن التوقع الرياضي لا غنى عنه عند إجراء المعالجة الإحصائيةوردت خلال بحث علمينتائج. كما يسمح لك بحساب احتمال نتيجة مرغوبة أو غير مرغوب فيها لتجربة أو دراسة ، اعتمادًا على مستوى تحقيق الهدف. بعد كل شيء ، يمكن أن يرتبط تحقيقه بالربح والربح ، وعدم تحقيقه - كخسارة أو خسارة.
استخدام التوقعات الرياضية في الفوركس
التطبيق العملي لهذه المعلمة الإحصائية ممكن عند إجراء المعاملات في سوق الصرف الأجنبي. يمكن استخدامه لتحليل نجاح المعاملات التجارية. علاوة على ذلك ، تشير الزيادة في قيمة التوقع إلى زيادة في نجاحهم.
من المهم أيضًا أن تتذكر أن التوقع الرياضي لا ينبغي اعتباره المعلمة الإحصائية الوحيدة المستخدمة لتحليل أداء المتداول. يؤدي استخدام العديد من المعلمات الإحصائية إلى جانب متوسط القيمة إلى زيادة دقة التحليل في بعض الأحيان.
أثبتت هذه المعلمة نفسها بشكل جيد في مراقبة ملاحظات حسابات التداول. بفضله ، يتم إجراء تقييم سريع للعمل المنجز على حساب الوديعة. في الحالات التي يكون فيها نشاط المتداول ناجحًا ويتجنب الخسائر ، لا يوصى باستخدام حساب التوقع الرياضي فقط. في هذه الحالات ، لا تؤخذ المخاطر في الاعتبار ، مما يقلل من فعالية التحليل.
تشير الدراسات التي أجريت على تكتيكات المتداولين إلى ما يلي:
- الأكثر فعالية هي التكتيكات القائمة على المدخلات العشوائية ؛
- الأقل فعالية هي التكتيكات القائمة على المدخلات المنظمة.
من أجل تحقيق نتائج إيجابية ، من المهم بنفس القدر:
- تكتيكات إدارة الأموال ؛
- استراتيجيات الخروج.
باستخدام مثل هذا المؤشر كتوقع رياضي ، يمكننا أن نفترض ما سيكون الربح أو الخسارة عند استثمار دولار واحد. من المعروف أن هذا المؤشر ، المحسوب لجميع الألعاب التي تمارس في الكازينو ، لصالح المؤسسة. هذا هو ما يسمح لك لكسب المال. في حالة وجود سلسلة طويلة من الألعاب ، يزداد احتمال خسارة العميل للمال بشكل كبير.
ألعاب اللاعبين المحترفين محدودة بفترات زمنية صغيرة ، مما يزيد من فرص الفوز ويقلل من مخاطر الخسارة. لوحظ نفس النمط في أداء عمليات الاستثمار.
يمكن للمستثمر أن يكسب مبلغًا كبيرًا مع توقع إيجابي وصنع عدد كبيرالمعاملات خلال فترة زمنية قصيرة.
يمكن اعتبار التوقع على أنه الفرق بين النسبة المئوية للربح (PW) مضروبة في متوسط الربح (AW) واحتمال الخسارة (PL) مضروبًا في متوسط الخسارة (AL).
كمثال ، ضع في اعتبارك ما يلي: المركز - 12.5 ألف دولار ، المحفظة - 100 ألف دولار ، المخاطرة لكل إيداع - 1٪. تبلغ ربحية المعاملات 40٪ من الحالات بمتوسط ربح 20٪. في حالة حدوث خسارة ، يكون متوسط الخسارة 5٪. يعطي حساب التوقع الرياضي للتداول قيمة 625 دولارًا.
يمكن أيضًا وصف المتغيرات العشوائية ، بالإضافة إلى قوانين التوزيع الخصائص العددية .
توقع رياضييسمى M (x) لمتغير عشوائي قيمته المتوسطة.
يتم حساب التوقع الرياضي لمتغير عشوائي منفصل بواسطة الصيغة
أين – قيم متغير عشوائي ، ص أنا-احتمالاتهم.
ضع في اعتبارك خصائص التوقع الرياضي:
1. التوقع الرياضي للثابت يساوي الثابت نفسه
2. إذا تم ضرب متغير عشوائي في رقم معين k ، فسيتم ضرب التوقع الرياضي بنفس الرقم
م (كس) = كم (س)
3. التوقع الرياضي لمجموع المتغيرات العشوائية يساوي مجموع توقعاتهم الرياضية
M (x 1 + x 2 + ... + x n) \ u003d M (x 1) + M (x 2) + ... + M (x n)
4. م (× 1 - × 2) \ u003d م (× 1) - م (× 2)
5. بالنسبة للمتغيرات العشوائية المستقلة × 1 ، × 2 ، ... × ن ، يكون التوقع الرياضي للمنتج مساويًا لمنتج توقعاتهم الرياضية
M (x 1، x 2، ... x n) \ u003d M (x 1) M (x 2) ... M (x n)
6. M (x - M (x)) \ u003d M (x) - M (M (x)) \ u003d M (x) - M (x) \ u003d 0
دعنا نحسب التوقع الرياضي للمتغير العشوائي من المثال 11.
م (س) == ![]() .
.
المثال 12.دع المتغيرات العشوائية x 1 ، x 2 تُعطى بواسطة قوانين التوزيع ، على التوالي:
× 1 الجدول 2
× 2 الجدول 3
احسب M (x 1) و M (x 2)
م (س 1) \ u003d (- 0.1) 0.1 + (- 0.01) 0.2 + 0 0.4 + 0.01 0.2 + 0.1 0.1 \ u003d 0
م (س 2) \ u003d (- 20) 0.3 + (- 10) 0.1 + 0 0.2 + 10 0.1 + 20 0.3 \ u003d 0
التوقعات الرياضية لكلا المتغيرين العشوائيين هي نفسها - إنها تساوي الصفر. ومع ذلك ، فإن توزيعها مختلف. إذا كانت قيم x 1 تختلف قليلاً عن توقعاتها الرياضية ، فإن قيم x 2 تختلف إلى حد كبير عن توقعاتها الرياضية ، واحتمالات مثل هذه الانحرافات ليست صغيرة. توضح هذه الأمثلة أنه من المستحيل تحديد الانحرافات التي تحدث من متوسط القيمة لأعلى ولأسفل. حتى مع نفس الشيء متوسطلا يمكن القول بأن هطول الأمطار السنوي في منطقتين مناسبتين للعمل الزراعي. وبالمثل ، من حيث المتوسط أجورلا يمكن الحكم جاذبية معينةالعمال ذوي الأجور المرتفعة والمنخفضة. لذلك ، يتم تقديمه خاصية عددية – تشتتد (خ) , التي تميز درجة انحراف متغير عشوائي عن قيمته المتوسطة:
د (س) = م (س - م (س)) 2. (2)
التشتت هو التوقع الرياضي للانحراف التربيعي لمتغير عشوائي عن التوقع الرياضي. بالنسبة للمتغير العشوائي المنفصل ، يتم حساب التباين بالصيغة:
د (س) = ![]() =
= ![]() (3)
(3)
ويترتب على تعريف التباين أن D (x) 0.
خصائص التشتت:
1. تشتت الثابت صفر
2. إذا تم ضرب متغير عشوائي في عدد ما ك ، فسيتم ضرب التباين في مربع هذا الرقم
د (ك س) = ك 2 د (خ)
3. D (x) \ u003d M (x 2) - M 2 (x)
4. للمتغيرات العشوائية الزوجية المستقلة x 1، x 2،… x n فرق المجموع يساوي مجموع الفروق.
D (x 1 + x 2 + ... + x n) = D (x 1) + D (x 2) + ... + D (x n)
دعنا نحسب التباين للمتغير العشوائي من المثال 11.
التوقع الرياضي M (x) = 1. لذلك ، وفقًا للصيغة (3) لدينا:
د (س) = (0 - 1) 2 1/4 + (1 - 1) 2 1/2 + (2-1) 2 1/4 = 1 1/4 +1 1/4 = 1/2
لاحظ أنه من الأسهل حساب التباين إذا استخدمنا الخاصية 3:
D (x) \ u003d M (x 2) - M 2 (x).
دعنا نحسب الفروق للمتغيرات العشوائية × 1 ، × 2 من المثال 12 باستخدام هذه الصيغة. التوقعات الرياضية لكلا المتغيرين العشوائيين تساوي الصفر.
د (س 1) \ u003d 0.01 0.1 + 0.0001 0.2 + 0.0001 0.2 + 0.01 0.1 \ u003d 0.001 + 0.00002 + 0.00002 + 0.001 \ u003d 0.00204
D (x 2) \ u003d (-20) 2 0.3 + (-10) 2 0.1 + 10 2 0.1 + 20 2 0.3 \ u003d 240 +20 = 260
كلما اقتربت قيمة التشتت من الصفر ، كلما قل انتشار المتغير العشوائي بالنسبة للقيمة المتوسطة.
القيمة تسمى الانحراف المعياري. أزياء عشوائية x نوع منفصل Mdهي قيمة المتغير العشوائي ، والتي تتوافق مع أعلى احتمال.
أزياء عشوائية x نوع مستمر Md، يسمى عدد حقيقي، تُعرَّف بأنها النقطة القصوى لكثافة التوزيع الاحتمالي f (x).
متوسط المتغير العشوائي x نوع مستمر Mnهو رقم حقيقي يحقق المعادلة
نظرية الاحتمالات - قسم خاصالرياضيات ، التي يدرسها طلاب مؤسسات التعليم العالي فقط. هل تحب الحسابات والصيغ؟ ألست خائفًا من احتمالات التعارف مع التوزيع الطبيعي ، وانتروبيا المجموعة ، والتوقع الرياضي وتباين المتغير العشوائي المنفصل؟ بعد ذلك سيكون هذا الموضوع ذا أهمية كبيرة لك. دعنا نلقي نظرة على بعض من أهمها مفاهيم أساسيةهذا فرع من العلوم.
دعونا نتذكر الأساسيات
حتى لو كنت تتذكر أكثر مفاهيم بسيطةنظرية الاحتمال ، لا تهمل الفقرات الأولى من المقال. الحقيقة هي أنه بدون فهم واضح للأساسيات ، لن تتمكن من التعامل مع الصيغ التي تمت مناقشتها أدناه.
لذلك هناك بعض حدث عشوائي، بعض التجارب. نتيجة للإجراءات التي تم تنفيذها ، يمكننا الحصول على العديد من النتائج - بعضها أكثر شيوعًا والبعض الآخر أقل شيوعًا. احتمال وقوع حدث هو نسبة عدد النتائج المتلقاة بالفعل من نوع واحد إلى الرقم الإجماليممكن. معرفة فقط التعريف الكلاسيكيمن هذا المفهوم ، يمكنك البدء في دراسة التوقع الرياضي والتباين للمتغيرات العشوائية المستمرة.
متوسط
بالعودة إلى المدرسة ، في دروس الرياضيات ، بدأت العمل بالمتوسط الحسابي. يستخدم هذا المفهوم على نطاق واسع في نظرية الاحتمالات ، وبالتالي لا يمكن تجاهله. الشيء الرئيسي بالنسبة لنا هذه اللحظةهو أننا سنواجهه في الصيغ الخاصة بالتوقع الرياضي والتباين لمتغير عشوائي.

لدينا سلسلة من الأرقام ونريد إيجاد المتوسط الحسابي. كل ما هو مطلوب منا هو جمع كل ما هو متاح وقسمته على عدد العناصر في التسلسل. دعونا نحصل على أرقام من 1 إلى 9. مجموع العناصر سيكون 45 ، وسوف نقسم هذه القيمة على 9. الإجابة: - 5.
تشتت
تتحدث لغة علمية، الفرق هو المربع الأوسطانحرافات القيم المميزة التي تم الحصول عليها عن المتوسط الحسابي. يُرمز إلى أحدهما بحرف لاتيني كبير D. ما المطلوب لحسابه؟ لكل عنصر من عناصر التسلسل ، نحسب الفرق بين الرقم المتاح والمتوسط الحسابي ونقوم بتربيعه. سيكون هناك العديد من القيم بالضبط بقدر ما يمكن أن تكون هناك نتائج للحدث الذي ندرسه. بعد ذلك ، نلخص كل ما تم استلامه ونقسمه على عدد العناصر في التسلسل. إذا كان لدينا خمس نتائج محتملة ، فاقسم على خمسة.

يحتوي التباين أيضًا على خصائص تحتاج إلى تذكرها من أجل تطبيقها عند حل المشكلات. على سبيل المثال ، إذا زاد المتغير العشوائي بمقدار X مرة ، فإن التباين يزيد بمقدار X مرة في المربع (أي X * X). لا تقل أبدًا عن الصفر ولا تعتمد على إزاحة القيم بمقدار قيمة متساويةصعودا أو هبوطا. أيضًا ، بالنسبة للتجارب المستقلة ، يكون التباين في المجموع مساويًا لمجموع الفروق.
الآن نحن بالتأكيد بحاجة إلى النظر في أمثلة تباين متغير عشوائي منفصل والتوقع الرياضي.
لنفترض أننا أجرينا 21 تجربة وحصلنا على 7 نتائج مختلفة. لاحظنا كل واحد منهم ، على التوالي ، 1،2،2،3،4،4 و 5 مرات. ماذا سيكون التباين؟
أولاً ، نحسب المتوسط الحسابي: مجموع العناصر ، بالطبع ، هو 21. نقسمه على 7 ، ونحصل على 3. الآن نطرح 3 من كل رقم في التسلسل الأصلي ، ونربّع كل قيمة ، ونجمع النتائج معًا . اتضح 12. الآن يتبقى لنا أن نقسم الرقم على عدد العناصر ، ويبدو أن هذا كل شيء. لكن هناك قبض! دعونا نناقشها.
الاعتماد على عدد التجارب
اتضح أنه عند حساب التباين ، يمكن أن يكون المقام واحدًا من رقمين: إما N أو N-1. هنا N هو عدد التجارب التي تم إجراؤها أو عدد العناصر في التسلسل (وهو في الأساس نفس الشيء). على ماذا تعتمد؟

إذا تم قياس عدد الاختبارات بالمئات ، فيجب علينا وضع N في المقام ، وإذا كان بالوحدات ، فعندئذٍ N-1. قرر العلماء رسم الحد بشكل رمزي تمامًا: اليوم يمتد على طول الرقم 30. إذا أجرينا أقل من 30 تجربة ، فسنقسم الكمية على N-1 ، وإذا كانت أكثر ، فسنقسمها على N.
مهمة
دعنا نعود إلى مثالنا في حل مشكلة التباين والتوقع. حصلنا على عدد متوسط وهو 12 ، والذي يجب أن نقسم على N أو N-1. نظرًا لأننا أجرينا 21 تجربة ، أي أقل من 30 تجربة ، فسنختار الخيار الثاني. إذن الجواب هو: الفرق هو 12/2 = 2.
القيمة المتوقعة
دعنا ننتقل إلى المفهوم الثاني ، الذي يجب أن نأخذ في الاعتبار في هذه المقالة. التوقع الرياضي هو نتيجة إضافة جميع النتائج الممكنة مضروبة في الاحتمالات المقابلة. من المهم أن نفهم أن القيمة التي تم الحصول عليها ، وكذلك نتيجة حساب التباين ، يتم الحصول عليها مرة واحدة فقط المهمة كلها، بغض النظر عن عدد النتائج التي تراها.

معادلة التوقع الرياضي بسيطة للغاية: نأخذ النتيجة ونضربها في احتمالية نضيفها للنتيجة الثانية والثالثة وما إلى ذلك. كل ما يتعلق بهذا المفهوم يسهل حسابه. على سبيل المثال ، مجموع التوقعات الرياضية يساوي التوقع الرياضي للمبلغ. نفس الشيء ينطبق على العمل. هذه عمليات بسيطةبعيدًا عن كل كمية في نظرية الاحتمال تسمح لنا بالوفاء بها. لنأخذ مهمة ونحسب قيمة مفهومين درسناهما في وقت واحد. بالإضافة إلى ذلك ، انشغلنا بالنظرية - حان وقت الممارسة.
مثال آخر
أجرينا 50 تجربة وحصلنا على 10 أنواع من النتائج - أرقام من 0 إلى 9 - تظهر بشكل مختلف نسبة مئوية. هذه على التوالي: 2٪ ، 10٪ ، 4٪ ، 14٪ ، 2٪ ، 18٪ ، 6٪ ، 16٪ ، 10٪ ، 18٪. تذكر أنه للحصول على الاحتمالات ، عليك قسمة قيم النسبة المئوية على 100. وهكذا ، نحصل على 0.02 ؛ 0.1 إلخ. دعونا نقدم مثالاً لحل مشكلة تباين المتغير العشوائي والتوقع الرياضي.
نحسب المتوسط الحسابي باستخدام الصيغة التي نتذكرها مدرسة ابتدائية: 50/10 = 5.
الآن دعونا نترجم الاحتمالات إلى عدد من النتائج "على شكل أجزاء" لجعلها أكثر ملاءمة للعد. نحصل على 1 و 5 و 2 و 7 و 1 و 9 و 3 و 8 و 5 و 9. قم بطرح المتوسط الحسابي من كل قيمة تم الحصول عليها ، وبعد ذلك نقوم بتربيع كل من النتائج التي تم الحصول عليها. شاهد كيفية القيام بذلك بالعنصر الأول كمثال: 1-5 = (-4). علاوة على ذلك: (-4) * (-4) = 16. للقيم الأخرى ، قم بهذه العمليات بنفسك. إذا فعلت كل شيء بشكل صحيح ، فبعد إضافة كل شيء ، ستحصل على 90.

دعنا نواصل حساب التباين ونعني بقسمة 90 على N. لماذا نختار N وليس N-1؟ هذا صحيح ، لأن عدد التجارب التي تم إجراؤها يتجاوز 30 تجربة. إذن: 90/10 = 9. حصلنا على التشتت. إذا حصلت على رقم مختلف ، فلا تيأس. على الأرجح ، لقد ارتكبت خطأ عاديًا في الحسابات. تحقق مرة أخرى مما كتبته ، وتأكد من أن كل شيء سيكون في مكانه الصحيح.
أخيرًا ، لنتذكر صيغة التوقع الرياضية. لن نقدم جميع الحسابات ، سنكتب فقط الإجابة التي يمكنك التحقق من خلالها بعد الانتهاء من جميع الإجراءات المطلوبة. ستكون القيمة المتوقعة 5.48. نتذكر فقط كيفية تنفيذ العمليات ، باستخدام مثال العناصر الأولى: 0 * 0.02 + 1 * 0.1 ... وهكذا. كما ترى ، نقوم ببساطة بضرب قيمة النتيجة في احتمالية حدوثها.
انحراف
مفهوم آخر يرتبط ارتباطًا وثيقًا بالتشتت والتوقع الرياضي هو الانحراف المعياري. تم وضع علامة إما بأحرف لاتينية sd ، أو "سيجما" اليونانية الصغيرة. هذا المفهوميوضح كيف تنحرف القيم في المتوسط عن السمة المركزية. للعثور على قيمتها ، تحتاج إلى حساب الجذر التربيعيمن التشتت.

إذا قمت بعمل رسم بياني التوزيع الطبيعيوترغب في رؤيتها مباشرة الانحراف المعياري، يمكن القيام بذلك في عدة خطوات. خذ نصف الصورة إلى يسار أو يمين الوضع (القيمة المركزية) ، ارسم عموديًا على المحور الأفقي بحيث تكون مساحات الأشكال الناتجة متساوية. ستكون قيمة المقطع بين منتصف التوزيع والإسقاط الناتج على المحور الأفقي هي الانحراف المعياري.
برمجة
كما يتضح من أوصاف الصيغ والأمثلة المقدمة ، فإن حساب التباين والتوقع الرياضي ليس أسهل إجراء من وجهة نظر حسابية. لكي لا تضيع الوقت ، فمن المنطقي استخدام البرنامج المستخدم في أعلى المؤسسات التعليمية- يطلق عليه "R". لديها وظائف تسمح لك بحساب القيم للعديد من المفاهيم من الإحصاءات ونظرية الاحتمالات.
على سبيل المثال ، يمكنك تحديد متجه من القيم. يتم ذلك على النحو التالي: ناقل<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.
أخيراً
التشتت والتوقعات الرياضية هما اللذان بدونهما يصعب حساب أي شيء في المستقبل. في الدورة الرئيسية للمحاضرات في الجامعات ، يتم اعتبارها بالفعل في الأشهر الأولى من دراسة الموضوع. وبسبب عدم فهم هذه المفاهيم البسيطة وعدم القدرة على حسابها على وجه التحديد ، يبدأ العديد من الطلاب على الفور في التخلف عن البرنامج ويتلقون لاحقًا درجات ضعيفة في نهاية الجلسة ، مما يحرمهم من المنح الدراسية.
مارس أسبوعًا واحدًا على الأقل لمدة نصف ساعة يوميًا ، وحل المهام المشابهة لتلك الواردة في هذه المقالة. بعد ذلك ، في أي اختبار نظرية احتمالية ، سوف تتعامل مع أمثلة بدون نصائح غريبة وأوراق الغش.
التوقع الرياضي هو التعريف
حصيرة الانتظارمن أهم المفاهيم في الإحصاء الرياضي ونظرية الاحتمالات التي تميز توزيع القيم أو الاحتمالاتمتغير عشوائي. عادة ما يتم التعبير عنها كمتوسط مرجح لجميع المعلمات الممكنة لمتغير عشوائي. يستخدم على نطاق واسع في التحليل الفني ، ودراسة سلسلة الأرقام ، ودراسة العمليات المستمرة وطويلة الأجل. إنه مهم في تقييم المخاطر ، والتنبؤ بمؤشرات الأسعار عند التداول في الأسواق المالية ، ويستخدم في تطوير استراتيجيات وأساليب تكتيكات اللعبة في نظرية القمار.
كش ملك في انتظار- هذامتوسط قيمة المتغير العشوائي ، التوزيع الاحتمالاتيعتبر المتغير العشوائي في نظرية الاحتمالات.
حصيرة الانتظارقياس متوسط قيمة متغير عشوائي في نظرية الاحتمالات. توقع الرياضيات لمتغير عشوائي xيعني م (س).
التوقع الرياضي (وسط السكان) هو
حصيرة الانتظار

حصيرة الانتظارفي نظرية الاحتمالات ، المتوسط المرجح لجميع القيم الممكنة التي يمكن أن يتخذها هذا المتغير العشوائي.

حصيرة الانتظارمجموع حاصل ضرب جميع القيم الممكنة لمتغير عشوائي من خلال احتمالات هذه القيم.
التوقع الرياضي (وسط السكان) هو
حصيرة الانتظارمتوسط الاستفادة من قرار معين ، بشرط أن يتم النظر في مثل هذا القرار في إطار نظرية الأعداد الكبيرة والمسافة الطويلة.

حصيرة الانتظارفي نظرية القمار ، مقدار المكاسب التي يمكن للمضارب أن يكسبها أو يخسرها ، في المتوسط ، لكل رهان. بلغة القمار المضاربونوهذا ما يسمى أحيانًا "بالميزة مضارب"(إذا كانت موجبة للمضارب) أو" حافة المنزل "(إذا كانت سلبية للمضارب).
التوقع الرياضي (وسط السكان) هو
Wir verwenden Cookies für die beste Präsentation unserer Website. Wenn Sie diese Website weiterhin nutzen، stimmen Sie dem zu. نعم

 تحويل كسر عشري إلى كسر عادي والعكس صحيح: قاعدة ، أمثلة
تحويل كسر عشري إلى كسر عادي والعكس صحيح: قاعدة ، أمثلة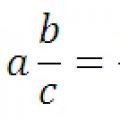 تحويل الأعداد العشرية إلى كسور مشتركة
تحويل الأعداد العشرية إلى كسور مشتركة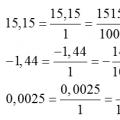 تحويل كسر عادي إلى كسر عشري والعكس قواعد وأمثلة
تحويل كسر عادي إلى كسر عشري والعكس قواعد وأمثلة