Бином на разпределение. Вероятностни разпределения на дискретни случайни променливи

Теорията на вероятностите невидимо присъства в живота ни. Ние не обръщаме внимание на това, но всяко събитие в живота ни има една или друга вероятност. Обръщам внимание на голяма сумасценарии, за нас става необходимо да определим най-вероятния и най-малко вероятния от тях. Най-удобно е да анализирате такива вероятностни данни графично. Разпределението може да ни помогне с това. Биномът е един от най-лесните и точни.

Преди да преминем директно към математиката и теорията на вероятностите, нека да разберем кой е първият, който е измислил този тип разпределение и каква е историята на развитието математически апаратза тази концепция.

История

Понятието вероятност е известно от древни времена. Древните математици обаче не му придават голямо значение и успяват само да положат основите на теория, която по-късно се превръща в теория на вероятностите. Те създадоха някои комбинаторни методи, което много помогна на онези, които по-късно създадоха и развиха самата теория.

През втората половина на седемнадесети век започва формирането на основните понятия и методи на теорията на вероятностите. Бяха въведени дефиниции на случайни променливи, методи за изчисляване на вероятността от прости и някои сложни независими и зависими събития. Такъв интерес към случайните променливи и вероятности е продиктуван от хазарт: Всеки искаше да знае какви са шансовете му да спечели играта.

Следващата стъпка беше прилагането на методите на математическия анализ в теорията на вероятностите. С тази задача се заемат видни математици като Лаплас, Гаус, Поасон и Бернули. Именно те напреднаха в тази област на математиката ново ниво. Джеймс Бернули е този, който открива закона за биномно разпределение. Между другото, както ще разберем по-късно, на базата на това откритие бяха направени още няколко, които направиха възможно създаването на закона за нормалното разпределение и много други.

Сега, преди да започнем да описваме биномното разпределение, ще освежим малко в паметта си понятията на теорията на вероятностите, вероятно вече забравени от училищната скамейка.

Основи на теорията на вероятностите

Ще разгледаме такива системи, в резултат на които са възможни само два резултата: "успех" и "неуспех". Това е лесно да се разбере с пример: хвърляме монета, предполагайки, че ще паднат опашки. Вероятностите за всяко от възможните събития (падане на опашки - "успех", падане на глави - "неуспех") са равни на 50 процента, ако монетата е идеално балансирана и няма други фактори, които могат да повлияят на експеримента.

Това беше най-простото събитие. Но също така има сложни системи, в които се извършват последователни действия и вероятностите за резултатите от тези действия ще се различават. Да разгледаме например следната система: в кутия, чието съдържание не можем да видим, има шест абсолютно еднакви топки, три чифта сини, червени и бели цветя. Трябва да вземем няколко топки на случаен принцип. Съответно, като извадим първо една от белите топки, ще намалим няколко пъти вероятността следващата също да получим бяла топка. Това се случва, защото броят на обектите в системата се променя.

AT следващия разделпомислете за по-сложни математически понятия, което ни доближава до думите " нормална дистрибуция"," биномно разпределение "и други подобни.

Елементи на математическата статистика

В статистиката, която е една от областите на приложение на теорията на вероятностите, има много примери, когато данните за анализ не са дадени изрично. Тоест не в числа, а под формата на разделение според характеристиките, например според пола. За да се приложи математическият апарат към такива данни и да се направят някои изводи от получените резултати, е необходимо първоначалните данни да се преобразуват в числов формат. Като правило, за да се приложи това, на положителен резултат се присвоява стойност 1, а на отрицателен се присвоява стойност 0. По този начин получаваме статистически данни, които могат да бъдат анализирани с помощта на математически методи.

Следващата стъпка в разбирането какво е биномното разпределение на случайна променлива е да се определи дисперсията на случайната променлива и математическо очакване. Ще говорим за това в следващия раздел.

Очаквана стойност

Всъщност разбирането какво е математическо очакване не е трудно. Помислете за система, в която има много различни събитияс техния различни вероятности. Математическото очакване ще се нарича стойност, равно на суматапродукти на стойностите на тези събития (и математическа форма, които обсъдихме в предишния раздел) относно вероятността за тяхното изпълнение.

Математическото очакване на биномното разпределение се изчислява по същата схема: вземаме стойността на случайна променлива, умножаваме я по вероятността за положителен резултат и след това обобщаваме получените данни за всички променливи. Много е удобно тези данни да се представят графично - по този начин разликата между математическите очаквания на различните стойности се възприема по-добре.

В следващия раздел ще ви разкажем малко за една различна концепция - дисперсията на случайна променлива. Също така е тясно свързано с такава концепция като биномно разпределение на вероятностите и е негова характеристика.

Дисперсия на биномно разпределение

Тази стойност е тясно свързана с предишната и също така характеризира разпределението на статистическите данни. Тя представлява среден квадратотклонения на стойностите от тяхното математическо очакване. Тоест дисперсията на случайна променлива е сумата от квадратите на разликите между стойността на случайна променлива и нейното математическо очакване, умножена по вероятността за това събитие.

Като цяло, това е всичко, което трябва да знаем за дисперсията, за да разберем какво е биномното разпределение на вероятностите. Сега да преминем към нашата основна тема. А именно какво се крие зад това привидно достатъчно сложна фраза„биномен закон за разпределение“.

Биномиално разпределение

Нека първо разберем защо това разпределение е биномно. Произлиза от думата "бином". Може би сте чували за бинома на Нютон - формула, която може да се използва за разширяване на сбора на произволни две числа a и b до всяка неотрицателна степен на n.

Както вероятно вече се досещате, биномната формула на Нютон и формулата за биномно разпределение са почти еднакви формули. С единственото изключение, което вторият има приложена стойностза конкретни количества, а първият е само общ математически инструмент, чиито приложения на практика могат да бъдат различни.

Формули за разпределение

Функцията на биномно разпределение може да бъде записана като сбор от следните членове:

(n!/(n-k)!k!)*p k *q n-k

Тук n е броят на независимите случайни експерименти, p е броят на успешните резултати, q е броят на неуспешните резултати, k е номерът на експеримента (може да приема стойности от 0 до n),! - обозначаване на факториел, такава функция на число, чиято стойност е равна на произведението на всички числа, отиващи до него (например за числото 4: 4!=1*2*3*4= 24).

Освен това функцията на биномното разпределение може да бъде написана като непълна бета функция. Това обаче вече е по-сложна дефиниция, която се използва само при решаване на сложни статистически задачи.

Биномиално разпределение, примери за които разгледахме по-горе, е един от най-много прости видоверазпределения в теорията на вероятностите. Има и нормално разпределение, което е вид биномно разпределение. Той е най-често използваният и най-лесният за изчисляване. Има и разпределение на Бернули, разпределение на Поасон, условно разпределение. Всички те характеризират графично областите на вероятност за даден процес при различни условия.

В следващия раздел ще разгледаме аспекти, свързани с приложението на този математически апарат в истинския живот. На пръв поглед, разбира се, изглежда, че това е друго математическо нещо, което, както обикновено, не намира приложение в реалния живот и като цяло не е необходимо на никого, освен на самите математици. Това обаче не е така. В крайна сметка всички видове дистрибуции и техните графични изображенияса създадени изключително за практически цели, а не като прищявка на учени.

Приложение

Досега най-важното приложение на разпределението се намира в статистиката, тъй като изисква комплексен анализмного данни. Както показва практиката, много масиви от данни имат приблизително еднакви разпределения на стойности: критичните области с много ниски и много високи стойности, като правило, съдържат по-малко елементи от средните стойности.

Анализът на големи масиви от данни е необходим не само в статистиката. Незаменим е, например, в физическа химия. В тази наука се използва за определяне на много величини, които са свързани със случайни вибрации и движения на атоми и молекули.

В следващия раздел ще обсъдим колко важно е използването на такива статистически концепции, като бином разпределение на случайна променлива в Ежедневиетоза теб и мен.

Защо ми трябва?

Много хора си задават този въпрос, когато стане дума за математика. И между другото, математиката не напразно е наричана кралицата на науките. То е в основата на физиката, химията, биологията, икономиката и във всяка от тези науки се използва и някакъв вид разпределение: дали е дискретно биномно разпределение или нормално, няма значение. И ако погледнем по-отблизо света около нас, ще видим, че математиката се прилага навсякъде: в ежедневието, на работа и дори човешките отношениямогат да бъдат представени под формата на статистически данни и анализирани (това, между другото, се прави от тези, които работят в специални организациисъбиране на информация).

Сега нека поговорим малко за това какво да направите, ако трябва да знаете много повече по тази тема от това, което сме описали в тази статия.

Информацията, която дадохме в тази статия, далеч не е пълна. Има много нюанси за това каква форма може да приеме разпространението. Биномиалното разпределение, както вече разбрахме, е един от основните видове, върху които се основава цялото математическа статистикаи теория на вероятностите.

Ако проявявате интерес или във връзка с работата си, трябва да знаете много повече по тази тема, ще трябва да проучите специализираната литература. Започнете с университетски курс математически анализи стигнете до раздела за теория на вероятностите. Също така знанията в областта на редовете ще бъдат полезни, тъй като биномното разпределение на вероятностите не е нищо повече от серия от последователни членове.

Заключение

Преди да завършим статията, бихме искали да ви кажем още нещо интересно. Засяга пряко темата на нашата статия и цялата математика като цяло.

Много хора казват, че математиката е безполезна наука и нищо, което са научили в училище, не им е било полезно. Но знанието никога не е излишно и ако нещо не ви е полезно в живота, това означава, че просто не го помните. Ако имате знания, те могат да ви помогнат, но ако ги нямате, тогава не можете да очаквате помощ от тях.

И така, разгледахме концепцията за биномното разпределение и всички дефиниции, свързани с него, и говорихме за това как се прилага в живота ни.

Разгледайте биномното разпределение, изчислете математическото му очакване, дисперсия, режим. Използвайки функцията на MS EXCEL BINOM.DIST(), ще начертаем графиките на функцията на разпределението и плътността на вероятността. Нека оценим параметъра на разпределението p, математическото очакване на разпределението и стандартно отклонение. Също така разгледайте разпределението на Бернули.

Определение. Нека се държат нтестове, във всеки от които могат да възникнат само 2 събития: събитието "успех" с вероятност стр или събитието "провал" с вероятността р =1-p (т.нар схема на Бернули,Бернулиизпитания).

Вероятност да получите точно х успех в тези н тестове е равно на:

Брой успехи в извадката х е случайна променлива, която има Биномиално разпределение(Английски) Биномразпространение) стри н– са параметри на това разпределение.

Спомнете си това, за да кандидатствате Схеми на Бернулии съответно биномно разпределение,трябва да бъдат изпълнени следните условия:

всяко изпитание трябва да има точно два резултата, условно наречени „успех” и „неуспех”.
резултатът от всеки тест не трябва да зависи от резултатите от предишни тестове (независимост на теста).
успеваемост стр трябва да бъде постоянно за всички тестове.

Биномиално разпределение в MS EXCEL

В MS EXCEL, като се започне от версия 2010, за Биномиално разпределениеима функция BINOM.DIST() , английско име- BINOM.DIST(), което ви позволява да изчислите вероятността извадката да бъде точна х"успехи" (т.е. функция на плътността на вероятността p(x), вижте формулата по-горе), и интегрална функция на разпределение(вероятност пробата да има хили по-малко "успехи", включително 0).

Преди MS EXCEL 2010, EXCEL имаше функцията BINOMDIST(), която също ви позволява да изчислявате разпределителна функцияи плътност на вероятността p(x). BINOMDIST() е оставен в MS EXCEL 2010 за съвместимост.

Примерният файл съдържа графики плътност на разпределение на вероятноститеи .

Биномиално разпределениеима обозначението б(н; стр) .

Забележка: За застрояване интегрална функция на разпределениеперфектен тип диаграма График, за плътност на разпространение – Хистограма с групиране. За повече информация относно изграждането на диаграми прочетете статията Основните типове диаграми.

Забележка: За удобство при писане на формули в примерния файл са създадени имена за параметри Биномиално разпределение: n и p.

Примерният файл показва различни вероятностни изчисления с помощта на функции на MS EXCEL:

Както се вижда на снимката по-горе, се предполага, че:

Безкрайната популация, от която е направена извадката, съдържа 10% (или 0,1) добри елементи (параметър стр, трети аргумент на функцията =BINOM.DIST() )
За да се изчисли вероятността в извадка от 10 елемента (параметър н, вторият аргумент на функцията) ще има точно 5 валидни елемента (първият аргумент), трябва да напишете формулата: =BINOM.DIST(5; 10; 0,1; FALSE)
Последният, четвърти елемент е зададен = FALSE, т.е. стойността на функцията се връща плътност на разпространение.

Ако стойността на четвъртия аргумент е TRUE, тогава функцията BINOM.DIST() връща стойността интегрална функция на разпределениеили просто разпределителна функция. В този случай можем да изчислим вероятността броят на добрите елементи в извадката да бъде от определен диапазон, например 2 или по-малко (включително 0).

За да направите това, трябва да напишете формулата:
= BINOM.DIST(2; 10; 0,1; TRUE)

Забележка: За стойност на x, която не е цяло число, . Например следните формули ще върнат същата стойност:
=BINOM.DIST( 2 ; 10; 0,1; ВЯРНО)
=BINOM.DIST( 2,9 ; 10; 0,1; ВЯРНО)

Забележка: В примерния файл плътност на вероятносттаи разпределителна функциясъщо се изчислява с помощта на дефиницията и функцията COMBIN().

Показатели за разпространение

AT примерен файл на лист Примерима формули за изчисляване на някои показатели за разпределение:

=n*p;
(стандартно отклонение на квадрат) = n*p*(1-p);
= (n+1)*p;
=(1-2*p)*ROOT(n*p*(1-p)).

Извеждаме формулата математическо очакване Биномиално разпределениеизползвайки Схема на Бернули.

А-приори произволна стойност X в Схема на Бернули(случайна променлива на Бернули) има разпределителна функция:

Това разпределение се нарича Разпределение на Бернули.

Забележка: Разпределение на Бернули – специален случай Биномиално разпределениес параметър n=1.

Нека генерираме 3 масива от 100 числа с различни вероятности за успех: 0.1; 0,5 и 0,9. За да направите това, в прозореца Поколение произволни числа комплект следните параметриза всяка вероятност p:

Забележка: Ако зададете опцията Случайно разпръскване (Случайно семе), тогава можете да изберете конкретен случаен наборгенерирани числа. Например, като зададете тази опция =25, можете да генерирате едни и същи набори от произволни числа на различни компютри (ако, разбира се, другите параметри на разпределение са еднакви). Стойността на опцията може да приема цели числа от 1 до 32 767. Име на опцията Случайно разпръскванеможе да обърка. Би било по-добре да го преведете като Задайте число със случайни числа.

В резултат на това ще имаме 3 колони от 100 числа, въз основа на които например можем да оценим вероятността за успех стрпо формулата: Брой успехи/100(см. примерен файлов лист Генериране на Bernoulli).

Забележка: За Разпределения на Бернулис p=0,5, можете да използвате формулата =RANDBETWEEN(0;1) , което съответства на .

Генериране на случайни числа. Биномиално разпределение

Да предположим, че в извадката има 7 дефектни артикула. Това означава, че е „много вероятно“ делът на дефектните продукти да се е променил. стр, което е характерно за нашия производствен процес. Въпреки че тази ситуация е „много вероятна“, има възможност (алфа риск, грешка тип 1, „фалшива аларма“), че стростава непроменена, а увеличеният брой дефектни продукти се дължи на случайна извадка.

Както може да се види на фигурата по-долу, 7 е броят на дефектните продукти, който е приемлив за процес с p=0,21 при същата стойност Алфа. Това илюстрира, че когато прагът на дефектни артикули в проба бъде надвишен, стр„вероятно“ се увеличи. Изразът „най-вероятно“ означава, че има само 10% шанс (100%-90%), че отклонението на процента дефектни продукти над прага се дължи само на случайни причини.

По този начин превишаването на праговия брой дефектни продукти в пробата може да служи като сигнал, че процесът е нарушен и е започнал да произвежда b относнопо-висок процент на дефектни продукти.

Забележка: Преди MS EXCEL 2010, EXCEL имаше функция CRITBINOM(), която е еквивалентна на BINOM.INV(). CRITBINOM() е оставен в MS EXCEL 2010 и по-нова версия за съвместимост.

Връзка на биномиалното разпределение с други разпределения

Ако параметърът н Биномиално разпределениеклони към безкрайност и стрклони към 0, тогава в този случай Биномиално разпределениеможе да бъде приблизително.
Възможно е да се формулират условия, когато апроксимацията Поасоново разпределениеработи добре:

стр<0,1 (по-малкото стри още н, толкова по-точно е приближението);
стр>0,9 (като се има предвид това р=1- стр, изчисленията в този случай трябва да се извършват с помощта на р(а хтрябва да се замени с н- х). Следователно, толкова по-малко ри още н, толкова по-точно е приближението).

На 0,1<=p<=0,9 и n*p>10 Биномиално разпределениеможе да бъде приблизително.

на свой ред Биномиално разпределениеможе да служи като добро приближение, когато размерът на популацията е N Хипергеометрично разпределениемного по-голям от размера на извадката n (т.е. N>>n или n/N<<1).

Можете да прочетете повече за връзката на горните разпределения в статията. Там са дадени и примери за приближение и са обяснени условията кога е възможно и с каква точност.

СЪВЕТ: Можете да прочетете за други дистрибуции на MS EXCEL в статията.

Биномиалното разпределение е едно от най-важните вероятностни разпределения за дискретно променяща се случайна променлива. Биномиалното разпределение е вероятностното разпределение на число мсъбитие Ив нвзаимно независими наблюдения. Често събитие Исе нарича "успех" на наблюдението, а обратното събитие - "неуспех", но това обозначение е много условно.

Членове на биномното разпределение:

извършено общо низпитания, при които събитието Иможе или не може да се случи;
събитие Ивъв всяко от изпитанията може да се случи с еднаква вероятност стр;
тестовете са взаимно независими.

Вероятността, че в нтестово събитие Иточно мпъти, може да се изчисли с помощта на формулата на Бернули:

където стр- вероятността за настъпване на събитието И;

р = 1 - стре вероятността да се случи противоположното събитие.

Нека да го разберем защо биномното разпределение е свързано с формулата на Бернули по описания по-горе начин . Събитие - броят на успехите при нтестовете е разделен на няколко варианта, във всеки от които се постига успех мизпитания, а неуспех - в н - мтестове. Помислете за една от тези опции - б1 . Съгласно правилото за добавяне на вероятности, ние умножаваме вероятностите за противоположни събития:

и ако обозначим р = 1 - стр, тогава

Същата вероятност ще има всяка друга опция, в която муспех и н - мнеуспехи. Броят на тези опции е равен на броя на начините, по които е възможно от нтест получите муспех.

Сумата от вероятностите за всички мномер на събитието И(цифри от 0 до н) е равно на едно:

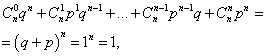
където всеки член е член на бинома на Нютон. Следователно разглежданото разпределение се нарича биномно разпределение.

На практика често е необходимо да се изчисляват вероятностите "най-много муспех в нтестове" или "поне муспех в нтестове". За това се използват следните формули.

Интегралната функция, т.е вероятност Е(м), че в нсъбитие за наблюдение Иняма да дойде повече мведнъж, може да се изчисли по формулата:

На свой ред вероятност Е(≥м), че в нсъбитие за наблюдение Иела поне мведнъж, се изчислява по формулата:

Понякога е по-удобно да се изчисли вероятността, че в нсъбитие за наблюдение Иняма да дойде повече мпъти, чрез вероятността от обратното събитие:

Коя от формулите да се използва зависи от това коя от тях съдържа по-малко членове.

Характеристиките на биномното разпределение се изчисляват по следните формули .

Очаквана стойност: .

дисперсия: .

Стандартно отклонение: .

Биномно разпределение и изчисления в MS Excel

Вероятност на биномно разпределение Пн ( м) и стойността на интегралната функция Е(м) може да се изчисли с помощта на функцията на MS Excel BINOM.DIST. Прозорецът за съответното изчисление е показан по-долу (кликнете с левия бутон на мишката, за да го увеличите).

MS Excel изисква да въведете следните данни:

брой успехи;
брой тестове;
вероятност за успех;
интеграл - логическа стойност: 0 - ако трябва да изчислите вероятността Пн ( м) и 1 - ако вероятността Е(м).

Пример 1Управителят на компанията обобщи информация за броя на продадените фотоапарати през последните 100 дни. Таблицата обобщава информацията и изчислява вероятността определен брой камери да бъдат продадени на ден.

Денят завършва с печалба, ако се продадат 13 или повече камери. Вероятността денят да приключи с печалба:

Вероятността денят да бъде отработен без печалба:

Нека вероятността денят да бъде изработен с печалба да е постоянна и равна на 0,61, а броят на продадените камери на ден не зависи от деня. След това можете да използвате биномното разпределение, където събитието И- денят ще бъде изработен с печалба, - без печалба.

Вероятността от 6 дни всички да бъдат изработени с печалба:

Получаваме същия резултат с помощта на функцията на MS Excel BINOM.DIST (стойността на интегралната стойност е 0):

П 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.

Вероятността от 6 дни 4 или повече дни да бъдат отработени с печалба:

където ,

Използвайки функцията на MS Excel BINOM.DIST, изчисляваме вероятността от 6 дни не повече от 3 дни да бъдат завършени с печалба (стойността на интегралната стойност е 1):

П 6 (≤3 ) = BINOM.DIST(3; 6; 0,61; 1) = 0,435.

Вероятността от 6 дни всички да бъдат отработени със загуби:

Изчисляваме същия индикатор с помощта на функцията на MS Excel BINOM.DIST:

П 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.

Решете проблема сами и след това вижте решението

Пример 2Една урна съдържа 2 бели топки и 3 черни. От урната се изважда топка, цветът се настройва и се връща обратно. Опитът се повтаря 5 пъти. Броят на появяванията на белите топки е дискретна случайна променлива х, разпределени по биномния закон. Съставете закона за разпределение на случайна променлива. Определете модата, математическото очакване и дисперсията.

Продължаваме да решаваме проблемите заедно

Пример 3От куриерската служба отиде до обектите н= 5 куриера. Всеки куриер с вероятност стр= 0.3 закъснява за обекта независимо от останалите. Дискретна случайна променлива х- броят на закъснелите куриери. Постройте серия на разпределение на тази случайна променлива. Намерете неговото математическо очакване, дисперсия, стандартно отклонение. Намерете вероятността поне двама куриери да закъснеят за предметите.

Биномиално разпределение

вероятностното разпределение на броя на случванията на дадено събитие при повтарящи се независими опити. Ако за всеки опит вероятността за настъпване на събитие е R,и 0 ≤ стр≤ 1, тогава броят μ повторения на това събитие за ннезависими опити, има случайна променлива, която приема стойностите м = 1, 2,.., нс вероятности

където р= 1 - п,а - биномни коефициенти (оттук и името Б. р.). Горната формула понякога се нарича формула на Бернули. Математическото очакване и дисперсията на величината μ, която има B.R., са равни на М(μ) = npи д(μ) = npq, съответно. На свобода н,по силата на теоремата на Лаплас (вижте теоремата на Лаплас), B. r. близко до нормално разпределение (виж Нормално разпределение), което се използва в практиката. На малки не необходимо да се използват таблици B. r.

Лит.:Болшев Л. Н., Смирнов Н. В., Таблици на математическата статистика, М., 1965.

Велика съветска енциклопедия. - М.: Съветска енциклопедия. 1969-1978 .

Вижте какво е "биномиалното разпределение" в други речници:

Вероятностна функция ... Уикипедия

- (биномиално разпределение) Разпределение, което ви позволява да изчислите вероятността за възникване на произволно събитие, получено в резултат на наблюдение на редица независими събития, ако вероятността за възникване на съставните му елементарни ... ... Икономически речник

- (разпределение на Бернули) вероятностното разпределение на броя на случванията на дадено събитие в повтарящи се независими опити, ако вероятността за възникване на това събитие във всеки опит е равна на p(0 p 1). Точно, номерът? има случаи на това събитие ... ... Голям енциклопедичен речник

биномно разпределение- - Телекомуникационни теми, основни понятия EN биномно разпределение ...

- (разпределение на Бернули), вероятностното разпределение на броя на случванията на някакво събитие в повтарящи се независими опити, ако вероятността за възникване на това събитие във всеки опит е p (0≤p≤1). А именно, броят μ повторения на това събитие… … енциклопедичен речник

биномно разпределение- 1,49. биномиално разпределение Вероятностното разпределение на дискретна случайна променлива X, приемаща всякакви цели числа от 0 до n, така че за x = 0, 1, 2, ..., n и параметри n = 1, 2, ... и 0< p < 1, где Источник … Речник-справочник на термините на нормативната и техническата документация

Разпределение на Бернули, разпределението на вероятността на случайна променлива X, което приема цели числа с вероятности, съответно (биномен коефициент; p параметър B. R., наречен вероятност за положителен резултат, който приема стойностите ... Математическа енциклопедия

- (разпределение на Бернули), вероятностното разпределение на броя на случванията на определено събитие в повтарящи се независими опити, ако вероятността за възникване на това събитие във всеки опит е p (0<или = p < или = 1). Именно, число м появлений … Естествени науки. енциклопедичен речник

Биномиално разпределение на вероятностите- (биномно разпределение) Разпределението, наблюдавано в случаите, когато резултатът от всеки независим експеримент (статистическо наблюдение) приема една от двете възможни стойности: победа или поражение, включване или изключване, плюс или ... Икономически и математически речник

биномно вероятностно разпределение- Разпределението, което се наблюдава в случаите, когато резултатът от всеки независим експеримент (статистическо наблюдение) приема една от двете възможни стойности: победа или поражение, включване или изключване, плюс или минус, 0 или 1. Това е ... ... Наръчник за технически преводач

Книги

Теория на вероятностите и математическа статистика в задачите. Повече от 360 задачи и упражнения, Д. А. Борзих. Предлаганото ръководство съдържа задачи с различни нива на сложност. Основният акцент обаче е поставен върху задачи със средна сложност. Това се прави умишлено, за да се насърчат учениците да...
Теория на вероятностите и математическа статистика в задачи: Повече от 360 задачи и упражнения, Borzykh D. Предлаганото ръководство съдържа задачи с различни нива на сложност. Основният акцент обаче е поставен върху задачи със средна сложност. Това се прави умишлено, за да се насърчат учениците да...

Глава 7

Специфични закони на разпределение на случайни величини

Видове закони на разпределение на дискретни случайни величини

Нека дискретна случайна променлива приема стойностите х 1 , х 2 , …, x n, … . Вероятностите на тези стойности могат да бъдат изчислени с помощта на различни формули, например с помощта на основните теореми на теорията на вероятностите, формулата на Бернули или някои други формули. За някои от тези формули законът за разпределение има собствено име.

Най-често срещаните закони на разпределение на дискретна случайна променлива са биномен, геометричен, хипергеометричен, закон на разпределение на Поасон.

Биномен закон на разпределение

Нека се произвежда ннезависими изпитания, във всяко от които дадено събитие може или не може да се случи И. Вероятността за настъпване на това събитие във всеки отделен опит е постоянна, не зависи от номера на опита и е равна на Р=Р(И). Оттук и вероятността събитието да не се случи Ивъв всеки тест също е постоянна и равна на р=1–Р. Помислете за случайна променлива хравен на броя повторения на събитието Ив нтестове. Очевидно е, че стойностите на това количество са равни на

х 1 =0 - събитие Ив нтестове не се появиха;

х 2 =1 – събитие Ив нопити се появиха веднъж;

х 3 =2 - събитие Ив низпитания се появиха два пъти;

…………………………………………………………..

x n +1 = н- събитие Ив нтестове се появи всичко нведнъж.

Вероятностите на тези стойности могат да бъдат изчислени с помощта на формулата на Бернули (4.1):

където да се=0, 1, 2, …,н .

Биномен закон на разпределение хравен на броя на успехите в нИзпитания на Бернули, с вероятност за успех Р.

И така, дискретна случайна променлива има биномиално разпределение (или се разпределя според биномиалния закон), ако нейните възможни стойности са 0, 1, 2, …, н, а съответните вероятности се изчисляват по формула (7.1).

Биномното разпределение зависи от две параметри Ри н.

Серията на разпределение на случайна променлива, разпределена според биномиалния закон, има формата:

х			…	к	…	н
Р			…		…

Пример 7.1 . Произвеждат се три независими изстрела по целта. Вероятността за уцелване на всеки удар е 0,4. Случайна стойност х- броят на попаденията в целта. Конструирайте неговите разпределителни серии.

Решение. Възможни стойности на случайна променлива хса х 1 =0; х 2 =1; х 3 =2; х 4=3. Намерете съответните вероятности, като използвате формулата на Бернули. Лесно е да се покаже, че прилагането на тази формула тук е напълно оправдано. Имайте предвид, че вероятността да не уцелите целта с един изстрел ще бъде равна на 1-0,4=0,6. Вземете

Серията на разпространение има следната форма:

х
Р	0,216	0,432	0,288	0,064

Лесно се проверява, че сумата от всички вероятности е равна на 1. Самата случайна променлива хразпределени по биномния закон. ■

Нека намерим математическото очакване и дисперсията на случайна променлива, разпределена според биномния закон.

При решаването на пример 6.5 беше показано, че математическото очакване на броя на събитията на събитие Ив ннезависими тестове, ако вероятността за възникване Ивъв всеки тест е постоянен и равен Р, се равнява н· Р

В този пример е използвана случайна променлива, разпределена според биномния закон. Следователно решението на пример 6.5 всъщност е доказателство на следната теорема.

Теорема 7.1.Математическото очакване на дискретна случайна променлива, разпределена според биномиалния закон, е равно на произведението от броя опити и вероятността за "успех", т.е. М(х)=н· Р.

Теорема 7.2.Дисперсията на дискретна случайна променлива, разпределена според биномиалния закон, е равна на произведението на броя опити с вероятността за "успех" и вероятността за "неуспех", т.е. д(х)=npq.

Асимметрията и ексцесът на случайна променлива, разпределени съгласно биномиалния закон, се определят от формулите

Тези формули могат да бъдат получени с помощта на концепцията за начален и централен момент.

Биномният закон за разпределение е в основата на много реални ситуации. За големи стойности нбиномното разпределение може да бъде апроксимирано чрез други разпределения, по-специално разпределението на Поасон.

Поасоново разпределение

Нека има нОпитите на Бернули, с броя на опитите ндостатъчно голям. По-рано беше показано, че в този случай (ако освен това вероятността Рразработки Имного малка), за да намерите вероятността дадено събитие Ида се появи тведнъж в тестовете можете да използвате формулата на Поасон (4.9). Ако случайната променлива хозначава броя на повторенията на събитието Ив нОпитите на Бернули, тогава вероятността, че хще придобие смисъла кможе да се изчисли по формулата

, (7.2)

където λ = np.

Закон за разпределение на Поасонсе нарича разпределение на дискретна случайна променлива х, за които възможните стойности са цели неотрицателни числа, и вероятностите p tтези стойности се намират по формула (7.2).

Стойност λ = npНаречен параметърПоасоново разпределение.

Случайна променлива, разпределена според закона на Поасон, може да приеме безкраен брой стойности. Тъй като за това разпределение вероятността Рпоявата на събитие във всеки опит е малка, тогава това разпределение понякога се нарича закон на редките явления.

Серията на разпределение на случайна променлива, разпределена според закона на Поасон, има формата

х					…	т	…
Р					…		…

Лесно е да се провери, че сумата от вероятностите на втория ред е равна на 1. За да направим това, трябва да запомним, че функцията може да бъде разширена в серия на Маклорен, която се събира за всеки х. В този случай имаме

. (7.3)

Както беше отбелязано, законът на Поасон в някои ограничаващи случаи замества биномния закон. Пример за това е случайна променлива х, чиито стойности са равни на броя на повреди за определен период от време при многократно използване на техническо средство. Предполага се, че това устройство е с висока надеждност, т.е. вероятността от неуспех в едно приложение е много малка.

Освен такива ограничаващи случаи на практика има случайни величини, разпределени по закона на Поасон, несвързани с биномното разпределение. Например, разпределението на Поасон често се използва, когато се работи с броя на събитията, които се случват за период от време (броя на обажданията до телефонната централа за един час, броя на колите, пристигнали на автомивката през деня, броя на спиранията на машината на седмица и т.н.). Всички тези събития трябва да образуват така наречения поток от събития, който е една от основните концепции на теорията на опашките. Параметър λ характеризира средната интензивност на потока от събития.