Това, което се нарича ред на квадратна матрица. Детерминанти на квадратни матрици
Квадратна матрица от ти ред, в която има единици на главния диагонал, а всички останали елементи са равни на нула, ще се нарича матрица на идентичност и ще се означава с или просто . Името "единична матрица" се свързва със следното свойство на матрицата: за всяка правоъгълна матрица
има равенства
![]() .
.
очевидно,
Нека е квадратна матрица. Тогава степента на матрицата се определя по обичайния начин:
От асоциативното свойство на матричното умножение следва:
Тук са произволни неотрицателни цели числа.
Помислете за полином (цяла рационална функция) с коефициенти от полето:
Тогава под имаме предвид матрицата
Ето как се дефинира полином в матрица.
Нека полиномът е равен на произведението на полиномите и:
![]() .
.
Полиномът се получава от и чрез почленно умножение и редукция на подобни членове. В този случай се използва правилото за умножение на степените: . Тъй като всички тези действия са валидни и при замяна на скаларна стойност с матрица, тогава
![]()
Следователно, по-специално,
два полинома в една и съща матрица винаги комутират един с друг.
Нека се съгласим, че ти супердиагонал (поддиагонал) в правоъгълна матрица е броят на елементите, за които (съответно). Означаваме с квадратна матрица от -ти ред, в която елементите на първия супердиагонал са равни на единица, а всички останали елементи са равни на нула. Тогава
 ,
,
 и др.;
и др.;
По силата на тези равенства, ако:
Полином по отношение на , тогава
 .
.
По същия начин, ако е квадратна матрица от ти ред, в която всички елементи на първия поддиагонал са равни на единица, а всички останали са равни на нула, тогава
 .
.
Каним читателя да провери следните свойства на матриците и:
1° В резултат на умножаване на произволна -матрица отляво на матрица (матрица) от -ти ред, всички редове на матрицата се смачкват (понижават) едно място нагоре (надолу), първият (последният) ред на матрицата изчезва, а последният (първи) ред на произведението се запълва с нули. Например,
 ,
,
 .
.
2° В резултат на умножаване на произволна -матрица отдясно на матрица от -ти ред, всички колони на матрицата се изместват надясно (наляво) с едно място, докато последната (първата) колона на матрицата изчезва, а първата (последната) колона на продукта се запълва с нули. Например,
 .
.
 .
.
2. Квадратна матрица ще се нарича сингулярна, ако . В противен случай квадратната матрица се нарича неособена.
Нека е неособена матрица (). Да разгледаме линейна трансформация с матрица на коефициента
Разглеждайки равенствата (23) като относителни уравнения и отбелязвайки, че детерминантата на системата от уравнения (23) е различна от нула по условие, можем уникално да изразим с помощта на добре известни формули чрез:
 . (24)
. (24)
Получихме "обратна" трансформация за (23). Матрицата на коефициента на тази трансформация
ще наричаме обратната матрица за матрицата . От (24) е лесно да се види това
![]() , (25)
, (25)
където е алгебричното допълнение (добавка) на елемента в детерминантата ![]() .
.
Така например, ако
 И ,
И ,
 .
.
Формирайки съставна трансформация от дадената трансформация (23) и обратната (24) в единия и в другия ред, и в двата случая получаваме идентична трансформация (с матрицата на идентичност на коефициентите); Ето защо
![]() . (26)
. (26)
Уравнения (26) могат също да бъдат проверени чрез директно умножаване на матриците и . Всъщност, поради (25)
![]()
![]() .
.
по същия начин
![]()
![]() .
.
Лесно се вижда, че матричните уравнения
те нямат други решения освен решението. Наистина, умножавайки двете части на първото уравнение отляво, а второто - отдясно по и използвайки асоциативното свойство на произведението на матриците, както и равенства (26), и в двата случая получаваме:
По същия начин се доказва, че всяко от матричните уравнения
където и са правоъгълни матрици с еднакъв размер, е квадратна матрица със съответния размер, има едно и само едно решение:
И съответно (29)
Матриците (29) са, така да се каже, "ляво" и "дясно" частно от "разделянето" на матрицата на матрицата. От (28) и (29) следва съответно (виж стр. 22) и , т.е. Сравнявайки с (28), имаме:
При умножаване на правоъгълна матрица отляво или отдясно с неособена матрица, рангът на оригиналната матрица не се променя.
Отбележете също, че (26) предполага, т.е.
За произведението на две неособени матрици имаме:
![]() . (30)
. (30)
3. Всички матрици от ти порядък образуват пръстен с единичен елемент . Тъй като в този пръстен е дефинирана операцията умножение с число от полето и има база от линейно независими матрици, през която всички матрици от -ти ред са линейно изразени, то пръстенът от матрици от -ти ред е алгебра.
Всички квадратни матрици от -ти ред образуват комутативна група по отношение на операцията събиране. Всички неособени матрици от -ти ред образуват (некомутативна) група по отношение на операцията умножение.
Квадратната матрица се нарича горна триъгълна (долна триъгълна), ако всички елементи на матрицата, разположени под главния диагонал (над главния диагонал), са равни на нула:
 ,
,  .
.
Диагоналната матрица е специален случай както на горната, така и на долната триъгълна матрица.
Тъй като детерминантата на триъгълна матрица е равна на произведението на нейните диагонални елементи, триъгълна (и по-специално диагонална) матрица е неособена само ако всички нейни диагонални елементи са различни от нула.
Лесно се проверява, че сумата и произведението на две диагонални (горна триъгълна, долна триъгълна) матрици е диагонална (съответно горна триъгълна, долна триъгълна) матрица и че обратната матрица за неособена диагонална (горна триъгълна, долна триъгълна) матрица е матрица от същия тип. Ето защо
1° Всички диагонални, всички горни триъгълни, всички долни триъгълни матрици от ти ред образуват три комутативни групи по отношение на операцията събиране.
2° Всички неособени диагонални матрици образуват комутативна група при умножение.
3° Всички неособени горни (долни) триъгълни матрици образуват (некомутативна) група по отношение на умножението
4. В заключение на този раздел посочваме две важни операции върху матрици - транспониране на матрица и преход към спрегната матрица., след това матрици.
Ако квадратна матрица съвпада с нейната транспонирана (), тогава такава матрица се нарича симетрична. Ако квадратната матрица съвпада със своя конюгат (), тогава тя се нарича ермитова. В симетричната матрица елементите, които са разположени симетрично спрямо главния диагонал, са равни, докато в ермитовата матрица те са комплексно спрегнати. Диагоналните елементи на ермитовата матрица винаги са реални. Обърнете внимание, че произведението на две симетрични (ермитови) матрици, най-общо казано, не е симетрична (ермитова) матрица. По силата на 3° това се случва само когато дадените две симетрични или ермитови матрици комутират една с друга.
Това води до равенство.
Ако квадратна матрица се различава с коефициент -1 от транспонираната (), тогава такава матрица се нарича косо-симетрична. В една косо-симетрична матрица всеки два елемента, разположени симетрично около главния диагонал, се различават един от друг с фактор -1, а диагоналните елементи са равни на нула. От 3° следва, че произведението на две косо симетрични матрици, които комутират една с друга, е симетрична матрица.
Матриците в математиката са един от най-важните обекти с приложно значение. Често една екскурзия в теорията на матриците започва с думите: "Матрицата е правоъгълна маса ...". Ще започнем тази екскурзия от малко по-различен ъгъл.
Телефонните указатели с всякакъв размер и с произволен брой абонатни данни не са нищо друго освен матрици. Тези матрици изглеждат така:
Ясно е, че всички ние използваме такива матрици почти всеки ден. Тези матрици се предлагат в различен брой редове (разграничават се като указател, издаден от телефонната компания, който може да съдържа хиляди, стотици хиляди и дори милиони редове, и нов бележник, който току-що сте започнали, който има по-малко от десет реда) и колони (директория на длъжностни лица на някаква организация, в която може да има колони като длъжност и номер на офис и същият вашия бележник, където може да няма други данни освен името, и по този начин има само две колони - име и телефонен номер).
Могат да се добавят и умножават всякакви матрици и да се извършват други операции върху тях, но няма нужда да добавяте и умножавате телефонни указатели, няма полза от това, а освен това можете да раздвижите ума си.
Но много матрици могат и трябва да се добавят и умножават и по този начин могат да се решават различни спешни задачи. По-долу са дадени примери за такива матрици.
Матрици, в които колоните са продукцията на единици от определен вид продукт, а редовете са годините, в които е записана продукцията на този продукт:

Можете да добавите матрици от този вид, които отчитат производството на подобни продукти от различни предприятия, за да получите обобщени данни за индустрията.
Или матрици, състоящи се например от една колона, в която редовете са средната цена на определен вид продукт:
Матриците от последните два вида могат да се умножават, като резултатът е редова матрица, съдържаща себестойността на всички видове продукти по години.
Матрици, основни определения
Правоъгълна таблица, състояща се от числа, подредени в млинии и нколони се нарича mn-матрица (или просто матрица ) и написано така:
 (1)
(1)
В матрица (1) числата се наричат нейни елементи (както в детерминанта, първият индекс означава номера на реда, вторият - колоната, в пресечната точка на която има елемент; аз = 1, 2, ..., м; й = 1, 2, н).
Матрицата се нарича правоъгълен , Ако .
Ако м = н, тогава се извиква матрицата квадрат , а числото n е неговото в ред .
Детерминантата на квадратната матрица А се нарича детерминантата, чиито елементи са елементите на матрицата А. Означава се със символа | А|.
Квадратната матрица се нарича неспециални (или неизродени , неединствен ), ако неговата детерминанта не е равна на нула, и специален (или изродени , единствено число ), ако неговата детерминанта е нула.
Матриците се наричат равен ако имат еднакъв брой редове и колони и всички съвпадащи елементи са еднакви.
Матрицата се нарича нула ако всички негови елементи са равни на нула. Нулевата матрица ще бъде обозначена със символа 0 или .
Например,
![]()
редова матрица (или малка буква ) се нарича 1 н-матрица и колонна матрица (или колонен ) – м 1-матрица.
Матрица А“, който се получава от матрицата Аразмяна на редове и колони в него се извиква транспониран по отношение на матрицата А. По този начин, за матрица (1), транспонираната матрица е

Преход към матрична работа А", транспониран по отношение на матрицата А, се нарича транспониране на матрицата А. За мн-транспонирана матрица е nm- матрица.
Матрицата, транспонирана по отношение на матрицата, е А, това е
(А")" = А .
Пример 1Намерете Матрицата А", транспониран по отношение на матрицата

и разберете дали детерминантите на оригиналната и транспонираната матрици са равни.
главен диагонал Квадратната матрица е въображаема линия, свързваща нейните елементи, за които и двата индекса са еднакви. Тези елементи се наричат диагонал .
Нарича се квадратна матрица, в която всички елементи извън главния диагонал са равни на нула диагонал . Не всички диагонални елементи на диагонална матрица непременно са различни от нула. Някои от тях може да са равни на нула.
Квадратна матрица, в която елементите на главния диагонал са равни на едно и също ненулево число, а всички останали са равни на нула, се нарича скаларна матрица .
матрица на идентичността се нарича диагонална матрица, в която всички диагонални елементи са равни на единица. Например матрицата на идентичност от трети ред е матрицата

Пример 2Матрични данни:


Решение. Нека изчислим детерминантите на тези матрици. Използвайки правилото на триъгълниците, намираме

Матрична детерминанта бизчислете по формулата 
![]()
Лесно го получаваме 
Следователно матриците Аи са неединични (неизродени, неединични), и матрицата б- специални (изродени, единични).
Детерминантата на единична матрица от всякакъв ред очевидно е равна на единица.
Решете сами проблема с матрицата и след това вижте решението
Пример 3Матрични данни
 ,
,
 ,
,
Определете кои от тях са неединични (неизродени, неединични).
Приложение на матриците в математическото и икономическо моделиране
Под формата на матрици структурираните данни за конкретен обект са написани просто и удобно. Матричните модели се създават не само за съхраняване на тези структурирани данни, но и за решаване на различни проблеми с тези данни с помощта на линейна алгебра.
Така добре познатият матричен модел на икономиката е моделът входно-изходен продукт, въведен от американския икономист от руски произход Василий Леонтиев. Този модел се основава на предположението, че целият производствен сектор на икономиката е разделен на нчисти индустрии. Всяка от индустриите произвежда само един вид продукт и различните индустрии произвеждат различни продукти. Поради това разделение на труда между отраслите съществуват междуотраслови отношения, чийто смисъл е, че част от продукцията на всяка индустрия се прехвърля в други отрасли като производствен ресурс.
Обем на производство аз-та индустрия (измерена с конкретна мерна единица), която е произведена през отчетния период, обозначена с и се нарича обща продукция азта индустрия. Изданията са удобно поставени в н-компонентен ред на матрицата.
Брой продуктови единици аз-та индустрия, която ще бъде изразходвана й-ти отрасъл за производство на единица продукция от него, се обозначава и нарича коефициент на преките разходи.
Операции с матрици и техните свойства.
Концепцията за детерминанта от втори и трети ред.Свойства на детерминантите и тяхното изчисляване.
3. Общо описание на задачата.
4. Изпълнение на задачите.
5. Изготвяне на доклад от лабораторната работа.
Терминологичен речник
Научете дефинициите на следното условия:
ИзмерениеМатрицата е съвкупност от две числа, състояща се от броя на нейните редове m и броя на колоните n.
Ако m=n, тогава се извиква матрицата квадратматрица от ред n.
Матрични операции: транспониране на матрица, умножение (деление) на матрица с число, събиране и изваждане, умножение на матрица по матрица.
Преходът от матрицата A към матрицата A m, чиито редове са колоните, а колоните са редовете на матрицата A, се нарича транспониранематрици а.
Пример: A= , A t = .
Да се умножете матрица по число, трябва да умножите всеки елемент от матрицата по това число.
Пример: 2A= 2 = .
Сума (разлика)матрици A и B с едно и също измерение се нарича матрица C \u003d A B, чиито елементи са равни с ij = a ij b ijза всички азИ й.
Пример: A = ; B = . A+B= ![]() = .
= .
работаматрица A m n към матрица B n k се нарича матрица C m k , всеки елемент от която c ij е равен на сумата от произведенията на елементите на i-тия ред на матрица A и съответния елемент на j-тата колона на матрица B:
c ij = a i1 b 1j + a i2 b 2j +…+ a in b nj .
За да можете да умножите матрица по матрица, те трябва да бъдат съгласенза умножение, т.е брой колонив първата матрица трябва да е равно на брой редовевъв втората матрица.
Пример: A= и B=.
A·B—невъзможно, защото те са непоследователни.
В·А= . = ![]() =
= ![]() .
.
Свойства на операцията умножение на матрица.
1. Ако матрицата A има размерността мн,и матрица B е измерението нк, то продуктът A · B съществува.
Продуктът B A може да съществува само когато m=k.
2. Матричното умножение не е комутативно, т.е. A · B не винаги е равно на B · A, дори и двата продукта да са дефинирани. Ако обаче отношението A B = B A е изпълнено, тогава матриците A и B се наричат пермутационен.
Пример. Изчисли .

Незначителенелемент е детерминантата на подредената матрица, получена чрез изтриване на -тия ред на -тата колона.
Алгебрично събиранеелемент се нарича.
Теорема за разширяване на Лаплас:
Детерминантата на квадратна матрица е равна на сумата от продуктите на елементите на всеки ред (колона) и техните алгебрични допълнения.
![]()
![]()
Пример. Изчисли .
Решение. .
Свойства на детерминанти от n-ти ред:
1) Стойността на детерминантата няма да се промени, ако редовете и колоните се разменят.
2) Ако детерминантата съдържа ред (колона) само с нули, тогава тя е равна на нула.
3) При размяна на два реда (колони) детерминантата променя знака.
4) Детерминанта с два еднакви реда (колони) е равна на нула.
5) Общият множител на елементите на всеки ред (колона) може да бъде изваден от знака на детерминантата.
6) Ако всеки елемент от определен ред (колона) е сумата от два термина, тогава детерминантата е равна на сумата от две детерминанти, във всяка от които всички редове (колони), с изключение на споменатия, са еднакви като в дадената детерминанта, а в споменатия ред ( колона) на първата детерминанта са първите термини, на втората - вторите.
7) Ако два реда (колони) са пропорционални в детерминантата, то тя е равна на нула.
8) Детерминантата няма да се промени, ако елементите на определен ред (колона) се добавят към съответните елементи на друг ред (колона), умножени по същото число.
9) Детерминантите на триъгълната и диагоналната матрици са равни на произведението на елементите на главния диагонал.
Методът за натрупване на нули за изчисляване на детерминанти се основава на свойствата на детерминантите.
Пример. Изчисли .
Решение. Изваждаме удвоената трета от първия ред, след което използваме теоремата за разширяване в първата колона.
~  .
.
Контролни въпроси(OK-1, OK-2, OK-11, PC-1) :
1. Какво се нарича детерминанта от втори ред?
2. Какви са основните свойства на детерминантите?
3. Какъв е минорът на елемента?
4. Какво се нарича алгебрично допълнение на детерминантния елемент?
5. Как да разширим детерминанта от трети ред с елементите на произволен ред (колона)?
6. Каква е сумата от продуктите на елементите на всеки ред (или колона), детерминантата чрез алгебрични допълнения на съответните елементи на друг ред (или колона)?
7. Какво е правилото на триъгълниците?
8. Как се изчисляват детерминантите от по-висок порядък чрез редукция на реда
10. Каква матрица се нарича квадратна? Нула? Какво е матрица-ред, матрица-колона?
11. Какви матрици се наричат равни?
12. Дайте дефиниции на операции събиране, матрично умножение, матрично умножение с число
13. Какви условия трябва да отговарят на размера на матриците по време на събиране, умножение?
14. Какви са свойствата на алгебричните операции: комутативност, асоциативност, дистрибутивност? Кои от тях се изпълняват за матрици при събиране, умножение и кои не?
15. Какво е обратна матрица? За кои матрици е дефинирано?
16. Формулирайте теорема за съществуването и единствеността на обратната матрица.
17. Формулирайте лема за транспонирането на произведението на матриците.
Практически задачи общ(OK-1, OK-2, OK-11, PC-1) :
номер 1. Намерете сбора и разликата на матриците A и B :
а) 
б) 
V) 
номер 2. Следвай тези стъпки :
в) Z \u003d -11A + 7B-4C + D
Ако 
номер 3. Следвай тези стъпки :
V) 
номер 4. Чрез прилагане на четири метода за изчисляване на детерминантата на квадратна матрица, намерете детерминантите на следните матрици :
номер 5. Намерете детерминанти от n-ти ред, по елементите на колоната (реда) :
а)  б)
б) 
номер 6. Намерете детерминантата на матрица, като използвате свойствата на детерминантите:
а)  б)
б) 
ДЕФИНИЦИЯ НА МАТРИЦА. ВИДОВЕ МАТРИЦИ
Размер на матрицата m× нсе нарича съвкупност m nчисла, подредени в правоъгълна таблица от млинии и нколони. Тази таблица обикновено е оградена в скоби. Например, матрицата може да изглежда така:
За краткост матрицата може да се обозначи с една главна буква, напр. Аили IN.
Като цяло, матрица на размера м× нпиши така
 .
.
Числата, които съставляват една матрица, се наричат матрични елементи. Удобно е да се доставят матрични елементи с два индекса aij: Първото показва номера на реда, а второто показва номера на колоната. Например, а 23– елементът е на 2-ри ред, 3-та колона.
Ако броят на редовете в една матрица е равен на броя на колоните, тогава матрицата се нарича квадрат, и се извиква броят на неговите редове или колони в редматрици. В примерите по-горе втората матрица е квадратна - редът й е 3, а четвъртата матрица - редът й е 1.
Извиква се матрица, в която броят на редовете не е равен на броя на колоните правоъгълен. В примерите това е първата матрица и третата.
Има и матрици, които имат само един ред или една колона.
Извиква се матрица само с един ред матрица - ред(или низ) и матрица, която има само една колона, матрица - колона.
Нарича се матрица, в която всички елементи са равни на нула нулаи се означава с (0) или просто 0. Например,
 .
.
главен диагоналКвадратната матрица е диагоналът, преминаващ от горния ляв до долния десен ъгъл.
Нарича се квадратна матрица, в която всички елементи под главния диагонал са равни на нула триъгълнаматрица.
 .
.
Квадратна матрица, в която всички елементи, с изключение може би тези на главния диагонал, са равни на нула, се нарича диагоналматрица. Например, или.
Извиква се диагонална матрица, в която всички диагонални записи са равни на единица единиченматрица и се обозначава с буквата E. Например матрицата за идентичност от 3-ти ред има формата  .
.
ДЕЙСТВИЯ ВЪРХУ МАТРИЦИ
Матрично равенство. Две матрици АИ бсе казват, че са равни, ако имат еднакъв брой редове и колони и съответните им елементи са равни aij = b ij. Така че, ако  И
И  , Че А=Б, Ако a 11 = b 11, a 12 = b 12, a 21 = b 21И a 22 = b 22.
, Че А=Б, Ако a 11 = b 11, a 12 = b 12, a 21 = b 21И a 22 = b 22.
Транспониране. Да разгледаме произволна матрица Аот млинии и нколони. Може да се свърже със следната матрица бот нлинии и мколони, където всеки ред е колона от матрицата Асъс същия номер (следователно всяка колона е ред от матрицата Асъс същия номер). Така че, ако  , Че
, Че  .
.
Тази матрица бНаречен транспониранматрица А, и преходът от АДа се Б транспониране.
По този начин транспонирането е обръщане на ролите на редове и колони на матрица. Матрица, транспонирана в матрица А, обикновено обозначаван А Т.
Комуникация между матрицата Аи неговото транспониране може да бъде записано като .
Например.Намерете матрицата, транспонирана към дадената.

Събиране на матрица.Нека матрици АИ бсе състоят от еднакъв брой редове и еднакъв брой колони, т.е. имат еднакви размери. След това, за да добавите матриците АИ бнеобходимост от матрични елементи Адобавете матрични елементи бстоящи на същите места. Така сумата от две матрици АИ бнаречена матрица ° С, което се определя от правилото, напр.
![]()
Примери.Намерете сумата на матриците:

Лесно се проверява, че събирането на матрици се подчинява на следните закони: комутативно A+B=B+Aи асоциативни ( A+B)+° С=А+(B+C).
Умножение на матрица по число.За умножаване на матрица Ана брой кнужда от всеки елемент от матрицата Аумножете по това число. И така, матричният продукт Ана брой кима нова матрица, която се определя от правилото  или .
или .
За всякакви числа аИ bи матрици АИ бса изпълнени равенства:
Примери.

Матрично умножение.Тази операция се извършва по особен закон. На първо място, отбелязваме, че размерите на матричните фактори трябва да бъдат последователни. Можете да умножавате само онези матрици, чийто брой колони на първата матрица съвпада с броя на редовете на втората матрица (т.е. дължината на първия ред е равна на височината на втората колона). работаматрици Ане е матрица бнаречена новата матрица C=AB, чиито елементи са съставени както следва:
Така, например, за да получите продукта (т.е. в матрицата ° С) елементът в 1-ви ред и 3-та колона от 13, трябва да вземете 1-вия ред в 1-вата матрица, 3-тата колона във 2-рата и след това да умножите елементите на реда по съответните елементи на колоната и да добавите получените продукти. И други елементи от матрицата на продукта се получават с помощта на подобно произведение на редовете на първата матрица по колоните на втората матрица.
Като цяло, ако умножим матрицата A = (aij)размер м× нда се матрица B = (bij)размер н× стр, тогава получаваме матрицата ° Сразмер м× стр, чиито елементи се изчисляват както следва: елемент c ijсе получава в резултат на произведението на елементите азред на матрицата Авърху съответните елементи й-та колона на матрицата би тяхното сумиране.
От това правило следва, че винаги можете да умножите две квадратни матрици от един и същи ред, като в резултат получаваме квадратна матрица от същия ред. По-специално, квадратната матрица винаги може да бъде умножена сама по себе си, т.е. квадрат нагоре.
Друг важен случай е умножаването на матрица-ред с матрица-колона, като ширината на първата трябва да е равна на височината на втората, в резултат на което получаваме матрица от първи ред (т.е. един елемент). Наистина ли,
 .
.
Примери.

По този начин тези прости примери показват, че матриците, най-общо казано, не комутират една с друга, т.е. A∙B ≠ B∙A . Следователно, когато умножавате матрици, трябва внимателно да следите реда на факторите.
Може да се провери, че умножението на матрицата се подчинява на асоциативните и разпределителните закони, т.е. (AB)C=A(BC)И (A+B)C=AC+BC.
Също така е лесно да се провери това при умножаване на квадратна матрица Акъм матрицата на идентичността дот същия ред, отново получаваме матрицата А, освен това AE=EA=A.
Може да се отбележи следният любопитен факт. Както е известно, произведението на 2 ненулеви числа не е равно на 0. При матриците това може да не е така, т.е. произведението на 2 ненулеви матрици може да бъде равно на нулевата матрица.
Например, Ако  , Че
, Че
![]() .
.
ПОНЯТИЕТО ЗА ДЕТЕРМИНАРИ
Нека е дадена матрица от втори ред - квадратна матрица, състояща се от два реда и две колони  .
.
Детерминанта от втори редсъответстващо на тази матрица е числото, получено както следва: a 11 a 22 – a 12 a 21.
Детерминантата се обозначава със символа  .
.
И така, за да намерите детерминанта от втори ред, трябва да извадите произведението на елементите по втория диагонал от произведението на елементите на главния диагонал.
Примери.Изчислете детерминанти от втори ред.
По подобен начин можем да разгледаме матрица от трети ред и съответния детерминант.
Детерминанта от трети ред, съответстващо на дадена квадратна матрица от трети ред, е число, обозначено и получено по следния начин:
 .
.
По този начин тази формула дава разширение на детерминанта от трети ред по отношение на елементите на първия ред а 11, а 12, а 13и редуцира изчисляването на детерминанта от трети ред до изчисляване на детерминанти от втори ред.
Примери.Изчислете детерминанта от трети ред.

По същия начин могат да се въведат понятията детерминанти на четвъртата, петата и т.н. порядъци, като понижават порядъка си чрез разширяване върху елементите от 1-ви ред, като знаците "+" и "-" за термините се редуват.
Така че, за разлика от матрицата, която е таблица с числа, детерминантата е число, което е присвоено по определен начин на матрицата.
Точки в пространството, продукт Rvдава друг вектор, който определя позицията на точката след въртенето. Ако vе вектор ред, същата трансформация може да се получи с помощта на vRТ, къде Р T - транспониран към Рматрица.
Енциклопедичен YouTube
1 / 5
C# - Конзола - Олимпийски игри - Квадратна спирала
Матрица: определение и основни понятия
Къде да получите сила и вдъхновение Презареждане 4 квадратна матрица
Сума и разлика на матрици, умножение на матрица с число
Транспонирана матрица / Транспонирана матрица
субтитри
Главен диагонал
Елементи а ii (аз = 1, ..., н) образуват главния диагонал на квадратна матрица. Тези елементи лежат на въображаема права линия, минаваща от горния ляв ъгъл до долния десен ъгъл на матрицата. Например главният диагонал на матрицата 4x4 на фигурата съдържа елементите а 11 = 9, а 22 = 11, а 33 = 4, а 44 = 10.
Диагоналът на квадратна матрица, минаващ през долния ляв и горния десен ъгъл, се нарича страна.
Специални видове
| Име | Пример с н = 3 |
|---|---|
| Диагонална матрица | [ a 11 0 0 0 a 22 0 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end(bmatrix))) |
| Долна триъгълна матрица | [ a 11 0 0 a 21 a 22 0 a 31 a 32 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\a_(21)&a_(22)&0\\a_(31)&a_( 32)&a_(33)\end(bmatrix))) |
| Горна триъгълна матрица | [ a 11 a 12 a 13 0 a 22 a 23 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&a_(12)&a_(13)\\0&a_(22)&a_(23)\\ 0&0&a_(33)\end(bmatrix))) |
Диагонални и триъгълни матрици
Ако всички елементи извън главния диагонал са нула, Анаречен диагонал. Ако всички елементи над (под) главния диагонал са нула, Асе нарича долна (горна) триъгълна матрица.
Идентификационна матрица
Q(х) = х T брадваприема само положителни стойности (съответно отрицателни стойности или и двете). Ако квадратичната форма приема само неотрицателни (съответно само неположителни) стойности, симетричната матрица се казва, че е положителна полуопределена (съответно отрицателна полуопределена). Една матрица е неопределена, ако не е нито положителна, нито отрицателна полуопределена.
Симетричната матрица е положително определена тогава и само ако всички нейни собствени стойности са положителни. Таблицата вдясно показва два възможни случая за 2×2 матрици.
Ако използваме два различни вектора, получаваме билинейна форма, свързана с А:
б А (х, г) = х T да.ортогонална матрица
ортогонална матрицае квадратна матрица с реални елементи, чиито колони и редове са ортогонални единични вектори (т.е. ортонормални). Човек може също да дефинира ортогонална матрица като матрица, чиято обратна е равна на транспонирането:
A T = A − 1 , (\displaystyle A^(\mathrm (T) )=A^(-1),)откъде следва
A T A = A A T = E (\displaystyle A^(T)A=AA^(T)=E),ортогонална матрица Авинаги обратимо ( А −1 = А T), унитарен ( А −1 = А*) и нормално ( А*А = АА*). Детерминантата на всяка ортонормална матрица е или +1, или −1. Като линейна карта всяка ортонормална матрица с детерминанта +1 е проста ротация, докато всяка ортонормална матрица с детерминанта −1 е или просто отражение, или композиция от отражение и ротация.
Операции
Писта
Определящо det( А) или | А| квадратна матрица Ае число, което определя някои свойства на матрицата. Една матрица е обратима тогава и само тогава, когато нейният детерминант е различен от нула.
 Преобразуване на десетична дроб в обикновена дроб и обратно: правило, примери
Преобразуване на десетична дроб в обикновена дроб и обратно: правило, примери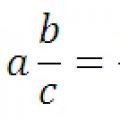 Преобразуване на десетични числа в обикновени дроби
Преобразуване на десетични числа в обикновени дроби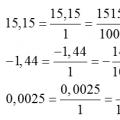 Преобразуване на обикновена дроб в десетична дроб и обратно, правила, примери
Преобразуване на обикновена дроб в десетична дроб и обратно, правила, примери