За какво са кръговете на Ойлер? кръг на Ойлер

Кръговете на Ойлер са геометрична диаграма. С негова помощ можете да изобразите връзките между подмножества (концепции) за визуално представяне.

Начинът на изобразяване на понятия под формата на кръгове ви позволява да развиете въображението и логическото мислене не само на децата, но и на възрастните. Започвайки от 4-5 години, децата могат да решават прости задачи с кръгове на Ойлер, първо с обяснения от възрастни, а след това самостоятелно. Овладяването на метода за решаване на задачи с помощта на кръгове на Ойлер развива способността на детето да анализира, сравнява, обобщава и групира своите знания за по-широко приложение.

Пример

Картината показва разнообразие от всички възможни играчки. Част от играчките са конструктори - откроени са в отделен овал. Това е част от голям набор от „играчки“ и в същото време отделен комплект (в края на краищата строителният комплект може да бъде „Лего“ или примитивни строителни комплекти, направени от блокове за деца). Част от голямото разнообразие от „играчки“ може да са играчки за навиване. Те не са конструктори, затова им рисуваме отделен овал. Жълтата овална „кола за навиване“ се отнася както за комплекта „играчка“, така и е част от по-малкия комплект „играчка за навиване“. Следователно той е изобразен вътре в двата овала наведнъж.

Ето няколко задачи за логическо мислене за малки деца:

Идентифицирайте кръговете, които отговарят на описанието на обекта. В този случай е препоръчително да се обърне внимание на онези качества, които обектът притежава постоянно и които има временно. Например стъклена чаша със сок винаги си остава стъклена, но не винаги има сок в нея. Или има някаква широка дефиниция, която включва различни понятия; такава класификация също може да бъде изобразена с помощта на кръгове на Ойлер. Например виолончелото е музикален инструмент, но не всеки музикален инструмент е виолончело.

За по-големи деца можете да предложите опции за проблеми с изчисления - от доста прости до много сложни. Освен това, самостоятелното измисляне на тези задачи за деца ще осигури на родителите много добра тренировка за ума.

1. От 27-те петокласници всички изучават чужди езици – английски и немски. 12 учат немски език и 19 учат английски език. Необходимо е да се определи колко петокласници изучават два чужди езика; колко хора не учат немски; колко хора не учат английски; Колко учат само немски и само английски?

В същото време първият въпрос на проблема подсказва най-общо пътя към решаването на този проблем, информирайки, че някои ученици изучават и двата езика, в който случай използването на диаграмата също улеснява децата да разберат проблема.

Между другото, ако не можете да решите коя професия да изберете, опитайте да нарисувате диаграма под формата на кръгове на Ойлер. Може би рисунка като тази ще ви помогне да направите своя избор:

Тези опции, които ще бъдат в пресечната точка на трите кръга, са професията, която не само ще може да ви нахрани, но и ще ви угоди.

И още един знак...

Ако мислите, че не знаете нищо за такова понятие като кръговете на Ойлер, тогава дълбоко грешите. Още от началното училище са известни схематични изображения или кръгове, които позволяват визуално разбиране на връзките между понятията и елементите на системата.

Методът, изобретен от Леонхард Ойлер, е използван от учения за решаване на сложни математически проблеми. Той изобразява множества в кръгове и прави тази диаграма основа на такава концепция като символична. Методът е предназначен да опрости възможно най-много разсъжденията, насочени към решаване на конкретен проблем, поради което техниката се използва активно както в началното училище, така и в академичната среда. Интересното е, че подобен подход е използван преди това от немския философ Лайбниц, а по-късно е възприет и приложен в различни модификации от известни умове в областта на математиката. Например, правоъгълни диаграми на чешките Болцано, Шрьодер, Вен, известни със създаването на популярна диаграма, базирана на този прост, но изненадващо ефективен метод.

Кръговете са в основата на така наречените „визуални интернет мемета“, които се основават на сходството на характеристиките на отделните набори. Това е смешно, визуално и най-важното, разбираемо.

Кръгове на мисълта

Кръговете ви позволяват ясно да опишете условията на даден проблем и незабавно да вземете правилното решение или да идентифицирате посоката на движение към правилния отговор. Обикновено кръговете на Ойлер се използват за решаване на логико-математически проблеми, включващи множества, техните съюзи или частични суперпозиции. Пресечната точка на кръгове включва обекти, които имат свойствата на всяко от множествата, изобразени в кръг. Обектите, които не са включени в комплекта, са разположени извън един или друг кръг. Ако понятията са абсолютно еквивалентни, те се означават с една окръжност, която е обединението на две множества с равни свойства и обеми.

Логика на взаимоотношенията

Използвайки кръговете на Ойлер, можете да решите редица ежедневни проблеми и дори да вземете решение за избора на бъдеща професия, просто трябва да анализирате вашите възможности и желания и да изберете тяхното максимално пресичане.

Сега става ясно, че кръговете на Ойлер изобщо не са абстрактна математическа и философска концепция от категорията на теоретичните знания, те имат много приложно и практическо значение, което ви позволява да се справяте не само с най-простите математически проблеми, но и да решавате важни житейски дилеми по нагледен и разбираем за всеки начин.

Всеки обект или явление има определени свойства (признаци).

Оказва се, че формирането на представа за даден обект означава преди всичко способността да се разграничи от други обекти, подобни на него.

Можем да кажем, че понятието е умственото съдържание на една дума.

Концепция -това е форма на мислене, която показва обектите в техните най-общи и съществени характеристики.

Понятието е форма на мисъл, а не форма на дума, тъй като думата е само етикет, с който отбелязваме тази или онази мисъл.

Думите могат да бъдат различни, но да означават една и съща концепция. На руски - "молив", на английски - "молив", на немски - bleistift. Една и съща мисъл има различни словесни изрази на различните езици.

ВРЪЗКИ МЕЖДУ ПОНЯТИЯТА. ОЙЛЕРОВИ КРЪГОВЕ.

Понятията, които имат общи черти в съдържанието си, се наричат СРАВНИМО(„юрист” и „депутат”; „студент” и „спортист”).

Иначе понятията се разглеждат НЕСРАВНИМО(„крокодил” и „тетрадка”; „човек” и „параход”).

Ако освен общи черти, понятията имат и общи елементи на обем, тогава те се наричат СЪВМЕСТИМ.

Има шест вида връзки между сравними понятия. Удобно е да се означават връзки между обемите на понятията с помощта на кръгове на Ойлер (кръгови диаграми, където всеки кръг означава обем на понятие).

ВИД ВРЪЗКА МЕЖДУ ПОНЯТИЯТА	ИЗОБРАЖЕНИЕ С ИЗПОЛЗВАНЕ НА ОЙЛЕРОВИ КРЪГОВЕ
РАВНОСТЪПНОСТ (ИДЕНТИЧНОСТ) Обхватът на понятията напълно съвпада. Тези. Това са различни по съдържание понятия, но в тях се мислят едни и същи обемни елементи.	1) A - Аристотел B - основател на логиката 2) A - квадрат B - равностранен правоъгълник
ПОДЧИНЕНОСТ (ПОДЧИНЕНОСТ) Обхватът на едно понятие се включва изцяло в обхвата на друго, но не го изчерпва.	1) A - човек B - ученик 2) A - животно B - слон
ПРЕСЪЧВАНЕ (ПРЕСИЧВАНЕ) Обемите на две понятия частично съвпадат. Тоест понятията съдържат общи елементи, но включват и елементи, които принадлежат само на едно от тях.	1) А - адвокат Б - заместник 2) А - студент Б - спортист
КООРДИНАЦИЯ (КООРДИНАЦИЯ) Понятията, които нямат общи елементи, се включват изцяло в обхвата на третото, по-широко понятие.	1) A - животно B - котка; C - куче; D - мишка 2) A - благороден метал B - злато; C - сребро; D - платина
ПРОТИВОПОСТАВНОСТ (КОНТРАПАРТНОСТ) Понятията А и Б не просто са включени в обхвата на третото понятие, но изглежда са на противоположните му полюси. Тоест понятието А има в съдържанието си такъв признак, който в понятието Б е заменен с противоположния.	1) A - бяла котка; B - червена котка (котките са черни и сиви) 2) A - горещ чай; студен чай (чаят може и топъл) т.е. концепциите А и Б не изчерпват целия обхват на концепцията, в която са включени.
ПРОТИВОРЕЧИЕ (КОНТРАДИЦИОННОСТ) Връзката между понятия, едното от които изразява наличието на някои характеристики, а другото - тяхното отсъствие, тоест просто отрича тези характеристики, без да ги заменя с други.	1) A - висока къща B - ниска къща 2) A - печеливш билет B - непечеливш билет Т.е. понятията А и не-А изчерпват целия обхват на понятието, в което са включени, тъй като между тях не може да се постави допълнително понятие.

Упражнение :Определете вида на връзката въз основа на обхвата на понятията по-долу. Начертайте ги с помощта на кръгове на Ойлер.

1) А - горещ чай; B - студен чай; C - чай с лимон

Горещият чай (B) и студеният чай (C) са в противоположна връзка.

Чаят с лимон (C) може да бъде горещ,

толкова студено, но може да бъде и например топло.

2)А- дърво; IN- камък; СЪС- структура; д- къща.

Всяка сграда (C) къща (D) ли е? - Не.

Всяка къща (D) сграда (C) ли е? - да

Нещо дървено (A) е задължително къща (D) или сграда (C) - Не.

Но можете да намерите дървена конструкция (например кабина),

Можете да намерите и дървена къща.

Нещо, направено от камък (B), не е непременно къща (D) или сграда (C).

Но може да има каменна сграда или каменна къща.

3)А- руски град; IN- столица на Русия;

СЪС- Москва; д- град на Волга; д- Углич.

Столицата на Русия (B) и Москва (C) са един и същи град.

Углич (E) е град на Волга (D).

В същото време Москва, Углич, както всеки град на Волга,

са руски градове (A)

Министерство на образованието, науката и младежта на Република Крим Малка академия на науките „Искател“

Направление: математика

Ж. Красноперекопск– 2017

Завършена работа:

Шумилина Мария Сергеевна,

ученик от 7-А клас на общински бюджет общо образованиеинституции „Средно общо образованиеУчилище № 5" общинско образувание район гр Красноперекопск

Научен ръководител:

Шейна Елена Николаевна,общински бюджет учител по математика общо образованиеинституции „Средно общо образованиеучилище No 5 » общинско образувание гр. район Красноперекопск

ВЪВЕДЕНИЕ ………………………………………………………………… 3

ГЛАВА 1. Малко история……………………………………. 5

ГЛАВА 2. От теорията на множествата…………………………………….7

2.1. Концепцията за набор.……………………………………………………..8

2.2. Операции върху множества.…………………………..9

ГЛАВА 3.Решаване на задачи с помощта на кръгове на Ойлер………………..10

ЗАКЛЮЧЕНИЕ…………………………………………………………..22

СПИСЪК НА ИЗПОЛЗВАНИТЕ ИЗТОЧНИЦИ………………….23

ВЪВЕДЕНИЕ

Нищо не помага

формиране на умствена култура,

като решение на логически проблеми. математика-

не суха и скучна наука, а пълна

необичайни и интересни открития

Решаването на логически задачи е много вълнуващо. Има хора, за които решаването на логическа задача е вълнуваща, но не и трудна задача. Техният мозък, като прожектор, веднага осветява всички гениални конструкции и те стигат до верния отговор необичайно бързо. Чудесно е, че не могат да обяснят как са стигнали до решението.

Логическите задачи представляват голям клас нестандартни задачи. Това включва на първо място текстови задачи, в които е необходимо да се разпознаят обекти или да се подредят в определен ред според съществуващите свойства.

Има много техники, които се използват за решаване на текстови логически проблеми. Много често решението помага да се намери чертеж. Използването на картина прави решаването на проблема лесно и ясно. Изобразяването на условията на даден проблем под формата на кръгове на Ойлер, като правило, опростява и улеснява пътя към неговото решение.

Уместност е, че задачите са с практическо естество, което е важно в съвременния живот. Проблемите ви карат да мислите, да подходите към решението на проблем от различен ъгъл, да можете да избирате от различни решения най-простия, най-лесния начин.

Цел на работата:

Запознаване с кръговете на Ойлер – Вен;

Научете се да прилагате метода за решаване на задачи с помощта на кръгове на Ойлер;

Създавайте задачи с практическо съдържание.

Глава 1. Малко история

Леонхард Ойлер, най-великият математикXVIIIc., роден в Швейцария през 1707 г.През 1727 г. по покана на Петербургската академия на науките той идва в Русия. В Санкт Петербург Ойлер се озовава в кръг от изключителни учени: математици, физици, астрономи и получава големи възможности да създава и публикува трудовете си. Работи със страст и скоро става, според единодушното признание на съвременниците си, първият математик в света. Научното наследство на Ойлер е поразително със своя обем и многостранност. Списъкът с неговите произведения включва повече от 800 заглавия. Пълното събрание на съчиненията на учения заема 72 тома. Сред трудовете му са първите учебници по диференциално и интегрално смятане. В теорията на числата Ойлер продължава работата на френския математик П. Ферма.

Ойлер работи много в областта на математическия анализ. Ученият е първият, който развива общо учение за логаритмичната функция. В геометрията Ойлер полага основите на напълно нова област на изследване, която по-късно прераства в самостоятелна наука - топология.

Името на Ойлер е дадено на формула, която свързва броя на върховете (B), ръбовете (P) и лицата (G) на изпъкнал полиедър: B -P + G = 2. Дори основните резултати от научната работа на Ойлер са трудни за списък. Тук е геометрията на кривите и повърхностите и първото представяне на вариационното смятане с множество нови конкретни резултати. Той пише трудове по хидравлика, корабостроене, артилерия, геометрична оптика и дори теория на музиката. За първи път той прави аналитично представяне на механиката вместо геометричното представяне на Нютон и конструира механиката на твърдо тяло, а не само на материална точка или твърда плоча. Едно от най-забележителните постижения на Ойлер е свързано с астрономията и небесната механика. Той изгради точна теория за движението на Луната, като отчита привличането не само на Земята, но и на Слънцето. Това е пример за решаване на много труден проблем.

Последните 17 години от живота на Ойлер са белязани от почти пълна загуба на зрение. Но той продължи да твори толкова интензивно, колкото в младостта си. Едва сега той вече не пишеше сам, а диктуваше на учениците си, които извършваха най-тромавите изчисления вместо него.

От 1761 до 1768 г. той пише известните „Писма до немска принцеса“, където Ойлер говори за своя метод, за изобразяване на множества под формата на кръгове. Ето защо чертежите под формата на кръгове обикновено се наричат „Ойлерови кръгове“. Ойлер отбеляза, че представянето на множества като кръгове „е много подходящо за улесняване на нашите разсъждения“.

След Ойлер същият метод е разработен от чешкия математик Бернард Болцано (1781 – 1848). Само, за разлика от Ойлер, той не рисува кръгли, а правоъгълни диаграми. Методът на кръга на Ойлер е използван и от немския математик Ернст Шрьодер (1841 – 1902). Този метод е широко използван в неговата книга Алгебра Логика. Но графичните методи достигат своя най-голям разцвет в писанията на английския логик Джон Вен (1843 - 1923). Той очерта този метод най-пълно в книгата си „Символна логика“, публикувана в Лондон през 1881 г. В чест на Вен, вместо кръгове на Ойлер, съответните чертежи понякога се наричат диаграми на Вен; в някои книги те се наричат още диаграми на Ойлер-Вен (или кръгове).

Глава 2. От теорията на множествата

2.1. Концепцията за набор.

Едно от основните понятия, използвани в математиката, е понятието множество. Не е дадено определение за него. Може да се обясни, че множеството е произволна колекция от обекти, а самите обекти са елементите на дадено множество. И така, можем да говорим за набор от ученици в клас (елементите са ученици), набор от дни от седмицата (елементите са дни от седмицата), набор от естествени делители на числото 6 (елементите са числа 1, 2, 3, 6) и т.н.

В курсовете по алгебра и алгебра началото на анализа най-често разглеждат множества, чиито елементи са числа, поради което се наричат набори от числа.

По правило наборите се обозначават с главни букви на латинската азбука. Например, ако наборътМсе състои от числа 1; 2; 3, тогава се обозначава, както следва:М= (1; 2; 3). Фактът, че числото 2 е включено в този комплект

(е елемент от този наборМ) се записва с помощта на специална икона както следва: 2М; и фактът, че числото 5 не е включено в това множество (не е елемент от това множествоМ), написана така: 5 М.

Можем да разгледаме и множество, което не съдържа нито един елемент - празното множество. Например: множеството от прости множители на числото 1 е празно множество.

За някои набори има специални обозначения. Така празното множество се обозначава със символа , множеството от всички естествени числа – букван, множеството от всички цели числа – букваЗ, множеството от всички рационални числа – букватаQ, а множеството от всички реални числа е букватаР. Използвайки кръговете на Ойлер-Вен, това може да бъде изобразено по следния начин:

Фиг. 1

Ако всеки елемент от множествотоАе елемент от множествотоБ, тогава казват, че наборътАе подмножество на множествотоБ.

Това е написано по следния начин:А Б.

Фиг.2

2.2. Операции върху множества.

Можете да извършвате определени действия върху множества: намиране на тяхното пресичане, обединение. Нека да дефинираме тези операции и да ги илюстрираме с кръгове.

Пресечна точка на множества А И Б наричаме тяхната обща част, тоест множеството° Свсички елементи, принадлежащи на двете групиА, и многоБ

Пресечната точка на множества се обозначава със знака∩ и запишетеА∩ Б .

Фиг.3

Обединение на комплекти А И Б обадете се на набор° С, състоящ се от всички елементи, принадлежащи към поне едно от тези множества (АилиБ). Обединението на множествата се обозначава със знака
и запишете А
Б

Глава 3. Решаване на задачи с помощта на кръгове на Ойлер

Задача No1.

От 52-ма ученици 23-ма колекционират значки, 35 събират печати, а 16 събират и значки, и марки.

Останалите не се интересуват от колекционерство. Колко ученици не се интересуват от колекционерство?

Решение.

Условията на този проблем не са толкова лесни за разбиране. Ако съберете 23 и 35, получавате повече от 52. Това се обяснява с факта, че тук броихме два пъти някои ученици, а именно тези, които събират значки и печати.

За да улесним решаването на проблема, нека представим данните му в следната диаграма

Фиг.5

В тази диаграма големият кръг представлява всички въпросни ученици. кръгЗ изобразява ученици, събиращи значки (общо 23) и кръгътМ - ученици, събиращи марки (общо 35). В пресечната точка на кръговеЗИ М Числото 16 струва - това са тези, които събират и значки, и печати. Това означава, че 23 - 16 = 7 души събират само значки, 35 - 16 = 19 души събират само печати. Общо 19 + 7 + 16 = 42 души събират печати и значки. Това оставя 52 - 42 = 10 души, които не са запалени по колекционирането. Този номер може да бъде въведен в свободното поле на кръга. Отговор: 10 души.

Задача 2.

В класа има 15 момчета. От тях 10 души се занимават с волейбол и 9 с баскетбол. Колко момчета правят и двете?

Решение.

Нека изобразим състоянието с помощта на окръжности на Ойлер. Тази цифра ни дава известна аргументация. Нека анализираме това разсъждение и във всяка от частите, образувани на диаграмата, въведем необходимото число.

Нека x момчета да играят всякакви спортове. Тогава само (10-то) момчета играят волейбол и само (9-то) момчета играят баскетбол. Нека съставим уравнение: 10 + x + 9 = 15, от което x = 4

10-те Б

х 9-ки

Фиг.6

Отговор: 4 човека.

Задача No3.

Някои момчета от нашия клас обичат да ходят на кино. Известно е, че 15 деца са гледали филма „Плашило“, 11 души са гледали филма „Над небето“, от които 6 са гледали едновременно „Плашило“ и„Над небето“. Колко хора са гледали само филма „Над небето”?

Решение:Нека начертаем два комплекта по този начин: Поставяме 6 души, които са гледали филмите „Плашило“ и „Над небето“ в пресечната точка на декорите.

15 – 6 = 9 – хора, които са гледали само „Плашило“.
11 – 6 = 5 – хора, които са гледали само „Над небето“.

Получаваме:

Фиг.7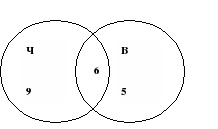

Отговор. 5 души са гледали само „Над небето“.

Задача No4.

В група от 80 туристи, дошли на екскурзия до Москва, 52 искат да посетят Болшой театър, 30 искат да посетят Художествения театър, 12 искат да посетят и двата театъра, останалите не искат да ходят на театри. Колко хора няма да отидат на театър?

Решение.

Само големият театър ще бъде посетен от: 52-12=40 туристи;

ще се посещава само арт театъра

30-12=18 туристи;

8
0-(40+18+12)=10 туристи няма да отидат на театър.

Фиг.8

Отговор: 10 души.

Задача No5.

На рафта имаше 26 магически книги за заклинания. 4 от тях са прочетени от Хари Потър и Рон. Хърмаяни прочете 7 книги, които нито Хари Потър, нито Рон бяха чели, и две книги, които Хари Потър беше чел. Общо Хари Потър е прочел 11 книги. Колко книги е прочел Рон?

Решение.

Като се имат предвид условията на проблема, чертежът ще бъде както следва:

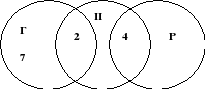
Фиг.9

Тъй като Хари Потър е прочел общо 11 книги, от които 4 книги са прочетени от Рон и 2 книги от Хърмаяни, тогава само Хари е прочел 11 - 4 - 2 = 5 - книги.

Следователно Рон е прочел 26 – 7 – 2 – 5 – 4 = 8 – книги.Отговор. Рон прочете 8 книги.

Задача No6.

В туристическа група от 100 души 75 души знаят немски, 65 души знаят английски, а 10 души не знаят нито немски, нито английски. Колко туристи говорят два езика? Решение.

Нека изобразим условията на задачата под формата на окръжности на Ойлер.

Лесно се вижда, че 90 туристи (100-10) знаят поне един език; Нека х туристи знаят и английски, и немски. След това (65-то) туристите знаят само английски, а (75-то) хората знаят само немски. Получаваме уравнението 65's + 75's + x = 90, от което x = 50 - туристите знаят и двата езика.Отговор: 50 туристи.

Задача No7.

Колко души участват в разходката, ако се знае, че 16 от тях са взели сандвич с шунка, 24 с наденица, 15 със сирене, 11 и с шунка, и с наденица, 8 и с шунка, и с кашкавал, 12 с наденица и с сирене, 6 - сандвичи от всякакъв вид, и 5 - взе пайове?Решение : Нека представим множествата по следния начин: Фиг.11

16+24+15-11-8-12+6=30 (човека) - участвали в разходката и взели сандвичи със себе си или 3+2+6+5+7+6+1=30 (човека)

30+5=35 (човека) - взеха участие в похода
Отговор. 35 души

Проблем No8

В 5 клас на нашето училище учат 22, в 6 клас - 16, в 7 клас - 23 деца. Известно е, че 4 души посещават клубове по ски, шах и спорт. Всеки две секции се посещават от 9 човека. Колко души отиват от всеки клас в секции? Колко ученици не посещават нито един спортен клуб?

Решение. Ако и в трите клуба има по 4 ученика, а във всеки два по 9 души, то две секции от 5 и 6 клас, от 6 и 7 клас и от 5 и 7 клас се посещават от 5

Човек.

Фиг.12

Получаваме 5+5+4=14 петокласници посещават кръжоци, 22-14=8 човека не посещават кръжоци. По разсъждения също, от шестокласниците 16-14=2 ученици не ходят никъде, а от седмокласниците – 23-14=9 души.

Отговор: 14 ученици от всеки клас посещават кръжоци; 7 ученици от 6-ти, 9 от 7-ми не посещават кръжоци.

Задача No9.

От 100 деца, посещаващи детски оздравителен лагер, 30 деца могат да карат сноуборд, 28 могат да карат ролери, 8 деца могат да карат скейтборд и сноуборд, 10 деца могат да карат скейтборд и ролери – 5, а на трите – 3. Колко момчета не знаят как да карат сноуборд, скейтборд или ролери?

Решение: IN Нека използваме кръговете на Ойлер.

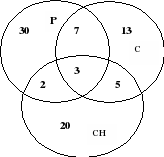
Фиг.13

Трима души притежават и трите спортни екипа, което означава, че в общата част на кръговете вписваме числото 3. 10 души могат да карат скейтборд и ролери, а 3 от тях и сноуборд. Следователно 10-3=7 момчета могат да карат само скейтборд и ролери. По същия начин откриваме, че само 8-3=5 момчета могат да карат скейтборд и сноуборд и само 5-3=2 души могат да карат сноуборд и ролери. Ние ще въведем тези данни в съответните части. Нека сега да определим колко души могат да карат само едно спортно оборудване. 30 души знаят как да карат сноуборд, но 5+3+2=10 от тях знаят и друго оборудване, следователно 20 души знаят как да карат сноуборд само. По същия начин откриваме, че 13 деца знаят само как да карат скейтборд, а 30 деца знаят как да карат само ролери. Според условията на задачата има само 100 момчета. 20+13+30+5+7+2+3=80 – момчетата знаят как да карат поне една спортна екипировка. Следователно 20 души не знаят как да карат никакво спортно оборудване.
Отговор. 20 човека не знаят как да карат никаква спортна екипировка.

Задача No10 .

В три седми класа учат 70 деца. От тях 27 се занимават с драматичен клуб, 32 пеят в хор, 22 се занимават със спорт. В драматичния клуб има 10 момчета от хор, 6 спортисти в хор, 8 спортисти в драматичен клуб; 3-ма състезатели посещават драматичен клуб и хор. Колко деца не пеят в хора, не се интересуват от спорт и не участват в драматичен клуб? Колко момчета се занимават само със спорт?

Решение . D - драматичен клуб; X - хор; S - спорт. В кръг D - 27 деца, в кръг X - 32 души, в кръг C - 22 ученици.Тези 10 момчета от драмклуба, които пеят в хора, ще бъдат в общата част на кръгове D и X. Трима от тях също са спортисти, те ще бъдат в общата част и на трите кръга. Останалите седем не се интересуват от спорт. По същия начин 8-3=5

спортисти, които не пеят в хора и 6-3=3, които не посещават драматичен клуб. Лесно се вижда, че 5+3+3=11 спортисти посещават хор или драматичен клуб, 22-(5+3+3)=11 се занимават само със спорт; 70-(11+12+19+7+3+3+5)=10 - не пеят в хор, не участват в драматичен клуб, не се интересуват от спорт.

Фиг.14Отговор: 10 души.

Задача No11 . В класа има 30 души. 20 от тях използват метро всеки ден, 15 използват автобус, 23 използват тролейбус, 10 използват и метро, и тролейбус, 12 използват и метро, и автобус, 9 използват и тролейбус, и автобус. Колко души използват и трите вида транспорт всеки ден?

Решение.

Фиг.15

Нека x човек използва и трите вида транспорт. След това използват само метро и тролейбус - (10 − x) души, само автобус и тролейбус - (9 − x) души, само метро и автобус - (12 − x) души. Нека разберем колко души използват само метрото:

20 − (12 − x) − (10 − x) − x = x − 2

По същия начин получаваме: x − 6 - само с автобус и x + 4 - само с тролейбус, тъй като има само 30 души, създаваме уравнението:

x + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30.

следователно x = 3.

Отговор: 3 души.

Задача No12.

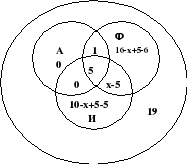
От служителите на компанията 16 са посетили Франция, 10 Италия, 6 Англия; в Англия и Италия - 5; в Англия и Франция -6; и в трите държави - 5 служители. Колко души са посетили Италия и Франция, ако във фирмата работят общо 19 души и всеки от тях е посетил поне една от посочените страни?

Решение:

Знаем, че имаше 5 служители и в трите държави. В Англия и Италия също има 5, което означава, че същите тези служители са били и във Франция и затова поставяме 0 в пресечната точка на кръговете A и I. Във Франция и Италия не знаем, така че пишем x-5 на пресечната точка на окръжности A и F. Защото в Англия имаше 6 души, тогава 6-5-1=0 пишем 0, във Франция има 16+5-6 и в Италия 10+5-5 и общо има 19 служители в компанията, тогава всичко това остава да се създаде и реши уравнението: 1 +16x+5-6+5+x-5+10x+5-5=19, следователно x=7, което означава, че 7-5=2 служители на компанията са посетили Италия и Франция.

Фиг.16

Отговор: 2 служители.

Задача No13.

Имаше 10 момчета, които искаха да си разменят различни видове списания. Сред тях 6 души са абонирани за K, 5 души за T, 5 души за Yu, 3 души за K и T, 2 души за T и Yu, 3 души за K и Yu и един човек не е абониран за нито едно списание .но чете всички тези списания в библиотеката. Трябва да разберем колко души са абонирани и за трите списания, колко за две и колко само за едно списание.

Решение. Нека голям кръг от 10 души е групата на всички момчета, които си разменят списания. Вътре в големия кръг ще нарисуваме три по-малки кръга: K, T, Yu, които изобразяват момчетата, които са се абонирали за съответните списания. Известно е, че един човек не се абонира за нито едно списание.

Нека x момчета се абонират за всичките три списания, тогава (3) момчета се абонират само за K и T, (2) само за T и Yu, (3) само за K и Yu. Това означава, че само списание K е абонирано за 6 - (3-x+x+3-x)=x хора, списание T 5-(3-x+x+2-x)=x, списание Yu 5-(3-x+x+2-x)= X .

Фиг.17

Нека съставим уравнение: x+3-x+3-x+x+x+x+x+2-x=9, 8+x=9,x=1

И така, 3 е броят на момчетата, които са се абонирали само за едно списание, 5 е броят на момчетата, които са се абонирали за две списания, и 1 е броят на момчетата, които са се абонирали и за трите списания.

ЗАКЛЮЧЕНИЕ

Предметът математика е толкова сериозен

това, което не можете да пропуснете възможността да направите

малко е забавно.

Б. Паскал

Сред математическите задачи логическите задачи заемат специално място. Решаването на такива задачи допринася за развитието на математическото мислене. Те се различават от повечето математически задачи по това, че решаването им често не изисква запас от специални знания, но като правило изисква интелигентност. Една от характерните черти на всяка логика е, че тя позволява, след като получи някаква информация, да извлече (идентифицира) новите знания, съдържащи се в нея.

Оказва се, че има няколко техники, с които можете да решавате текстови логически проблеми. Те са разнообразни и всеки от тях има своя област на приложение.

Работата ми разглежда проблеми, които се състои от много данни.Намерените решения следват същия метод: направете чертеж; въведете първоначалните данни в кръгове; анализирайки и разсъждавайки, записваме резултатите в части от кръгчетата; Търсим и записваме отговора.Изобразяването на условията на даден проблем под формата на кръгове на Ойлер, като правило, опростява и улеснява пътя към неговото решение. Освен това с тяхна помощ можете да отговорите на много въпроси, зададени към едно условие на проблема.

Тази тема разшири математическите ми хоризонти и обогати арсенала ми от инструменти, използвани при решаването на различни задачи.

Списък на използваните източници:

1. Гаврилова Т.Д.. Занимателна математика. 5 - 11 клас. Волгоград: Учител, 2005.-96 с.

2. Германович П.Ю. "Сборник задачи по математика за съобразителност."

3. Гетманова A.D. Логически основи на математиката, 10-11 клас: учебник. – М.: Дропла, 2005.

4. Глейзър Г.И. . - М.: Образование, 1964. - С. 232.

5. Гусев В.А., Орлов А.И., Розентал А.Л. "Извънкласна работа по математика." М.: Образование, 1984.

6. Нелин Е.П., Долгова О.Е.. Учебник по алгебра и начало на анализа, 11 клас.

Резюмета за работата

Темата на моята изследователска работа е „Решаване на задачи с помощта на кръгове на Ойлер“. Когато се подготвях за олимпиадата, бях изправен пред задачи, които включваха голямо количество данни. Оказва се, че така наречените кръгове на Ойлер помагат за опростяване на решението на такива проблеми, с помощта на които можете да изобразите много елементи, които имат определено свойство. Целта на тази работа е да проучи този метод и да може да го прилага за решаване на проблеми.

Работата разглежда проблеми, чието решение се подчинява на един алгоритъм: изготвяне на чертеж; Въвеждаме началните данни в кръгове, като започваме с условието, което съдържа повече свойства; анализирайки и разсъждавайки, записваме резултатите в части от кръга; запишете отговора.

Уместността се състои в това, че задачите са с практическо естество, което е важно в съвременния живот. Проблемите ви карат да мислите, да подходите към решението на проблем от различен ъгъл, да можете да избирате от различни решения най-простия, най-лесния начин. Методът, разгледан в работатадостъпен и лесен за разбиране, което ви позволява да разширите обхвата на неговото приложение. Кръговете на Ойлер могат да бъдат намерени в историята, биологията и при изучаването на други предмети.

Материалът, който беше изучен в работата, както и практическата част,може да се използва в допълнителни часове при подготовка за математически олимпиади.

Преглед на материала

Математиката е един от любимите ми предмети в гимназията. Обичам да решавам различни математически пъзели и логически задачи. В математическия клуб се запознаваме с различни начини за решаване на задачи. Един ден по време на клубен час ни беше дадена домашна задача да решим следната задача: „Има 35 ученици в класа, 12 са в кръжок по математика, 9 са в кръжок по биология и 16 деца не посещават тези кръжоци . Колко биолози се интересуват от математика? Реших го по следния начин:

35 - 16=19 (деца) - посещават клубове

19- 9 = 10 (деца) – посещават математически клуб

12 - 10=2 (биолози) – увличат се по математика.

И тя ме помоли да проверя решението на проблема на по-големия ми брат. Той каза това

Проблемът е решен правилно, но има по-удобен и по-бърз начин за решаването му. Оказва се, че така наречените кръгове на Ойлер помагат да се опрости решението на този проблем, с помощта на който можете да изобразите много елементи, които имат определено свойство. Интересувах се от нов начин за решаване на проблема и реших да напиша научна статия на тема: „Решаване на задачи с помощта на кръгове на Ойлер“

Поставих си цел: да науча нов начин за решаване на нестандартни задачи с помощта на кръгове на Ойлер.

За разкриване на темата на моята изследователска работа бяха поставени следните задачи:

Научете се да използвате научна литература.

Научете какво представляват кръговете на Ойлер.

Създайте алгоритъм за решаване на проблеми.

Научете се да решавате задачи с помощта на кръгове на Ойлер.

Съставете селекция от задачи за използване в часовете по математика.

Изследователски методи:

Проучване и анализ на научна литература;

Метод на индуктивното обобщение, конкретизация.

Обект на изследване: кръгове на Ойлер

Предмет на изследване: концепцията за набор, основните действия с тях, необходими при решаване на задачи с помощта на кръгове на Ойлер

Участници в изследването: ученици от 5-9 клас на гимназията

Изследователска хипотеза: Методът на Ойлер опростява разсъжденията при решаването на определени проблеми и улеснява пътя към тяхното решение.

Уместността на изследването се състои в това, че има много техники и начини за решаване на нестандартни логически проблеми. Често при решаване на проблем се използват чертежи, което прави решаването на проблема по-просто и визуално. Един такъв визуален и удобен начин за решаване на проблеми е методът на кръга на Ойлер. Този метод ви позволява да решавате проблеми с тромави условия и с много данни.

Задачи, решени с помощта на кръгове на Ойлер, често се предлагат на математически олимпиади. Такива задачи често са от практическо естество, което е важно в съвременния живот. Карат те да мислиш и да подходиш към решаването на даден проблем от различни ъгли. Те ви учат да избирате най-простия и лесен от различни методи.

Теоретична част

Кратка историческа справка.

Леонхард Ойлер (1707-1783) – велик математик от Петербургската академия от 18 век. Роден в швейцарския град Базел. Той рано открива математически способности. На 13-годишна възраст той става студент във факултета по изкуствата на университета в Базел, където се преподават както математика, така и астрономия. На 17 години получава магистърска степен. На 20-годишна възраст Ойлер е поканен да работи в Академията на науките в Санкт Петербург, а на 23 години вече е професор по физика, а три години по-късно получава катедрата по висша математика.

През дългия си живот Леонхард Ойлер оставя важни трудове по различни клонове на математиката, механиката, физиката, астрономията и редица приложни науки и написва повече от 850 научни статии. В един от тях се появиха тези кръгове.

Какво представляват кръговете на Ойлер?

Отговорът на този въпрос намерих, като прочетох различна учебна литература. Леонхард Ойлер вярва, че „кръговете са много подходящи за улесняване на нашето мислене“. При решаването на редица проблеми той използва идеята за представяне на множества с помощта на кръгове, поради което те са наречени „Ойлерови кръгове“.

В математиката наборът е колекция, колекция от всякакви обекти (обекти). Обектите, които съставят едно множество, се наричат негови елементи. Традиционно се приема, че кръг визуално изобразява обема на едно понятие. Например нашият 5 клас е набор, а броят на учениците в класа е неговите елементи.

В математиката множествата се означават с главни букви, а техните елементи с главни букви. Често се записва във формата A = (a, b, c, ...), където елементите на множеството A са посочени във къдрави скоби.

Ако всеки елемент от множество A е същевременно елемент от множество B, тогава те казват, че A е подмножество от множество B. Например множеството от ученици от 5-ти клас в нашата гимназия е подмножество от всички ученици в гимназията .

С множествата, както и с обектите, можете да извършвате определени действия (операции). За по-ясно представяне на действията с множества се използват специални чертежи - диаграми на Ойлер (окръжности). Нека се запознаем с някои от тях.

Множеството от общи елементи A и B се нарича пресечна точка на множествата A и B и се означава със знака ∩.

A∩B = (m), C ∩B = (e, u).

Множествата A и C нямат общи елементи, така че пресечната точка на тези множества е празното множество: A∩C =∅.

Ако създадете ново множество от елементите на множества A и B, състоящо се от всички елементи на тези множества и не съдържащо други елементи, тогава получавате обединение на множества A и B, което се обозначава със знака ∪.

Разгледайте пример: Нека A = (t, o, h, k, a), B = (t, i, p, e), C = (d, e, f, u, s).

A∪B = (t, o, h, k, a, i, p, e), B∪ C = (t, i, p, e, d, f, s), A ∪ B ∪ C = (t , o, h, k, a, i, p, e, d, f, s).

Изводи: Кръговете на Ойлер са геометрична диаграма, която ви позволява да направите по-ясни логически връзки между явления и понятия. Също така помага да се изобрази връзката между комплект и неговата част.

Можете да проверите това с примерна задача.

Всички мои приятели отглеждат цветя в апартаментите си. Шест от тях отглеждат кактуси, а пет теменужки. И само две имат и кактуси, и теменужки. Колко приятелки имам?

Нека определим колко множества има в задачата (т.е. колко кръга ще начертаем, когато решаваме задачата).

В задачата приятелите отглеждат 2 вида цветя: кактуси и теменужки.

Това означава първият набор (1 кръг е приятели, които отглеждат кактуси).

Вторият комплект (2-ри кръг са приятели, които отглеждат теменужки).

В първия кръг ще посочим собствениците на кактуси, а във втория кръг собствениците на теменужки.

Избираме условието, което съдържа повече свойства за рисуване на кръгове. Някои приятели имат и двете цветя, така че нека нарисуваме кръгове, така че да имат обща част.

Да направим чертежа.

В общата част поставяме числото 2, тъй като двама приятели имат и кактуси, и теменужки.

Според условията на задачата 6 приятели отглеждат кактуси, а 2 вече са в общата част, след което в останалата част от кактусите поставяме числото 4 (6-2 = 4).

5 приятели отглеждат теменужки, а 2 вече са в общата част, след което в останалата част от теменужките поставяме числото 3 (5-2=3)

Самата картинка ни казва отговора 4+2+3=9. Записваме отговора.

Отговор: 9 приятелки

Практическа част

Решаване на задачи с помощта на кръгове на Ойлер

След като разбрах какви са кръговете на Ойлер въз основа на примера на проблема и изучения материал, реших да премина към съставяне на алгоритъм за решаване на проблеми с помощта на този метод.

2.1 Алгоритъм за решаване на задачи

Внимателно изучаваме и записваме накратко условията на проблема.

Ние определяме броя на комплектите и ги обозначаваме.

Да направим чертежа. Построяваме пресечната точка на множества.

Пишем първоначалните данни в кръгове.

Изберете условието, което съдържа повече свойства.

Записваме липсващите данни в кръгове на Ойлер (разсъждение и анализиране)

Проверяваме решението на задачата и записваме отговора.

След като създадох алгоритъм за решаване на проблеми с помощта на кръгове на Ойлер, реших да го работя върху още няколко проблема.

Задачи, включващи пресичане и обединение на две множества

Задача 1.

В моя клас има 15 ученика. От тях 9 се занимават в секцията по лека атлетика, 5 в секцията по плуване и 3 в двете секции. Колко ученици в класа не посещават секции?

Решение.

Проблемът има едно множество и две подмножества. 1 кръг - общо ученици. 2 кръг – брой ученици, занимаващи се с лека атлетика. 3 кръг - броят на учениците, занимаващи се с плуване.

Нека представим всички ученици с по-голям кръг. Ще поставим по-малки кръгове вътре и ще ги нарисуваме така, че да имат обща част (тъй като трима момчета учат и в двата раздела).

Обща сума

Да направим чертежа.

В голям кръг има 15 ученици. В общата част на по-малките кръгове поставяме числото 3. В останалата част на кръга l/a поставяме числото 6 (9-3=6). В останалата част от кръга n - поставете числото 2 (5-3=2).

5. Записваме отговора от картинката: 15-(6+3+2) = 4 (ученици) не са ангажирани в нито една от тези секции.

Задача 2. (която реших по различен начин, но сега ще я реша с помощта на кръгове на Ойлер)

В класа има 35 ученици, 12 са в кръжок по математика, 9 в кръжок по биология, а 16 деца не посещават тези кръжоци. Колко биолози се интересуват от математика?

Решение:

Проблемът има едно множество и две подмножества. 1 кръг - общо ученици в класа. 2-ро кръгче броя на учениците, обучаващи се в математически кръжок (обозначава се с буквата М). 3-ти кръг - броят на учениците, обучаващи се в кръга по биология (обозначен с буквата B).

Нека представим всички ученици в класа с голям кръг. Вътре ще поставим по-малки кръгове, които имат обща част, т.к Няколко биолози се интересуват от математика.

Да направим рисунката:

В големия кръг има само 35 ученици. 35-16 = 19 (ученици) посещават тези клубове. В кръг M поставяме 12 ученици, които учат в математически кръг. В кръг B поставяме 9 ученици, които учат в клуба по биология.

Да напишем отговора от картинката: (12 + 9) – 19 = 2 (ученици) – обичат биологията и математиката. Отговор: 2 ученика.

2.3. Задачи, включващи пресичане и обединение на три множества

Задача 3.

В класа има 40 души. От тях 19 души са с тройка по руски език, 17 по математика и 22 по история. Само по един предмет има оценки „C”: по руски език - 4 души, по математика - 4 души, по история - 11 души. Седем ученици са с „С” и по математика, и по история, а 5 ученици са с „С” по всички предмети. Колко хора учат без оценки? Колко хора имат C по два от три предмета?

Решение:

Проблемът има едно множество и три подмножества. 1 голям кръг - общо ученици в класа. 2-ри кръг е броят на учениците с тройка по математика (обозначен с буквата М), 3-ти кръг е по-малък - броят на учениците с тройка по руски език (обозначен с буквата Р), 4-ти кръг е по-малък - брой ученици с оценки C по история (означени с буквата I)

Нека начертаем окръжности на Ойлер. Вътре в по-големия кръг, изобразяващ всички ученици в класа, ще поставим три по-малки кръга M, R, I, което означава съответно математика, руски език и история, и трите кръга се пресичат, тъй като 5 ученици имат оценки "C" във всички предмети.

Нека напишем данните в кръгове, като разсъждаваме, анализираме и извършваме необходимите изчисления. Тъй като броят на учениците с „В” оценки по математика и история е 7, броят на учениците само с две „В” оценки – по математика и история е 7-5 = 2. Тогава 17-4-5-2=6 ученици имат две оценки „Ч” – по математика и руски език, а 22-5-2-11=4 ученици имат само две оценки „Ч” – по история и руски език. . В този случай 40-22-4-6-4 = 4 студенти учат без „С“. А 6+2+4=12 души имат „С” оценки по два предмета от три.

7-5=2 - броят на учениците само с две оценки "В" - М, І.

17-4-5-2=6 - броят на учениците само с две оценки "В" - М, Р.

22-5-2-11=4 - броят на учениците само с две оценки "В" - I,R.

40-22-4-6-4=4 - броят на студентите, обучаващи се без „С“

6+2+4=12 - броят на учениците с оценка "В" - по два от три предмета

Отговор: 4 ученици учат без „С“ оценки, 12 ученици имат „С“ по два от три предмета

Задача 4.

В класа има 30 души. 20 от тях използват метро всеки ден, 15 използват автобус, 23 използват тролейбус, 10 използват и метро, и тролейбус, 12 използват и метро, и автобус, 9 използват и тролейбус, и автобус. Колко души използват и трите вида транспорт всеки ден?

Решение. 1 начин. За да решим, отново използваме кръгове на Ойлер:

20 − (12 − x) − (10 − x) − x = x − 2

По същия начин получаваме: 15 –(12 − x) -(9 − x) - x = x − 6 - само с автобус и

23 - (9 − x) - (10 − x) – x = x + 4 - само с тролейбус, тъй като има само 30 души, създаваме уравнението:

X + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30. Следователно x = 3.

Метод 2. Или можете да разрешите този проблем по друг начин:

20+15+23-10-12-9+x=30, 27+x=30, x=3.

Отговор: 3 души използват трите вида транспорт всеки ден.

2.4. Подготовка на задачи с практическо значение

Задача 1. В 5А клас има 15 души. В кръжок „Ерудит” ходят 5 души, в кръжок „Път към словото” – 13, спортна секция – 3 души. Освен това 2 човека посещават кръжок „Ерудит” и кръжок „Път към словото”, „Ерудиция” и спортна секция, спортна секция и „Път към словото”. Колко души посещават и трите клуба?

Решение:

1. Тогава нека x души посещават и трите клуба

2. 5+13+3-2-2-2+x=15, 13+x=15, x=2

Отговор: И в трите клуба посещават 2 човека.

Проблем 2

Известно е, че учениците от 6Б клас са регистрирани в социалните мрежи: „VK“, „Odnoklassniki“, „Galaxy за запознанства“. 2 студенти не са регистрирани в никоя социална мрежа, 7 студенти са регистрирани в Odnoklassniki и VK; 2 ученика само в Odnoklassniki и 1 само във VK; и 2 ученика са регистрирани и в 3-те социални мрежи. Колко човека от класа са регистрирани във всяка социална мрежа? Колко души от класа участваха в анкетата?

Решение:

Използвайки кръговете на Ойлер, получаваме:

Във VK са регистрирани 1+5+2=8 души,

В Odnoklassniki има 2+5+2=9 души,

В Галактиката за запознанства има само 2 души.

В анкетата участваха общо 1+5+2+2+2=12 души

2.5. Задачи за използване в часовете на кръжока по математика

Задача 1: „Хари Потър, Рон и Хърмаяни“

На рафта имаше 26 магически книги за заклинания, всички бяха прочетени. 4 от тях са прочетени от Хари Потър и Рон. Хърмаяни прочете 7 книги, които нито Хари Потър, нито Рон бяха чели, и две книги, които Хари Потър беше чел. Общо Хари Потър е прочел 11 книги. Колко книги е прочел сам Рон?

Задача 2: „Пионерски лагер“

Задача 3: „Екстремно“

Задача 4: "Футболен отбор"

Футболният отбор на Спартак има 30 футболисти, включително 18 нападатели, 11 полузащитници, 17 защитници и вратари. Известно е, че трима могат да бъдат нападатели и защитници, 10 защитници и полузащитници, 6 нападатели и защитници, а 1 може да бъде нападател, защитник и халф. Вратарите са незаменими. Колко вратари има в отбора на Спартак?

Задача 5: „Магазин“

65 души са посетили магазина. Известно е, че те са закупили 35 хладилника, 36 микровълнови печки, 37 телевизора. 20 от тях са закупили и хладилник, и микровълнова печка, 19 са закупили и микровълнова печка, и телевизор, 15 са закупили хладилник и телевизор, като и трите покупки са направени от трима души. Имаше ли посетител сред тях, който не си купи нищо?

Задача 6: „Детска градина“

В детската градина се обучават 52 деца. Всеки от тях обича или торта, или сладолед, или и двете. Половината от децата харесват торта, а 20 души обичат торта и сладолед. Колко деца обичат сладолед?

Задача 7: „Студентска бригада“

В ученическия производствен екип са 86 гимназисти. 8 от тях не знаят да управляват нито трактор, нито комбайн. 54 ученици владеят добре трактора, 62 - комбайна. Колко души от този екип могат да работят и на трактор, и на комбайн?

Изследователска част

Цел: използване на метода на Ойлер от ученици от гимназията при решаване на нестандартни проблеми.

Експериментът е проведен с участието на ученици от 5-9 клас, които се интересуват от математика. Те бяха помолени да решат следните два проблема:

Шестима ученика от класа посещават музикално училище, десет се занимават с футболна секция, а други десет посещават художествено ателие. Трима от тях посещават както футболно, така и музикално училище. Колко хора има в класа?

От 10 участници (2 души от всеки паралелен клас) на експеримента само 4 души решиха първата задача, само двама решиха втората задача (ученици от 8 и 9 клас). След като им представих моята изследователска работа, в която говорих за кръгове на Ойлер, анализирах решението на няколко прости и предложени задачи с помощта на този метод, учениците можеха сами да решават прости задачи.

В края на експеримента децата получиха следната задача:

В пионерския лагер има 70 деца. От тях 27 се занимават с драматичен клуб, 32 пеят в хор, 22 се занимават със спорт. В драматичния клуб има 10 момчета от хор, 6 спортисти в хор, 8 спортисти в драматичен клуб; 3-ма състезатели посещават драматичен клуб и хор. Колко деца не пеят, не се интересуват от спорт, не участват в драматичен клуб? Колко момчета се занимават само със спорт?

От 10-те участници в експеримента всички се справиха с тази задача.

Заключение: Решаването на задачи с помощта на кръгове на Ойлер развива логическото мислене и прави възможно решаването на задачи, които могат да бъдат решени по обичайния начин само чрез съставяне на система от три уравнения с три неизвестни. Учениците от 5-7 клас не знаят как да решават системи от уравнения, но могат да решават същите задачи. Това означава, че децата трябва да знаят този метод за решаване на задачи с помощта на кръгове на Ойлер.

Приложения