Екстремуми на функция - с прости думи за комплекса. Как да намерим екстремни точки на функция

Екстремалната точка на функция е точката в областта на функцията, където стойността на функцията приема минимална или максимална стойност. Стойностите на функцията в тези точки се наричат екстремуми (минимум и максимум) на функцията.

Определение. Точка х1 функционален обхват f(х) е наречен максимална точка на функцията , ако стойността на функцията в тази точка е по-голяма от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството f(х0 ) > f(х 0 + Δ х) х1 максимум.

Определение. Точка х2 функционален обхват f(х) е наречен минимална точка на функцията, ако стойността на функцията в тази точка е по-малка от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството f(х0 ) < f(х 0 + Δ х) ). В този случай се казва, че функцията има в точката х2 минимум.

Да кажем точката х1 - максимална точка на функцията f(х) . След това в интервала до х1 функцията се увеличава, така че производната на функцията е по-голяма от нула ( f "(х) > 0 ), и в интервала след х1 функцията намалява, така че производна на функцияпо-малко от нула ( f "(х) < 0 ). Тогда в точке х1

Нека приемем също, че точката х2 - минимална точка на функцията f(х) . След това в интервала до х2 функцията е намаляваща и производната на функцията е по-малка от нула ( f "(х) < 0 ), а в интервале после х2 функцията нараства и производната на функцията е по-голяма от нула ( f "(х) > 0 ). В този случай също в точката х2 производната на функцията е нула или не съществува.

Теорема на Ферма (необходим критерий за съществуване на екстремум на функция). Ако точка х0 - екстремна точка на функцията f(х), тогава в тази точка производната на функцията е равна на нула ( f "(х) = 0 ) или не съществува.

Определение. Наричат се точките, в които производната на функцията е равна на нула или не съществува критични точки .

Пример 1Нека разгледаме функция.

В точката х= 0 производната на функцията е равна на нула, следователно точката х= 0 е критичната точка. Въпреки това, както може да се види на графиката на функцията, тя нараства в цялата област на дефиниция, така че точката х= 0 не е екстремна точка на тази функция.

По този начин условията, че производната на функция в точка е равна на нула или не съществува, са необходими условия за екстремум, но не са достатъчни, тъй като могат да бъдат дадени други примери за функции, за които тези условия са изпълнени, но функцията няма екстремум в съответната точка. Ето защо трябва да има достатъчно индикации, които позволяват да се прецени дали има екстремум в дадена критична точка и какъв – максимум или минимум.

Теорема (първият достатъчен критерий за съществуване на екстремум на функция).Критична точка х0 f(х), ако производната на функцията промени знака при преминаване през тази точка и ако знакът се промени от "плюс" на "минус", тогава максималната точка, а ако от "минус" на "плюс", тогава минималната точка .

Ако е близо до точката х0 , вляво и вдясно от нея, производната запазва знака си, това означава, че функцията или само намалява, или само нараства в някаква околност на точката х0 . В този случай в точката х0 няма екстремум.

Така, за да определите екстремалните точки на функцията, трябва да направите следното :

Намерете производната на функция.
Приравнете производната на нула и определете критичните точки.
Мислено или на хартия маркирайте критичните точки на цифровата ос и определете знаците на производната на функцията в получените интервали. Ако знакът на производната се промени от "плюс" на "минус", тогава критичната точка е максималната точка, а ако от "минус" на "плюс", тогава критичната точка е минималната точка.
Изчислете стойността на функцията в точките на екстремума.

Пример 2Намерете екстремуми на функция .

Решение. Нека намерим производната на функцията:

Приравнете производната на нула, за да намерите критичните точки:

Тъй като за всякакви стойности на "x" знаменателят не е равен на нула, тогава приравняваме числителя на нула:

Имам една критична точка х= 3 . Определяме знака на производната в интервалите, ограничени от тази точка:

в диапазона от минус безкрайност до 3 - знак минус, тоест функцията намалява,

в диапазона от 3 до плюс безкрайност - знак плюс, тоест функцията се увеличава.

Тоест точка х= 3 е минималната точка.

Намерете стойността на функцията в минималната точка:

Така се намира екстремната точка на функцията: (3; 0) и тя е минималната точка.

Теорема (вторият достатъчен критерий за съществуване на екстремум на функция).Критична точка х0 е екстремната точка на функцията f(х), ако втората производна на функцията в тази точка не е равна на нула ( f ""(х) ≠ 0 ), освен това, ако втората производна е по-голяма от нула ( f ""(х) > 0 ), тогава максималната точка и ако втората производна е по-малка от нула ( f ""(х) < 0 ), то точкой минимума.

Забележка 1. Ако в точка х0 както първата, така и втората производна изчезват, тогава в този момент е невъзможно да се прецени наличието на екстремум въз основа на втория достатъчен знак. В този случай трябва да използвате първия достатъчен критерий за екстремума на функцията.

Забележка 2. Вторият достатъчен критерий за екстремум на функция също е неприложим, когато първата производна не съществува в стационарната точка (тогава втората производна също не съществува). В този случай също е необходимо да се използва първият достатъчен критерий за екстремума на функцията.

Локалният характер на екстремумите на функцията

От горните дефиниции следва, че екстремумът на функцията има локален характер - това е най-голямата и най-малката стойност на функцията в сравнение с най-близките стойности.

Да предположим, че смятате приходите си за период от една година. Ако през май сте спечелили 45 000 рубли, а през април 42 000 рубли и през юни 39 000 рубли, тогава майската печалба е максимумът на функцията за печалба в сравнение с най-близките стойности. Но през октомври сте спечелили 71 000 рубли, през септември 75 000 рубли, а през ноември 74 000 рубли, така че приходите през октомври са минимумът на функцията за печалба в сравнение със близките стойности. И можете лесно да видите, че максимумът сред стойностите на април-май-юни е по-малък от минимума на септември-октомври-ноември.

Най-общо казано, една функция може да има няколко екстремума на интервал и може да се окаже, че всеки минимум на функцията е по-голям от всеки максимум. И така, за функцията, показана на фигурата по-горе, .

Тоест не трябва да се мисли, че максимумът и минимумът на функцията са съответно нейните максимални и минимални стойности за целия разглеждан сегмент. В точката на максимума функцията има най-голяма стойност само в сравнение с онези стойности, които има във всички точки, достатъчно близки до максималната точка, а в точката на минимум, най-малката стойност само в сравнение с тези стойности че има във всички точки достатъчно близо до минималната точка.

Следователно можем да прецизираме концепцията за екстремни точки на функция, дадена по-горе, и да наречем минималните точки локални минимални точки, а максималните точки - локални максимални точки.

Търсим заедно екстремума на функцията

Пример 3

Решение Функцията е дефинирана и непрекъсната на цялата числова ос. Негова производна също съществува на цялата числова ос. Следователно в този случай като критични точки служат само тези, при които , т.е. , откъде и . Критични точки и разделете цялата област на функцията на три интервала на монотонност: . Избираме по една контролна точка във всяка от тях и намираме знака на производната в тази точка.

За интервала референтната точка може да бъде: намираме . Като вземем точка в интервала, получаваме , И като вземем точка в интервала, имаме . И така, в интервалите и , и в интервала . Според първия достатъчен знак на екстремума, в точката няма екстремум (тъй като производната запазва знака си в интервала), а функцията има минимум в точката (тъй като производната променя знака от минус на плюс при преминаване през тази точка). Намерете съответните стойности на функцията: , и . В интервала функцията намалява, тъй като в този интервал , а в интервала нараства, тъй като в този интервал.

За да изясним конструкцията на графиката, намираме нейните точки на пресичане с координатните оси. Когато получим уравнение, чиито корени и , т.е. две точки (0; 0) и (4; 0) от графиката на функцията са намерени. Използвайки цялата получена информация, изграждаме графика (вижте в началото на примера).

Пример 4Намерете екстремума на функцията и изградете нейната графика.

Домейнът на функцията е цялата числова ос, с изключение на точката, т.е. .

За да съкратим изследването, можем да използваме факта, че тази функция е четна, тъй като . Следователно неговата графика е симетрична спрямо оста Ойи изследването може да се извърши само за интервала .

Намиране на производната и критични точки на функцията:

1) ;

2) ,

но функцията претърпява прекъсване в тази точка, така че не може да бъде точка на екстремум.

Така дадената функция има две критични точки: и . Като вземем предвид паритета на функцията, проверяваме само точката по втория достатъчен знак на екстремума. За да направим това, намираме втората производна и определете неговия знак при : получаваме . Тъй като и , тогава е минималната точка на функцията, докато .

За да получите по-пълна картина на графиката на функцията, нека разберем нейното поведение в границите на областта на дефиниция:

(тук символът показва желанието хдо нула вдясно и хостава положителен; по подобен начин означава стремеж хдо нула вляво и хостава отрицателна). По този начин, ако , тогава . След това намираме

тези. ако , тогава .

Графиката на функцията няма пресечни точки с осите. Картината е в началото на примера.

Продължаваме заедно да търсим екстремуми на функцията

Пример 8Намерете екстремума на функцията.

Решение. Намерете домейна на функцията. Тъй като неравенството трябва да е в сила, получаваме от .

Нека намерим първата производна на функцията:

Нека намерим критичните точки на функцията.

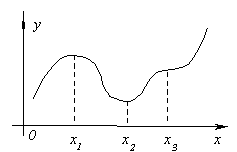
Разгледайте графиката на непрекъсната функция y=f(x)показано на фигурата.

Стойност на функцията в точка х 1 ще бъде по-голяма от стойностите на функцията във всички съседни точки както отляво, така и отдясно на х 1 . В този случай се казва, че функцията има в точката х 1 макс. В точката хФункцията 3 очевидно също има максимум. Ако разгледаме точката х 2 , то стойността на функцията в него е по-малка от всички съседни стойности. В този случай се казва, че функцията има в точката х 2 минимум. По същия начин за точката х 4 .

функция y=f(x)в точката х 0 има максимум, ако стойността на функцията в тази точка е по-голяма от нейните стойности във всички точки на някакъв интервал, съдържащ точката х 0, т.е. ако има такава близост на точката х 0, което е за всички х≠х 0 , принадлежащи към този квартал, имаме неравенството f(x)<f(x 0 ) .

функция y=f(x)То има минимумв точката х 0 , ако има такава близост на точката х 0 , това, което е за всички х≠х 0, принадлежащ на тази околия, имаме неравенството f(x)>f(x0.

Точките, в които функцията достига своя максимум и минимум, се наричат точки на екстремум, а стойностите на функцията в тези точки са екстремуми на функцията.

Нека обърнем внимание на факта, че функция, дефинирана върху сегмент, може да достигне своя максимум и минимум само в точки, съдържащи се в рамките на разглеждания сегмент.

Обърнете внимание, че ако дадена функция има максимум в точка, това не означава, че в тази точка функцията има максимална стойност в цялата област. На фигурата, обсъдена по-горе, функцията в точката х 1 има максимум, въпреки че има точки, в които стойностите на функцията са по-големи, отколкото в точката х 1 . В частност, f(х 1) < f(х 4) т.е. минимумът на функцията е по-голям от максимума. От дефиницията на максимума следва само, че това е най-голямата стойност на функцията в точки, достатъчно близки до максималната точка.

Теорема 1. (Необходимо условие за съществуването на екстремум.)Ако диференцируемата функция y=f(x)има в точката х= х 0 екстремум, тогава нейната производна в тази точка изчезва.

Доказателство. Нека, за категоричност, в точката х 0 функцията има максимум. Тогава за достатъчно малки увеличения Δ хние имаме f(x 0 + Δ х) 0 ) , т.е. Но след това

Преминавайки в тези неравенства до границата като Δ х→ 0 и като се има предвид, че производната f "(х 0) съществува и следователно границата отляво не зависи от това как Δ х→ 0, получаваме: за Δ х → 0 – 0 е"(х 0) ≥ 0 и при Δ х → 0 + 0 е"(х 0) ≤ 0. Тъй като е"(х 0) дефинира число, тогава тези две неравенства са съвместими само ако е"(х 0) = 0.

Доказаната теорема гласи, че максималните и минималните точки могат да бъдат само сред тези стойности на аргумента, за които производната е нула.

Разгледахме случая, когато една функция има производна във всички точки на определен сегмент. Какво се случва, когато производното не съществува? Разгледайте примери.

Примери.

г=|х|.
Функцията няма производна в точка х=0 (в тази точка графиката на функцията няма определен тангенс), но в тази точка функцията има минимум, тъй като г(0)=0 и за всички х≠ 0г > 0.

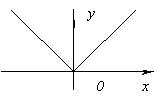
Функцията няма производна при х=0, тъй като отива в безкрайност, когато х=0. Но в този момент функцията има максимум.

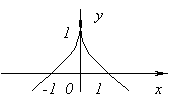
Функцията няма производна при х=0 защото при х→0. В този момент функцията няма нито максимум, нито минимум. Наистина ли, f(x)=0 и при х<0f(x)<0, а при х>0f(x)>0.

Така от дадените примери и формулираната теорема става ясно, че функцията може да има екстремум само в два случая: 1) в точките, където производната съществува и е равна на нула; 2) в точката, където производната не съществува.

Ако обаче в даден момент х 0 знаем това f"(x 0 ) =0, то от това не може да се заключи, че в точката х 0 функцията има екстремум.

Например. .

Но точка х=0 не е екстремна точка, тъй като вляво от тази точка стойностите на функцията са разположени под оста вол, и горе вдясно.

Стойностите на аргумент от домейна на функция, за които производната на функцията изчезва или не съществува, се наричат критични точки.

От казаното по-горе следва, че екстремалните точки на функцията са сред критичните точки, но не всяка критична точка е екстремна точка. Следователно, за да намерите екстремума на функцията, трябва да намерите всички критични точки на функцията и след това да изследвате всяка от тези точки поотделно за максимум и минимум. За това служи следната теорема.

Теорема 2. (Достатъчно условие за съществуване на екстремум.)Нека функцията е непрекъсната на някакъв интервал, съдържащ критичната точка х 0 и е диференцируем във всички точки от този интервал (освен, може би, самата точка х 0). Ако при преминаване отляво надясно през тази точка производната промени знака от плюс на минус, тогава в точката х = х 0 функцията има максимум. Ако при преминаване през х 0 отляво надясно, производната променя знака от минус на плюс, тогава функцията има минимум в тази точка.

По този начин, ако

Доказателство. Нека първо приемем, че при преминаване през х 0, производната променя знака от плюс на минус, т.е. за всички хблизо до точката х 0 f "(x)> 0 за х< x 0 , f"(x)< 0 за x > x 0 . Нека приложим теоремата на Лагранж към разликата f(x) - f(x 0 ) = f "(c)(x- x 0), където ° Слежи между хИ х 0 .

Позволявам х< x 0 . Тогава ° С< x 0 и f "(c)> 0. Ето защо f "(c)(x-x 0)< 0 и следователно
f(x) - f(x 0 )< 0, т.е. f(x)< f(x 0 ).

Позволявам x > x 0 . Тогава c>x 0 и е"(в)< 0. Средства f "(c)(x-x 0)< 0. Ето защо f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Така за всички стойности хдостатъчно близо до х 0 f(x)< f(x 0 ) . А това означава, че в точката х 0 функцията има максимум.

Втората част от теоремата за минимума се доказва по подобен начин.

Нека илюстрираме значението на тази теорема на фигурата. Позволявам f"(x 1 ) =0 и за всякакви х,достатъчно близо до х 1 , неравенствата

f"(x)< 0 при х< x 1 , f "(x)> 0 при x > x 1 .

След това вляво от точката х 1 функцията е нарастваща и намаляваща отдясно, следователно, когато х = х 1 функция преминава от нарастваща към намаляваща, тоест има максимум.

По същия начин може да се разгледат точките х 2 и х 3 .

Схематично всичко по-горе може да бъде изобразено на снимката:

Правилото за изследване на функцията y=f(x) за екстремум

Намерете обхвата на функция f(x).

Намерете първата производна на функция f"(x).

Определете критичните точки за това:
намерете истинските корени на уравнението f"(x)=0;

намери всички стойности хпри които производната f"(x)не съществува.

Определете знака на производната отляво и отдясно на критичната точка. Тъй като знакът на производната остава постоянен между две критични точки, достатъчно е да се определи знакът на производната във всяка точка отляво и в една точка отдясно на критичната точка.

Изчислете стойността на функцията в точките на екстремума.

Примери. Разгледайте функции за минимум и максимум.

НАЙ-ГОЛЕМИТЕ И МИНИМАЛНИТЕ ФУНКЦИОНАЛНИ СТОЙНОСТИ НА ИНТЕРСЕПТА

най-великиястойността на функция в сегмент е най-голямата от всички нейни стойности в този сегмент и най-малкое най-малката от всички негови стойности.

Помислете за функцията y=f(x)непрекъснат на сегмента [ а, б]. Както е известно, такава функция достига своите максимални и минимални стойности или на границата на сегмента, или вътре в него. Ако максималната или минималната стойност на функцията е достигната във вътрешната точка на сегмента, тогава тази стойност е максималната или минималната стойност на функцията, т.е. достига се в критични точки.

Така получаваме следното правилото за намиране на най-големите и най-малките стойности на функция в сегмента [ а, б] :

Намерете всички критични точки на функция в интервала ( а, б) и изчислете стойностите на функцията в тези точки.

Изчислете стойностите на функцията в краищата на сегмента за x=a, x=b.

От всички получени стойности изберете най-голямата и най-малката.

Нека функцията $z=f(x,y)$ е дефинирана в някаква околност на точката $(x_0,y_0)$. Казва се, че $(x_0,y_0)$ е точка на (локален) максимум, ако за всички точки $(x,y)$ в някакъв околност на $(x_0,y_0)$ неравенството $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, тогава точката $(x_0,y_0)$ се нарича (локална) минимална точка.

Високите и ниските точки често се наричат с общия термин точки на екстремум.

Ако $(x_0,y_0)$ е максимална точка, тогава стойността на функцията $f(x_0,y_0)$ в тази точка се нарича максимум на функцията $z=f(x,y)$. Съответно, стойността на функцията в минималната точка се нарича минимум на функцията $z=f(x,y)$. Минимумите и максимумите на функцията се обединяват от общ термин - екстремуми на функция.

Алгоритъм за изследване на функцията $z=f(x,y)$ за екстремум

Намерете частните производни на $\frac(\partial z)(\partial x)$ и $\frac(\partial z)(\partial y)$. Съставете и решете системата от уравнения $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 \ end(aligned) \right.$ Точките, чиито координати отговарят на определената система, се наричат стационарни.

Намерете $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ и изчислете стойността $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\ frac (\partial^2z)(\partial x\partial y) \right)^2$ във всяка стационарна точка. След това използвайте следната схема:
Ако $\Delta > 0$ и $\frac(\partial^2z)(\partial x^2) > 0$ (или $\frac(\partial^2z)(\partial y^2) > 0$), тогава в изследваната точка е минималната точка.

Ако $\Delta > 0$ и $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.

Ако $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.

Ако $\Delta = 0$, тогава нищо определено не може да се каже за наличието на екстремум; необходими са допълнителни изследвания.

Забележка (желателно за по-добро разбиране на текста): покажи\скрий

Ако $\Delta > 0$, тогава $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\ partial ^2z)(\partial x\partial y) \right)^2 > 0$. И от това следва, че $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z ) (\partial x\partial y) \right)^2 ≥ 0$. Тези. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Ако произведението на някои количества е по-голямо от нула, тогава тези количества имат еднакъв знак. Това е, например, ако $\frac(\partial^2z)(\partial x^2) > 0$, тогава $\frac(\partial^2z)(\partial y^2) > 0$. Накратко, ако $\Delta > 0$, тогава знаците на $\frac(\partial^2z)(\partial x^2)$ и $\frac(\partial^2z)(\partial y^2)$ са същото.

Пример #1

Изследвайте функцията $z=4x^2-6xy-34x+5y^2+42y+7$ за екстремум.

$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$
$$ \left \( \begin(подравнено) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(подравнено) \right. $$
Нека намалим всяко уравнение на тази система с $2$ и прехвърлим числата в дясната страна на уравненията:
$$ \left \( \begin(подравнено) & 4x-3y=17;\\ & -3x+5y=-21. \end(подравнено) \right. $$
Получихме система от линейни алгебрични уравнения. В тази ситуация ми се струва най-удобното приложение на метода на Крамър за решаване на получената система.
$$ \begin(aligned) & \Delta=\left| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \ & \Delta_x=\наляво| \begin(array) (cc) 17 & -3\\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \ & \Delta_y=\left| \begin(array) (cc) 4 & 17\\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(aligned) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$
Стойностите $x=2$, $y=-3$ са координатите на стационарната точка $(2;-3)$.
$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$
Нека изчислим стойността на $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$
Тъй като $\Delta > 0$ и $\frac(\partial^2 z)(\partial x^2) > 0$, тогава според точката $(2;-3)$ е минималната точка на функцията $ z$. Намираме минимума на функцията $z$, като заместваме координатите на точката $(2;-3)$ в дадената функция:
$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot(-3)+7=-90. $$
Отговор: $(2;-3)$ - минимална точка; $z_(мин)=-90$.

Пример #2

Изследвайте функцията $z=x^3+3xy^2-15x-12y+1$ за екстремум.

Ние ще следваме горното. Първо, нека намерим частните производни от първи ред:
$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y)=6xy-12. $$
Съставете системата от уравнения $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \ край (подравнен)\десен.$:
$$ \left \( \begin(подравнено) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(подравнено) \right. $$
Намалете първото уравнение с 3, а второто с 6.
$$ \left \( \begin(aligned) & x^2+y^2-5=0;\\ & xy-2=0. \end(aligned) \right. $$
Ако $x=0$, тогава второто уравнение ще ни доведе до противоречие: $0\cdot y-2=0$, $-2=0$. Оттук и заключението: $x\neq 0$. Тогава от второто уравнение имаме: $xy=2$, $y=\frac(2)(x)$. Като заместим $y=\frac(2)(x)$ в първото уравнение, имаме:
$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$
Имаме биквадратно уравнение. Правим замяната $t=x^2$ (имаме предвид, че $t > 0$):
$$ t^2-5t+4=0;\\ \begin(aligned) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(подравнено) $$
Ако $t=1$, тогава $x^2=1$. Следователно имаме две стойности на $x$: $x_1=1$, $x_2=-1$. Ако $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Спомняйки си, че $y=\frac(2)(x)$, получаваме:
\begin(aligned) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2)=-1. \край (подравнено)
И така, имаме четири стационарни точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Това завършва първата стъпка от алгоритъма.

Сега да преминем към алгоритъма. Нека намерим частни производни от втори ред:
$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$
Намерете $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$
Сега ще изчислим стойността на $\Delta$ във всяка от предварително намерените стационарни точки. Да започнем от точката $M_1(1;2)$. В този момент имаме: $\Delta(M_1)=36(1^2-2^2)=-108$. Тъй като $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

Нека изследваме точката $M_2(-1;-2)$. В този момент имаме: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Тъй като $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

Нека разгледаме точката $M_3(2;1)$. В този момент получаваме:
$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$
Тъй като $\Delta(M_3) > 0$ и $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, тогава според $M_3(2; 1)$ е минималната точка на функцията $z$. Намираме минимума на функцията $z$, като заместваме координатите на точката $M_3$ в дадената функция:
$$ z_(min)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$
Остава да изследваме точката $M_4(-2;-1)$. В този момент получаваме:
$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$
Тъй като $\Delta(M_4) > 0$ и $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$
Екстремалното изследване е завършено. Остава само да запиша отговора.

Отговор:

$(2;1)$ - минимална точка, $z_(min)=-27$;

$(-2;-1)$ - максимална точка, $z_(max)=29$.

Забележка

В общия случай няма нужда да изчисляваме стойността на $\Delta$, тъй като се интересуваме само от знака, а не от конкретната стойност на този параметър. Например, за пример № 2, разгледан по-горе, в точка $M_3(2;1)$ имаме $\Delta=36\cdot(2^2-1^2)$. Тук е очевидно, че $\Delta > 0$ (тъй като и двата фактора $36$ и $(2^2-1^2)$ са положителни) и е възможно да не се намери конкретна стойност на $\Delta$. Вярно е, че тази забележка е безполезна за типичните изчисления - те изискват изчисленията да бъдат приведени до число :)

Пример #3

Изследвайте функцията $z=x^4+y^4-2x^2+4xy-2y^2+3$ за екстремум.

Ще последваме. Първо, нека намерим частните производни от първи ред:
$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$
Съставете системата от уравнения $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \ край (подравнен)\десен.$:
$$ \left \( \begin(подравнено) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(подравнено) \right. $$
Нека намалим двете уравнения с $4$:
$$ \left \( \begin(подравнено) & x^3-x+y=0;\\ & y^3+x-y=0. \end(подравнено) \right. $$
Нека добавим първото уравнение към второто и изразим $y$ чрез $x$:
$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$
Замествайки $y=-x$ в първото уравнение на системата, ще имаме:
$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$
От полученото уравнение имаме: $x=0$ или $x^2-2=0$. От уравнението $x^2-2=0$ следва, че $x=-\sqrt(2)$ или $x=\sqrt(2)$. И така, намерени са три стойности на $x$, а именно: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Тъй като $y=-x$, тогава $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.

Първата стъпка от решението приключи. Имаме три стационарни точки: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .

Сега да преминем към алгоритъма. Нека намерим частни производни от втори ред:
$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$
Намерете $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$
Сега ще изчислим стойността на $\Delta$ във всяка от предварително намерените стационарни точки. Да започнем от точката $M_1(0;0)$. В този момент имаме: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Тъй като $\Delta(M_1) = 0$ са необходими допълнителни изследвания, тъй като не може да се каже нищо определено за наличието на екстремум в разглежданата точка. Нека оставим тази точка на мира за момента и да преминем към други точки.

Нека разгледаме точката $M_2(-\sqrt(2),\sqrt(2))$. В този момент получаваме:
\begin(aligned) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \край (подравнено)
Тъй като $\Delta(M_2) > 0$ и $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, тогава според $M_2(-\ sqrt(2),\sqrt(2))$ е минималната точка на функцията $z$. Намираме минимума на функцията $z$, като заместваме координатите на точката $M_2$ в дадената функция:
$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$
Подобно на предишната точка, разглеждаме точката $M_3(\sqrt(2),-\sqrt(2))$. В този момент получаваме:
\begin(aligned) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \край (подравнено)
Тъй като $\Delta(M_3) > 0$ и $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, тогава според $M_3(\sqrt (2),-\sqrt(2))$ е минималната точка на функцията $z$. Намираме минимума на функцията $z$, като заместваме координатите на точката $M_3$ в дадената функция:
$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2 ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$
Време е да се върнем към точката $M_1(0;0)$, където $\Delta(M_1) = 0$. Необходими са допълнителни изследвания. Тази уклончива фраза означава "правете каквото искате" :). Няма общ начин за разрешаване на подобни ситуации - и това е разбираемо. Ако имаше такъв метод, той отдавна щеше да е влязъл във всички учебници. Междувременно трябва да търсим специален подход към всяка точка, в която $\Delta = 0$. Е, нека проучим поведението на функцията в близост до точката $M_1(0;0)$. Веднага отбелязваме, че $z(M_1)=z(0;0)=3$. Да приемем, че $M_1(0;0)$ е минимална точка. Тогава за всяка точка $M$ от някаква околност на точката $M_1(0;0)$ получаваме $z(M) > z(M_1) $, т.е. $z(M) > 3$. Ами ако някой квартал съдържа точки, където $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Разгледайте точки, за които $y=0$, т.е. точки от формата $(x,0)$. В тези точки функцията $z$ ще приеме следните стойности:
$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$
Във всички достатъчно малки квартали $M_1(0;0)$ имаме $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Но може би точката $M_1(0;0)$ е максимална точка? Ако това е така, тогава за всяка точка $M$ от някаква околност на точката $M_1(0;0)$ получаваме $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3$? Тогава определено няма да има максимум в точката $M_1$.

Разгледайте точки, за които $y=x$, т.е. точки от формата $(x,x)$. В тези точки функцията $z$ ще приеме следните стойности:
$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$
Тъй като във всяка околност на точката $M_1(0;0)$ имаме $2x^4 > 0$, тогава $2x^4+3 > 3$. Заключение: всяка околност на точката $M_1(0;0)$ съдържа точки, където $z > 3$, така че точката $M_1(0;0)$ не може да бъде максимална точка.

Точката $M_1(0;0)$ не е нито максимум, нито минимум. Заключение: $M_1$ изобщо не е крайна точка.

Отговор: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ - минимални точки на функцията $z$. И в двете точки $z_(min)=-5$.

Какво е екстремум на функция и какво е необходимото условие за екстремум?

Екстремумът на функция е максимумът и минимумът на функцията.

Необходимото условие за максимума и минимума (екстремума) на функцията е следното: ако функцията f(x) има екстремум в точката x = a, тогава в тази точка производната е или нула, или безкрайна, или не съществува.

Това условие е необходимо, но не достатъчно. Производната в точката x = a може да изчезне, да отиде до безкрайност или да не съществува, без функцията да има екстремум в тази точка.

Кое е достатъчното условие за екстремума на функцията (максимум или минимум)?

Първо условие:

Ако, в достатъчна близост до точката x = a, производната f?(x) е положителна отляво на a и отрицателна отдясно на a, тогава в самата точка x = a функцията f(x) има максимум

Ако в достатъчна близост до точката x = a, производната f?(x) е отрицателна отляво на a и положителна отдясно на a, тогава в самата точка x = a функцията f(x) има минимумпри условие, че функцията f(x) тук е непрекъсната.

Вместо това можете да използвате второто достатъчно условие за екстремума на функцията:

Нека в точката x = и първата производна f?(x) изчезва; ако втората производна f??(а) е отрицателна, тогава функцията f(x) има максимум в точката x = a, ако е положителна, тогава минимум.

Каква е критичната точка на функция и как да я намерим?

Това е стойността на аргумента на функцията, при която функцията има екстремум (т.е. максимум или минимум). За да го намерите, трябва намерете производнатафункция f?(x) и приравнявайки я на нула, реши уравнението f?(x) = 0. Корените на това уравнение, както и онези точки, в които не съществува производната на тази функция, са критични точки, т.е. стойностите на аргумента, при които може да има екстремум . Те могат лесно да бъдат идентифицирани, като се вгледат производна графика: интересуваме се от тези стойности на аргумента, при които графиката на функцията пресича абсцисната ос (ос Ox) и тези, при които графиката претърпява прекъсвания.

Например, да намерим екстремум на параболата.

Функция y(x) = 3x2 + 2x - 50.

Производна на функция: y?(x) = 6x + 2

Решаваме уравнението: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

В този случай критичната точка е x0=-1/3. Именно за тази стойност на аргумента функцията има екстремум. Да го вземеш намирам, заместваме намереното число в израза за функцията вместо "x":

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Как да определим максимума и минимума на една функция, т.е. неговите най-големи и най-малки стойности?

Ако знакът на производната се промени от "плюс" на "минус" при преминаване през критичната точка x0, тогава x0 е максимална точка; ако знакът на производната се промени от минус на плюс, тогава x0 е минимална точка; ако знакът не се променя, то в точката x0 няма нито максимум, нито минимум.

За разглеждания пример:

Вземаме произволна стойност на аргумента вляво от критичната точка: x = -1

Когато x = -1, стойността на производната ще бъде y? (-1) = 6 * (-1) + 2 = -6 + 2 = -4 (т.е. знакът минус).

Сега вземаме произволна стойност на аргумента вдясно от критичната точка: x = 1

За x = 1, стойността на производната ще бъде y(1) = 6 * 1 + 2 = 6 + 2 = 8 (т.е. знакът плюс).

Както можете да видите, при преминаване през критичната точка производната промени знака от минус на плюс. Това означава, че при критичната стойност на x0 имаме минимална точка.

Най-голямата и най-малката стойност на функцията на интервала(на сегмента) се намират по същата процедура, само като се вземе предвид фактът, че може би не всички критични точки ще лежат в определения интервал. Онези критични точки, които са извън интервала, трябва да бъдат изключени от разглеждане. Ако има само една критична точка вътре в интервала, тя ще има или максимум, или минимум. В този случай, за да определим най-големите и най-малките стойности на функцията, ние също вземаме предвид стойностите на функцията в края на интервала.

Например, нека намерим най-голямата и най-малката стойност на функцията

y (x) \u003d 3 sin (x) - 0,5x

на интервали:

Така че производната на функцията е

y?(x) = 3cos(x) - 0,5

Решаваме уравнението 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

x \u003d ± arccos (0,16667) + 2πk.

Намираме критични точки на интервала [-9; 9]:

x \u003d arccos (0,16667) - 2π * 2 \u003d -11,163 (не е включено в интервала)

x \u003d -arccos (0,16667) - 2π * 1 \u003d -7,687

x \u003d arccos (0,16667) - 2π * 1 \u003d -4,88

x \u003d -arccos (0,16667) + 2π * 0 \u003d -1,403

x \u003d arccos (0,16667) + 2π * 0 \u003d 1,403

x \u003d -arccos (0,16667) + 2π * 1 \u003d 4,88

x \u003d arccos (0,16667) + 2π * 1 \u003d 7,687

x \u003d -arccos (0,16667) + 2π * 2 \u003d 11,163 (не е включено в интервала)

Намираме стойностите на функцията при критични стойности на аргумента:

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

Вижда се, че на интервала [-9; 9] функцията има най-голяма стойност при x = -4,88:

x = -4,88, y = 5,398,

и най-малката - при x = 4,88:

x = 4,88, y = -5,398.

На интервала [-6; -3] имаме само една критична точка: x = -4,88. Стойността на функцията при x = -4,88 е y = 5,398.

Намираме стойността на функцията в краищата на интервала:

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

На интервала [-6; -3] имаме най-голямата стойност на функцията

y = 5,398 при x = -4,88

най-малката стойност е

y = 1,077 при x = -3

Как да намерим точките на инфлексия на графика на функция и да определим страните на изпъкналост и вдлъбнатост?

За да намерите всички точки на огъване на линията y \u003d f (x), трябва да намерите второто производно, да го приравните към нула (решете уравнението) и да тествате всички тези стойности на x, за които второто производно е нула , безкрайно или не съществува. Ако при преминаване през една от тези стойности втората производна промени знака, тогава графиката на функцията има инфлексия в тази точка. Ако не се променя, значи няма инфлексия.

Корените на уравнението f ? (x) = 0, както и възможните точки на прекъсване на функцията и втората производна, разделят областта на функцията на няколко интервала. Изпъкналостта на всеки техен интервал се определя от знака на втората производна. Ако втората производна в точка от изследвания интервал е положителна, тогава линията y = f(x) тук е вдлъбната нагоре, а ако е отрицателна, тогава надолу.

Как да намерим екстремуми на функция на две променливи?

За да намерите екстремумите на функцията f(x, y), диференцируема в областта на нейното присвояване, трябва:

1) намерете критичните точки и за това решете системата от уравнения

fx? (x,y) = 0, fy? (x,y) = 0

2) за всяка критична точка P0(a;b), проучете дали знакът на разликата остава непроменен

за всички точки (x; y), достатъчно близки до P0. Ако разликата запазва положителен знак, тогава в точката P0 имаме минимум, ако е отрицателен, тогава максимум. Ако разликата не запазва знака си, то в точка Р0 няма екстремум.

По същия начин екстремумите на функцията се определят за по-голям брой аргументи.

Кой е официалният сайт на певицата Мика Нютън и нейната група
Ново украинско чудо - Мика Нютон! Това е група от 5 души, които свирят поп-рок, наслаждават се на живота, дават драйв и гледат позитивно на този живот. Момчетата се събраха в Киев, където живеят в момента. Момчетата не са съгласни със стандартните основи в музиката и живота, откриват новото си звучене и нарушават всякакви стандарти. Ръководител екип -
Как да конвертирате милилитри в кубични метри
Основната единица за дължина в системата SI е метърът. Въз основа на това основната единица за обем трябва да се счита за кубичен метър или, както се нарича още, кубичен метър или кубичен метър. Това е обемът на куб с ръбове, равни на един метър. На практика обаче не винаги е удобно обемът да се изрази в кубични метри. Например, удобно е да изразите обема на помещението в кубични метри: умножете дължината на
Какво е калоричното съдържание на грис
Калорична храна, таблица с калории. Човешката енергийна нужда се измерва в килокалории (kcal). Думата "калория" идва от латински език и означава "топлина". Във физиката енергията се измерва в калории. Една килокалория е количеството енергия
Кои са етапите на развитие на реализма в литературата
Реализмът (лат. реален, реален) е течение в литературата и изкуството, което има за цел вярно възпроизвеждане на действителността в нейните характерни черти. Общи черти: Художествено изобразяване на живота в образи, съответстващи на същността на явленията от самия живот. Реалността е средство за познание на човека за себе си и света около него. Въвеждане
Каква е връзката между беркелий и 117-ия елемент от периодичната таблица
Berkelium, Berkelium, Bk - 97-ият елемент от периодичната таблица. Открит през декември 1949 г. от Томпсън, Гиорсо и Сиборг в Калифорнийския университет в Бъркли. Чрез облъчване на 241Am с алфа частици те получават изотопа на Berkelium 243Bk. Тъй като Bk е структурно подобен на тербия, който носи името си от г-н Ytterby в
С какво е известен Ярослав Мъдри?
Ярослав Мъдри (980-1054), велик княз на Киев (1019). Син на Владимир I Святославович. Той изгонва Святополк I Проклети, воюва с брат му Мстислав, разделя с него държавата (1025 г.), а през 1035 г. отново я обединява. Редица победи осигуриха южните и западните граници на Русия. Установява династични връзки с много страни на ев
Как възникна традицията да се вика "Горчиво!"
Преди много време имаше традиция по време на сватбения празник да се вика: "Горчиво!", Принуждавайки младоженците да станат от местата си и да се целунат. Днес мнозина дори не предполагат какво е значението на тази церемония.В старите времена на сватби викаха "Горчиво!", Давайки да се разбере, че виното в купите се твърди, че е неподсладено. А
Какви са симптомите на ларингит
Ларингитът (от др. гръцки λ?ρυγξ - ларинкс) е възпаление на ларинкса, обикновено свързано с настинка или инфекциозни заболявания като морбили, скарлатина, магарешка кашлица. Развитието на заболяването се улеснява от хипотермия, дишане през устата, прах
Дали се определят род и склонение за съществителни, които имат само форма за множествено число
Числото е граматична категория, която изразява количествените характеристики на обекта. 1. Повечето съществителни се изменят по числа, т.е. Има две форми – единствено и множествено число. В единствено число съществителното обозначава един обект, в множествено число няколко обекта:
С какво е полезна руската каша
Овесена каша от елда Елдата е специална зърнена култура. От него се оказва може би една от най-полезните зърнени храни. Нищо чудно, че го наричаме първия. Елдата съдържа фибри, цял набор от витамини - Е, РР, В1, В2, фолиева и органична киселини, както и голям процент нишесте, което допринася за поглъщането на правилното количество нео

Интерактивна карта на град Архангелск можете да видите на следните сайтове: Map1 - сателитна и стандартна карта Map2 - стандартна карта (1:350 000); Map3 - има имена на улици, номера на къщи, възможно е търсене по улица; Map4 - карта с имена на улици; Map5 - интерактивна карта на града; Map6 - интерактивна карта на града.

Точката x 0 се нарича максимална точка(минимум) на функцията f(х), ако в някаква околност на точката x 0 е изпълнено неравенството f(х) ≤f(х 0) (f(х) ≥f(х 0)).
Стойността на функцията в тази точка се извиква съответно максимумили минимумфункции. Максимумът и минимумът на функцията се комбинират с общо име екстремумфункции.
Екстремумът на функция в този смисъл често се нарича локален екстремум, подчертавайки факта, че това понятие се свързва само с достатъчно малка околност на точката x 0 . В един и същ интервал една функция може да има няколко локални максимума и минимума, които не е задължително да съвпадат с глобален максимумили минимум(т.е. най-голямата или най-малката стойност на функцията за целия интервал).
Необходимо условие за екстремум. За да има една функция екстремум в дадена точка, е необходимо нейната производна в тази точка да е равна на нула или да не съществува.
За диференцируемите функции това условие следва от теоремата на Ферма. В допълнение, той предвижда случая, когато функцията има екстремум в точка, в която не е диференцируема.
Точките, в които е изпълнено необходимото екстремално условие, се наричат критичен(или стационаренза диференцируема функция). Тези точки трябва да са в обхвата на функцията.
По този начин, ако има екстремум във всяка точка, тогава тази точка е критична (условие на необходимост). Обърнете внимание, че обратното не е вярно. Критичната точка не е непременно екстремна точка, т.е. посоченото условие не е достатъчно.
Първото достатъчно условие за екстремум. Ако при преминаване през определена точка производната на диференцируема функция промени знака си от плюс на минус, тогава това е максималната точка на функцията, а ако от минус на плюс, тогава минималната точка.
Доказателството за това условие следва от условието за достатъчна монотонност (когато знакът на производната се промени, преходът настъпва или от нарастване на функцията към намаляване, или от намаляване към нарастване).
Второто достатъчно условие за екстремум. Ако първата производна на два пъти диференцируема функция е нула в дадена точка, а втората производна е положителна в тази точка, тогава това е минималната точка на функцията; и ако втората производна е отрицателна, тогава това е максималната точка.
Доказателството на това условие също се основава на условието за достатъчна монотонност. Наистина, ако втората производна е положителна, тогава първата производна е нарастваща функция. Тъй като в разглежданата точка е равна на нула, следователно при преминаване през нея променя знака от минус на плюс, което ни връща към първото достатъчно условие за локален минимум. По същия начин, ако втората производна е отрицателна, тогава първата намалява и променя знака от плюс на минус, което е достатъчно условие за локален максимум.
Изследване на функция до екстремумв съответствие с формулираните теореми включва следните стъпки:
1. Намерете първата производна на функцията f`(x).
2. Проверете изпълнението на необходимото екстремално условие, т.е. намиране на критични точки на функцията f(x), при които производната f`(x) = 0 или не съществува.
3. Проверете изпълнението на достатъчното екстремално условие, т.е. или изследвайте знака на производната отляво и отдясно на всяка критична точка, или намерете втората производна f``(x) и определете нейния знак във всяка критична точка. Направете заключение за наличието на екстремуми на функцията.
4. Намерете екстремуми (крайни стойности) на функцията.
Намиране на глобалния максимум и минимум на функцияна определен интервал също е от голямо практическо значение. Решението на този проблем на сегмент се основава на теоремата на Weierstrass, според която непрекъсната функция приема своите максимални и минимални стойности на сегмент. Те могат да бъдат постигнати както в екстремни точки, така и в краищата на сегмента. Следователно решението включва следните стъпки:
1. Намерете производната на функцията f`(x).
2. Намерете критичните точки на функцията f(x), в които производната f`(x) = 0 или не съществува.
3. Намерете стойностите на функцията в критичните точки и в краищата на сегмента и изберете най-голямата и най-малката от тях.