Линейна зависимост на два вектора. Линейно зависими и линейно независими вектори

За да се провери дали една система от вектори е линейно зависима, е необходимо да се състави линейна комбинация от тези вектори и да се провери дали тя може да бъде нула, ако поне един коефициент е нула.

Случай 1. Системата от вектори е дадена от вектори

Правим линейна комбинация

Получихме хомогенна система от уравнения. Ако има ненулево решение, тогава детерминантата трябва да е равна на нула. Нека направим детерминанта и да намерим нейната стойност.

Детерминантата е нула, следователно векторите са линейно зависими.

Случай 2. Системата от вектори е дадена от аналитични функции:

а)
, ако идентичността е вярна, тогава системата е линейно зависима.

Нека направим линейна комбинация.

Необходимо е да се провери дали има такива a, b, c (поне един от които не е равен на нула), за които дадения израз е равен на нула.

Записваме хиперболичните функции

,
, тогава

тогава линейната комбинация от вектори ще приеме формата:

Където
, вземете, например, тогава линейната комбинация е равна на нула, следователно системата е линейно зависима.

Отговор: Системата е линейно зависима.

б)
, съставяме линейна комбинация

Линейна комбинация от вектори трябва да бъде нула за всякакви стойности на x.

Да проверим за специални случаи.

Линейна комбинация от вектори е нула само ако всички коефициенти са нула.

Следователно системата е линейно независима.

Отговор: Системата е линейно независима.

5.3. Намерете някакъв базис и определете размерността на линейното пространство на решенията.

Нека формираме разширена матрица и я доведем до формата на трапец, използвайки метода на Гаус.

За да получим някаква основа, заместваме произволни стойности:

Вземете останалите координати

Отговор:

5.4. Намерете координатите на вектора X в базиса, ако е даден в базиса.

Намирането на координатите на вектора в новата основа се свежда до решаване на системата от уравнения

Метод 1. Намиране с помощта на матрицата на прехода

Съставете матрицата на прехода

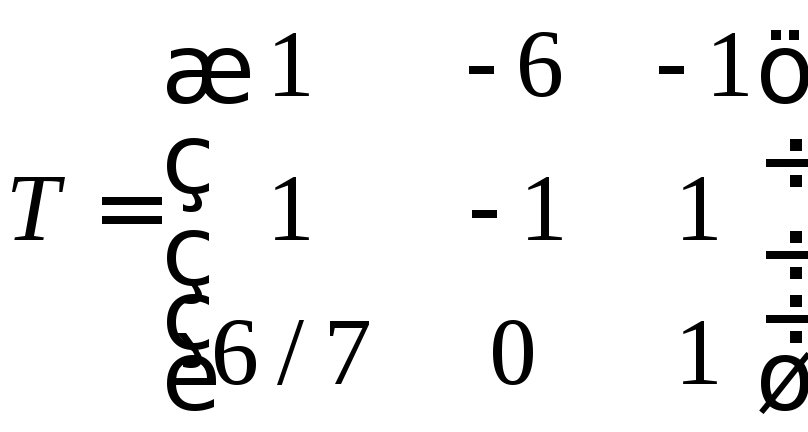
Нека намерим вектора в новата основа по формулата

Намерете обратната матрица и направете умножението

,

Метод 2. Намиране чрез съставяне на система от уравнения.

Съставете базисните вектори от коефициентите на базиса

,
,

Намирането на вектор в нова основа има формата

, където дтова е даден вектор х.

Полученото уравнение може да бъде решено по всякакъв начин, отговорът ще бъде същият.

Отговор: вектор в нова база
.

5.5. Нека x = (х 1 , х 2 , х 3 ) . Линейни ли са следните трансформации.

Нека съставим матрици от линейни оператори от коефициентите на дадени вектори.

Нека проверим свойството на линейните операции за всяка матрица на линеен оператор.

Лявата страна се намира чрез умножение на матрицата НОна вектор

Намираме дясната страна, като умножим дадения вектор по скалар
.

Виждаме това
така че трансформацията не е линейна.

Нека проверим други вектори.

, трансформацията не е линейна.

, трансформацията е линейна.

Отговор: о- не линейна трансформация, Vx- не линейни Cx- линеен.

Забележка.Можете да изпълните тази задача много по-лесно, като внимателно разгледате дадените вектори. AT овиждаме, че има термини, които не съдържат елементи х, които не могат да бъдат получени в резултат на линейна операция. AT Vxима елемент хна трета степен, което също не можеше да се получи чрез умножение по вектор х.

5.6. дадени х = { х 1 , х 2 , х 3 } , брадва = { х 2 – х 3 , х 1 , х 1 + х 3 } , bx = { х 2 , 2 х 3 , х 1 } . Изпълнете дадената операция: ( А ( б – А )) х .

Нека напишем матриците на линейните оператори.

Нека извършим операция върху матрици

Когато умножим получената матрица по X, получаваме

Отговор:

Задача 1.Разберете дали системата от вектори е линейно независима. Системата от вектори ще бъде определена от матрицата на системата, чиито колони се състоят от координатите на векторите.

.

Решение.Нека линейната комбинация е равно на нула. Записвайки това равенство в координати, получаваме следната система от уравнения:

.

Такава система от уравнения се нарича триъгълна. Тя има единственото решение. . Оттук и векторите са линейно независими.

Задача 2.Разберете дали системата от вектори е линейно независима.

.

Решение.Вектори са линейно независими (вижте задача 1). Нека докажем, че векторът е линейна комбинация от вектори . Коефициенти на векторно разширение се определят от системата от уравнения

.

Тази система, подобно на триъгълната, има уникално решение.

Следователно системата от вектори линейно зависими.

Коментирайте. Матрици като в задача 1 се наричат триъгълна , а в задача 2 – стъпаловидно триъгълно . Въпросът за линейната зависимост на система от вектори се решава лесно, ако матрицата, съставена от координатите на тези вектори, е стъпаловидно триъгълна. Ако матрицата не специален вид, след което използвате елементарни низови трансформации , запазвайки линейните връзки между колоните, тя може да бъде намалена до стъпаловидна триъгълна форма.

Елементарни трансформациилинииматрици (EPS) се наричат ​​следните операции върху матрицата:

1) пермутация на линии;

2) умножаване на низ с различно от нула число;

3) добавяне към низа на друг низ, умножен по произволно число.

Задача 3.Намерете максималната линейно независима подсистема и изчислете ранга на системата от вектори

.

Решение.Нека намалим матрицата на системата с помощта на EPS до стъпаловидна триъгълна форма. За да се обясни процедурата, редът с номера на матрицата, която трябва да се трансформира, ще бъде обозначен със символа . Колоната след стрелката показва действията, които трябва да се извършат върху редовете на преобразуваната матрица, за да се получат редовете на новата матрица.

.

Очевидно първите две колони на получената матрица са линейно независими, третата колона е тяхната линейна комбинация, а четвъртата не зависи от първите две. Вектори се наричат ​​основни. Те формират максимално линейно независимата подсистема на системата , а рангът на системата е три.

Основа, координати

Задача 4.Намерете основата и координатите на векторите в тази основа върху множеството геометрични вектори, чиито координати отговарят на условието .

Решение. Множеството е равнина, минаваща през началото. Произволен базис на равнината се състои от два неколинеарни вектора. Координатите на векторите в избрания базис се определят чрез решаване на съответната система от линейни уравнения.

Има друг начин за решаване на този проблем, когато можете да намерите основата по координати.

Координати пространствата не са координати в равнината, тъй като са свързани с релацията , тоест не са независими. Независимите променливи и (те се наричат ​​свободни) еднозначно определят вектора на равнината и следователно могат да бъдат избрани като координати в . След това основата се състои от вектори, лежащи в и съответстващи на набори от свободни променливи и , това е .

Задача 5.Намерете основата и координатите на векторите в тази база върху множеството от всички вектори в пространството , чиито нечетни координати са равни една на друга.

Решение. Избираме, както в предишната задача, координати в пространството.

защото , след това свободните променливи уникално дефинират вектор от и следователно са координати. Съответният базис се състои от вектори.

Задача 6.Намерете основата и координатите на векторите в тази основа върху множеството от всички матрици на формата , където са произволни числа.

Решение. Всяка матрица от може да бъде уникално представена като:

Тази връзка е разширение на вектора от по отношение на основата
с координати .

Задача 7.Намерете размерността и основата на линейния обхват на система от вектори

.

Решение.Използвайки EPS, ние трансформираме матрицата от координатите на системните вектори в стъпаловидно-триъгълна форма.

.

колони на последната матрица са линейно независими, а колоните се изразяват линейно чрез тях. Оттук и векторите формират основата , и .

Коментирайте. Основа в избран нееднозначно. Например вектори също формират основата .

а 1 = { 3, 5, 1 , 4 }, а 2 = { –2, 1, -5 , -7 }, а 3 = { -1, –2, 0, –1 }.

Решение.Търсят общо решениесистеми от уравнения

а 1 х 1 + а 2 х 2 + а 3 х 3 = Θ

Метод на Гаус. За да направим това, записваме тази хомогенна система в координати:

Системна матрица

Разрешената система изглежда така: (r A = 2, н= 3). Системата е последователна и недефинирана. Неговото общо решение ( х 2 – свободна променлива): х 3 = 13х 2 ; 3х 1 – 2х 2 – 13х 2 = 0 => х 1 = 5х 2 => хо = . Наличието на ненулево частно решение, например, показва, че векторите а 1 , а 2 , а 3 линейно зависими.

Пример 2

Разберете дали е така тази системавектори, линейно зависими или линейно независими:

1. а 1 = { -20, -15, - 4 }, а 2 = { –7, -2, -4 }, а 3 = { 3, –1, –2 }.

Решение.Разгледайте хомогенната система от уравнения а 1 х 1 + а 2 х 2 + а 3 х 3 = Θ

или разширено (по координати)

Системата е хомогенна. Ако не е изродено, то има уникално решение. Кога хомогенна системае нулевото (тривиално) решение. Следователно в този случай системата от вектори е независима. Ако системата е изродена, тогава тя има ненулеви решения и следователно е зависима.

Проверка на системата за израждане:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Системата е неизродена и следователно векторите а 1 , а 2 , а 3 са линейно независими.

Задачи.Разберете дали дадената система от вектори е линейно зависима или линейно независима:

1. а 1 = { -4, 2, 8 }, а 2 = { 14, -7, -28 }.

2. а 1 = { 2, -1, 3, 5 }, а 2 = { 6, -3, 3, 15 }.

3. а 1 = { -7, 5, 19 }, а 2 = { -5, 7 , -7 }, а 3 = { -8, 7, 14 }.

4. а 1 = { 1, 2, -2 }, а 2 = { 0, -1, 4 }, а 3 = { 2, -3, 3 }.

5. а 1 = { 1, 8 , -1 }, а 2 = { -2, 3, 3 }, а 3 = { 4, -11, 9 }.

6. а 1 = { 1, 2 , 3 }, а 2 = { 2, -1 , 1 }, а 3 = { 1, 3, 4 }.

7. а 1 = {0, 1, 1 , 0}, а 2 = {1, 1 , 3, 1}, а 3 = {1, 3, 5, 1}, а 4 = {0, 1, 1, -2}.

8. а 1 = {-1, 7, 1 , -2}, а 2 = {2, 3 , 2, 1}, а 3 = {4, 4, 4, -3}, а 4 = {1, 6, -11, 1}.

9. Докажете, че система от вектори ще бъде линейно зависима, ако съдържа:

а) два равни вектора;

б) два пропорционални вектора.

Вектори, техните свойства и действия с тях

Вектори, действия с вектори, линейно векторно пространство.

Векторите са подредена колекция от краен брой реални числа.

Действия: 1. Умножаване на вектор по число: ламбда * вектор x \u003d (ламбда * x 1, ламбда * x 2 ... ламбда * x n). (3.4, 0. 7) * 3 \u003d (9, 12,0.21 )

2. Добавяне на вектори (те принадлежат към едно и също векторно пространство) вектор x + вектор y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Вектор 0=(0,0…0)---n E n – n-мерен (линейно пространство) вектор x + вектор 0 = вектор x

Теорема. За да бъде линейно зависима система от n вектора в n-мерно линейно пространство, е необходимо и достатъчно един от векторите да бъде линейна комбинация от останалите.

Теорема. Всеки набор от n+ 1-ви вектор на n-мерно линейно пространство yavl. линейно зависими.

Събиране на вектори, умножение на вектори с числа. Изваждане на вектори.

Сумата от два вектора е векторът, насочен от началото на вектора към края на вектора, при условие че началото съвпада с края на вектора. Ако векторите са дадени чрез техните разширения по отношение на базисни вектори, тогава добавянето на векторите добавя съответните им координати.

Нека разгледаме това на примера на декартова координатна система. Позволявам

Нека покажем това

Фигура 3 показва това

Количеството на всяка крайно числовекторите могат да бъдат намерени с помощта на правилото на многоъгълника (фиг. 4): за да се изгради сумата от краен брой вектори, достатъчно е да се комбинира началото на всеки следващ вектор с края на предишния и да се изгради вектор, свързващ началото на първия вектор с края на последния.

Свойства на операцията за събиране на вектори:

В тези изрази m, n са числа.

Разликата на векторите се нарича вектор.Вторият член е вектор, противоположен на вектора по посока, но равен на него по дължина.

Така операцията за векторно изваждане се заменя с операцията за събиране

Векторът, чието начало е в началото на координатите, а краят в точката A (x1, y1, z1), се нарича радиус вектор на точка A и се обозначава или просто. Тъй като неговите координати съвпадат с координатите на точка А, неговото разлагане по вектори има формата

Вектор, започващ в точка A(x1, y1, z1) и завършващ в точка B(x2, y2, z2), може да бъде записан като

където r 2 е радиус векторът на точка B; r 1 - радиус вектор на точка А.

Следователно, разширяването на вектора по отношение на orts има формата

Дължината му е равна на разстоянието между точките А и В

УМНОЖЕНИЕ

Така че в случай проблем със самолетапроизведението на вектор от a = (ax; ay) и число b се намира по формулата

a b = (ax b; ay b)

Пример 1. Намерете произведението на вектора a = (1; 2) по 3.

3 a = (3 1; 3 2) = (3; 6)

Така че в случай пространствен проблемпроизведението на вектора a = (ax; ay; az) и числото b се намира по формулата

a b = (ax b; ay b; az b)

Пример 1. Намерете произведението на вектора a = (1; 2; -5) по 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Точково произведение на вектори и където е ъгълът между векторите и ; ако едно от двете, тогава

От дефиницията на скаларното произведение следва, че

където например е стойността на проекцията на вектора върху посоката на вектора .

Скаларен квадрат на вектор:

Свойства на точков продукт:

Точково произведение в координати

Ако тогава

Ъгъл между векторите

Ъгъл между векторите - ъгълът между посоките на тези вектори (най-малък ъгъл).

Векторно произведение (Векторното произведение на два вектора.)-това е псевдовектор, перпендикулярна на равнината, изградена от два фактора, която е резултат от двоичната операция „векторно умножение“ върху вектори в тримерното евклидово пространство. Продуктът не е нито комутативен, нито асоциативен (той е антикомутативен) и е различен от точковия продукт на векторите. В много инженерни и физични задачи е необходимо да можете да построите вектор, перпендикулярен на два съществуващи - векторното произведение предоставя тази възможност. Кръстосаното произведение е полезно за "измерване" на перпендикулярността на векторите - дължината на кръстосаното произведение на два вектора е равна на произведението на дължините им, ако са перпендикулярни, и намалява до нула, ако векторите са успоредни или антипаралелни.

Векторният продукт се дефинира само в триизмерни и седемизмерни пространства. Резултатът от векторното произведение, подобно на скаларното произведение, зависи от метриката на евклидовото пространство.

За разлика от формулата за изчисляване на точковото произведение от координатите на векторите в тримерна правоъгълна координатна система, формулата за кръстосаното произведение зависи от ориентацията правоъгълна системакоординати или, с други думи, неговата "хиралност"

Колинеарност на вектори.

Два ненулеви (не равни на 0) вектора се наричат ​​колинеарни, ако лежат на успоредни прави или на една права. Допускаме, но не препоръчваме, синоним - "паралелни" вектори. Колинеарни векторимогат да бъдат насочени в същата посока („сънасочени“) или противоположно насочени (в последен случайте понякога се наричат ​​"антиколинеарни" или "антипаралелни").

Смесено произведение на вектори ( а,б,в)- скаларно произведение на вектор a и векторно произведение на вектори b и c:

(a,b,c)=a ⋅(b×c)

понякога наричан троен скаларно произведениевектори, очевидно поради факта, че резултатът е скалар (по-точно псевдоскалар).

геометричен смисъл: Модулът на смесения продукт е числено равен на обема на паралелепипеда, образуван от векторите (a,b,c) .

Имоти

Смесеният продукт е косо симетричен по отношение на всички свои аргументи: т.е. д. пермутация на всеки два фактора променя знака на произведението. От това следва, че смесеният продукт вдясно Декартова системакоординати (в ортонормална база) е равна на детерминантата на матрица, съставена от вектори и:

Смесеният продукт в лявата декартова координатна система (в ортонормална основа) е равен на детерминантата на матрица, съставена от вектори и взета със знак минус:

По-специално,

Ако всеки два вектора са успоредни, тогава с всеки трети вектор те образуват смесен продукт, равен на нула.

Ако три вектора са линейно зависими (т.е. компланарни, лежат в една и съща равнина), тогава техният смесен продукт е нула.

Геометричен смисъл - Смесен продукт от абсолютна стойносте равен на обема на паралелепипеда (виж фигурата), образуван от векторите и; знакът зависи от това дали тази тройка вектори е дясна или лява.

Компланарност на вектори.

Три вектора (или Повече ▼) се наричат ​​копланарни, ако те, като се свеждат до общо начало, лежат в една и съща равнина

Свойства на компланарност

Ако поне един от три вектора- нула, тогава трите вектора също се считат за компланарни.

Тройка вектори, съдържаща двойка колинеарни вектори, е компланарна.

Смесено произведение на копланарни вектори. Това е критерий за копланарност на три вектора.

Копланарните вектори са линейно зависими. Това също е критерий за копланарност.

В тримерното пространство 3 некомпланарни вектора образуват основа

Линейно зависими и линейно независими вектори.

Линейно зависими и независими системи от вектори.Определение. Системата от вектори се нарича линейно зависими, ако има поне една нетривиална линейна комбинация от тези вектори, равна на нулевия вектор. В противен случай, т.е. ако само тривиална линейна комбинация от дадени вектори е равна на нулевия вектор, векторите се извикват линейно независими.

Теорема (критерий за линейна зависимост). За да бъде система от вектори в линейно пространство линейно зависима, е необходимо и достатъчно поне един от тези вектори да бъде линейна комбинация от останалите.

1) Ако сред векторите има поне един нулев вектор, тогава цялата система от вектори е линейно зависима.

Наистина, ако, например, , тогава, ако приемем, имаме нетривиална линейна комбинация .▲

2) Ако някои от векторите образуват линейно зависима система, то цялата система е линейно зависима.

Наистина, нека векторите , , са линейно зависими. Следователно съществува нетривиална линейна комбинация, равна на нулевия вектор. Но тогава, ако приемем , ние също получаваме нетривиална линейна комбинация, равна на нулевия вектор.

2. Основание и измерение. Определение. Система от линейно независими вектори векторно пространствоНаречен базатова пространство, ако всеки вектор от може да бъде представен като линейна комбинация от векторите на тази система, т.е. за всеки вектор има реални числа такова, че равенството е в сила.Това равенство се нарича векторно разлаганеспоред основата и числата Наречен векторни координати спрямо основата(или в основата) .

Теорема (за уникалността на разширението по отношение на основата). Всеки пространствен вектор може да бъде разширен по отношение на основата по уникален начин, т.е. координати на всеки вектор в основата се определят еднозначно.

Системата от вектори се нарича линейно зависими, ако има такива числа, сред които поне едно е различно от нула, че равенството https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src =" >.

Ако това равенство е в сила само ако всички , тогава системата от вектори се нарича линейно независими.

Теорема.Системата от вектори ще линейно зависимитогава и само ако поне един от неговите вектори е линейна комбинация от останалите.

Пример 1Полином е линейна комбинация от полиноми https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Полиномите представляват линейно независима система, тъй като https полином: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Пример 2Матричната система, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> е линейно независима, тъй като линейната комбинация е равна на нулева матрица само когато https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text/78/ 624 /images/image022_26.gif" width="40" height="21"> линейно зависима.

Решение.

Съставете линейна комбинация от тези вектори https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" height =" 22">.

Приравняване на едноименните координати равни вектори, получаваме https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Накрая получаваме

и

Системата има само един тривиално решение, така че линейната комбинация от тези вектори е равна на нула само в случай, че всички коефициенти са равни на нула. Следователно тази система от вектори е линейно независима.

Пример 4Векторите са линейно независими. Какви ще бъдат системите от вектори

а).;

б).?

Решение.

а).Съставете линейна комбинация и я приравнете на нула

Използвайки свойствата на операциите с вектори в линейно пространство, пренаписваме последното равенство във формата

Тъй като векторите са линейно независими, коефициентите за трябва да са равни на нула, т.е..gif" width="12" height="23 src=">

Получената система от уравнения има уникално тривиално решение .

От равенството (*) изпълнява се само на https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – линейно независим;

б).Съставете равенството https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Прилагайки подобни разсъждения, получаваме

Решавайки системата от уравнения по метода на Гаус, получаваме

или

Последната система има безкрайно множестворешения https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. По този начин има ненулев набор от коефициенти, за които равенството (**) . Следователно системата от вектори е линейно зависим.

Пример 5Векторната система е линейно независима, а векторната система е линейно зависима..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

В равенство (***) . Наистина, за , системата ще бъде линейно зависима.

От връзката (***) получаваме или Обозначете .

Вземете

Задачи за независимо решение(в публиката)

1. Система, съдържаща нулев вектор, е линейно зависима.

2. Едновекторна система а, е линейно зависим тогава и само ако, а=0.

3. Система, състояща се от два вектора, е линейно зависима тогава и само тогава, когато векторите са пропорционални (т.е. единият от тях се получава от другия чрез умножение по число).

4. Ако k е линейно зависима системадобавите вектор, получавате линейно зависима система.

5. Ако от линейни независима системаизтриете вектор, тогава получената система от вектори е линейно независима.

6. Ако системата Слинейно независим, но става линейно зависим, когато се добави вектор b, след това вектора bлинейно изразени чрез векторите на системата С.

° С).Системата от матрици , , в пространството на матриците от втори ред.

10. Нека системата от вектори а,б,° Свекторното пространство е линейно независимо. Докажи линейна независимост следните системивектори:

а).а+b, b, c.

б).а+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">–произволно число

° С).а+b, a+c, b+c.

11. Позволявам а,б,° Сса три вектора в равнината, които могат да се използват за образуване на триъгълник. Тези вектори ще бъдат ли линейно зависими?

12. Дадени са два вектора a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Вземете още два 4D вектора a3 иa4така че системата a1,а2,a3,a4беше линейно независим .