Dekompozicija brojeva na proste faktore, metode i primjeri dekompozicije. Dobiti kanonsku dekompoziciju broja na proste faktore

Predavanje 14 Slučajni procesi Kanonsko proširenje slučajnih procesa. Spektralna dekompozicija stacionarno slučajni proces. SluLecture 14
slučajni procesi
Kanonsko proširenje slučajnih procesa.
Spektralna dekompozicija stacionarnog slučajnog
proces. Slučajni procesi sa nezavisnim
sekcije. Markovljevi procesi i Markovljevi lanci.
Normalni slučajni procesi. Periodično
nestacionarni slučajni procesi
(Akhmetov S.K.)

Kanonska dekompozicija stohastičkih procesa

Bilo koji SP X(t) može biti predstavljen u
oblik njegove ekspanzije, tj. kao suma
elementarni procesi:
Vk- slučajne varijable
φk(t) su neslučajne funkcije (sinusoidi, eksponenti, stepen
funkcije itd.)
Poseban slučaj takve dekompozicije je kanonski
raspadanje
SP X(t) ima oblik
mx(t) = M – matematičko očekivanje SP X(t)
V1, V2…Vk – nekorelirani i centrirani SW
D1, D2…Dk- SW disperzije V1, V2…Vk
φk(t) su neslučajne funkcije argumenta t
Slučajne varijable V1, V2…Vk nazivaju se koeficijenti kanonika
raspadanje,
i neslučajne funkcije φ1(t), φ2(t) φk(t) - koordinatne funkcije
kanonska dekompozicija

Glavne karakteristike SP-a date kanonskom ekspanzijom

M – matematičko očekivanje SP X(t)
Kx(t,t’) – korelacione funkcije SP X(t)
Izraz
- kanonsko proširenje korelacije
funkcije
Ako je t=t', onda u skladu sa prvim
svojstvo korelacione funkcije
Izraz
Dk(t) -
disperzija
kanonsko proširenje varijanse SP X(t)

Spektralna dekompozicija stacionarnog SP

Stacionarno zajedničko ulaganje može biti. predstavljeno kanonskom dekompozicijom
Vk i Uk su nekorelirani i centrirani SW s disperzijama
D=D=Dk
ω - neslučajna vrijednost (učestalost)
U ovom slučaju, kanonska ekspanzija korelacijske funkcije
je definisan izrazom
Zastupljen
kanonski
raspadanje
zajedničko ulaganje
X(t)
pozvao
spektralna dekompozicija SP i
izraženo kao
Θk - faza harmonijske oscilacije osnovno stacionarno zajedničko ulaganje,
koji je SW jednoliko raspoređen u intervalu (0, 2π);
Zk - SW, što je amplituda harmonijske oscilacije
osnovno stacionarno zajedničko ulaganje

Spektralna dekompozicija stacionarnog SP (2)

Slučajne varijable Θk i Zk su zavisne i za njih vrijedi sljedeće:
Vk = Zk cos Θk
Uk = Zk sin Θk
Stacionarno zajedničko ulaganje može biti. predstavljen kao zbir harmonika
oscilacije sa slučajnim amplitudama Zk i slučajnim fazama Θk on
različite neslučajne frekvencije ωk
Korelaciona funkcija stacionarnog SP X(t) je parna
funkciju njegovog argumenta, tj. kx(τ) = kx(-τ). Stoga je na intervalu (-T,
T) može se proširiti u Fourierov red u parnim (kosinusnim) harmonicima:
Varijanca stacionarnog SP X(t) je jednaka
suma
varijanse
sve
harmonike
njegov
spektralna dekompozicija
Zavisnost Dk = f(wk) naziva se diskretnim spektrom varijansi ili
diskretni spektar stacionarnog SP.

Spektralna dekompozicija stacionarnog SP (3)

Na ∆ω
→ 0 doći će do prijelaza na kontinuirani spektar
Sx(ω) - spektralna gustina
Dakle, korelaciona funkcija i spektralna gustoća
povezani su kosinusnom Fourierovom transformacijom. Dakle, spektralni
gustina stacionarnog zajedničkog ulaganja može biti izraženo kroz korelaciju
funkcija po formuli

Slučajni procesi sa nezavisnim presecima

U hidrologiji se smatra da serija odgovara modelu slučajnog
vrijednosti ako ne postoji značajna korelacija između članova ove serije
za bilo koji pomak τ.
Nasumični proces sa nezavisnim sekcijama je SP za koji
za t i t'
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx za τ = 0 i 0 za τ ≠ 0)
Takav proces je stacionaran i ergodičan
imovine
Za takve procese, karakteristike jednodimenzionalnog zakona raspodjele
može se procijeniti i za bilo koji dio i za bilo koji (dovoljno je
kontinuirana) implementacija
Takvi procesi nemaju korelaciju između članova unutar bilo kojeg
implementacija
Prihvaćajući takav model, pretpostavlja se da određeni broj hidroloških veličina
predstavlja jednu implementaciju zajedničkog ulaganja
Ponekad se naziva slučajni proces sa nezavisnim sekcijama
"bijeli šum" po analogiji s bijelim svjetlom

Markovljevi procesi i Markovljevi lanci

slučajni proces
se zove Markov ako za bilo koji
trenutak vremena t vjerovatnoća svakog od stanja sistema u budućnosti
(za t > t0) zavisi samo od njegovog stanja u sadašnjosti (za t = t0) i ne
zavisi od njenog stanja u prošlosti (u t< t0)
Markov lanac ili jednostavan Markov lanac pozvao
Markovljev proces sa diskretnim stanjem i diskretnim vremenom
Markov SP je u potpunosti opisan dvodimenzionalnim zakonom
distribucija. Ako a Markov proces je nepomičan i
ergodičan, onda se njegove karakteristike mogu procijeniti iz jedinice
implementacija.
Lanac u kojem uslovne vjerovatnoće države u budućnosti zavise
iz svog stanja u nekoliko prethodnih koraka, naziva se složenim
Markov lanac.

Normalni (Gaussovi) slučajni procesi

Poziva se normalni (Gausov) slučajni proces X(t).
SP, u kojem u svim sekcijama SW X(ti) ima normalu
distribucija
Periodično nestacionarni SP
Prilikom učenja godišnje, mjesečno, dnevno itd. procesi, obično
postoje intra-godišnji itd. fluktuacije. U ovom slučaju, kao
matematički model, možete periodično koristiti model
nestacionarni stohastički proces (PNSP)
Za slučajni proces se kaže da je periodično nestacionaran ako
njegove probabilističke karakteristike su invarijantne prema pomacima za
pozitivan broj T. Na primjer, sa diskretnim korakom od jednog mjeseca
invarijantnost se mora sačuvati u smjenama 12, 24, 36 itd.

Ovaj članak daje odgovore na pitanje o faktoriranju broja u listove. Razmislite opšta ideja o dekompoziciji sa primjerima. Hajde da analiziramo kanonski oblik proširenja i njen algoritam. Sve alternativne metode će se razmatrati korištenjem znakova djeljivosti i tablice množenja.

Yandex.RTB R-A-339285-1

Šta znači rastaviti broj u proste faktore?

Hajde da analiziramo koncept primarni faktori. Poznato je da je svaki prosti faktor prost broj. U proizvodu oblika 2 7 7 23 imamo da imamo 4 prosta faktora u obliku 2 , 7 , 7 , 23 .

Faktoring uključuje njegovu reprezentaciju kao proizvode prostih brojeva. Ako trebate razložiti broj 30, onda ćemo dobiti 2, 3, 5. Unos će imati oblik 30 = 2 3 5 . Moguće je da se množitelji mogu ponoviti. Broj poput 144 ima 144 = 2 2 2 2 3 3 .

Nisu svi brojevi skloni razgradnji. Brojevi koji su veći od 1 i cijeli su brojevi mogu se rastaviti na faktore. Prosti brojevi su djeljivi samo sa 1 i sami kada se razlože, tako da je nemoguće ove brojeve predstaviti kao proizvod.

Kada se z odnosi na cijele brojeve, predstavlja se kao proizvod a i b, gdje je z podijeljeno sa a i b. Složeni brojevi se rastavljaju na proste faktore koristeći osnovnu aritmetičku teoremu. Ako je broj veći od 1, onda je njegova faktorizacija p 1 , p 2 , … , p n ima oblik a = p 1 , p 2 , … , p n . Dekompozicija se pretpostavlja u jednoj varijanti.

Kanonska dekompozicija broja na proste faktore

Faktori se mogu ponoviti tokom razlaganja. Napisane su kompaktno koristeći diplomu. Ako pri dekomponovanju broja a imamo faktor p 1 koji se javlja s 1 puta i tako dalje p n - s n puta. Dakle, dekompozicija poprima oblik a=p 1 s 1 a = p 1 s 1 p 2 s 2 … p n s n. Ovaj unos se zove kanonska dekompozicija broja na proste faktore.

Kada dekomponujemo broj 609840, dobijamo da je 609 840 = 2 2 2 2 3 3 5 7 11 11, njegov kanonski oblik će biti 609 840 = 2 4 3 2 5 7 11 2 . Koristeći kanonsko proširenje, možete pronaći sve djelitelje broja i njihov broj.

Da biste pravilno faktorizirali, morate imati razumijevanje prostih i složenih brojeva. Poenta je da dobijete uzastopni broj djelitelja oblika p 1 , p 2 , … , p n brojevi a , a 1 , a 2 , … , a n - 1, to omogućava dobijanje a = p 1 a 1, gdje je a 1 \u003d a: p 1, a \u003d p 1 a 1 \u003d p 1 p 2 a 2, gdje je a 2 \u003d a 1: p 2, ..., a \u003d p 1 p2. .. ... p n a n , gdje a n = a n - 1: p n. Po primitku a n = 1, zatim jednakost a = p 1 p 2 … p n dobijamo traženu dekompoziciju broja a na proste faktore. primeti, to p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Da nađem najmanju zajednički djelitelji morate koristiti tabelu prostih brojeva. To se radi na primjeru pronalaženja najmanjeg prostog djelitelja broja z. Kada uzimamo proste brojeve 2, 3, 5, 11 i tako dalje, i sa njima dijelimo broj z. Pošto z nije prost broj, imajte na umu da najmanji prosti djelitelj neće biti veći od z. Može se vidjeti da nema djelitelja z , tada je jasno da je z prost broj.

Primjer 1

Razmotrimo primjer broja 87. Kada se podijeli sa 2, imamo da je 87: 2 = 43 s ostatkom od 1. Iz toga slijedi da 2 ne može biti djelitelj, podjela se mora izvršiti u potpunosti. Kada se podijeli sa 3, dobijamo da je 87: 3 = 29. Otuda zaključak - 3 je najmanji prost djelitelj broja 87.

Prilikom dekompozicije na proste faktore potrebno je koristiti tabelu prostih brojeva, gdje je a. Prilikom dekompozicije 95 treba koristiti oko 10 prostih brojeva, a kod razlaganja 846653 oko 1000.

Uzmimo u obzir algoritam za osnovnu faktorizaciju:

pronalaženje najmanjeg faktora sa djeliteljem p 1 broja a po formuli a 1 \u003d a: p 1, kada je a 1 = 1, tada je a prost broj i uključen je u faktorizaciju, kada nije jednako 1, tada a \u003d p 1 a 1 i slijedite dolje;
pronalaženje prostog djelitelja p 2 od 1 uzastopnim nabrajanjem prostih brojeva, koristeći a 2 = a 1: p 2 , kada je a 2 = 1 , tada ekspanzija ima oblik a = p 1 p 2 , kada je 2 = 1, onda a = p 1 p 2 a 2 , i vršimo prijelaz na sljedeći korak;
ponavljanje prostih brojeva i pronalaženje prostog djelitelja p 3 brojevi a 2 prema formuli a 3 = a 2: p 3 kada je a 3 = 1 , onda dobijamo da je a = p 1 p 2 p 3 , kada nije jednako 1 tada je a = p 1 p 2 p 3 a 3 i pređite na sljedeći korak;
naći prosti djelitelj p n brojevi a n - 1 nabrajanjem prostih brojeva sa p n - 1, kao i a n = a n - 1: p n, gdje je a n = 1, korak je konačan, kao rezultat dobijamo da je a = p 1 p 2 … p n .

Rezultat algoritma je zapisan u obliku tabele sa dekomponovanim faktorima sa vertikalnom trakom uzastopno u koloni. Razmotrite sliku ispod.

Rezultirajući algoritam se može primijeniti razlaganjem brojeva na proste faktore.

Prilikom rastavljanja osnovnih faktora, potrebno je slijediti osnovni algoritam.

Primjer 2

Rastavite broj 78 na proste faktore.

Rješenje

Da bismo pronašli najmanji prosti djelitelj, potrebno je nabrojati sve proste brojeve u 78 . To jest, 78:2 = 39. Deljenje bez ostatka, tako da je ovo prvi prosti djelitelj, koji označavamo kao p 1. Dobijamo da je a 1 = a: p 1 = 78: 2 = 39. Došli smo do jednakosti oblika a = p 1 a 1 , gdje je 78 = 2 39 . Tada je 1 = 39, to jest, trebali biste preći na sljedeći korak.

Fokusirajmo se na pronalaženje prostog djelitelja p2 brojevi a 1 = 39. Trebali biste razvrstati proste brojeve, odnosno 39: 2 = 19 (preostalo 1). Pošto dijeljenje ima ostatak, 2 nije djelitelj. Kada biramo broj 3, dobijamo da je 39: 3 = 13. To znači da je p 2 = 3 najmanji prosti djelitelj broja 39 sa a 2 = a 1: p 2 = 39: 3 = 13 . Dobijamo jednakost oblika a = p 1 p 2 a 2 u obliku 78 = 2 3 13 . Imamo da a 2 = 13 nije jednako 1, onda treba da idemo dalje.

Najmanji prosti djelitelj broja a 2 = 13 nalazi se nabrajanjem brojeva, počevši od 3. Dobijamo da je 13: 3 = 4 (odmor 1). Ovo pokazuje da 13 nije deljivo sa 5, 7, 11, jer je 13: 5 = 2 (odmor 3), 13: 7 = 1 (odmor 6) i 13: 11 = 1 (odmor 2). Može se vidjeti da je 13 prost broj. Formula izgleda ovako: a 3 = a 2: p 3 = 13: 13 = 1. Dobili smo da je a 3 = 1, što znači kraj algoritma. Sada su faktori zapisani kao 78 = 2 3 13 (a = p 1 p 2 p 3) .

odgovor: 78 = 2 3 13 .

Primjer 3

Rastavite broj 83,006 na proste faktore.

Rješenje

Prvi korak uključuje faktoring p 1 = 2 i a 1 = a: p 1 = 83 006: 2 = 41 503, gdje je 83 006 = 2 41 503 .

Drugi korak pretpostavlja da 2, 3 i 5 nisu prosti djelitelji za 1 = 41503, ali je 7 prosti djelitelj jer je 41503: 7 = 5929. Dobijamo da je p 2 = 7, a 2 = a 1: p 2 = 41 503: 7 = 5 929. Očigledno, 83 006 = 2 7 5 929 .

Pronalaženje najmanjeg prostog djelitelja p 4 na broj a 3 = 847 je 7 . Može se vidjeti da je a 4 = a 3: p 4 = 847: 7 = 121, dakle 83 006 = 2 7 7 7 121.

Da bismo pronašli prosti djelitelj broja a 4 = 121, koristimo broj 11, odnosno p 5 = 11. Tada dobijamo izraz forme a 5 = a 4: p 5 = 121: 11 \u003d 11, i 83 006 = 2 7 7 7 11 11 .

Za broj a 5 = 11 broj p6 = 11 je najmanji prosti djelitelj. Dakle, 6 = a 5: p 6 = 11: 11 = 1. Tada je a 6 = 1. Ovo ukazuje na kraj algoritma. Množitelji će biti zapisani kao 83006 = 2 7 7 7 11 11 .

Kanonska notacija odgovora će imati oblik 83 006 = 2 7 3 11 2 .

odgovor: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2 .

Primjer 4

Faktorizirajte broj 897 924 289.

Rješenje

Da biste pronašli prvi prosti faktor, iterirajte proste brojeve, počevši od 2. Kraj nabrajanja pada na broj 937. Tada je p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 i 897 924 289 = 937 958 297.

Drugi korak algoritma je nabrajanje manjih prostih brojeva. Odnosno, počinjemo sa brojem 937. Broj 967 se može smatrati prostim, jer je prost djelitelj broja a 1 = 958 297. Odavde dobijamo da je p 2 = 967, zatim 2 = a 1: p 1 = 958 297: 967 = 991 i 897 924 289 = 937 967 991.

Treći korak kaže da je 991 prost broj, jer nema prosti djelitelj koji je manji ili jednak 991. Približna vrijednost radikalnog izraza je 991< 40 2 . Иначе запишем как 991 < 40 2 . Iz ovoga se može vidjeti da je p 3 = 991 i a 3 = a 2: p 3 = 991: 991 = 1. Dobijamo da se razlaganje broja 897 924 289 na proste faktore dobije kao 897 924 289 \u003d 937 967 991.

odgovor: 897 924 289 = 937 967 991 .

Korištenje testova djeljivosti za osnovnu faktorizaciju

Da biste rastavili broj na proste faktore, morate slijediti algoritam. Kada postoje mali brojevi, dozvoljeno je koristiti tablicu množenja i znakove djeljivosti. Pogledajmo ovo na primjerima.

Primjer 5

Ako je potrebno faktorizirati 10, tabela pokazuje: 2 5 = 10. Rezultirajući brojevi 2 i 5 su prosti, tako da su prosti činioci za broj 10.

Primjer 6

Ako je potrebno razložiti broj 48, tabela pokazuje: 48 = 6 8. Ali 6 i 8 nisu prosti faktori, jer se takođe mogu razložiti kao 6 = 2 3 i 8 = 2 4 . Onda potpuna razgradnja odavde ispada kao 48 = 6 8 = 2 3 2 4 . Kanonska notacija će imati oblik 48 = 2 4 3 .

Primjer 7

Prilikom razlaganja broja 3400 možete koristiti znakove djeljivosti. AT ovaj slučaj relevantni su znaci djeljivosti sa 10 i sa 100. Odavde dobijamo da je 3400 = 34 100, pri čemu se 100 može podijeliti sa 10, odnosno zapisati kao 100 \u003d 10 10, što znači da je 3400 = 34 10 10. Na osnovu znaka djeljivosti dobijamo da je 3400 = 34 10 10 = 2 17 2 5 2 5 . Svi faktori su jednostavni. Kanonska ekspanzija poprima oblik 3400 = 2 3 5 2 17.

Kada pronađemo proste faktore, potrebno je koristiti znakove djeljivosti i tablicu množenja. Ako broj 75 predstavljate kao proizvod faktora, onda morate uzeti u obzir pravilo djeljivosti sa 5. Dobijamo da je 75 = 5 15 i 15 = 3 5 . Odnosno, željena dekompozicija je primjer oblika proizvoda 75 = 5 · 3 · 5 .

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Poziva se slučajna varijabla V centriran , ako je njegovo matematičko očekivanje jednako 0. Elementarni centrirani slučajni proces je proizvod centrirane slučajne varijable V i neslučajne funkcije φ(t):X(t)=Vφ(t). Elementarno centriran slučajni proces ima sljedeće karakteristike:

Izražavanje forme
, gdje je φ k ( t ), k =1;2;…-neslučajne funkcije; , k =1;2;… - nekorelirane centrirane slučajne varijable, naziva se kanonska ekspanzija slučajnog procesaX ( t ), dok su slučajne varijable nazivaju se koeficijenti kanonske ekspanzije; dok neslučajne funkcije φ k ( t ) - koordinatne funkcije kanonske ekspanzije.

Razmotrite karakteristike slučajnog procesa

Pošto prema uslovu
onda

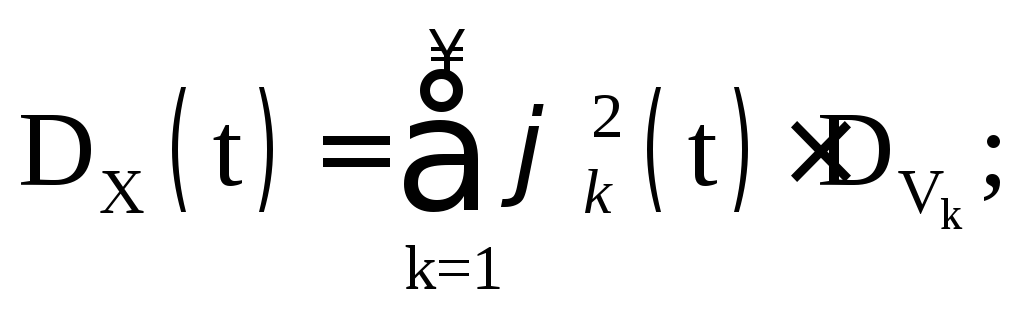
Očigledno, isti slučajni proces ima različite vrste kanonsko proširenje ovisno o izboru koordinatnih funkcija. Štaviše, čak i kod izbora koordinatnih funkcija postoji proizvoljnost u distribuciji slučajnih varijabli V k. U praksi se na osnovu rezultata eksperimenata dobijaju procjene matematičkog očekivanja i korelacijske funkcije:
. Nakon raspadanja
u dvostrukom Fourierovom redu u koordinatnim funkcijama φ do (t):

dobiti vrijednosti varijansi
slučajne varijable V k .

4.2. Koncept generalizirane funkcije. Diracova delta funkcija. Integralno kanonsko predstavljanje slučajnih procesa.

Generalizirana funkcija naziva se granica niza jednoparametarske porodice kontinuiranih funkcija.

Diracova delta funkcija
- je generalizirana funkcija koja je rezultat prelaska na granicu na
u porodici funkcija

Među nekretninama -karakteristike imajte na umu sljedeće:

3. Ako je f(t)- kontinuirana funkcija, onda

Slučajni proces X( t ), čija korelaciona funkcija ima oblik koji se naziva nestacionarni "bijeli šum". Ako a W ( t 1 )= W - konst , zatim X( t )-stacionarni "bijeli šum".

Kao što slijedi iz definicije, ne postoje dva, čak proizvoljno bliska, poprečna presjeka “bijelog šuma”. Poziva se izraz W(t). intenzitet belog šuma.

Integralni kanonski prikaz slučajnog procesa X( t ) naziva se izraz oblika
gdje
- nasumično centrirana funkcija;
- neslučajna funkcija kontinuiranih argumenata

Korelaciona funkcija takvog slučajnog procesa ima oblik:

Može se pokazati da postoji neslučajna funkcija G(λ) takva da

gdje je G(λ 1) gustina disperzije; δ(x) - Diracova delta funkcija. Dobijamo

Prema tome, varijansa slučajnog procesa X(t):

4.3. Linearne i nelinearne transformacije slučajnih procesa

Razmatra se sledeći problem: na ulaz sistema (uređaja, pretvarača) S dolazi „ulazni signal“, koji ima karakter slučajnog procesa X(t). Sistem ga pretvara u "izlazni signal" Y(t):

Formalno, transformacija slučajnog procesa X(t) u Y(t) može se opisati pomoću takozvanog sistemskog operatora A t:

Y(t)=A t (X(t)).

Indeks t označava da ovaj operator vrši transformaciju u vremenu. Moguće su sljedeće formulacije problema transformacije slučajnog procesa.

Poznati su zakoni distribucije ili Opće karakteristike slučajni proces X(t) na ulazu u sistem S, zadan je operator A t sistema S, potrebno je odrediti zakon distribucije ili opšte karakteristike slučajnog procesa Y(t) na izlazu sistema S.

Poznati su zakoni distribucije (opće karakteristike) slučajnog procesa X(t) i zahtjevi za slučajni proces Y(t); potrebno je odrediti oblik operatora A t sistema S koji najbolje zadovoljava zadate zahtjeve kY(t).

Poznati su zakoni distribucije (opće karakteristike) slučajnog procesa Y(t) i dat je operator A t sistema S; potrebno je odrediti zakone raspodjele ili opšte karakteristike slučajnog procesa X(t).

P rinyata sledeća klasifikacija operatori A t sistema S:

Operateri sistema

Linear LNonlinearN

Linearno homogeno L 0 Linearno nehomogeno L n

Razmotrite uticaj linearnog nehomogenog sistema

L n (...) \u003d L 0 (...) + φ (t)

na slučajnom procesu X(t) koji ima sljedeću kanonsku ekspanziju:

Dobijamo:

uvodimo notaciju

tada kanonska dekompozicija Y(t) ima oblik:

Matematičko očekivanje slučajnog procesa Y(t):

korelaciona funkcija slučajnog procesa Y(t):

shodno tome,

S druge strane

Disperzija slučajnog procesa Y(t):

U zaključku ovog odeljka napominjemo da su operatori diferencijacije i integracije slučajnih procesa linearno homogeni.

2. Kvadratnom transformacijom se smatra:

Y(t)=(X(t)) 2 ,

V k -centrirane slučajne varijable koje imaju distribuciju simetričnu oko nule; svaka četiri od njih su kolektivno nezavisna. Onda

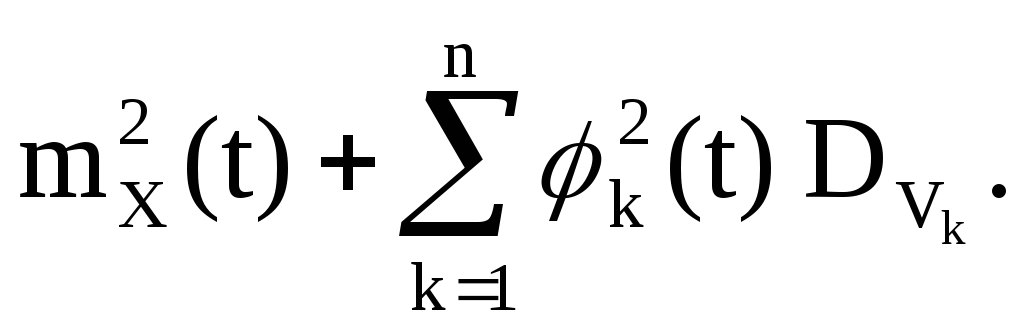
Uvodimo neslučajne funkcije

i slučajne varijable

tada slučajni proces Y(t) poprima oblik

Dobija se kanonska dekompozicija slučajnog procesa Y(t). Korelaciona funkcija Y(t):

Formulacija. Dato prirodni broj n (n > 1). Dobiti njegovu kanonsku dekompoziciju na proste faktore, odnosno predstaviti ga kao proizvod prostih faktora. U ovom slučaju je u dekompoziciji dozvoljeno navesti faktor 1. Na primjer, 264 = 2 * 2 * 2 * 3 * 11 (dozvoljeno je da program da odgovor 264 = 1 * 2 * 2 * 2 * 3 * 11).

Rješenje. Ovaj zadatak ima prilično lepo rešenje.

Od osnovna teorema aritmetike poznato je da za bilo koji prirodan broj veći od 1 postoji njegova kanonska dekompozicija na proste faktore, a ta je dekompozicija jedinstvena do reda faktora. To jest, na primjer, 12 = 2 * 2 * 2 i 12 = 3 * 2 * 2 su ista proširenja.

Razmotrimo kanonski oblik bilo kojeg broja na konkretan primjer. Na primjer, 264 = 2 * 2 * 2 * 3 * 11. Kako se ova struktura može otkriti? Da bismo odgovorili na ovo pitanje, prisjetimo se školski kurs pravila algebre za podelu monoma, zamišljajući da su brojevi u kanonskoj dekompoziciji promenljive. Kao što znate, ako podijelite izraz na varijablu u određenom stepenu sadržanu u ovom izrazu u istom stepenu, on se briše u njegovom zapisu.

To jest, ako podijelimo 264 sa 2, tada će jedna dvojka nestati u svojoj kanonskoj dekompoziciji. Tada možemo provjeriti da li je rezultujući količnik opet djeljiv sa 2. Odgovor je da, ali treći dio će dati ostatak. Zatim morate uzeti u obzir sljedeći prirodni broj 3 - količnik će se jednom podijeliti na njega. Kao rezultat toga, prolazeći brojevnu pravu u pozitivnom smjeru, doći ćemo do broja 11, a nakon dijeljenja sa 11 n postaje jednako 1, što će ukazivati na potrebu okončanja postupka.

Zašto ovakvim “brisanjem” pronađenih faktora ne dobijemo djeljivost složenim brojevima? U stvari, ovdje je sve jednostavno - bilo koji složeni broj je proizvod prostih faktora koji su manji od njega. Kao rezultat toga, ispada da ćemo izbrisati iz n sve faktore bilo kojeg složenog broja, dok ne dođemo do samog sebe u lancu podjela. Na primjer, s takvom iteracijom n nikada neće biti podijeljeno sa 4, jer ćemo "na putu" do ovog broja precrtati n svi faktori su dva.

Algoritam na prirodnom jeziku:

1) Ulaz n;

2) Dodjela varijabli str brojevi 2;

3) Izlaz broja n, znak jednakosti i jedinica za ukrašavanje dekompozicije;

4) Izvođenje petlje sa preduvjetom n< > 1 . u petlji:

Ako a mmodp = 0, zatim prikažite znak množenja i varijablu p, a zatim podijelite n na str, inače povećajte vrijednost i od 1;

program PrimeFactors;
n, p: riječ;
početi
p:= 2;
readln(n);
write(n, '=1');
dok n<>1 počinjem
ako je (n mod p) = 0 onda počnite
write('*', p);
n:= n div p
inače početi
inc(p)