Эксцентриситет линии второго порядка. Эллипс и его каноническое уравнение

Рассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.

Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат Ox_1x_2 может быть задано уравнением вида p(x_1,x_2)=0, где p(x_1,x_2) - многочлен второй степени двух переменных Ox_1x_2 . Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.

Результатом решения поставленной задачи является следующая основная теорема (3.3)

Классификация алгебраических линий второго порядка (теорема 3.3)

Для любой алгебраической линии второго порядка существует прямоугольная система координат Oxy , в которой уравнение этой линии принимает один из следующих девяти канонических видов:

Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) - мнимыми.

Приведем доказательство теоремы, поскольку оно фактически содержит алгоритм решения поставленной задачи.

Без ограничения общности можно предполагать, что уравнение линии второго порядка задано в прямоугольной системе координат Oxy . В противном случае можно перейти от непрямоугольной системы координат Ox_1x_2 к прямоугольной Oxy , при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 3.1 об инвариантности порядка алгебраической линии.

Пусть в прямоугольной системе координат Oxy алгебраическая линия второго порядка задана уравнением

A_{11}x^2+2a_{12}xy+a_{22}y^2+2a_1x+2a_2y+a_0=0,

в котором хотя бы один из старших коэффициентов a_{11},a_{12},a_{22} отличен от нуля, т.е. левая часть (3.34) - многочлен двух переменных x,y второй степени. Коэффициенты при первых степенях переменных x и y , а также при их произведении x\cdot y взяты удвоенными просто для удобства дальнейших преобразований.

Для приведения уравнения (3.34) к каноническому виду используются следующие преобразования прямоугольных координат:

– поворот на угол \varphi

\begin{cases}x=x"\cdot\cos\varphi-y"\cdot\sin\varphi,\\y=x"\cdot\sin\varphi+y"\cdot\cos\varphi;\end{cases}

– параллельный перенос

\begin{cases}x=x_0+x",\\y=y_0+y";\end{cases}

– изменение направлений координатных осей (отражения в координатных осях):

оси ординат \begin{cases}x=x",\\y=-y",\end{cases} оси абсцисс \begin{cases}x=-x",\\y=y",\end{cases} обеих осей \begin{cases}x=-x",\\y=-y";\end{cases}

– переименование координатных осей (отражение в прямой y=x )

\begin{cases}x=y",\\y=x",\end{cases}

где x,y и x",y" - координаты произвольной точки в старой (Oxy) и новой O"x"y" системах координат соответственно.

Кроме преобразования координат обе части уравнения можно умножать на отличное от нуля число.

Рассмотрим сначала частные случаи, когда уравнение (3.34) имеет вид:

\begin{aligned} &\mathsf{(I)\colon}~ \lambda_2\cdot y^2+a_0,~\lambda_2\ne0;\\ &\mathsf{(II)\colon}~ \lambda_2\cdot y^2+2\cdot a_1\cdot x,~\lambda_2\ne0,~a_1\ne0;\\ &\mathsf{(III)\colon}~ \lambda_1\cdot x^2+\lambda_2\cdot y^2+a_0,~\lambda_1\ne0,~\lambda_2\ne0. \end{aligned}

Эти уравнения (также многочлены в левых частях) называются приведенными. Покажем, что приведенные уравнения (I), (II), (III) сводятся к каноническим (1)–(9).

Уравнение (I). Если в уравнении (I) свободный член равен нулю (a_0=0) , то, разделив обе части уравнения \lambda_2y^2=0 на старший коэффициент (\lambda_0\ne0) , получим y^2=0 - уравнение двух совпадающих прямых (9), содержащих ось абсцисс y=0 . Если же свободный член отличен от нуля a_0\ne0 , то разделим обе части уравнения (I) на старший коэффициент (\lambda_2\ne0): y^2+\frac{a_0}{\lambda_2}=0 . Если величина отрицательная, то, обозначив ее через -b^2 , где b=\sqrt{-\frac{a_0}{\lambda_2}} , получаем y^2-b^2=0 - уравнение пары параллельных прямых (7): y=b или y=-b . Если же величина \frac{a_0}{\lambda_2} положительная, то, обозначив ее через b^2 , где b=\sqrt{\frac{a_0}{\lambda_2}} , получаем y^2+b^2=0 - уравнение пары мнимых параллельных прямых (8). Это уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, отвечающих этому уравнению. Однако в области комплексных чисел уравнение y^2+b^2=0 имеет два сопряженных решения y=\pm ib , которые иллюстрируются штриховыми линиями (см. пункт 8 теоремы 3.3).

Уравнение (II). Разделим уравнение на старший коэффициент (\lambda_2\ne0) и перенесем линейный член в правую часть: y^2=-\frac{2a_1}{\lambda_2}\,x . Если величина отрицательная, то, обозначая p=-\frac{a_1}{\lambda_2}>0 , получаем y^2=2px - уравнение параболы (6). Если величина \frac{a_1}{\lambda_2} положительная, то, изменяя направление оси абсцисс, т.е. выполняя второе преобразование в (3.37), получаем уравнение (y")^2=\frac{2a_1}{\lambda_2}\,x" или (y")^2=2px" , где p=\frac{a_1}{\lambda_2}>0 . Это уравнение параболы в новой системе координат Ox"y" .

Уравнение (III). Возможны два случая: либо старшие коэффициенты одного знака (эллиптический случай), либо противоположных знаков (гиперболический случай).

В эллиптическом случае (\lambda_1\lambda_2>0)

\mathsf{(III)}\quad\Leftrightarrow\quad \lambda_1\cdot x^2+\lambda_2\cdot y^2=-a_0\quad \Leftrightarrow \quad \frac{\lambda_1}{-a_0}\cdot x^2+\frac{\lambda_2}{-a_0}\cdot y^2=1

Противоположен знаку a_0 , то, обозначая положительные величины и \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 - уравнение эллипса (1).

Если знак старших коэффициентов \lambda_1,\lambda_2 совпадает со знаком a_0 , то, обозначая положительные величины \frac{a_0}{\lambda_1} и \frac{a_0}{\lambda_2} через a^2 и b^2 , получаем -\frac{x^2}{a^2}-\frac{y^2}{b^2}=1~\Leftrightarrow~\frac{x^2}{a^2}+\frac{y^2}{b^2}=-1 - уравнение мнимого эллипса (2). Это уравнение не имеет действительных решений. Однако оно имеет решения в области комплексных чисел, которые иллюстрируются штриховой линией (см. пункт 2 теоремы 3.3).

Можно считать, что в уравнениях эллипса (действительного или мнимого) коэффициенты удовлетворяют неравенству a\geqslant b , в противном случае этого можно добиться, переименовывая координатные оси, т.е. делая преобразование (3.38) системы координат.

Если свободный член уравнения (III) равен нулю (a_0=0) , то, обозначая положительные величины \frac{1}{|\lambda_1|} и \frac{1}{|\lambda_2|} через a^2 и b^2 , получаем \frac{x^2}{a^2}+\frac{y^2}{b^2}=0 - уравнение пары мнимых пересекающихся прямых (3). Этому уравнению удовлетворяет только точка с координатами x=0 и y=0 , т.е. точка O - начало координат. Однако в области комплексных чисел левую часть уравнения можно разложить на множители \frac{x^2}{a^2}+\frac{y^2}{b^2}=\left(\frac{y}{b}+i\,\frac{x}{a}\right)\!\!\left(\frac{y}{b}-i\,\frac{x}{a}\right) , поэтому уравнение имеет сопряженные решения y=\pm i\,\frac{b}{a}\,x , которые иллюстрируются штриховыми линиями, пересекающимися в начале координат (см. пункт 3 теоремы 3.3).

В гиперболическом случае (\lambda_1,\lambda_2<0) при a_0\ne0 переносим свободный член в правую часть и делим обе части на -a_0\ne0 :

\mathsf{(III)}\quad \Leftrightarrow \quad \lambda_1\cdot x^2+\lambda_2\cdot y^2=-a_0 \quad \Leftrightarrow \quad \frac{\lambda_1}{-a_0}\cdot x^2+\frac{\lambda_2}{-a_0}\cdot y^2=1.

Величины \frac{-a_0}{\lambda_1} и \frac{-a_0}{\lambda_2} имеют противоположные знаки. Без ограничения общности считаем, что знак \lambda_2 совпадает со знаком свободного члена a_0 , т.е. \frac{a_0}{\lambda_2}>0 . В противном случае нужно переименовать координатные оси, т.е. сделать преобразование (3.38) системы координат. Обозначая положительные величины \frac{-a_0}{\lambda_1} и \frac{a_0}{\lambda_2} через a^2 и b^2 , получаем \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 - уравнение гиперболы (4).

Пусть в уравнении (III) свободный член равен нулю (a_0=0) . Тогда можно считать, что \lambda_1>0 , а \lambda_2<0 (в противном случае обе части уравнения умножим на –1) . Обозначая положительные величины \frac{1}{\lambda_1} и -\frac{1}{\lambda_2} через a^2 и b^2 , получаем \frac{x^2}{a^2}-\frac{y^2}{b^2}=0 - уравнение пары пересекающихся прямых (5). Уравнения прямых находятся в результате разложения на множители левой части уравнения

\frac{x^2}{a^2}-\frac{y^2}{b^2}=\left(\frac{x}{a}-\frac{y}{b}\right)\!\!\left(\frac{x}{a}+\frac{y}{b}\right)=0 , то есть y=\pm\frac{b}{a}\cdot x

Таким образом, приведенные уравнения (I),(II),(III) алгебраической линии второго порядка сводятся к одному из канонических видов (1)–(9), перечисленных в теореме 3.3.

Осталось показать, что общее уравнение (3.34) можно свести к приведенным при помощи преобразований прямоугольной системы координат.

Упрощение общего уравнения (3.34) производится в два этапа. На первом этапе при помощи поворота системы координат "уничтожается" член с произведением неизвестных. Если произведения неизвестных нет (a_{12}=0) , то поворот делать не надо (в этом случае переходим сразу ко второму этапу). На втором этапе при помощи параллельного переноса "уничтожаются" один или оба члена первой степени. В результате получаются приведенные уравнения (I),(II),(III).

Первый этап: преобразование уравнения линии второго порядка при повороте прямоугольной системы координат.

Если коэффициент a_{12}\ne0 , выполним поворот системы координат на угол \varphi . Подставляя выражения (3.35) в уравнение (3.34), получаем:

\begin{gathered} a_{11}(x"\cos\varphi-y"\sin\varphi)^2+2a_{12}(x"\cos\varphi-y"\sin\varphi)(x"\sin\varphi+y"\cos\varphi)+a_{22}(x"\sin\varphi+y"\cos\varphi)^2+\\ +2a_1(x"\cos\varphi-y"\sin\varphi)+2a_2(x"\cos\varphi-y"\sin\varphi)+a_0=0. \end{gathered}

Приводя подобные члены, приходим к уравнению вида (3.34):

A"_{11}(x")^2+2a"_{12}x"y"+a"_{22}(y")^2+2a"_1x"+2a"_2y"+a"_0=0,

\begin{aligned}a"_{11}&=a_{11}\cos^2\varphi+2a_{12}\cos\varphi\sin\varphi+a_{22}\sin^2\varphi;\\ a"_{12}&=-a_{11}\cos\varphi\sin\varphi+a_{12}(\cos^2\varphi-\sin^2\varphi)+a_{22}\cos\varphi\sin\varphi;\\ a"_{22}&=a_{11}\sin^2\varphi-2a_{12}\cos\varphi\sin\varphi+a_{22}\cos^2\varphi;\\ a"_1&=a_1\cos\varphi+a_2\sin\varphi;\quad a"_2=-a_1\sin\varphi+a_2\cos\varphi; \quad a"_0=a_0. \end{aligned}

Определим угол \varphi так, чтобы a"_{12}=0 . Преобразуем выражение для a"_{12} , переходя к двойному углу:

A"_{12}= -\frac{1}{2}\,a_{11}\sin2\varphi+a_{12}\cos2\varphi+\frac{1}{2}\,a_{22}\sin2\varphi= \frac{a_{22}-a_{11}}{2}\,\sin2\varphi+a_{12}\cos2\varphi.

Угол \varphi должен удовлетворять однородному тригонометрическому уравнению \frac{a_{22}-a_{11}}{2}\,\sin2\varphi+a_{12}\cos2\varphi=0 , которое равносильно уравнению

\operatorname{ctg}2\varphi=\frac{a_{11}-a_{22}}{2a_{12}},

поскольку a_{12}\ne 0 . Это уравнение имеет бесконечное количество корней

\varphi=\frac{1}{2}\operatorname{arcctg}\frac{a_{11}-a_{22}}{2a_{12}}+\frac{\pi}{2}\,n, \quad n\in\mathbb{Z}.

Выберем любой из них, например, угол \varphi из интервала 0<\varphi<\frac{\pi}{2} . Тогда в уравнении (3.39) исчезнет член 2a"_{12}x"y" , поскольку a"_{12}=0 .

Обозначив оставшиеся старшие коэффициенты через \lambda_1= a" и \lambda_2=a"_{22} , получим уравнение

\lambda_1\cdot(x")^2+\lambda_2\cdot(y")^2+2\cdot a"_1\cdot x"+2\cdot a"_2\cdot y"+a"_0=0.

Согласно теореме 3.1, уравнение (3.41) является уравнением второй степени (при преобразовании (3.35) порядок линии сохраняется), т.е. хотя бы один из старших коэффициентов \lambda_1 или \lambda_2 отличен от нуля. Далее будем считать, что именно коэффициент при (y")^2 не равен нулю (\lambda_2\ne0) . В противном случае (при \lambda_2=0 и \lambda_1\ne0 ) следует сделать поворот системы координат на угол \varphi+\frac{\pi}{2} , который также удовлетворяет условию (3.40). Тогда вместо координат x",y" в (3.41) получим y",-x" соответственно, т.е. отличный от нуля коэффициент \lambda_1 будет при (y")^2 .

Второй этап: преобразование уравнения линии второго порядка при параллельном переносе прямоугольной системы координат.

Уравнение (3.41) можно упростить, выделяя полные квадраты. Нужно рассмотреть два случая: \lambda_1\ne0 или \lambda_1=0 (согласно предположению \lambda_2\ne0 ), которые называются центральный (включающий эллиптический и гиперболический случаи) или параболический соответственно. Геометрический смысл этих названий раскрывается в дальнейшем.

Центральный случай: \lambda_1\ne0 и \lambda_2\ne0 . Выделяя полные квадраты по переменным x",y" , получаем

\begin{gathered}\lambda_1\left[(x")^2+2\,\frac{a"_1}{\lambda_1}\,x"+{\left(\frac{a"_1}{\lambda_1}\right)\!}^2\right]+ \lambda_2\left[(y")^2+2\,\frac{a"_2}{\lambda_2}\,y"+{\left(\frac{a"_2}{\lambda_2}\right)\!}^2\right]- \lambda_1{\left(\frac{a"_1}{\lambda_1}\right)\!}^2-\lambda_2{\left(\frac{a"_2}{\lambda_2}\right)\!}^2+a"_0=0~\Leftrightarrow\\ \Leftrightarrow~ \lambda_1{\left(x"+\frac{a"_1}{\lambda_1}\right)\!}^2+\lambda_2{\left(y"+\frac{a"_2}{\lambda_2}\right)\!}^2- \lambda_1{\left(\frac{a"_1}{\lambda_1}\right)\!}^2-\lambda_2{\left(\frac{a"_2}{\lambda_2}\right)\!}^2+a"_0=0. \end{gathered}

После замены переменных

\left\{\begin{aligned} x""&=x"+\frac{a"_1}{\lambda_1},\\ y""&=y"+\frac{a"_2}{\lambda_2}, \end{aligned}\right.

получаем уравнение

\lambda_1\,(x"")^2+\lambda_2\,(y"")^2+a""_0=0,

где a""_0=-\lambda_1{\left(\frac{a"_1}{\lambda_1}\right)\!}^2-\lambda_2{\left(\frac{a"_2}{\lambda_2}\right)\!}^2+a"_0 .

Параболический случай: \lambda_1=0 и \lambda_2\ne0 . Выделяя полный квадрат по переменной y" , получаем

\begin{gathered} \lambda_2\left[(y")^2+2\cdot\frac{a"_2}{\lambda_2}\cdot y"+{\left(\frac{a"_2}{\lambda_2}\right)\!}^2\right]+2\cdot a"_1\cdot x"-\lambda_2{\left(\frac{a"_2}{\lambda_2}\right)\!}^2+a"_0=0 \quad \Leftrightarrow \\ \Leftrightarrow \quad \lambda_2{\left(y"+\frac{a"_2}{\lambda_2}\right)\!}^2+2\cdot a"_1\cdot x"-\lambda_2{\left(\frac{a"_2}{\lambda_2}\right)\!}^2+a"_0=0.\end{gathered}

Если a"_1\ne0 , то последнее уравнение приводится к виду

\lambda_2{\left(y"+ \frac{a"_2}{\lambda_2}\right)\!}^2+ 2\cdot a"_1\left=0.

Сделав замену переменных

\left\{\begin{aligned} x""&=x"+\frac{a"_0}{2a"_1}- \frac{\lambda_2}{2a"_1}{\left(\frac{a"_2}{\lambda_2}\right)\!}^2,\\ y""&=y"+ \frac{a"_2}{\lambda_2}, \end{aligned}\right.

получим, где a""_1=a"_1

\lambda_2\cdot(y"")^2+2\cdot a""_1\cdot x""=0,

Если a"_1=0 , то уравнение (3.44) приводится к виду, где a""_0=-\lambda_2{\left(\frac{a"_2}{\lambda_2} \right)\!}^2+a"_0 ,

\lambda_2\cdot(y"")^2+a""_0,

\left\{\begin{aligned}x""&=x",\\y""&=y"+\frac{a"_2}{\lambda_2}.\end{aligned}\right.

Замены переменных (3.42), (3.45), (3.48) соответствуют параллельному переносу системы координат Ox"y" (см. пункт 1"a" замечаний 2.3).

Таким образом, при помощи параллельного переноса системы координат Ox"y" получаем новую систему координат O""x""y"" , в которой уравнение линии второго порядка принимает вид (3.43), или (3.46), или (3.47). Эти уравнения являются приведенными (вида (III),(II) или (I) соответственно).

Основная теорема 3.3 о приведении уравнения алгебраической линии второго порядка к каноническому виду доказана.

Замечания 3.8

1. Система координат, в которой уравнение алгебраической линии второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной y на (-y) не изменяет уравнений (1)–(9). Поэтому ориентация канонической системы координат не имеет принципиального значения, ее всегда можно сделать правой, изменив при необходимости направление оси ординат.

2. Ранее показано, что преобразования прямоугольных систем координат на плоскости сводятся к одному из преобразований (2.9) или (2.10):

\begin{cases} x=x_0+x"\cdot\cos\varphi-y"\cdot\sin\varphi,\\ y=y_0+x"\cdot\sin\varphi+y"\cdot\cos\varphi, \end{cases}\quad \begin{cases} x=x_0+x"\cdot\cos\varphi+y"\cdot\sin\varphi,\\ y=y_0+x"\cdot\sin\varphi-y"\cdot\cos\varphi.\end{cases}

Поэтому задача приведения уравнения линии второго порядка к каноническому виду сводится к нахождению начала O"(x_0,y_0) канонической системы координат O"x"y" и угла \varphi наклона ее оси абсцисс O"x" к оси абсцисс Ox исходной системы координат Oxy .

3. В случаях (3),(5),(7),(8),(9) линии называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Малый дискриминант 5 (§ 66) для эллипса положителен (см. пример 1 § 66), для гиперболы отрицателен, для параболы равен нулю.

Доказательство. Эллипс представляется уравнением . У этого уравнения малый дискриминант При преобразовании координат сохраняет свою величину, а при умножении обеих частей уравнения на какое-либо число дискриминант умножается на (§ 66, замечание). Следовательно, дискриминант эллипса положителен в любой системе координат. В случае гиперболы и в случае параболы доказательство аналогично.

Согласно с этим различают три типа линий второго порядка (и уравнений второй степени):

1. Эллиптический тип, характеризующийся условием

К нему относятся, кроме действительного эллипса, также мнимый эллипс (§ 58, пример 5) и пара мнимых прямых, пересекающихся в действительной точке (§ 58, пример 4).

2. Гиперболический тип, характеризующийся условием

К нему относится, кроме гиперболы, пара действительных пересекающихся прямых (§ 58, пример 1).

3. Параболический тип, характеризующийся условием

К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).

Пример 1. Уравнение

принадлежит к параболическому типу, так как

Поскольку большой дискриминант

не равен нулю, то уравнение (1) представляет нераспадающуюся линию, т. е. параболу (ср. §§ 61-62, пример 2).

Пример 2. Уравнение

принадлежит к гиперболическому типу, так как

поскольку

то уравнение (2) представляет пару пересекающихся прямых. Их уравнения можно найти по способу § 65.

Пример 3. Уравнение

принадлежит к эллиптическому типу, так как

Поскольку

то линия не распадается и, значит, является эллипсом.

Замечание. Однотипные линии геометрически связаны так: пара пересекающихся мнимых прямых (т. е. одна действительная точка) есть предельный случай эллипса, «стягивающегося в точку» (рис. 88); пара пересекающихся действительных прямых - предельный случай гиперболы, приближающейся к своим асимптотам (рис. 89); пара параллельных прямых - предельный случай параболы, у которой ось и одна пара точек симметричных относительно оси (рис. 90), неподвижны, а вершина удаляется в бесконечность.

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка : приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

$$9x^2-4y^2-90x-8y+185=0.$$

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

$$6x^2+2\sqrt{5}xy+2y^2=21.$$

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

$$3x^2-6y^2-12x-108y-492=0.$$

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

$$9x^2+25y^2-18x-100y-116=0.$$

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $\sqrt{2/5}$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=\pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

Скачать с Depositfiles

Лекция № 9. Тема 3 : Линии второго порядка

Пусть в некоторой ДСК задана линия, определяемая уравнением второй степени

где коэффициенты
одновременно не равны нулю. Эта линия назы-вается кривой или линией второго порядка .

Может случиться, что нет точек
с действительными коорди-натами, удовлетворяющими уравнению (1). В этом случае считают, что уравнение (1) определяет мнимую линию второго порядка. Например,
 это уравнение мнимой окружности.

Рассмотрим три важных частных случаев уравнения (1).

3.1. Эллипс

Эллипс определяется уравнением

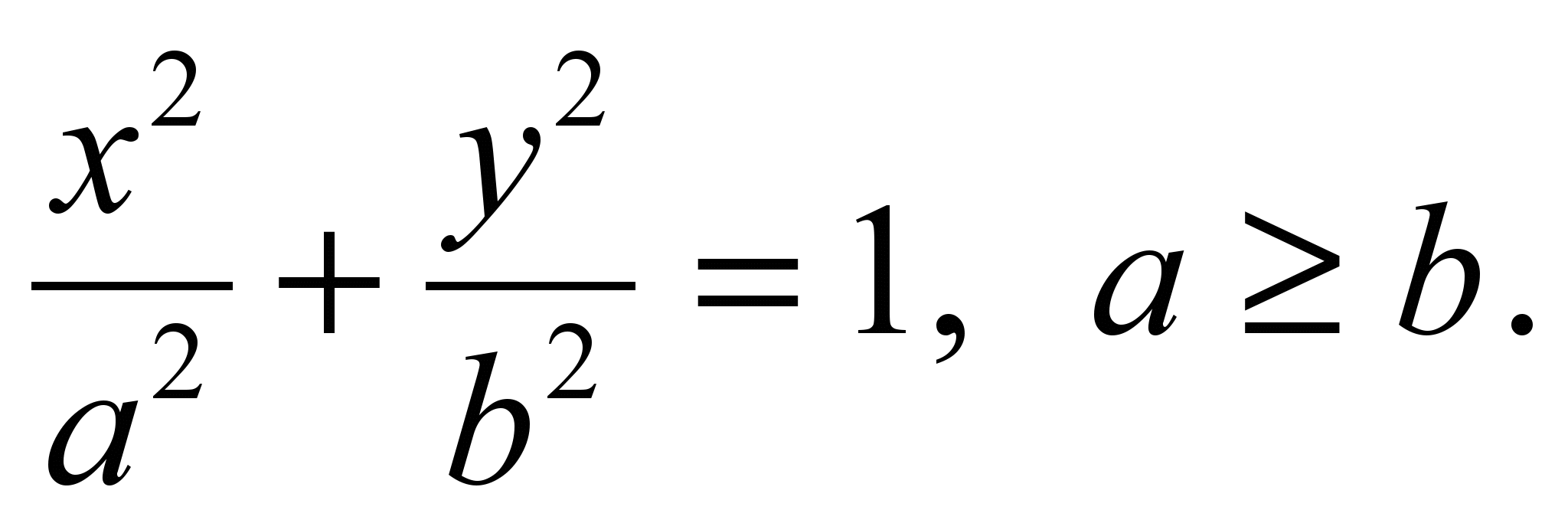(2)

Коэффициенты а и b называются соответственно большой и малой полуосями, а уравнение (2) – каноническим уравнением эллипса.

Положим
и отметим на оси Ох точки

называемые фокусами эллипса. Тогда эллипс можно определить как

геометрическое место точек, сумма расстояний от которых до фокусов есть величина постоянная, равная 2а .

M K

— а F 1 O F 2 a x

— b

Покажем это. Пусть точка
 текущая точка эллипса. В этом случае получаем Тогда должно выполняться равенство

Выражение (3) представим в виде

и возведём в квадрат обе части выражения

Отсюда получаем

Еще раз возведём это выражение в квадрат и воспользуемся соотно-шением
, тогда

(4)

Разделив обе части выражения (4) на
, окончательно получаем каноническое уравнение эллипса

Исследуем уравнение (2). Если в уравнении заменить , то уравнение (2) не изменится. Это означает, что эллипс симметричен относительно координатных осей. Поэтому рассмотрим подробно часть эллипса, находящуюся в первой четверти. Она определяется уравнением
Очевидно, что эллипс проходит через точки
. Выполнив схематическое построение в первой четверти, симметрично отобразим его график во все четверти. Таким образом, эллипс является непрерывной замкнутой кривой. Точки называются вершинами эллипса.

Отношение
называется эксцентриситетом эллипса. Для эллипса
.

Прямые
называются директрисами эллипса.

Справедливо следующее свойство директрис :

Отношение расстояний от фокуса и директрисы для точек эллипса есть величина постоянная, равная эксцентриситету, т.е.

Доказывается аналогично, как и равенство (3).

Замечание 1. Окружность
является частным случаем эллипса. Для неё

3.2. Гипербола

Каноническое уравнение гиперболы имеет вид

т.е. в уравнении (1) нужно положить

Коэффициенты а и b называются соответственно вещественной и мнимой полуосями.

Положив
, отметим на оси Ох точки
на-зываемые фокусами гиперболы. Тогда гиперболу можно определить как

геометрическое место точек, разность расстояний от которых до фокусов по абсолютной величине равна 2 а , т.е.

К М

F 1 —а О а F 2 х

Доказывается аналогично, как и для эллипса. По виду уравнения гиперболы так же заключаем, что её график симметричен относительно осей системы координат. Часть гиперболы, лежащая в первой четверти, имеет уравнение
Из этого уравнения видно, что при достаточно больших х гипербола близка к прямой
. После схематичного построения в первой четверти симметрично отобра-жаем график во все четверти.