Πώς προέκυψε η αρχή της ελάχιστης δράσης; Αρχή της ελάχιστης δράσης

Όταν έμαθα για πρώτη φορά για αυτήν την αρχή, είχα ένα αίσθημα κάποιου είδους μυστικισμού. Φαίνεται ότι η φύση περνά μυστηριωδώς από όλα τα πιθανά μονοπάτια κίνησης του συστήματος και επιλέγει την καλύτερη.

Σήμερα θέλω να μιλήσω λίγο για μια από τις πιο αξιόλογες αρχές της φυσικής - την αρχή της ελάχιστης δράσης.

Ιστορικό

Από την εποχή του Γαλιλαίου, είναι γνωστό ότι τα σώματα που δεν ασκούνται από καμία δύναμη κινούνται σε ευθείες γραμμές, δηλαδή κατά μήκος της συντομότερης διαδρομής. Οι ακτίνες φωτός ταξιδεύουν επίσης σε ευθείες γραμμές.

Όταν ανακλάται, το φως κινείται επίσης με τέτοιο τρόπο ώστε να φτάνει από το ένα σημείο στο άλλο με τον συντομότερο δυνατό τρόπο. Στην εικόνα, η συντομότερη διαδρομή θα είναι η πράσινη διαδρομή, στην οποία η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης. Οποιαδήποτε άλλη διαδρομή, για παράδειγμα, κόκκινο, θα είναι μεγαλύτερη.

Αυτό είναι εύκολο να αποδειχθεί αντανακλώντας απλώς τις διαδρομές των ακτίνων στην αντίθετη πλευρά του καθρέφτη. Φαίνονται με διακεκομμένες γραμμές στην εικόνα.

Φαίνεται ότι το πράσινο μονοπάτι ACB μετατρέπεται σε ευθεία ACB'. Και το κόκκινο μονοπάτι μετατρέπεται σε μια διακεκομμένη γραμμή ADB’, η οποία, φυσικά, είναι μεγαλύτερη από την πράσινη.

Το 1662, ο Pierre Fermat πρότεινε ότι η ταχύτητα του φωτός σε πυκνή ύλη, όπως το γυαλί, είναι μικρότερη από τον αέρα. Πριν από αυτό, η εκδοχή του Descartes ήταν γενικά αποδεκτή, σύμφωνα με την οποία η ταχύτητα του φωτός στην ύλη πρέπει να είναι μεγαλύτερη από τον αέρα για να ληφθεί ο σωστός νόμος διάθλασης. Για τον Fermat, η υπόθεση ότι το φως μπορούσε να κινηθεί πιο γρήγορα σε ένα πιο πυκνό μέσο από ό,τι σε ένα σπάνιο φαινόταν αφύσικη. Επομένως, υπέθεσε ότι όλα ήταν ακριβώς το αντίθετο και απέδειξε ένα εκπληκτικό πράγμα - με αυτήν την υπόθεση, το φως διαθλάται με τέτοιο τρόπο ώστε να φτάσει στον προορισμό του στον ελάχιστο χρόνο.

Και πάλι, το πράσινο χρώμα δείχνει τη διαδρομή κατά μήκος της οποίας πραγματικά ταξιδεύει η δέσμη φωτός. Η διαδρομή που σημειώνεται με κόκκινο είναι η συντομότερη, αλλά όχι η πιο γρήγορη, επειδή το φως έχει μια μακρύτερη διαδρομή για να ταξιδέψει μέσα από το γυαλί και είναι πιο αργή εκεί. Η ταχύτερη διαδρομή είναι η πραγματική διαδρομή της δέσμης φωτός.

Όλα αυτά τα γεγονότα υποδηλώνουν ότι η φύση ενεργεί με κάποιο ορθολογικό τρόπο, το φως και τα σώματα κινούνται με τον βέλτιστο τρόπο, καταβάλλοντας όσο το δυνατόν λιγότερη προσπάθεια. Αλλά τι είδους προσπάθειες είναι αυτές και πώς να τις υπολογίσετε παρέμεινε ένα μυστήριο.

Το 1744, ο Maupertuis εισήγαγε την έννοια της «δράσης» και διατύπωσε την αρχή σύμφωνα με την οποία η πραγματική τροχιά ενός σωματιδίου διαφέρει από οποιαδήποτε άλλη στο ότι η δράση για αυτό είναι ελάχιστη. Ωστόσο, ο ίδιος ο Maupertuis δεν μπόρεσε ποτέ να δώσει έναν σαφή ορισμό του τι σημαίνει αυτή η ενέργεια. Μια αυστηρή μαθηματική διατύπωση της αρχής της ελάχιστης δράσης αναπτύχθηκε ήδη από άλλους μαθηματικούς - τον Euler, τον Lagrange και τελικά δόθηκε από τον William Hamilton:

Στη μαθηματική γλώσσα, η αρχή της ελάχιστης δράσης διατυπώνεται αρκετά σύντομα, αλλά δεν μπορούν όλοι οι αναγνώστες να κατανοήσουν το νόημα της σημειογραφίας που χρησιμοποιείται. Θέλω να προσπαθήσω να εξηγήσω αυτή την αρχή πιο ξεκάθαρα και με απλούστερους όρους.

Ελεύθερο σώμα

Φανταστείτε, λοιπόν, ότι κάθεστε σε ένα αυτοκίνητο σε ένα σημείο και τη δεδομένη στιγμή σας δίνεται μια απλή εργασία: τη στιγμή που θα χρειαστεί να οδηγήσετε το αυτοκίνητο στο σημείο .

Τα καύσιμα για ένα αυτοκίνητο είναι ακριβά και, φυσικά, θέλετε να ξοδέψετε όσο το δυνατόν λιγότερα από αυτά. Το αυτοκίνητό σας είναι κατασκευασμένο χρησιμοποιώντας τις πιο πρόσφατες σούπερ τεχνολογίες και μπορεί να επιταχύνει ή να φρενάρει όσο πιο γρήγορα θέλετε. Ωστόσο, είναι σχεδιασμένο με τέτοιο τρόπο ώστε όσο πιο γρήγορα πηγαίνει, τόσο περισσότερο καύσιμο καταναλώνει. Επιπλέον, η κατανάλωση καυσίμου είναι ανάλογη του τετραγώνου της ταχύτητας. Εάν οδηγείτε δύο φορές πιο γρήγορα, θα καταναλώσετε 4 φορές περισσότερο καύσιμο την ίδια χρονική περίοδο. Εκτός από την ταχύτητα, η κατανάλωση καυσίμου επηρεάζεται φυσικά και από το βάρος του οχήματος. Όσο πιο βαρύ το αυτοκίνητό μας, τόσο περισσότερο καύσιμο καταναλώνει. Η κατανάλωση καυσίμου του αυτοκινήτου μας σε κάθε χρονική στιγμή είναι ίση, δηλ. ακριβώς ίση με την κινητική ενέργεια του αυτοκινήτου.

Πώς πρέπει λοιπόν να οδηγείτε για να φτάσετε στον προορισμό σας ακριβώς την καθορισμένη ώρα και να καταναλώνετε όσο το δυνατόν λιγότερα καύσιμα; Είναι σαφές ότι πρέπει να πάτε σε ευθεία γραμμή. Καθώς η διανυθείσα απόσταση αυξάνεται, δεν θα καταναλωθεί λιγότερο καύσιμο. Και τότε μπορείτε να επιλέξετε διαφορετικές τακτικές. Για παράδειγμα, μπορείτε να φτάσετε γρήγορα στο σημείο εκ των προτέρων και απλώς να καθίσετε και να περιμένετε μέχρι να έρθει η ώρα. Η ταχύτητα οδήγησης, άρα και η κατανάλωση καυσίμου σε κάθε στιγμή, θα είναι υψηλή, αλλά και ο χρόνος οδήγησης θα μειωθεί. Ίσως η συνολική κατανάλωση καυσίμου να μην είναι τόσο μεγάλη. Ή μπορείτε να οδηγείτε ομοιόμορφα, με την ίδια ταχύτητα, ώστε, χωρίς να βιάζεστε, να φτάσετε ακριβώς τη στιγμή της ώρας. Ή οδηγείτε ένα μέρος της διαδρομής γρήγορα και αποχωρίστε πιο αργά. Ποιος είναι ο καλύτερος τρόπος να πάτε;

Αποδεικνύεται ότι ο βέλτιστος, πιο οικονομικός τρόπος οδήγησης είναι να οδηγείτε με σταθερή ταχύτητα, έτσι ώστε να φτάσετε στον προορισμό ακριβώς την καθορισμένη ώρα. Οποιαδήποτε άλλη επιλογή θα καταναλώσει περισσότερο καύσιμο. Μπορείτε να το ελέγξετε μόνοι σας χρησιμοποιώντας πολλά παραδείγματα. Ο λόγος είναι ότι η κατανάλωση καυσίμου αυξάνεται με το τετράγωνο της ταχύτητας. Επομένως, καθώς αυξάνεται η ταχύτητα, η κατανάλωση καυσίμου αυξάνεται πιο γρήγορα από ότι μειώνεται ο χρόνος οδήγησης και η συνολική κατανάλωση καυσίμου αυξάνεται επίσης.

Έτσι, ανακαλύψαμε ότι αν ένα αυτοκίνητο κάθε στιγμή καταναλώνει καύσιμο σε αναλογία με την κινητική του ενέργεια, τότε ο πιο οικονομικός τρόπος για να φτάσετε από σημείο σε σημείο ακριβώς την καθορισμένη ώρα είναι να οδηγείτε ομοιόμορφα και σε ευθεία, ακριβώς ο τρόπος που κινείται ένα σώμα απουσία δυνάμεων που δρουν πάνω του Οποιαδήποτε άλλη μέθοδος οδήγησης θα έχει ως αποτέλεσμα υψηλότερη συνολική κατανάλωση καυσίμου.

Στο πεδίο της βαρύτητας

Τώρα ας βελτιώσουμε λίγο το αυτοκίνητό μας. Ας προσαρτήσουμε κινητήρες τζετ σε αυτό, ώστε να μπορεί να πετά ελεύθερα προς οποιαδήποτε κατεύθυνση. Σε γενικές γραμμές, η σχεδίαση παρέμεινε η ίδια, επομένως η κατανάλωση καυσίμου παρέμεινε και πάλι αυστηρά ανάλογη με την κινητική ενέργεια του αυτοκινήτου. Εάν τώρα δοθεί το καθήκον να πετάξουμε από ένα σημείο σε ένα σημείο του χρόνου και να φτάσουμε σε ένα σημείο σε μια χρονική στιγμή, τότε ο πιο οικονομικός τρόπος, όπως και πριν, φυσικά, θα είναι να πετάξουμε ομοιόμορφα και ευθύγραμμα για να τελειώσουμε σε ένα σημείο την ακριβή καθορισμένη ώρα. Αυτό αντιστοιχεί και πάλι στην ελεύθερη κίνηση ενός σώματος σε τρισδιάστατο χώρο.

Ωστόσο, μια ασυνήθιστη συσκευή εγκαταστάθηκε στο τελευταίο μοντέλο αυτοκινήτου. Αυτή η συσκευή μπορεί να παράγει καύσιμο κυριολεκτικά από το τίποτα. Αλλά ο σχεδιασμός είναι τέτοιος ώστε όσο υψηλότερο είναι το αυτοκίνητο, τόσο περισσότερο καύσιμο παράγει η συσκευή ανά πάσα στιγμή. Η παραγωγή καυσίμου είναι ευθέως ανάλογη με το υψόμετρο στο οποίο βρίσκεται αυτή τη στιγμή το αυτοκίνητο. Επίσης, όσο πιο βαρύ είναι το αυτοκίνητο, τόσο πιο ισχυρή είναι εγκατεστημένη πάνω του η συσκευή και τόσο περισσότερο καύσιμο παράγει και η παραγωγή είναι ευθέως ανάλογη με το βάρος του αυτοκινήτου. Η συσκευή αποδείχθηκε τέτοια ώστε η παραγωγή καυσίμου να είναι ακριβώς ίση με (πού είναι η επιτάχυνση της ελεύθερης πτώσης), δηλ. δυναμική ενέργεια του αυτοκινήτου.

Η κατανάλωση καυσίμου σε κάθε χρονική στιγμή είναι ίση με την κινητική ενέργεια μείον τη δυναμική ενέργεια του αυτοκινήτου (μείον δυναμική ενέργεια, επειδή η εγκατεστημένη συσκευή παράγει καύσιμο και δεν το καταναλώνει). Τώρα το έργο μας να μετακινούμε το αυτοκίνητο μεταξύ σημείων όσο πιο αποτελεσματικά γίνεται γίνεται πιο δύσκολο. Η ευθύγραμμη ομοιόμορφη κίνηση αποδεικνύεται ότι δεν είναι η πιο αποτελεσματική σε αυτή την περίπτωση. Αποδεικνύεται ότι είναι καλύτερο να κερδίσετε λίγο υψόμετρο, να μείνετε εκεί για λίγο, να καταναλώνετε περισσότερο καύσιμο και μετά να κατεβείτε στο σημείο . Με τη σωστή τροχιά πτήσης, η συνολική παραγωγή καυσίμου λόγω της ανάβασης θα καλύψει το πρόσθετο κόστος καυσίμου για την αύξηση του μήκους της διαδρομής και την αύξηση της ταχύτητας. Αν υπολογίσετε προσεκτικά, ο πιο οικονομικός τρόπος για ένα αυτοκίνητο θα είναι να πετάξει με παραβολή, με την ίδια ακριβώς τροχιά και με την ίδια ακριβώς ταχύτητα που θα πετούσε μια πέτρα στο βαρυτικό πεδίο της Γης.

Αξίζει εδώ να γίνει μια διευκρίνιση. Φυσικά, μπορείτε να πετάξετε μια πέτρα από ένα σημείο με πολλούς διαφορετικούς τρόπους, ώστε να χτυπήσει στο σημείο. Αλλά πρέπει να το πετάξετε με τέτοιο τρόπο ώστε, έχοντας απογειωθεί από το σημείο τη στιγμή του χρόνου, να χτυπήσει στο σημείο ακριβώς τη στιγμή του χρόνου. Είναι αυτή η κίνηση που θα είναι η πιο οικονομική για το αυτοκίνητό μας.

Συνάρτηση Lagrange και αρχή της ελάχιστης δράσης

Τώρα μπορούμε να μεταφέρουμε αυτή την αναλογία σε πραγματικά φυσικά σώματα. Ένα ανάλογο του ρυθμού κατανάλωσης καυσίμου για αμαξώματα ονομάζεται συνάρτηση Lagrange ή Lagrange (προς τιμήν του Lagrange) και συμβολίζεται με το γράμμα . Το Lagrangian δείχνει πόσα «καύσιμα» καταναλώνει ένα σώμα σε μια δεδομένη στιγμή. Για ένα σώμα που κινείται σε ένα δυναμικό πεδίο, το Lagrangian είναι ίσο με την κινητική του ενέργεια μείον τη δυναμική ενέργεια.

Ένα ανάλογο της συνολικής ποσότητας καυσίμου που καταναλώθηκε κατά τη διάρκεια ολόκληρης της περιόδου κίνησης, δηλ. η τιμή Lagrange που συσσωρεύεται σε όλη τη διάρκεια της κίνησης ονομάζεται «δράση».

Η αρχή της ελάχιστης δράσης είναι ότι το σώμα κινείται με τέτοιο τρόπο ώστε η δράση (η οποία εξαρτάται από την τροχιά της κίνησης) να είναι ελάχιστη. Ταυτόχρονα, δεν πρέπει να ξεχνάμε ότι προσδιορίζονται οι αρχικές και οι τελικές προϋποθέσεις, δηλ. όπου το σώμα βρίσκεται τη στιγμή του χρόνου και τη στιγμή του χρόνου.

Σε αυτή την περίπτωση, το αμάξωμα δεν χρειάζεται απαραίτητα να κινείται σε ένα ομοιόμορφο βαρυτικό πεδίο, το οποίο θεωρήσαμε για το αυτοκίνητό μας. Μπορούν να εξεταστούν εντελώς διαφορετικές καταστάσεις. Ένα σώμα μπορεί να ταλαντώνεται σε μια ελαστική ταινία, να ταλαντεύεται σε ένα εκκρεμές ή να πετάει γύρω από τον Ήλιο, σε όλες αυτές τις περιπτώσεις κινείται με τέτοιο τρόπο ώστε να ελαχιστοποιεί τη «συνολική κατανάλωση καυσίμου» π.χ. δράση.

Εάν ένα σύστημα αποτελείται από πολλά σώματα, τότε το Lagrangian ενός τέτοιου συστήματος θα είναι ίσο με τη συνολική κινητική ενέργεια όλων των σωμάτων μείον τη συνολική δυναμική ενέργεια όλων των σωμάτων. Και πάλι, όλα τα σώματα θα κινούνται συντονισμένα, έτσι ώστε η επίδραση ολόκληρου του συστήματος κατά τη διάρκεια μιας τέτοιας κίνησης να είναι ελάχιστη.

Όχι τόσο απλό

Στην πραγματικότητα, απάτησα λίγο λέγοντας ότι τα σώματα κινούνται πάντα με τρόπο που ελαχιστοποιεί τη δράση. Αν και αυτό ισχύει σε πολλές περιπτώσεις, είναι δυνατό να σκεφτούμε καταστάσεις στις οποίες η δράση δεν είναι σαφώς ελάχιστη.

Για παράδειγμα, ας πάρουμε μια μπάλα και ας την τοποθετήσουμε σε κενό χώρο. Σε κάποια απόσταση από αυτό θα τοποθετήσουμε έναν ελαστικό τοίχο. Ας πούμε ότι θέλουμε η μπάλα να καταλήξει στο ίδιο μέρος μετά από κάποιο χρονικό διάστημα. Υπό αυτές τις δεδομένες συνθήκες, η μπάλα μπορεί να κινηθεί με δύο διαφορετικούς τρόπους. Πρώτον, μπορεί απλά να παραμείνει στη θέση του. Δεύτερον, μπορείτε να το σπρώξετε προς τον τοίχο. Η μπάλα θα πετάξει στον τοίχο, θα αναπηδήσει από αυτόν και θα επιστρέψει. Είναι ξεκάθαρο ότι μπορείς να το σπρώξεις με τέτοια ταχύτητα ώστε να επιστρέψει ακριβώς την κατάλληλη στιγμή.

Και οι δύο επιλογές για την κίνηση της μπάλας είναι δυνατές, αλλά η δράση στη δεύτερη περίπτωση θα είναι μεγαλύτερη, γιατί όλο αυτό το διάστημα η μπάλα θα κινείται με μη μηδενική κινητική ενέργεια.

Πώς μπορούμε να σώσουμε την αρχή της ελάχιστης δράσης ώστε να ισχύει σε τέτοιες καταστάσεις; Θα μιλήσουμε για αυτό στο.

Εξετάσαμε εν συντομία μια από τις πιο αξιοσημείωτες φυσικές αρχές - την αρχή της ελάχιστης δράσης, και σταματήσαμε σε ένα παράδειγμα που φαινόταν να την έρχεται σε αντίθεση. Σε αυτό το άρθρο θα εξετάσουμε αυτήν την αρχή με λίγο περισσότερες λεπτομέρειες και θα δούμε τι συμβαίνει σε αυτό το παράδειγμα.

Αυτή τη φορά θα χρειαστούμε λίγο περισσότερα μαθηματικά. Ωστόσο, θα προσπαθήσω και πάλι να παρουσιάσω το κύριο μέρος του άρθρου σε στοιχειώδες επίπεδο. Θα επισημάνω ελαφρώς πιο αυστηρά και πολύπλοκα σημεία στο χρώμα που μπορούν να παραβλεφθούν χωρίς να διακυβεύεται η βασική κατανόηση του άρθρου.

Συνοριακές συνθήκες

Θα ξεκινήσουμε με το απλούστερο αντικείμενο - μια μπάλα που κινείται ελεύθερα στο διάστημα, πάνω στην οποία δεν δρουν δυνάμεις. Μια τέτοια μπάλα, όπως είναι γνωστό, κινείται ομοιόμορφα και ευθύγραμμα. Για απλότητα, ας υποθέσουμε ότι κινείται κατά μήκος του άξονα:

Για να περιγραφεί με ακρίβεια η κίνησή του, κατά κανόνα, καθορίζονται οι αρχικές συνθήκες. Για παράδειγμα, διευκρινίζεται ότι την αρχική στιγμή η μπάλα βρισκόταν σε σημείο με συντεταγμένες και είχε ταχύτητα . Έχοντας ορίσει τις αρχικές συνθήκες σε αυτή τη μορφή, προσδιορίζουμε ξεκάθαρα την περαιτέρω κίνηση της μπάλας - θα κινηθεί με σταθερή ταχύτητα και η θέση της τη στιγμή του χρόνου θα είναι ίση με την αρχική θέση συν την ταχύτητα πολλαπλασιασμένη με τον χρόνο που έχει παρέλθει : . Αυτή η μέθοδος ρύθμισης των αρχικών συνθηκών είναι πολύ φυσική και διαισθητικά οικεία. Έχουμε καθορίσει όλες τις απαραίτητες πληροφορίες σχετικά με την κίνηση της μπάλας την αρχική χρονική στιγμή και στη συνέχεια η κίνησή της καθορίζεται από τους νόμους του Νεύτωνα.

Ωστόσο, αυτός δεν είναι ο μόνος τρόπος για να καθορίσετε την κίνηση της μπάλας. Ένας άλλος εναλλακτικός τρόπος είναι να ορίσετε τη θέση της μπάλας σε δύο διαφορετικούς χρόνους και . Εκείνοι. ρωτήστε το:

1) τη στιγμή που η μπάλα ήταν σε ένα σημείο (με συντεταγμένη).
2) τη στιγμή που η μπάλα ήταν στο σημείο (με συντεταγμένη ).

Η έκφραση «ήταν στο σημείο» δεν σημαίνει ότι η μπάλα ήταν σε ηρεμία στο σημείο. Τη στιγμή του χρόνου μπορούσε να πετάξει μέσα από το σημείο. Αυτό σημαίνει ότι η θέση του τη στιγμή του χρόνου συνέπεσε με το σημείο. Το ίδιο ισχύει και για το σημείο.

Αυτές οι δύο συνθήκες καθορίζουν επίσης μοναδικά την κίνηση της μπάλας. Η κίνησή του είναι εύκολο να υπολογιστεί. Για να ικανοποιηθούν και οι δύο προϋποθέσεις, η ταχύτητα της μπάλας πρέπει προφανώς να είναι . Η θέση της μπάλας τη στιγμή του χρόνου θα είναι και πάλι ίση με την αρχική θέση συν την ταχύτητα πολλαπλασιαζόμενη με τον χρόνο που έχει παρέλθει:

Σημειώστε ότι στις συνθήκες του προβλήματος δεν χρειάστηκε να ρυθμίσουμε την αρχική ταχύτητα. Καθορίστηκε μοναδικά από τις συνθήκες 1) και 2).

Η ρύθμιση συνθηκών με τον δεύτερο τρόπο φαίνεται ασυνήθιστη. Μπορεί να είναι ασαφές γιατί μπορεί να είναι απαραίτητο να τους ρωτήσετε με αυτή τη μορφή. Ωστόσο, στην αρχή της ελάχιστης δράσης, χρησιμοποιούνται οι συνθήκες με τη μορφή 1) και 2) και όχι με τη μορφή προσδιορισμού της αρχικής θέσης και της αρχικής ταχύτητας.

Μονοπάτι με την ελάχιστη δράση

Τώρα ας ξεφύγουμε λίγο από την πραγματική ελεύθερη κίνηση της μπάλας και ας εξετάσουμε το ακόλουθο καθαρά μαθηματικό πρόβλημα. Ας πούμε ότι έχουμε μια μπάλα που μπορούμε να την μετακινήσουμε χειροκίνητα με όποιον τρόπο θέλουμε. Σε αυτήν την περίπτωση, πρέπει να εκπληρώσουμε τις προϋποθέσεις 1) και 2). Εκείνοι. στο χρονικό διάστημα μεταξύ και πρέπει να το μετακινήσουμε από σημείο σε σημείο. Αυτό μπορεί να γίνει με εντελώς διαφορετικούς τρόπους. Κάθε τέτοια μέθοδο θα ονομάζουμε τροχιά της κίνησης της μπάλας και μπορεί να περιγραφεί με συνάρτηση της θέσης της μπάλας σε σχέση με το χρόνο. Ας σχεδιάσουμε αρκετές από αυτές τις τροχιές σε ένα γράφημα της θέσης της μπάλας σε σχέση με το χρόνο:

Για παράδειγμα, μπορούμε να κινήσουμε την μπάλα με την ίδια ταχύτητα ίση με (πράσινη τροχιά). Ή μπορούμε να το κρατήσουμε στο σημείο το μισό χρόνο και μετά να το μετακινήσουμε στο σημείο με διπλή ταχύτητα (μπλε τροχιά). Μπορείτε πρώτα να το μετακινήσετε προς την αντίθετη κατεύθυνση και μετά να το μετακινήσετε σε (καφέ τροχιά). Μπορείτε να το μετακινήσετε εμπρός και πίσω (κόκκινη διαδρομή). Γενικά, μπορείτε να το μετακινήσετε όπως θέλετε, αρκεί να πληρούνται οι προϋποθέσεις 1) και 2).

Για κάθε τέτοια τροχιά μπορούμε να συσχετίσουμε έναν αριθμό. Στο παράδειγμά μας, δηλ. ελλείψει δυνάμεων που ασκούνται στην μπάλα, αυτός ο αριθμός είναι ίσος με τη συνολική συσσωρευμένη κινητική ενέργεια καθ' όλη τη διάρκεια της κίνησής της στο χρονικό διάστημα μεταξύ και και ονομάζεται δράση.

Σε αυτή την περίπτωση, η λέξη «συσσωρευμένη» κινητική ενέργεια δεν αποδίδει το νόημα με μεγάλη ακρίβεια. Στην πραγματικότητα, η κινητική ενέργεια δεν συσσωρεύεται πουθενά, η συσσώρευση χρησιμοποιείται μόνο για τον υπολογισμό της δράσης για την τροχιά. Στα μαθηματικά υπάρχει μια πολύ καλή ιδέα για μια τέτοια συσσώρευση - το ολοκλήρωμα:

Η δράση συνήθως υποδεικνύεται με το γράμμα . Το σύμβολο σημαίνει κινητική ενέργεια. Αυτό το ολοκλήρωμα σημαίνει ότι η δράση είναι ίση με τη συσσωρευμένη κινητική ενέργεια της μπάλας στο χρονικό διάστημα από έως.

Για παράδειγμα, ας πάρουμε μια μπάλα μάζας 1 kg, θέσουμε ορισμένες οριακές συνθήκες και υπολογίσουμε τη δράση για δύο διαφορετικές τροχιές. Αφήστε το σημείο να βρίσκεται σε απόσταση 1 μέτρου από το σημείο και ο χρόνος απέχει 1 δευτερόλεπτο από το χρόνο. Εκείνοι. πρέπει να μετακινήσουμε την μπάλα, η οποία την αρχική στιγμή βρισκόταν στο σημείο , σε ένα δευτερόλεπτο σε απόσταση 1 m κατά μήκος του άξονα.

Στο πρώτο παράδειγμα (πράσινη τροχιά) μετακινήσαμε την μπάλα ομοιόμορφα, δηλ. με την ίδια ταχύτητα, η οποία προφανώς θα έπρεπε να είναι ίση με: m/s. Η κινητική ενέργεια της μπάλας σε κάθε χρονική στιγμή είναι ίση με: = 1/2 J. Σε ένα δευτερόλεπτο θα συσσωρευτεί 1/2 J κινητικής ενέργειας. Εκείνοι. δράση για μια τέτοια τροχιά ισούται με: J s.

Τώρα ας μην μετακινήσουμε αμέσως τη μπάλα από σημείο σε σημείο, αλλά ας την κρατήσουμε στο σημείο για μισό δευτερόλεπτο και, στη συνέχεια, στον υπόλοιπο χρόνο, ας την μετακινήσουμε ομοιόμορφα σε σημείο. Στο πρώτο μισό του δευτερολέπτου, η μπάλα είναι σε ηρεμία και η κινητική της ενέργεια είναι μηδενική. Επομένως, η συμβολή στη δράση αυτού του τμήματος της τροχιάς είναι επίσης μηδενική. Το δεύτερο μισό δευτερόλεπτο μετακινούμε την μπάλα με διπλή ταχύτητα: m/s. Η κινητική ενέργεια θα είναι ίση με = 2 J. Η συμβολή αυτής της χρονικής περιόδου στη δράση θα είναι ίση με 2 J φορές μισό δευτερόλεπτο, δηλ. 1 J s. Επομένως, η συνολική δράση για μια τέτοια τροχιά είναι ίση με J s.

Ομοίως, οποιαδήποτε άλλη τροχιά με τις οριακές συνθήκες 1) και 2) που δίνονται από εμάς αντιστοιχεί σε έναν ορισμένο αριθμό ίσο με την ενέργεια για αυτήν την τροχιά. Ανάμεσα σε όλες αυτές τις τροχιές, υπάρχει μια τροχιά που έχει τη λιγότερη δράση. Μπορεί να αποδειχθεί ότι αυτή η τροχιά είναι η πράσινη τροχιά, δηλ. ομοιόμορφη κίνηση της μπάλας. Για οποιαδήποτε άλλη τροχιά, όσο δύσκολη κι αν είναι, η δράση θα είναι μεγαλύτερη από το 1/2.

Στα μαθηματικά, μια τέτοια σύγκριση για κάθε συνάρτηση ενός συγκεκριμένου αριθμού ονομάζεται συνάρτηση. Αρκετά συχνά στη φυσική και στα μαθηματικά προκύπτουν προβλήματα παρόμοια με τα δικά μας, δηλ. για να βρείτε μια συνάρτηση για την οποία η τιμή μιας συγκεκριμένης συνάρτησης είναι ελάχιστη. Για παράδειγμα, ένα από τα προβλήματα που είχε μεγάλη ιστορική σημασία για την ανάπτυξη των μαθηματικών είναι το πρόβλημα του βαχιστόχρονου. Εκείνοι. βρίσκοντας την καμπύλη κατά μήκος της οποίας η μπάλα κυλάει πιο γρήγορα. Και πάλι, κάθε καμπύλη μπορεί να αναπαρασταθεί από μια συνάρτηση h(x) και κάθε συνάρτηση μπορεί να συσχετιστεί με έναν αριθμό, σε αυτήν την περίπτωση τον χρόνο κύλισης της μπάλας. Και πάλι, το πρόβλημα έγκειται στην εύρεση μιας συνάρτησης για την οποία η τιμή της συνάρτησης είναι ελάχιστη. Ο κλάδος των μαθηματικών που ασχολείται με τέτοια προβλήματα ονομάζεται λογισμός μεταβολών.

Αρχή της ελάχιστης δράσης

Στα παραδείγματα που συζητήθηκαν παραπάνω, έχουμε δύο ειδικές τροχιές που λαμβάνονται με δύο διαφορετικούς τρόπους.

Η πρώτη τροχιά λαμβάνεται από τους νόμους της φυσικής και αντιστοιχεί στην πραγματική τροχιά μιας ελεύθερης μπάλας, στην οποία δεν ασκούνται δυνάμεις και για την οποία ορίζονται οριακές συνθήκες στη μορφή 1) και 2).

Η δεύτερη τροχιά προκύπτει από το μαθηματικό πρόβλημα εύρεσης τροχιάς με δεδομένες οριακές συνθήκες 1) και 2), για την οποία η δράση είναι ελάχιστη.

Η αρχή της ελάχιστης δράσης δηλώνει ότι αυτές οι δύο τροχιές πρέπει να συμπίπτουν. Με άλλα λόγια, εάν είναι γνωστό ότι η μπάλα κινήθηκε με τέτοιο τρόπο ώστε να ικανοποιούνται οι οριακές συνθήκες 1) και 2), τότε αναγκαστικά κινήθηκε κατά μήκος μιας τροχιάς για την οποία η δράση είναι ελάχιστη σε σύγκριση με οποιαδήποτε άλλη τροχιά με το ίδιο όριο. συνθήκες.

Θα μπορούσε κανείς να το θεωρήσει αυτό ως απλή σύμπτωση. Υπάρχουν πολλά προβλήματα στα οποία εμφανίζονται ομοιόμορφες τροχιές και ευθείες γραμμές. Ωστόσο, η αρχή της ελάχιστης δράσης αποδεικνύεται ότι είναι μια πολύ γενική αρχή, που ισχύει σε άλλες καταστάσεις, για παράδειγμα, για την κίνηση μιας μπάλας σε ένα ομοιόμορφο βαρυτικό πεδίο. Για να γίνει αυτό, χρειάζεται απλώς να αντικαταστήσετε την κινητική ενέργεια με τη διαφορά μεταξύ κινητικής και δυναμικής ενέργειας. Αυτή η διαφορά ονομάζεται Lagrangian ή Lagrangian συνάρτηση και η δράση γίνεται πλέον ίση με το σύνολο του Lagrangian που έχει συσσωρευτεί. Στην πραγματικότητα, η συνάρτηση Lagrange περιέχει όλες τις απαραίτητες πληροφορίες για τις δυναμικές ιδιότητες του συστήματος.

Εάν εκτοξεύσουμε μια μπάλα σε ένα ομοιόμορφο βαρυτικό πεδίο με τέτοιο τρόπο ώστε να περνάει ένα σημείο σε μια στιγμή του χρόνου και να φτάνει σε ένα σημείο σε μια στιγμή του χρόνου, τότε, σύμφωνα με τους νόμους του Νεύτωνα, θα πετάξει κατά μήκος μιας παραβολής. Αυτή η παραβολή είναι που θα συμπέσει με τις τροχιές για τις οποίες η δράση θα είναι ελάχιστη.

Έτσι, για ένα σώμα που κινείται σε δυναμικό πεδίο, για παράδειγμα, στο βαρυτικό πεδίο της Γης, η συνάρτηση Lagrange ισούται με: . Η κινητική ενέργεια εξαρτάται από την ταχύτητα του σώματος και η δυναμική ενέργεια εξαρτάται από τη θέση του, δηλ. συντεταγμένες Στην αναλυτική μηχανική, ολόκληρο το σύνολο των συντεταγμένων που καθορίζουν τη θέση του συστήματος συνήθως συμβολίζεται με ένα γράμμα. Για μια μπάλα που κινείται ελεύθερα σε ένα βαρυτικό πεδίο, σημαίνει συντεταγμένες και .

Για να υποδείξουν το ρυθμό μεταβολής οποιασδήποτε ποσότητας, στη φυσική πολύ συχνά απλώς βάζουν μια τελεία πάνω από αυτήν την ποσότητα. Για παράδειγμα, υποδηλώνει το ρυθμό αλλαγής της συντεταγμένης ή, με άλλα λόγια, την ταχύτητα του σώματος προς την κατεύθυνση. Χρησιμοποιώντας αυτές τις συμβάσεις, η ταχύτητα της μπάλας μας στην αναλυτική μηχανική συμβολίζεται ως . Εκείνοι. σημαίνει συνιστώσες ταχύτητας.

Δεδομένου ότι η συνάρτηση Lagrange εξαρτάται από την ταχύτητα και τις συντεταγμένες και μπορεί επίσης να εξαρτάται ρητά από τον χρόνο (ρητά εξαρτάται από τον χρόνο σημαίνει ότι η τιμή είναι διαφορετική σε διαφορετικούς χρόνους, για τις ίδιες ταχύτητες και θέσεις της μπάλας), τότε η ενέργεια γενικά γράφεται όπως και

Όχι πάντα minimal

Ωστόσο, στο τέλος του προηγούμενου μέρους εξετάσαμε ένα παράδειγμα όπου η αρχή της ελάχιστης δράσης σαφώς δεν λειτουργεί. Για να το κάνουμε αυτό, πήραμε ξανά μια ελεύθερη μπάλα, πάνω στην οποία δεν δρουν δυνάμεις, και τοποθετήσαμε έναν τοίχο ελατηρίου δίπλα της.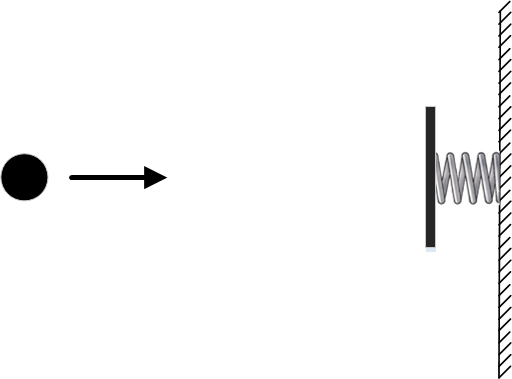

Θέτουμε τις οριακές συνθήκες έτσι ώστε τα σημεία και να συμπίπτουν. Εκείνοι. τόσο τη στιγμή του χρόνου όσο και τη στιγμή που η μπάλα πρέπει να βρίσκεται στο ίδιο σημείο. Μία από τις πιθανές τροχιές θα είναι η μπάλα να στέκεται ακίνητη. Εκείνοι. ολόκληρο το χρονικό διάστημα μεταξύ και θα σταθεί στο σημείο. Η κινητική και δυναμική ενέργεια σε αυτή την περίπτωση θα είναι ίση με μηδέν, επομένως η δράση για μια τέτοια τροχιά θα είναι επίσης ίση με μηδέν.

Αυστηρά μιλώντας, η δυναμική ενέργεια μπορεί να θεωρηθεί ότι είναι ίση όχι με το μηδέν, αλλά με οποιονδήποτε αριθμό, αφού η διαφορά της δυναμικής ενέργειας σε διαφορετικά σημεία του χώρου είναι σημαντική. Ωστόσο, η αλλαγή της τιμής δυναμικής ενέργειας δεν επηρεάζει την αναζήτηση τροχιάς με ελάχιστη δράση. Απλώς για όλες τις τροχιές η τιμή της δράσης θα αλλάξει στον ίδιο αριθμό και η τροχιά με την ελάχιστη ενέργεια θα παραμείνει η τροχιά με την ελάχιστη ενέργεια. Για ευκολία, για τη μπάλα μας θα επιλέξουμε τη δυναμική ενέργεια ίση με μηδέν.

Μια άλλη πιθανή φυσική τροχιά με τις ίδιες οριακές συνθήκες θα ήταν μια τροχιά στην οποία η μπάλα πετάει πρώτα προς τα δεξιά, περνώντας το σημείο κάθε φορά. Στη συνέχεια, συγκρούεται με το ελατήριο, το συμπιέζει, το ελατήριο, ισιώνοντας, σπρώχνει την μπάλα προς τα πίσω και αυτή ξαναπετάει πέρα ​​από το σημείο. Μπορείτε να επιλέξετε την ταχύτητα της μπάλας έτσι ώστε να αναπηδά από τον τοίχο και να περνά το σημείο ακριβώς τη στιγμή. Η δράση σε μια τέτοια τροχιά θα είναι βασικά ίση με τη συσσωρευμένη κινητική ενέργεια κατά τη διάρκεια της πτήσης μεταξύ του σημείου και του τοίχου και της πλάτης. Θα υπάρξει κάποια χρονική περίοδος που η μπάλα θα συμπιέσει το ελατήριο και η δυνητική ενέργειά του θα αυξηθεί, και κατά τη διάρκεια αυτής της χρονικής περιόδου η δυνητική ενέργεια θα έχει αρνητική συμβολή στη δράση. Αλλά μια τέτοια χρονική περίοδος δεν θα είναι πολύ μεγάλη και δεν θα μειώσει σημαντικά το αποτέλεσμα.

Το σχήμα δείχνει και τις δύο φυσικώς πιθανές τροχιές της κίνησης της μπάλας. Η πράσινη τροχιά αντιστοιχεί σε μια μπάλα σε ηρεμία, ενώ η μπλε τροχιά αντιστοιχεί σε μια μπάλα που αναπηδά από έναν τοίχο ελατηρίου.

Ωστόσο, μόνο ένα από αυτά έχει ελάχιστο αποτέλεσμα, δηλαδή το πρώτο! Η δεύτερη τροχιά έχει περισσότερη δράση. Αποδεικνύεται ότι σε αυτό το πρόβλημα υπάρχουν δύο φυσικά πιθανές τροχιές και μόνο μία με ελάχιστη δράση. Εκείνοι. Σε αυτή την περίπτωση, η αρχή της ελάχιστης δράσης δεν λειτουργεί.

Σταθερά σημεία

Για να κατανοήσουμε τι συμβαίνει εδώ, ας αγνοήσουμε την αρχή της ελάχιστης δράσης προς το παρόν και ας προχωρήσουμε στις συνηθισμένες λειτουργίες. Ας πάρουμε μια συνάρτηση και ας σχεδιάσουμε το γράφημά της:

Στο γράφημα σημείωσα τέσσερα ειδικά σημεία με πράσινο χρώμα. Τι κοινό έχουν αυτά τα σημεία; Ας φανταστούμε ότι το γράφημα μιας συνάρτησης είναι μια πραγματική διαφάνεια κατά μήκος της οποίας μπορεί να κυλήσει μια μπάλα. Τα τέσσερα καθορισμένα σημεία είναι ιδιαίτερα στο ότι αν τοποθετήσετε την μπάλα ακριβώς σε αυτό το σημείο, δεν θα κυλήσει πουθενά. Σε όλα τα άλλα σημεία, για παράδειγμα, το σημείο Ε, δεν θα μπορεί να μείνει ακίνητος και θα αρχίσει να γλιστράει προς τα κάτω. Τέτοια σημεία ονομάζονται ακίνητα. Η εύρεση τέτοιων σημείων είναι μια χρήσιμη εργασία, καθώς οποιοδήποτε μέγιστο ή ελάχιστο μιας συνάρτησης, εάν δεν έχει απότομες διακοπές, πρέπει απαραίτητα να είναι ένα ακίνητο σημείο.

Αν ταξινομήσουμε με μεγαλύτερη ακρίβεια αυτά τα σημεία, τότε το σημείο Α είναι το απόλυτο ελάχιστο της συνάρτησης, δηλ. η τιμή του είναι μικρότερη από οποιαδήποτε άλλη τιμή συνάρτησης. Το σημείο Β δεν είναι ούτε μέγιστο ούτε ελάχιστο και ονομάζεται σημείο σέλας. Το σημείο Γ ονομάζεται τοπικό μέγιστο, δηλ. η τιμή σε αυτό είναι μεγαλύτερη από ό,τι σε γειτονικά σημεία της συνάρτησης. Και το σημείο Δ είναι ένα τοπικό ελάχιστο, δηλ. η τιμή σε αυτό είναι μικρότερη από ό,τι σε γειτονικά σημεία της συνάρτησης.

Η αναζήτηση τέτοιων σημείων πραγματοποιείται από έναν κλάδο των μαθηματικών που ονομάζεται μαθηματική ανάλυση. Διαφορετικά, μερικές φορές ονομάζεται απειροελάχιστη ανάλυση, αφού μπορεί να λειτουργήσει με απειροελάχιστα μεγέθη. Από την άποψη της μαθηματικής ανάλυσης, τα ακίνητα σημεία έχουν μια ειδική ιδιότητα, χάρη στην οποία βρίσκονται. Για να καταλάβουμε ποια είναι αυτή η ιδιότητα, πρέπει να καταλάβουμε πώς φαίνεται η συνάρτηση σε πολύ μικρές αποστάσεις από αυτά τα σημεία. Για να το κάνουμε αυτό, θα πάρουμε ένα μικροσκόπιο και θα το κοιτάξουμε μέσα από τα σημεία μας. Το σχήμα δείχνει πώς φαίνεται η συνάρτηση κοντά σε διάφορα σημεία σε διαφορετικές μεγεθύνσεις.

Μπορεί να φανεί ότι σε πολύ υψηλή μεγέθυνση (δηλαδή για πολύ μικρές αποκλίσεις x) τα ακίνητα σημεία φαίνονται ακριβώς τα ίδια και είναι πολύ διαφορετικά από το μη ακίνητο σημείο. Είναι εύκολο να καταλάβουμε ποια είναι αυτή η διαφορά - το γράφημα μιας συνάρτησης σε ένα ακίνητο σημείο γίνεται αυστηρά οριζόντια γραμμή όταν αυξάνεται, και σε ένα μη ακίνητο σημείο γίνεται κεκλιμένη γραμμή. Αυτός είναι ο λόγος για τον οποίο μια μπάλα που είναι εγκατεστημένη σε ακίνητο σημείο δεν θα κυλήσει προς τα κάτω.

Η οριζοντιότητα μιας συνάρτησης σε ένα ακίνητο σημείο μπορεί να εκφραστεί διαφορετικά: η συνάρτηση σε ένα ακίνητο σημείο πρακτικά δεν αλλάζει με μια πολύ μικρή αλλαγή στο όρισμά της, ακόμη και σε σύγκριση με την ίδια την αλλαγή στο όρισμα. Η συνάρτηση σε μη ακίνητο σημείο με μικρή αλλαγή αλλάζει ανάλογα με τη μεταβολή. Και όσο μεγαλύτερη είναι η κλίση της συνάρτησης, τόσο περισσότερο αλλάζει η συνάρτηση όταν . Στην πραγματικότητα, όσο αυξάνεται η συνάρτηση, γίνεται όλο και περισσότερο σαν μια εφαπτομένη στο γράφημα στο εν λόγω σημείο.

Στην αυστηρή μαθηματική γλώσσα, η έκφραση "μια συνάρτηση πρακτικά δεν αλλάζει σε ένα σημείο με πολύ μικρή αλλαγή" σημαίνει ότι ο λόγος μιας αλλαγής σε μια συνάρτηση και μιας αλλαγής στο όρισμά της τείνει στο 0 καθώς τείνει στο 0:

$$εμφάνιση$$\lim_(∆x \έως 0) \frac (∆y(x_0))(∆x) = \lim_(x \έως 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$εμφάνιση$$

Για ένα μη ακίνητο σημείο, αυτός ο λόγος τείνει σε έναν μη μηδενικό αριθμό, ο οποίος είναι ίσος με την εφαπτομένη της κλίσης της συνάρτησης σε αυτό το σημείο. Αυτός ο ίδιος αριθμός ονομάζεται παράγωγος της συνάρτησης σε ένα δεδομένο σημείο. Η παράγωγος μιας συνάρτησης δείχνει πόσο γρήγορα αλλάζει η συνάρτηση γύρω από ένα δεδομένο σημείο με μια μικρή αλλαγή στο όρισμά της. Έτσι, ακίνητα σημεία είναι τα σημεία στα οποία η παράγωγος της συνάρτησης είναι ίση με 0.

Στατικές τροχιές

Κατ' αναλογία με ακίνητα σημεία, μπορούμε να εισαγάγουμε την έννοια των στατικών τροχιών. Ας θυμηθούμε ότι κάθε τροχιά αντιστοιχεί σε μια συγκεκριμένη τιμή ενέργειας, δηλ. κάποιο νούμερο. Τότε μπορεί να υπάρξει μια τροχιά τέτοια ώστε για τροχιές κοντά σε αυτήν με τις ίδιες οριακές συνθήκες, οι αντίστοιχες τιμές δράσης πρακτικά δεν θα διαφέρουν από την ενέργεια για την ίδια την ακίνητη τροχιά. Μια τέτοια τροχιά ονομάζεται ακίνητη. Με άλλα λόγια, οποιαδήποτε τροχιά κοντά σε ακίνητη θα έχει μια τιμή δράσης που διαφέρει πολύ λίγο από την ενέργεια για αυτήν την ακίνητη τροχιά.

Και πάλι, στη μαθηματική γλώσσα, το «ελαφρώς διαφορετικό» έχει την ακόλουθη ακριβή σημασία. Ας υποθέσουμε ότι έχουμε μια δεδομένη συνάρτηση για συναρτήσεις με τις απαιτούμενες οριακές συνθήκες 1) και 2), δηλ. Και . Ας υποθέσουμε ότι η τροχιά είναι ακίνητη.

Μπορούμε να πάρουμε οποιαδήποτε άλλη συνάρτηση έτσι ώστε να παίρνει μηδενικές τιμές στα άκρα, δηλ. = = 0. Ας πάρουμε και μια μεταβλητή, την οποία θα κάνουμε όλο και μικρότερη. Από αυτές τις δύο συναρτήσεις και τη μεταβλητή, μπορούμε να συνθέσουμε μια τρίτη συνάρτηση, η οποία θα ικανοποιεί επίσης τις οριακές συνθήκες και. Καθώς μειώνεται, η τροχιά που αντιστοιχεί στη συνάρτηση θα πλησιάζει όλο και περισσότερο την τροχιά.

Επιπλέον, για σταθερές τροχιές σε μικρές τιμές του λειτουργικού για τις τροχιές θα διαφέρει πολύ λίγο από την τιμή του λειτουργικού για ακόμη και σε σύγκριση με το . Εκείνοι.

$$εμφάνιση$$\lim_(ε \to 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε \to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$εμφάνιση$$

Επιπλέον, αυτό θα πρέπει να ισχύει για οποιαδήποτε τροχιά που ικανοποιεί τις οριακές συνθήκες = = 0.

Μια αλλαγή στη συνάρτηση με μια μικρή αλλαγή στη συνάρτηση (ακριβέστερα, το γραμμικό μέρος της μεταβολής της συνάρτησης, ανάλογο με την αλλαγή της συνάρτησης) ονομάζεται παραλλαγή της συνάρτησης και συμβολίζεται με . Το όνομα «λογισμός μεταβολών» προέρχεται από τον όρο «παραλλαγή».

Για σταθερές τροχιές, παραλλαγή της λειτουργικής.

Μια μέθοδος για την εύρεση σταθερών συναρτήσεων (όχι μόνο για την αρχή της ελάχιστης δράσης, αλλά και για πολλά άλλα προβλήματα) βρέθηκε από δύο μαθηματικούς - τον Euler και τον Lagrange. Αποδεικνύεται ότι μια ακίνητη συνάρτηση, της οποίας η συνάρτηση εκφράζεται με ένα ολοκλήρωμα παρόμοιο με το ολοκλήρωμα δράσης, πρέπει να ικανοποιεί μια ορισμένη εξίσωση, η οποία τώρα ονομάζεται εξίσωση Euler-Lagrange.

Στατική αρχή

Η κατάσταση με μια ελάχιστη ενέργεια για τις τροχιές είναι παρόμοια με την κατάσταση με την ελάχιστη ενέργεια για τις συναρτήσεις. Για να έχει μια τροχιά το μικρότερο αποτέλεσμα, πρέπει να είναι μια σταθερή τροχιά. Ωστόσο, δεν είναι όλες οι σταθερές τροχιές ελάχιστες τροχιές δράσης. Για παράδειγμα, μια σταθερή τροχιά μπορεί να έχει ελάχιστη επίδραση τοπικά. Εκείνοι. η δράση του θα είναι μικρότερη από αυτή οποιασδήποτε άλλης γειτονικής τροχιάς. Ωστόσο, κάπου μακριά μπορεί να υπάρχουν άλλες τροχιές για τις οποίες η δράση θα είναι ακόμη λιγότερη.

Αποδεικνύεται ότι τα πραγματικά σώματα μπορεί να μην κινούνται απαραίτητα κατά μήκος τροχιών με την ελάχιστη δράση. Μπορούν να κινηθούν κατά μήκος ενός ευρύτερου συνόλου ειδικών τροχιών, δηλαδή σταθερών τροχιών. Εκείνοι. η πραγματική τροχιά του σώματος θα είναι πάντα ακίνητη. Επομένως, η αρχή της ελάχιστης δράσης ονομάζεται ορθότερα αρχή της στατικής δράσης. Ωστόσο, σύμφωνα με την καθιερωμένη παράδοση, ονομάζεται συχνά η αρχή της ελάχιστης δράσης, υπονοώντας όχι μόνο την ελάχιστη, αλλά και τη σταθερότητα των τροχιών.

Τώρα μπορούμε να γράψουμε την αρχή της στατικής δράσης στη μαθηματική γλώσσα, όπως συνήθως γράφεται στα σχολικά βιβλία: .

Εδώ αυτές είναι γενικευμένες συντεταγμένες, δηλ. ένα σύνολο μεταβλητών που καθορίζουν μοναδικά τη θέση του συστήματος.
- ρυθμός μεταβολής γενικευμένων συντεταγμένων.
- Συνάρτηση Lagrange, η οποία εξαρτάται από τις γενικευμένες συντεταγμένες, τις ταχύτητες τους και, πιθανώς, τον χρόνο.
- μια ενέργεια που εξαρτάται από τη συγκεκριμένη τροχιά του συστήματος (δηλαδή στις ).

Οι πραγματικές τροχιές του συστήματος είναι στάσιμες, δηλ. για αυτούς μια παραλλαγή της δράσης.

Αν επιστρέψουμε στο παράδειγμα με μια μπάλα και έναν ελαστικό τοίχο, τότε η εξήγηση αυτής της κατάστασης γίνεται πλέον πολύ απλή. Υπό δεδομένες οριακές συνθήκες που η μπάλα πρέπει να καταλήξει σε ένα σημείο τόσο την ώρα όσο και την ώρα, υπάρχουν δύο ακίνητες τροχιές. Και η μπάλα μπορεί πραγματικά να κινηθεί κατά μήκος οποιασδήποτε από αυτές τις τροχιές. Για να επιλέξετε ρητά μία από τις τροχιές, μπορείτε να επιβάλετε έναν επιπλέον όρο στην κίνηση της μπάλας. Για παράδειγμα, πείτε ότι η μπάλα πρέπει να αναπηδήσει από τον τοίχο. Τότε η τροχιά θα καθοριστεί αναμφίβολα.

Μερικές αξιοσημείωτες συνέπειες προκύπτουν από την αρχή της ελάχιστης (ακριβέστερα στατικής) δράσης, την οποία θα συζητήσουμε στο επόμενο μέρος.

Το υπακούουν και επομένως αυτή η αρχή είναι μια από τις βασικές διατάξεις της σύγχρονης φυσικής. Οι εξισώσεις κίνησης που λαμβάνονται με τη βοήθειά του ονομάζονται εξισώσεις Euler-Lagrange.

Η πρώτη διατύπωση της αρχής δόθηκε από τον P. Maupertuis το έτος, επισημαίνοντας αμέσως την καθολική φύση της, θεωρώντας την εφαρμόσιμη στην οπτική και τη μηχανική. Από αυτή την αρχή έβγαλε τους νόμους της ανάκλασης και της διάθλασης του φωτός.

Ιστορία

Ο Maupertuis κατέληξε σε αυτήν την αρχή από την αίσθηση ότι η τελειότητα του Σύμπαντος απαιτεί μια ορισμένη οικονομία στη φύση και έρχεται σε αντίθεση με κάθε άχρηστη δαπάνη ενέργειας. Η φυσική κίνηση πρέπει να είναι τέτοια ώστε να κάνει μια ορισμένη ποσότητα ελάχιστη. Το μόνο που έπρεπε να κάνει ήταν να βρει αυτή την αξία, την οποία συνέχισε να κάνει. Ήταν το γινόμενο της διάρκειας (χρόνου) της κίνησης μέσα στο σύστημα κατά διπλάσια τιμή, που τώρα ονομάζουμε κινητική ενέργεια του συστήματος.

Euler (σε "Réflexions sur quelques loix générales de la nature", 1748) υιοθετεί την αρχή της ελάχιστης δράσης, αποκαλώντας τη δράση «προσπάθεια». Η έκφρασή του σε στατική αντιστοιχεί σε αυτό που θα ονομάζαμε τώρα δυναμική ενέργεια, έτσι ώστε η δήλωση της ελάχιστης δράσης του στη στατική είναι ισοδύναμη με την συνθήκη ελάχιστης δυναμικής ενέργειας για μια διαμόρφωση ισορροπίας.

Στην κλασική μηχανική

Η αρχή της ελάχιστης δράσης χρησιμεύει ως η θεμελιώδης και τυπική βάση των διατυπώσεων της μηχανικής Lagrangian και Hamilton.

Αρχικά, ας δούμε την κατασκευή ως εξής: Λαγκρανζική μηχανική. Χρησιμοποιώντας το παράδειγμα ενός φυσικού συστήματος με έναν βαθμό ελευθερίας, ας υπενθυμίσουμε ότι μια ενέργεια είναι μια συνάρτηση σε σχέση με (γενικευμένες) συντεταγμένες (στην περίπτωση ενός βαθμού ελευθερίας - μία συντεταγμένη), δηλαδή εκφράζεται μέσω έτσι ώστε κάθε πιθανή εκδοχή της συνάρτησης να σχετίζεται με έναν ορισμένο αριθμό - μια ενέργεια (με αυτή την έννοια, μπορούμε να πούμε ότι μια ενέργεια ως συνάρτηση είναι ένας κανόνας που επιτρέπει σε κάθε δεδομένη συνάρτηση να υπολογίσει έναν εντελώς συγκεκριμένο αριθμό - που ονομάζεται επίσης μια δράση). Η δράση μοιάζει με:

όπου είναι το Lagrangian του συστήματος, ανάλογα με τη γενικευμένη συντεταγμένη, η πρώτη του παράγωγος ως προς το χρόνο, και επίσης, ενδεχομένως, ρητά στον χρόνο. Εάν το σύστημα έχει μεγαλύτερο αριθμό βαθμών ελευθερίας, τότε ο Λαγκραντζιανός εξαρτάται από μεγαλύτερο αριθμό γενικευμένων συντεταγμένων και των πρώτων παραγώγων τους ως προς το χρόνο. Έτσι, η δράση είναι βαθμωτή λειτουργική ανάλογα με την τροχιά του σώματος.

Το γεγονός ότι η ενέργεια είναι βαθμωτή καθιστά εύκολη τη γραφή της σε οποιεσδήποτε γενικευμένες συντεταγμένες, το κύριο πράγμα είναι ότι η θέση (διαμόρφωση) του συστήματος χαρακτηρίζεται ξεκάθαρα από αυτές (για παράδειγμα, αντί για καρτεσιανές συντεταγμένες, αυτές μπορεί να είναι πολικές συντεταγμένες, αποστάσεις μεταξύ σημείων του συστήματος, γωνίες ή συναρτήσεις τους κ.λπ. .δ.).

Η δράση μπορεί να υπολογιστεί για μια εντελώς αυθαίρετη τροχιά, ανεξάρτητα από το πόσο «άγρια» και «αφύσικη» μπορεί να είναι. Ωστόσο, στην κλασική μηχανική, ανάμεσα σε ολόκληρο το σύνολο των πιθανών τροχιών, υπάρχει μόνο μία κατά μήκος της οποίας θα κινηθεί πραγματικά το σώμα. Η αρχή της ακίνητης δράσης δίνει ακριβώς την απάντηση στο ερώτημα πώς θα κινηθεί πραγματικά το σώμα:

Αυτό σημαίνει ότι εάν δοθεί το Lagrangian του συστήματος, τότε χρησιμοποιώντας τον λογισμό των παραλλαγών μπορούμε να καθορίσουμε πώς ακριβώς θα κινηθεί το σώμα παίρνοντας πρώτα τις εξισώσεις κίνησης - τις εξισώσεις Euler-Lagrange και στη συνέχεια λύνοντάς τις. Αυτό επιτρέπει όχι μόνο τη σοβαρή γενίκευση της διατύπωσης της μηχανικής, αλλά και την επιλογή των πιο βολικών συντεταγμένων για κάθε συγκεκριμένο πρόβλημα, χωρίς να περιορίζεται στα καρτεσιανά, που μπορεί να είναι πολύ χρήσιμα για τη λήψη των απλούστερων και πιο εύκολα λυμένων εξισώσεων.

πού είναι η συνάρτηση Hamilton αυτού του συστήματος; - (γενικευμένες) συντεταγμένες, - συζευγμένες (γενικευμένες) παρορμήσεις, οι οποίες μαζί χαρακτηρίζουν σε κάθε δεδομένη χρονική στιγμή τη δυναμική κατάσταση του συστήματος και, καθεμία συνάρτηση του χρόνου, χαρακτηρίζοντας έτσι την εξέλιξη (κίνηση) του συστήματος. Σε αυτή την περίπτωση, για να ληφθούν οι εξισώσεις κίνησης του συστήματος με τη μορφή των κανονικών εξισώσεων του Hamilton, είναι απαραίτητο να μεταβληθεί η ενέργεια που γράφτηκε με αυτόν τον τρόπο ανεξάρτητα για όλους και .

Πρέπει να σημειωθεί ότι εάν από τις συνθήκες του προβλήματος είναι καταρχήν δυνατό να βρεθεί ο νόμος της κίνησης, τότε αυτό γίνεται αυτόματα Δενσημαίνει ότι είναι δυνατό να κατασκευαστεί μια συνάρτηση που παίρνει μια σταθερή τιμή κατά την πραγματική κίνηση. Ένα παράδειγμα είναι η κοινή κίνηση ηλεκτρικών φορτίων και μονοπόλων -μαγνητικά φορτία- σε ένα ηλεκτρομαγνητικό πεδίο. Οι εξισώσεις κίνησής τους δεν μπορούν να προκύψουν από την αρχή της ακίνητης δράσης. Ομοίως, ορισμένα συστήματα Χαμιλτονίου έχουν εξισώσεις κίνησης που δεν μπορούν να προκύψουν από αυτήν την αρχή.

Παραδείγματα

Ασήμαντα παραδείγματα βοηθούν στην αξιολόγηση της χρήσης της αρχής λειτουργίας μέσω των εξισώσεων Euler-Lagrange. Ελεύθερο σωματίδιο (μάζα Μκαι ταχύτητα v) στον Ευκλείδειο χώρο κινείται σε ευθεία γραμμή. Χρησιμοποιώντας τις εξισώσεις Euler-Lagrange, αυτό μπορεί να φανεί σε πολικές συντεταγμένες ως εξής. Ελλείψει δυναμικού, η συνάρτηση Lagrange είναι απλώς ίση με την κινητική ενέργεια

σε ένα ορθογώνιο σύστημα συντεταγμένων.

Στις πολικές συντεταγμένες, η κινητική ενέργεια, και επομένως η συνάρτηση Lagrange, γίνεται

Οι ακτινικές και γωνιακές συνιστώσες των εξισώσεων γίνονται, αντίστοιχα:

Επίλυση αυτών των δύο εξισώσεων

Εδώ είναι μια υπό όρους συμβολισμός για άπειρα πολλαπλή συναρτητική ολοκλήρωση σε όλες τις τροχιές x(t) και είναι η σταθερά του Planck. Τονίζουμε ότι, καταρχήν, η δράση στην εκθετική εμφανίζεται (ή μπορεί να εμφανιστεί) η ίδια κατά τη μελέτη του τελεστή εξέλιξης στην κβαντομηχανική, αλλά για συστήματα που έχουν ακριβές κλασσικό (μη κβαντικό) ανάλογο, είναι ακριβώς ίση με το συνηθισμένο κλασική δράση.

Η μαθηματική ανάλυση αυτής της έκφρασης στο κλασικό όριο - για αρκετά μεγάλες, δηλαδή για πολύ γρήγορες ταλαντώσεις της φανταστικής εκθετικής - δείχνει ότι η συντριπτική πλειοψηφία όλων των πιθανών τροχιών σε αυτό το ολοκλήρωμα ακυρώνει η μία την άλλη στο όριο (τυπικά για ). Σχεδόν για οποιοδήποτε μονοπάτι υπάρχει μια διαδρομή στην οποία η μετατόπιση φάσης θα είναι ακριβώς το αντίθετο, και θα αθροίζονται ως μηδενική συνεισφορά. Μόνο εκείνες οι τροχιές για τις οποίες η δράση είναι κοντά στην ακραία τιμή (για τα περισσότερα συστήματα - στο ελάχιστο) δεν μειώνονται. Αυτό είναι ένα καθαρά μαθηματικό γεγονός από τη θεωρία των συναρτήσεων μιας μιγαδικής μεταβλητής. Για παράδειγμα, η μέθοδος στατικής φάσης βασίζεται σε αυτήν.

Ως αποτέλεσμα, το σωματίδιο, σε πλήρη συμφωνία με τους νόμους της κβαντικής μηχανικής, κινείται ταυτόχρονα κατά μήκος όλων των τροχιών, αλλά υπό κανονικές συνθήκες μόνο τροχιές κοντά σε ακίνητες (δηλαδή κλασικές) συμβάλλουν στις παρατηρούμενες τιμές. Δεδομένου ότι η κβαντική μηχανική μετατρέπεται σε κλασική μηχανική στο όριο των υψηλών ενεργειών, μπορούμε να υποθέσουμε ότι αυτό είναι κβαντομηχανική εξαγωγή της κλασικής αρχής της στασιμότητας της δράσης.

Στην κβαντική θεωρία πεδίου

Στην κβαντική θεωρία πεδίου εφαρμόζεται επίσης με επιτυχία η αρχή της ακίνητης δράσης. Η πυκνότητα Lagrangi εδώ περιλαμβάνει τους τελεστές των αντίστοιχων κβαντικών πεδίων. Αν και είναι πιο σωστό εδώ στην ουσία (με εξαίρεση το κλασικό όριο και εν μέρει τα σχεδόν κλασσικά) να μην μιλάμε για την αρχή της σταθερότητας της δράσης, αλλά για την ολοκλήρωση Feynman κατά μήκος τροχιών στη διαμόρφωση ή στο χώρο φάσης αυτών των πεδίων - χρησιμοποιώντας η μόλις αναφερθείσα Lagrange πυκνότητα.

Περαιτέρω γενικεύσεις

Ευρύτερα, μια ενέργεια νοείται ως μια συνάρτηση που ορίζει μια αντιστοίχιση από έναν χώρο διαμόρφωσης σε ένα σύνολο πραγματικών αριθμών και, γενικά, δεν χρειάζεται να είναι ολοκλήρωμα, επειδή οι μη τοπικές ενέργειες είναι κατ' αρχήν δυνατές, τουλάχιστον θεωρητικά. Επιπλέον, ένας χώρος διαμόρφωσης δεν είναι απαραίτητα ένας χώρος συναρτήσεων, επειδή μπορεί να έχει μη μεταθετική γεωμετρία.

Η αρχή της ελάχιστης δράσης, που διατυπώθηκε για πρώτη φορά ακριβώς από τον Jacobi, είναι παρόμοια με την αρχή του Hamilton, αλλά λιγότερο γενική και πιο δύσκολο να αποδειχθεί. Αυτή η αρχή εφαρμόζεται μόνο στην περίπτωση που οι συνδέσεις και η συνάρτηση δύναμης δεν εξαρτώνται από το χρόνο και όταν, επομένως, υπάρχει ένα ολοκλήρωμα ζωντανής δύναμης.

Αυτό το ολοκλήρωμα έχει τη μορφή:

Η αρχή του Hamilton που αναφέρθηκε παραπάνω δηλώνει ότι η παραλλαγή του ολοκληρώματος

ισούται με μηδέν κατά τη μετάβαση της πραγματικής κίνησης σε οποιαδήποτε άλλη απείρως κοντινή κίνηση, η οποία μεταφέρει το σύστημα από την ίδια αρχική θέση στην ίδια τελική θέση στην ίδια χρονική περίοδο.

Η αρχή του Jacobi, αντίθετα, εκφράζει μια ιδιότητα κίνησης που δεν εξαρτάται από το χρόνο. Ο Jacobi θεωρεί το αναπόσπαστο

καθοριστική δράση. Η αρχή που καθιέρωσε δηλώνει ότι η μεταβολή αυτού του ολοκληρώματος είναι μηδέν όταν συγκρίνουμε την πραγματική κίνηση του συστήματος με οποιαδήποτε άλλη απείρως στενή κίνηση που οδηγεί το σύστημα από την ίδια αρχική θέση στην ίδια τελική θέση. Σε αυτή την περίπτωση, δεν δίνουμε προσοχή στη χρονική περίοδο που δαπανάται, αλλά παρατηρούμε την εξίσωση (1), δηλαδή την εξίσωση του ανθρώπινου δυναμικού με την ίδια τιμή της σταθεράς h όπως στην πραγματική κίνηση.

Αυτή η απαραίτητη προϋπόθεση για ένα άκρο οδηγεί, γενικά, σε ένα ελάχιστο ολοκλήρωμα (2), εξ ου και η ονομασία αρχή της ελάχιστης δράσης. Η ελάχιστη συνθήκη φαίνεται να είναι η πιο φυσική, αφού η τιμή του Τ είναι ουσιαστικά θετική και επομένως το ολοκλήρωμα (2) πρέπει απαραίτητα να έχει ελάχιστο. Η ύπαρξη ενός ελάχιστου μπορεί να αποδειχθεί αυστηρά εάν μόνο η χρονική περίοδος είναι αρκετά μικρή. Η απόδειξη αυτής της θέσης βρίσκεται στη διάσημη πορεία του Darboux για τη θεωρία της επιφάνειας. Εμείς, ωστόσο, δεν θα το παρουσιάσουμε εδώ και θα περιοριστούμε στην εξαγωγή της συνθήκης

432. Απόδειξη της αρχής της ελάχιστης δράσης.

Στον πραγματικό υπολογισμό συναντάμε μια δυσκολία που δεν υπάρχει στην απόδειξη του θεωρήματος του Hamilton. Η μεταβλητή t δεν παραμένει πλέον ανεξάρτητη από την παραλλαγή. επομένως παραλλαγές των q i και q. σχετίζονται με τη μεταβολή του t με μια μιγαδική σχέση που προκύπτει από την εξίσωση (1). Ο απλούστερος τρόπος για να ξεπεράσετε αυτήν τη δυσκολία είναι να αλλάξετε την ανεξάρτητη μεταβλητή, επιλέγοντας μια της οποίας οι τιμές εμπίπτουν μεταξύ σταθερών ορίων που δεν εξαρτώνται από το χρόνο. Έστω k μια νέα ανεξάρτητη μεταβλητή, τα όρια της οποίας θεωρούνται ανεξάρτητα από το t. Όταν μετακινείτε το σύστημα, οι παράμετροι και το t θα είναι συναρτήσεις αυτής της μεταβλητής

Έστω γράμματα με πρώτους q υποδηλώνουν παράγωγα των παραμέτρων q ως προς το χρόνο.

Εφόσον οι συνδέσεις, κατά την υπόθεση, δεν εξαρτώνται από το χρόνο, οι καρτεσιανές συντεταγμένες x, y, z είναι συναρτήσεις του q που δεν περιέχουν χρόνο. Επομένως, οι παράγωγοί τους θα είναι γραμμικές ομοιογενείς συναρτήσεις του q και το 7 θα είναι μια ομοιογενής τετραγωνική μορφή του q, οι συντελεστές της οποίας είναι συναρτήσεις του q. Εχουμε

Για να διακρίνουμε τα παράγωγα του q ως προς το χρόνο, δηλώνουμε, χρησιμοποιώντας παρενθέσεις, (q), τα παράγωγα του q λαμβάνονται ως προς και που τίθενται σύμφωνα με αυτό.

τότε θα έχουμε

και το ολοκλήρωμα (2), που εκφράζεται μέσω της νέας ανεξάρτητης μεταβλητής Α, θα λάβει τη μορφή.

Η παράγωγος μπορεί να εξαλειφθεί χρησιμοποιώντας το θεώρημα της ζωντανής δύναμης. Πράγματι, το αναπόσπαστο του ανθρώπινου δυναμικού θα είναι

Αντικαθιστώντας αυτήν την έκφραση στον τύπο για, ανάγουμε το ολοκλήρωμα (2) στη μορφή

Το ολοκλήρωμα που ορίζει τη δράση πήρε έτσι την τελική του μορφή (3). Η συνάρτηση ολοκληρώματος είναι η τετραγωνική ρίζα της τετραγωνικής μορφής των μεγεθών

Ας δείξουμε ότι οι διαφορικές εξισώσεις των ακραίων του ολοκληρώματος (3) είναι ακριβώς οι εξισώσεις Lagrange. Οι εξισώσεις των ακραίων, με βάση τους γενικούς τύπους του λογισμού των μεταβολών, θα είναι:

Ας πολλαπλασιάσουμε τις εξισώσεις επί 2 και ας κάνουμε μερικές διαφοροποιήσεις, λαμβάνοντας υπόψη ότι δεν περιέχει, τότε παίρνουμε, αν δεν γράψουμε δείκτη,

Αυτές είναι εξισώσεις ακραίων που εκφράζονται με όρους της ανεξάρτητης μεταβλητής Το καθήκον τώρα είναι να επιστρέψουμε στην ανεξάρτητη μεταβλητή

Εφόσον το Γ είναι ομοιογενής συνάρτηση του δεύτερου βαθμού και είναι ομοιογενής συνάρτηση του πρώτου βαθμού, έχουμε

Από την άλλη πλευρά, το θεώρημα της ζωντανής δύναμης μπορεί να εφαρμοστεί στους παράγοντες των παραγώγων στις εξισώσεις των ακραίων, γεγονός που οδηγεί, όπως είδαμε παραπάνω, στην υποκατάσταση

Ως αποτέλεσμα όλων των αντικαταστάσεων, οι εξισώσεις των ακραίων μειώνονται στη μορφή

Φτάσαμε λοιπόν στις εξισώσεις Lagrange.

433. Η περίπτωση που δεν υπάρχουν κινητήριες δυνάμεις.

Στην περίπτωση που δεν υπάρχουν κινητήριες δυνάμεις, υπάρχει εξίσωση ζωντανής δύναμης και έχουμε

Η προϋπόθεση για το ολοκλήρωμα να είναι ελάχιστο είναι σε αυτή την περίπτωση ότι η αντίστοιχη τιμή του -10 πρέπει να είναι η μικρότερη. Έτσι, όταν δεν υπάρχουν κινητήριες δυνάμεις, τότε μεταξύ όλων των κινήσεων στις οποίες η ζωντανή δύναμη διατηρεί την ίδια δεδομένη τιμή, η πραγματική κίνηση είναι αυτή που μεταφέρει το σύστημα από την αρχική του θέση στην τελική του θέση στο συντομότερο χρόνο.

Εάν το σύστημα μειωθεί σε ένα σημείο που κινείται σε μια ακίνητη επιφάνεια, τότε η πραγματική κίνηση, μεταξύ όλων των κινήσεων στην επιφάνεια που συμβαίνουν με την ίδια ταχύτητα, είναι η κίνηση κατά την οποία το σημείο μετακινείται από την αρχική του θέση στην τελική θέση στο συντομότερος

χρονικό διάστημα. Με άλλα λόγια, ένα σημείο περιγράφει στην επιφάνεια τη συντομότερη γραμμή μεταξύ των δύο θέσεων του, δηλαδή μια γεωδαισιακή γραμμή.

434. Σημ.

Η αρχή της ελάχιστης δράσης προϋποθέτει ότι το σύστημα έχει πολλούς βαθμούς ελευθερίας, αφού αν υπήρχε μόνο ένας βαθμός ελευθερίας, τότε μια εξίσωση θα ήταν αρκετή για να καθορίσει την κίνηση. Εφόσον η κίνηση μπορεί σε αυτή την περίπτωση να προσδιοριστεί πλήρως από την εξίσωση της ζωντανής δύναμης, τότε η πραγματική κίνηση θα είναι η μόνη που ικανοποιεί αυτήν την εξίσωση και επομένως δεν μπορεί να συγκριθεί με καμία άλλη κίνηση.

P. Maupertuis) το 1744, επισημαίνοντας αμέσως την καθολική φύση του και θεωρώντας το εφαρμόσιμο στην οπτική και τη μηχανική. Από αυτή την αρχή έβγαλε τους νόμους της ανάκλασης και της διάθλασης του φωτός.

Εγκυκλοπαιδικό YouTube

• 1 / 5

  Η μαθηματική έρευνα και ανάπτυξη της αρχής του Fermat πραγματοποιήθηκε από τον Christiaan Huygens, μετά τον οποίο το θέμα συζητήθηκε ενεργά από τους μεγαλύτερους επιστήμονες του 17ου αιώνα. Ο Λάιμπνιτς εισήγαγε τη θεμελιώδη έννοια της δράσης στη φυσική το 1669: «Οι τυπικές ενέργειες της κίνησης είναι ανάλογες… προς το γινόμενο της ποσότητας της ύλης, τις αποστάσεις στις οποίες κινούνται και την ταχύτητα».

  Παράλληλα με την ανάλυση των θεμελιωδών αρχών της μηχανικής, αναπτύχθηκαν μέθοδοι επίλυσης μεταβλητών προβλημάτων. Ο Ισαάκ Νεύτων στις «Μαθηματικές αρχές της φυσικής φιλοσοφίας» (1687) έθεσε και έλυσε το πρώτο μεταβλητό πρόβλημα: να βρει μια μορφή σώματος περιστροφής που κινείται σε ένα ανθεκτικό μέσο κατά μήκος του άξονά του για το οποίο η αντίσταση που παρουσιάστηκε θα ήταν η ελάχιστη. Σχεδόν ταυτόχρονα, εμφανίστηκαν και άλλα μεταβλητά προβλήματα: το πρόβλημα του βραχιστόχρονου (1696), η μορφή μιας γραμμής αλυσίδας κ.λπ.

  Αποφασιστικά γεγονότα έλαβαν χώρα το 1744. Ο Leonhard Euler δημοσίευσε το πρώτο γενικό έργο για τον λογισμό των παραλλαγών («Μέθοδος εύρεσης καμπυλών που κατέχουν τις ιδιότητες μέγιστου ή ελάχιστου») και ο Pierre-Louis de Maupertuis, στην πραγματεία του «The Reconciliation of Various Laws of Nature, Who Hitherto Feed. Ασυμβίβαστο», έδωσε η πρώτη διατύπωση της αρχής της ελάχιστης δράσης: «το μονοπάτι που ακολουθεί το φως είναι το μονοπάτι για το οποίο η ποσότητα της δράσης θα είναι η μικρότερη». Απέδειξε την εκπλήρωση αυτού του νόμου τόσο για την ανάκλαση όσο και για τη διάθλαση του φωτός. Σε απάντηση στο άρθρο του Maupertuis, ο Euler δημοσίευσε (το ίδιο έτος 1744) το έργο «Σχετικά με τον προσδιορισμό της κίνησης των πεταμένων σωμάτων σε ένα μη αντιστασιακό μέσο με τη μέθοδο των μέγιστων και ελάχιστων» και σε αυτό το έργο έδωσε τον Maupertuis' αρχή ενός γενικού μηχανικού χαρακτήρα: «Δεδομένου ότι όλα τα φυσικά φαινόμενα ακολουθούν κάποιους. μέγιστο ή ελάχιστο. Ο Euler διατύπωσε περαιτέρω αυτόν τον νόμο: η τροχιά ενός σώματος επιτυγχάνει ένα ελάχιστο ∫ m v d s (\displaystyle \int mv\ ds). Στη συνέχεια το εφάρμοσε, εξάγοντας τους νόμους της κίνησης σε ένα ομοιόμορφο βαρυτικό πεδίο και σε αρκετές άλλες περιπτώσεις.

  Το 1746, ο Maupertuis, σε ένα νέο έργο, συμφώνησε με τη γνώμη του Euler και διακήρυξε την πιο γενική εκδοχή της αρχής του: «Όταν συμβαίνει κάποια αλλαγή στη φύση, το μέγεθος της δράσης που απαιτείται για αυτήν την αλλαγή είναι το λιγότερο δυνατό. Η ποσότητα δράσης είναι το γινόμενο της μάζας των σωμάτων από την ταχύτητά τους και την απόσταση που διανύουν». Στην ευρεία συζήτηση που ακολούθησε, ο Euler υποστήριξε την προτεραιότητα του Maupertuis και υποστήριξε την καθολική φύση του νέου νόμου: «όλη η δυναμική και η υδροδυναμική μπορούν να αποκαλυφθούν με εκπληκτική ευκολία μόνο μέσω της μεθόδου των μέγιστων και ελάχιστων».

  Ένα νέο στάδιο ξεκίνησε το 1760-1761, όταν ο Joseph Louis Lagrange εισήγαγε την αυστηρή έννοια της παραλλαγής μιας συνάρτησης, έδωσε στον λογισμό των μεταβολών μια σύγχρονη μορφή και επέκτεινε την αρχή της ελάχιστης δράσης σε ένα αυθαίρετο μηχανικό σύστημα (δηλαδή, όχι μόνο σε ελεύθερα υλικά σημεία). Αυτό σηματοδότησε την αρχή της αναλυτικής μηχανικής. Μια περαιτέρω γενίκευση της αρχής πραγματοποιήθηκε από τον Carl Gustav Jacob Jacobi το 1837 - θεώρησε το πρόβλημα γεωμετρικά, ως εύρεση των ακραίων σημείων ενός μεταβλητού προβλήματος σε ένα χώρο διαμόρφωσης με μια μη Ευκλείδεια μετρική. Συγκεκριμένα, ο Jacobi επεσήμανε ότι ελλείψει εξωτερικών δυνάμεων, η τροχιά του συστήματος αντιπροσωπεύει μια γεωδαισιακή γραμμή στο χώρο διαμόρφωσης.

  Η προσέγγιση του Hamilton έχει αποδειχθεί καθολική και εξαιρετικά αποτελεσματική στα μαθηματικά μοντέλα της φυσικής, ειδικά για την κβαντική μηχανική. Η ευρετική του δύναμη επιβεβαιώθηκε στη δημιουργία της Γενικής Σχετικότητας, όταν ο Ντέιβιντ Χίλμπερτ εφάρμοσε την αρχή του Χάμιλτον για να εξαγάγει τις τελικές εξισώσεις του βαρυτικού πεδίου (1915).

  Στην κλασική μηχανική

  Η αρχή της ελάχιστης δράσης χρησιμεύει ως η θεμελιώδης και τυπική βάση των διατυπώσεων της μηχανικής Lagrangian και Hamilton.

  Αρχικά, ας δούμε την κατασκευή ως εξής: Λαγκρανζική μηχανική. Χρησιμοποιώντας το παράδειγμα ενός φυσικού συστήματος με έναν βαθμό ελευθερίας, ας υπενθυμίσουμε ότι η δράση είναι συνάρτηση σε σχέση με (γενικευμένες) συντεταγμένες (στην περίπτωση ενός βαθμού ελευθερίας - μία συντεταγμένη), δηλαδή εκφράζεται μέσω q (t) (\displaystyle q(t))ώστε κάθε νοητή παραλλαγή της συνάρτησης q (t) (\displaystyle q(t))συγκρίνεται ένας συγκεκριμένος αριθμός - μια ενέργεια (με αυτή την έννοια μπορούμε να πούμε ότι μια ενέργεια ως συνάρτηση είναι ένας κανόνας που επιτρέπει οποιαδήποτε δεδομένη συνάρτηση q (t) (\displaystyle q(t))υπολογίστε έναν πολύ συγκεκριμένο αριθμό - που ονομάζεται επίσης δράση). Η δράση μοιάζει με:

  S [ q ] = ∫ L (q (t) , q ˙ (t) , t) d t , (\displaystyle S[q]=\int (\mathcal (L))(q(t),(\dot ( q))(t),t)dt,)

  Οπου L (q (t) , q ˙ (t) , t) (\style display (\mathcal (L))(q(t),(\dot (q))(t),t))είναι το Lagrange του συστήματος, ανάλογα με τη γενικευμένη συντεταγμένη q (\displaystyle q), η πρώτη του παράγωγος q ˙ (\displaystyle (\dot (q))), και επίσης, ενδεχομένως, ρητά από τον χρόνο t (\displaystyle t). Αν το σύστημα έχει περισσότερους βαθμούς ελευθερίας n (\displaystyle n), τότε η Lagrangian εξαρτάται από μεγαλύτερο αριθμό γενικευμένων συντεταγμένων q i (t) , i = 1 , 2 , … , n (\displaystyle q_(i)(t),\ i=1,2,\dots ,n)και τα παράγωγά τους για πρώτη φορά. Έτσι, η δράση είναι βαθμωτή λειτουργική ανάλογα με την τροχιά του σώματος.

  Το γεγονός ότι η ενέργεια είναι βαθμωτή καθιστά εύκολη τη γραφή της σε οποιεσδήποτε γενικευμένες συντεταγμένες, το κύριο πράγμα είναι ότι η θέση (διαμόρφωση) του συστήματος χαρακτηρίζεται ξεκάθαρα από αυτές (για παράδειγμα, αντί για καρτεσιανές συντεταγμένες, αυτές μπορεί να είναι πολικές συντεταγμένες, αποστάσεις μεταξύ σημείων του συστήματος, γωνίες ή συναρτήσεις τους κ.λπ. .δ.).

  Η δράση μπορεί να υπολογιστεί για μια εντελώς αυθαίρετη τροχιά q (t) (\displaystyle q(t)), όσο «άγριο» και «αφύσικο» κι αν είναι. Ωστόσο, στην κλασική μηχανική, ανάμεσα σε ολόκληρο το σύνολο των πιθανών τροχιών, υπάρχει μόνο μία κατά μήκος της οποίας θα κινηθεί πραγματικά το σώμα. Η αρχή της ακίνητης δράσης δίνει ακριβώς την απάντηση στο ερώτημα πώς θα κινηθεί πραγματικά το σώμα:

  Αυτό σημαίνει ότι εάν δοθεί το Lagrangian του συστήματος, τότε χρησιμοποιώντας τον λογισμό των μεταβολών μπορούμε να καθορίσουμε πώς ακριβώς θα κινηθεί το σώμα, λαμβάνοντας πρώτα τις εξισώσεις κίνησης - τις εξισώσεις Euler-Lagrange, και στη συνέχεια λύνοντάς τις. Αυτό επιτρέπει όχι μόνο τη σοβαρή γενίκευση της διατύπωσης της μηχανικής, αλλά και την επιλογή των πιο βολικών συντεταγμένων για κάθε συγκεκριμένο πρόβλημα, χωρίς να περιορίζεται στα καρτεσιανά, που μπορεί να είναι πολύ χρήσιμα για τη λήψη των απλούστερων και πιο εύκολα λυμένων εξισώσεων.

  S [ p , q ] = ∫ (∑ i p i d q i − H (q , p , t) d t) = ∫ (∑ i p i q ˙ i − H (q , p , t)) d t , (\displaystyle S=\int (\ μεγάλο ()\sum _(i)p_(i)dq_(i)-(\mathcal (H))(q,p,t)dt(\big))=\int (\big ()\sum _( i)p_(i)(\dot (q))_(i)-(\mathcal (H))(q,p,t)(\big))dt,)

  Οπου H (q , p , t) ≡ H (q 1 , q 2 , … , q N , p 1 , p 2 , … , p N , t) (\displaystyle (\mathcal (H))(q,p, t)\ ισοδύναμο (\mathcal (H))(q_(1),q_(2),\dots ,q_(N),p_(1),p_(2),\dots ,p_(N),t) )- Λειτουργία Hamilton αυτού του συστήματος. q ≡ q 1 , q 2 , … , q N (\displaystyle q\equiv q_(1),q_(2),\dots ,q_(N))- (γενικευμένες) συντεταγμένες, p ≡ p 1 , p 2 , … , p N (\displaystyle p\equiv p_(1),p_(2),\dots ,p_(N))- οι (γενικευμένες) παρορμήσεις συζευγνύονται με αυτό, οι οποίες μαζί χαρακτηρίζουν σε κάθε δεδομένη χρονική στιγμή τη δυναμική κατάσταση του συστήματος και, καθεμία συνάρτηση του χρόνου, χαρακτηρίζοντας έτσι την εξέλιξη (κίνηση) του συστήματος. Σε αυτήν την περίπτωση, για να ληφθούν οι εξισώσεις κίνησης του συστήματος με τη μορφή των κανονικών εξισώσεων του Hamilton, είναι απαραίτητο να μεταβληθεί η ενέργεια που γράφτηκε με αυτόν τον τρόπο ανεξάρτητα για όλους q i (\displaystyle q_(i))Και p i (\displaystyle p_(i)).

  Πρέπει να σημειωθεί ότι εάν από τις συνθήκες του προβλήματος είναι καταρχήν δυνατό να βρεθεί ο νόμος της κίνησης, τότε αυτό γίνεται αυτόματα Δενσημαίνει ότι είναι δυνατό να κατασκευαστεί μια συνάρτηση που παίρνει μια σταθερή τιμή κατά την πραγματική κίνηση. Ένα παράδειγμα είναι η κοινή κίνηση ηλεκτρικών φορτίων και μονοπόλων -μαγνητικά φορτία- σε ένα ηλεκτρομαγνητικό πεδίο. Οι εξισώσεις κίνησής τους δεν μπορούν να προκύψουν από την αρχή της ακίνητης δράσης. Ομοίως, ορισμένα συστήματα Χαμιλτονίου έχουν εξισώσεις κίνησης που δεν μπορούν να προκύψουν από αυτήν την αρχή.

  Παραδείγματα

  Ασήμαντα παραδείγματα βοηθούν στην αξιολόγηση της χρήσης της αρχής λειτουργίας μέσω των εξισώσεων Euler-Lagrange. Ελεύθερο σωματίδιο (μάζα Μκαι ταχύτητα v) στον Ευκλείδειο χώρο κινείται σε ευθεία γραμμή. Χρησιμοποιώντας τις εξισώσεις Euler-Lagrange, αυτό μπορεί να φανεί σε πολικές συντεταγμένες ως εξής. Ελλείψει δυναμικού, η συνάρτηση Lagrange είναι απλώς ίση με την κινητική ενέργεια

  1 2 m v 2 = 1 2 m (x ˙ 2 + y ˙ 2) (\displaystyle (\frac (1)(2))mv^(2)=(\frac (1)(2))m\left( (\dot (x))^(2)+(\dot (y))^(2)\δεξιά)) ψ = ∫ [D x ] e (i S [ x ] / ℏ) . (\displaystyle \psi =\int e^(((iS[x])/(\hbar )))\,.)

  Εδώ ∫ [ D x ] (\displaystyle \int)είναι ένας συμβολισμός υπό όρους για άπειρη πολλαπλή συναρτητική ολοκλήρωση σε όλες τις τροχιές x(t), και ℏ (\displaystyle \hbar)- Σταθερά του Planck. Τονίζουμε ότι, καταρχήν, η δράση στην εκθετική εμφανίζεται (ή μπορεί να εμφανιστεί) η ίδια κατά τη μελέτη του τελεστή εξέλιξης στην κβαντομηχανική, αλλά για συστήματα που έχουν ακριβές κλασσικό (μη κβαντικό) ανάλογο, είναι ακριβώς ίση με το συνηθισμένο κλασική δράση.

  Μαθηματική ανάλυση αυτής της έκφρασης στο κλασικό όριο - για αρκετά μεγάλο S / ℏ (\displaystyle S/\hbar), δηλαδή με πολύ γρήγορες ταλαντώσεις της φανταστικής εκθετικής - δείχνει ότι η συντριπτική πλειονότητα όλων των πιθανών τροχιών σε αυτό το ολοκλήρωμα αλληλοακυρώνονται στο όριο (τυπικά στο S / ℏ → ∞ (\displaystyle S/\hbar \δεξιό βέλος \infty)). Σχεδόν για οποιοδήποτε μονοπάτι υπάρχει μια διαδρομή στην οποία η μετατόπιση φάσης θα είναι ακριβώς το αντίθετο, και θα αθροίζονται ως μηδενική συνεισφορά. Μόνο εκείνες οι τροχιές για τις οποίες η δράση είναι κοντά στην ακραία τιμή (για τα περισσότερα συστήματα - στο ελάχιστο) δεν μειώνονται. Αυτό είναι ένα καθαρά μαθηματικό γεγονός από