Το εμβαδόν ενός τριγώνου είναι το Πυθαγόρειο θεώρημα. Διαφορετικοί τρόποι απόδειξης του Πυθαγόρειου Θεωρήματος: παραδείγματα, περιγραφή και κριτικές
Όταν πρωτοξεκίνησες να μαθαίνεις τετραγωνικές ρίζες και πώς να λύνεις παράλογες εξισώσεις(ισότητες που περιέχουν το άγνωστο κάτω από το σύμβολο της ρίζας), πιθανότατα πήρατε την πρώτη ιδέα για αυτές πρακτική χρήση. Η ικανότητα εξαγωγής Τετραγωνική ρίζατων αριθμών είναι επίσης απαραίτητο για την επίλυση προβλημάτων σχετικά με την εφαρμογή του Πυθαγόρειου θεωρήματος. Αυτό το θεώρημα συσχετίζει τα μήκη των πλευρών οποιουδήποτε ορθογωνίου τριγώνου.
Αφήστε τα μήκη των σκελών ενός ορθογωνίου τριγώνου (αυτές τις δύο πλευρές που συγκλίνουν σε ορθή γωνία) να συμβολίζονται με τα γράμματα και και το μήκος της υποτείνουσας (η μεγαλύτερη πλευρά του τριγώνου απέναντι ορθή γωνία) θα συμβολίζεται με το γράμμα . Τότε τα αντίστοιχα μήκη συσχετίζονται με την ακόλουθη σχέση:
Αυτή η εξίσωση σας επιτρέπει να βρείτε το μήκος μιας πλευράς ενός ορθογωνίου τριγώνου στην περίπτωση που το μήκος των άλλων δύο πλευρών του είναι γνωστό. Επιπλέον, σας επιτρέπει να προσδιορίσετε εάν το εξεταζόμενο τρίγωνο είναι ορθογώνιο, υπό τον όρο ότι τα μήκη όλων τρεις πλευρέςγνωστό εκ των προτέρων.
Επίλυση προβλημάτων χρησιμοποιώντας το Πυθαγόρειο θεώρημα
Για να εμπεδώσουμε το υλικό, θα λύσουμε τα παρακάτω προβλήματα για την εφαρμογή του Πυθαγόρειου θεωρήματος.

Δίνεται λοιπόν:
- Το μήκος ενός από τα πόδια είναι 48, η υποτείνουσα είναι 80.
- Το μήκος του ποδιού είναι 84, η υποτείνουσα είναι 91.
Πάμε στη λύση:
α) Η αντικατάσταση των δεδομένων στην παραπάνω εξίσωση δίνει τα ακόλουθα αποτελέσματα:
48 2 + σι 2 = 80 2
2304 + σι 2 = 6400
σι 2 = 4096
σι= 64 ή σι = -64
Επειδή το μήκος μιας πλευράς ενός τριγώνου δεν μπορεί να εκφραστεί αρνητικός αριθμός, η δεύτερη επιλογή απορρίπτεται αυτόματα.
Απάντηση στην πρώτη εικόνα: σι = 64.
β) Το μήκος του σκέλους του δεύτερου τριγώνου βρίσκεται με τον ίδιο τρόπο:
84 2 + σι 2 = 91 2
7056 + σι 2 = 8281
σι 2 = 1225
σι= 35 ή σι = -35
Όπως και στην προηγούμενη περίπτωση, η αρνητική λύση απορρίπτεται.
Απάντηση στη δεύτερη εικόνα: σι = 35

Μας δίνονται:
- Τα μήκη των μικρότερων πλευρών του τριγώνου είναι 45 και 55, αντίστοιχα, και των μεγαλύτερων είναι 75.
- Τα μήκη των μικρότερων πλευρών του τριγώνου είναι 28 και 45, αντίστοιχα, και των μεγαλύτερων είναι 53.
Λύνουμε το πρόβλημα:
α) Είναι απαραίτητο να ελέγξουμε αν το άθροισμα των τετραγώνων των μηκών των μικρότερων πλευρών ενός δεδομένου τριγώνου είναι ίσο με το τετράγωνο του μήκους του μεγαλύτερου:
45 2 + 55 2 = 2025 + 3025 = 5050
Επομένως, το πρώτο τρίγωνο δεν είναι ορθογώνιο.
β) Εκτελείται η ίδια πράξη:
28 2 + 45 2 = 784 + 2025 = 2809
Επομένως, το δεύτερο τρίγωνο είναι ορθογώνιο.
Πρώτα βρίσκουμε το μήκος μεγαλύτερο τμήμα, που σχηματίζονται από σημεία με συντεταγμένες (-2, -3) και (5, -2). Για αυτό χρησιμοποιούμε γνωστός τύποςγια να βρείτε την απόσταση μεταξύ των σημείων ορθογώνιο σύστημασυντεταγμένες:
Ομοίως, βρίσκουμε το μήκος του τμήματος που περικλείεται μεταξύ των σημείων με συντεταγμένες (-2, -3) και (2, 1):
Τέλος, προσδιορίζουμε το μήκος του τμήματος μεταξύ σημείων με συντεταγμένες (2, 1) και (5, -2):
Εφόσον υπάρχει ισότητα:
τότε το αντίστοιχο τρίγωνο είναι ορθογώνιο.
Έτσι, μπορούμε να διατυπώσουμε την απάντηση στο πρόβλημα: αφού το άθροισμα των τετραγώνων των πλευρών με το μικρότερο μήκος είναι ίσο με το τετράγωνο της πλευράς με μεγαλύτερο μήκος, τα σημεία είναι οι κορυφές ενός ορθογωνίου τριγώνου.
Η βάση (βρίσκεται αυστηρά οριζόντια), η λαβή (βρίσκεται αυστηρά κάθετα) και το καλώδιο (τεντωμένο διαγώνια) σχηματίζουν ένα ορθογώνιο τρίγωνο, αντίστοιχα, το Πυθαγόρειο θεώρημα μπορεί να χρησιμοποιηθεί για να βρεθεί το μήκος του καλωδίου:
Έτσι, το μήκος του καλωδίου θα είναι περίπου 3,6 μέτρα.
Δίνεται: η απόσταση από το σημείο R έως το σημείο P (το σκέλος του τριγώνου) είναι 24, από το σημείο R στο σημείο Q (υποτείνουσα) - 26.
Έτσι, βοηθάμε τη Vitya να λύσει το πρόβλημα. Δεδομένου ότι οι πλευρές του τριγώνου που φαίνονται στο σχήμα υποτίθεται ότι σχηματίζουν ένα ορθογώνιο τρίγωνο, μπορείτε να χρησιμοποιήσετε το Πυθαγόρειο θεώρημα για να βρείτε το μήκος της τρίτης πλευράς:
Έτσι, το πλάτος της λίμνης είναι 10 μέτρα.
Σεργκέι Βαλέριεβιτς
Πυθαγόρειο θεώρημα
Πυθαγόρειο θεώρημα- ένα από τα θεμελιώδη θεωρήματα της Ευκλείδειας γεωμετρίας, που καθιερώνει τη σχέση
ανάμεσα στις πλευρές ενός ορθογώνιου τριγώνου.
Πιστεύεται ότι αποδείχθηκε από τον Έλληνα μαθηματικό Πυθαγόρα, από τον οποίο πήρε το όνομά του.
Γεωμετρική διατύπωση του Πυθαγόρειου θεωρήματος.
Το θεώρημα αρχικά διατυπώθηκε ως εξής:
Σε ένα ορθογώνιο τρίγωνο, το εμβαδόν του τετραγώνου που χτίζεται στην υποτείνουσα είναι ίσο με το άθροισμα των εμβαδών των τετραγώνων,
χτισμένο σε καθετήρες.
Αλγεβρική διατύπωση του Πυθαγόρειου θεωρήματος.
Σε ένα ορθογώνιο τρίγωνο, το τετράγωνο του μήκους της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των μηκών των σκελών.
Δηλαδή, που δηλώνει το μήκος της υποτείνουσας του τριγώνου διέλευσης ντο, και τα μήκη των ποδιών μέσα ένακαι σι:
Και τα δύο σκευάσματα Πυθαγόρεια θεωρήματαείναι ισοδύναμα, αλλά η δεύτερη διατύπωση είναι πιο στοιχειώδης, δεν το κάνει
απαιτεί την έννοια της περιοχής. Δηλαδή, η δεύτερη δήλωση μπορεί να επαληθευτεί χωρίς να γνωρίζουμε τίποτα για την περιοχή και
μετρώντας μόνο τα μήκη των πλευρών ενός ορθογωνίου τριγώνου.
Το αντίστροφο Πυθαγόρειο θεώρημα.
Αν το τετράγωνο της μιας πλευράς ενός τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των άλλων δύο πλευρών, τότε
το τρίγωνο είναι ορθογώνιο.
Ή, με άλλα λόγια:
Για κάθε τριπλό θετικών αριθμών ένα, σικαι ντο, τέτοιο που
υπάρχει ένα ορθογώνιο τρίγωνο με πόδια ένακαι σικαι υποτείνουσα ντο.
Το Πυθαγόρειο θεώρημα για ισοσκελές τρίγωνο.

Πυθαγόρειο θεώρημα για ισόπλευρο τρίγωνο.

Αποδείξεις του Πυθαγόρειου θεωρήματος.
Αυτή τη στιγμή, 367 αποδείξεις αυτού του θεωρήματος έχουν καταγραφεί στην επιστημονική βιβλιογραφία. Μάλλον το θεώρημα
Ο Πυθαγόρας είναι το μόνο θεώρημα με τόσο εντυπωσιακό αριθμό αποδείξεων. Τέτοια ποικιλομορφία
μπορεί να εξηγηθεί μόνο από τη θεμελιώδη σημασία του θεωρήματος για τη γεωμετρία.
Φυσικά, εννοιολογικά, όλα μπορούν να χωριστούν σε μικρό αριθμό τάξεων. Οι πιο διάσημοι από αυτούς:
απόδειξη του μέθοδος περιοχής, αξιωματικόςκαι εξωτικά στοιχεία(για παράδειγμα,
με τη χρήση διαφορικές εξισώσεις).
1. Απόδειξη του Πυθαγόρειου θεωρήματος ως προς όμοια τρίγωνα.
Η παρακάτω απόδειξη της αλγεβρικής διατύπωσης είναι η απλούστερη από τις αποδείξεις που κατασκευάστηκαν
απευθείας από τα αξιώματα. Συγκεκριμένα, δεν χρησιμοποιεί την έννοια του εμβαδού μιας φιγούρας.
Αφήνω αλφάβητουπάρχει ένα ορθογώνιο τρίγωνο ντο. Ας τραβήξουμε ένα ύψος από ντοκαι δηλώνουν
η ίδρυσή του μέσω H.
Τρίγωνο ACHπαρόμοιο με ένα τρίγωνο ΑΒ C σε δύο γωνίες. Το ίδιο και το τρίγωνο CBHπαρόμοιος αλφάβητο.
Εισάγοντας τη σημειογραφία:

παίρνουμε:
![]() ,
,
που ταιριάζει -
Έχοντας διπλώσει ένα 2 και σι 2, παίρνουμε:
ή , που έπρεπε να αποδειχθεί.
2. Απόδειξη του Πυθαγόρειου θεωρήματος με τη μέθοδο της περιοχής.
Οι παρακάτω αποδείξεις, παρά τη φαινομενική απλότητά τους, δεν είναι καθόλου τόσο απλές. Ολα τους
χρησιμοποιήστε τις ιδιότητες της περιοχής, η απόδειξη της οποίας είναι πιο περίπλοκη από την απόδειξη του ίδιου του Πυθαγόρειου θεωρήματος.
- Απόδειξη μέσω ισοσυμπλήρωσης.
 Τοποθετήστε τέσσερα ίσα ορθογώνια
Τοποθετήστε τέσσερα ίσα ορθογώνια
τρίγωνο όπως φαίνεται στην εικόνα
στα δεξιά.
Τετράπλευρο με πλευρές ντο- τετράγωνο,
αφού το άθροισμα δύο οξειών γωνιών είναι 90°, και
η αναπτυγμένη γωνία είναι 180°.
Το εμβαδόν ολόκληρου του σχήματος είναι, αφενός,
εμβαδόν τετραγώνου με πλευρά ( α+β), και από την άλλη το άθροισμα των εμβαδών τέσσερα τρίγωνακαι
![]()
![]()
Q.E.D.
3. Απόδειξη του Πυθαγόρειου θεωρήματος με την απειροελάχιστη μέθοδο.

Λαμβάνοντας υπόψη το σχέδιο που φαίνεται στο σχήμα, και
βλέποντας την πλευρά να αλλάζειένα, μπορούμε
γράψτε την παρακάτω σχέση για το άπειρο
μικρό πλαϊνές αυξήσειςΜεκαι ένα(χρησιμοποιώντας ομοιότητα
τρίγωνα):
Χρησιμοποιώντας τη μέθοδο διαχωρισμού μεταβλητών, βρίσκουμε:
Μια γενικότερη έκφραση για την αλλαγή της υποτείνουσας στην περίπτωση αυξήσεων και των δύο ποδιών:
Ενσωμάτωση δεδομένη εξίσωσηκαι χρησιμοποιώντας τις αρχικές συνθήκες, παίρνουμε:
Έτσι, καταλήγουμε στην επιθυμητή απάντηση:
Όπως είναι εύκολο να δούμε, η τετραγωνική εξάρτηση στον τελικό τύπο εμφανίζεται λόγω της γραμμικής
αναλογικότητα μεταξύ των πλευρών του τριγώνου και των προσαυξήσεων, ενώ το άθροισμα σχετίζεται με το ανεξάρτητο
συνεισφορές από την αύξηση των διαφορετικών ποδιών.
Μια απλούστερη απόδειξη μπορεί να ληφθεί αν υποθέσουμε ότι το ένα από τα πόδια δεν παρουσιάζει αύξηση
(σε αυτή η υπόθεσηπόδι σι). Τότε για τη σταθερά ολοκλήρωσης παίρνουμε:
(σύμφωνα με τον Πάπυρο 6619 του Μουσείου του Βερολίνου). Σύμφωνα με τον Κάντορ, οι άρπεδοναπτες ή «εντατήρες χορδών», κατασκεύαζαν ορθές γωνίες χρησιμοποιώντας ορθογώνια τρίγωνα με πλευρές 3, 4 και 5.
Είναι πολύ εύκολο να αναπαραχθεί ο τρόπος κατασκευής τους. Ας πάρουμε ένα σχοινί μήκους 12 m και το δέσουμε σε μια χρωματιστή λωρίδα σε απόσταση 3 m από τη μία άκρη και 4 μέτρα από την άλλη. Μια ορθή γωνία θα περικλείεται μεταξύ των πλευρών μήκους 3 και 4 μέτρων. Θα μπορούσε να αντιταχθεί στους Harpedonapts ότι η μέθοδος κατασκευής τους καθίσταται περιττή εάν, για παράδειγμα, χρησιμοποιείται το ξύλινο τετράγωνο που χρησιμοποιούν όλοι οι ξυλουργοί. Πράγματι, είναι γνωστά αιγυπτιακά σχέδια στα οποία βρίσκεται ένα τέτοιο εργαλείο - για παράδειγμα, σχέδια που απεικονίζουν ένα εργαστήριο ξυλουργικής.
Λίγο περισσότερα είναι γνωστά για το Πυθαγόρειο θεώρημα μεταξύ των Βαβυλωνίων. Σε ένα κείμενο που χρονολογείται στην εποχή του Χαμουραμπί, δηλαδή στο 2000 π.Χ. μι. , δίνεται ένας κατά προσέγγιση υπολογισμός της υποτείνουσας ενός ορθογωνίου τριγώνου. Από αυτό μπορούμε να συμπεράνουμε ότι στη Μεσοποταμία μπορούσαν να κάνουν υπολογισμούς με ορθογώνια τρίγωνα, τουλάχιστον σε ορισμένες περιπτώσεις. Βασισμένος, αφενός, στο τρέχον επίπεδο γνώσης των Αιγυπτιακών και Βαβυλωνιακών μαθηματικών και, αφετέρου, σε μια κριτική μελέτη ελληνικών πηγών, ο van der Waerden (Ολλανδός μαθηματικός) κατέληξε στο συμπέρασμα ότι υπήρχε μεγάλη πιθανότητα η Το θεώρημα του τετραγώνου της υποτείνουσας ήταν γνωστό στην Ινδία ήδη γύρω στον 18ο αιώνα π.Χ. μι.
Γύρω στο 400 π.Χ. ε., σύμφωνα με τον Πρόκλο, ο Πλάτων έδωσε μια μέθοδο για την εύρεση πυθαγόρειων τριπλών, συνδυάζοντας άλγεβρα και γεωμετρία. Γύρω στο 300 π.Χ. μι. Τα Στοιχεία του Ευκλείδη περιέχουν την παλαιότερη αξιωματική απόδειξη του Πυθαγόρειου θεωρήματος.
Διατύπωση
Γεωμετρική διατύπωση:
Το θεώρημα αρχικά διατυπώθηκε ως εξής:
Αλγεβρική διατύπωση:
Δηλαδή, δηλώνοντας το μήκος της υποτείνουσας του τριγώνου διέλευσης, και τα μήκη των άκρων και:
Και οι δύο διατυπώσεις του θεωρήματος είναι ισοδύναμες, αλλά η δεύτερη διατύπωση είναι πιο στοιχειώδης, δεν απαιτεί την έννοια του εμβαδού. Δηλαδή, η δεύτερη πρόταση μπορεί να επαληθευτεί χωρίς να γνωρίζουμε τίποτα για το εμβαδόν και μετρώντας μόνο τα μήκη των πλευρών ενός ορθογωνίου τριγώνου.
Αντίστροφο Πυθαγόρειο θεώρημα:
Απόδειξη
Αυτή τη στιγμή, 367 αποδείξεις αυτού του θεωρήματος έχουν καταγραφεί στην επιστημονική βιβλιογραφία. Πιθανώς, το Πυθαγόρειο θεώρημα είναι το μόνο θεώρημα με τόσο εντυπωσιακό αριθμό αποδείξεων. Μια τέτοια ποικιλία μπορεί να εξηγηθεί μόνο από τη θεμελιώδη σημασία του θεωρήματος για τη γεωμετρία.
Φυσικά, εννοιολογικά, όλα μπορούν να χωριστούν σε μικρό αριθμό τάξεων. Οι πιο διάσημες από αυτές: αποδείξεις με τη μέθοδο της περιοχής, αξιωματικές και εξωτικές αποδείξεις (για παράδειγμα, χρησιμοποιώντας διαφορικές εξισώσεις).
Μέσα από παρόμοια τρίγωνα
Η ακόλουθη απόδειξη της αλγεβρικής διατύπωσης είναι η απλούστερη από τις αποδείξεις που χτίστηκαν απευθείας από τα αξιώματα. Συγκεκριμένα, δεν χρησιμοποιεί την έννοια της περιοχής σχήματος.

Αφήνω αλφάβητουπάρχει ένα ορθογώνιο τρίγωνο ντο. Ας τραβήξουμε ένα ύψος από ντοκαι να συμβολίσετε τη βάση του με H. Τρίγωνο ACHπαρόμοιο με ένα τρίγωνο αλφάβητοσε δύο γωνίες. Το ίδιο και το τρίγωνο CBHπαρόμοιος αλφάβητο. Παρουσιάζοντας τη σημειογραφία
παίρνουμε
Τι είναι ισοδύναμο
Προσθέτοντας, παίρνουμε
, που έπρεπε να αποδειχτείΑποδείξεις περιοχής
Οι παρακάτω αποδείξεις, παρά τη φαινομενική απλότητά τους, δεν είναι καθόλου τόσο απλές. Όλοι χρησιμοποιούν τις ιδιότητες της περιοχής, η απόδειξη των οποίων είναι πιο περίπλοκη από την απόδειξη του ίδιου του Πυθαγόρειου θεωρήματος.
Απόδειξη μέσω Ισοδυναμίας
- Τοποθετήστε τέσσερα ίσα ορθογώνια τρίγωνα όπως φαίνεται στο σχήμα 1.
- Τετράπλευρο με πλευρές ντοείναι τετράγωνο γιατί το άθροισμα δύο οξειών γωνιών είναι 90° και της ευθείας γωνίας είναι 180°.
- Το εμβαδόν ολόκληρου του σχήματος είναι ίσο, αφενός, με το εμβαδόν ενός τετραγώνου με πλευρά (a + b) και, αφετέρου, το άθροισμα των εμβαδών τεσσάρων τριγώνων και του εμβαδού της εσωτερικής πλατείας.
Q.E.D.
Η απόδειξη του Ευκλείδη
Η ιδέα της απόδειξης του Ευκλείδη είναι η εξής: ας προσπαθήσουμε να αποδείξουμε ότι το μισό εμβαδόν του τετραγώνου που χτίζεται στην υποτείνουσα είναι ίσο με το άθροισμα των μισών εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη και μετά τα εμβαδά του τα μεγάλα και τα δύο μικρά τετράγωνα είναι ίσα.
Εξετάστε το σχέδιο στα αριστερά. Κατασκευάσαμε τετράγωνα στις πλευρές ενός ορθογώνιου τριγώνου πάνω του και σχεδιάσαμε μια ακτίνα s από την κορυφή της ορθής γωνίας C κάθετη στην υποτείνουσα AB, κόβει το τετράγωνο ABIK, χτισμένο στην υποτείνουσα, σε δύο ορθογώνια - BHJI και HAKJ , αντίστοιχα. Αποδεικνύεται ότι τα εμβαδά αυτών των ορθογωνίων είναι ακριβώς ίσα με τα εμβαδά των τετραγώνων που είναι χτισμένα στα αντίστοιχα σκέλη.
Ας προσπαθήσουμε να αποδείξουμε ότι το εμβαδόν του τετραγώνου DECA είναι ίσο με το εμβαδόν του ορθογωνίου AHJK Για να το κάνουμε αυτό, χρησιμοποιούμε μια βοηθητική παρατήρηση: Το εμβαδόν ενός τριγώνου με το ίδιο ύψος και βάση με το δεδομένο ορθογώνιο είναι ίσο με το μισό του εμβαδού του δεδομένου ορθογωνίου. Αυτό είναι συνέπεια του ορισμού του εμβαδού ενός τριγώνου ως το μισό του γινόμενου της βάσης και του ύψους. Από αυτή την παρατήρηση προκύπτει ότι το εμβαδόν του τριγώνου ACK είναι ίσο με το εμβαδόν του τριγώνου AHK (δεν φαίνεται), το οποίο, με τη σειρά του, είναι ίσο με το μισό του εμβαδού του ορθογωνίου AHJK.
Ας αποδείξουμε τώρα ότι το εμβαδόν του τριγώνου ACK είναι επίσης ίσο με το μισό του εμβαδού του τετραγώνου DECA. Το μόνο πράγμα που πρέπει να γίνει για αυτό είναι να αποδειχθεί η ισότητα των τριγώνων ACK και BDA (καθώς το εμβαδόν του τριγώνου BDA είναι ίσο με το μισό του εμβαδού του τετραγώνου από την παραπάνω ιδιότητα). Αυτή η ισότητα είναι προφανής: τα τρίγωνα είναι ίσα σε δύο πλευρές και τη γωνία μεταξύ τους. Δηλαδή - AB=AK, AD=AC - η ισότητα των γωνιών CAK και BAD είναι εύκολο να αποδειχθεί με τη μέθοδο της κίνησης: ας περιστρέψουμε το τρίγωνο CAK 90 ° αριστερόστροφα, τότε είναι προφανές ότι οι αντίστοιχες πλευρές των δύο θεωρούμενων τριγώνων θα συμπίπτουν (λόγω του ότι η γωνία στην κορυφή του τετραγώνου είναι 90°).
Το επιχείρημα για την ισότητα των εμβαδών του τετραγώνου BCFG και του ορθογωνίου BHJI είναι εντελώς ανάλογο.
Έτσι, αποδείξαμε ότι το εμβαδόν του τετραγώνου που είναι χτισμένο στην υποτείνουσα είναι το άθροισμα των εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη. Ιδέα αυτό το στοιχείοαπεικονίζεται περαιτέρω με την παραπάνω κινούμενη εικόνα.
Απόδειξη του Λεονάρντο ντα Βίντσι
Τα κύρια στοιχεία της απόδειξης είναι η συμμετρία και η κίνηση.
Εξετάστε το σχέδιο, όπως φαίνεται από τη συμμετρία, το τμήμα κόβει το τετράγωνο σε δύο πανομοιότυπα μέρη (καθώς τα τρίγωνα είναι ίσα στην κατασκευή).
Χρησιμοποιώντας μια αριστερόστροφη περιστροφή 90 μοιρών γύρω από το σημείο, βλέπουμε την ισότητα των σκιασμένων σχημάτων και .
Τώρα είναι σαφές ότι το εμβαδόν του σχήματος που έχουμε σκιάσει είναι ίσο με το άθροισμα των μισών εμβαδών των μικρών τετραγώνων (χτισμένα στα πόδια) και του εμβαδού του αρχικού τριγώνου. Από την άλλη πλευρά, είναι ίσο με το μισό του εμβαδού του μεγάλου τετραγώνου (χτισμένο στην υποτείνουσα) συν το εμβαδόν του αρχικού τριγώνου. Έτσι, το μισό άθροισμα των εμβαδών των μικρών τετραγώνων είναι ίσο με το μισό του εμβαδού του μεγάλου τετραγώνου, και επομένως το άθροισμα των εμβαδών των τετραγώνων που είναι χτισμένα στα πόδια είναι ίσο με το εμβαδόν του τετραγώνου που έχει κατασκευαστεί στην υποτείνουσα.
Απόδειξη με την απειροελάχιστη μέθοδο
Η ακόλουθη απόδειξη μέσω διαφορικών εξισώσεων αποδίδεται συχνά στα γνωστά Άγγλος μαθηματικόςΧάρντι, που έζησε στο πρώτο μισό του 20ού αιώνα.
Λαμβάνοντας υπόψη το σχέδιο που φαίνεται στο σχήμα και παρατηρώντας την αλλαγή στην πλευρά ένα, μπορούμε να γράψουμε την παρακάτω σχέση για απειροελάχιστες πλευρικές προσαυξήσεις Μεκαι ένα(χρησιμοποιώντας παρόμοια τρίγωνα):
Χρησιμοποιώντας τη μέθοδο διαχωρισμού μεταβλητών, βρίσκουμε
Μια γενικότερη έκφραση για την αλλαγή της υποτείνουσας στην περίπτωση αυξήσεων και των δύο ποδιών
Ενσωματώνοντας αυτή την εξίσωση και χρησιμοποιώντας τις αρχικές συνθήκες, παίρνουμε
Έτσι, φτάνουμε στην επιθυμητή απάντηση
Όπως γίνεται εύκολα αντιληπτό, η τετραγωνική εξάρτηση στον τελικό τύπο εμφανίζεται λόγω της γραμμικής αναλογικότητας μεταξύ των πλευρών του τριγώνου και των προσαυξήσεων, ενώ το άθροισμα οφείλεται στις ανεξάρτητες συνεισφορές από την αύξηση των διαφορετικών σκελών.
Μια απλούστερη απόδειξη μπορεί να ληφθεί εάν υποθέσουμε ότι ένα από τα πόδια δεν παρουσιάζει αύξηση (στην περίπτωση αυτή, το πόδι). Τότε για τη σταθερά ολοκλήρωσης παίρνουμε
Παραλλαγές και γενικεύσεις
Παρόμοια γεωμετρικά σχήματα σε τρεις πλευρές
Γενίκευση για παρόμοια τρίγωνα, εμβαδόν πράσινων μορφών A + B = εμβαδόν μπλε C
Πυθαγόρειο θεώρημα χρησιμοποιώντας παρόμοια ορθογώνια τρίγωνα
Μια γενίκευση του Πυθαγόρειου θεωρήματος έγινε από τον Ευκλείδη στο έργο του Αρχές, επεκτείνοντας τα εμβαδά των τετραγώνων στις πλευρές στα εμβαδά των ομοίων γεωμετρικά σχήματα :
Αν κατασκευάσουμε παρόμοια γεωμετρικά σχήματα (βλέπε Ευκλείδεια γεωμετρία) στις πλευρές ενός ορθογωνίου τριγώνου, τότε το άθροισμα των δύο μικρότερων σχημάτων θα ισούται με το εμβαδόν του μεγαλύτερου σχήματος.
Η κύρια ιδέα αυτής της γενίκευσης είναι ότι το εμβαδόν ενός τέτοιου γεωμετρικού σχήματος είναι ανάλογο με το τετράγωνο οποιασδήποτε από τις γραμμικές του διαστάσεις και, ειδικότερα, με το τετράγωνο του μήκους οποιασδήποτε πλευράς. Επομένως, για παρόμοια στοιχεία με περιοχές ΕΝΑ, σικαι ντοχτισμένο σε πλευρές με μήκος ένα, σικαι ντο, έχουμε:
Όμως, σύμφωνα με το Πυθαγόρειο θεώρημα, ένα 2 + σι 2 = ντο 2, λοιπόν ΕΝΑ + σι = ντο.
Αντίστροφα, αν μπορούμε να το αποδείξουμε ΕΝΑ + σι = ντογια τρία παρόμοια γεωμετρικά σχήματα χωρίς να χρησιμοποιήσουμε το Πυθαγόρειο θεώρημα, τότε μπορούμε να αποδείξουμε το ίδιο το θεώρημα, μεταβαίνοντας στο αντίστροφη κατεύθυνση. Για παράδειγμα, το αρχικό κεντρικό τρίγωνο μπορεί να επαναχρησιμοποιηθεί ως τρίγωνο ντοστην υποτείνουσα και δύο παρόμοια ορθογώνια τρίγωνα ( ΕΝΑκαι σι) χτισμένο στις άλλες δύο πλευρές, που σχηματίζονται ως αποτέλεσμα της διαίρεσης του κεντρικού τριγώνου με το ύψος του. Το άθροισμα των δύο μικρότερων εμβαδών των τριγώνων είναι τότε προφανώς ίσο με το εμβαδόν του τρίτου, επομένως ΕΝΑ + σι = ντοκαι, ακολουθώντας τις προηγούμενες αποδείξεις στο αντίστροφη σειρά, παίρνουμε το Πυθαγόρειο θεώρημα a 2 + b 2 = c 2 .
Θεώρημα συνημιτονίου
Το Πυθαγόρειο θεώρημα είναι ειδική περίπτωσηπερισσότερο γενικό θεώρημασυνημίτονα, που συσχετίζει τα μήκη των πλευρών σε ένα αυθαίρετο τρίγωνο:
όπου θ είναι η γωνία μεταξύ των πλευρών ένακαι σι.
Αν το θ είναι 90 μοίρες τότε συν θ = 0 και ο τύπος απλοποιείται στο συνηθισμένο Πυθαγόρειο θεώρημα.
Αυθαίρετο τρίγωνο
Σε οποιαδήποτε επιλεγμένη γωνία ενός αυθαίρετου τριγώνου με πλευρές α, β, γεγγράψετε ένα ισοσκελές τρίγωνο με τέτοιο τρόπο ώστε ίσες γωνίεςστη βάση του, το θ ισοδυναμούσε με την επιλεγμένη γωνία. Ας υποθέσουμε ότι η επιλεγμένη γωνία θ βρίσκεται απέναντι από την πλευρά που υποδεικνύεται ντο. Ως αποτέλεσμα, πήραμε ένα τρίγωνο ABD με γωνία θ, το οποίο βρίσκεται απέναντι από την πλευρά ένακαι πάρτι r. Το δεύτερο τρίγωνο σχηματίζεται από τη γωνία θ, η οποία βρίσκεται απέναντι από την πλευρά σικαι πάρτι Μεμήκος μικρό, όπως φαίνεται στην εικόνα. Ο Thabit Ibn Qurra δήλωσε ότι οι πλευρές σε αυτά τα τρία τρίγωνα σχετίζονται ως εξής:
Καθώς η γωνία θ πλησιάζει το π/2, η βάση ισοσκελές τρίγωνομειώνεται και οι δύο πλευρές r και s αλληλοεπικαλύπτονται όλο και λιγότερο. Όταν θ = π/2, το ADB μετατρέπεται σε ορθογώνιο τρίγωνο, r + μικρό = ντοκαι παίρνουμε το αρχικό Πυθαγόρειο θεώρημα.
Ας δούμε ένα από τα επιχειρήματα. Τρίγωνο ABCέχει τις ίδιες γωνίες με το τρίγωνο ABD, αλλά με αντίστροφη σειρά. (Τα δύο τρίγωνα έχουν κοινή γωνία στην κορυφή Β, και τα δύο έχουν γωνία θ, και έχουν επίσης την ίδια τρίτη γωνία, με το άθροισμα των γωνιών του τριγώνου) Συνεπώς, το ABC είναι παρόμοιο με την ανάκλαση ABD του τριγώνου DBA, όπως φαίνεται στο κάτω σχήμα. Ας γράψουμε τη σχέση μεταξύ αντίθετες πλευρέςκαι δίπλα στη γωνία θ,
Έτσι είναι η αντανάκλαση ενός άλλου τριγώνου,
Πολλαπλασιάστε τα κλάσματα και προσθέστε αυτούς τους δύο λόγους:
Q.E.D.
Γενίκευση για αυθαίρετα τρίγωνα μέσω παραλληλογραμμών
Γενίκευση για αυθαίρετα τρίγωνα,
περιοχή του πράσινου οικόπεδο = έκτασημπλε
Απόδειξη της διατριβής ότι στο παραπάνω σχήμα
Ας κάνουμε μια περαιτέρω γενίκευση για τα μη ορθογώνια τρίγωνα, χρησιμοποιώντας παραλληλόγραμμα σε τρεις πλευρές αντί για τετράγωνα. (τα τετράγωνα είναι μια ειδική περίπτωση.) Το επάνω σχήμα δείχνει ότι για οξύ τρίγωνοτο εμβαδόν του παραλληλογράμμου στη μεγάλη πλευρά είναι ίσο με το άθροισμα των παραλληλόγραμμων στις άλλες δύο πλευρές, με την προϋπόθεση ότι το παραλληλόγραμμο στη μεγάλη πλευρά είναι κατασκευασμένο όπως φαίνεται στο σχήμα (οι διαστάσεις που σημειώνονται με βέλη είναι οι ίδιες και προσδιορίστε τις πλευρές του κάτω παραλληλογράμμου). Αυτή η αντικατάσταση τετραγώνων από παραλληλόγραμμα έχει σαφή ομοιότητα με το αρχικό Πυθαγόρειο θεώρημα και πιστεύεται ότι διατυπώθηκε από τον Πάππο της Αλεξάνδρειας το 4 μ.Χ. μι.
Το κάτω σχήμα δείχνει την πρόοδο της απόδειξης. Ας δούμε την αριστερή πλευρά του τριγώνου. Το αριστερό πράσινο παραλληλόγραμμο έχει την ίδια περιοχή με την αριστερή πλευρά του μπλε παραλληλογράμμου επειδή έχουν την ίδια βάση σικαι ύψος η. Επίσης, το αριστερό πράσινο πλαίσιο έχει την ίδια περιοχή με το αριστερό πράσινο πλαίσιο στην επάνω εικόνα επειδή έχουν κοινά σημεία(ανώτερος αριστερή πλευράτρίγωνο) και το συνολικό ύψος κάθετο σε εκείνη την πλευρά του τριγώνου. Με το ίδιο επιχείρημα για τη δεξιά πλευρά του τριγώνου, αποδεικνύουμε ότι το κάτω παραλληλόγραμμο έχει το ίδιο εμβαδόν με τα δύο πράσινα παραλληλόγραμμα.
Μιγαδικοί αριθμοί
Το Πυθαγόρειο θεώρημα χρησιμοποιείται για την εύρεση της απόστασης μεταξύ δύο σημείων σε ένα καρτεσιανό σύστημα συντεταγμένων και αυτό το θεώρημα ισχύει για όλες τις αληθινές συντεταγμένες: απόσταση μικρόανάμεσα σε δύο σημεία ( α, β) και ( γ, δ) ισοδυναμεί
Δεν υπάρχουν προβλήματα με τον τύπο εάν οι μιγαδικοί αριθμοί αντιμετωπίζονται ως διανύσματα με πραγματικές συνιστώσες Χ + i y = (Χ, y). . Για παράδειγμα, η απόσταση μικρόμεταξύ 0 + 1 Εγώκαι 1 + 0 Εγώυπολογίστε ως συντελεστή διανύσματος (0, 1) − (1, 0) = (−1, 1), ή
Ωστόσο, για πράξεις με διανύσματα με μιγαδικές συντεταγμένες, είναι απαραίτητο να γίνει κάποια βελτίωση στον Πυθαγόρειο τύπο. Απόσταση μεταξύ σημείων με μιγαδικοί αριθμοί (ένα, σι) και ( ντο, ρε); ένα, σι, ντο, και ρεείναι όλα περίπλοκα, διατυπώνουμε χρησιμοποιώντας απόλυτες τιμές. Απόσταση μικρόμε βάση τη διανυσματική διαφορά (ένα − ντο, σι − ρε) σε παρακάτω φόρμα: αφήστε τη διαφορά ένα − ντο = Π+i q, όπου Πείναι το πραγματικό μέρος της διαφοράς, qείναι το φανταστικό μέρος, και i = √(−1). Ομοίως, ας σι − ρε = r+i μικρό. Επειτα:
πού βρίσκεται το σύνθετο συζυγές του . Για παράδειγμα, η απόσταση μεταξύ των σημείων (ένα, σι) = (0, 1) και (ντο, ρε) = (Εγώ, 0) , υπολογίστε τη διαφορά (ένα − ντο, σι − ρε) = (−Εγώ, 1) και το αποτέλεσμα θα ήταν 0 αν δεν χρησιμοποιήθηκαν σύμπλοκα συζυγή. Επομένως, χρησιμοποιώντας τη βελτιωμένη φόρμουλα, παίρνουμε
Η ενότητα ορίζεται ως εξής:
Στερεομετρία
Μια σημαντική γενίκευση του Πυθαγόρειου θεωρήματος για τον τρισδιάστατο χώρο είναι το θεώρημα του de Gua, που πήρε το όνομά του από τον J.-P. de Gua: αν ένα τετράεδρο έχει ορθή γωνία (όπως σε έναν κύβο), τότε το τετράγωνο της επιφάνειας της όψης απέναντι από τη σωστή γωνία είναι ίσο με το άθροισμα των τετραγώνων των περιοχών των άλλων τριών όψεων. Αυτό το συμπέρασμα μπορεί να συνοψιστεί ως " n-διαστατικό Πυθαγόρειο θεώρημα":
Το θεώρημα του Πυθαγόρα τρισδιάστατο χώροσυνδέει τη διαγώνιο ΑΔ με τρεις πλευρές.
Μια άλλη γενίκευση: Το Πυθαγόρειο θεώρημα μπορεί να εφαρμοστεί στη στερεομετρία με την ακόλουθη μορφή. Σκεφτείτε κυβοειδές, όπως φαίνεται στην εικόνα. Βρείτε το μήκος της διαγωνίου BD χρησιμοποιώντας το Πυθαγόρειο θεώρημα:
όπου τρεις πλευρές σχηματίζουν ένα ορθογώνιο τρίγωνο. Χρησιμοποιήστε την οριζόντια διαγώνιο BD και την κατακόρυφη ακμή AB για να βρείτε το μήκος της διαγωνίου AD, χρησιμοποιώντας και πάλι το Πυθαγόρειο θεώρημα:
ή, αν όλα είναι γραμμένα σε μία εξίσωση:
Αυτό το αποτέλεσμα είναι μια τρισδιάστατη έκφραση για τον προσδιορισμό του μεγέθους του διανύσματος v(διαγώνιος AD) εκφρασμένη ως προς τις κάθετες συνιστώσες της ( vια) (τρεις αμοιβαία κάθετες πλευρές):
Αυτή η εξίσωση μπορεί να θεωρηθεί ως γενίκευση του Πυθαγόρειου θεωρήματος για έναν πολυδιάστατο χώρο. Ωστόσο, το αποτέλεσμα στην πραγματικότητα δεν είναι τίποτα άλλο από την επαναλαμβανόμενη εφαρμογή του Πυθαγόρειου θεωρήματος σε μια ακολουθία ορθογωνίων τριγώνων σε διαδοχικά κάθετα επίπεδα.
διανυσματικός χώρος
Στην περίπτωση ενός ορθογώνιου συστήματος διανυσμάτων, λαμβάνει χώρα μια ισότητα, η οποία ονομάζεται επίσης Πυθαγόρειο θεώρημα:
Αν είναι η προβολή του διανύσματος επάνω άξονες συντεταγμένων, τότε αυτός ο τύπος συμπίπτει με την Ευκλείδεια απόσταση - και σημαίνει ότι το μήκος του διανύσματος είναι ίσο με τη ρίζα τετραγωνικό άθροισματετράγωνα των συστατικών του.
Ανάλογο αυτής της ισότητας στην υπόθεση ατελείωτο σύστημαδιανύσματα ονομάζεται ισότητα Parseval.
Μη Ευκλείδεια γεωμετρία
Το Πυθαγόρειο θεώρημα προέρχεται από τα αξιώματα της Ευκλείδειας γεωμετρίας και, στην πραγματικότητα, δεν ισχύει για τη μη Ευκλείδεια γεωμετρία, με τη μορφή που γράφτηκε παραπάνω. (Δηλαδή, το Πυθαγόρειο θεώρημα αποδεικνύεται ότι είναι ένα είδος ισοδύναμο με το αξίωμα του Ευκλείδη για παραλληλισμό) Με άλλα λόγια, στη μη Ευκλείδεια γεωμετρία, η αναλογία μεταξύ των πλευρών του τριγώνου θα είναι απαραίτητα σε μια μορφή διαφορετική από το Πυθαγόρειο θεώρημα . Για παράδειγμα, στη σφαιρική γεωμετρία, και οι τρεις πλευρές ενός ορθογωνίου τριγώνου (ας πούμε ένα, σικαι ντο) που δεσμεύει την οκτάδα (ένα όγδοο) της μοναδιαίας σφαίρας έχουν μήκος π/2, το οποίο έρχεται σε αντίθεση με το πυθαγόρειο θεώρημα επειδή ένα 2 + σι 2 ≠ ντο 2 .
Εξετάστε εδώ δύο περιπτώσεις μη Ευκλείδειας γεωμετρίας - σφαιρική και υπερβολική γεωμετρία. Και στις δύο περιπτώσεις, όπως για τον Ευκλείδειο χώρο για τα ορθογώνια τρίγωνα, το αποτέλεσμα που αντικαθιστά το Πυθαγόρειο θεώρημα προκύπτει από το θεώρημα του συνημιτόνου.
Ωστόσο, το Πυθαγόρειο θεώρημα παραμένει έγκυρο για υπερβολική και ελλειπτική γεωμετρία εάν η απαίτηση ότι το τρίγωνο είναι ορθογώνιο αντικατασταθεί από την προϋπόθεση ότι το άθροισμα δύο γωνιών του τριγώνου πρέπει να είναι ίσο με την τρίτη, ας πούμε. ΕΝΑ+σι = ντο. Τότε η αναλογία μεταξύ των πλευρών μοιάζει με αυτό: το άθροισμα των εμβαδών των κύκλων με διαμέτρους ένακαι σιίσο με το εμβαδόν ενός κύκλου με διάμετρο ντο.
σφαιρική γεωμετρία
Για κάθε ορθογώνιο τρίγωνο σε σφαίρα με ακτίνα R(για παράδειγμα, αν η γωνία γ στο τρίγωνο είναι ορθή) με πλευρές ένα, σι, ντοη σχέση μεταξύ των μερών θα μοιάζει με αυτό:
Αυτή η ισότητα μπορεί να προκύψει ως ειδική περίπτωσηΘεώρημα σφαιρικού συνημιτόνου, το οποίο ισχύει για όλα τα σφαιρικά τρίγωνα:
όπου cosh είναι το υπερβολικό συνημίτονο. Αυτός ο τύπος είναι μια ειδική περίπτωση του θεωρήματος του υπερβολικού συνημιτόνου, που ισχύει για όλα τα τρίγωνα:
όπου γ είναι η γωνία της οποίας η κορυφή είναι απέναντι από την πλευρά ντο.
όπου σολ ijονομάζεται μετρικός τανυστής. Μπορεί να είναι συνάρτηση θέσης. Τέτοιοι καμπυλόγραμμοι χώροι περιλαμβάνουν τη γεωμετρία του Ρίμαν όπως γενικό παράδειγμα. Αυτή η διατύπωση είναι επίσης κατάλληλη για τον Ευκλείδειο χώρο όταν χρησιμοποιούνται καμπυλόγραμμες συντεταγμένες. Για παράδειγμα, για πολικές συντεταγμένες:
διανυσματικό προϊόν
Το Πυθαγόρειο θεώρημα συνδέει δύο παραστάσεις για το μέγεθος ενός διανυσματικού γινομένου. Μια προσέγγιση για τον ορισμό ενός διασταυρούμενου προϊόντος απαιτεί να ικανοποιεί την εξίσωση:
αυτός ο τύπος χρησιμοποιεί το προϊόν με κουκκίδες. Η δεξιά πλευρά της εξίσωσης ονομάζεται ορίζουσα του Gram για ένακαι σι, το οποίο είναι ίσο με το εμβαδόν του παραλληλογράμμου που σχηματίζεται από αυτά τα δύο διανύσματα. Με βάση αυτή την απαίτηση, καθώς και την απαίτηση το διανυσματικό γινόμενο να είναι κάθετο στα συστατικά του ένακαι σιέπεται ότι, εκτός από τις ασήμαντες περιπτώσεις του 0- και 1-διάστατου χώρου, το διανυσματικό γινόμενο ορίζεται μόνο σε τρεις και επτά διαστάσεις. Χρησιμοποιούμε τον ορισμό της γωνίας in n-διαστατικός χώρος:
αυτή η ιδιότητα του διανυσματικού προϊόντος δίνει την τιμή της με την ακόλουθη μορφή:
Μέσω των θεμελιωδών τριγωνομετρική ταυτότητα Pythagoras, έχουμε μια διαφορετική μορφή γραφής της αξίας του:
Μια εναλλακτική προσέγγιση για τον ορισμό ενός διασταυρούμενου προϊόντος χρησιμοποιεί μια έκφραση για το μέγεθός του. Στη συνέχεια, επιχειρηματολογώντας με αντίστροφη σειρά, αποκτούμε μια σύνδεση με κλιμακωτό προϊόν:
δείτε επίσης
Σημειώσεις
- Θέμα ιστορίας: Το θεώρημα του Πυθαγόρα στα βαβυλωνιακά μαθηματικά
- ( , σελ. 351) σελ. 351
- ( , τόμος I, σελ. 144)
- Συζήτηση ιστορικά γεγονόταδίνεται στο (, σελ. 351) σελ. 351
- Kurt Von Fritz (Απρ., 1945). «Η ανακάλυψη της ασυμμετρίας από τον Ιππάσο του Μεταπόντου». The Annals of Mathematics, Δεύτερη Σειρά(Annals of Mathematics) 46 (2): 242–264.
- Lewis Carroll, «The story with knots», M., Mir, 1985, σελ. 7
- Άσγκερ ΑαμπόεΕπεισόδια από την πρώιμη ιστορία των μαθηματικών. - Mathematical Association of America, 1997. - P. 51. - ISBN 0883856131
- Πυθαγόρεια πρότασηαπό τον Elisha Scott Loomis
- του Ευκλείδη Στοιχεία: Βιβλίο VI, Πρόταση VI 31: "Στα ορθογώνια τρίγωνα το σχήμα στην πλευρά που υποβάλλει τη σωστή γωνία είναι ίσο με τα παρόμοια και παρόμοια περιγραφόμενα σχήματα στις πλευρές που περιέχουν τη σωστή γωνία."
- Lawrence S. Leff αναφερόμενη εργασία. - Barron's Educational Series. - Σ. 326. - ISBN 0764128922
- Howard Whitley Eves§4.8:...γενίκευση του Πυθαγόρειου θεωρήματος // Μεγάλες στιγμές στα μαθηματικά (πριν από το 1650) . - Mathematical Association of America, 1983. - P. 41. - ISBN 0883853108
- Ο Tâbit ibn Qorra (πλήρες όνομα Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 μ.Χ.) ήταν ένας γιατρός που ζούσε στη Βαγδάτη και έγραψε εκτενώς για τα Στοιχεία του Ευκλείδη και άλλοιμαθηματικά θέματα.
- Aydin Sayili (Μάρ. 1960). «Γενίκευση του Πυθαγόρειου Θεωρήματος του Thâbit ibn Qurra». Ίσις 51 (1): 35–37. DOI: 10.1086/348837.
- Judith D. Sally, Paul SallyΆσκηση 2.10(ii) // Αναφερόμενη εργασία . - Σ. 62. - ISBN 0821844032
- Για λεπτομέρειες μιας τέτοιας κατασκευής, βλ Τζορτζ ΤζένινγκςΕικόνα 1.32: Το γενικευμένο Πυθαγόρειο θεώρημα // Σύγχρονη γεωμετρία με εφαρμογές: με 150 σχήματα . - 3ος. - Springer, 1997. - P. 23. - ISBN 038794222X
- Arlen Brown, Carl M. Pearcyείδος ντο: Κανόνας για ένα αυθαίρετο n-tuple ... // Εισαγωγή στην ανάλυση . - Springer, 1995. - P. 124. - ISBN 0387943692Βλέπε επίσης σελίδες 47-50.
- Alfred Gray, Elsa Abbena, Simon SalamonΣύγχρονη διαφορική γεωμετρία καμπυλών και επιφανειών με το Mathematica. - 3ος. - CRC Press, 2006. - P. 194. - ISBN 1584884487
- Rajendra Bhatiaανάλυση μήτρας. - Springer, 1997. - P. 21. - ISBN 0387948465
- Stephen W. Hawking αναφερόμενη εργασία. - 2005. - Σ. 4. - ISBN 0762419229
- Eric W. Weiststein CRC συνοπτική εγκυκλοπαίδεια των μαθηματικών. - 2ο. - 2003. - Σελ. 2147. - ISBN 1584883472
- Alexander R. Pruss
Μέσο επίπεδο
Ορθογώνιο τρίγωνο. Πλήρης εικονογραφημένος οδηγός (2019)
ΟΡΘΟΓΩΝΙΟ ΤΡΙΓΩΝΟ. ΠΡΩΤΟ ΕΠΙΠΕΔΟ.
Στα προβλήματα, μια ορθή γωνία δεν είναι καθόλου απαραίτητη - η κάτω αριστερή, επομένως πρέπει να μάθετε πώς να αναγνωρίζετε ένα ορθογώνιο τρίγωνο σε αυτήν τη μορφή,

και σε τέτοια

και σε τέτοια 
Τι είναι καλό σε ένα ορθογώνιο τρίγωνο; Λοιπόν... πρώτα από όλα, υπάρχουν ειδικές όμορφα ονόματαγια τα πλευρά του.
Προσοχή στο σχέδιο!

Θυμηθείτε και μην μπερδεύετε: πόδια - δύο, και η υποτείνουσα - μόνο ένα(το μοναδικό, μοναδικό και μακρύτερο)!
Λοιπόν, συζητήσαμε τα ονόματα, τώρα το πιο σημαντικό πράγμα: το Πυθαγόρειο Θεώρημα.
Πυθαγόρειο θεώρημα.
Αυτό το θεώρημα είναι το κλειδί για την επίλυση πολλών προβλημάτων που αφορούν ένα ορθογώνιο τρίγωνο. Το απέδειξε ο Πυθαγόρας σε εντελώς αμνημονεύτων χρόνων, και από τότε έχει φέρει πολλά οφέλη σε όσους το γνωρίζουν. Και το καλύτερο για εκείνη είναι ότι είναι απλή.
Ετσι, Πυθαγόρειο θεώρημα:
Θυμάστε το αστείο: «Το πυθαγόρειο παντελόνι είναι ίσο από όλες τις πλευρές!»;
Ας ζωγραφίσουμε αυτά τα πολύ πυθαγόρεια παντελόνια και ας τα δούμε. 
Μοιάζει πραγματικά με σορτς; Λοιπόν, σε ποιες πλευρές και πού είναι ίσες; Γιατί και από πού προήλθε το αστείο; Και αυτό το αστείο συνδέεται ακριβώς με το Πυθαγόρειο θεώρημα, πιο συγκεκριμένα με τον τρόπο που διατύπωσε ο ίδιος ο Πυθαγόρας το θεώρημά του. Και το διατύπωσε ως εξής:
"Αθροισμα περιοχή των πλατειών, χτισμένο στα πόδια, ισούται με τετραγωνική έκτασηχτισμένο πάνω στην υποτείνουσα.
Δεν ακούγεται λίγο διαφορετικό, έτσι δεν είναι; Και έτσι, όταν ο Πυθαγόρας σχεδίασε τη δήλωση του θεωρήματός του, αποδείχθηκε ακριβώς μια τέτοια εικόνα.

Σε αυτήν την εικόνα, το άθροισμα των εμβαδών των μικρών τετραγώνων είναι ίσο με το εμβαδόν του μεγάλου τετραγώνου. Και για να θυμούνται καλύτερα τα παιδιά ότι το άθροισμα των τετραγώνων των ποδιών είναι ίσο με το τετράγωνο της υποτείνουσας, κάποιος πνευματώδης επινόησε αυτό το αστείο για το πυθαγόρειο παντελόνι.
Γιατί διατυπώνουμε τώρα το Πυθαγόρειο θεώρημα
Υπέφερε ο Πυθαγόρας και μίλησε για τετράγωνα;
Βλέπετε, στα αρχαία χρόνια δεν υπήρχε ... άλγεβρα! Δεν υπήρχαν σημάδια και ούτω καθεξής. Δεν υπήρχαν επιγραφές. Μπορείτε να φανταστείτε πόσο τρομερό ήταν για τους φτωχούς αρχαίους μαθητές να απομνημονεύουν τα πάντα με λέξεις;;! Και μπορούμε να χαιρόμαστε που έχουμε μια απλή διατύπωση του Πυθαγόρειου θεωρήματος. Ας το επαναλάβουμε για να θυμηθούμε καλύτερα:
Τώρα πρέπει να είναι εύκολο:
| Το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των ποδιών. |
Λοιπόν, συζητήθηκε το πιο σημαντικό θεώρημα για ένα ορθογώνιο τρίγωνο. Αν αναρωτιέστε πώς αποδεικνύεται, διαβάστε παρακάτω. επόμενα επίπεδαθεωρία, και τώρα ας προχωρήσουμε… στο σκοτεινό δάσος... τριγωνομετρία! Στις φοβερές λέξεις ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη.
Ημίτονο, συνημίτονο, εφαπτομένη, συνεφαπτομένη σε ορθογώνιο τρίγωνο.
Στην πραγματικότητα, δεν είναι όλα τόσο τρομακτικά. Φυσικά, ο «πραγματικός» ορισμός του ημιτονοειδούς, συνημίτονος, εφαπτομένης και συνεφαπτομένης θα πρέπει να εξεταστεί στο άρθρο. Αλλά πραγματικά δεν θέλετε, έτσι δεν είναι; Μπορούμε να χαρούμε: για να λύσετε προβλήματα σχετικά με ένα ορθογώνιο τρίγωνο, μπορείτε απλά να συμπληρώσετε τα ακόλουθα απλά πράγματα:
Γιατί είναι όλα για τη γωνία; Πού είναι η γωνία; Για να το καταλάβετε αυτό, πρέπει να ξέρετε πώς γράφονται με λέξεις οι προτάσεις 1 - 4. Κοίτα, κατάλαβε και θυμήσου!
1.
Στην πραγματικότητα ακούγεται κάπως έτσι:
Τι γίνεται με τη γωνία; Υπάρχει ένα πόδι που είναι απέναντι από τη γωνία, δηλαδή το αντίθετο πόδι (για τη γωνία); Φυσικά και έχουν! Αυτός είναι ένας καθετήρας!
Τι γίνεται όμως με τη γωνία; Κοίτα προσεκτικά. Ποιο πόδι είναι δίπλα στη γωνία; Φυσικά, η γάτα. Έτσι, για τη γωνία, το πόδι είναι γειτονικό, και
Και τώρα, προσοχή! Δείτε τι πήραμε:
Δείτε πόσο υπέροχο είναι:
Τώρα ας περάσουμε στην εφαπτομένη και την συνεφαπτομένη.
Πώς να το εκφράσω τώρα με λέξεις; Τι είναι το πόδι σε σχέση με τη γωνία; Απέναντι, φυσικά - «βρίσκεται» απέναντι από τη γωνία. Και ο καθετήρας; Δίπλα στη γωνία. Τι πήραμε λοιπόν;
Δείτε πώς αντιστρέφονται ο αριθμητής και ο παρονομαστής;
Και τώρα πάλι οι γωνίες και έγινε η ανταλλαγή:
Περίληψη
Ας γράψουμε εν συντομία όσα μάθαμε.
 |
Πυθαγόρειο θεώρημα: |
Το θεώρημα του κύριου ορθογωνίου τριγώνου είναι το Πυθαγόρειο θεώρημα.
Πυθαγόρειο θεώρημα
Παρεμπιπτόντως, θυμάσαι καλά τι είναι τα πόδια και η υποτείνουσα; Αν όχι, τότε κοιτάξτε την εικόνα - ανανεώστε τις γνώσεις σας

Είναι πιθανό να έχετε ήδη χρησιμοποιήσει το Πυθαγόρειο θεώρημα πολλές φορές, αλλά έχετε αναρωτηθεί ποτέ γιατί ισχύει ένα τέτοιο θεώρημα. Πώς θα το αποδείκνυες; Ας κάνουμε όπως οι αρχαίοι Έλληνες. Ας σχεδιάσουμε ένα τετράγωνο με μια πλευρά.

Βλέπετε πόσο πονηρά χωρίσαμε τις πλευρές του σε τμήματα μήκους και!
Τώρα ας συνδέσουμε τα σημειωμένα σημεία

Εδώ, ωστόσο, σημειώσαμε κάτι άλλο, αλλά εσείς οι ίδιοι δείτε την εικόνα και σκεφτείτε γιατί.
Ποιο είναι το εμβαδόν του μεγαλύτερου τετραγώνου; Σωστά, . Τι γίνεται με τη μικρότερη περιοχή; Φυσικά, . Το συνολικό εμβαδόν των τεσσάρων γωνιών παραμένει. Φανταστείτε ότι πήραμε δύο από αυτά και ακουμπήσαμε ο ένας στον άλλο με υποτείνουσες. Τι συνέβη? Δύο ορθογώνια. Έτσι, η περιοχή των "μοσχευμάτων" είναι ίση.
Ας τα βάλουμε όλα μαζί τώρα.
Ας μεταμορφώσουμε:
Επισκεφτήκαμε λοιπόν τον Πυθαγόρα - αποδείξαμε το θεώρημά του με αρχαίο τρόπο.
Ορθογώνιο τρίγωνο και τριγωνομετρία
Για ένα ορθογώνιο τρίγωνο ισχύουν οι ακόλουθες σχέσεις:

Κόλπος οξεία γωνίαίση με την αναλογία του αντίθετου σκέλους προς την υποτείνουσα
Το συνημίτονο μιας οξείας γωνίας ισούται με την αναλογία του διπλανού σκέλους προς την υποτείνουσα.
Η εφαπτομένη μιας οξείας γωνίας είναι ίση με την αναλογία του απέναντι σκέλους προς το διπλανό σκέλος.
Η συνεφαπτομένη μιας οξείας γωνίας είναι ίση με την αναλογία του διπλανού σκέλους προς το αντίθετο σκέλος.
Και για άλλη μια φορά, όλα αυτά με τη μορφή ενός πιάτου:
Είναι πολύ άνετο!
Σημάδια ισότητας ορθογωνίων τριγώνων
I. Σε δύο πόδια

II. Με το πόδι και την υπόταση

III. Με υποτείνουσα και οξεία γωνία

IV. Κατά μήκος του ποδιού και οξεία γωνία
ένα) 
σι) 
Προσοχή! Εδώ είναι πολύ σημαντικό τα πόδια να είναι «αντίστοιχα». Για παράδειγμα, αν πάει ως εξής:

ΤΟΤΕ ΤΑ ΤΡΙΓΩΝΑ ΔΕΝ ΕΙΝΑΙ ΙΣΑ, παρά το γεγονός ότι έχουν μια ίδια οξεία γωνία.
Πρέπει να και στα δύο τρίγωνα το πόδι ήταν δίπλα, ή και στα δύο - απέναντι.
Έχετε παρατηρήσει πώς διαφέρουν τα σημάδια ισότητας ορθογωνίων τριγώνων από τα συνηθισμένα σημάδια ισότητας τριγώνων; Κοιτάξτε το θέμα «και δώστε προσοχή στο γεγονός ότι για την ισότητα των «συνηθισμένων» τριγώνων, χρειάζεστε την ισότητα των τριών στοιχείων τους: δύο πλευρές και μια γωνία μεταξύ τους, δύο γωνίες και μια πλευρά μεταξύ τους ή τρεις πλευρές. Για την ισότητα όμως των ορθογώνιων τριγώνων αρκούν μόνο δύο αντίστοιχα στοιχεία. Είναι υπέροχο, σωστά;
Περίπου η ίδια κατάσταση με σημάδια ομοιότητας ορθογωνίων τριγώνων.
Σημάδια ομοιότητας ορθογωνίων τριγώνων
Ι. Οξεία γωνία

II. Σε δύο πόδια

III. Με το πόδι και την υπόταση

Διάμεσος σε ορθογώνιο τρίγωνο
Γιατί έτσι?
Θεωρήστε ένα ολόκληρο ορθογώνιο αντί για ένα ορθογώνιο τρίγωνο.
Ας σχεδιάσουμε μια διαγώνιο και ας εξετάσουμε ένα σημείο - το σημείο τομής των διαγωνίων. Τι γνωρίζετε για τις διαγώνιες ενός ορθογωνίου;
Και τι προκύπτει από αυτό;
Έγινε λοιπόν αυτό
- - διάμεσος:
Θυμηθείτε αυτό το γεγονός! Βοηθάει πολύ!
Αυτό που προκαλεί ακόμη μεγαλύτερη έκπληξη είναι ότι ισχύει και το αντίστροφο.
Τι καλό μπορεί να ωφεληθεί από το γεγονός ότι η διάμεσος που σύρεται στην υποτείνουσα είναι ίση με τη μισή υποτείνουσα; Ας δούμε την εικόνα
Κοίτα προσεκτικά. Έχουμε: , δηλαδή, οι αποστάσεις από το σημείο και στις τρεις κορυφές του τριγώνου αποδείχθηκαν ίσες. Αλλά σε ένα τρίγωνο υπάρχει μόνο ένα σημείο, οι αποστάσεις από το οποίο περίπου και οι τρεις κορυφές του τριγώνου είναι ίσες, και αυτό είναι το ΚΕΝΤΡΟ ΤΟΥ ΠΕΡΙΓΡΑΦΟΥ. Λοιπόν τι έγινε?
Ας ξεκινήσουμε λοιπόν με αυτό το «άλλωστε...».
Ας δούμε το i.
Αλλά σε παρόμοια τρίγωνα όλες οι γωνίες είναι ίσες!
Το ίδιο μπορεί να ειπωθεί για και
Τώρα ας το σχεδιάσουμε μαζί:
Τι χρήση μπορεί να αντλήσει από αυτή την «τριπλή» ομοιότητα.
Λοιπόν, για παράδειγμα - δύο τύποι για το ύψος ενός ορθογωνίου τριγώνου.
Γράφουμε τις σχέσεις των αντίστοιχων μερών:

Για να βρούμε το ύψος, λύνουμε την αναλογία και παίρνουμε πρώτος τύπος "Ύψος σε ορθογώνιο τρίγωνο":
Ας εφαρμόσουμε λοιπόν την ομοιότητα: .

Τι θα γίνει τώρα;
Και πάλι λύνουμε την αναλογία και παίρνουμε τον δεύτερο τύπο:
Και οι δύο αυτοί τύποι πρέπει να θυμόμαστε πολύ καλά και αυτός που είναι πιο βολικό να εφαρμοστεί. Ας τα ξαναγράψουμε.
Πυθαγόρειο θεώρημα:
Σε ένα ορθογώνιο τρίγωνο, το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των σκελών:.

Σημάδια ισότητας ορθογωνίων τριγώνων:
- σε δύο πόδια:
- κατά μήκος του ποδιού και της υποτείνουσας: ή
- κατά μήκος του σκέλους και της παρακείμενης οξείας γωνίας: ή
- κατά μήκος του σκέλους και της αντίθετης οξείας γωνίας: ή
- κατά υποτείνουσα και οξεία γωνία: ή.
Σημάδια ομοιότητας ορθογωνίων τριγώνων:
- μια αιχμηρή γωνία: ή
- από την αναλογικότητα των δύο ποδιών:
- από την αναλογικότητα του ποδιού και της υποτείνουσας: ή.
Ημίτονο, συνημίτονο, εφαπτομένη, συνεφαπτομένη σε ορθογώνιο τρίγωνο
- Το ημίτονο οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος του αντίθετου σκέλους προς την υποτείνουσα:
- Το συνημίτονο οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος του διπλανού σκέλους προς την υποτείνουσα:
- Η εφαπτομένη οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος του απέναντι σκέλους προς το διπλανό:
- Η συνεφαπτομένη οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος του διπλανού σκέλους προς το αντίθετο:.
Ύψος ορθογωνίου τριγώνου: ή.
Σε ένα ορθογώνιο τρίγωνο, η διάμεσος που αντλείται από την κορυφή της ορθής γωνίας είναι ίση με το μισό της υποτείνουσας: .
Εμβαδόν ορθογωνίου τριγώνου:
- μέσω των καθετήρων:
 Ομοίως, το τρίγωνο CBH είναι παρόμοιο με το ABC. Παρουσιάζοντας τη σημειογραφία
Ομοίως, το τρίγωνο CBH είναι παρόμοιο με το ABC. Παρουσιάζοντας τη σημειογραφία  1. Τοποθετήστε τέσσερα ίσα ορθογώνια τρίγωνα όπως φαίνεται στο σχήμα.
1. Τοποθετήστε τέσσερα ίσα ορθογώνια τρίγωνα όπως φαίνεται στο σχήμα. 
 Η ιδέα της απόδειξης του Ευκλείδη είναι η εξής: ας προσπαθήσουμε να αποδείξουμε ότι το μισό εμβαδόν του τετραγώνου που χτίζεται στην υποτείνουσα είναι ίσο με το άθροισμα των μισών εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη και μετά τα εμβαδά του τα μεγάλα και τα δύο μικρά τετράγωνα είναι ίσα. Εξετάστε το σχέδιο στα αριστερά. Κατασκευάσαμε τετράγωνα στις πλευρές ενός ορθογώνιου τριγώνου πάνω του και σχεδιάσαμε μια ακτίνα s από την κορυφή της ορθής γωνίας C κάθετη στην υποτείνουσα AB, κόβει το τετράγωνο ABIK, χτισμένο στην υποτείνουσα, σε δύο ορθογώνια - BHJI και HAKJ , αντίστοιχα. Αποδεικνύεται ότι τα εμβαδά αυτών των ορθογωνίων είναι ακριβώς ίσα με τα εμβαδά των τετραγώνων που είναι χτισμένα στα αντίστοιχα σκέλη. Ας προσπαθήσουμε να αποδείξουμε ότι το εμβαδόν του τετραγώνου DECA είναι ίσο με το εμβαδόν του ορθογωνίου AHJK Για να το κάνουμε αυτό, χρησιμοποιούμε μια βοηθητική παρατήρηση: Το εμβαδόν ενός τριγώνου με το ίδιο ύψος και βάση με το δεδομένο ορθογώνιο είναι ίσο με το μισό του εμβαδού του δεδομένου ορθογωνίου. Αυτό είναι συνέπεια του ορισμού του εμβαδού ενός τριγώνου ως το μισό του γινόμενου της βάσης και του ύψους. Από αυτή την παρατήρηση προκύπτει ότι το εμβαδόν του τριγώνου ACK είναι ίσο με το εμβαδόν του τριγώνου AHK (δεν φαίνεται), το οποίο, με τη σειρά του, είναι ίσο με το μισό του εμβαδού του ορθογωνίου AHJK. Ας αποδείξουμε τώρα ότι το εμβαδόν του τριγώνου ACK είναι επίσης ίσο με το μισό του εμβαδού του τετραγώνου DECA. Το μόνο πράγμα που πρέπει να γίνει για αυτό είναι να αποδειχθεί η ισότητα των τριγώνων ACK και BDA (καθώς το εμβαδόν του τριγώνου BDA είναι ίσο με το μισό του εμβαδού του τετραγώνου από την παραπάνω ιδιότητα). Αυτή η ισότητα είναι προφανής, τα τρίγωνα είναι ίσα σε δύο πλευρές και η μεταξύ τους γωνία. Δηλαδή - AB=AK,AD=AC - η ισότητα των γωνιών CAK και BAD είναι εύκολο να αποδειχθεί με τη μέθοδο της κίνησης: ας περιστρέψουμε το τρίγωνο CAK 90 ° αριστερόστροφα, τότε είναι προφανές ότι οι αντίστοιχες πλευρές των δύο υπό εξέταση τριγώνων θα συμπίπτουν (λόγω του γεγονότος ότι η γωνία στην κορυφή του τετραγώνου είναι 90°). Το επιχείρημα για την ισότητα των εμβαδών του τετραγώνου BCFG και του ορθογωνίου BHJI είναι εντελώς ανάλογο. Έτσι, αποδείξαμε ότι το εμβαδόν του τετραγώνου που είναι χτισμένο στην υποτείνουσα είναι το άθροισμα των εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη.
Η ιδέα της απόδειξης του Ευκλείδη είναι η εξής: ας προσπαθήσουμε να αποδείξουμε ότι το μισό εμβαδόν του τετραγώνου που χτίζεται στην υποτείνουσα είναι ίσο με το άθροισμα των μισών εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη και μετά τα εμβαδά του τα μεγάλα και τα δύο μικρά τετράγωνα είναι ίσα. Εξετάστε το σχέδιο στα αριστερά. Κατασκευάσαμε τετράγωνα στις πλευρές ενός ορθογώνιου τριγώνου πάνω του και σχεδιάσαμε μια ακτίνα s από την κορυφή της ορθής γωνίας C κάθετη στην υποτείνουσα AB, κόβει το τετράγωνο ABIK, χτισμένο στην υποτείνουσα, σε δύο ορθογώνια - BHJI και HAKJ , αντίστοιχα. Αποδεικνύεται ότι τα εμβαδά αυτών των ορθογωνίων είναι ακριβώς ίσα με τα εμβαδά των τετραγώνων που είναι χτισμένα στα αντίστοιχα σκέλη. Ας προσπαθήσουμε να αποδείξουμε ότι το εμβαδόν του τετραγώνου DECA είναι ίσο με το εμβαδόν του ορθογωνίου AHJK Για να το κάνουμε αυτό, χρησιμοποιούμε μια βοηθητική παρατήρηση: Το εμβαδόν ενός τριγώνου με το ίδιο ύψος και βάση με το δεδομένο ορθογώνιο είναι ίσο με το μισό του εμβαδού του δεδομένου ορθογωνίου. Αυτό είναι συνέπεια του ορισμού του εμβαδού ενός τριγώνου ως το μισό του γινόμενου της βάσης και του ύψους. Από αυτή την παρατήρηση προκύπτει ότι το εμβαδόν του τριγώνου ACK είναι ίσο με το εμβαδόν του τριγώνου AHK (δεν φαίνεται), το οποίο, με τη σειρά του, είναι ίσο με το μισό του εμβαδού του ορθογωνίου AHJK. Ας αποδείξουμε τώρα ότι το εμβαδόν του τριγώνου ACK είναι επίσης ίσο με το μισό του εμβαδού του τετραγώνου DECA. Το μόνο πράγμα που πρέπει να γίνει για αυτό είναι να αποδειχθεί η ισότητα των τριγώνων ACK και BDA (καθώς το εμβαδόν του τριγώνου BDA είναι ίσο με το μισό του εμβαδού του τετραγώνου από την παραπάνω ιδιότητα). Αυτή η ισότητα είναι προφανής, τα τρίγωνα είναι ίσα σε δύο πλευρές και η μεταξύ τους γωνία. Δηλαδή - AB=AK,AD=AC - η ισότητα των γωνιών CAK και BAD είναι εύκολο να αποδειχθεί με τη μέθοδο της κίνησης: ας περιστρέψουμε το τρίγωνο CAK 90 ° αριστερόστροφα, τότε είναι προφανές ότι οι αντίστοιχες πλευρές των δύο υπό εξέταση τριγώνων θα συμπίπτουν (λόγω του γεγονότος ότι η γωνία στην κορυφή του τετραγώνου είναι 90°). Το επιχείρημα για την ισότητα των εμβαδών του τετραγώνου BCFG και του ορθογωνίου BHJI είναι εντελώς ανάλογο. Έτσι, αποδείξαμε ότι το εμβαδόν του τετραγώνου που είναι χτισμένο στην υποτείνουσα είναι το άθροισμα των εμβαδών των τετραγώνων που είναι χτισμένα στα σκέλη.  Εξετάστε το σχέδιο, όπως φαίνεται από τη συμμετρία, το τμήμα CI κόβει το τετράγωνο ABHJ σε δύο πανομοιότυπα μέρη (καθώς τα τρίγωνα ABC και JHI είναι ίσα στην κατασκευή). Χρησιμοποιώντας μια αριστερόστροφη περιστροφή 90 μοιρών, βλέπουμε την ισότητα των σκιασμένων σχημάτων CAJI και GDAB. Τώρα είναι σαφές ότι η περιοχή της φιγούρας που σκιάζεται από εμάς είναι ίση με το άθροισμα των μισών περιοχών των τετραγώνων που είναι χτισμένα στα πόδια και της περιοχής του αρχικού τριγώνου. Από την άλλη πλευρά, είναι ίσο με το μισό εμβαδόν του τετραγώνου που είναι χτισμένο στην υποτείνουσα, συν το εμβαδόν του αρχικού τριγώνου. Το τελευταίο βήμα της απόδειξης αφήνεται στον αναγνώστη.
Εξετάστε το σχέδιο, όπως φαίνεται από τη συμμετρία, το τμήμα CI κόβει το τετράγωνο ABHJ σε δύο πανομοιότυπα μέρη (καθώς τα τρίγωνα ABC και JHI είναι ίσα στην κατασκευή). Χρησιμοποιώντας μια αριστερόστροφη περιστροφή 90 μοιρών, βλέπουμε την ισότητα των σκιασμένων σχημάτων CAJI και GDAB. Τώρα είναι σαφές ότι η περιοχή της φιγούρας που σκιάζεται από εμάς είναι ίση με το άθροισμα των μισών περιοχών των τετραγώνων που είναι χτισμένα στα πόδια και της περιοχής του αρχικού τριγώνου. Από την άλλη πλευρά, είναι ίσο με το μισό εμβαδόν του τετραγώνου που είναι χτισμένο στην υποτείνουσα, συν το εμβαδόν του αρχικού τριγώνου. Το τελευταίο βήμα της απόδειξης αφήνεται στον αναγνώστη.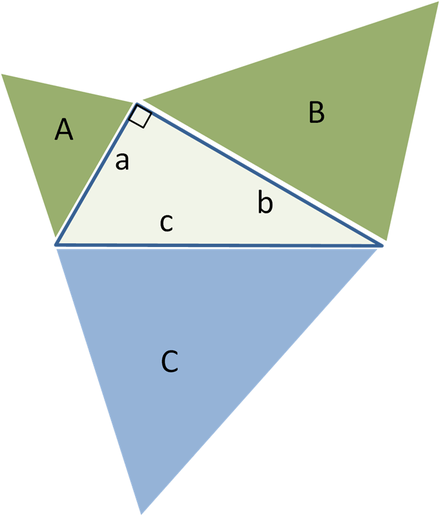




 Φοιτητής παιδαγωγικού πανεπιστημίου: ζωή και επαγγελματικές προοπτικές: Μονογραφία Επαγγελματική δραστηριότητα νεαρού δασκάλου
Φοιτητής παιδαγωγικού πανεπιστημίου: ζωή και επαγγελματικές προοπτικές: Μονογραφία Επαγγελματική δραστηριότητα νεαρού δασκάλου Χαρακτηριστικά της εκπαίδευσης βάσει ικανοτήτων Προετοιμασία για το μάθημα
Χαρακτηριστικά της εκπαίδευσης βάσει ικανοτήτων Προετοιμασία για το μάθημα Ψυχολογικές και παιδαγωγικές προσεγγίσεις για την αξιολόγηση των αποτελεσμάτων της εκπαίδευσης με βάση τις ικανότητες III
Ψυχολογικές και παιδαγωγικές προσεγγίσεις για την αξιολόγηση των αποτελεσμάτων της εκπαίδευσης με βάση τις ικανότητες III