Definition. Let a function f(x) be defined on some interval and x 0 be a point in this interval. If , then f(x) is said to be continuous at the point x 0 .
From the definition it follows that we can talk about continuity only in relation to those points at which f(x) is defined (when defining the limit of a function, such a condition was not set). For continuous functions , that is, the operations f and lim are commutable. Accordingly, two definitions of the limit of a function at a point can be given two definitions of continuity - “in the language of sequences” and “in the language of inequalities” (in the language of ε-δ). It is suggested that you do this yourself.
For practical use, it is sometimes more convenient to define continuity in the language of increments.
The value Δx=x-x 0 is called the increment of the argument, and Δy=f(x)-f(x 0) is the increment of the function when moving from point x 0 to point x.
Definition. Let f(x) be defined at point x 0 . A function f(x) is called continuous at a point x 0 if an infinitesimal increment of the argument at this point corresponds to an infinitesimal increment of the function, that is, Δy→0 for Δx→0.

Example No. 1. Prove that the function y=sinx is continuous for any value of x.
Solution. Let x 0 be an arbitrary point. Giving it an increment Δx, we get the point x=x 0 +Δx. Then Δy=f(x)-f(x 0) = sin(x 0 +Δx)-sin(x) = . We get .

Definition . The function y=f(x) is called continuous at the point x 0 on the right (left) if
.
A function continuous at an interior point will be both right and left continuous. The converse is also true: if a function is continuous at a point on the left and right, then it will be continuous at that point. However, a function can only be continuous on one side. For example, for , , f(1)=1, therefore, this function is continuous only on the left (for the graph of this function, see paragraph 5.7.2 above).
Definition. A function is called continuous on some interval if it is continuous at every point of this interval.
In particular, if the interval is a segment, then one-sided continuity is implied at its ends.

Properties of continuous functions

1. All elementary functions are continuous in their domain of definition.
2. If f(x) and φ(x), given on a certain interval, are continuous at the point x 0 of this interval, then the functions will also be continuous at this point.
3. If y=f(x) is continuous at the point x 0 from X, and z=φ(y) is continuous at the corresponding point y 0 =f(x 0) from Y, then the complex function z=φ(f(x )) will be continuous at point x 0 .

Function breaks and their classification

A sign of continuity of the function f(x) at the point x 0 is the equality, which implies the presence of three conditions:
1) f(x) is defined at point x 0 ;
2) ;
3) .
If at least one of these requirements is violated, then x 0 is called the break point of the function. In other words, a break point is a point at which this function is not continuous. From the definition of break points it follows that the break points of a function are:
a) points belonging to the domain of definition of the function at which f(x) loses the property of continuity,
b) points not belonging to the domain of definition of f(x), which are adjacent points of two intervals of the domain of definition of the function.
For example, for a function, the point x=0 is a break point, since the function at this point is not defined, and the function has a discontinuity at the point x=1, which is adjacent to two intervals (-∞,1) and (1,∞) of the domain of definition of f(x) and does not exist.

The following classification is adopted for break points.
1) If at the point x 0 there are finite And , but f(x 0 +0)≠f(x 0 -0), then x 0 is called discontinuity point of the first kind , and is called function jump .

Example 2. Consider the function
The function can only be broken at the point x=2 (at other points it is continuous like any polynomial).
We'll find , . Since the one-sided limits are finite, but not equal to each other, then at the point x=2 the function has a discontinuity of the first kind. notice, that , therefore the function at this point is continuous on the right (Fig. 2).
2) Discontinuity points of the second kind are called points at which at least one of the one-sided limits is equal to ∞ or does not exist.

Example 3. The function y=2 1/ x is continuous for all values ​​of x except x=0. Let's find one-sided limits: , , therefore x=0 is a discontinuity point of the second kind (Fig. 3).
3) Point x=x 0 is called removable break point , if f(x 0 +0)=f(x 0 -0)≠f(x 0).
We will “eliminate” the gap in the sense that it is enough to change (redefine or redefine) the value of the function at this point by setting , and the function will become continuous at the point x 0 .
Example 4. It is known that , and this limit does not depend on the way x tends to zero. But the function at point x=0 is not defined. If we redefine the function by setting f(0)=1, then it turns out to be continuous at this point (at other points it is continuous as the quotient of the continuous functions sinx and x).
Example 5. Examine the continuity of a function .
Solution. The functions y=x 3 and y=2x are defined and continuous everywhere, including in the indicated intervals. Let's examine the junction point of the intervals x=0:
, , . We obtain that , which implies that at the point x=0 the function is continuous.
Definition. A function that is continuous on an interval except for a finite number of discontinuity points of the first kind or removable discontinuity is called piecewise continuous on this interval.

Examples of discontinuous functions

Example 1. The function is defined and continuous on (-∞,+∞) except at the point x=2. Let's determine the type of break. Because the And , then at the point x=2 there is a discontinuity of the second kind (Fig. 6).
Example 2. The function is defined and continuous for all x except x=0, where the denominator is zero. Let's find one-sided limits at the point x=0:
One-sided limits are finite and different, therefore, x=0 is a discontinuity point of the first kind (Fig. 7).
Example 3. Determine at what points and what kind of discontinuities the function has
This function is defined on [-2,2]. Since x 2 and 1/x are continuous in the intervals [-2,0] and , respectively, the discontinuity can only occur at the junction of the intervals, that is, at the point x=0. Since , then x=0 is a discontinuity point of the second kind.

Example 4. Is it possible to eliminate function gaps:
A) at point x=2;
b) at point x=2;
V) at point x=1?
Solution. Regarding example a) we can immediately say that the discontinuity f(x) at the point x=2 cannot be eliminated, since at this point there are infinite one-sided limits (see example 1).
b) The function g(x) although has finite one-sided limits at the point x=2

(,),

but they do not coincide, so the gap cannot be eliminated either.
c) The function φ(x) at the discontinuity point x=1 has equal one-sided finite limits: . Therefore, the gap can be eliminated by redefining the function at x=1 by putting f(1)=1 instead of f(1)=2.

Example No. 5. Show that the Dirichlet function

discontinuous at every point on the numerical axis.
Solution. Let x 0 be any point from (-∞,+∞). In any of its neighborhoods there are both rational and irrational points. This means that in any neighborhood of x 0 the function will have values ​​equal to 0 and 1. In this case, there cannot be a limit of the function at the point x 0 either on the left or on the right, which means that the Dirichlet function has discontinuities of the second kind at each point on the real axis.

Example 6. Find function breakpoints

and determine their type.
Solution. Points suspected of breaking are points x 1 =2, x 2 =5, x 3 =3.
At the point x 1 =2 f(x) has a discontinuity of the second kind, since
.
The point x 2 =5 is a point of continuity, since the value of the function at this point and in its vicinity is determined by the second line, and not the first: .
Let's examine the point x 3 =3: , , from which it follows that x=3 is a discontinuity point of the first kind.

For independent decision.
Examine functions for continuity and determine the type of discontinuity points:
1) ; Answer: x=-1 – point of removable discontinuity;
2) ; Answer: Discontinuity of the second kind at point x=8;
3) ; Answer: Discontinuity of the first kind at x=1;
4)
Answer: At the point x 1 =-5 there is a removable gap, at x 2 =1 there is a gap of the second kind and at the point x 3 =0 there is a gap of the first kind.
5) How should the number A be chosen so that the function

would be continuous at x=0?
Answer: A=2.
6) Is it possible to choose the number A so that the function

would be continuous at x=2?
Answer: no.

Definition of continuity according to Heine

The function of a real variable \(f\left(x \right)\) is said to be continuous at the point \(a \in \mathbb(R)\) (\(\mathbb(R)-\)set of real numbers), if for any sequence \(\left\( ((x_n)) \right\)\ ), such that \[\lim\limits_(n \to \infty ) (x_n) = a,\] the relation \[\lim\limits_(n \to \infty ) f\left(((x_n)) \right) = f\left(a \right).\] In practice, it is convenient to use the following \(3\) conditions for the continuity of the function \(f\left(x \right)\) at the point \(x = a\) ( which must be executed simultaneously):

1. The function \(f\left(x \right)\) is defined at the point \(x = a\);
2. The limit \(\lim\limits_(x \to a) f\left(x \right)\) exists;
3. The equality \(\lim\limits_(x \to a) f\left(x \right) = f\left(a \right)\) holds.

Definition of Cauchy continuity (notation \(\varepsilon - \delta\))

Consider a function \(f\left(x \right)\) that maps the set of real numbers \(\mathbb(R)\) to another subset \(B\) of the real numbers. The function \(f\left(x \right)\) is said to be continuous at the point \(a \in \mathbb(R)\), if for any number \(\varepsilon > 0\) there is a number \(\delta > 0\) such that for all \(x \in \mathbb (R)\), satisfying the relation \[\left| (x - a) \right| Definition of continuity in terms of increments of argument and function

The definition of continuity can also be formulated using increments of argument and function. The function is continuous at the point \(x = a\) if the equality \[\lim\limits_(\Delta x \to 0) \Delta y = \lim\limits_(\Delta x \to 0) \left[ ( f\left((a + \Delta x) \right) - f\left(a \right)) \right] = 0,\] where \(\Delta x = x - a\).

The above definitions of continuity of a function are equivalent on the set of real numbers.

The function is continuous on a given interval , if it is continuous at every point of this interval.

Continuity theorems

Theorem 1.
Let the function \(f\left(x \right)\) be continuous at the point \(x = a\) and \(C\) be a constant. Then the function \(Cf\left(x \right)\) is also continuous for \(x = a\).

Theorem 2.
Given two functions \((f\left(x \right))\) and \((g\left(x \right))\), continuous at the point \(x = a\). Then the sum of these functions \((f\left(x \right)) + (g\left(x \right))\) is also continuous at the point \(x = a\).

Theorem 3.
Suppose that two functions \((f\left(x \right))\) and \((g\left(x \right))\) are continuous at the point \(x = a\). Then the product of these functions \((f\left(x \right)) (g\left(x \right))\) is also continuous at the point \(x = a\).

Theorem 4.
Given two functions \((f\left(x \right))\) and \((g\left(x \right))\), continuous for \(x = a\). Then the ratio of these functions \(\large\frac((f\left(x \right)))((g\left(x \right)))\normalsize\) is also continuous for \(x = a\) subject to , that \((g\left(a \right)) \ne 0\).

Theorem 5.
Suppose that the function \((f\left(x \right))\) is differentiable at the point \(x = a\). Then the function \((f\left(x \right))\) is continuous at this point (i.e., differentiability implies continuity of the function at the point; the converse is not true).

Theorem 6 (Limit value theorem).
If a function \((f\left(x \right))\) is continuous on a closed and bounded interval \(\left[ (a,b) \right]\), then it is bounded above and below on this interval. In other words, there are numbers \(m\) and \(M\) such that \ for all \(x\) in the interval \(\left[ (a,b) \right]\) (Figure 1).

Fig.1		Fig.2

Theorem 7 (Intermediate value theorem).
Let the function \((f\left(x \right))\) be continuous on a closed and bounded interval \(\left[ (a,b) \right]\). Then, if \(c\) is some number greater than \((f\left(a \right))\) and less than \((f\left(b \right))\), then there exists a number \(( x_0)\), such that \ This theorem is illustrated in Figure 2.

Continuity of elementary functions

All elementary functions are continuous at any point in their domain of definition.

The function is called elementary , if it is built from a finite number of compositions and combinations
(using \(4\) operations - addition, subtraction, multiplication and division) . A bunch of basic elementary functions includes:

Continuity of function. Breaking points.

The bull walks, sways, sighs as he goes:
- Oh, the board is running out, now I’m going to fall!

In this lesson we will examine the concept of continuity of a function, the classification of discontinuity points and a common practical problem continuity studies of functions. From the very name of the topic, many intuitively guess what will be discussed and think that the material is quite simple. This is true. But it is simple tasks that are most often punished for neglect and a superficial approach to solving them. Therefore, I recommend that you study the article very carefully and catch all the subtleties and techniques.

What do you need to know and be able to do? Not very much. To learn the lesson well, you need to understand what it is limit of a function. For readers with a low level of preparation, it is enough to comprehend the article Function limits. Examples of solutions and look at the geometric meaning of the limit in the manual Graphs and properties of elementary functions. It is also advisable to familiarize yourself with geometric transformations of graphs, since practice in most cases involves constructing a drawing. The prospects are optimistic for everyone, and even a full kettle will be able to cope with the task on its own in the next hour or two!

Continuity of function. Breakpoints and their classification

Concept of continuity of function

Let's consider some function that is continuous on the entire number line:

Or, to put it more succinctly, our function is continuous on (the set of real numbers).

What is the “philistine” criterion of continuity? Obviously, the graph of a continuous function can be drawn without lifting the pencil from the paper.

In this case, two simple concepts should be clearly distinguished: domain of a function And continuity of function. In general it's not the same thing. For example:

This function is defined on the entire number line, that is, for everyone The meaning of “x” has its own meaning of “y”. In particular, if , then . Note that the other point is punctuated, because by the definition of a function, the value of the argument must correspond to the only thing function value. Thus, domain our function: .

However this function is not continuous on ! It is quite obvious that at the point she is suffering gap. The term is also quite intelligible and visual; indeed, here the pencil will have to be torn off the paper anyway. A little later we will look at the classification of breakpoints.

Continuity of a function at a point and on an interval

In a particular mathematical problem, we can talk about the continuity of a function at a point, the continuity of a function on an interval, a half-interval, or the continuity of a function on a segment. That is, there is no “mere continuity”– the function can be continuous SOMEWHERE. And the fundamental “building block” of everything else is continuity of function at the point .

The theory of mathematical analysis gives a definition of the continuity of a function at a point using “delta” and “epsilon” neighborhoods, but in practice there is a different definition in use, to which we will pay close attention.

First let's remember one-sided limits who burst into our lives in the first lesson about function graphs. Consider an everyday situation:

If we approach the axis to the point left(red arrow), then the corresponding values ​​of the “games” will go along the axis to the point (crimson arrow). Mathematically, this fact is fixed using left-hand limit:

Pay attention to the entry (reads “x tends to ka on the left”). The “additive” “minus zero” symbolizes , essentially this means that we are approaching the number from the left side.

Similarly, if you approach the point “ka” on right(blue arrow), then the “games” will come to the same value, but along the green arrow, and right-hand limit will be formatted as follows:

"Additive" symbolizes , and the entry reads: “x tends to ka on the right.”

If one-sided limits are finite and equal(as in our case): , then we will say that there is a GENERAL limit. It's simple, the general limit is our “usual” limit of a function, equal to a finite number.

Note that if the function is not defined at (poke out the black dot on the graph branch), then the above calculations remain valid. As has already been noted several times, in particular in the article on infinitesimal functions, expressions mean that "x" infinitely close approaches the point, while DOESN'T MATTER, whether the function itself is defined at a given point or not. A good example will be found in the next paragraph, when the function is analyzed.

Definition: a function is continuous at a point if the limit of the function at a given point is equal to the value of the function at that point: .

The definition is detailed in the following terms:

1) The function must be defined at the point, that is, the value must exist.

2) There must be a general limit of the function. As noted above, this implies the existence and equality of one-sided limits: .

3) The limit of the function at a given point must be equal to the value of the function at this point: .

If violated at least one of the three conditions, then the function loses the property of continuity at the point .

Continuity of a function over an interval is formulated ingeniously and very simply: a function is continuous on the interval if it is continuous at every point of the given interval.

In particular, many functions are continuous on an infinite interval, that is, on the set of real numbers. This is a linear function, polynomials, exponential, sine, cosine, etc. And in general, any elementary function continuous on its domain of definition, for example, a logarithmic function is continuous on the interval . Hopefully by now you have a pretty good idea of ​​what graphs of basic functions look like. More detailed information about their continuity can be obtained from a kind man named Fichtenholtz.

With the continuity of a function on a segment and half-intervals, everything is also not difficult, but it is more appropriate to talk about this in class about finding the minimum and maximum values ​​of a function on a segment, but for now let’s not worry about it.

Classification of break points

The fascinating life of functions is rich in all sorts of special points, and break points are only one of the pages of their biography.

Note : just in case, I’ll dwell on an elementary point: the breaking point is always single point– there are no “several break points in a row”, that is, there is no such thing as a “break interval”.

These points, in turn, are divided into two large groups: ruptures of the first kind And ruptures of the second kind. Each type of gap has its own characteristic features, which we will look at right now:

Discontinuity point of the first kind

If the continuity condition is violated at a point and one-sided limits finite , then it is called discontinuity point of the first kind.

Let's start with the most optimistic case. According to the original idea of ​​the lesson, I wanted to tell the theory “in general terms,” but in order to demonstrate the reality of the material, I settled on the option with specific characters.

It’s sad, like a photo of newlyweds against the backdrop of the Eternal Flame, but the following shot is generally accepted. Let us depict the graph of the function in the drawing:


This function is continuous on the entire number line, except for the point. And in fact, the denominator cannot be equal to zero. However, in accordance with the meaning of the limit, we can infinitely close approach “zero” both from the left and from the right, that is, one-sided limits exist and, obviously, coincide:
(Condition No. 2 of continuity is satisfied).

But the function is not defined at the point, therefore, Condition No. 1 of continuity is violated, and the function suffers a discontinuity at this point.

A break of this type (with the existing general limit) are called repairable gap. Why removable? Because the function can redefine at the breaking point:

Does it look weird? Maybe. But such a function notation does not contradict anything! Now the gap is closed and everyone is happy:


Let's perform a formal check:

2) – there is a general limit;
3)

Thus, all three conditions are satisfied, and the function is continuous at a point by the definition of continuity of a function at a point.

However, matan haters can define the function in a bad way, for example :


It is interesting that the first two continuity conditions are satisfied here:
1) – the function is defined at a given point;
2) – there is a general limit.

But the third boundary has not been passed: , that is, the limit of the function at the point not equal the value of a given function at a given point.

Thus, at a point the function suffers a discontinuity.

The second, sadder case is called rupture of the first kind with a jump. And sadness is evoked by one-sided limits that finite and different. An example is shown in the second drawing of the lesson. Such a gap usually occurs in piecewise defined functions, which have already been mentioned in the article about graph transformations.

Consider the piecewise function and we will complete its drawing. How to build a graph? Very simple. On a half-interval we draw a fragment of a parabola (green), on an interval - a straight line segment (red) and on a half-interval - a straight line (blue).

Moreover, due to the inequality, the value is determined for the quadratic function (green dot), and due to the inequality, the value is determined for the linear function (blue dot):

In the most difficult case, you should resort to point-by-point construction of each piece of the graph (see the first lesson about graphs of functions).

Now we will only be interested in the point. Let's examine it for continuity:

2) Let's calculate one-sided limits.

On the left we have a red line segment, so the left-sided limit is:

On the right is the blue straight line, and the right-hand limit:

As a result, we received finite numbers, and they not equal. Since one-sided limits finite and different: , then our function tolerates discontinuity of the first kind with a jump.

It is logical that the gap cannot be eliminated - the function really cannot be further defined and “glued together”, as in the previous example.

Discontinuity points of the second kind

Usually, all other cases of rupture are cleverly classified into this category. I won’t list everything, because in practice, in 99% of problems you will encounter endless gap– when left-handed or right-handed, and more often, both limits are infinite.

And, of course, the most obvious picture is the hyperbola at point zero. Here both one-sided limits are infinite: , therefore, the function suffers a discontinuity of the second kind at the point .

I try to fill my articles with as diverse content as possible, so let's look at the graph of a function that has not yet been encountered:

according to the standard scheme:

1) The function is not defined at this point because the denominator goes to zero.

Of course, we can immediately conclude that the function suffers a discontinuity at point , but it would be good to classify the nature of the discontinuity, which is often required by the condition. For this:

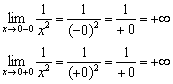
Let me remind you that by recording we mean infinitesimal negative number, and under the entry - infinitesimal positive number.

One-sided limits are infinite, which means that the function suffers a discontinuity of the 2nd kind at the point . The y-axis is vertical asymptote for the graph.

It is not uncommon for both one-sided limits to exist, but only one of them is infinite, for example:

This is the graph of the function.

We examine the point for continuity:

1) The function is not defined at this point.

2) Let's calculate one-sided limits:

We will talk about the method of calculating such one-sided limits in the last two examples of the lecture, although many readers have already seen and guessed everything.

The left-hand limit is finite and equal to zero (we “do not go to the point itself”), but the right-hand limit is infinite and the orange branch of the graph approaches infinitely close to its vertical asymptote, given by the equation (black dotted line).

So the function suffers second kind discontinuity at point .

As for a discontinuity of the 1st kind, the function can be defined at the discontinuity point itself. For example, for a piecewise function Feel free to put a black bold dot at the origin of coordinates. On the right is a branch of a hyperbola, and the right-hand limit is infinite. I think almost everyone has an idea of ​​what this graph looks like.

What everyone was looking forward to:

How to examine a function for continuity?

The study of a function for continuity at a point is carried out according to an already established routine scheme, which consists of checking three conditions of continuity:

Example 1

Explore function

Solution:

1) The only point within the scope is where the function is not defined.

2) Let's calculate one-sided limits:

One-sided limits are finite and equal.

Thus, at the point the function suffers a removable discontinuity.

What does the graph of this function look like?

I would like to simplify , and it seems like an ordinary parabola is obtained. BUT the original function is not defined at point , so the following clause is required:

Let's make the drawing:

Answer: the function is continuous on the entire number line except the point at which it suffers a removable discontinuity.

The function can be further defined in a good or not so good way, but according to the condition this is not required.

You say this is a far-fetched example? Not at all. This has happened dozens of times in practice. Almost all of the site’s tasks come from real independent work and tests.

Let's get rid of our favorite modules:

Example 2

Explore function for continuity. Determine the nature of the function discontinuities, if they exist. Execute the drawing.

Solution: For some reason, students are afraid and don’t like functions with a module, although there is nothing complicated about them. We have already touched on such things a little in the lesson. Geometric transformations of graphs. Since the module is non-negative, it is expanded as follows: , where “alpha” is some expression. In this case, and our function should be written piecewise:

But the fractions of both pieces must be reduced by . The reduction, as in the previous example, will not take place without consequences. The original function is not defined at the point since the denominator goes to zero. Therefore, the system should additionally specify the condition , and make the first inequality strict:

Now about a VERY USEFUL decision technique: before finalizing the task on a draft, it is advantageous to make a drawing (regardless of whether it is required by the conditions or not). This will help, firstly, to immediately see points of continuity and points of discontinuity, and, secondly, it will 100% protect you from errors when finding one-sided limits.

Let's do the drawing. In accordance with our calculations, to the left of the point it is necessary to draw a fragment of a parabola (blue color), and to the right - a piece of a parabola (red color), while the function is not defined at the point itself:

If in doubt, take a few x values ​​and plug them into the function (remembering that the module destroys the possible minus sign) and check the graph.

Let us examine the function for continuity analytically:

1) The function is not defined at the point, so we can immediately say that it is not continuous at it.

2) Let’s establish the nature of the discontinuity; to do this, we calculate one-sided limits:

The one-sided limits are finite and different, which means that the function suffers a discontinuity of the 1st kind with a jump at the point . Note again that when finding limits, it does not matter whether the function at the break point is defined or not.

Now all that remains is to transfer the drawing from the draft (it was made as if with the help of research ;-)) and complete the task:

Answer: the function is continuous on the entire number line except for the point at which it suffers a discontinuity of the first kind with a jump.

Sometimes they require additional indication of the discontinuity jump. It is calculated simply - from the right limit you need to subtract the left limit: , that is, at the break point our function jumped 2 units down (as the minus sign tells us).

Example 3

Explore function for continuity. Determine the nature of the function discontinuities, if they exist. Make a drawing.

This is an example for you to solve on your own, a sample solution at the end of the lesson.

Let's move on to the most popular and widespread version of the task, when the function consists of three parts:

Example 4

Examine a function for continuity and plot a graph of the function .

Solution: it is obvious that all three parts of the function are continuous on the corresponding intervals, so it remains to check only two points of “junction” between the pieces. First, let's make a draft drawing; I commented on the construction technique in sufficient detail in the first part of the article. The only thing is that we need to carefully follow our singular points: due to the inequality, the value belongs to the straight line (green dot), and due to the inequality, the value belongs to the parabola (red dot):


Well, in principle, everything is clear =) All that remains is to formalize the decision. For each of the two “joining” points, we standardly check 3 continuity conditions:

I) We examine the point for continuity

1)

The one-sided limits are finite and different, which means that the function suffers a discontinuity of the 1st kind with a jump at the point .

Let us calculate the discontinuity jump as the difference between the right and left limits:
, that is, the graph jerked up one unit.

II) We examine the point for continuity

1) – the function is defined at a given point.

2) Find one-sided limits:

– one-sided limits are finite and equal, which means there is a general limit.

3) – the limit of a function at a point is equal to the value of this function at a given point.

At the final stage, we transfer the drawing to the final version, after which we put the final chord:

Answer: the function is continuous on the entire number line, except for the point at which it suffers a discontinuity of the first kind with a jump.

Example 5

Examine a function for continuity and construct its graph .

This is an example for independent solution, a short solution and an approximate sample of the problem at the end of the lesson.

You may get the impression that at one point the function must be continuous, and at another there must be a discontinuity. In practice, this is not always the case. Try not to neglect the remaining examples - there will be several interesting and important features:

Example 6

Given a function . Investigate the function for continuity at points. Build a graph.

Solution: and again immediately execute the drawing on the draft:

The peculiarity of this graph is that the piecewise function is given by the equation of the abscissa axis. Here this area is drawn in green, but in a notebook it is usually highlighted in bold with a simple pencil. And, of course, don’t forget about our rams: the value belongs to the tangent branch (red dot), and the value belongs to the straight line.

Everything is clear from the drawing - the function is continuous along the entire number line, all that remains is to formalize the solution, which is brought to full automation literally after 3-4 similar examples:

I) We examine the point for continuity

1) – the function is defined at a given point.

2) Let's calculate one-sided limits:

, which means there is a general limit.

Just in case, let me remind you of a trivial fact: the limit of a constant is equal to the constant itself. In this case, the limit of zero is equal to zero itself (left-handed limit).

3) – the limit of a function at a point is equal to the value of this function at a given point.

Thus, a function is continuous at a point by the definition of continuity of a function at a point.

II) We examine the point for continuity

1) – the function is defined at a given point.

2) Find one-sided limits:

And here – the limit of one is equal to the unit itself.

– there is a general limit.

3) – the limit of a function at a point is equal to the value of this function at a given point.

Thus, a function is continuous at a point by the definition of continuity of a function at a point.

As usual, after research we transfer our drawing to the final version.

Answer: the function is continuous at the points.

Please note that in the condition we were not asked anything about studying the entire function for continuity, and it is considered good mathematical form to formulate precise and clear the answer to the question posed. By the way, if the conditions do not require you to build a graph, then you have every right not to build it (although later the teacher can force you to do this).

A small mathematical “tongue twister” for solving it yourself:

Example 7

Given a function 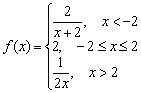. Investigate the function for continuity at points. Classify breakpoints, if any. Execute the drawing.

Try to “pronounce” all the “words” correctly =) And draw the graph more precisely, accuracy, it will not be superfluous everywhere;-)

As you remember, I recommended immediately completing the drawing as a draft, but from time to time you come across examples where you can’t immediately figure out what the graph looks like. Therefore, in some cases, it is advantageous to first find one-sided limits and only then, based on the study, depict the branches. In the final two examples we will also learn a technique for calculating some one-sided limits:

Example 8

Examine the function for continuity and construct its schematic graph.

Solution: the bad points are obvious: (reduces the denominator of the exponent to zero) and (reduces the denominator of the entire fraction to zero). It is not clear what the graph of this function looks like, which means it is better to do some research first.

Definition. Let the function y = f(x) be defined at the point x0 and some of its neighborhood. The function y = f(x) is called continuous at point x0, If:

1. exists
2. this limit is equal to the value of the function at point x0:

When defining the limit, it was emphasized that f(x) may not be defined at the point x0, and if it is defined at this point, then the value of f(x0) does not participate in any way in determining the limit. When determining continuity, it is fundamental that f(x0) exists, and this value must be equal to lim f(x).

Definition. Let the function y = f(x) be defined at the point x0 and some of its neighborhood. A function f(x) is called continuous at a point x0 if for all ε>0 there is a positive number δ such that for all x in the δ-neighborhood of the point x0 (i.e. |x-x0|
Here it is taken into account that the value of the limit must be equal to f(x0), therefore, in comparison with the definition of the limit, the condition of puncture of the δ-neighborhood 0 is removed
Let us give one more (equivalent to the previous) definition in terms of increments. Let's denote Δх = x - x0; we will call this value the increment of the argument. Since x->x0, then Δx->0, i.e. Δx - b.m. (infinitesimal) quantity. Let us denote Δу = f(x)-f(x0), we will call this value the increment of the function, since |Δу| should be (for sufficiently small |Δх|) less than an arbitrary number ε>0, then Δу- is also b.m. value, therefore

Definition. Let the function y = f(x) be defined at the point x0 and some of its neighborhood. The function f(x) is called continuous at point x0, if an infinitesimal increment in the argument corresponds to an infinitesimal increment in the function.

Definition. The function f(x), which is not continuous at the point x0, called discontinuous at this point.

Definition. A function f(x) is called continuous on a set X if it is continuous at every point of this set.

Theorem on the continuity of a sum, product, quotient

Theorem on the passage to the limit under the sign of a continuous function

Theorem on the continuity of superposition of continuous functions

Let the function f(x) be defined on an interval and be monotonic on this interval. Then f(x) can have only discontinuity points of the first kind on this segment.

Intermediate value theorem. If the function f(x) is continuous on a segment and at two points a and b (a is less than b) takes unequal values ​​A = f(a) ≠ B = f(b), then for any number C lying between A and B, there is a point c ∈ at which the value of the function is equal to C: f(c) = C.

Theorem on the boundedness of a continuous function on an interval. If a function f(x) is continuous on an interval, then it is bounded on this interval.

Theorem on reaching minimum and maximum values. If the function f(x) is continuous on an interval, then it reaches its lower and upper bounds on this interval.

Theorem on the continuity of the inverse function. Let the function y=f(x) be continuous and strictly increasing (decreasing) on ​​the interval [a,b]. Then on the segment there exists an inverse function x = g(y), also monotonically increasing (decreasing) on ​​and continuous.

The process of studying a function for continuity is inextricably linked with the skill of finding one-sided limits of a function. Therefore, in order to begin studying the material in this article, it is advisable to first examine the topic of the limit of a function.

Definition 1

Function f(x) is continuous at point x 0, if the limit on the left is equal to the limit on the right and coincides with the value of the function at point x 0, i.e.: lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) = f(x0)

This definition allows us to derive a corollary: the value of the limit of a function at points of continuity coincides with the value of the function at these points.

Example 1

The function f (x) = 1 6 (x - 8) 2 - 8 is given. It is necessary to prove its continuity at the point x 0 = 2.

Solution

First of all, we determine the existence of a limit on the left. To do this, we use a sequence of arguments x n, which reduces to x 0 = 2 · (x n< 2) . Например, такой последовательностью может быть:

2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2

The corresponding sequence of function values ​​looks like this:

f(-2); f (0) ; f (1) ; f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16 ; . . . ; f 1 1023 1024 ; . . . = = 8 . 667; 2. 667; 0 . 167; - 0 . 958; - 1 . 489; - 1 . 747; - 1 . 874; . . . ; - 1 . 998; . . . → - 2

in the drawing they are indicated in green.

It is quite obvious that such a sequence reduces to - 2, which means lim x → 2 - 0 1 6 (x - 8) 2 - 8 = - 2.

Let us determine the existence of a limit on the right: we use a sequence of arguments x n, which reduces to x 0 = 2 (x n > 2). For example, this sequence could be:

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

The corresponding sequence of functions:

f (6) ; f (4) ; f (3) ; f 2 1 2 ; f 2 1 4 ; f 2 1 8 ; f 2 1 16 ; . . . ; f 2 1 1024 ; . . . = = - 7 . 333; - 5 . 333; - 3. 833; - 2. 958; - 2. 489; - 2. 247; - 2. 247; - 2. 124; . . . ; - 2. 001 ; . . . → - 2

indicated in blue in the figure.

And this sequence reduces to - 2, then lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2.

The actions above showed that the limits on the right and left are equal, which means there is a limit of the function f (x) = 1 6 x - 8 2 - 8 at the point x 0 = 2, while lim x → 2 1 6 (x - 8 ) 2 - 8 = - 2 .

After calculating the value of the function at a given point, the equality is obvious:

lim x → 2 - 0 f (x) = lim x → 2 + 0 f (x) = f (2) = 1 6 (2 - 8) 2 - 8 = - 2 which indicates the continuity of the given function at a given point.

Let's show it graphically:

Answer: The continuity of the function f (x) = 1 6 (x - 8) 2 - 8 in the given part has been proven.

Removable rupture of the first kind

Definition 2

The function has removable rupture of the first kind at point x 0, when the limits on the right and left are equal, but not equal to the value of the function at the point, i.e.:

lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) ≠ f (x 0)

Example 2

The function f (x) = x 2 - 25 x - 5 is given. It is necessary to determine the points of its break and determine their type.

Solution

First, let's denote the domain of definition of the function: D (f (x)) ⇔ D x 2 - 25 x - 5 ⇔ x - 5 ≠ 0 ⇔ x ∈ (- ∞ ; 5) ∪ (5 ; + ∞)

In a given function, only the boundary point of the domain of definition can serve as a break point, i.e. x 0 = 5. Let us examine the function for continuity at this point.

Let's simplify the expression x 2 - 25 x - 5: x 2 - 25 x - 5 = (x - 5) (x + 5) x - 5 = x + 5.

Let's define the limits on the right and left. Since the function g(x) = x + 5 is continuous for any real x, then:

lim x → 5 - 0 (x + 5) = 5 + 5 = 10 lim x → 5 + 0 (x + 5) = 5 + 5 = 10

Answer: the limits on the right and left are equal, and the given function at the point x 0 = 5 is not defined, i.e. at this point the function has a removable discontinuity of the first kind.

An irremovable discontinuity of the first kind is also determined by the jump point of the function.

Definition 3 Example 3

Given a piecewise continuous function f (x) = x + 4 , x< - 1 , x 2 + 2 , - 1 ≤ x < 1 2 x , x ≥ 1 . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.

Solution

Discontinuities of this function can only be at the point x 0 = - 1 or at the point x 0 = 1.

Let us determine the limits to the right and left of these points and the value of the given function at these points:

• to the left of the point x 0 = - 1 the given function is f (x) = x + 4, then due to the continuity of the linear function: lim x → - 1 - 0 f (x) = lim x → - 1 - 0 (x + 4 ) = - 1 + 4 = 3 ;
• directly at the point x 0 = - 1 the function takes the form: f (x) = x 2 + 2, then: f (- 1) = (- 1) 2 + 2 = 3;
• on the interval (- 1 ; 1) the given function is: f (x) = x 2 + 2. Based on the property of continuity of a quadratic function, we have: lim x → - 1 + 0 f (x) = lim x → - 1 + 0 (x 2 + 2) = (- 1) 2 + 2 = 3 lim x → 1 - 0 f (x) = lim x → 1 - 0 (x 2 + 2) = (1) 2 + 2 = 3
• at point x 0 = - 1 the function has the form: f (x) = 2 x and f (1) = 2 1 = 2.
• to the right of the point x 0 the given function is f (x) = 2 x. Due to the continuity of the linear function: lim x → 1 + 0 f (x) = lim x → 1 + 0 (2 x) = 2 1 = 2

Answer: ultimately we got:

• lim x → - 1 - 0 f (x) = lim x → - 1 + 0 f (x) = f (- 1) = 3 - this means that at the point x 0 = - 1 the given piecewise function is continuous;
• lim x → - 1 - 0 f (x) = 3, lim x → 1 + 0 f (x) = 2 - thus, at the point x 0 = 1 an irremovable discontinuity of the first kind (jump) is defined.

All we have to do is prepare a drawing for this task.

Definition 4

The function has second kind discontinuity at the point x 0, when any of the limits on the left lim x → x 0 - 0 f (x) or on the right lim x → x 0 + 0 f (x) does not exist or is infinite.

Example 4

The function f (x) = 1 x is given. It is necessary to examine the given function for continuity, determine the type of break points, and prepare a drawing.

Solution

Let us write down the domain of definition of the function: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) .

Let's find the limits to the right and left of the point x 0 = 0.

Let us specify an arbitrary sequence of argument values ​​converging to x 0 on the left. Eg:

8 ; - 4 ; - 2 ; - 1 ; - 1 2 ; - 1 4 ; . . . ; - 1 1024 ; . . .

It corresponds to the sequence of function values:

f (- 8) ; f (- 4) ; f(-2); f (- 1) ; f - 1 2 ; f - 1 4 ; . . . ; f - 1 1024 ; . . . = = - 1 8 ; - 14 ; - 12 ; - 1 ; - 2; - 4 ; . . . ; - 1024; . . .

Obviously, this sequence is infinitely large negative, then lim x → 0 - 0 f (x) = lim x → 0 - 0 1 x = - ∞ .

Now let's specify an arbitrary sequence of argument values ​​converging to x 0 from the right. For example: 8 ; 4 ; 2 ; 1 ; 12 ; 14 ; . . . ; 1 1024 ; . . . , and it corresponds to the sequence of function values:

f (8) ; f (4) ; f (2) ; f (1) ; f 1 2 ; f 1 4 ; . . . ; f 1 1024 ; . . . = = 1 8 ; 14 ; 12 ; 1 ; 2 ; 4 ; . . . ; 1024 ; . . .

This sequence is infinitely large positive, which means lim x → 0 + 0 f (x) = lim x → 0 + 0 1 x = + ∞ .

Answer: point x 0 = 0 is the discontinuity point of a function of the second kind.

Let's illustrate:

If you notice an error in the text, please highlight it and press Ctrl+Enter