Funktsiooni äärmus - lihtsas sõnastuses keeruliste asjade kohta. Kuidas leida funktsiooni äärmuspunkte

Nende ebavõrdsuste üleminek piirini Δ juures x→ 0 ja võttes arvesse, et tuletis f "(x 0) on olemas ja seetõttu ei sõltu vasakpoolne piirang sellest, kuidas Δ x→ 0, saame: juures Δ x → 0 – 0 f"(x 0) ≥ 0 a juures Δ x → 0 + 0 f"(x 0) ≤ 0. Alates f"(x 0) defineerib arvu, siis on need kaks võrratust ühilduvad ainult siis, kui f"(x 0) = 0.

Tõestatud teoreem väidab, et maksimum- ja miinimumpunktid võivad olla ainult nende argumendi väärtuste hulgas, mille korral tuletis muutub nulliks.

Vaatlesime juhtumit, kui funktsioonil on tuletis teatud segmendi kõigis punktides. Milline on olukord juhtudel, kui tuletist ei eksisteeri? Vaatame näiteid.

Näited.

1. y=|x|.

   Funktsioonil ei ole punktis tuletist x=0 (sellel hetkel ei ole funktsiooni graafikul defineeritud puutujat), kuid sellel hetkel on funktsioonil miinimum, kuna y(0)=0 ja kõigi jaoks x≠ 0y > 0.



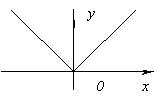
Funktsioonil ei ole tuletist at x=0, kuna see läheb lõpmatusse punktis x=0. Kuid sel hetkel on funktsioonil maksimum.



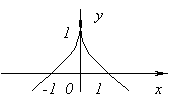
Funktsioonil ei ole tuletist at x=0, alates juures x→0. Sel hetkel ei ole funktsioonil ei maksimumi ega miinimumi. Tõesti, f(x)=0 ja at x<0f(x)<0, а при x>0f(x)>0.



Seega on toodud näidete ja sõnastatud teoreemi põhjal selge, et funktsioonil saab ekstreemum olla ainult kahel juhul: 1) punktides, kus tuletis eksisteerib ja on võrdne nulliga; 2) kohas, kus tuletist ei eksisteeri.

Kui aga ühel hetkel x 0 me teame seda f "(x 0 ) =0, siis ei saa sellest järeldada, et punktis x 0 funktsioonil on äärmus.

Näiteks. .



Aga periood x=0 ei ole äärmuspunkt, kuna sellest punktist vasakul asuvad funktsiooni väärtused telje all Ox ja ülal paremal.

Argumendi väärtusi funktsiooni domeenist, mille juures funktsiooni tuletis kaob või ei eksisteeri, nimetatakse kriitilised punktid.




Kõigest eelnevast järeldub, et funktsiooni äärmuspunktid kuuluvad kriitiliste punktide hulka, kuid mitte iga kriitiline punkt ei ole äärmuspunkt. Seetõttu peate funktsiooni ekstreemumi leidmiseks leidma kõik funktsiooni kriitilised punktid ja seejärel uurima iga punkti eraldi maksimumi ja miinimumi jaoks. Seda täidab järgmine teoreem.

Teoreem 2. (Piisav tingimus ekstreemumi olemasoluks.) Olgu funktsioon pidev mingil kriitilist punkti sisaldaval intervallil x 0 ja on diferentseeritav selle intervalli kõigis punktides (välja arvatud võib-olla punkt ise x 0). Kui selle punkti kaudu vasakult paremale liikudes muudab tuletis märgi plussist miinusesse, siis punktis x = x Funktsioonil 0 on maksimum. Kui läbimisel x 0 vasakult paremale, tuletis muudab märgi miinusest plussiks, siis on funktsioonil selles punktis miinimum.

Seega, kui

Tõestus. Oletame esmalt, et läbisõidul x 0 tuletis muudab märgi plussist miinusesse, st. kõigi ees x, punkti lähedal x 0 f "(x)> 0 eest x< x 0 , f "(x)< 0 eest x> x 0 . Rakendame erinevusele Lagrange'i teoreemi f(x) - f(x 0 ) = f "(c)(x-x 0), kus c jääb vahele x Ja x 0 .

1. Lase x< x 0 . Siis c< x 0 ja f "(c)> 0. Sellepärast f "(c)(x-x 0)< 0 ja seetõttu

   f(x) - f(x 0 )< 0, st. f(x)< f(x 0 ).

2. Lase x > x 0 . Siis c>x 0 ja f "(c)< 0. Tähendab f "(c)(x-x 0)< 0. Sellepärast f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Seega kõikide väärtuste puhul x piisavalt lähedal x 0 f(x)< f(x 0 ) . Ja see tähendab, et hetkel x Funktsioonil 0 on maksimum.

Samamoodi on tõestatud ka miinimumteoreemi teine ​​osa.



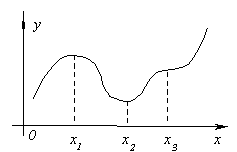
Illustreerime selle teoreemi tähendust joonisel. Lase f "(x 1 ) =0 ja mis tahes x, piisavalt lähedal x 1, on ebavõrdsused täidetud

f "(x)< 0 kl x< x 1 , f "(x)> 0 kl x> x 1 .

Seejärel punktist vasakule x 1 funktsioon suureneb ja väheneb paremal, seega millal x = x 1 funktsioon läheb suurenevalt kahanemisele, see tähendab, et sellel on maksimum.

Samamoodi võime kaaluda punkte x 2 ja x 3 .


Kõik ülaltoodud on skemaatiliselt kujutatud pildil:

Ekstreemumi funktsiooni y=f(x) uurimise reegel

1. Leia funktsiooni domeen f(x).
2. Leia funktsiooni esimene tuletis f "(x).
3. Määrake selle jaoks kriitilised punktid:
   1. leida võrrandi tegelikud juured f "(x)=0;
   2. leida kõik väärtused x mille puhul tuletis f "(x) ei eksisteeri.
4. Määrake kriitilisest punktist vasakul ja paremal asuva tuletise märk. Kuna tuletise märk jääb kahe kriitilise punkti vahel konstantseks, siis piisab tuletise märgi määramisest kriitilisest punktist ühes punktis vasakul ja üks punkt paremal.
5. Arvutage funktsiooni väärtus äärmuspunktides.

Näited. Uurige miinimum- ja maksimumfunktsioone.




Segmendi FUNKTSIOONIDE MAKSIMAALSED JA VÄIKSEIMAD VÄÄRTUSED

Suurim funktsiooni väärtus intervallil on suurim kõigist selle intervalli väärtustest ja kõige väiksem– kõigist selle väärtustest väikseim.

Mõelge funktsioonile y=f(x) pidev lõigul [ a, b]. Teatavasti saavutab selline funktsioon oma maksimum- ja miinimumväärtused kas lõigu piiril või selle sees. Kui funktsiooni suurim või väikseim väärtus saavutatakse segmendi sisemises punktis, siis on see väärtus funktsiooni maksimum või miinimum, see tähendab, et see saavutatakse kriitilistes punktides.

Seega saame järgmise reegel funktsiooni suurima ja väikseima väärtuse leidmiseks segmendis[ a, b] :

1. Leia kõik funktsiooni kriitilised punktid vahemikus ( a, b) ja arvutage nendes punktides funktsiooni väärtused.
2. Arvutage funktsiooni väärtused segmendi otstes, kui x = a, x = b.
3. Valige kõigi saadud väärtuste hulgast suurim ja väikseim.

Olgu funktsioon $z=f(x,y)$ defineeritud mingis punkti $(x_0,y_0)$ läheduses. Nad ütlevad, et $(x_0,y_0)$ on (lokaalne) maksimumpunkt, kui kõikide punktide $(x,y)$ jaoks punkti $(x_0,y_0)$ naabruses on ebavõrdsus $f(x,y) on rahul< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, siis punkti $(x_0,y_0)$ nimetatakse (kohalikuks) miinimumpunktiks.

Maksimaalset ja miinimumpunkti nimetatakse sageli üldmõisteks – äärmuspunktideks.

Kui $(x_0,y_0)$ on maksimumpunkt, siis funktsiooni $f(x_0,y_0)$ väärtust selles punktis nimetatakse funktsiooni $z=f(x,y)$ maksimumiks. Vastavalt sellele nimetatakse funktsiooni väärtust miinimumpunktis funktsiooni $z=f(x,y)$ miinimumiks. Funktsiooni miinimumi ja maksimume ühendab ühine termin - funktsiooni ekstreem.

Algoritm funktsiooni $z=f(x,y)$ ekstreemumi uurimiseks

1. Leidke osatuletised $\frac(\partial z)(\partial x)$ ja $\frac(\partial z)(\partial y)$. Koostage ja lahendage võrrandisüsteem $ \left \( \begin(joondatud) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 \ end(joondatud) \right.$ Punkte, mille koordinaadid vastavad määratud süsteemile, nimetatakse statsionaarseteks.
2. Otsige üles $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ ja arvuta $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ igas statsionaarses punktis. Pärast seda kasutage järgmist skeemi:
   1. Kui $\Delta > 0$ ja $\frac(\partial^2z)(\partial x^2) > 0$ (või $\frac(\partial^2z)(\partial y^2) > 0$, siis uuritav punkt on miinimumpunkt.
   2. Kui $\Delta > 0$ ja $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Kui $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Kui $\Delta = 0$, siis ekstreemumi olemasolu kohta midagi kindlat öelda ei saa; on vaja täiendavaid uuringuid.

Märkus (soovitav teksti täielikumaks mõistmiseks): näita\peida

Kui $\Delta > 0$, siis $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\ osaline^2z)(\partial x\partial y) \right)^2 > 0$. Sellest järeldub, et $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) ( \partial x\partial y)\right)^2 ≥ 0$. Need. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Kui teatud suuruste korrutis on suurem kui null, siis on need suurused sama märgiga. See tähendab, et näiteks kui $\frac(\partial^2z)(\partial x^2) > 0$, siis $\frac(\partial^2z)(\partial y^2) > 0$. Lühidalt, kui $\Delta > 0$, siis $\frac(\partial^2z)(\partial x^2)$ ja $\frac(\partial^2z)(\partial y^2)$ märgid langevad kokku .

Näide nr 1

Uurige funktsiooni $z=4x^2-6xy-34x+5y^2+42y+7$ selle ekstreemumi jaoks.

$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$

$$ \left \( \begin (joondatud) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end (joondatud) \right. $$

Vähendame selle süsteemi iga võrrandit $2 $ võrra ja liigutame arvud võrrandite paremale küljele:

$$ \left \( \begin (joondatud) & 4x-3y=17;\\ & -3x+5y=-21. \end (joondatud) \right. $$

Oleme saanud lineaarsete algebraliste võrrandite süsteemi. Selles olukorras tundub mulle kõige mugavam kasutada tekkinud süsteemi lahendamiseks Crameri meetodit.

$$ \begin(joondatud) & \Delta=\left| \begin(massiivi) (cc) 4 & -3\\ -3 & 5 \end(massiivi)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\left| \begin(massiivi) (cc) 17 & -3\\ -21 & 5 \end(massiivi)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\left| \begin(massiivi) (cc) 4 & 17\\ -3 & -21 \end(massiivi)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(joondatud) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$

Väärtused $x=2$, $y=-3$ on statsionaarse punkti $(2;-3)$ koordinaadid.

$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$

Arvutame $\Delta$ väärtuse:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$

Kuna $\Delta > 0$ ja $\frac(\partial^2 z)(\partial x^2) > 0$, siis vastavalt punktile $(2;-3)$ on funktsiooni $ miinimumpunkt z$. Leiame funktsiooni $z$ miinimumi, asendades punkti $(2;-3)$ koordinaadid antud funktsiooniga:

$$ z_(min)=z(2;-3)=4\cpunkt 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$

Vastus: $(2;-3)$ - miinimumpunkt; $z_(min) = -90 $.

Näide nr 2

Uurige funktsiooni $z=x^3+3xy^2-15x-12y+1$ selle ekstreemumi jaoks.

Järgime ülaltoodut. Esiteks leiame esimest järku osatuletised:

$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y)=6xy-12. $$

Loome võrrandisüsteemi $ \left \( \begin(joondatud) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( joondatud) \right.$:

$$ \left \( \begin (joondatud) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end (joondatud) \paremale. $$

Vähendame esimest võrrandit 3 võrra ja teist 6 võrra.

$$ \left \( \begin (joondatud) & x^2+y^2-5=0;\\ & xy-2=0. \end(joondatud) \right. $$

Kui $x=0$, siis teine ​​võrrand viib meid vastuoluni: $0\cdot y-2=0$, $-2=0$. Siit järeldus: $x\neq 0$. Seejärel saame teisest võrrandist: $xy=2$, $y=\frac(2)(x)$. Asendades esimeses võrrandis $y=\frac(2)(x)$, saame:

$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$

Saime bikvadraatvõrrandi. Teeme asendus $t=x^2$ (see tähendab, et $t > 0$):

$$ t^2-5t+4=0;\\ \begin(joondatud) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(joondatud) $$

Kui $t=1$, siis $x^2=1$. Seega on meil kaks väärtust $x$: $x_1=1$, $x_2=-1$. Kui $t=4$, siis $x^2=4$, st. $x_3=2$, $x_4=-2$. Pidades meeles, et $y=\frac(2)(x)$, saame:

\begin(joondatud) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2) = -1. \end (joondatud)

Niisiis, meil on neli statsionaarset punkti: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. See lõpetab algoritmi esimese sammu.

Nüüd alustame algoritmiga. Leiame teist järku osatuletised:

$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$

Leiame $\Delta$:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$

Nüüd arvutame igas varem leitud statsionaarses punktis $\Delta$ väärtuse. Alustame punktist $M_1(1;2)$. Sel hetkel on meil: $\Delta(M_1)=36(1^2-2^2)=-108$. Alates $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

Uurime punkti $M_2(-1;-2)$. Sel hetkel on meil: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Alates $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

Uurime punkti $M_3(2;1)$. Sel hetkel saame:

$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$

Kuna $\Delta(M_3) > 0$ ja $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, siis vastavalt $M_3(2; 1)$ on funktsiooni $z$ miinimumpunkt. Leiame funktsiooni $z$ miinimumi, asendades antud funktsiooniga punkti $M_3$ koordinaadid:

$$ z_(min)=z(2;1)=2^3+3\cpunkt 2\cpunkt 1^2-15\cpunkt 2-12\cpunkt 1+1=-27. $$

Jääb üle uurida punkti $M_4(-2;-1)$. Sel hetkel saame:

$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$

Alates $\Delta(M_4) > 0$ ja $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$

Ekstreemuuring on lõpetatud. Jääb üle vaid vastus kirja panna.

Vastus:

• $(2;1)$ - miinimumpunkt, $z_(min)=-27$;
• $(-2;-1)$ – maksimaalne punkt, $z_(max)=29$.

Märkus

Üldjuhul pole $\Delta$ väärtust vaja arvutada, sest meid huvitab ainult märk, mitte selle parameetri konkreetne väärtus. Näiteks eespool vaadeldud nr 2 punktis $M_3(2;1)$ on meil $\Delta=36\cdot(2^2-1^2)$. Siin on ilmne, et $\Delta > 0$ (kuna mõlemad tegurid $36$ ja $(2^2-1^2)$ on positiivsed) ja $\Delta$ konkreetset väärtust on võimalik mitte leida. Tõsi, standardarvutuste jaoks on see märkus kasutu - need nõuavad arvutuste viimist numbrini :)

Näide nr 3

Uurige funktsiooni $z=x^4+y^4-2x^2+4xy-2y^2+3$ selle ekstreemumi kohta.

Me järgime. Esiteks leiame esimest järku osatuletised:

$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$

Loome võrrandisüsteemi $ \left \( \begin(joondatud) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( joondatud) \right.$:

$$ \left \( \begin (joondatud) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(joondatud) \right. $$

Vähendame mõlemat võrrandit 4 $ võrra:

$$ \left \( \begin (joondatud) & x^3-x+y=0;\\ & y^3+x-y=0. \end(joondatud) \right. $$

Lisame esimese võrrandi teisele ja väljendame $y$ väärtusega $x$:

$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$

Asendades süsteemi esimeses võrrandis $y=-x$, saame:

$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$

Saadud võrrandist saame: $x=0$ või $x^2-2=0$. Võrrandist $x^2-2=0$ järeldub, et $x=-\sqrt(2)$ või $x=\sqrt(2)$. Seega leitakse kolm $x$ väärtust, nimelt: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Kuna $y=-x$, siis $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.

Lahenduse esimene samm on lõpetatud. Saime kolm statsionaarset punkti: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .

Nüüd alustame algoritmiga. Leiame teist järku osatuletised:

$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$

Leiame $\Delta$:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$

Nüüd arvutame igas varem leitud statsionaarses punktis $\Delta$ väärtuse. Alustame punktist $M_1(0;0)$. Siin on meil: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Kuna $\Delta(M_1) = 0$, siis on vaja täiendavaid uuringuid, kuna ekstreemumi olemasolu kohta vaadeldavas punktis midagi kindlat öelda ei saa. Jätame selle punkti praegu rahule ja liigume edasi teiste punktide juurde.

Uurime punkti $M_2(-\sqrt(2),\sqrt(2))$. Sel hetkel saame:

\begin(joondatud) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end (joondatud)

Kuna $\Delta(M_2) > 0$ ja $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, siis vastavalt $M_2(-\ sqrt(2),\sqrt(2))$ on funktsiooni $z$ miinimumpunkt. Leiame funktsiooni $z$ miinimumi, asendades antud funktsiooniga punkti $M_2$ koordinaadid:

$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$

Sarnaselt eelmise punktiga uurime punkti $M_3(\sqrt(2),-\sqrt(2))$. Sel hetkel saame:

\begin(joondatud) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end (joondatud)

Kuna $\Delta(M_3) > 0$ ja $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, siis vastavalt $M_3(\sqrt (2),-\sqrt(2))$ on funktsiooni $z$ miinimumpunkt. Leiame funktsiooni $z$ miinimumi, asendades antud funktsiooniga punkti $M_3$ koordinaadid:

$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2) ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$

On aeg naasta punkti $M_1(0;0)$, kus $\Delta(M_1) = 0$. Selle kohaselt on vaja täiendavaid uuringuid. See kõrvalepõiklev fraas tähendab "tee, mida tahad" :). Üldist viisi selliste olukordade lahendamiseks ei ole ja see on mõistetav. Kui selline meetod oleks olemas, oleks see juba ammu kõikides õpikutes sees. Vahepeal peame otsima spetsiaalset lähenemist igale punktile, kus $\Delta = 0$. Noh, uurime funktsiooni käitumist punkti $M_1(0;0)$ läheduses. Pangem kohe tähele, et $z(M_1)=z(0;0)=3$. Oletame, et $M_1(0;0)$ on miinimumpunkt. Seejärel saame mis tahes punkti $M$ jaoks punkti $M_1(0;0)$ mõnest naabrusest $z(M) > z(M_1)$, s.t. $z(M) > 3$. Mis siis, kui mõni naabruskond sisaldab punkte, kus $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Vaatleme punkte, mille puhul $y=0$, s.t. punktid kujul $(x,0)$. Nendel punktidel võtab funktsioon $z$ järgmised väärtused:

$$ z(x,0)=x^4+0^4-2x^2+4x\cpunkt 0-2\cpunkt 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$

Kõigis piisavalt väikestes piirkondades $M_1(0;0)$ on meil $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Aga võib-olla on punkt $M_1(0;0)$ maksimumpunkt? Kui see on nii, siis mis tahes punkti $M$ jaoks punkti $M_1(0;0)$ mõnest naabrusest saame $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3 dollarit? Siis punktis $M_1$ maksimumi kindlasti ei tule.

Vaatleme punkte, mille puhul $y=x$, s.t. punktid kujul $(x,x)$. Nendel punktidel võtab funktsioon $z$ järgmised väärtused:

$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$

Kuna punkti $M_1(0;0)$ mis tahes naabruses on meil $2x^4 > 0$, siis $2x^4+3 > 3$. Järeldus: punkti $M_1(0;0)$ mis tahes naabruskond sisaldab punkte, kus $z > 3$, mistõttu punkt $M_1(0;0)$ ei saa olla maksimumpunkt.

Punkt $M_1(0;0)$ ei ole ei maksimum- ega miinimumpunkt. Järeldus: $M_1$ ei ole üldse äärmuspunkt.

Vastus: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ on funktsiooni $z$ miinimumpunktid. Mõlemas punktis $z_(min)=-5$.

Mis on funktsiooni ekstreemum ja mis on ekstreemumi vajalik tingimus?

Funktsiooni ekstreemum on funktsiooni maksimum ja miinimum.

Funktsiooni maksimumi ja miinimumi (ekstreemumi) vajalik tingimus on järgmine: kui funktsioonil f(x) on ekstreemum punktis x = a, siis selles punktis on tuletis kas null või lõpmatu või ei ei eksisteeri.

See tingimus on vajalik, kuid mitte piisav. Tuletis punktis x = a võib minna nulli, lõpmatusse või mitte eksisteerida, ilma et funktsioonil oleks selles punktis ekstreemum.

Mis on funktsiooni ekstreemumi (maksimum või miinimum) piisav tingimus?

Esimene tingimus:

Kui punkti x = a piisavas läheduses on tuletis f?(x) positiivne a-st vasakul ja negatiivne a-st paremal, siis punktis x = a on funktsioonil f(x) maksimaalselt

Kui punktile x = a piisavalt lähedal on tuletis f?(x) a-st vasakul negatiivne ja a-st paremal positiivne, siis punktis x = a on funktsioonil f(x) miinimum eeldusel, et funktsioon f(x) on siin pidev.

Selle asemel võite kasutada funktsiooni ekstreemumi jaoks teist piisavat tingimust:

Olgu punktis x = a esimene tuletis f?(x) kaob; kui teine ​​tuletis f??(a) on negatiivne, siis on funktsioonil f(x) maksimum punktis x = a, kui positiivne, siis miinimum.

Mis on funktsiooni kriitiline punkt ja kuidas seda leida?

See on funktsiooni argumendi väärtus, mille juures funktsioonil on ekstreemum (st maksimum või miinimum). Selle leidmiseks vajate leia tuletis funktsioon f?(x) ja võrdsustades selle nulliga, lahendage võrrand f?(x) = 0. Selle võrrandi juured, aga ka punktid, kus selle funktsiooni tuletist ei eksisteeri, on kriitilised punktid, st argumendi väärtused, mille juures võib esineda ekstreemum. Neid saab hõlpsalt tuvastada vaadates tuletisgraafik: meid huvitavad need argumendi väärtused, mille juures funktsiooni graafik lõikub abstsisstelljega (Ox-telg) ja need, mille juures graafikul esineb katkestusi.

Näiteks leiame parabooli äärmus.

Funktsioon y(x) = 3x2 + 2x - 50.

Funktsiooni tuletis: y?(x) = 6x + 2

Lahendage võrrand: y?(x) = 0

6x + 2 = 0, 6x = -2, x = -2/6 = -1/3

Sel juhul on kriitiline punkt x0=-1/3. Funktsioonil on selle argumendi väärtusega äärmus. Temale leida, asendage "x" asemel funktsiooni avaldises leitud arv:

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Kuidas määrata funktsiooni maksimumi ja miinimumi, s.t. selle suurimad ja väikseimad väärtused?

Kui tuletise märk kriitilise punkti x0 läbimisel muutub plussist miinusseks, siis on x0 maksimaalne punkt; kui tuletise märk muutub miinusest plussiks, siis on x0 miinimumpunkt; kui märk ei muutu, siis punktis x0 pole ei maksimumi ega miinimumi.

Vaadeldava näite puhul:

Võtame kriitilisest punktist vasakul oleva argumendi suvalise väärtuse: x = -1

Kui x = -1, on tuletise väärtus y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (st märk on "miinus").

Nüüd võtame kriitilisest punktist paremal oleva argumendi suvalise väärtuse: x = 1

Kui x = 1, on tuletise väärtus y(1) = 6*1 + 2 = 6 + 2 = 8 (st märk on "pluss").

Nagu näete, muutis tuletis kriitilise punkti läbimisel märgi miinusest plussiks. See tähendab, et kriitilise väärtuse x0 juures on meil minimaalne punkt.

Funktsiooni suurim ja väikseim väärtus intervallil(segmendil) leitakse sama protseduuri abil, võttes arvesse ainult asjaolu, et võib-olla ei asu kõik kriitilised punktid määratud intervalli sees. Need kriitilised punktid, mis jäävad väljaspoole intervalli, tuleb vaatlusest välja jätta. Kui intervallis on ainult üks kriitiline punkt, on sellel kas maksimum või miinimum. Sel juhul võtame funktsiooni suurima ja väikseima väärtuse määramiseks arvesse ka funktsiooni väärtusi intervalli lõpus.

Näiteks leiame funktsiooni suurimad ja väikseimad väärtused

y(x) = 3sin(x) - 0,5x

intervallidega:

Niisiis, funktsiooni tuletis on

y?(x) = 3cos(x) - 0,5

Lahendame võrrandi 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

x = ±arccos(0,16667) + 2πk.

Leiame kriitilised punktid intervallilt [-9; 9]:

x = arccos(0,16667) - 2π*2 = -11,163 (ei sisaldu intervallis)

x = -arccos(0,16667) – 2π*1 = -7,687

x = arccos(0,16667) - 2π*1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos(0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos(0,16667) + 2π*1 = 7,687

x = -arccos(0,16667) + 2π*2 = 11,163 (ei sisaldu intervallis)

Leiame funktsiooni väärtused argumendi kriitiliste väärtuste juures:

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

On näha, et intervallil [-9; 9] funktsioonil on suurim väärtus x = -4,88:

x = -4,88, y = 5,398,

ja väikseim - x = 4,88:

x = 4,88, y = -5,398.

Intervallil [-6; -3] meil on ainult üks kriitiline punkt: x = -4,88. Funktsiooni väärtus x = -4,88 võrdub y = 5,398.

Leidke funktsiooni väärtus intervalli lõpus:

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

Intervallil [-6; -3] meil on funktsiooni suurim väärtus

y = 5,398 x = -4,88 juures

väikseim väärtus -

y = 1,077 x = -3 juures

Kuidas leida funktsioonigraafiku käändepunkte ning määrata kumer ja nõgus pool?

Kõikide sirge y = f(x) käändepunktide leidmiseks peate leidma teise tuletise, võrdsustama selle nulliga (lahendama võrrandi) ja testima kõiki neid x väärtusi, mille puhul teine ​​tuletis on null, lõpmatu või seda pole olemas. Kui ühe neist väärtustest läbides muutub teine ​​tuletis märki, siis funktsiooni graafikul on selles punktis kääne. Kui see ei muutu, siis pole kurvi.

Võrrandi f juured? (x) = 0, samuti funktsiooni ja teise tuletise võimalikud katkestuspunktid jagavad funktsiooni definitsioonipiirkonna mitmeks intervalliks. Iga nende intervalli kumerus määratakse teise tuletise märgiga. Kui teine ​​tuletis uuritava intervalli punktis on positiivne, siis sirge y = f(x) on nõgus ülespoole ja kui negatiivne, siis allapoole.

Kuidas leida kahe muutuja funktsiooni äärmusi?

Funktsiooni f(x,y) ekstreemi leidmiseks, mis on selle spetsifikatsiooni domeenis diferentseeruv, on vaja:

1) leidke kriitilised punktid ja lahendage selleks võrrandisüsteem

fх? (x,y) = 0, fу? (x,y) = 0

2) iga kriitilise punkti P0(a;b) puhul uuri, kas erinevuse märk jääb muutumatuks

kõigi punktide (x;y) jaoks, mis on piisavalt lähedal P0-le. Kui erinevus jääb positiivseks, siis punktis P0 on meil miinimum, kui negatiivne, siis maksimum. Kui erinevus ei säilita oma märki, siis punktis P0 ekstreemumit pole.

Funktsiooni äärmused määratakse sarnaselt suurema arvu argumentide korral.

Mis on laulja Mika Newtoni ja tema bändi ametlik veebisait?
Uus Ukraina ime - Mika Newton! See on 5-liikmeline bänd, mis mängib pop-rocki, naudib elu, annab hoogu ja on positiivse ellusuhtumisega. Poisid kogunesid Kiievisse, kus nad praegu elavad. Poisid ei nõustu üldse muusika ja elu standardsete alustega, avastades oma uue kõla ja rikkudes kõikvõimalikke standardeid. Meeskonna juht -

Kuidas teisendada milliliitrit kuupmeetriteks
SI-süsteemi pikkuse põhiühikuks on meeter. Sellest lähtuvalt tuleks mahu põhiühikuks lugeda kuupmeetrit või, nagu seda ka nimetatakse, kuupmeetrit või kuupi. See on kuubi maht, mille servad on võrdsed ühe meetriga. Praktikas ei ole aga alati mugav mahtu kuupmeetrites väljendada. Näiteks on mugav väljendada ruumi mahtu kuupmeetrites: korrutage selle pikkus

Mis on manna kalorisisaldus?
Toidu kalorisisaldus, kalorisisalduse tabel. Inimese energiavajadust mõõdetakse kilokalorites (kcal). Sõna "kalor" tuleb ladina keelest ja tähendab "soojust". Füüsikas mõõdavad kalorid energiat. Üks kilokalor on energia hulk

Millised on realismi arenguetapid kirjanduses?
Realism (ladina keeles material, real) on kirjanduse ja kunsti suund, mille eesmärk on tõetruult reprodutseerida tegelikkust selle tüüpilistes joontes. Üldised omadused: Elu kunstiline kujutamine kujundites, mis vastab elu enda nähtuste olemusele. Reaalsus on inimese jaoks vahend iseenda ja ümbritseva maailma mõistmiseks. Tippimine

Milline on seos berkeeli ja perioodilisuse tabeli elemendi 117 vahel
Berkelium, Berkelium, Bk on perioodilisuse tabeli 97. element, mille avastasid 1949. aasta detsembris Thompson, Ghiorso ja Seaborg California ülikoolist Berkeleys. 241Am alfaosakestega kiiritamisel saadi berkeliumi isotoop 243Bk. Kuna Bk-l on struktuurne sarnasus terbiumiga, mis sai oma nime hr Ytterbylt aastal

Mille poolest on kuulus Jaroslav Tark?
Jaroslav Tark (980-1054), Kiievi suurvürst (1019). Vladimir I Svjatoslavovitši poeg. Ta saatis välja Svjatopolk I Neetud, võitles oma venna Mstislaviga, jagas temaga riigi (1025) ja ühendas 1035 uuesti. Mitmete võitudega kindlustas ta Venemaa lõuna- ja läänepiiri. Loonud dünastilised sidemed paljude ev-riikidega

Kuidas tekkis traditsioon hüüda pulmas "kibe!"
Ammu oli kombeks pulmapeo ajal karjuda: “Mõru!”, sundides noorpaari oma kohalt tõusma ja suudlema. Tänapäeval ei tea paljud inimesed isegi, mida see rituaal tähendab. Vanasti hüüti pulmades "Mõru!", andes mõista, et tassides olev vein oli väidetavalt magustamata. A

Millised on larüngiidi sümptomid
Larüngiit (vanakreeka keelest λ?ρυγξ – kõri) on kõripõletik, mida tavaliselt seostatakse külmetuse või nakkushaigustega nagu leetrid, sarlakid, läkaköha. Haiguse arengut soodustab alajahtumine, hingamine läbi suu, tolmune

Kas sugu ja kääne on määratud nimisõnadele, millel on ainult mitmuse vorm?
Arv on grammatiline kategooria, mis väljendab objekti kvantitatiivseid omadusi. 1. Enamik nimisõnu muutub vastavalt numbritele, s.t. on kaks vormi - ainsuses ja mitmuses. Ainsuse vormis tähistab nimisõna ühte objekti, mitmuses - mitut objekti:

Mis kasu on vene pudrust?
Tatrapuder Tatar on eriline teravili. Selgub, võib-olla üks kasulikumaid pudrusid. Pole ime, et me nimetame seda esimeseks. Tatar sisaldab kiudaineid, tervet rida vitamiine - E, PP, B1, B2, fool- ja orgaanilisi happeid, samuti suures koguses tärklist, mis aitab organismil saada õiges koguses neo.

Arhangelski linna interaktiivset kaarti saab vaadata järgmistel saitidel: Map1 - satelliit- ja standardkaart 2 - standardkaart (1:350 000); Map3 - seal on tänavanimed, majanumbrid, saate otsida tänavate järgi Map4 - kaart koos tänavanimedega Map6 - interaktiivne linna kaart;

Punkti x 0 nimetatakse maksimaalne punkt(miinimum) funktsiooni f(x), kui punkti x 0 mõnes läheduses on täidetud võrratus f(x) ≤f(x 0) (f(x) ≥f(x 0)).

Funktsiooni väärtust selles punktis kutsutakse vastavalt maksimaalselt või miinimum funktsioonid. Maksimaalset ja minimaalset funktsiooni ühendab ühine nimi äärmus funktsioonid.

Funktsiooni ekstreemumiks selles tähenduses nimetatakse sageli kohalik äärmus, rõhutades asjaolu, et seda mõistet seostatakse ainult punkti x 0 piisavalt väikese naabruskonnaga. Samal intervallil võib funktsioonil olla mitu kohalikku maksimumi ja miinimumi, mis ei pruugi nendega kokku langeda globaalne maksimum või miinimum(st funktsiooni suurim või väikseim väärtus kogu intervalli jooksul).

Ekstreemi jaoks vajalik tingimus. Selleks, et funktsioonil oleks punktis ekstreemum, on vajalik, et selle tuletis selles punktis oleks võrdne nulliga või seda ei eksisteeri.

Diferentseeruvate funktsioonide puhul tuleneb see tingimus Fermat' teoreemist. Lisaks näeb see ette ka juhud, kui funktsioonil on ekstreemum punktis, kus see ei ole diferentseeritav.

Nimetatakse punkte, kus vajalik äärmuslik tingimus on täidetud kriitiline(või paigal diferentseeruva funktsiooni jaoks). Need punktid peavad jääma funktsiooni valdkonda.

Seega, kui mingis punktis on ekstreemum, siis see punkt on kriitiline (vajalik tingimus). Pange tähele, et vastupidine pole tõsi. Kriitiline punkt ei pruugi olla äärmuspunkt, s.t. märgitud tingimus ei ole piisav.

Ekstreemumi esimene piisav tingimus. Kui teatud punkti läbimisel muudab diferentseeruva funktsiooni tuletis oma märgi plussist miinusesse, siis on see funktsiooni maksimumpunkt ja kui miinusest plussiks, siis see on miinimumpunkt.

Selle tingimuse tõestus tuleneb monotoonsuse piisavast tingimusest (tuletise märgi muutumisel toimub üleminek kas funktsiooni suurenemiselt vähenemisele või kahanemiselt suurenemisele).

Ekstreemumi teine ​​piisav tingimus. Kui kaks korda diferentseeruva funktsiooni esimene tuletis on mingil hetkel null ja teine ​​tuletis selles punktis on positiivne, siis on see funktsiooni miinimumpunkt; ja kui teine ​​tuletis on negatiivne, siis on see maksimumpunkt.

Selle tingimuse tõestuse aluseks on ka monotoonsuse piisav tingimus. Tegelikult, kui teine ​​tuletis on positiivne, siis esimene tuletis on kasvav funktsioon. Kuna vaadeldavas punktis on see võrdne nulliga, muudab see selle läbimisel märgi miinusest plussiks, mis tagastab meid kohaliku miinimumi esimese piisava tingimuse juurde. Samamoodi, kui teine ​​tuletis on negatiivne, siis esimene väheneb ja muudab märgi plussist miinusesse, mis on piisav tingimus lokaalseks maksimumiks.

Ekstreemumi funktsiooni uurimine sõnastatud teoreemide kohaselt sisaldab see järgmisi etappe:

1. Leia funktsiooni f`(x) esimene tuletis.

2. Kontrolli vajaliku ekstreemtingimuse täitmist, s.o. leida funktsiooni f(x) kriitilised punktid, kus tuletist f`(x) = 0 või ei eksisteeri.

3. Kontrolli ekstreemumi piisava tingimuse täitmist, s.o. kas uurige igast kriitilisest punktist vasakul ja paremal asuva tuletise märki või leidke teine ​​tuletis f``(x) ja määrake selle märk igas kriitilises punktis. Tehke järeldus funktsiooni äärmuste olemasolu kohta.

4. Leia funktsiooni äärmused (äärmuslikud väärtused).

Funktsiooni globaalse maksimumi ja miinimumi leidmine teatud aja jooksul on sellel ka suur praktiline tähendus. Selle ülesande lahendus segmendil põhineb Weierstrassi teoreemil, mille kohaselt pidev funktsioon võtab lõigul oma suurimad ja väikseimad väärtused. Neid saab saavutada nii äärmuslikes punktides kui ka segmendi otstes. Seetõttu sisaldab lahendus järgmisi samme:

1. Leia funktsiooni f`(x) tuletis.

2. Leia funktsiooni f(x) kriitilised punktid, kus tuletist f`(x) = 0 või ei eksisteeri.

3. Leidke funktsiooni väärtused kriitilistes punktides ja lõigu otstes ning valige nende hulgast suurim ja väikseim.