Vektorite süsteemi lineaarne sõltuvus ja lineaarne sõltumatus. Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid Uurige, kas vektorid on lineaarselt sõltumatud
Definitsioon. Lineaarne vektorite kombinatsioon a 1 , ..., a n koefitsientidega x 1 , ..., x n nimetatakse vektoriks
x 1 a 1 + ... + x n a n .
triviaalne, kui kõik koefitsiendid x 1 , ..., x n on võrdsed nulliga.
Definitsioon. Nimetatakse lineaarkombinatsioon x 1 a 1 + ... + x n a n mittetriviaalne, kui vähemalt üks koefitsientidest x 1, ..., x n ei ole võrdne nulliga.
lineaarselt sõltumatu, kui nende vektorite mittetriviaalne kombinatsioon ei ole võrdne nullvektoriga.
See tähendab, et vektorid a 1, ..., a n on lineaarselt sõltumatud, kui x 1 a 1 + ... + x n a n = 0 siis ja ainult siis, kui x 1 = 0, ..., x n = 0.
Definitsioon. Nimetatakse vektoreid a 1, ..., a n lineaarselt sõltuv, kui nende vektorite mittetriviaalne kombinatsioon on võrdne nullvektoriga.
Lineaarselt sõltuvate vektorite omadused:
N-mõõtmeliste vektorite jaoks.
n + 1 vektorid on alati lineaarselt sõltuvad.
Kahe- ja kolmemõõtmeliste vektorite jaoks.
Kaks lineaarselt sõltuvat vektorit on kollineaarsed. (Kollineaarsed vektorid on lineaarselt sõltuvad.)
3-mõõtmeliste vektorite jaoks.
Kolm lineaarselt sõltuvat vektorit on tasapinnalised. (Kolm samatasandilist vektorit on lineaarselt sõltuvad.)
Vektorite lineaarse sõltuvuse ja lineaarse sõltumatuse probleemide näited:
Näide 1. Kontrollige, kas vektorid a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) on lineaarselt sõltumatud .
Lahendus:
Vektorid on lineaarselt sõltuvad, kuna vektorite mõõde on väiksem kui vektorite arv.
Näide 2. Kontrollige, kas vektorid a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) on lineaarselt sõltumatud.
Lahendus:
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
lahutage esimesest reast teine; lisage kolmandale reale teine rida:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
See lahendus näitab, et süsteemil on palju lahendusi, st arvude x 1, x 2, x 3 väärtuste nullist erinev kombinatsioon on selline, et vektorite a, b, c lineaarne kombinatsioon on võrdne nullvektor, näiteks:
A + b + c = 0
ja see tähendab, et vektorid a, b, c on lineaarselt sõltuvad.
Vastus: vektorid a, b, c on lineaarselt sõltuvad.
Näide 3. Kontrollige, kas vektorid a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) on lineaarselt sõltumatud.
Lahendus: Leiame koefitsientide väärtused, mille korral nende vektorite lineaarne kombinatsioon on võrdne nullvektoriga.
x 1 a + x 2 b + x 3 c 1 = 0Selle vektorvõrrandi saab kirjutada lineaarsete võrrandite süsteemina
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + 2x 3 = 0 |
Lahendame selle süsteemi Gaussi meetodil
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
lahutage esimene teisest reast; lahutage esimene kolmandast reast:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
lahutage esimesest reast teine; lisage kolmandale reale sekund.
Selles artiklis käsitleme:
- mis on kollineaarsed vektorid;
- millised on vektorite kollineaarsuse tingimused;
- millised on kollineaarsete vektorite omadused;
- milline on kollineaarsete vektorite lineaarne sõltuvus.
Kollineaarsed vektorid on vektorid, mis on paralleelsed ühe sirgega või asuvad ühel sirgel.
Näide 1
Vektorite kollineaarsuse tingimused
Kaks vektorit on kollineaarsed, kui mõni järgmistest tingimustest on tõene:
- tingimus 1 . Vektorid a ja b on kollineaarsed, kui on olemas arv λ, mille puhul a = λ b;
- tingimus 2 . Vektorid a ja b on kollineaarsed võrdsete koordinaatide suhetega:
a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2
- tingimus 3 . Vektorid a ja b on kollineaarsed eeldusel, et ristkorrutis ja nullvektor on võrdsed:
a ∥ b ⇔ a, b = 0
Märkus 1
Tingimus 2 ei kehti, kui üks vektori koordinaatidest on null.
Märkus 2
Tingimus 3 kehtib ainult nendele vektoritele, mis on määratud ruumis.
Ülesannete näited vektorite kollineaarsuse uurimiseks
Näide 1Uurime vektorite a = (1; 3) ja b = (2; 1) kollineaarsust.
Kuidas lahendada?
Sel juhul on vaja kasutada 2. kolineaarsuse tingimust. Antud vektorite puhul näeb see välja järgmine:
Võrdsus on vale. Sellest võime järeldada, et vektorid a ja b on mittekollineaarsed.
Vastus : a | | b
Näide 2
Milline vektori a = (1; 2) ja b = (- 1; m) väärtus m on vajalik, et vektorid oleksid kollineaarsed?
Kuidas lahendada?
Kasutades teist kollineaarsustingimust, on vektorid kollineaarsed, kui nende koordinaadid on võrdelised:
See näitab, et m = -2.
Vastus: m = -2.
Vektorsüsteemide lineaarse sõltuvuse ja lineaarse sõltumatuse kriteeriumid
TeoreemVektoriruumis olev vektorite süsteem on lineaarselt sõltuv ainult siis, kui süsteemi üht vektorit saab väljendada selle süsteemi ülejäänud vektoritega.
Tõestus
Olgu süsteem e 1 , e 2 , . . . , e n on lineaarselt sõltuv. Kirjutame selle süsteemi lineaarse kombinatsiooni, mis on võrdne nullvektoriga:
a 1 e 1 + a 2 e 2 + . . . + a n e n = 0
milles vähemalt üks kombinatsiooni koefitsient ei ole võrdne nulliga.
Olgu a k ≠ 0 k ∈ 1 , 2 , . . . , n.
Jagame võrdsuse mõlemad pooled nullist erineva koefitsiendiga:
a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0
Tähistame:
A k - 1 a m , kus m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n
Sel juhul:
β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0
või e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n
Sellest järeldub, et süsteemi üht vektorit väljendatakse kõigi teiste süsteemi vektorite kaudu. Mida oli vaja tõestada (jne).
Adekvaatsus
Olgu üks vektoritest lineaarselt väljendatud kõigi teiste süsteemi vektorite kaudu:
e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n
Viime vektori e k selle võrrandi paremale poole:
0 = γ 1 e 1 +. . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n
Kuna vektori e k koefitsient on võrdne - 1 ≠ 0, saame nulli mittetriviaalse esituse vektorite süsteemiga e 1, e 2, . . . , e n ja see omakorda tähendab, et see vektorite süsteem on lineaarselt sõltuv. Mida oli vaja tõestada (jne).
Tagajärg:
- Vektorite süsteem on lineaarselt sõltumatu, kui ühtki selle vektorit ei saa väljendada süsteemi kõigi teiste vektoritega.
- Nullvektorit või kahte võrdset vektorit sisaldav vektorite süsteem on lineaarselt sõltuv.
Lineaarselt sõltuvate vektorite omadused
- 2- ja 3-mõõtmeliste vektorite puhul on täidetud järgmine tingimus: kaks lineaarselt sõltuvat vektorit on kollineaarsed. Kaks kollineaarset vektorit on lineaarselt sõltuvad.
- 3-mõõtmeliste vektorite puhul on täidetud järgmine tingimus: kolm lineaarselt sõltuvat vektorit on tasapinnalised. (3 samatasandilist vektorit on lineaarselt sõltuvad).
- N-mõõtmeliste vektorite puhul on täidetud järgmine tingimus: n + 1 vektorit on alati lineaarselt sõltuvad.
Näited probleemide lahendamisest, mis hõlmavad vektorite lineaarset sõltuvust või lineaarset sõltumatust
Näide 3Kontrollime vektorite a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 lineaarset sõltumatust.
Lahendus. Vektorid on lineaarselt sõltuvad, kuna vektorite mõõde on väiksem kui vektorite arv.
Näide 4
Kontrollime vektorite a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 lineaarset sõltumatust.
Lahendus. Leiame koefitsientide väärtused, mille korral lineaarne kombinatsioon võrdub nullvektoriga:
x 1 a + x 2 b + x 3 c 1 = 0
Kirjutame vektorvõrrandi lineaarsel kujul:
x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0
Lahendame selle süsteemi Gaussi meetodiga:
1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~
2. realt lahutame 1., 3. - 1.:
~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~
1. realt lahutame 2., 3. lisame teise:
~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0
Lahendusest järeldub, et süsteemil on palju lahendusi. See tähendab, et selliste arvude x 1, x 2, x 3 väärtustest on nullist erinev kombinatsioon, mille puhul a, b, c lineaarne kombinatsioon võrdub nullvektoriga. Seetõttu on vektorid a, b, c lineaarselt sõltuv.
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
Lineaarne sõltuvus ja vektori sõltumatus
Lineaarselt sõltuvate ja sõltumatute vektorsüsteemide definitsioonid
Definitsioon 22
Olgu meil n-vektorite süsteem ja arvude hulk  , Siis
, Siis
(11)
nimetatakse antud vektorite süsteemi lineaarseks kombinatsiooniks antud koefitsientide hulgaga.
Definitsioon 23
Vektorsüsteem  nimetatakse lineaarselt sõltuvaks, kui selline koefitsientide hulk on olemas
nimetatakse lineaarselt sõltuvaks, kui selline koefitsientide hulk on olemas  , millest vähemalt üks ei ole võrdne nulliga, et antud vektorite süsteemi lineaarne kombinatsioon selle koefitsientide komplektiga on võrdne nullvektoriga:
, millest vähemalt üks ei ole võrdne nulliga, et antud vektorite süsteemi lineaarne kombinatsioon selle koefitsientide komplektiga on võrdne nullvektoriga:
Lase  , Siis
, Siis

Definitsioon 24 ( süsteemi ühe vektori esitamise kaudu teiste lineaarse kombinatsioonina)
Vektorsüsteem  nimetatakse lineaarselt sõltuvaks, kui vähemalt ühte selle süsteemi vektorit saab esitada selle süsteemi ülejäänud vektorite lineaarse kombinatsioonina.
nimetatakse lineaarselt sõltuvaks, kui vähemalt ühte selle süsteemi vektorit saab esitada selle süsteemi ülejäänud vektorite lineaarse kombinatsioonina.
3. väide
Definitsioonid 23 ja 24 on samaväärsed.
Definitsioon 25(null lineaarse kombinatsiooni kaudu)
Vektorsüsteem  nimetatakse lineaarselt sõltumatuks, kui selle süsteemi nullline lineaarne kombinatsioon on võimalik ainult kõigi jaoks
nimetatakse lineaarselt sõltumatuks, kui selle süsteemi nullline lineaarne kombinatsioon on võimalik ainult kõigi jaoks  võrdne nulliga.
võrdne nulliga.
Definitsioon 26(kuna süsteemi üht vektorit on võimatu esitada teiste lineaarse kombinatsioonina)
Vektorsüsteem  nimetatakse lineaarselt sõltumatuks, kui ühtegi selle süsteemi vektorit ei saa esitada selle süsteemi teiste vektorite lineaarse kombinatsioonina.
nimetatakse lineaarselt sõltumatuks, kui ühtegi selle süsteemi vektorit ei saa esitada selle süsteemi teiste vektorite lineaarse kombinatsioonina.
Lineaarselt sõltuvate ja sõltumatute vektorsüsteemide omadused
Teoreem 2 (nullvektor vektorite süsteemis)
Kui vektorite süsteemil on nullvektor, siis on süsteem lineaarselt sõltuv.
Lase  , Siis.
, Siis.
Me saame  , seega lineaarselt sõltuva vektorite süsteemi definitsiooni kaudu null-lineaarse kombinatsiooni kaudu (12)
süsteem on lineaarselt sõltuv.
, seega lineaarselt sõltuva vektorite süsteemi definitsiooni kaudu null-lineaarse kombinatsiooni kaudu (12)
süsteem on lineaarselt sõltuv.
Teoreem 3 (sõltuv alamsüsteem vektorsüsteemis)
Kui vektorite süsteemil on lineaarselt sõltuv alamsüsteem, siis on kogu süsteem lineaarselt sõltuv.
Lase  - lineaarselt sõltuv alamsüsteem
- lineaarselt sõltuv alamsüsteem  , mille hulgas vähemalt üks ei ole võrdne nulliga:
, mille hulgas vähemalt üks ei ole võrdne nulliga:
See tähendab 23. definitsiooni järgi, et süsteem on lineaarselt sõltuv.
4. teoreem
Lineaarselt sõltumatu süsteemi mis tahes alamsüsteem on lineaarselt sõltumatu.
Vastupidiselt. Olgu süsteem lineaarselt sõltumatu ja sellel on lineaarselt sõltuv alamsüsteem. Kuid siis, vastavalt teoreemile 3, on ka kogu süsteem lineaarselt sõltuv. Vastuolu. Järelikult ei saa lineaarselt sõltumatu süsteemi alamsüsteem olla lineaarselt sõltuv.
Vektorisüsteemi lineaarse sõltuvuse ja sõltumatuse geomeetriline tähendus
5. teoreem
Kaks vektorit  Ja
Ja  on lineaarselt sõltuvad siis ja ainult siis
on lineaarselt sõltuvad siis ja ainult siis  .
.
Vajadus.
 Ja
Ja  - lineaarselt sõltuv
- lineaarselt sõltuv  et tingimus on täidetud
et tingimus on täidetud  . Siis
. Siis  , st.
, st.  .
.
Adekvaatsus.
Lineaarselt sõltuv.
Järeldus 5.1
Nullvektor on mis tahes vektori suhtes kollineaarne
Järeldus 5.2
Selleks, et kaks vektorit oleks lineaarselt sõltumatud, on vajalik ja piisav, et  ei olnud kollineaarne
ei olnud kollineaarne  .
.
6. teoreem
Selleks, et kolmest vektorist koosnev süsteem oleks lineaarselt sõltuv, on vajalik ja piisav, et need vektorid oleksid tasapinnalised .
Vajadus.
 - on lineaarselt sõltuvad, seetõttu saab ühte vektorit esitada kahe teise vektori lineaarse kombinatsioonina.
- on lineaarselt sõltuvad, seetõttu saab ühte vektorit esitada kahe teise vektori lineaarse kombinatsioonina.
 ,
(13)
,
(13)
Kus  Ja
Ja  . Rööpkülikureegli järgi
. Rööpkülikureegli järgi  on külgedega rööpküliku diagonaal
on külgedega rööpküliku diagonaal  , kuid rööpkülik on lame kujund
, kuid rööpkülik on lame kujund  koplanaarne
koplanaarne  - on samuti tasapinnalised.
- on samuti tasapinnalised.
Adekvaatsus.
 - koplanaarne. Rakendame punktile O kolm vektorit:
- koplanaarne. Rakendame punktile O kolm vektorit:


 C
C
 B`
B`

 – lineaarselt sõltuv
– lineaarselt sõltuv
Järeldus 6.1
Nullvektor on samatasandiline mis tahes vektoripaariga.
Järeldus 6.2
Selleks, et vektorid  olid lineaarselt sõltumatud, on vajalik ja piisav, et need ei oleks tasapinnalised.
olid lineaarselt sõltumatud, on vajalik ja piisav, et need ei oleks tasapinnalised.
Järeldus 6.3
Tasapinna mis tahes vektorit saab esitada mis tahes kahe sama tasandi mittekollineaarse vektori lineaarse kombinatsioonina.
7. teoreem
Kõik neli vektorit ruumis on lineaarselt sõltuvad .
Vaatleme 4 juhtumit:
Joonistame tasapinna läbi vektorite, seejärel tasapinna läbi vektorite ja tasapinna läbi vektorite. Seejärel joonistame vektoripaaridega paralleelsed tasapinnad, mis läbivad punkti D; ; vastavalt. Ehitame rööptahuka piki tasandite lõikejooni 1 O.B. 1 C 1 D.

ABDC ; vastavalt. Ehitame rööptahuka piki tasandite lõikejooni 1
O.B. 1
C 1
Mõelgem  .
.
– rööpkülik konstruktsiooni järgi rööpkülikureegli järgi  Vaatleme OADD 1 – rööpkülikut (rööptahuka omadusest)
Vaatleme OADD 1 – rööpkülikut (rööptahuka omadusest)
, Siis
EMBED võrrand.3 .  1. teoreemi järgi
1. teoreemi järgi  selline, et. Siis
selline, et. Siis
, ja definitsiooni 24 järgi on vektorite süsteem lineaarselt sõltuv.
Järeldus 7.1
Kolme mittetasapinnalise vektori summa ruumis on vektor, mis ühtib nendele kolmele vektorile ehitatud rööptahuka diagonaaliga, mis on rakendatud ühisele alguspunktile, ja summavektori alguspunkt langeb kokku nende kolme vektori ühise alguspunktiga.
Järeldus 7.2
Kui võtta ruumis 3 mittetasatasandilist vektorit, siis saab selle ruumi suvalise vektori lagundada nende kolme vektori lineaarseks kombinatsiooniks.. Lineaarne vektorite kombinatsioon on nende vektorite ja skalaaride korrutiste summa  :
:
2. definitsioon. Vektorsüsteem  nimetatakse lineaarselt sõltuvaks süsteemiks, kui nende lineaarne kombinatsioon (2.8) kaob:
nimetatakse lineaarselt sõltuvaks süsteemiks, kui nende lineaarne kombinatsioon (2.8) kaob:
ja numbrite hulgas  on vähemalt üks, mis erineb nullist.
on vähemalt üks, mis erineb nullist.
3. definitsioon. Vektorid  nimetatakse lineaarseks sõltumatuteks, kui nende lineaarne kombinatsioon (2.8) kaob ainult juhul, kui kõik arvud.
nimetatakse lineaarseks sõltumatuteks, kui nende lineaarne kombinatsioon (2.8) kaob ainult juhul, kui kõik arvud.
Nendest määratlustest võib saada järgmised järeldused.
Järeldus 1. Lineaarselt sõltuvas vektorite süsteemis saab vähemalt ühte vektorit väljendada teiste lineaarse kombinatsioonina.
Tõestus. Olgu (2.9) rahuldatud ja määravuse huvides koefitsient  . Meil on siis:
. Meil on siis:  . Pange tähele, et ka vastupidine on tõsi.
. Pange tähele, et ka vastupidine on tõsi.
Järeldus 2. Kui vektorite süsteem  sisaldab nullvektorit, siis on see süsteem (tingimata) lineaarselt sõltuv – tõestus on ilmne.
sisaldab nullvektorit, siis on see süsteem (tingimata) lineaarselt sõltuv – tõestus on ilmne.
Järeldus 3. Kui hulgas n vektorid  ükskõik milline k(
ükskõik milline k( ) vektorid on lineaarselt sõltuvad, siis on kõik n vektorid on lineaarselt sõltuvad (jätame tõestuse välja).
) vektorid on lineaarselt sõltuvad, siis on kõik n vektorid on lineaarselt sõltuvad (jätame tõestuse välja).
2 0 . Kahe, kolme ja nelja vektori lineaarsed kombinatsioonid. Vaatleme vektorite lineaarse sõltuvuse ja sõltumatuse küsimusi sirgel, tasapinnal ja ruumis. Esitame vastavad teoreemid.
1. teoreem. Selleks, et kaks vektorit oleks lineaarselt sõltuvad, on vajalik ja piisav, et nad oleksid kollineaarsed.
Vajadus. Las vektorid  Ja
Ja  lineaarselt sõltuv. See tähendab, et nende lineaarne kombinatsioon
lineaarselt sõltuv. See tähendab, et nende lineaarne kombinatsioon  =0 ja (selguse huvides)
=0 ja (selguse huvides)  . See tähendab võrdsust
. See tähendab võrdsust  , ja (vektori arvuga korrutamise definitsiooni järgi) vektorid
, ja (vektori arvuga korrutamise definitsiooni järgi) vektorid  Ja
Ja  kollineaarne.
kollineaarne.
Adekvaatsus. Las vektorid  Ja
Ja  kollineaarne (
kollineaarne (  ║
║ ) (oletame, et need erinevad nullvektorist; vastasel juhul on nende lineaarne sõltuvus ilmne).
) (oletame, et need erinevad nullvektorist; vastasel juhul on nende lineaarne sõltuvus ilmne).
Teoreemi (2.7) järgi (vt §2.1, punkt 2 0) siis  selline et
selline et  , või
, või  – lineaarne kombinatsioon on võrdne nulliga ja koefitsient at
– lineaarne kombinatsioon on võrdne nulliga ja koefitsient at  võrdub 1-ga – vektorid
võrdub 1-ga – vektorid  Ja
Ja  lineaarselt sõltuv.
lineaarselt sõltuv.
Sellest teoreemist tuleneb järgmine järeldus.
Tagajärg. Kui vektorid  Ja
Ja  ei ole kollineaarsed, siis on nad lineaarselt sõltumatud.
ei ole kollineaarsed, siis on nad lineaarselt sõltumatud.
2. teoreem. Selleks, et kolm vektorit oleksid lineaarselt sõltuvad, on vajalik ja piisav, et need oleksid tasapinnalised.
Vajadus. Las vektorid  ,
, Ja
Ja  lineaarselt sõltuv. Näitame, et need on tasapinnalised.
lineaarselt sõltuv. Näitame, et need on tasapinnalised.
Vektorite lineaarse sõltuvuse definitsioonist järeldub arvude olemasolu  Ja
Ja  nii et lineaarne kombinatsioon
nii et lineaarne kombinatsioon  , ja samal ajal (kui olla täpne)
, ja samal ajal (kui olla täpne)  . Siis saame sellest võrdsusest väljendada vektori
. Siis saame sellest võrdsusest väljendada vektori  :
: =
= , see tähendab vektorit
, see tähendab vektorit  võrdne selle võrrandi paremal küljel asuvatele vektoritele konstrueeritud rööpküliku diagonaaliga (joonis 2.6). See tähendab, et vektorid
võrdne selle võrrandi paremal küljel asuvatele vektoritele konstrueeritud rööpküliku diagonaaliga (joonis 2.6). See tähendab, et vektorid  ,
, Ja
Ja  lamavad samas tasapinnas.
lamavad samas tasapinnas.
Adekvaatsus. Las vektorid  ,
, Ja
Ja  koplanaarne. Näitame, et need on lineaarselt sõltuvad.
koplanaarne. Näitame, et need on lineaarselt sõltuvad.
Jätame välja mis tahes vektoripaari kollineaarsuse juhtumi (sest siis on see paar lineaarselt sõltuv ja Järeldus 3 järgi (vt lõik 1 0) on kõik kolm vektorit lineaarselt sõltuvad). Pange tähele, et see eeldus välistab ka nullvektori olemasolu nende kolme hulgas.
Liigutame kolm tasapinnalist vektorit ühte tasapinda ja viime need ühisesse algpunkti. Läbi vektori otsa  tõmmake vektoritega paralleelsed jooned
tõmmake vektoritega paralleelsed jooned  Ja
Ja  ; saame vektorid
; saame vektorid  Ja
Ja  (joon. 2.7) - nende olemasolu tagab see, et vektorid
(joon. 2.7) - nende olemasolu tagab see, et vektorid  Ja
Ja  vektorid, mis ei ole eeldusel kollineaarsed. Sellest järeldub, et vektor
vektorid, mis ei ole eeldusel kollineaarsed. Sellest järeldub, et vektor  =
= +
+ . Selle võrdsuse ümberkirjutamine kujul (–1)
. Selle võrdsuse ümberkirjutamine kujul (–1)  +
+ +
+ =0, järeldame, et vektorid
=0, järeldame, et vektorid  ,
, Ja
Ja  lineaarselt sõltuv.
lineaarselt sõltuv.
Tõestatud teoreemist tuleneb kaks järeldust.
Järeldus 1. Lase  Ja
Ja  mittekollineaarsed vektorid, vektor
mittekollineaarsed vektorid, vektor  – suvaline, mis asub vektorite poolt määratletud tasapinnal
– suvaline, mis asub vektorite poolt määratletud tasapinnal  Ja
Ja  , vektor. Siis on numbrid
, vektor. Siis on numbrid  Ja
Ja  selline et
selline et
 =
= +
+ .
(2.10)
.
(2.10)
Järeldus 2. Kui vektorid  ,
, Ja
Ja  ei ole tasapinnalised, siis on nad lineaarselt sõltumatud.
ei ole tasapinnalised, siis on nad lineaarselt sõltumatud.
3. teoreem. Kõik neli vektorit on lineaarselt sõltuvad.
Jätame tõestuse välja; mõningate muudatustega kopeerib see teoreemi 2 tõestuse. Toome selle teoreemi järelduse.
Tagajärg. Mis tahes mittetasapinnaliste vektorite jaoks  ,
, ,
, ja mis tahes vektorit
ja mis tahes vektorit  Ja
Ja  selline et
selline et
 .
(2.11)
.
(2.11)
Kommenteeri. (Kolmemõõtmelises) ruumis olevate vektorite puhul on lineaarse sõltuvuse ja sõltumatuse mõistetel, nagu ülaltoodud teoreemidest 1-3, lihtne geomeetriline tähendus.
Olgu kaks lineaarselt sõltuvat vektorit  Ja
Ja  . Sel juhul on üks neist teise lineaarne kombinatsioon, see tähendab, et see erineb sellest lihtsalt numbrilise teguri poolest (näiteks
. Sel juhul on üks neist teise lineaarne kombinatsioon, see tähendab, et see erineb sellest lihtsalt numbrilise teguri poolest (näiteks  ). Geomeetriliselt tähendab see, et mõlemad vektorid on ühisel sirgel; neil võib olla sama või vastupidine suund (joonis 2.8 xx).
). Geomeetriliselt tähendab see, et mõlemad vektorid on ühisel sirgel; neil võib olla sama või vastupidine suund (joonis 2.8 xx).
Kui kaks vektorit asetsevad üksteise suhtes nurga all (joonis 2.9 xx), siis sel juhul ei saa ühte neist saada, kui korrutada teist arvuga - sellised vektorid on lineaarselt sõltumatud. Seetõttu on kahe vektori lineaarne sõltumatus  Ja
Ja  tähendab, et neid vektoreid ei saa paigutada ühele sirgele.
tähendab, et neid vektoreid ei saa paigutada ühele sirgele.
Selgitame välja kolme vektori lineaarse sõltuvuse ja sõltumatuse geomeetrilise tähenduse.
Las vektorid  ,
, Ja
Ja  on lineaarselt sõltuvad ja olgu (konkreetseks) vektoriks
on lineaarselt sõltuvad ja olgu (konkreetseks) vektoriks  on vektorite lineaarne kombinatsioon
on vektorite lineaarne kombinatsioon  Ja
Ja  st asub vektoreid sisaldaval tasapinnal
st asub vektoreid sisaldaval tasapinnal  Ja
Ja  . See tähendab, et vektorid
. See tähendab, et vektorid  ,
, Ja
Ja  lamavad samas tasapinnas. Tõsi on ka vastupidi: kui vektorid
lamavad samas tasapinnas. Tõsi on ka vastupidi: kui vektorid  ,
, Ja
Ja  asuvad samal tasapinnal, siis on nad lineaarselt sõltuvad.
asuvad samal tasapinnal, siis on nad lineaarselt sõltuvad.
Seega vektorid  ,
, Ja
Ja  on lineaarselt sõltumatud siis ja ainult siis, kui nad ei asu samal tasapinnal.
on lineaarselt sõltumatud siis ja ainult siis, kui nad ei asu samal tasapinnal.
3 0 . Aluse mõiste. Lineaar- ja vektoralgebra üks olulisemaid mõisteid on aluse mõiste. Tutvustame mõningaid määratlusi.
Kui võtta ruumis 3 mittetasatasandilist vektorit, siis saab selle ruumi suvalise vektori lagundada nende kolme vektori lineaarseks kombinatsiooniks.. Vektoripaari nimetatakse järjestatuks, kui on määratud, millist selle paari vektorit peetakse esimeseks ja millist teiseks.
2. definitsioon. Tellitud paar  ,
, mittekollineaarseid vektoreid nimetatakse baasiks antud vektorite poolt määratletud tasandil.
mittekollineaarseid vektoreid nimetatakse baasiks antud vektorite poolt määratletud tasandil.
1. teoreem. Mis tahes vektor  tasapinnal võib kujutada vektorite baassüsteemi lineaarse kombinatsioonina
tasapinnal võib kujutada vektorite baassüsteemi lineaarse kombinatsioonina  ,
, :
:
 (2.12)
(2.12)
ja see esitus on ainus.
Tõestus. Las vektorid  Ja
Ja  moodustavad aluse. Siis mis tahes vektor
moodustavad aluse. Siis mis tahes vektor  saab esitada kujul
saab esitada kujul  .
.
Ainulaadsuse tõestamiseks eeldame, et on veel üks lagunemine  . Meil on siis = 0 ja vähemalt üks erinevustest erineb nullist. Viimane tähendab, et vektorid
. Meil on siis = 0 ja vähemalt üks erinevustest erineb nullist. Viimane tähendab, et vektorid  Ja
Ja  lineaarselt sõltuv, st kollineaarne; see on vastuolus väitega, et need moodustavad aluse.
lineaarselt sõltuv, st kollineaarne; see on vastuolus väitega, et need moodustavad aluse.
Kuid siis on ainult lagunemine.
3. definitsioon. Vektorite kolmikut nimetatakse järjestatuks, kui on määratud, millist vektorit peetakse esimeseks, millist teiseks ja kumba kolmandaks.
4. määratlus. Mitte-tasapinnaliste vektorite järjestatud kolmikut nimetatakse ruumi baasiks.
Siin kehtib ka lagunemise ja kordumatuse teoreem.
2. teoreem. Mis tahes vektor  saab esitada baasvektorisüsteemi lineaarse kombinatsioonina
saab esitada baasvektorisüsteemi lineaarse kombinatsioonina  ,
, ,
, :
:
 (2.13)
(2.13)
ja see esitus on ainulaadne (jätame teoreemi tõestuse välja).
Laiendustes (2.12) ja (2.13) kogused  nimetatakse vektorkoordinaatideks
nimetatakse vektorkoordinaatideks  antud alusel (täpsemalt afiinsete koordinaatide järgi).
antud alusel (täpsemalt afiinsete koordinaatide järgi).
Fikseeritud alusega  Ja
Ja  sa võid kirjutada
sa võid kirjutada  .
.
Näiteks kui alus on antud  ja see on antud
ja see on antud  , siis see tähendab, et on olemas esitus (lagundamine)
, siis see tähendab, et on olemas esitus (lagundamine)  .
.
4 0 . Lineaartehted vektoritel koordinaatkujul. Aluse kasutuselevõtt võimaldab vektoritega tehtud lineaartehteid asendada tavaliste lineaartehtetega arvudega – nende vektorite koordinaatidega.
Olgu mingi alus antud  . Ilmselgelt määrab vektori koordinaatide määramine sellel alusel täielikult vektori enda. Kehtivad järgmised ettepanekud:
. Ilmselgelt määrab vektori koordinaatide määramine sellel alusel täielikult vektori enda. Kehtivad järgmised ettepanekud:
a) kaks vektorit  Ja
Ja  on võrdsed siis ja ainult siis, kui nende vastavad koordinaadid on võrdsed:
on võrdsed siis ja ainult siis, kui nende vastavad koordinaadid on võrdsed:
b) vektori korrutamisel  numbri kohta
numbri kohta  selle koordinaadid korrutatakse selle arvuga:
selle koordinaadid korrutatakse selle arvuga:
 ;
(2.15)
;
(2.15)
c) vektorite lisamisel lisatakse nendele vastavad koordinaadid:
Jätame nende omaduste tõendid välja; Tõestagem omadust b) ainult näitena. Meil on
 ==
==
Kommenteeri. Kosmoses (lennukil) saab valida lõpmatult palju aluseid.
Toome näite üleminekust ühelt aluselt teisele ja loome seosed vektori koordinaatide vahel erinevates alustes.
Näide 1. Põhisüsteemis  on antud kolm vektorit:
on antud kolm vektorit:  ,
, Ja
Ja  . Alusel
. Alusel  ,
, ,
, vektor
vektor  on lagunemine. Otsige vektori koordinaadid
on lagunemine. Otsige vektori koordinaadid  alusel
alusel  .
.
Lahendus. Meil on laiendused:  ,
, ,
, ; seega,
; seega,  =
= +2
+2 +
+ =
=
=
= , see tähendab
, see tähendab  alusel
alusel  .
.
Näide 2. Laske mingi alus sisse  Neli vektorit on antud nende koordinaatidega:
Neli vektorit on antud nende koordinaatidega:  ,
, ,
, Ja
Ja  .
.
Uurige, kas vektorid moodustuvad  alus; kui vastus on positiivne, leia vektori lagunemine
alus; kui vastus on positiivne, leia vektori lagunemine  sellel alusel.
sellel alusel.
Lahendus. 1) vektorid moodustavad aluse, kui nad on lineaarselt sõltumatud. Teeme vektorite lineaarse kombinatsiooni  (
( ) ja uurige, milles
) ja uurige, milles  Ja
Ja  see läheb nulli:
see läheb nulli:  =0. Meil on:
=0. Meil on:
 =
= +
+ +
+ =
=
Defineerides vektorite võrdsuse koordinaatide kujul, saame järgmise (lineaarsete homogeensete algebraliste) võrrandite süsteemi:  ;
; ;
; , mille määraja
, mille määraja  =1
=1 , see tähendab, et süsteemil on (ainult) triviaalne lahendus
, see tähendab, et süsteemil on (ainult) triviaalne lahendus  . See tähendab vektorite lineaarset sõltumatust
. See tähendab vektorite lineaarset sõltumatust  ja seetõttu moodustavad nad aluse.
ja seetõttu moodustavad nad aluse.
2) laiendada vektorit  sellel alusel. Meil on:
sellel alusel. Meil on:  =
= või koordinaatide kujul.
või koordinaatide kujul.
Liikudes vektorite võrdsuse juurde koordinaatide kujul, saame lineaarsete mittehomogeensete algebraliste võrrandite süsteemi:  ;
; ;
; . Selle lahendamisel (näiteks Crameri reegli abil) saame:
. Selle lahendamisel (näiteks Crameri reegli abil) saame:  ,
, ,
, Ja (
Ja (  )
) . Meil on vektori lagunemine
. Meil on vektori lagunemine  alusel
alusel  :
: =.
=.
5
0
. Vektori projektsioon teljele. Projektsioonide omadused. Olgu mingi telg l, st sirgjoon, millele on valitud suund ja olgu antud mingi vektor  Defineerime vektorprojektsiooni mõiste
Defineerime vektorprojektsiooni mõiste  telje kohta l.
telje kohta l.
Definitsioon. Vektorprojektsioon  telje kohta l nimetatakse selle vektori mooduli ja teljevahelise nurga koosinuse korrutist l ja vektor (joonis 2.10):
telje kohta l nimetatakse selle vektori mooduli ja teljevahelise nurga koosinuse korrutist l ja vektor (joonis 2.10):
 .
(2.17)
.
(2.17)
Selle määratluse tagajärg on väide, et võrdsetel vektoritel on võrdsed projektsioonid (samal teljel).
Märgime projektsioonide omadused.
1) vektorite summa projektsioon mõnele teljele l võrdne samale teljele vektorite projektsioonide summaga:
2) skalaari korrutise projektsioon vektori järgi on võrdne selle skalaari korrutisega vektori projektsiooniga samale teljele:
 =
= .
(2.19)
.
(2.19)
Tagajärg. Vektorite lineaarse kombinatsiooni projektsioon teljele on võrdne nende projektsioonide lineaarse kombinatsiooniga:
Jätame ära omaduste tõendid.
6
0
. Ristkülikukujuline Descartes'i koordinaatsüsteem ruumis.Vektori lagunemine telgede ühikvektorites. Olgu aluseks võtta kolm üksteisega risti asetsevat ühikvektorit; tutvustame nende jaoks erimärke  . Asetades nende algused ühte punkti O, suuname neid mööda (vastavalt ort
. Asetades nende algused ühte punkti O, suuname neid mööda (vastavalt ort  ) koordinaatteljed Ox,Oy ja O z(sellele valitud positiivse suuna, alguspunkti ja pikkuseühikuga telge nimetatakse koordinaatteljeks).
) koordinaatteljed Ox,Oy ja O z(sellele valitud positiivse suuna, alguspunkti ja pikkuseühikuga telge nimetatakse koordinaatteljeks).
Definitsioon. Kolmest vastastikku risti asetsevast koordinaatteljest koosnevat järjestatud süsteemi, millel on ühine alguspunkt ja ühine pikkusühik, nimetatakse ruumis ristkülikukujuliseks Descartes'i koordinaatsüsteemiks.
Telg Ox nimetatakse abstsissteljeks, Oy– ordinaattelg uO z – telje aplikaator.
Käsitleme suvalise vektori laiendamist baasis  . Teoreemist (vt §2.2, lõik 3 0, (2.13)) järeldub, et
. Teoreemist (vt §2.2, lõik 3 0, (2.13)) järeldub, et  saab unikaalselt laiendada üle aluse
saab unikaalselt laiendada üle aluse  (siin koordinaatide määramise asemel
(siin koordinaatide määramise asemel  kasutada
kasutada  ):
):
 .
(2.21)
.
(2.21)
B (2,21)  olemuse (Cartesiuse ristkülikukujulised) vektori koordinaadid
olemuse (Cartesiuse ristkülikukujulised) vektori koordinaadid  . Descartes'i koordinaatide tähendus määratakse järgmise teoreemiga.
. Descartes'i koordinaatide tähendus määratakse järgmise teoreemiga.
Teoreem. Descartes'i ristkülikukujulised koordinaadid  vektor
vektor  on selle vektori projektsioonid vastavalt teljel Ox,Oy ja O z.
on selle vektori projektsioonid vastavalt teljel Ox,Oy ja O z.
Tõestus. Asetame vektori  koordinaatsüsteemi alguspunkti - punkt O. Siis langeb selle lõpp mingi punktiga kokku
koordinaatsüsteemi alguspunkti - punkt O. Siis langeb selle lõpp mingi punktiga kokku  .
.
Joonistame punkti läbi  kolm koordinaattasanditega paralleelset tasapinda Oyz,Oxz Ja Oxy(joonis 2.11 xx). Seejärel saame:
kolm koordinaattasanditega paralleelset tasapinda Oyz,Oxz Ja Oxy(joonis 2.11 xx). Seejärel saame:
 .
(2.22)
.
(2.22)
In (2.22) vektorid
 Ja
Ja
 nimetatakse vektorkomponentideks
nimetatakse vektorkomponentideks  mööda telgesid Ox,Oy ja O z.
mööda telgesid Ox,Oy ja O z.
Lase läbi  Ja
Ja  vektori moodustatud nurgad on näidatud vastavalt
vektori moodustatud nurgad on näidatud vastavalt  ortidega
ortidega  . Seejärel saame komponentide jaoks järgmised valemid:
. Seejärel saame komponentide jaoks järgmised valemid:
 =
=
 =
= ,
,
 =
=
 =
= ,
,
 =
=
 =
= (2.23)
(2.23)
Alates (2.21), (2.22) (2.23) leiame:
 =
= =
= ;
; =
= =
= ;
; =
= =
= (2.23)
(2.23)
- koordinaadid  vektor
vektor  on selle vektori projektsioonid koordinaattelgedele Ox,Oy ja O z vastavalt.
on selle vektori projektsioonid koordinaattelgedele Ox,Oy ja O z vastavalt.
Kommenteeri. Numbrid  nimetatakse vektori suunakoosinusteks
nimetatakse vektori suunakoosinusteks  .
.
Vektormoodul  (ristkülikukujulise rööptahuka diagonaal) arvutatakse järgmise valemiga:
(ristkülikukujulise rööptahuka diagonaal) arvutatakse järgmise valemiga:
 .
(2.24)
.
(2.24)
Valemitest (2.23) ja (2.24) järeldub, et suunakoosinused saab arvutada valemite abil:
 =
= ;
; =
= ;
; =
= .
(2.25)
.
(2.25)
Tõstades (2.25) iga võrdsuse mõlemat poolt ja liites saadud võrrandite vasaku ja parema külje termini haaval, saame valemi:
– mitte suvalised kolm nurka ei moodusta ruumis kindlat suunda, vaid ainult need, mille koosinused on omavahel seotud (2.26).
7 0 . Raadiuse vektor ja punkti koordinaadid.Vektori määramine selle alguse ja lõpu järgi. Tutvustame määratlust.
Definitsioon. Raadiuse vektor (tähistatud  ) on alguspunkti ühendav vektor O selle punktiga (joonis 2.12 xx):
) on alguspunkti ühendav vektor O selle punktiga (joonis 2.12 xx):
 .
(2.27)
.
(2.27)
Iga punkt ruumis vastab teatud raadiusvektorile (ja vastupidi). Seega on ruumipunktid vektoralgebras esindatud nende raadiusvektoritega.
Ilmselgelt koordinaadid  punktid M on selle raadiusvektori projektsioonid
punktid M on selle raadiusvektori projektsioonid  koordinaattelgedel:
koordinaattelgedel:
 (2.28’)
(2.28’)
ja seega
 (2.28)
(2.28)
– punkti raadiuse vektor on vektor, mille projektsioonid koordinaattelgedel on võrdsed selle punkti koordinaatidega. See toob kaasa kaks kirjet:  Ja
Ja  .
.
Saame vektorprojektsioonide arvutamise valemid  selle lähtepunkti koordinaatide järgi - punkt
selle lähtepunkti koordinaatide järgi - punkt  ja lõpp-punkt
ja lõpp-punkt  .
.
Joonistame raadiuse vektorid  ja vektor
ja vektor  (joonis 2.13). Me saame sellest aru
(joonis 2.13). Me saame sellest aru
 =
= =(2.29)
=(2.29)
– vektori projektsioonid koordinaatühiku vektoritele on võrdsed vektori lõpu ja alguse vastavate koordinaatide erinevustega.
8 0 . Mõned ristkoordinaatidega seotud probleemid.
1)
vektorite kollineaarsuse tingimused
. Teoreemist (vt §2.1, lõik 2 0, valem (2.7)) järeldub, et vektorite kollineaarsuse korral  Ja
Ja  see on vajalik ja piisav järgmise seose kehtimiseks:
see on vajalik ja piisav järgmise seose kehtimiseks:  =
=
 . Sellest vektorvõrdsusest saame kolm võrdsust koordinaadikujul:, mis eeldab koordinaadikujul vektorite kollineaarsuse tingimust:
. Sellest vektorvõrdsusest saame kolm võrdsust koordinaadikujul:, mis eeldab koordinaadikujul vektorite kollineaarsuse tingimust:
 (2.30)
(2.30)
– vektorite kollineaarsuse jaoks  Ja
Ja  on vajalik ja piisav, et nende vastavad koordinaadid oleksid proportsionaalsed.
on vajalik ja piisav, et nende vastavad koordinaadid oleksid proportsionaalsed.
2)
punktide vaheline kaugus
. Esitusest (2.29) järeldub, et kaugus  punktide vahel
punktide vahel  Ja
Ja  määratakse valemiga
määratakse valemiga
 =
= =.
(2.31)
=.
(2.31)
3)
segmendi jagamine etteantud suhtega
. Lastakse punkte anda  Ja
Ja  ja suhtumist
ja suhtumist  . Vaja leida
. Vaja leida  – punkti koordinaadid M
(joonis 2.14).
– punkti koordinaadid M
(joonis 2.14).
Vektorite kollineaarsuse tingimuse põhjal saame:  , kus
, kus  Ja
Ja
 .
(2.32)
.
(2.32)
Alates (2.32) saame koordinaatide kujul:
Valemitest (2,32’) saame valemid lõigu keskkoha koordinaatide arvutamiseks  , eeldades
, eeldades  :
:
Kommenteeri. Loendame segmente  Ja
Ja  positiivsed või negatiivsed olenevalt sellest, kas nende suund kattub suunaga algusest peale
positiivsed või negatiivsed olenevalt sellest, kas nende suund kattub suunaga algusest peale  segment lõpuni
segment lõpuni  ,
või ei sobi. Seejärel saate valemite (2.32) – (2.32”) abil leida lõiku jagava punkti koordinaadid
,
või ei sobi. Seejärel saate valemite (2.32) – (2.32”) abil leida lõiku jagava punkti koordinaadid  väliselt ehk nii, et eralduspunkt M on segmendi jätkamisel
väliselt ehk nii, et eralduspunkt M on segmendi jätkamisel  ja mitte selle sees. Samal ajal muidugi
ja mitte selle sees. Samal ajal muidugi  .
.
4)
sfäärilise pinna võrrand
.
Koostame sfäärilise pinna võrrandi – punktide geomeetrilise lookuse  , võrdsel kaugusel
, võrdsel kaugusel  mingist fikseeritud keskpunktist – punktist
mingist fikseeritud keskpunktist – punktist  . On ilmne, et antud juhul
. On ilmne, et antud juhul  ja võttes arvesse valemit (2.31)
ja võttes arvesse valemit (2.31)
Võrrand (2.33) on soovitud sfäärilise pinna võrrand.
Vormi väljendamine helistas vektorite lineaarne kombinatsioon A 1, A 2,...,A n koefitsientidega λ 1, λ 2,...,λ n.
Vektorite süsteemi lineaarse sõltuvuse määramine
Vektorsüsteem A 1, A 2,...,A n helistas lineaarselt sõltuv, kui on nullist erinev arvude hulk λ 1, λ 2,...,λ n, milles vektorite lineaarne kombinatsioon λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n võrdne nullvektoriga, see tähendab võrrandisüsteemi: on nullist erinev lahendus.
Numbrite komplekt λ 1, λ 2,...,λ n on nullist erinev, kui vähemalt üks arvudest λ 1, λ 2,...,λ n nullist erinev.
Vektorite süsteemi lineaarse sõltumatuse määramine
Näide 29.1Vektorsüsteem A 1, A 2,...,A n helistas lineaarselt sõltumatu, kui nende vektorite lineaarne kombinatsioon λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n võrdne nullvektoriga ainult nullarvude hulga puhul λ 1, λ 2,...,λ n , see tähendab võrrandisüsteemi: A 1 x 1 +A 2 x 2 +...+A n x n =Θ omab ainulaadset nulllahendust.
Kontrollige, kas vektorite süsteem on lineaarselt sõltuv
Lahendus:

1. Koostame võrrandisüsteemi:
2. Lahendame selle Gaussi meetodil. Süsteemi Jordanano teisendused on toodud tabelis 29.1. Arvutamisel süsteemi paremaid külgi üles ei kirjutata, kuna need on võrdsed nulliga ega muutu Jordani teisenduste käigus.

3. Tabeli kolmest viimasest reast kirjutage üles lahendatud süsteem, mis on samaväärne algse süsteemiga süsteem:
![]()
4. Saame süsteemi üldlahenduse:
5. Olles määranud vaba muutuja väärtuse x 3 =1 oma äranägemise järgi, saame konkreetse nullist erineva lahenduse X=(-3,2,1).
Vastus: Seega nullist erineva arvude hulga (-3,2,1) korral võrdub vektorite lineaarne kombinatsioon nullvektoriga -3A 1 +2A 2 +1A 3 =Θ. Seega vektorsüsteem lineaarselt sõltuv.
Vektorsüsteemide omadused
Vara (1)
Kui vektorite süsteem on lineaarselt sõltuv, siis vähemalt ühte vektorit laiendatakse teiste suhtes ja vastupidi, kui vähemalt ühte süsteemi vektorit laiendatakse teiste suhtes, siis vektorite süsteem. on lineaarselt sõltuv.
Vara (2)
Kui mis tahes vektorite alamsüsteem on lineaarselt sõltuv, siis on lineaarselt sõltuv kogu süsteem.
Vara (3)
Kui vektorite süsteem on lineaarselt sõltumatu, siis on iga selle alamsüsteem lineaarselt sõltumatu.
Kinnistu (4)
Iga nullvektorit sisaldav vektorite süsteem on lineaarselt sõltuv.
Kinnisvara (5)
M-mõõtmeliste vektorite süsteem on alati lineaarselt sõltuv, kui vektorite arv n on suurem kui nende mõõde (n>m)
Vektorsüsteemi alused
Vektorsüsteemi alus A 1 , A 2 ,..., A sellist alamsüsteemi B 1 , B 2 ,...,B r nimetatakse(iga vektorid B 1, B 2,..., B r on üks vektoritest A 1, A 2,..., A n), mis vastab järgmistele tingimustele:
1. B 1 ,B 2 ,...,B r lineaarselt sõltumatu vektorite süsteem;
2. mis tahes vektor A j Süsteemi A 1 , A 2 ,..., A n väljendatakse lineaarselt läbi vektorite B 1 , B 2 ,..., B rr— baasis sisalduvate vektorite arv.
Teoreem 29.1 Vektorite süsteemi ühiku alusel.Kui m-mõõtmeliste vektorite süsteem sisaldab m erinevat ühikvektorit E 1 E 2 ,..., E m , siis moodustavad need süsteemi aluse.
Algoritm vektorite süsteemi aluse leidmiseks
Vektorite süsteemi A 1 ,A 2 ,...,A n aluse leidmiseks on vaja:
- Loo homogeenne vektorisüsteemile vastav võrrandisüsteem A 1 x 1 +A 2 x 2 +...+A n x n =Θ
- Tooge see süsteem
 Viipekeele lühisõnastik, kuidas sõnaraamat töötab ja kuidas seda kasutada Viipekeele tõlk võrgus
Viipekeele lühisõnastik, kuidas sõnaraamat töötab ja kuidas seda kasutada Viipekeele tõlk võrgus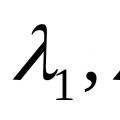 Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid Uurige, kas vektorid on lineaarselt sõltumatud
Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid Uurige, kas vektorid on lineaarselt sõltumatud Mida on vaja teada, et tunda end iirlasena?
Mida on vaja teada, et tunda end iirlasena?