Функция распределения непрерывной величины. Случайной величины
Пусть непрерывная случайная величина Х задана функцией распределения f(x) . Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b ].
Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку , называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.
Определение. Модой М 0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным . Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным .
Определение. Медианой M D случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам. Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
Определение. Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х k .
Начальный момент первого порядка равен математическому ожиданию.
Определение. Центральным моментом порядка k случайной величины Х называется математическое ожидание величины
Для дискретной случайной величины: .
Для непрерывной случайной величины: .
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии .
Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом .
Кроме рассмотренных величин используются также так называемые абсолютные моменты:
Абсолютный начальный момент: . Абсолютный центральный момент: . Абсолютный центральный момент первого порядка называется средним арифметическим отклонением .
Пример. Для рассмотренного выше примера определить математическое ожидание и дисперсию случайной величины Х.
Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.
Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).
Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна
Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий.
1) Белый шар не появился вовсе:
2) Белый шар появился один раз:
3) Белый шар появиться два раза: .
Функцией распределения случайной величины X называется функция F(x), выражающая для каждого х вероятность того, что случайная величина X примет значение , меньшее х
Пример 2.5. Дан ряд распределения случайной величины
Найти и изобразить графически ее функцию распределения. Решение. В соответствии с определением
F(jc) = 0 при х х
F(x) = 0,4 + 0,1 = 0,5 при 4 F{x) = 0,5 + 0,5 = 1 при х > 5.
Итак (см. рис. 2.1):


Свойства функции распределения:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
![]()
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. при х 2 >х
![]()
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности - равна единице, т.е.
4. Вероятность попадания случайной величины X в интервал равна определенному интегралу от ее плотности вероятности в пределах от а до b (см. рис. 2.2), т.е.

Рис. 2.2
3. Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле:
F(x)= Jp (*)*. (2.10)
4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:
Геометрически свойства / и 4 плотности вероятности означают, что ее график - кривая распределения - лежит не ниже оси абсцисс , и полная площадь фигуры , ограниченной кривой распределения и осью абсцисс , равна единице.
Для непрерывной случайной величины X математическое ожидание М(Х) и дисперсия D(X) определяются по формулам:
(если интеграл абсолютно сходится); или

(если приведенные интегралы сходятся).
Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек.
Квантилем уровня q (или q-квантилем) называется такое значение x q случайной величины , при котором функция ее распределения принимает значение , равное q, т. е.
- 100q%-ou точкой называется квантиль X~ q .
- ? Пример 2.8.
По данным примера 2.6 найти квантиль xqj и 30%-ную точку случайной величины X.
Решение. По определению (2.16) F(xo t3)= 0,3, т. е.
~Y~ = 0,3, откуда квантиль х 0 3 = 0,6. 30%-ная точка случайной величины X , или квантиль Х)_о,з = xoj » находится аналогично из уравнения ^ = 0,7 . откуда *,= 1,4. ?
Среди числовых характеристик случайной величины выделяют начальные v* и центральные р* моменты к-го порядка , определяемые для дискретных и непрерывных случайных величин по формулам:

4. Плотность распределения вероятностей непрерывной случайной величины
Непрерывную случайную величину можно задать с помощью функции распределения F (x ) . Этот способ задания не является единственным. Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда её называют дифференциальной функцией).
Определение4.1: Плотностью распределения непрерывной случайной величины Х называют функцию f (x ) - первую производную от функции распределения F (x ) :
f ( x ) = F "( x ) .
Из этого определения следует, что функция распределения является первообразной для плотности распределения. Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Вероятность попадания непрерывной случайной величины в заданный интервал
Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.
Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащие интервалу (a , b ), равна определённому интегралу от плотности распределения, взятому в пределах от a до b :
Доказательство: Используем соотношение
P (a ≤ X b ) = F (b ) – F (a ).
По формуле Ньютона-Лейбница,
Таким образом,
 .
.
Так как P (a ≤ X b )= P (a X b ) , то окончательно получим
 .
.
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a , b ), равна площади криволинейной трапеции, ограниченной осью Ox , кривой распределения f (x ) и прямыми x = a и x = b .
Замечание: В частности, если f (x ) – чётная функция и концы интервала симметричны относительно начала координат, то
 .
.
Пример. Задана плотность вероятности случайной величины Х

Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу (0,5; 1).
Решение: Искомая вероятность
Нахождение функции распределения по известной плотности распределения
Зная плотность распределения f (x ) , можно найти функцию распределения F (x ) по формуле
 .
.
Действительно, F (x ) = P (X x ) = P (-∞ X x ) .
Следовательно,
 .
.
Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения можно найти плотность распределения , а именно:
f (x ) = F "(x ).
Пример. Найти функцию распределения по данной плотности распределения:

Решение:
Воспользуемся формулой

Если x ≤ a , то f (x ) = 0 , следовательно, F (x ) = 0 . Если a , то f(x) = 1/(b-a) ,
следовательно,
 .
.
Если x > b , то
 .
.
Итак, искомая функция распределения

Замечание: Получили функцию распределения равномерно распределенной случайной величины (см. равномерное распределение).
Свойства плотности распределения
Свойство 1: Плотность распределения - неотрицательная функция:
f ( x ) ≥ 0 .
Свойство 2: Несобственный интеграл от плотности распределения в пределах от -∞ до ∞ равен единице:
 .
.
Замечание: График плотности распределения называют кривой распределения .
Замечание: Плотность распределения непрерывной случайной величины также называют законом распределения.
Пример. Плотность распределения случайной величины имеет следующий вид:

Найти постоянный параметр a .
Решение: Плотность распределения должна удовлетворять условию , поэтому потребуем, чтобы выполнялось равенство
 .
.
Отсюда
 .
Найдём
неопределённый интеграл:
.
Найдём
неопределённый интеграл:
 .
.
Вычислим несобственный интеграл:
Таким образом, искомый параметр
 .
.
Вероятный смысл плотности распределения
Пусть F (x ) – функция распределения непрерывной случайной величины X . По определению плотности распределения, f (x ) = F "(x ) , или
 .
.
Разность F (x +∆х) - F (x ) определяет вероятность того, что X примет значение, принадлежащее интервалу (x , x +∆х) . Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу (x , x +∆х) , к длине этого интервала (при ∆х→0 ) равен значению плотности распределения в точке х .
Итак, функция f (x ) определяет плотность распределения вероятности для каждой точки х . Из дифференциального исчисления известно,что приращение функции приближенно равно дифференциалу функции, т.е.
Так как F "(x ) = f (x ) и dx = ∆ x , то F (x +∆ x ) - F (x ) ≈ f (x )∆ x .
Вероятностный смысл этого равенства таков: вероятность того, что случайная величина примет значение принадлежащее интервалу (x , x +∆ x ) ,приближенно равна произведению плотности вероятности в точке х на длину интервала ∆х .
Геометрически этот результат можно истолковать так : вероятность того, что случайная величина примет значение принадлежащее интервалу (x , x +∆ x ) ,приближенно равна площади прямоугольника с основанием ∆х и высотой f (x ).
5. Типовые распределения дискретных случайных величин
5.1. Распределение Бернулли
Определение5.1: Случайная величина X , принимающая два значения 1 и 0 с вероятностями (“успеха”) p и (“неуспеха”) q , называется Бернуллиевской :
, где k =0,1.
5.2. Биномиальное распределение
Пусть производится n независимых испытаний, в каждом из которых событие A может появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 - p ).
Рассмотрим случайную величину X – число появлений события A в этих испытаниях. Случайная величина X принимает значения 0,1,2,… n с вероятностями, вычисленными по формуле Бернулли: , где k = 0,1,2,… n .
Определение5.2: Биномиальным называют раcпределение вероятностей, определяемое формулой Бернулли.
Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти ее ряд распределения.
Решение: Случайная величина X принимает значения 0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, где n = 3, p = 0,8 (вероятность попадания), q = 1 - 0,8 = = 0,2 (вероятность непопадания).
Таким образом, ряд распределения имеет следующий вид:
Пользоваться формулой Бернулли при больших значениях n достаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико.
Локальная
теорема Лапласа
: Если вероятность p
появления события A
 того, что событие A
появится в n
испытаниях
ровно k
раз, приближенно
равна (тем точнее, чем больше n
)
значению функции
того, что событие A
появится в n
испытаниях
ровно k
раз, приближенно
равна (тем точнее, чем больше n
)
значению функции
 ,
где
,
где
 ,
,
 .
.
Замечание1:
Таблицы, в которых помещены значения
функции
 ,
даны в приложении 1, причем
,
даны в приложении 1, причем
 .
Функция
является плотностью стандартного
нормального распределения (смотри
нормальное распределение).
.
Функция
является плотностью стандартного
нормального распределения (смотри
нормальное распределение).
Пример: Найти вероятность того, что событие A наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение:
По условию n
= 400,
k
= 80,
p
= 0,2
, q
= 0,8
.
Вычислим определяемое данными задачи
значение x
:
 .
По таблице приложения 1 находим
.
По таблице приложения 1 находим
 .
Тогда искомая вероятность будет:
.
Тогда искомая вероятность будет:
Если нужно вычислить вероятность того, что событие A появится в n испытаниях не менее k 1 раз и не более k 2 раз, то нужно использовать интегральную теорему Лапласа:
Интегральная
теорема Лапласа
: Если вероятность p
появления события A
в каждом испытании постоянна и отлична
от нуля и единицы, то вероятность
 того, что событие A
появится в n
испытаниях
от k
1
до
k
2
раз,
приближенно равна определенному
интегралу
того, что событие A
появится в n
испытаниях
от k
1
до
k
2
раз,
приближенно равна определенному
интегралу
 ,
где
,
где
 и
и
 .
.
Другими словами, вероятность того, что событие A появится в n испытаниях от k 1 до k 2 раз, приближенно равна
где
 ,
и
.
,
и
.
Замечание2:
Функцию
 называют функцией Лапласа (смотри
нормальное распределение). Таблицы, в
которых помещены значения функции
,
даны в приложении 2, причем
называют функцией Лапласа (смотри
нормальное распределение). Таблицы, в
которых помещены значения функции
,
даны в приложении 2, причем
 .
.
Пример: Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей, если вероятность того, что деталь не прошла проверку ОТК, равна 0,2.
Решение: По условию n = 400, p = 0,2 , q = 0,8, k 1 = 70, k 2 = 100 . Вычислим нижний и верхний пределы интегрирования:
 ;
;
 .
.
Таким образом, имеем:
По таблице
приложения 2 находим, что
 и
.
Тогда искомая вероятность равна:
и
.
Тогда искомая вероятность равна:
Замечание3: В сериях независимых испытаний (когда n велико, p мало) для вычисления вероятности наступления события ровно k раз используют формулу Пуассона (смотри распределение Пуассона).
5.3. Распределение Пуассона
Определение5.3: Дискретную случайную величину называют Пуассоновской, если ее закон распределения имеет следующий вид:
 ,
где
,
где
 и
и
 (постоянное
значение).
(постоянное
значение).
Примеры Пуассоновских случайных величин:
Число вызовов на автоматическую станцию за промежуток времени T .
Число частиц распада некоторого радиоактивного вещества за промежуток времени T .
Число телевизоров, которые поступают в мастерскую за промежуток времени T в большом городе.
Число автомобилей, которые поступят к стоп-линии перекрестка в большом городе.
Замечание1: Специальные таблицы для вычисления данных вероятностей приведены в приложении 3.
Замечание2:
В сериях независимых испытаний (когда
n
велико, p
мало) для вычисления вероятности
наступления события ровно k
раз используют формулу Пуассона:
 ,
где
,
где
 ,
то есть среднее число появлений
событий остается постоянным.
,
то есть среднее число появлений
событий остается постоянным.
Замечание3: Если есть случайная величина, которая распределена по закону Пуассона, то обязательно есть случайная величина, которая распределена по показательному закону и, наоборот (см. Показательное распределение).
Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002 . Найти вероятность, что на базу прибудут ровно три негодных изделия.
Решение: По условию n = 5000, p = 0,0002, k = 3. Найдем λ: λ = np = 5000·0,0002 = 1 .
По формуле Пуассона искомая вероятность равна:
 ,
где случайная величина X
– число негодных изделий.
,
где случайная величина X
– число негодных изделий.
5.4. Геометрическое распределение
Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна p (0 p
q = 1 - p . Испытания заканчиваются, как только появится событие А . Таким образом, если событие А появилось в k -м испытании, то в предшествующих k – 1 испытаниях оно не появлялось.
Обозначим через Х дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А . Очевидно, возможными значениями Х являются натуральные числа х 1 = 1, х 2 = 2, …
Пусть в первых k -1 испытаниях событие А не наступило, а в k -м испытании появилось. Вероятность этого “сложного события”, по теореме умножения вероятностей независимых событий, P (X = k ) = q k -1 p .
Определение5.4: Дискретная случайная величина имеет геометрическое распределение , если ее закон распределения имеет следующий вид:
P
(
X
=
k
) =
q
k
-1
p
,
где
 .
.
Замечание1: Полагая k = 1,2,… , получим геометрическую прогрессию с первым членом p и знаменателем q (0q . По этой причине распределение называют геометрическим.
Замечание2:
Ряд
 сходится и сумма его равна единице.
Действительно сумма ряда равна
сходится и сумма его равна единице.
Действительно сумма ряда равна
 .
.
Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p = 0,6 . Найти вероятность того, что попадание произойдет при третьем выстреле.
Решение: По условию p = 0,6, q = 1 – 0,6 = 0,4, k = 3. Искомая вероятность равна:
P (X = 3) = 0,4 2 ·0,6 = 0,096.
5.5. Гипергеометрическое распределение
Рассмотрим следующую задачу. Пусть в партии из N изделий имеется M стандартных (M N ). Из партии случайно отбирают n изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь не применима).
Обозначим через X случайную величину – число m стандартных изделий среди n отобранных. Тогда возможными значениями X будут 0, 1, 2,…, min ; обозначим их и, ... по значениям независимой переменной (Fonds) воспользуемся кнопкой (раздел ...
Учебно-методический комплекс по дисциплине «Общий психологический практикум»
Учебно-методический комплекс... методические указания по выполнению практических работ 5.1 Методические рекомендации по выполнению учебных проектов 5.2 Методические рекомендации по ... чувствительности), одномерного и многомерного... случайного компонента в величине ... с разделом «Представление...
Учебно-методический комплекс по дисциплине физика (название)
Учебно-методический комплекс... разделов в учебниках. Решение задач по каждой теме. Проработка методических указаний к лабораторным работам по ... случайной и приборной погрешности измерений 1.8 Тематика контрольных работ и методические указания по ... Частица в одномерной потенциальной яме. ...
Методические указания к лабораторным работам по дисциплине информатика
Методические указания... Методические указания к ЛАБОРАТОРНым РАБОТАМ по ... величиной , а наибольшей суммой величин ... массива случайными числами... 3.0 4.0 3.0 -2.5 14.3 16.2 18.0 1.0 а) одномерный массив б) двумерный массив Рис. 2– Файлы... описываются в разделе реализации после...
Непрерывные случайные величины имеют бесконечное число возможных значений. Поэтому ввести для них ряд распределения нельзя.
Вместо вероятности того, что случайная величина Х примет значение, равное х, т.е. p(X = x), рассматривают вероятность того, что Х примет значение, меньшее, чем х, т.е. Р(Х < х).
Введем новую характеристику случайных величин - функцию распределения и рассмотрим ее свойства.
Функция распределения - самая универсальная характеристика случайной величины. Она может быть определена как для дискретных, так и для непрерывных случайных величин:
F(x) = p(X < x).
Свойства функции распределения.
Функция распределения является неубывающей функцией своего аргумента, т.е. если:
На минус бесконечности функция распределения равна нулю:
На плюс бесконечности функция распределения равна единице:
Вероятность попадания случайной величины на заданный интервал определяется формулой:
Функция f(x), равная производной от функции распределения, называется плотностью вероятности случайной величины Х или плотностью распределения:
Выразим вероятность попадания на участок б до в через f(x). Она равна сумме элементов вероятности на этом участке, т.е. интегралу:
Отсюда можно выразить функцию распределения через плотность вероятности:
Свойства плотности вероятности.
Плотность вероятности является неотрицательной функцией (так как функция распределения является неубывающей функцией):
Плотность вероятно
сти является непрерывной функцией.
Интеграл в бесконечных пределах от плотности вероятности равен 1:
Плотность вероятности имеет размерность случайной величины.
Математическое ожидание и дисперсия непрерывной случайной величины
Смысл математического ожидания и дисперсии остается таким же, как и в случае дискретных случайных величин. Меняется вид формул для их нахождения путем замены:
Тогда получаем формулы для расчета математического ожидания и дисперсии непрерывной случайной величины:
Пример. Функция распределения непрерывной случайной величины задана выражением:

Найти величину a, плотность вероятности, вероятность попадания на участок (0,25-0,5), математическое ожидание и дисперсию.
Так как функция распределения F(x) непрерывна, то при х = 1 ax2 = 1, следовательно, a = 1.
Плотность вероятности находится, как производная от функции распределения:

Вычисление вероятности попадания на заданный участок может быть произведено двумя способами: с помощью функции распределения и с помощью плотности вероятности.
- 1-й способ. Используем формулу нахождения вероятности через функцию распределения:
- 2-й способ. Используем формулу нахождения вероятности через плотность вероятности:
Находим математическое ожидание:
Находим дисперсию:
Равномерное распределение
Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в некотором интервале и равновероятны.
Плотность вероятности такой случайной величины будет иметь вид:
где с - некоторая постоянная.
График плотности вероятности изобразится следующим образом:

Выразим параметр с через б и в. Для этого используем тот факт, что интеграл от плотности вероятности по всей области должен быть равен 1:
Плотность распределения равномерно распределенной случайной величины

Найдем функцию распределения:

Функция распределения равномерно распределенной случайной величины
Построим график функции распределения:

Вычислим математическое ожидание и дисперсию случайной величины, подчиняющейся равномерному распределению.



Тогда среднеквадратичное отклонение будет иметь вид:
Нормальное (Гауссово) распределение
Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами a, у > 0, если она имеет плотность вероятности:
Кривая распределение случайной величины, имеет вид:

Контрольная работа 2
Задание 1. Составить закон распределения дискретной случайной величины Х, вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 1
ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0,7. Проверено 20 изделий. Найти закон распределения случайной величины Х - числа стандартных изделий среди проверенных. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 2
В урне 4 шара, на которых указаны очки 2; 4; 5; 5. Наудачу вынимается шар. Найти закон распределения случайной величины Х - числа очков на нем. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 3
Охотник стреляет по дичи до попадания, но может сделать не более трех выстрелов. Вероятность попадания при каждом выстреле равна 0,6. Составить закон распределения случайной величины Х - числа выстрелов сделанных стрелком. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 4
Вероятность превысить заданную точность при измерении равна 0,4. Составить закон распределения случайной величины Х - число ошибок при 10 измерениях. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 5
Вероятность попадания в цель при одном выстреле равна 0,45. Произведено 20 выстрелов. Составить закон распределения случайной величины Х - числа попаданий. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 6
Изделия некоторого завода содержит 5% брака. Составить закон распределения случайной величины Х - числа бракованных изделий среди пяти взятых на удачу. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 7
Нужные сборщику детали находятся в трех из пяти ящиков. Сборщик вскрывает ящики до тех пор пока не найдет нужные детали. Составить закон распределения случайной величины Х - числа вскрытых ящиков. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 8
В урне 3 черных и 2 белых шара. Производится последовательное без возвращения извлечение шаров до появления черного. Составить закон распределения случайной величины Х - числа извлеченных шаров. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 9
Студент знает 15 вопросов из 20. В билете 3 вопроса. Составить закон распределения случайной величины Х - числа известных студенту вопросов в билете. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Вариант 10
Имеется 3 лампочки, каждая из которых с вероятностью 0,4 имеет дефект. При включении дефектная лампочка перегорает и заменяется другой. Составить закон распределения случайной величины Х - числа испробованных ламп. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Задание 2. Случайная величина Х задана функцией распределения F(X). Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал (б, в). Построить графики функций F(X) и f(X).
Вариант 1

Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10









Вопросы к экзамену
Классическое определение вероятности.
Элементы комбинаторики. Размещение. Примеры.
Элементы комбинаторики. Перестановка. Примеры.
Элементы комбинаторики. Сочетания. Примеры.
Теорема о сумме вероятностей.
Теорема умножения вероятностей.
Операции над событиями.
Формула полной вероятности.
Формула Байеса.
Повторение испытаний. Формула Бернулли.
Дискретные случайные величины. Ряд распределения. Пример.
Математическое ожидание дискретной случайной величины.
Дисперсия дискретной случайной величины.
Биномиальное распределение случайной величины.
Распределение Пуассона.
Распределение по закону геометрической прогрессии.
Непрерывные случайные величины. Функция распределения и ее свойства.
Плотность вероятности и ее свойства.
Математическое ожидание непрерывной случайной величины.
Дисперсия непрерывной случайной величины.
Равномерное распределение непрерывной случайной величины.
Нормальный закон распределения.
Понятия математического ожидания М (Х ) и дисперсии D (X ), введенные ранее для дискретной случайной величины, можно распространить на непрерывные случайные величины.
· Математическое ожидание М (Х ) непрерывной случайной величины Х определяется равенством:
при условии, что этот интеграл сходится.
· Дисперсия D (X ) непрерывной случайной величины Х определяется равенством:
· Среднее квадратическое отклонение σ(Х ) непрерывной случайной величины определяется равенством:
Все свойства математического ожидания и дисперсии, рассмотренные ранее для дискретных случайных величин, справедливы и для непрерывных.
Задача 5.3. Случайная величина Х задана дифференциальной функцией f (x ):
Найти M (X ), D (X ), σ(Х ), а также P (1 < х < 5).
Решение:
M (X )= =
+ = 8/9 0+9/6 4/6=31/18,
D (X )=
= = /
P 1 =
Задачи
5.1. Х
f (x ), а также
Р (‒1/2 < Х < 1/2).
5.2. Непрерывная случайная величина Х задана функцией распределения:
Найти дифференциальную функцию распределения f (x ), а также
Р (2π /9 < Х < π /2).
5.3. Непрерывная случайная величина Х
Найти: а) число с ; б) М (Х ), D (X ).
5.4. Непрерывная случайная величина Х задана плотностью распределения:
Найти: а) число с ; б) М (Х ), D (X ).
5.5. Х :
Найти: а) F (х ) и построить ее график; б) M (X ), D (X ), σ(Х ); в) вероятность того, что в четырех независимых испытаниях величина Х примет ровно 2 раза значение, принадлежащее интервалу (1;4).
5.6. Задана плотность распределения вероятностей непрерывной случайной величины Х :
Найти: а) F (х ) и построить ее график; б) M (X ), D (X ), σ(Х ); в) вероятность того, что в трех независимых испытаниях величина Х примет ровно 2 раза значение, принадлежащее отрезку .
5.7. Функция f (х ) задана в виде:
с Х ; б) функцию распределения F (x ).
5.8. Функция f (x ) задана в виде:
Найти: а) значение постоянной с , при которой функция будет плотностью вероятности некоторой случайной величины Х ; б) функцию распределения F (x ).
5.9. Случайная величина Х , сосредоточенная на интервале (3;7), задана функцией распределения F (х )= Х примет значение: а) меньше 5, б) не меньше 7.
5.10. Случайная величина Х , сосредоточенная на интервале (-1;4), задана функцией распределения F (х )= . Найти вероятность того, что случайная величина Х примет значение: а) меньше 2, б) меньше 4.
5.11.
Найти: а) число с ; б) М (Х ); в) вероятность Р (Х > М (Х )).
5.12. Случайная величина задана дифференциальной функцией распределения:
Найти: а) М (Х ); б) вероятность Р (Х ≤ М (Х )).
5.13. Распределение Ремя задается плотностью вероятности:
Доказать, что f (x ) действительно является плотностью распределения вероятностей.
5.14. Задана плотность распределения вероятностей непрерывной случайной величины Х :
Найти число с .
5.15. Случайная величина Х распределена по закону Симпсона (равнобедренного треугольника) на отрезке [-2;2] (рис. 5.4). Найти аналитическое выражение для плотности вероятности f (x ) на всей числовой оси.
Рис. 5.4 Рис. 5.5
5.16. Случайная величина Х распределена по закону "прямоугольного треугольника" в интервале (0;4) (рис. 5.5). Найти аналитическое выражение для плотности вероятности f (x ) на всей числовой оси.
Ответы
P (-1/2<X <1/2)=2/3.
P (2π /9<Х < π /2)=1/2.
5.3. а) с =1/6, б) М (Х )=3 , в) D (X )=26/81.
5.4. а) с =3/2, б) М (Х )=3/5, в) D (X )=12/175.
б) M (X )= 3 , D (X )= 2/9, σ(Х )= /3.
б) M (X )=2 , D (X )= 3 , σ(Х )= 1,893.
5.7. а) с = ; б)
5.8. а) с =1/2; б)
5.9. а)1/4; б) 0.
5.10. а)3/5; б) 1.
5.11. а) с = 2; б) М (Х )= 2; в) 1-ln 2 2 ≈ 0,5185.
5.12. а) М (Х )= π /2 ; б) 1/2
 Корпускулярные и волновые свойства частиц
Корпускулярные и волновые свойства частиц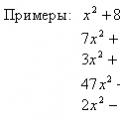 Уравнения онлайн X 5 0 решение
Уравнения онлайн X 5 0 решение Предельные монокарбоновые кислоты
Предельные монокарбоновые кислоты