Ograničena funkcija online kalkulatora s rješenjem. Limit funkcije – definicije, teoremi i svojstva
Prvo značajno ograničenje je sljedeća jednakost:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Budući da za $\alpha\to(0)$ imamo $\sin\alpha\to(0)$, kažu da prva značajna granica otkriva nesigurnost oblika $\frac(0)(0)$. Općenito govoreći, u formuli (1) umjesto varijable $\alpha$ ispod znaka sinusa i nazivnika može se staviti bilo koji izraz, ako su ispunjena dva uvjeta:
- Izrazi pod znakom sinusa i u nazivniku istovremeno teže nuli, tj. postoji nesigurnost oblika $\frac(0)(0)$.
- Izrazi pod znakom sinusa i u nazivniku su isti.
Korolari iz prve izvanredne granice također se često koriste:
\begin(jednadžba) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \kraj(jednadžba)
Na ovoj stranici riješeno je jedanaest primjera. Primjer br. 1 posvećen je dokazu formula (2)-(4). Primjeri br. 2, br. 3, br. 4 i br. 5 sadrže rješenja s detaljnim komentarima. Primjeri br. 6-10 sadrže rješenja praktički bez komentara, jer su detaljna objašnjenja data u prethodnim primjerima. Rješenje koristi neke trigonometrijske formule koje se mogu pronaći.
Dopustite mi da primijetim da prisutnost trigonometrijskih funkcija zajedno s nesigurnošću $\frac (0) (0)$ ne znači nužno primjenu prve značajne granice. Ponekad su dovoljne jednostavne trigonometrijske transformacije - na primjer, vidi.
Primjer br. 1
Dokažite da je $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Budući da je $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, tada:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Budući da $\lim_(\alpha\to(0))\cos(0)=1$ i $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Da:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Napravimo promjenu $\alpha=\sin(y)$. Budući da je $\sin(0)=0$, tada iz uvjeta $\alpha\to(0)$ imamo $y\to(0)$. Osim toga, postoji okolina nule u kojoj je $\arcsin\alpha=\arcsin(\sin(y))=y$, pa je:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
Dokazana je jednakost $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$.
c) Napravimo zamjenu $\alpha=\tg(y)$. Budući da je $\tg(0)=0$, tada su uvjeti $\alpha\to(0)$ i $y\to(0)$ ekvivalentni. Osim toga, postoji okolina nule u kojoj $\arctg\alpha=\arctg\tg(y))=y$, prema tome, na temelju rezultata točke a), imat ćemo:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
Dokazana je jednakost $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
Jednakosti a), b), c) često se koriste uz prvu značajnu granicu.
Primjer br. 2
Izračunajte granicu $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) (x+7))$.
Budući da $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ i $\lim_( x \to(2))\sin\lijevo(\frac(x^2-4)(x+7)\desno)=\sin(0)=0$, tj. a brojnik i nazivnik razlomka istovremeno teže nuli, onda se ovdje radi o nesigurnosti oblika $\frac(0)(0)$, tj. Gotovo. Osim toga, jasno je da se izrazi pod znakom sinusa i u nazivniku podudaraju (tj. i da je zadovoljeno):
Dakle, ispunjena su oba uvjeta navedena na početku stranice. Iz ovoga slijedi da je formula primjenjiva, tj. $\lim_(x\to(2)) \frac(\sin\lijevo(\frac(x^2-4)(x+7)\desno))(\frac(x^2-4)(x+ 7 ))=1$.
Odgovor: $\lim_(x\to(2))\frac(\sin\lijevo(\frac(x^2-4)(x+7)\desno))(\frac(x^2-4)(x +7))=1$.
Primjer br. 3
Pronađite $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Budući da $\lim_(x\to(0))\sin(9x)=0$ i $\lim_(x\to(0))x=0$, tada imamo posla s nesigurnošću oblika $\frac (0 )(0)$, tj. Gotovo. Međutim, izrazi pod znakom sinusa i u nazivniku se ne podudaraju. Ovdje je potrebno prilagoditi izraz u nazivniku željenom obliku. Trebamo izraz $9x$ da bude u nazivniku, tada će postati istina. U biti, nedostaje nam faktor od 9$ u nazivniku, koji nije tako teško unijeti—samo pomnožite izraz u nazivniku s 9$. Naravno, da biste kompenzirali množenje s 9$, morat ćete odmah podijeliti s 9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Sada se izrazi u nazivniku i pod znakom sinusa podudaraju. Oba uvjeta za granicu $\lim_(x\to(0))\frac(\sin(9x))(9x)$ su zadovoljena. Prema tome, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. A to znači da:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Odgovor: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Primjer br. 4
Pronađite $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Budući da $\lim_(x\to(0))\sin(5x)=0$ i $\lim_(x\to(0))\tg(8x)=0$, ovdje se radi o nesigurnosti oblika $\frac(0)(0)$. Međutim, forma prve izvanredne granice je prekršena. Brojnik koji sadrži $\sin(5x)$ zahtijeva nazivnik $5x$. U ovoj situaciji, najlakši način je podijeliti brojnik s $5x$ i odmah pomnožiti s $5x$. Osim toga, izvršit ćemo sličnu operaciju s nazivnikom, množenjem i dijeljenjem $\tg(8x)$ s $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Smanjujući za $x$ i uzimajući konstantu $\frac(5)(8)$ izvan graničnog znaka, dobivamo:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Imajte na umu da $\lim_(x\to(0))\frac(\sin(5x))(5x)$ u potpunosti zadovoljava zahtjeve za prvu značajnu granicu. Za pronalaženje $\lim_(x\to(0))\frac(\tg(8x))(8x)$ primjenjiva je sljedeća formula:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Odgovor: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Primjer br. 5
Pronađite $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Budući da je $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (zapamtite da $\cos(0)=1$) i $\ lim_(x\to(0))x^2=0$, tada imamo posla s nesigurnošću oblika $\frac(0)(0)$. Međutim, kako biste primijenili prvu značajnu granicu, trebali biste se riješiti kosinusa u brojniku i prijeći na sinuse (kako biste zatim primijenili formulu) ili tangente (kako biste zatim primijenili formulu). To se može učiniti sljedećom transformacijom:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\lijevo(1-\cos^2(5x)\desno)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\lijevo(1-\cos^2(5x)\desno)=\cos(5x)\cdot\sin^2(5x).$$
Vratimo se na limit:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\lijevo(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\desno) $$
Razlomak $\frac(\sin^2(5x))(x^2)$ već je blizu oblika potrebnog za prvu značajnu granicu. Poradimo malo s razlomkom $\frac(\sin^2(5x))(x^2)$, prilagođavajući ga prvoj značajnoj granici (imajte na umu da se izrazi u brojniku i ispod sinusa moraju podudarati):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\lijevo(\frac(\sin(5x))(5x)\desno)^2$$
Vratimo se na limit o kojem je riječ:
$$ \lim_(x\to(0))\lijevo(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\desno) =\lim_(x\to(0) ))\lijevo(25\cos(5x)\cdot\lijevo(\frac(\sin(5x))(5x)\desno)^2\desno)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\lijevo(\frac(\sin(5x))(5x)\desno)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Odgovor: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Primjer br. 6
Pronađite granicu $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Budući da $\lim_(x\to(0))(1-\cos(6x))=0$ i $\lim_(x\to(0))(1-\cos(2x))=0$, tada imamo posla s neizvjesnošću $\frac(0)(0)$. Otkrijmo to uz pomoć prve značajne granice. Da bismo to učinili, prijeđimo s kosinusa na sinuse. Budući da je $1-\cos(2\alpha)=2\sin^2(\alpha)$, tada:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Prelazeći na sinuse u zadanoj granici, imat ćemo:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\lijevo(\ frac(\sin(3x))(3x)\desno)^2\cdot(9x^2))(\lijevo(\frac(\sin(x))(x)\desno)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\lijevo(\frac(\sin(3x))(3x)\desno)^2)(\displaystyle\lim_(x \to(0))\lijevo(\frac(\sin(x))(x)\desno)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Odgovor: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Primjer br. 7
Izračunajte granicu $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ podložno $\alpha\neq \ beta$.
Detaljna objašnjenja dana su ranije, ali ovdje jednostavno napominjemo da ponovno postoji nesigurnost $\frac(0)(0)$. Prijeđimo s kosinusa na sinuse pomoću formule
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Pomoću ove formule dobivamo:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\lijevo|\frac(0)( 0)\desno| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\lijevo(x\cdot\frac(\alpha+\beta )(2)\desno)\cdot\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x^2) =-2\cdot\lim_(x\to( 0))\lijevo(\frac(\sin\lijevo(x\cdot\frac(\alpha+\beta)(2)\desno))(x)\cdot\frac(\sin\lijevo(x\cdot\frac (\alpha-\beta)(2)\desno))(x)\desno)=\\ =-2\cdot\lim_(x\to(0))\lijevo(\frac(\sin\lijevo(x) \cdot\frac(\alpha+\beta)(2)\desno))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\desno)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\lijevo(x\cdot\frac(\alpha+\beta)(2)\desno))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alfa^2)(2). $$
Odgovor: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.
Primjer br. 8
Pronađite granicu $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Budući da je $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (zapamtite da je $\sin(0)=\tg(0)=0$) i $\ lim_(x\to(0))x^3=0$, onda se ovdje radi o nesigurnosti oblika $\frac(0)(0)$. Raščlanimo to na sljedeći način:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\lijevo(\frac(1)(\cos(x))-1\desno))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\lijevo(1-\cos(x)\desno))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\lijevo(\frac(\sin(x))(x)\cdot\lijevo(\frac(\sin\frac(x)(2))(\frac(x)( 2))\desno)^2\cdot\frac(1)(\cos(x))\desno) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Odgovor: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Primjer br. 9
Pronađite granicu $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Budući da je $\lim_(x\to(3))(1-\cos(x-3))=0$ i $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, tada postoji nesigurnost oblika $\frac(0)(0)$. Prije nego što prijeđete na njezino širenje, zgodno je napraviti promjenu varijable na takav način da nova varijabla teži nuli (imajte na umu da je u formulama varijabla $\alpha \to 0$). Najlakši način je uvesti varijablu $t=x-3$. Međutim, radi pogodnosti daljnjih transformacija (ova se korist može vidjeti u tijeku rješenja danog u nastavku), vrijedi izvršiti sljedeću zamjenu: $t=\frac(x-3)(2)$. Napominjem da su obje zamjene primjenjive u ovom slučaju, samo što će vam druga zamjena omogućiti manje rada s razlomcima. Budući da je $x\to(3)$, onda $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\lijevo|\frac (0)(0)\desno| =\lijevo|\početak(poravnano)&t=\frac(x-3)(2);\\&t\to(0)\kraj(poravnano)\desno| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\lijevo(\frac(\sin(t))(t)\cdot\cos(t)\desno) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Odgovor: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Primjer br. 10
Pronađite granicu $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^ 2 )$.
Opet imamo posla s neizvjesnošću $\frac(0)(0)$. Prije nego što prijeđete na njezino širenje, zgodno je napraviti promjenu varijable na takav način da nova varijabla teži nuli (imajte na umu da je u formulama varijabla $\alpha\to(0)$). Najlakši način je uvesti varijablu $t=\frac(\pi)(2)-x$. Budući da $x\to\frac(\pi)(2)$, onda $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^2) =\lijevo|\frac(0)(0)\desno| =\lijevo|\početak(poravnano)&t=\frac(\pi)(2)-x;\\&t\to(0)\kraj(poravnano)\desno| =\lim_(t\to(0))\frac(1-\sin\lijevo(\frac(\pi)(2)-t\desno))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\lijevo(\frac(\sin\frac(t)(2))(\frac(t)(2))\desno)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Odgovor: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^2) =\frac(1)(2)$.
Primjer br. 11
Pronađite granice $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
U ovom slučaju ne moramo koristiti prvu divnu granicu. Imajte na umu da i prva i druga granica sadrže samo trigonometrijske funkcije i brojeve. Često je u primjerima ove vrste moguće pojednostaviti izraz koji se nalazi ispod znaka granice. Štoviše, nakon spomenutog pojednostavljenja i smanjenja nekih faktora, nesigurnost nestaje. Dao sam ovaj primjer samo s jednom svrhom: da pokažem da prisutnost trigonometrijskih funkcija ispod znaka granice ne znači nužno korištenje prve značajne granice.
Budući da je $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (zapamtite da $\sin\frac(\pi)(2)=1$ ) i $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (da vas podsjetim da $\cos\frac(\pi)(2)=0$), tada imamo koji se bave nesigurnošću oblika $\frac(0)(0)$. Međutim, to ne znači da ćemo morati koristiti prvu divnu granicu. Da bi se otkrila nesigurnost, dovoljno je uzeti u obzir da je $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\lijevo|\frac(0)(0)\desno| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Slično rješenje nalazi se iu Demidovičevu rješeniku (br. 475). Što se tiče druge granice, kao u prethodnim primjerima u ovom odjeljku, imamo nesigurnost oblika $\frac(0)(0)$. Zašto nastaje? Nastaje jer $\tg\frac(2\pi)(3)=-\sqrt(3)$ i $2\cos\frac(2\pi)(3)=-1$. Koristimo ove vrijednosti za transformaciju izraza u brojniku i nazivniku. Cilj našeg djelovanja je da zbroj u brojniku i nazivniku zapišemo kao umnožak. Usput, često je unutar sličnog tipa zgodno promijeniti varijablu, napravljenu na takav način da nova varijabla teži nuli (vidi, na primjer, primjere br. 9 ili br. 10 na ovoj stranici). Međutim, u ovom primjeru nema smisla zamjenjivati, iako po želji zamjenu varijable $t=x-\frac(2\pi)(3)$ nije teško implementirati.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ do\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\lijevo(\cos(x)+\frac(1)(2)\desno )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\lijevo(\ cos(x)-\cos\frac(2\pi)(3)\desno))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \lijevo(x-\frac(2\pi)(3)\desno))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\lijevo(x-\frac(2\pi)(3)\desno))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\lijevo(-\frac(1)(2)\desno)\cdot\lijevo( -\frac(1)(2)\desno)) =-\frac(4)(\sqrt(3)). $$
Kao što vidite, nismo morali primijeniti prvo divno ograničenje. Naravno, možete to učiniti ako želite (vidi napomenu ispod), ali nije nužno.
Koje je rješenje korištenjem prve značajne granice? pokazati\sakrij
Korištenjem prve značajne granice dobivamo:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\lijevo(x-\frac(2\pi)(3)\desno))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\lijevo(\frac(\sin\lijevo(x-\frac(2\pi)(3)\ desno))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\desno) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\lijevo(-\frac(1)(2)\desno)\cdot\lijevo(-\frac(1)(2)\desno)) =-\frac(4)(\sqrt( 3)). $$
Odgovor: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Otopina ograničenja mrežne funkcije. Naći graničnu vrijednost funkcije ili funkcionalnog niza u točki, izračunati krajnji vrijednost funkcije u beskonačnosti. određivanje konvergencije niza brojeva i mnogo više se može učiniti zahvaljujući našoj online usluzi -. Omogućujemo vam brzo i točno pronalaženje ograničenja funkcija na internetu. Vi sami upisujete funkcionalnu varijablu i granicu kojoj ona teži, a naš servis za vas obavlja sve izračune dajući točan i jednostavan odgovor. I za pronalaženje granice online možete unijeti i numeričke serije i analitičke funkcije koje sadrže konstante u doslovnom izrazu. U ovom slučaju, pronađena granica funkcije sadržavat će ove konstante kao konstantne argumente u izrazu. Naša usluga rješava sve složene probleme pronalaska ograničenja online, dovoljno je naznačiti funkciju i točku u kojoj je potrebno izračunati granična vrijednost funkcije. Računanje online ograničenja, možete koristiti različite metode i pravila za njihovo rješavanje, dok provjeravate dobiveni rezultat s rješavanje ograničenja online na www.site, što će dovesti do uspješnog izvršenja zadatka - izbjeći ćete vlastite pogreške i pogreške u pisanju. Ili nam možete potpuno vjerovati i koristiti naš rezultat u svom radu, bez trošenja dodatnog truda i vremena na samostalno izračunavanje limita funkcije. Dopuštamo unos graničnih vrijednosti kao što je beskonačnost. Potrebno je unijeti zajednički član brojčanog niza i www.site izračunat će vrijednost ograničiti online do plus ili minus beskonačnosti.
Jedan od osnovnih pojmova matematičke analize je granica funkcije I ograničenje niza u točki i u beskonačnosti, važno je znati točno riješiti granice. Uz našu uslugu to neće biti teško. Odluka je donesena ograničenja online u roku od nekoliko sekundi odgovor je točan i potpun. Proučavanje matematičke analize počinje s prijelaz do granice, granice koriste se u gotovo svim područjima više matematike, pa je korisno imati pri ruci poslužitelj za online limit rješenja, koja je stranica.
Za one koji žele naučiti kako pronaći granice, u ovom članku ćemo govoriti o tome. Nećemo ulaziti u teoriju; nastavnici je obično drže na predavanjima. Dakle, "dosadnu teoriju" trebate zabilježiti u svoje bilježnice. Ako to nije slučaj, onda možete čitati udžbenike preuzete iz knjižnice obrazovne ustanove ili s drugih internetskih izvora.
Dakle, koncept limita je vrlo važan u proučavanju više matematike, posebno kada naiđete na integralni račun i razumijete vezu između limita i integrala. Ovaj materijal će pogledati jednostavne primjere, kao i načine za njihovo rješavanje.
Primjeri rješenja
| Primjer 1 |
| Izračunajte a) $ \lim_(x \to 0) \frac(1)(x) $; b)$ \lim_(x \to \infty) \frac(1)(x) $ |
| Otopina |
|
a) $$ \lim \limits_(x \to 0) \frac(1)(x) = \infty $$ b)$$ \lim_(x \to \infty) \frac(1)(x) = 0 $$ Ljudi nam često šalju ta ograničenja sa zahtjevom da im pomognemo riješiti ih. Odlučili smo ih istaknuti kao zaseban primjer i objasniti da se ta ograničenja u pravilu samo trebaju zapamtiti. Ako ne možete riješiti svoj problem, pošaljite nam ga. Mi ćemo pružiti detaljno rješenje. Moći ćete vidjeti napredak izračuna i dobiti informacije. To će vam pomoći da na vrijeme dobijete ocjenu od svog učitelja! |
| Odgovor |
| $$ \text(a)) \lim \limits_(x \to 0) \frac(1)(x) = \infty \text( b))\lim \limits_(x \to \infty) \frac(1 )(x) = 0 $$ |
Što učiniti s nesigurnošću oblika: $ \bigg [\frac(0)(0) \bigg ] $
| Primjer 3 |
| Riješite $ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) $ |
| Otopina |
|
Kao i uvijek, počinjemo zamjenom vrijednosti $ x $ u izraz ispod znaka granice. $$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = \frac((-1)^2-1)(-1+1)=\frac( 0)(0) $$ Što je sada sljedeće? Što bi se na kraju trebalo dogoditi? Budući da se radi o neizvjesnosti, ovo još nije odgovor i nastavljamo s izračunom. Budući da imamo polinom u brojnicima, faktorizirat ćemo ga pomoću formule poznate svima iz škole $$ a^2-b^2=(a-b)(a+b) $$. sjećaš li se odlično! Sada samo naprijed i iskoristi to uz pjesmu :) Nalazimo da je brojnik $ x^2-1=(x-1)(x+1) $ Nastavljamo rješavati uzimajući u obzir gornju transformaciju: $$ \lim \limits_(x \to -1)\frac(x^2-1)(x+1) = \lim \limits_(x \to -1)\frac((x-1)(x+ 1) ))(x+1) = $$ $$ = \lim \limits_(x \to -1)(x-1)=-1-1=-2 $$ |
| Odgovor |
| $$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = -2 $$ |
Pomaknimo granicu u zadnja dva primjera do beskonačnosti i razmotrimo nesigurnost: $ \bigg [\frac(\infty)(\infty) \bigg ] $
| Primjer 5 |
| Izračunajte $ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) $ |
| Otopina |
|
$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \frac(\infty)(\infty) $ Što učiniti? Što da radim? Ne paničarite, jer nemoguće je moguće. Potrebno je izbaciti x i u brojniku i u nazivniku, a zatim ga smanjiti. Nakon toga pokušajte izračunati granicu. Pokušajmo... $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) =\lim \limits_(x \to \infty) \frac(x^2(1-\frac (1)(x^2)))(x(1+\frac(1)(x))) = $$ $$ = \lim \limits_(x \to \infty) \frac(x(1-\frac(1)(x^2)))((1+\frac(1)(x))) = $$ Koristeći definiciju iz primjera 2 i zamjenjujući beskonačnost za x, dobivamo: $$ = \frac(\infty(1-\frac(1)(\infty)))((1+\frac(1)(\infty))) = \frac(\infty \cdot 1)(1+ 0) = \frac(\infty)(1) = \infty $$ |
| Odgovor |
| $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \infty $$ |
Algoritam za izračunavanje granica
Dakle, sažmimo ukratko primjere i izradimo algoritam za rješavanje granica:
- Zamijenite točku x u izraz iza znaka granice. Ako se dobije određeni broj ili beskonačnost, tada je limit potpuno riješen. U suprotnom, imamo nesigurnost: "nula podijeljena s nulom" ili "beskonačno podijeljeno s beskonačnom" i prijeđite na sljedeće točke uputa.
- Da biste eliminirali nesigurnost "nule podijeljene s nulom", trebate faktorizirati brojnik i nazivnik. Smanjite slične. Zamijenite točku x u izraz ispod znaka granice.
- Ako je nesigurnost "beskonačnost podijeljena s beskonačnošću", tada izbacujemo i brojnik i nazivnik x do najvećeg stupnja. Skraćujemo X-ove. Zamjenjujemo vrijednosti x ispod granice u preostali izraz.
U ovom ste članku naučili osnove rješavanja granica, koje se često koriste u tečaju Računa. Naravno, ovo nisu sve vrste zadataka koje nude ispitivači, već samo najjednostavnije granice. O drugim vrstama zadataka govorit ćemo u budućim člancima, ali prvo morate naučiti ovu lekciju kako biste krenuli naprijed. Raspravljajmo o tome što učiniti ako postoje korijeni, stupnjevi, proučavajmo infinitezimalne ekvivalentne funkcije, izvanredne granice, L'Hopitalovo pravilo.
Ako ne možete sami odrediti granice, nemojte paničariti. Uvijek nam je drago pomoći!
Pojmovi limita nizova i funkcija. Kada je potrebno pronaći limes niza, piše se na sljedeći način: lim xn=a. U takvom nizu nizova, xn teži a, a n teži beskonačno. Niz se obično predstavlja kao niz, na primjer:
x1, x2, x3...,xm,...,xn... .
Nizovi se dijele na rastuće i opadajuće. Na primjer:
xn=n^2 - rastući niz
yn=1/n - niz
Tako, na primjer, granica niza xn=1/n^ :
lim 1/n^2=0
x→∞
Ova granica je jednaka nuli, jer n→∞, a niz 1/n^2 teži nuli.
Tipično, varijabilna veličina x teži konačnoj granici a, a x se stalno približava a, a veličina a je konstantna. Ovo se piše na sljedeći način: limx =a, dok n također može težiti nuli ili beskonačnosti. Postoje beskonačne funkcije, za koje granica teži beskonačnosti. U drugim slučajevima, kada, na primjer, funkcija usporava vlak, granica teži nuli.
Granice imaju niz svojstava. Tipično, svaka funkcija ima samo jedno ograničenje. Ovo je glavno svojstvo granice. Ostali su navedeni u nastavku:
* Limit iznosa jednak je zbroju limita:
lim(x+y)=lim x+lim y
* Granica proizvoda jednaka je umnošku granica:
lim(xy)=lim x*lim y
* Granica kvocijenta jednaka je kvocijentu granica:
lim(x/y)=lim x/lim y
* Konstantni faktor uzet je izvan graničnog znaka:
lim(Cx)=C lim x
Zadana je funkcija 1 /x u kojoj je x →∞, njezina granica je nula. Ako je x→0, granica takve funkcije je ∞.
Za trigonometrijske funkcije postoje neka od ovih pravila. Budući da funkcija sin x uvijek teži jedinici kada se približava nuli, za nju vrijedi identitet:
lim sin x/x=1
U nizu funkcija postoje funkcije kod kojih se kod izračuna granica javlja nesigurnost - situacija u kojoj se granica ne može izračunati. Jedini izlaz iz ove situacije je L'Hopital. Postoje dvije vrste neizvjesnosti:
* nesigurnost oblika 0/0
* nesigurnost oblika ∞/∞
Na primjer, data je granica sljedećeg oblika: lim f(x)/l(x), i f(x0)=l(x0)=0. U tom slučaju nastaje nesigurnost oblika 0/0. Da bi se riješio takav problem, obje se funkcije diferenciraju, nakon čega se nalazi granica rezultata. Za nesigurnosti tipa 0/0, granica je:
lim f(x)/l(x)=lim f"(x)/l"(x) (pri x→0)
Isto pravilo vrijedi i za nesigurnosti tipa ∞/∞. Ali u ovom slučaju vrijedi sljedeća jednakost: f(x)=l(x)=∞
Koristeći L'Hopitalovo pravilo, možete pronaći vrijednosti svih granica u kojima se pojavljuju nesigurnosti. Preduvjet za
volumen - nema grešaka pri pronalaženju izvedenica. Tako je, na primjer, derivacija funkcije (x^2)" jednaka 2x. Odavde možemo zaključiti da:
f"(x)=nx^(n-1)
Teorija granica- jedan od dijelova matematičke analize koji neki mogu savladati, dok drugi imaju poteškoća u izračunavanju granica. Pitanje pronalaženja granica prilično je općenito, budući da postoje deseci tehnika granice rješenja razne vrste. Iste granice mogu se pronaći i korištenjem L'Hopitalovog pravila i bez njega. Događa se da vam raspoređivanje niza infinitezimalnih funkcija omogućuje brzo postizanje željenog rezultata. Postoji niz tehnika i trikova koji vam omogućuju da pronađete granicu funkcije bilo koje složenosti. U ovom ćemo članku pokušati razumjeti glavne vrste ograničenja koja se najčešće susreću u praksi. Ovdje nećemo davati teoriju i definiciju granice; na Internetu se o tome govori mnogo izvora. Stoga, bacimo se na praktične izračune, ovdje su nas učili "ne znam!"
Izračunavanje limita metodom supstitucije
Primjer 1. Pronađite limit funkcije
Lim((x^2-3*x)/(2*x+5),x=3).
Rješenje: Primjeri ove vrste mogu se teoretski izračunati koristeći uobičajenu zamjenu
Limit je 18/11.
U takvim granicama nema ništa komplicirano ni mudro - zamijenili smo vrijednost, izračunali je i kao odgovor zapisali granicu. Međutim, na temelju takvih ograničenja, svi su poučeni da prije svega trebaju zamijeniti vrijednost u funkciju. Nadalje, granice postaju kompliciranije, uvodeći koncept beskonačnosti, neizvjesnosti i slično.
Granica s neizvjesnošću poput beskonačnosti podijeljene s beskonačnošću. Tehnike otkrivanja neizvjesnosti
Primjer 2. Pronađite limit funkcije
Lim((x^2+2x)/(4x^2+3x-4),x=beskonačno).
Rješenje: dana je granica polinoma oblika podijeljenog s polinomom, a varijabla teži beskonačnosti ![]()
Jednostavna zamjena vrijednosti do koje treba pronaći varijablu neće pomoći u pronalaženju granica; dobit ćemo nesigurnost oblika beskonačno podijeljeno na beskonačnost.
Prema teoriji granica, algoritam za izračun granice je pronaći najveću potenciju "x" u brojniku ili nazivniku. Zatim se brojnik i nazivnik pojednostavljuju na to i nalazi se granica funkcije 
Budući da vrijednost teži nuli kada se varijabla približi beskonačnosti, one se zanemaruju, odnosno upisuju u konačni izraz u obliku nula 
Odmah iz prakse možete dobiti dva zaključka koji su nagovještaj u izračunima. Ako varijabla teži beskonačnosti, a stupanj brojnika je veći od stupnja nazivnika, tada je granica jednaka beskonačnosti. Inače, ako je polinom u nazivniku višeg reda nego u brojniku, granica je nula.
Granica se može napisati formulama poput ove: 
Ako imamo funkciju oblika običnog polja bez razlomaka, tada je njezin limit jednak beskonačnosti ![]()
Sljedeća vrsta ograničenja tiče se ponašanja funkcija blizu nule.
Primjer 3. Pronađite limit funkcije
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Rješenje: Ovdje nema potrebe uklanjati vodeći faktor polinoma. Upravo suprotno, potrebno je pronaći najmanju potenciju brojnika i nazivnika i izračunati granicu ![]()
x^2 vrijednost; x teže nuli kada varijabla teži nuli, stoga se zanemaruju, pa dobivamo ![]()
da je granica 2,5.
Sada znate kako pronaći limit funkcije oblika, podijelite polinom s polinomom ako varijabla teži beskonačnosti ili 0. Ali ovo je samo mali i laki dio primjera. Iz sljedećeg materijala naučit ćete kako otkriti nesigurnosti u granicama funkcije.
Granica s nesigurnošću tipa 0/0 i metode njezina izračuna
Svi se odmah sjećaju pravila da ne možete dijeliti s nulom. Međutim, teorija granica u ovom kontekstu podrazumijeva infinitezimalne funkcije.
Pogledajmo nekoliko primjera radi jasnoće.
Primjer 4. Pronađite limit funkcije
Lim((3x^2+10x+7)/(x+1), x=-1).
Rješenje: Kada u nazivnik zamijenimo vrijednost varijable x = -1, dobijemo nulu, a isto to dobijemo i u brojniku. Tako da imamo nesigurnost oblika 0/0.
Suočavanje s takvom nesigurnošću je jednostavno: potrebno je rastaviti polinom na faktore, odnosno odabrati faktor koji pretvara funkciju u nulu. 
Nakon proširenja, granica funkcije može se napisati kao 
To je cijela metoda za izračunavanje limita funkcije. Isto radimo ako postoji granica polinoma oblika podijeljenog s polinomom.
Primjer 5. Pronađite limit funkcije
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Rješenje: Izravna zamjena pokazuje
2*4-7*2+6=0;
3*4-2-10=0
što imamo vrsta 0/0 nesigurnosti.
Podijelimo polinome faktorom koji uvodi singularitet ![]()
![]()
Ima učitelja koji uče da se polinome 2. reda, odnosno tipa “kvadratne jednadžbe”, treba rješavati preko diskriminante. Ali stvarna praksa pokazuje da je to duže i zbunjujuće, stoga se riješite značajki unutar ograničenja prema navedenom algoritmu. Dakle, funkciju zapisujemo u obliku jednostavnih faktora i izračunavamo je u limitu 
Kao što vidite, nema ništa komplicirano u izračunavanju takvih granica. Dok proučite limite, znate dijeliti polinome, barem po programu ste ga već trebali položiti.
Među zadacima na vrsta 0/0 nesigurnosti Postoje neki u kojima morate koristiti skraćene formule množenja. Ali ako ih ne znate, tada dijeljenjem polinoma s monomom možete dobiti željenu formulu.
Primjer 6. Pronađite limit funkcije
Lim((x^2-9)/(x-3), x=3).
Rješenje: Imamo nesigurnost tipa 0/0. U brojniku koristimo formulu skraćenog množenja ![]()
i izračunajte traženi limit ![]()
Metoda otkrivanja nesigurnosti množenjem njezinim konjugatom
Metoda se primjenjuje na granice u kojima nesigurnost generiraju iracionalne funkcije. Brojnik ili nazivnik pretvaraju se u nulu u točki izračuna i ne zna se kako pronaći granicu.
Primjer 7. Pronađite limit funkcije
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Otopina: Predstavimo varijablu u formuli limita
Kod zamjene dobivamo nesigurnost tipa 0/0.
Prema teoriji granica, način da se zaobiđe ova značajka je množenje iracionalnog izraza njegovim konjugatom. Kako bi se osiguralo da se izraz ne mijenja, nazivnik se mora podijeliti s istom vrijednošću 
Koristeći pravilo razlike kvadrata, pojednostavljujemo brojnik i izračunavamo limit funkcije
Pojednostavljujemo pojmove koji stvaraju singularnost u limitu i izvodimo zamjenu
Primjer 8. Pronađite limit funkcije
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Rješenje: Izravna supstitucija pokazuje da granica ima singularitet oblika 0/0. ![]()
Da bismo proširili, množimo i dijelimo s konjugatom brojnika 
Zapisujemo razliku kvadrata
Pojednostavljujemo pojmove koji uvode singularitet i nalazimo limit funkcije
![]()
Primjer 9. Pronađite limit funkcije
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Rješenje: Zamijenite dva u formulu ![]()
Dobivamo nesigurnost 0/0.
Nazivnik se mora pomnožiti s konjugiranim izrazom, au brojniku kvadratna jednadžba mora biti riješena ili faktorizirana, uzimajući u obzir singularitet. Budući da je poznato da je 2 korijen, drugi korijen nalazimo pomoću Vietinog teorema
Dakle, zapisujemo brojnik u obliku ![]()
i zamijenite ga u limit
Smanjenjem razlike kvadrata rješavamo se singularnosti u brojniku i nazivniku
Koristeći gornju metodu, moguće je riješiti se singularnosti u mnogim primjerima, a primjenu treba primijetiti gdje god se zadana razlika korijena pretvara u nulu tijekom supstitucije. Ostale vrste ograničenja odnose se na eksponencijalne funkcije, infinitezimalne funkcije, logaritme, posebne granice i druge tehnike. Ali o tome možete pročitati u dolje navedenim člancima o ograničenjima.
 Rješavanje usporedbi prvog stupnja
Rješavanje usporedbi prvog stupnja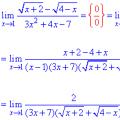 Limit sekvence i funkcije
Limit sekvence i funkcije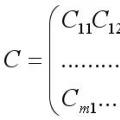 Označavanje elemenata matrice
Označavanje elemenata matrice