"primjena svojstava funkcije u rješavanju jednadžbi i nejednadžbi". „Rješenje jednadžbi nestandardnim metodama, korištenjem svojstava funkcija

Tema: Metode korištenja ograničenih funkcija.
Život je dobar zato što je možeš raditi matematiku. (Leonhard Euler)Ciljevi: razvoj novog razmišljanja izvan okvira koje se može uspješno primijeniti u drugim područjima ljudska aktivnost(kibernetika, računalna tehnologija, ekonomija, radiofizika, kemija itd.).
Zadaci: - osposobljenost za procjenu objektivne i subjektivne težine zadataka i razumnog izbora tih zadataka na ispitu;

Stvaranje "kasice-prasice" netradicionalnog i neobičnog zaključivanja.

Tijekom nastave:

Org. trenutak. Formuliranje teme lekcije od strane učenika ispunjavanjem zadataka Jedinstvenog državnog ispita dijelova A i B i dekodiranjem teme u padajućem redoslijedu dobivenih odgovora. (Prema očekivanim riječima, šifrirajte 12 kartica s brojevima od -2 do 10) (Dodatak 1 i 2)

ograničenja

2. Podijelite učenike u 2 grupe, zadajte im skup "Teorija + 10 zadataka" (Prilog 3 i 4), zamolite ih da odaberu one zadatke koje je moguće riješiti u ovom teorijskom dijelu, opravdati svoj izbor.3. Pokažite napredak ovih zadataka na ploči učenika: Noskova K., Dedevshin I., Veselov I.4. Podijelite zadatke s kartice u 2 grupe kako biste ih riješili, nakon čega slijedi samoprovjera na listu gotova rješenja. (Prilog 5)5. Podijelite listove grupama s opisom novih nestandardnih metoda za rješavanje jednadžbi i nejednadžbi za odabir sljedeća tema(kao domaći zadatak za pronaći u zbirkama UPOTREBA zadataka, koji se može riješiti ovom metodom) (Prilog 6)6. Refleksija učenika (ispunjavanje tablice) F.I. student

Dodatak 1.
Riješite ove zadatke i rasporedite odgovore silaznim redoslijedom, prikupite temu naše lekcije prema odgovorima.

Pronađite apscisu točke grafa funkcije y \u003d 3x 2 -7x + 7, u kojoj je tangent kuta tangente -1.

Dodatak 2
9 2 0 7Istraživanje funkcija uz pomoć derivacije. 10 5 1 -1 Metoda korištenja ograničenih funkcija. 4 -2 8 12 Rješavanje nejednadžbi grafički.
3 11 6Rješenja funkcionalnih jednadžbi.
Studija

Dodatak 3

Jedan od učinkovite metode rješavanje jednadžbi ili nejednadžbi je metoda koja se temelji na korištenju ograničenih funkcija. Najpoznatijem ograničene funkcije uključuju, na primjer, neke trigonometrijske; obrnuto trigonometrijske funkcije; funkcije koje sadrže modul, stupanj, korijen c čak i stupanj drugo.

Najčešće nejednakosti su:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

, a f ( x ) >0, (f(x) ± g(x))2n ≥ 0,
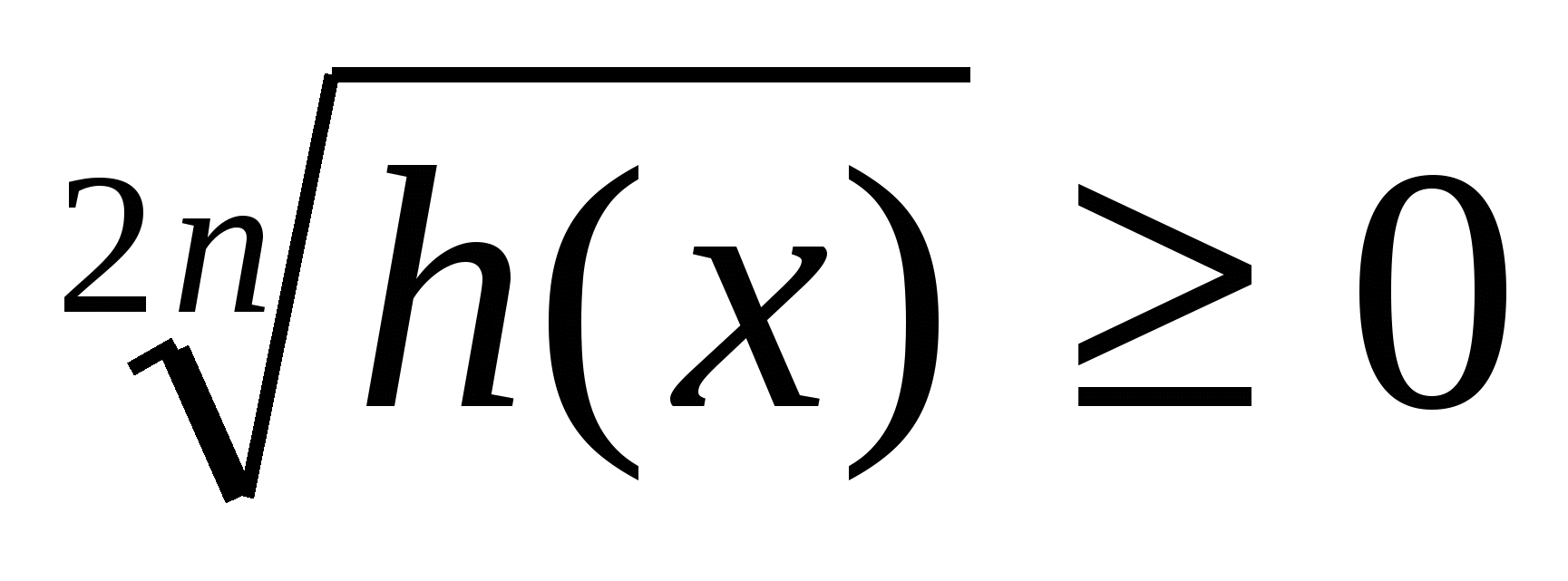, a+ ≥ 2, b+ ≤ -2 i mnogi drugi. Ovdje n -prirodni broj, h(x) ≥ 0, a>0, b 0.

Osim gore navedenih najjednostavnijih nejednakosti, postoje i one složenije, posebno, trigonometrijske nejednakosti -,

,

te nejednakosti s modulima oblika
.

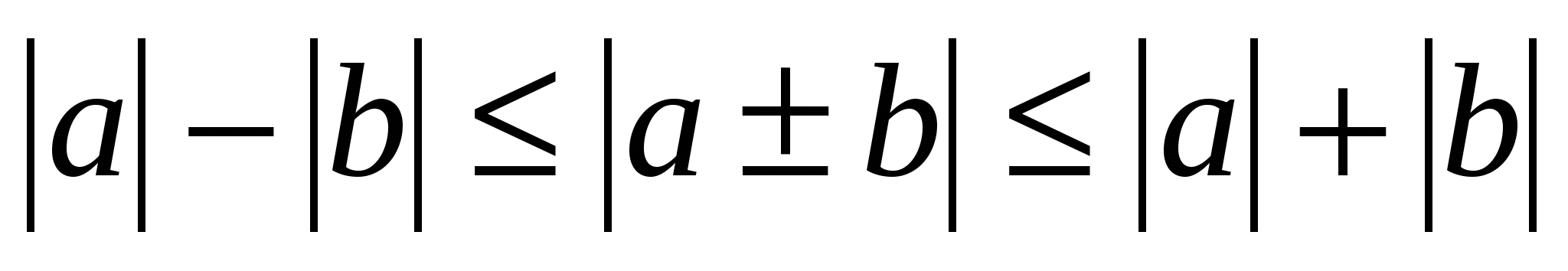Primjer 1Riješite jednadžbu:

Odluka: izdvojiti pun kvadrat na desnoj strani jednadžbe, tj. . Otuda slijedi da
. Budući da se u isto vrijeme grijeh π x ≤ 1, tada dobivamo sustav jednadžbi

Rješavajući drugu jednadžbu sustava, dobivamo da je x=. Zamjenom u prvu jednadžbu osiguravamo da je pronađena vrijednost x rješenje sustava, što znači da je rješenje izvorne jednadžbe.

Odgovor: x=.

Primjer 2Riješite jednadžbu:

Odluka: budući da Međutim sin2 π x ≤ 1. Dakle, 5+4 sin2 π x ≤ 9. Tako dobivamo sustav jednadžbi:

Odavde dobivamo sustav jednadžbi
, iz prve jednadžbe nalazimo x \u003d. Zamijenite ga u drugu jednadžbu sustava i uvjerite se da je x= rješenje sustava, a time i rješenje izvorne jednadžbe.

Odgovor: x=

Dodatak 4 S predloženog popisa zadataka odaberite one koji se mogu riješiti metodom ograničenih funkcija. 1. Riješite jednadžbu x 2 -4 x=(2-cos
2. Pronađite količinu cjelobrojna rješenja nejednakosti x 2ctg 2
3. Riješite jednadžbu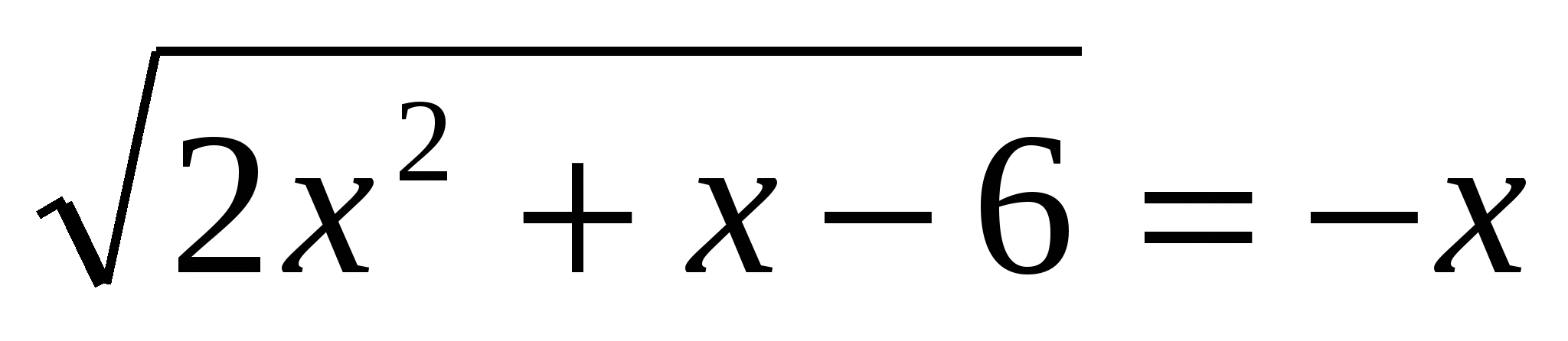
4. Riješite jednadžbu 3-(5. Pronađite broj cjelobrojnih rješenja nejednakosti 16-x 2 ≥0 koja zadovoljavaju uvjet 3 tg 2
6. Riješite jednadžbu
7. Riješite jednadžbu -25x 2 +40x-23 = ( cos
8. Pronađite umnožak korijena jednadžbe x
9. Riješite jednadžbu
10. Riješite jednadžbu 3- jer 2

List za samoprovjeru. Dodatak 5 1. riješiti jednadžbu Rješenje: jer , zatim od i onda
dobivamo sustav jednadžbi

rješavamo prvu jednadžbu, dobivamo x = , tu vrijednost zamjenjujemo u drugu jednadžbu

2 . riješiti jednadžbu 3- cos 2 Rješenje: jer , zatim od i onda
dobivamo sustav jednadžbi

rješavamo drugu jednadžbu, dobivamo x \u003d, zamijenimo ovu vrijednost u prvoj jednadžbi

pa je x= rješenje izvorne jednadžbe. Odgovor: x=
3 . Pronađite broj cjelobrojnih rješenja nejednadžbe x 2 +7h-8≤0 zadovoljavajući uvjet ctg 2 a zatim, za bilo koje dopuštene vrijednosti x, nalazimo nule kvadratnog trinoma, prema Vietinom teoremu, rješavamo nejednakost metodom intervala
zatim. mi to znamo
cjelobrojne vrijednosti x su brojevi koje isključujemo. Odgovor: 8 cjelobrojnih rješenja 4 . Pronađite broj cjelobrojnih rješenja 16-x nejednadžbe 2 ≥0 koja zadovoljavaju uvjet 3 tg 2 a zatim za sve dopuštene vrijednosti x Nađite nule izraza, x= i x= Riješite nejednakost koristeći intervalnu metodu
zatim. mi to znamo

cjelobrojne vrijednosti x su brojevi koje isključujemo. Odgovor: 7 cjelobrojnih rješenja
Dodatak 6

Metoda korištenja monotonosti funkcija. Prilikom rješavanja jednadžbe tipa f (x) = g (x) u nekim slučajevima učinkovita je metoda koja koristi monotonost funkcija y = f (x) i y = g (x). Ako je funkcija y = f (x ) je kontinuiran i raste (opada) na intervalu a≤ x ≤ b, a funkcija y = g (x) je kontinuirana i smanjuje se (povećava) na istom segmentu, tada je jednadžba f (x) = g (x) na segmentu a≤ x ≤ b ne može imati više od jednog korijena, tada je potrebno ili pokušati izborom pronaći jedinstveni korijen jednadžbe ili pokazati da takav korijen ne postoji. Ova metoda je posebno učinkovita u slučaju kada su oba dijela jednadžbe f(x)=g(x) "nezgodna" za zajedničko proučavanje funkcije. Komentar: Ako je funkcija y= f(x) raste, a funkcija y= g(x) opada za a≤ x ≤ b i pri čemu f(a)>g(a), zatim korijeni jednadžbe među a≤ x ≤ b Ne.

Primjer: riješiti jednadžbuOdluka: Raspon valjanih vrijednosti jednadžbe je x
. Lako je vidjeti da se na ovom području lijeva strana jednadžbe povećava, a desna smanjuje, t.j. funkcijaf(x)=
raste, a funkcijag(x)=
- opadajući. U tom smislu, izvorna jednadžba može imati samo jedan korijen (ako postoji). Odabirom nalazimo ovaj korijen jednadžbe x= 2.Odgovor: x=2
Metoda rješavanja funkcionalnih jednadžbi. Među najvećim izazovni zadaci USE uključuje zadatke čije se rješavanje svodi na razmatranje funkcionalnih jednadžbi oblika f(f(….f(x)…))=x ili f(g(x))=f(h(x)), gdje su f(x),g(x),h(x) neke funkcije i n≥ 2
Metode rješavanja ovih funkcionalnih jednadžbi temelje se na primjeni mnogih teorema, razmotrimo jedan od njih.
Teorem 1. Korijeni jednadžbe f(x)=0 su korijeni jednadžbe f(f(….f(x)…))=x
Primjer: Riješite jednadžbu x=
, gdje Korijen zauzeto jenputa in≥ 1 Odluka: Iz uvjeta zadatka slijedi da je x> 0. Nekaf(x)=
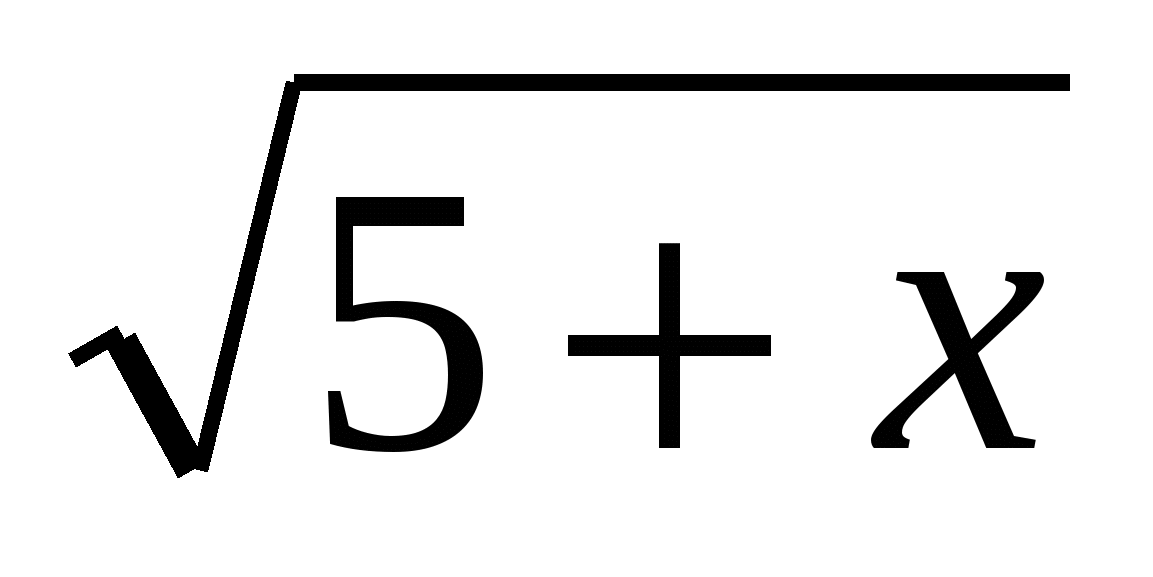, tada se naša jednadžba može predstaviti kao funkcionalna f( f(…. f( x)…))= x. Budući da za x> 0 funkcijaf(x)= povećava if(x) > 0, tada je jednadžba x= ekvivalentna jednadžbif(x)= x, tj. \u003d x, čije je pozitivno rješenje x \u003d
Odgovor: x=

Pripremio i vodi profesor matematike

MKOU "Srednja škola br. 1", Povorino

Voronješka regija

Kartashova S. A.

2014

Tema lekcije:„Rješavanje jednadžbi nestandardne metode, koristeći svojstva funkcija"

Oblik lekcije je predavanje nakon kojeg slijedi pojačanje. Dizajniran za 2 lekcije

(Slajd #1)

Ciljevi lekcije:

Ponoviti i sažeti znanje na temu: "Svojstva funkcija"

Naučiti primijeniti funkcionalnu metodu rješavanja jednadžbi

Razviti logično mišljenje, promatranje

Njegovati aktivnost, kreativnu inicijativu.

(slajd broj 2)

Oprema: interaktivna ploča, računalo s prezentacijom.

Plan učenja:

Organiziranje vremena.

Motivacija aktivnosti učenja(poruka teme, ciljevi sata).

Aktualizacija temeljnih znanja (ponavljanje svojstava glavnih funkcija).

Učenje novog gradiva (funkcionalna metoda rješavanja jednadžbi).

Učvršćivanje znanja (rješavanje vježbi).

Rezimirajući. Procjene.

Tijekom nastave.

Učitelj, nastavnik, profesor:

Za rješavanje većine jednadžbi koje se susreću na ispitima dovoljno je savladati školski kolegij matematike, ali je u isto vrijeme potrebno biti sposoban rješavati ne samo standardnim tehnikama dizajniranim za potpuno određene vrste jednadžbe, ali i „nestandardne“ metode o kojima ćemo danas na satu. Jedna od takvih metoda za rješavanje jednadžbi je funkcionalna, koja se temelji na korištenju svojstava funkcija. Za razliku od grafička metoda, poznavanje svojstava funkcija omogućuje vam da pronađete točne korijene jednadžbe, bez potrebe za crtanjem grafova funkcija. Korištenje svojstava funkcija pridonosi racionalizaciji rješenja jednadžbi.

(slajd broj 3)

Odgovorit ćemo na pitanja:

Što je jednadžba?

Koji je korijen jednadžbe?

Što znači riješiti jednadžbu?

Što se zove funkcija?

Koji je opseg funkcije?

Koji je opseg funkcije?

(slajd broj 4)

Smatrati(slajd broj 5)

PRIMJER 1. Riješite jednadžbu:

Rješenje: ODZ:

Odgovor: Ne postoje rješenja.

(slajd broj 6)

PRIMJER 2. Riješite jednadžbu:

Rješenje: ODZ:

ODZ se sastoji od jedne točke x=1. Ostaje provjeriti je li x=1 korijen jednadžbe. Zamjenom vidimo da je x=1 korijen jednadžbe.

Odgovor: x=1.

Učitelj, nastavnik, profesor:

Ponekad se pokaže da je dovoljno uzeti u obzir ne cijelu domenu funkcije, već samo njezin podskup, na kojem funkcija uzima vrijednosti koje zadovoljavaju određene uvjete (na primjer, samo nenegativne vrijednosti)

(slajd br. 7 )

PRIMJER 3.

Odluka. Nađimo sjecište područja definicija funkcija u desnom i lijevom dijelu jednadžbe:

D 1

Ograničimo skupD, s obzirom na to da je lijeva strana jednadžbe nenegativna, pa bi prema tome ista trebala biti desni dio Yu Da biste to učinili, razmotrite sjecište skupaDs mnogo rješenja nejednakosti , odnosno s mnogima . Stoga je dovoljno razmotriti jednadžbu na skupu .

Zamjenom osiguravamo da oba elementa služe kao rješenje jednadžbe.

Odgovor: -3; 2.

(slajd br. 8 )

PRIMJER 4.

Odluka.

Uzimajući u obzir činjenicu da korijen jednadžbe je x=4.

Odgovor: 4.

Učitelj, nastavnik, profesor:

Prijeđimo na rješavanje jednadžbi koristeći koncept raspona funkcije.

(slajd #9-#10)

(slajd broj 11)

PRIMJER 1.

Odluka. Kao , tada jednadžba nema rješenja.

Odgovor: nema rješenja.

PRIMJER 2.

Odluka. ODZ:

Odgovor: nema rješenja.

Učitelj, nastavnik, profesor:

Ako je funkcija f ( x ) na intervalu X omeđena je odozgo, a funkcija g ( x ) ograničena je odozdo, onda jednadžba f ( x ) = g ( x ) je ekvivalentan sustavu

(slajd broj 12)

PRIMJER 3.

Odluka. A-priorat,

Jednakost se postiže ako

Riješimo prvu jednadžbu sustava:

arccos(x-1)=π, x-1=-1, x=0.

Kod x=0 druga se jednadžba pretvara u točnu brojčanu jednakost.

Stoga je rješenje sustava i ove jednadžbe x=0.

Odgovor: 0.

(slajd №13-14)

PRIMJER 4.

Odluka.

Nađimo maksimum ove funkcije na intervalu (2;4) koristeći derivaciju.

= 0,

g' + -

g 2 3 4 x

Maks

g(3)=2.Imamo

Zatim zadana jednadžba jednako je sustavu

Nakon što smo riješili prvu jednadžbu sustava, dobivamo x = 3, provjerom, zamjenom u drugu jednadžbu, uvjerit ćemo se da je x = 3 rješenje sustava i ove jednadžbe.

Odgovor: 3.

(slajd broj 15)

Učitelj, nastavnik, profesor:

Ova metoda se često nalazi na ispitu iz matematike. Ova metoda sastoji se u tome da je jedan dio jednadžbe odozgo omeđen određenim brojem M, a drugi dio jednadžbe odozdo omeđen istim brojem M. Broj M obično se nazivamajorant a ova metoda jemajorantna metoda . U majorantnoj metodi, kao što ste možda pogodili, morate dobro razumjeti što je funkcija, biti u stanju istražiti svojstva funkcija.

(slajd broj 16)

Vježbe za učvršćivanje, razvoj vještina i sposobnosti.

Razred je podijeljen u 2 grupe prema mogućnostima.

1 opcija.

Dokažite da jednadžba nema korijena.

Riješite jednadžbe: Odgovor: 2.6.

Odgovor: 2.

Učitelj, nastavnik, profesor:

Danas smo razmatrali nestandardnu ​​metodu rješavanja jednadžbi pomoću svojstava funkcija, koja je primjenjiva i za rješavanje nejednakosti, ali o tome ćemo govoriti u nekoliko narednih lekcija.

Sumiranje, evaluacija.

(slajd broj 17)

Domaća zadaća:

"Opseg funkcije" - Opseg definicije kvadratna funkcija- bilo koji pravi broj. Funkcija se zove logaritamska ako varijabla stoji pod znakom logaritma. logaritamska funkcija. Funkcija čija se varijabla nalazi u eksponentu naziva se eksponencijalna. Kvadratna funkcija.

"Opća svojstva funkcija" - Opća svojstva funkcije. Pronađite opseg funkcije. Ravnomjerna funkcija. Je li ova funkcija parna ili neparna. Odredite skup vrijednosti funkcije iz grafa. Iz grafa odredite vrijednosti X. Iz grafa odredite intervale opadajuće funkcije. Funkcija f(x) raste. Zadana je funkcija y=f(x).

"Povećanje i smanjenje funkcije" - Povećanje i smanjenje funkcije sinusa. Razmotrimo još jedan primjer. Intervali padajućeg kosinusa su segmenti, n je cijeli broj. Neka je, na primjer, funkcija f parna i raste na intervalu , gdje je b>a?0. Povećajuće i opadajuće funkcije. Povećana i opadajuća kosinusna funkcija. Slika ispod prikazuje graf funkcije definirane na segmentu [-1;10].

"Primjena kontinuiteta" - Značenje izraza. geometrijski smisao izvedenica. intervalna metoda. Napišite jednadžbu za tangentu na graf funkcije. Tangenta na graf funkcije. Graf je blizu tangente. Formula. Izračunajmo po formuli. Tangenta na krivulju u danoj točki M je granični položaj sekante NM. Hiperbola.

"Ekstremum funkcije" - Ovisnost tlaka plina o temperaturi. Tema sata: „Znakovi rastućih i opadajućih funkcija. Test. Promjena jačine struje kada se krug otvori. Istraživanje funkcije do ekstrema”. Promijeniti naizmjenična struja. Plan: Ovisnost jačine struje o naponu. Ovisnost tlaka plina o volumenu. Tema: „Znakovi rastućih i opadajućih funkcija.

"Funkcije i njihova svojstva" - Nezavisna varijabla se zove - argument. Povećanje funkcije. Definicija funkcije. Čak i neparne funkcije. Monotonost funkcije. Vrijednosti zavisne varijable nazivaju se vrijednostima funkcije. Sve vrijednosti nezavisne varijable čine domenu funkcije -D (f). 1. Vrijednosti funkcije su pozitivne.

Ukupno u temi 23 prezentacije

Neobavezna aktivnost"Primjena svojstva ograničene funkcije"

Materijal koji se odnosi na jednadžbe i nejednakosti čini značajan dio školskog kolegija matematike, ali nam vremenski okvir sata ne dopušta razmatranje svih pitanja.

Osim toga, utvrđuje se obvezni minimum sadržaja nastave matematike, utvrđen državnim standardom za osnovnu školu edukativni materijal za obvezno razmatranje, ali ne i za obveznu asimilaciju (npr. nestandardne metode za rješavanje jednadžbi i nejednadžbi, metode za rješavanje jednadžbi i nejednadžbi s parametrom itd.).

S obzirom na važnost i obimnost materijala povezanog s pojmovima jednadžbi i nejednačina, njihovo proučavanje u moderna metodologija matematika je organizirana u sadržajno-metodičku liniju – red jednadžbi i nejednakosti. Postoje tri glavna smjera za postavljanje ove linije u školski tečaj matematika.

Primijenjena orijentacija linije jednadžbi i nejednadžbi otkriveno uglavnom u studiji algebarska metoda rješenja problemi s riječima. Jednadžbe i nejednadžbe glavni su dio matematičkih alata koji se koriste u rješavanju riječnih zadataka.

Teorijsko-matematičko usmjerenje otkriva se u dva aspekta: u proučavanju najvažnijih klasa jednadžbi, nejednadžbi i njihovih sustava, te u proučavanju generaliziranih pojmova i metoda vezanih uz pravac u cjelini.

Linija jednadžbi i nejednadžbi također je usko povezana s funkcionalnom linijom. S jedne strane, primjena metoda razvijenih u nizu jednadžbi i nejednakosti na proučavanje funkcije. S druge strane, funkcionalna linija ima značajan utjecaj kako na sadržaj linije jednadžbi i nejednakosti, tako i na stil njezina proučavanja. Konkretno, funkcionalni prikazi služe kao osnova za privlačenje grafičke vizualizacije u rješavanje i proučavanje jednadžbi i nejednačina.

U kolegiju algebre, koji proučavamo pod uredništvom Mordkovicha, kao prioritet se bira funkcionalno-grafička linija. Sav materijal izgrađen je prema krutoj shemi: funkcija-transformacija-jednadžba.

Na ispitu se često nalaze zadaci koji se rješavaju pomoću svojstava funkcija. Stoga je preporučljivo ovaj materijal donijeti na izborne kolegije. Ali ipak, radije razmatram neke od ovih zadataka u nastavi, počevši od 9. razreda.

Primjena svojstava funkcija pri rješavanju jednadžbi i nejednadžbi

Korištenje ograničenog svojstva.

Korištenje opsega funkcije.

Korištenje monotonosti funkcija u rješavanju jednadžbi i nejednadžbi.

Koristeći koncept opsega funkcije.

- Korištenje svojstava parnih ili neparnih i periodičnosti funkcija.

SLAJD 2.

U mom govoru pojavila se samo jedna od nestandardnih metoda za rješavanje jednadžbi i nejednadžbi na temelju svojstva ograničenosti funkcija uključenih u jednadžbu (nejednakost). Zadaci koje predlažem mogu se uzeti u obzir u satima predviđenim za pripremu učenika za ispit (tri ili četiri sata), ili koristiti jedan ili dva zadatka po satu, također dati materijal može se koristiti u izbornoj nastavi (ili u izbornom kolegiju).

Već u 9. razredu, proučavajući svojstvo omeđenosti, skrećem pozornost na važnost ovog svojstva i mogućnost njegovog korištenja kada

Pronalaženje najmanje i najveće vrijednosti funkcije;

Pronalaženje skupa vrijednosti funkcije.

SLAJD3.

Razmatraju se rješenja nekih zadataka. Najprije treba ponoviti osnovne definicije. SLAJD 4.

Na SLAJDOVIMA 5-9 razmatraju se zadaci za pronalaženje najmanjih ili najvećih vrijednosti funkcije.

SLAJD 10.

Primjena svojstva ograničenosti funkcija na rješavanje jednadžbi i nejednadžbi.

1. METODA MAJORANT (METOD OCJENE)

Glavna ideja majorantne metode je sljedeća:

Neka imamo jednadžbu i postoji takav broj M, što za bilo koje x iz područja definicije https://pandia.ru/text/78/376/images/image003_26.gif" width="160" height="23">. Tada je jednadžba ekvivalentna sustavu https://pandia. ru/text/78 /376/images/image005_16.gif" width="96" height="35 src=">.

Odluka. Procijenimo obje strane jednadžbe.

Za sve vrijednosti x nejednakosti https://pandia.ru/text/78/376/images/image007_10.gif" width="188" height="59 src="> su točne.

Dobiveni sustav nema rješenja, budući da https://pandia.ru/text/78/376/images/image009_6.gif" width="20" height="20">

Primjer 1.2 ..gif" width="157" height="20">.gif" width="75" height="51 src=">.

Rješenje prve jednadžbe sustava su vrijednosti https://pandia.ru/text/78/376/images/image014_3.gif" width="201" height="48 src=">.

Stoga, sustavno rješenje.

Odgovor: .

Primjer 1.3. Riješite nejednakost https://pandia.ru/text/78/376/images/image016_0.gif" width="56" height="19">.gif" width="84" height="21">.gif " width="156 height=61" height="61">.

Obrnuta zamjena: x + 1 = 0 .

Odgovor: - 1.

Primjer 1.4. Pronađite sve vrijednosti parametara a, za svaku od kojih jednadžba ima rješenja. Pronađite ova rješenja.

Odluka.

Prepišimo jednadžbu u obliku . Za sve vrijednosti x izraz pa https://pandia.ru/text/78/376/images/image026_0.gif" width="87" height="19 src="> i ..gif" width="405" height="91">

Odgovor: https://pandia.ru/text/78/376/images/image031_0.gif" width="51" height="41 src=">

2. "UPOZNAJTE SE NA RUBI"

Varijanta majorantne metode su zadaci (“ susret na rubu”) u kojem skupovi vrijednosti lijevog i desnog dijela jednadžbe ili nejednadžbe imaju jedinstvenu zajednička točka, što je najveća vrijednost za jedan dio, a najmanja za drugi.

Kako početi rješavati takve probleme? Prije svega, donesi zadane jednadžbe ili nejednakost na više običan prizor: faktoringom, uklanjanjem modula, logaritama itd. Zatim morate ponovno pažljivo pročitati zadatak, pokušati nacrtati grafičku sliku funkcija uključenih u zadatak.

Primjer 2.1. Riješite jednadžbu.

Odluka. Korijen jednadžbe je lako pogoditi - to jest x= 1. Ali nije moguće dokazati njegovu jedinstvenost iz razmatranja monotonosti, jer ni lijeva ni desna strana jednadžbe nisu monotone funkcije. Ovdje se koristi druga ideja..gif" width="191" height="51">. Najveća vrijednost desne strane rezultirajuće jednadžbe je 1 i uzima se u točki x= 1..gif" width="185" height="52 src=">). Stoga lijeva strana doseže do x= 1 vlastiti najmanju vrijednost, što je također jednako 1. Zaključak: jednakost je zadovoljena ako i samo ako su oba dijela istovremeno jednaka 1, tj. x = 1.

Primjer 2.2. Riješite jednadžbu.

1 način.

Odluka: Imajte na umu da lijeva strana jednadžbe ne prelazi 1, dok desna strana nije manja od 1. Prema tome, izvorna jednadžba ima rješenje samo ako su obje strane jednake jedinici. To je moguće samo s .

Odgovor: .

2 način. Ova se jednadžba može riješiti grafički. Da bismo to učinili, izgradit ćemo grafove desnog i lijevog dijela jednadžbe u istom koordinatnom sustavu, tj. graf funkcije i graf funkcije https://pandia.ru/text/78/376/ images/image008_7.gif" width="37" height=" 19">.

Odgovor: .

Primjer 2. 3. Riješite jednadžbu https://pandia.ru/text/78/376/images/image042_0.gif" width="301" height="35 src=">

onda je ova jednadžba zadovoljena samo ako je sustav . Prva jednadžba sustava ima jedan korijen x= 1, ali ovaj korijen ne zadovoljava drugu jednadžbu. Dakle, sustav nema rješenja.

Odgovor: Æ

Primjer 2.4. Riješite jednadžbu https://pandia.ru/text/78/376/images/image045_0.gif" width="105" height="21">, tada lijeva strana jednadžbe uzima vrijednost od do 2.. gif" width=" 137" height="53">..gif" width="217" height="24"> ima rješenje.

Odluka.

Procijenimo obje strane nejednakosti. Da bismo to učinili, transformiramo desnu stranu nejednakosti odabirom cijelog kvadrata ..gif" width="71" height="19">.gif" width="121" height="24 src=">.gif " width="51" height ="41">(odnosno, postoji "sastanak na rubu").

Odgovor:

Primjer 2.6. Pronađite sve vrijednosti parametara a pod kojim jednadžba

Galaeva Ekaterina, učenica 11. razreda srednje škole broj 149 MAOU, Nižnji Novgorod

Djelo je primijenjene i istraživačke prirode. Radi cjelovitosti, studija je razmatrala sljedeća pitanja:

– Kako se svojstva funkcije odražavaju pri rješavanju jednadžbi i nejednadžbi?

– Koje se jednadžbe i nejednadžbe rješavaju kroz definiranje svojstava domene definicije, skupa vrijednosti, invarijantnosti?

– Koji je algoritam rješenja?

- Razmotreni su zadaci s parametrom predloženim u KIM materijalima u pripremi za ispit.

Ekaterina je u svom radu istraživala širok spektar zadataka i sistematizirala ih prema izgled.

Preuzimanje datoteka:

Pregled:

https://accounts.google.com

Naslovi slajdova:

Riješite nejednakost Rješenje. Funkcija f (x) = monotono raste na cijeloj realnoj liniji, a funkcija g (x) = monotono opada u cijeloj domeni definicije. Stoga je nejednakost f (x) > g (x) zadovoljena ako je x >

Hvala na pažnji!

Pregled:

Za korištenje pregleda prezentacija stvorite Google račun (račun) i prijavite se: https://accounts.google.com

Naslovi slajdova:

Primjena svojstava funkcije pri rješavanju jednadžbi i nejednačina Završio rad: Galaeva Ekaterina MBOU srednja škola br. 149 Moskovskog okruga Učenici 11 "A" razreda Voditelj: Fadeeva I. A. Nastavnica matematike

Glavni smjerovi: Proučavanje svojstava funkcije: monotonost, ograničenost, područje definicije i nepromjenjivost Naučiti glavne tvrdnje koje se najčešće koriste u rješavanju jednadžbi, nejednačina i sustava Rješavanje zadataka iz KIM materijala za pripremu ispita

Monotoničnost Funkcija se povećava ako veća vrijednost argument odgovara većoj vrijednosti funkcije. Funkcija se smanjuje ako veća vrijednost argumenta odgovara manjoj vrijednosti funkcije. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2

Tvrdnja 1. Ako je funkcija y \u003d f (x) monotona, tada jednadžba f (x) \u003d c ima najviše jedan korijen. x =2 f(x) = - monotono opadajuća, pa nema drugih rješenja. Odgovor: x=2

Tvrdnja 2. Ako je funkcija y \u003d f (x) monotono rastuća, a funkcija y \u003d g (x) monotono opadajuća, tada jednadžba f (x) \u003d g (x) ima najviše jedan korijen. 2 - x \u003d lg (x + 11) + 1 g (x) \u003d 2 - x se monotono smanjuje, a funkcija f (x) \u003d lg (x + 11) + 1 monotono raste u domeni, što znači da jednadžba f (x ) = g (x) ima najviše jedan korijen. Odabirom utvrđujemo da je x \u003d -1. Gornja tvrdnja potvrđuje jedinstvenost rješenja.

a) f (x) ≤ g (x) ako i samo ako je x ϵ (- ∞ ; x 0 ]; b) f (x) ≥ g (x) ako i samo ako je x ϵ [x 0; +∞). Vizualno značenje ove izjave je očito. Tvrdnja 3. Ako se funkcija y = f (x) monotono povećava na cijeloj realnoj liniji, funkcija y = g (x) monotono se smanjuje na cijeloj realnoj liniji i f (x 0) \u003d g (x 0), tada su sljedeće tvrdnje istinite:

Riješite nejednakost Rješenje. Funkcija f (x) = monotono raste na cijeloj realnoj liniji, a funkcija g (x) = monotono opada u cijeloj domeni definicije. Dakle, nejednakost f (x) > g (x) je zadovoljena ako je x > 2. Dodajmo domenu nejednadžbe. Tako dobivamo sistemski odgovor: (2; 5).

Tvrdnja 4. Ako je funkcija y = f (x) monotono rastuća, tada jednadžbe f (x) = x i f (f (x)) = x imaju isti skup korijena, bez obzira na broj ulaganja. Posljedica. Ako je n prirodan broj, a funkcija y \u003d f (x) monotono raste, tada jednadžbe f (x) = x i n puta imaju isti skup korijena.

Riješite jednadžbu. Odgovor: Odluka. Za x ≥1, desna strana jednadžbe nije manja od 1, a lijeva strana je manja od 1. Stoga, ako jednadžba ima korijene, tada je bilo koja od njih manja od 1. Za x ≤0, desna strana strana jednadžbe nije pozitivna, a lijeva strana je pozitivna, zbog činjenice da . Dakle, bilo koji korijen ove jednadžbe pripada intervalu (0; 1). Pomnožimo obje strane ove jednadžbe s x i podijelimo brojnik i nazivnik lijeve strane s x, dobivamo

Gdje je = . Označavajući kroz t, gdje je t 0, dobivamo jednadžbu = t. Razmotrimo funkciju f (t)= 1+ koja raste u svojoj domeni definicije. Rezultirajuća jednadžba se može napisati kao f (f (f (f (t))))= t , a prema posljedici izjave 4, ima isti skup rješenja kao i jednadžba f (t)= t , tj. jednadžba 1 + = t, odakle. jedini pozitivan korijen ovog kvadratnog s obzirom na jednadžbu je. Dakle, gdje, tj. , ili. Odgovor:

Tvrdnja 1. Ako je max f (x) = c i min g (x) = c, tada jednadžba f (x) = g (x) ima isti skup rješenja kao i sustav Ograničenost Maksimalna vrijednost lijeve strane je 1 i minimalna vrijednost na desnoj strani 1 , što znači da se rješenje jednadžbe može svesti na sustav jednadžbi: , iz druge jednadžbe nalazimo mogućeg kandidata x=0 , te se uvjeravamo da je rješenje prve jednadžbe . Odgovor: x=1 .

Riješite jednadžbu Rješenje. Budući da sin3x≤1 i cos4x≤1, lijeva strana ove jednadžbe ne prelazi 7. Može biti jednaka 7 ako i samo ako je odakle je k , n ϵ Z . Ostaje utvrditi postoje li cijeli brojevi k i n takvi da najnoviji sustav ima rješenja. Odgovor: Z

U problemima s nepoznatim x i parametrom a, pod područjem definicije podrazumijeva se skup svih uređenih parova brojeva (x; a), od kojih je svaki takav da nakon zamjene odgovarajućih vrijednosti x i a u sve relacije uključeni u problem, oni će se utvrditi. Primjer 1. Za svaku vrijednost parametra a riješite nejednakost Rješenje. Nađimo područje definicije ove nejednakosti. Iz čega je jasno da sustav nema rješenja. To znači da domena nejednadžbe ne sadrži par brojeva x i a, pa stoga nejednadžba nema rješenja. Opseg odgovor:

Invarijantnost, tj. nepromjenjivost jednadžbe ili nejednakosti s obzirom na zamjenu varijable nekim algebarski izraz iz ove varijable. Najjednostavniji primjer invarijantnosti je parnost: ako je − ravnomjerna funkcija, tada je jednadžba invarijantna prema promjeni x i – x , budući da je = 0. Invarijantnost

Pronađite korijene jednadžbe. Odluka. Imajte na umu da je par nepromjenjiv u odnosu na zamjenu. Zamjenom u jednakosti, dobivamo. Pomnožimo oba dijela ove jednakosti s 2 i oduzmemo član po član od rezultirajuće jednakosti, nalazimo 3, odakle. Sada ostaje riješiti jednadžbu, odakle su korijeni jednadžbe brojevi. Odgovor: .

Pronađite sve vrijednosti a za svaku od kojih jednadžba ima više od tri razna rješenja. Rješavanje problema s parametrom svojstva monotoničnosti

|x|= pozitivno X= |x|= Da bi postojala dva korijena, brojnik mora biti pozitivan. Dakle, kada se korijeni prve i druge jednadžbe podudaraju, što ne ispunjava uvjet uvjeta: prisutnost više od tri korijena. Odgovor: .

Pronađite sve vrijednosti a za svaku od kojih jednadžba ima dva korijena. Pretvorimo jednadžbu u oblik I razmotrimo funkciju f(x)= definiranu i kontinuiranu na cijeloj realnoj liniji. Graf ove funkcije je izlomljena linija, koja se sastoji od odsječaka i zraka, čija je svaka karika dio ravne linije oblika y= kt+l . f(x)= Za bilo koje proširenje modula prvog izraza, k ne prelazi 8, pa će povećanje i smanjenje funkcije f(x) ovisiti o proširenju drugog modula. Za vrijeme x, f(x) će se smanjiti, a za x će se povećati. To jest, za x=3 funkcija će uzeti najviša vrijednost. Da bi jednadžba imala dva korijena, potrebno je da je f(3) svojstvo monotonosti

f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Odgovor: a

Pronađite sve vrijednosti parametra a, za svaku od kojih je, za bilo koju realnu vrijednost x, nejednakost zadovoljena. Prepišemo nejednakost u obliku, uvedemo novu varijablu t = i razmotrimo funkciju f (t) = , definiran i kontinuiran na cijeloj realnoj liniji. Graf ove funkcije je izlomljena linija, koja se sastoji od segmenata i zraka, od kojih je svaka karika dio ravne linije, gdje se

Budući da je tada t ϵ [-1; jedan]. Zbog monotonog smanjenja funkcije y = f (t), dovoljno je provjeriti lijevi rub ovog segmenta. Z. Točno je A. To znači da je moguće samo ako brojevi u i v imaju isti predznak ili je bilo koji od njih jednak nuli. , = () () 0. Faktorizirajući kvadratne trinome, dobivamo nejednakost (, iz koje nalazimo da je a ϵ (-∞; -1) U (2) U [ 4; +∞). Odgovor: (-∞ ; -1]U(2)U)