Maclaurin proširenje online. Taylorova ekspanzija

Studenti više matematike trebaju biti svjesni da je zbroj nekog reda potencija koji pripada intervalu konvergencije zadanog niza kontinuirana i neograničen broj puta diferencirana funkcija. Postavlja se pitanje: je li moguće ustvrditi da je zadana proizvoljna funkcija f(x) zbroj nekog reda potencija? Odnosno, pod kojim se uvjetima funkcija f(x) može prikazati potencijskim redom? Važnost ovog pitanja leži u činjenici da je moguće aproksimativno zamijeniti funkciju f(x) zbrojem prvih nekoliko članova potencijskog niza, odnosno polinomom. Takva zamjena funkcije prilično jednostavnim izrazom - polinomom - također je prikladna pri rješavanju nekih problema, naime: pri rješavanju integrala, pri računanju itd.

Dokazano je da za neku funkciju f(x), u kojoj se mogu izračunati derivacije do (n + 1) reda, uključujući i posljednju, u blizini (α - R; x 0 + R) neke točka x = α formula:

Ova formula je dobila ime po poznatom znanstveniku Brooku Tayloru. Niz koji se dobije iz prethodnog zove se Maclaurinov red:

Pravilo koje omogućuje proširenje u Maclaurinov niz:

Odredi izvodnice prvog, drugog, trećeg ... reda.
Izračunajte kolike su derivacije pri x=0.
Napišite Maclaurinov red za tu funkciju, a zatim odredite interval njezine konvergencije.
Odredite interval (-R;R), gdje je ostatak Maclaurinove formule

R n (x) -> 0 za n -> beskonačno. Ako postoji, funkcija f(x) u njemu mora koincidirati sa zbrojem Maclaurinovog reda.

Razmotrite sada seriju Maclaurin za pojedinačne funkcije.

1. Dakle, prvi će biti f(x) = e x. Naravno, prema svojim značajkama, takva funkcija ima izvodnice vrlo različitih redova, i f (k) (x) \u003d e x, gdje je k jednako sve. Zamijenimo x \u003d 0. Dobivamo f (k) (0) \u003d e 0 \u003d 1, k \u003d 1,2 ... Na temelju prethodnog, niz e x izgledat će ovako:

2. Maclaurinov red za funkciju f(x) = sin x. Odmah pojasnite da će funkcija za sve nepoznanice imati izvode, osim f "(x) \u003d cos x \u003d sin (x + n / 2), f "" (x) \u003d -sin x \u003d sin (x + 2*n/2)..., f(k)(x)=sin(x+k*n/2), gdje je k jednako bilo kojem prirodnom broju. To jest, jednostavnim izračunima možemo zaključiti da serija za f(x) = sin x će izgledati ovako:

3. Pokušajmo sada razmotriti funkciju f(x) = cos x. Ima izvodnice proizvoljnog reda za sve nepoznanice i |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Dakle, naveli smo najvažnije funkcije koje se mogu proširiti u Maclaurinovim serijama, ali su za neke funkcije dopunjene Taylorovim serijama. Sada ćemo ih navesti. Također je vrijedno napomenuti da su Taylorov i Maclaurinov redovi važan dio prakse rješavanja nizova u višoj matematici. Dakle, serija Taylor.

1. Prvi će biti red za f-ii f (x) = ln (1 + x). Kao i u prethodnim primjerima, s obzirom na f (x) = ln (1 + x), možemo dodati niz koristeći opći oblik Maclaurinovog niza. međutim, za ovu funkciju, Maclaurinov niz se može dobiti mnogo jednostavnije. Nakon integriranja određenog geometrijskog niza, dobivamo niz za f (x) = ln (1 + x) takvog uzorka:

2. A drugi, koji će biti konačni u našem članku, bit će niz za f (x) \u003d arctg x. Za x koji pripada intervalu [-1; 1] vrijedi proširenje:

To je sve. U ovom članku razmatrani su najčešće korišteni Taylor i Maclaurin nizovi u višoj matematici, posebice na ekonomskim i tehničkim sveučilištima.

Kako umetnuti matematičke formule na stranicu?

Ako ikada budete trebali dodati jednu ili dvije matematičke formule na web stranicu, onda je najlakši način da to učinite kako je opisano u članku: matematičke formule se lako umeću na stranicu u obliku slika koje Wolfram Alpha automatski generira. Osim jednostavnosti, ova univerzalna metoda pomoći će poboljšati vidljivost stranice u tražilicama. Radi već dugo (i mislim da će raditi zauvijek), ali je moralno zastario.

Ako stalno koristite matematičke formule na svojoj web stranici, preporučujem vam da koristite MathJax, posebnu JavaScript biblioteku koja prikazuje matematičku notaciju u web preglednicima koristeći MathML, LaTeX ili ASCIIMathML oznake.

Postoje dva načina da počnete koristiti MathJax: (1) korištenjem jednostavnog koda, možete brzo povezati MathJax skriptu sa svojim web mjestom, koja će se automatski učitati s udaljenog poslužitelja u pravo vrijeme (popis poslužitelja); (2) prenesite skriptu MathJax s udaljenog poslužitelja na svoj poslužitelj i povežite je sa svim stranicama svoje stranice. Druga metoda je složenija i dugotrajnija te će vam omogućiti da ubrzate učitavanje stranica vaše stranice, a ako nadređeni MathJax poslužitelj iz nekog razloga postane privremeno nedostupan, to ni na koji način neće utjecati na vašu vlastitu stranicu. Unatoč tim prednostima, odabrao sam prvu metodu jer je jednostavnija, brža i ne zahtijeva tehničke vještine. Slijedite moj primjer i u roku od 5 minuta moći ćete koristiti sve značajke MathJaxa na svojoj web stranici.

Možete povezati skriptu MathJax biblioteke s udaljenog poslužitelja koristeći dvije opcije koda preuzete s glavnog MathJax web mjesta ili sa stranice dokumentacije:

Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kôd vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake . Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako umetnete prvi kod, morat ćete ga povremeno ažurirati. Ako zalijepite drugi kod, tada će se stranice učitavati sporije, ali nećete morati stalno pratiti ažuriranja MathJaxa.

Najlakši način povezivanja MathJaxa je u Bloggeru ili WordPressu: na kontrolnoj ploči web-mjesta dodajte widget dizajniran za umetanje JavaScript koda treće strane, kopirajte prvu ili drugu verziju gornjeg koda za učitavanje u njega i postavite widget bliže početak predloška (usput, to uopće nije potrebno jer se MathJax skripta učitava asinkrono). To je sve. Sada naučite sintaksu označavanja MathML, LaTeX i ASCIIMathML i spremni ste ugraditi matematičke formule u svoje web stranice.

Svaki fraktal izgrađen je prema određenom pravilu, koje se dosljedno primjenjuje neograničen broj puta. Svako takvo vrijeme naziva se iteracija.

Iterativni algoritam za konstruiranje Mengerove spužve prilično je jednostavan: originalna kocka sa stranicom 1 podijeljena je ravninama paralelnim s njezinim stranama na 27 jednakih kocki. Iz nje se uklanjaju jedna središnja kocka i 6 kocki uz nju duž strana. Ispada set koji se sastoji od 20 preostalih manjih kockica. Postupivši isto sa svakom od ovih kockica, dobivamo set od 400 manjih kockica. Nastavljajući ovaj proces na neodređeno vrijeme, dobivamo Mengerovu spužvu.

Među funkcionalnim redovima najvažnije mjesto zauzimaju potencionski redovi.

Niz potencija naziva se niz

čiji su članovi potencije raspoređene u rastuće nenegativne cijele potencije x, a c0 , c 1 , c 2 , c n su konstantne vrijednosti. Brojke c1 , c 2 , c n - koeficijenti članova serije, c0 - besplatan član. Članovi potencije definirani su na cijelom brojevnom pravcu.

Upoznajmo se s konceptom područje konvergencije reda potencija. Ovo je skup vrijednosti varijable x za koje niz konvergira. Redovi potencija imaju prilično jednostavno područje konvergencije. Za stvarne vrijednosti varijable x područje konvergencije sastoji se ili od jedne točke, ili je određeni interval (interval konvergencije), ili se poklapa s cijelom osi Vol .

Pri zamjeni u potencijskom nizu vrijednosti x= 0 dobivate niz brojeva

c0 +0+0+...+0+... ,

koji konvergira.

Stoga, na x= 0 konvergira bilo koji red potencije i, prema tome, njegovo područje konvergencije ne može biti prazan skup. Struktura područja konvergencije svih redova potencija je ista. Može se utvrditi pomoću sljedećeg teorema.

Teorem 1 (Abelov teorem). Ako red potencija konvergira na nekoj vrijednosti x = x 0 , koja je različita od nule, tada konvergira, i štoviše, apsolutno, za sve vrijednosti |x| < |x 0 | . Imajte na umu: i početna vrijednost "x je nula" i bilo koja vrijednost "x" koja se uspoređuje s početnom vrijednošću uzimaju se modulo - bez uzimanja u obzir predznaka.

Posljedica. Ako a niz potencija divergira na neku vrijednost x = x 1 , tada divergira za sve vrijednosti |x| > |x 1 | .

Kao što smo ranije saznali, bilo koji red potencije konvergira za vrijednost x= 0. Postoje potencijski redovi koji konvergiraju samo za x= 0 i divergiraju za ostale vrijednosti x. Isključujući ovaj slučaj iz razmatranja, pretpostavljamo da red potencije konvergira na nekoj vrijednosti x = x 0 , različit od nule. Tada, prema Abelovom teoremu, konvergira u svim točkama intervala ]-| x0 |, |x 0 |[ (interval, čija su lijeva i desna granica vrijednosti x, na kojima konvergira red potencije, uzet redom s znakom minus i znakom plus), simetričan u odnosu na ishodište.

Ako red potencije divergira na nekoj vrijednosti x = x 1 , tada, na temelju korolara Abelovog teorema, također divergira u svim točkama izvan segmenta [-| x1 |, |x 1 |] . Slijedi da za bilo koji potencijski niz postoji interval , simetričan u odnosu na ishodište, tzv interval konvergencije , u čijoj svakoj točki niz konvergira, može konvergirati na granicama ili se može razilaziti, a ne nužno istovremeno, ali izvan segmenta, niz se razilazi. Broj R naziva se radijus konvergencije reda potencija.

U posebnim slučajevima interval konvergencije redova potencija može degenerirati do točke (tada niz konvergira samo za x= 0 i pretpostavlja se da je R= 0) ili predstavljaju cijeli brojevni pravac (tada niz konvergira u svim točkama brojevnog pravca i pretpostavlja se da je ).

Dakle, definicija područja konvergencije niza potencija je određivanje njegove radijus konvergencije R i proučavanje konvergencije niza na granicama intervala konvergencije (za).

Teorem 2. Ako su svi koeficijenti niza snaga, počevši od određenog, različiti od nule, tada je njegov radijus konvergencije jednak granici na omjeru apsolutnih vrijednosti koeficijenata općih sljedećih članova niza, tj.

Primjer 1. Odredite područje konvergencije potencijskog reda

Riješenje. Ovdje

Koristeći formulu (28), nalazimo radijus konvergencije ovog niza:

Proučimo konvergenciju niza na krajevima intervala konvergencije. Primjer 13 pokazuje da ovaj niz konvergira za x= 1 i divergira na x= -1. Stoga je područje konvergencije poluinterval.

Primjer 2. Odredite područje konvergencije potencijskog reda

Riješenje. Koeficijenti niza su pozitivni, i

Nađimo granicu ovog omjera, tj. radijus konvergencije niza potencija:

Istražujemo konvergenciju niza na krajevima intervala. Zamjena vrijednosti x= -1/5 i x= 1/5 u ovoj seriji daje:

Prvi od ovih nizova konvergira (vidi primjer 5). Ali tada, na temelju teorema paragrafa "Apsolutna konvergencija", drugi niz također konvergira, a područje njegove konvergencije je segment

Primjer 3. Odredite područje konvergencije potencijskog reda

Riješenje. Ovdje

Pomoću formule (28) nalazimo radijus konvergencije niza:

Proučimo konvergenciju niza za vrijednosti. Zamjenjujući ih u ovoj seriji, dobivamo

Oba niza divergiraju jer nužni uvjet konvergencije nije zadovoljen (njihovi zajednički članovi ne teže nuli na ). Dakle, na oba kraja intervala konvergencije ovaj niz divergira, a područje njegove konvergencije je interval .

Primjer 5. Odredite područje konvergencije potencijskog reda

Riješenje. Nalazimo odnos , gdje je , i :

Prema formuli (28), radijus konvergencije ovog niza

odnosno niz konvergira samo kada x= 0 i divergira za ostale vrijednosti x.

Primjeri pokazuju da se serije ponašaju različito na krajevima intervala konvergencije. U primjeru 1 niz konvergira na jednom kraju intervala konvergencije, a divergira na drugom, u primjeru 2 konvergira na oba kraja, u primjeru 3 divergira na oba kraja.

Formula za radijus konvergencije reda potencija dobiva se pod pretpostavkom da su svi koeficijenti članova niza, počevši od nekih, različiti od nule. Stoga je primjena formule (28) dopuštena samo u tim slučajevima. Ako je ovaj uvjet prekršen, tada treba tražiti radijus konvergencije reda snage pomoću znak d'Alemberta, ili, promjenom varijable, transformacijom serije u oblik u kojem je navedeni uvjet zadovoljen.

Primjer 6. Odredite interval konvergencije potencijskog reda

Riješenje. Ovaj niz ne sadrži pojmove s neparnim stupnjevima x. Stoga transformiramo niz postavljanjem . Onda dobivamo seriju

formula (28) može se koristiti za pronalaženje radijusa konvergencije od kojih. Budući da je , i , tada je radijus konvergencije ovog niza

Iz jednakosti dobivamo stoga ovaj niz konvergira na intervalu .

Zbroj redova potencija. Diferenciranje i integracija potencijskih redova

Neka za potencijski niz

radijus konvergencije R> 0, tj. ovaj niz konvergira na intervalu .

Zatim svaka vrijednost x iz intervala konvergencije odgovara nekom zbroju niza. Stoga je zbroj reda potencija funkcija od x na intervalu konvergencije. Označavajući ga kroz f(x), možemo napisati jednakost

shvaćajući ga u smislu da zbroj niza u svakoj točki x iz intervala konvergencije jednaka je vrijednosti funkcije f(x) u ovom trenutku. U istom smislu ćemo reći da red potencija (29) konvergira funkciji f(x) na intervalu konvergencije.

Izvan intervala konvergencije jednakost (30) nema značenja.

Primjer 7 Nađi zbroj potencijskih nizova

Riješenje. Ovo je geometrijski niz a= 1, i q= x. Stoga je njegov zbroj funkcija . Niz konvergira ako je , i njegov je interval konvergencije. Dakle, jednakost

vrijedi samo za vrijednosti, iako funkcija definiran za sve vrijednosti x, Osim x= 1.

Može se pokazati da zbroj potencijskih nizova f(x) kontinuirana i diferencijabilna na bilo kojem intervalu unutar intervala konvergencije, posebno u bilo kojoj točki intervala konvergencije niza.

Predstavimo teoreme o diferencijaciji i integraciji potencijskih redova po članu.

Teorem 1. Red potencije (30) u intervalu svoje konvergencije može se diferencirati član po član neograničeni broj puta, a rezultirajući red potencije ima isti radijus konvergencije kao i izvorni niz, a njihovi zbrojevi redom su jednaki .

Teorem 2. Red potencije (30) može se integrirati član po član neograničeni broj puta u rasponu od 0 do x, ako , i rezultirajući niz potencija ima isti radijus konvergencije kao izvorni niz, a njihovi zbrojevi su redom jednaki

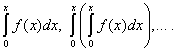
Proširenje funkcija u potencijski red

Neka funkcija f(x), koji treba proširiti u potencijski niz, tj. predstaviti u obliku (30):

Problem je odrediti koeficijente red (30). Da bismo to učinili, diferencirajući jednakost (30) pojam po pojam, uzastopno nalazimo:

……………………………………………….. (31)

Pretpostavljajući u jednakosti (30) i (31) x= 0, nalazimo

Zamjenom pronađenih izraza u jednakost (30) dobivamo

(32)

Nađimo Maclaurinov niz nekih elementarnih funkcija.

Primjer 8 Proširite funkciju u Maclaurinovu nizu

Riješenje. Izvodnice ove funkcije su iste kao i sama funkcija:

Stoga, kada x= 0 imamo

Zamjenom ovih vrijednosti u formulu (32) dobivamo željeno proširenje:

(33)

Ovaj niz konvergira na cijelom brojevnom pravcu (njegov radijus konvergencije je ).

Ako funkcija f(x) ima derivacije svih redova na nekom intervalu koji sadrži točku a, tada se na nju može primijeniti Taylorova formula:
,
gdje rn- takozvani rezidualni član ili ostatak niza, može se procijeniti pomoću Lagrangeove formule:
, gdje se broj x nalazi između x i a.

Pravila unosa funkcija:

Ako za neku vrijednost x rn→0 at n→∞, tada se u limitu Taylorova formula pretvara za ovu vrijednost u konvergentnu Taylorova serija:
,
Stoga se funkcija f(x) može proširiti u Taylorov niz u razmatranoj točki x ako:
1) ima izvedenice svih redova;
2) konstruirani niz konvergira u ovoj točki.

Za a = 0 dobivamo niz tzv blizu Maclaurina:
,
Proširenje najjednostavnijih (elementarnih) funkcija u Maclaurinov red:
eksponencijalne funkcije
, R=∞
Trigonometrijske funkcije
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funkcija actgx se ne proširuje po x, jer ctg0=∞
Hiperboličke funkcije

Logaritamske funkcije
, -1
Binomni nizovi
.

Primjer #1. Proširite funkciju u potencijski niz f(x)= 2x.
Riješenje. Nađimo vrijednosti funkcije i njezinih izvoda na x=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2=ln2;
f""(x) = 2x U 2 2, f""( 0) = 2 0 log 2 2= log 2 2;
…
f(n)(x) = 2x ul n 2, f(n)( 0) = 2 0 ul n 2=ln n 2.
Zamjenom dobivenih vrijednosti izvedenica u formulu Taylorovog niza dobivamo:

Polumjer konvergencije ovog niza jednak je beskonačnosti, pa ovo širenje vrijedi za -∞<x<+∞.

Primjer #2. Napišite Taylorov niz u potencijama ( x+4) za funkciju f(x)= e x.
Riješenje. Nalaženje derivacija funkcije e x i njihove vrijednosti u točki x=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Stoga željeni Taylorov red funkcije ima oblik:

Ova ekspanzija vrijedi i za -∞<x<+∞.

Primjer #3. Proširi funkciju f(x)=ln x u nizu po stupnjevima ( X- 1),
(tj. u Taylorovom nizu u blizini točke x=1).
Riješenje. Pronalazimo derivacije ove funkcije.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f(n)=(- 1) n-1 (n-1)!
Zamjenom ovih vrijednosti u formulu dobivamo željeni Taylorov niz:

Uz pomoć d'Alembertova testa, može se potvrditi da niz konvergira na ½x-1½<1 . Действительно,

Niz konvergira ako je ½ X- 1½<1, т.е. при 0<x<2. При x=2 dobivamo izmjenični niz koji zadovoljava uvjete Leibnizova testa. Za x=0 funkcija nije definirana. Dakle, područje konvergencije Taylorovog niza je poluotvoreni interval (0;2].

Primjer #4. Proširi funkciju u potencijski niz.
Riješenje. U dekompoziciji (1) zamijenimo x s -x 2, dobivamo:
, -∞

Primjer broj 5. Proširite funkciju u Maclaurinovu nizu.
Riješenje. Imamo
Koristeći formulu (4), možemo napisati:

zamjenjujući umjesto x u formuli -x, dobivamo:

Odavde nalazimo: ln(1+x)-ln(1-x) = -
Proširivanjem zagrada, preuređivanjem uvjeta serije i smanjenjem sličnih izraza, dobivamo
. Ovaj niz konvergira u intervalu (-1;1) jer je dobiven iz dva niza od kojih svaki konvergira u tom intervalu.

Komentar .
Formule (1)-(5) također se mogu koristiti za proširenje odgovarajućih funkcija u Taylorov niz, tj. za proširenje funkcija na pozitivne cijele potencije ( Ha). Za to je potrebno izvršiti takve identične transformacije na zadanoj funkciji da bi se dobila jedna od funkcija (1) - (5), u kojoj umjesto x košta k( Ha) m , gdje je k konstantan broj, m je pozitivan cijeli broj. Često je zgodno promijeniti varijablu t=Ha i proširiti rezultirajuću funkciju s obzirom na t u Maclaurinovom nizu.

Ova se metoda temelji na teoremu o jedinstvenosti proširenja funkcije u potencijski niz. Bit ovog teorema je da se u blizini iste točke ne mogu dobiti dva različita niza potencije koji bi konvergirali istoj funkciji, bez obzira na način na koji se izvodi njezino širenje.

Primjer br. 5a. Proširite funkciju u Maclaurinovom nizu, označite područje konvergencije.
Riješenje. Prvo nalazimo 1-x-6x 2 =(1-3x)(1+2x) , .
do osnovnog:

Razlomak 3/(1-3x) može se promatrati kao zbroj beskonačno opadajuće geometrijske progresije s nazivnikom 3x ako je |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

s područjem konvergencije |x|< 1/3.

Primjer broj 6. Proširi funkciju u Taylorov niz u blizini točke x = 3.
Riješenje. Ovaj problem se može riješiti, kao i prije, pomoću definicije Taylorovog niza, za koji je potrebno pronaći derivacije funkcija i njihove vrijednosti na x=3. Međutim, bit će lakše koristiti postojeću dekompoziciju (5):
=
Rezultirajući niz konvergira na ili -3

Primjer broj 7. Napišite Taylorov red potencijama (x -1) funkcije ln(x+2) .
Riješenje.

Niz konvergira na , ili -2< x < 5.

Primjer broj 8. Proširite funkciju f(x)=sin(πx/4) u Taylorov niz oko točke x =2.
Riješenje. Napravimo zamjenu t=x-2:

Koristeći ekspanziju (3), u kojoj zamijenimo x s π / 4 t, dobivamo:

Rezultirajući niz konvergira zadanoj funkciji na -∞< π / 4 t<+∞, т.е. при (-∞Na ovaj način,
, (-∞

Približni proračuni korištenjem potencijskih redova

Redovi potencija naširoko se koriste u približnim proračunima. Uz njihovu pomoć, s određenom točnošću, možete izračunati vrijednosti korijena, trigonometrijske funkcije, logaritme brojeva, određene integrale. Redovi se također koriste u integraciji diferencijalnih jednadžbi.
Razmotrimo proširenje funkcije u niz potencija:

Za izračunavanje približne vrijednosti funkcije u danoj točki x, koji pripada području konvergencije naznačenog niza, prvi nčlanovi ( n je konačan broj), a preostali članovi se odbacuju:

Za procjenu pogreške dobivene približne vrijednosti potrebno je procijeniti odbačeni ostatak r n (x) . Za to se koriste sljedeće metode:

ako je rezultirajući niz izmjeničan, tada se koristi sljedeće svojstvo: za izmjenični niz koji zadovoljava Leibnizove uvjete, apsolutna vrijednost ostatka niza ne prelazi prvi odbačeni član.
ako je zadani niz konstantnog predznaka, tada se niz sastavljen od odbačenih članova uspoređuje s beskonačno padajućom geometrijskom progresijom.
u općem slučaju, za procjenu ostatka Taylorovog niza, možete koristiti Lagrangeovu formulu: a x ).

Primjer #1. Izračunajte ln(3) s točnošću 0,01.
Riješenje. Upotrijebimo dekompoziciju, gdje je x=1/2 (pogledajte primjer 5 u prethodnoj temi):

Provjerimo možemo li odbaciti ostatak nakon prva tri člana proširenja, za to ga procjenjujemo koristeći zbroj beskonačno opadajuće geometrijske progresije:

Dakle, možemo odbaciti ovaj ostatak i dobiti

Primjer #2. Izračunajte do najbližih 0,0001.
Riješenje. Upotrijebimo binomni niz. Budući da je 5 3 najbliža cjelobrojna kocka 130, preporučljivo je predstaviti broj 130 kao 130=5 3 +5.

budući da je četvrti član dobivenog predznakoizmjeničnog niza koji zadovoljava Leibnizov test već manji od tražene točnosti:
, tako da se on i uvjeti nakon njega mogu odbaciti.
Mnogi praktično potrebni definitivni ili nepravi integrali ne mogu se izračunati pomoću Newton-Leibnizove formule, jer je njezina primjena povezana s pronalaženjem antiderivacije, koja često nema izraz u elementarnim funkcijama. Također se događa da je pronalaženje antiderivata moguće, ali nepotrebno naporno. Međutim, ako se integrand proširi u red potencije, a granice integracije pripadaju intervalu konvergencije tog niza, tada je moguć aproksimativni izračun integrala s unaprijed određenom točnošću.

Primjer #3. Izračunajte integral ∫ 0 1 4 sin (x) x s točnošću od 10 -5 .
Riješenje. Odgovarajući neodređeni integral ne može se izraziti elementarnim funkcijama, tj. je "nemoguć integral". Ovdje se ne može primijeniti Newton-Leibnizova formula. Izračunajmo približno integral.
Dijeljenje pojam po pojam serije za grijeh x na x, dobivamo:

Integrirajući ovaj niz član po član (ovo je moguće jer granice integracije pripadaju intervalu konvergencije ovog niza), dobivamo:

Budući da dobiveni niz zadovoljava Leibnizove uvjete, dovoljno je uzeti zbroj prva dva člana da bi se dobila željena vrijednost sa zadanom točnošću.
Dakle, nalazimo
.

Primjer #4. Izračunajte integral ∫ 0 1 4 e x 2 s točnošću 0,001.
Riješenje.
. Provjerimo možemo li odbaciti ostatak nakon drugog člana rezultirajućeg niza.
0,0001<0.001. Следовательно, .

U teoriji funkcionalnih nizova središnje mjesto zauzima dio posvećen rastavljanju funkcije u niz.

Dakle, postavlja se problem: za zadanu funkciju potrebno je pronaći takav niz potencija

koji je konvergirao na nekom intervalu i njegov je zbroj bio jednak
, oni.

= ..

Ovaj zadatak se zove problem proširenja funkcije u potencijski niz.

Nužan uvjet za proširenje funkcije u potencijski niz je njegova diferencijabilnost beskonačan broj puta – to proizlazi iz svojstava konvergentnih redova potencije. Ovaj uvjet je u pravilu zadovoljen za elementarne funkcije u njihovoj domeni definiranja.

Dakle, pretpostavimo da funkcija
ima izvedenice bilo kojeg reda. Može li se proširiti u potencijski niz, ako može, kako pronaći taj niz? Drugi dio problema je lakše riješiti, pa krenimo od njega.

Pretpostavimo da funkcija
može se predstaviti kao zbroj redova potencija koji konvergiraju u intervalu koji sadrži točku x 0 :

= .. (*)

gdje a 0 ,a 1 ,a 2 ,...,a P ,... – neizvjesni (još) koeficijenti.

Stavimo u jednakost (*) vrijednost x = x 0 , onda dobivamo

Razlikujemo redove potencija (*) član po član

= ..

i stavljajući ovdje x = x 0 , dobivamo

Sljedećim diferenciranjem dobivamo niz

= ..

pretpostavljajući x = x 0 , dobivamo
, gdje
.

Nakon P-fold diferencijaciju dobivamo

Uz pretpostavku u posljednjoj jednakosti x = x 0 , dobivamo
, gdje

Dakle, koeficijenti su pronađeni

,
,
, …,
,….,

zamjenom koje u red (*), dobivamo

Dobiveni niz naziva se blizu Taylora za funkciju
.

Dakle, to smo utvrdili ako se funkcija može proširiti u niz potencija potencijama (x - x 0 ), tada je ovo širenje jedinstveno i rezultirajući niz je nužno Taylorov niz.

Imajte na umu da se Taylorov red može dobiti za bilo koju funkciju koja ima derivacije bilo kojeg reda u točki x = x 0 . Ali to još ne znači da se između funkcije i rezultirajućeg niza može staviti znak jednakosti, tj. da je zbroj niza jednak izvornoj funkciji. Prvo, takva jednakost može imati smisla samo u području konvergencije, a Taylorov niz dobiven za funkciju može divergirati, i drugo, ako Taylorov niz konvergira, tada se njegov zbroj možda neće podudarati s izvornom funkcijom.

3.2. Dovoljni uvjeti za proširenje funkcije u Taylorov red

Formulirajmo tvrdnju uz pomoć koje ćemo riješiti navedeni problem.

Ako funkcija
u nekoj okolini točke x 0 ima derivacije do (n+ 1)-tog reda uključujući, onda u ovom susjedstvu imamoformula Taylor

gdjeR n (x)-rezidualni član Taylorove formule - ima oblik (Lagrangeov oblik)

gdje točkaξ leži između x i x 0 .

Imajte na umu da postoji razlika između Taylorovog niza i Taylorove formule: Taylorova formula je konačna suma, tj. P - fiksni broj.

Podsjetimo da je zbroj niza S(x) može se definirati kao granica funkcionalnog niza parcijalnih suma S P (x) u nekom intervalu x:

Prema ovome, proširiti funkciju u Taylorov niz znači pronaći niz takav da za bilo koji xx

Taylorovu formulu zapisujemo u obliku gdje je

primijeti da
definira pogrešku koju dobivamo, zamijenite funkciju f(x) polinom S n (x).

Ako a
, onda
,oni. funkcija se proširuje u Taylorov niz. Nasuprot tome, ako
, onda
.

Dakle, dokazali smo kriterij za proširenje funkcije u Taylorov red.

Da bi u nekom intervalu funkcijaf(x) proširuje u Taylorov niz, potrebno je i dovoljno da na tom intervalu
, gdjeR n (x) je ostatak Taylorovog niza.

Uz pomoć formuliranog kriterija može se dobiti dostatanuvjeti za proširenje funkcije u Taylorov niz.

Ako uneka okolina točke x 0 apsolutne vrijednosti svih izvodnica funkcije ograničene su istim brojem M≥ 0, tj.

, to u ovom susjedstvu, funkcija se proširuje u Taylorov niz.

Iz navedenog proizlazi algoritamproširenje funkcije f(x) u Taylorovom nizu u blizini točke x 0 :

1. Nalaženje derivacije funkcije f(x):

f(x), f’(x), f”(x), f’”(x), f (n) (x),…

2. Izračunavamo vrijednost funkcije i vrijednosti njezinih izvodnica u točki x 0

f(x 0 ), f'(x 0 ), f”(x 0 ), f’”(x 0 ), f (n) (x 0 ),…

3. Formalno pišemo Taylorov red i nalazimo područje konvergencije rezultirajućeg reda potencija.

4. Provjeravamo ispunjenje dovoljnih uvjeta, t.j. ustanoviti za koji x iz regije konvergencije, preostali član R n (x) teži nuli pri
ili
.

Proširenje funkcija u Taylorov niz prema ovom algoritmu naziva se proširenje funkcije u Taylorov red po definiciji ili izravna dekompozicija.