Tablica sinusa od 60 stupnjeva. Sinus, kosinus, tangens i kotangens - sve što trebate znati na OGE i USE

Trigonometrija, kao znanost, nastala je na Starom istoku. Prve trigonometrijske omjere razvili su astronomi kako bi stvorili točan kalendar i orijentirali se prema zvijezdama. Ovi izračuni odnosili su se na sfernu trigonometriju, dok se u školskom tečaju proučava omjer stranica i kut ravnog trokuta.

Trigonometrija je grana matematike koja se bavi svojstvima trigonometrijskih funkcija i odnosom stranica i kutova trokuta.

Tijekom procvata kulture i znanosti u 1. tisućljeću nove ere, znanje se proširilo od starog istoka do Grčke. Ali glavna otkrića trigonometrije zasluga su ljudi arapskog kalifata. Konkretno, turkmenski znanstvenik al-Marazvi uveo je takve funkcije kao što su tangens i kotangens, sastavio je prve tablice vrijednosti za sinuse, tangente i kotangense. Pojam sinusa i kosinusa uveli su indijski znanstvenici. Mnogo je pažnje posvećeno trigonometriji u djelima velikih ličnosti antike kao što su Euklid, Arhimed i Eratosten.

Osnovne veličine trigonometrije

Osnovne trigonometrijske funkcije numeričkog argumenta su sinus, kosinus, tangens i kotangens. Svaki od njih ima svoj graf: sinus, kosinus, tangens i kotangens.

Formule za izračunavanje vrijednosti ovih veličina temelje se na Pitagorinom teoremu. Školarcima je poznatija u formulaciji: "Pitagorejske hlače, jednake u svim smjerovima", budući da se dokaz daje na primjeru jednakokračnog pravokutnog trokuta.

Sinus, kosinus i druge ovisnosti uspostavljaju odnos između oštrih kutova i stranica bilo kojeg pravokutnog trokuta. Dajemo formule za izračunavanje ovih veličina za kut A i pratimo odnos trigonometrijskih funkcija:

Kao što vidite, tg i ctg su inverzne funkcije. Ako krak a predstavimo kao umnožak sin A i hipotenuze c, a krak b kao cos A * c, tada ćemo dobiti sljedeće formule za tangens i kotangens:

trigonometrijski krug

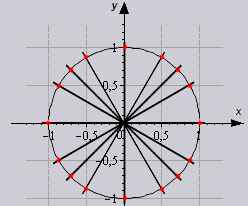
Grafički se odnos navedenih veličina može prikazati na sljedeći način:

Krug, u ovom slučaju, predstavlja sve moguće vrijednosti kuta α - od 0° do 360°. Kao što se može vidjeti sa slike, svaka funkcija ima negativnu ili pozitivnu vrijednost ovisno o kutu. Na primjer, sin α će biti sa znakom "+" ako α pripada I i II četvrtini kruga, odnosno nalazi se u rasponu od 0 ° do 180 °. Uz α od 180° do 360° (III i IV četvrtina), sin α može biti samo negativna vrijednost.

Pokušajmo sastaviti trigonometrijske tablice za određene kutove i saznati značenje količina.

Vrijednosti α jednake 30°, 45°, 60°, 90°, 180° i tako dalje nazivaju se posebnim slučajevima. Vrijednosti trigonometrijskih funkcija za njih izračunavaju se i prikazuju u obliku posebnih tablica.

Ovi kutovi nisu odabrani slučajno. Oznaka π u tablicama je za radijane. Rad je kut pod kojim duljina kružnog luka odgovara njegovom polumjeru. Ova je vrijednost uvedena kako bi se uspostavio univerzalni odnos; kada se računa u radijanima, stvarna duljina polumjera u cm nije važna.

Kutovi u tablicama za trigonometrijske funkcije odgovaraju vrijednostima radijana:

Dakle, nije teško pogoditi da je 2π puni krug ili 360°.

Svojstva trigonometrijskih funkcija: sinus i kosinus

Da bismo razmotrili i usporedili osnovna svojstva sinusa i kosinusa, tangensa i kotangensa, potrebno je nacrtati njihove funkcije. To se može učiniti u obliku krivulje koja se nalazi u dvodimenzionalnom koordinatnom sustavu.

Razmotrite usporednu tablicu svojstava za sinusni val i kosinusni val:

sinusoida	kosinusni val
y = sin x	y = cos x
ODZ [-1; jedan]	ODZ [-1; jedan]
sin x = 0, za x = πk, gdje je k ϵ Z	cos x = 0, za x = π/2 + πk, gdje je k ϵ Z
sin x = 1, za x = π/2 + 2πk, gdje je k ϵ Z	cos x = 1, za x = 2πk, gdje je k ϵ Z
sin x = - 1, pri x = 3π/2 + 2πk, gdje je k ϵ Z	cos x = - 1, za x = π + 2πk, gdje je k ϵ Z
sin (-x) = - sin x, tj. neparna funkcija	cos (-x) = cos x, tj. funkcija je parna
	funkcija je periodična, najmanji period je 2π
sin x › 0, pri čemu x pripada četvrtinama I i II ili od 0° do 180° (2πk, π + 2πk)	cos x › 0, pri čemu x pripada četvrtima I i IV ili od 270° do 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, pri čemu x pripada četvrtinama III i IV ili od 180° do 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, pri čemu x pripada četvrtinama II i III ili od 90° do 270° (π/2 + 2πk, 3π/2 + 2πk)
raste na intervalu [- π/2 + 2πk, π/2 + 2πk]	raste na intervalu [-π + 2πk, 2πk]
opada na intervalima [ π/2 + 2πk, 3π/2 + 2πk]	smanjuje u intervalima
izvod (sin x)' = cos x	izvod (cos x)’ = - sin x

Određivanje je li neka funkcija parna ili nije vrlo je jednostavno. Dovoljno je zamisliti trigonometrijski krug sa znakovima trigonometrijskih veličina i mentalno "presaviti" graf u odnosu na OX os. Ako su predznaci isti, funkcija je parna; u protivnom je neparna.

Uvođenje radijana i nabrajanje glavnih svojstava sinusoide i kosinusnog vala omogućuju nam da donesemo sljedeći obrazac:

Vrlo je lako provjeriti ispravnost formule. Na primjer, za x = π/2, sinus je jednak 1, kao i kosinus od x = 0. Provjera se može obaviti pregledom tablica ili praćenjem krivulja funkcije za dane vrijednosti.

Svojstva tangentoida i kotangentoida

Grafovi funkcija tangensa i kotangensa bitno se razlikuju od sinusoide i kosinusnog vala. Vrijednosti tg i ctg su inverzne jedna drugoj.

Y = tgx.
Tangens teži vrijednostima y na x = π/2 + πk, ali ih nikada ne doseže.
Najmanji pozitivni period tangentoida je π.
Tg (- x) \u003d - tg x, tj. funkcija je neparna.
Tg x = 0, za x = πk.
Funkcija se povećava.
Tg x › 0, za x ϵ (πk, π/2 + πk).
Tg x ‹ 0, za x ϵ (— π/2 + πk, πk).
Derivacija (tg x)' = 1/cos 2 ⁡x .

Razmotrite grafički prikaz kotangentoida u nastavku teksta.

Glavna svojstva kotangentoida:

Y = ctgx.
Za razliku od sinusne i kosinusne funkcije, u tangentoidu Y može poprimiti vrijednosti skupa svih realnih brojeva.
Kotangentoid teži vrijednostima y pri x = πk, ali ih nikada ne doseže.
Najmanji pozitivni period kotangentoida je π.
Ctg (- x) \u003d - ctg x, tj. funkcija je neparna.
Ctg x = 0, za x = π/2 + πk.
Funkcija se smanjuje.
Ctg x › 0, za x ϵ (πk, π/2 + πk).
Ctg x ‹ 0, za x ϵ (π/2 + πk, πk).
Derivacija (ctg x)' = - 1/sin 2 ⁡x Fiks

Referentni podaci za tangens (tg x) i kotangens (ctg x). Geometrijska definicija, svojstva, grafikoni, formule. Tablica tangensa i kotangenata, derivacije, integrali, proširenja nizova. Izrazi kroz kompleksne varijable. Veza s hiperboličkim funkcijama.

Geometrijska definicija

|BD| - duljina kružnog luka sa središtem u točki A.
α je kut izražen u radijanima.

Tangenta ( tgα) je trigonometrijska funkcija koja ovisi o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine suprotnog kraka |BC| na duljinu susjednog kraka |AB| .

Kotangens ( ctgα) je trigonometrijska funkcija koja ovisi o kutu α između hipotenuze i kraka pravokutnog trokuta, jednaka omjeru duljine susjednog kraka |AB| na duljinu suprotnog kraka |BC| .

Tangens

Gdje n- cijeli.

U zapadnoj literaturi tangenta se označava na sljedeći način:
.
;
;
.

Graf funkcije tangensa, y = tg x

Kotangens

Gdje n- cijeli.

U zapadnoj literaturi kotangens se označava na sljedeći način:
.
Također je usvojena sljedeća oznaka:
;
;
.

Graf kotangens funkcije, y = ctg x

Svojstva tangensa i kotangensa

Periodičnost

Funkcije y= tg x i y= ctg x su periodične s periodom π.

Paritet

Funkcije tangens i kotangens su neparne.

Područja definiranja i vrijednosti, uzlazno, silazno

Funkcije tangens i kotangens su kontinuirane na svojoj domeni definicije (vidi dokaz kontinuiteta). Glavna svojstva tangensa i kotangensa prikazana su u tablici ( n- cijeli broj).

	y= tg x	y= ctg x
Opseg i kontinuitet
Raspon vrijednosti	-∞ < y < +∞	-∞ < y < +∞
Uzlazni		-
Silazni	-
Krajnosti	-	-
Nule, y= 0
Točke presjeka s osi y, x = 0	y= 0	-

Formule

Izrazi pomoću sinusa i kosinusa

; ;
; ;
;

Formule za tangens i kotangens zbroja i razlike

Ostale formule lako je nabaviti, na primjer

Umnožak tangenti

Formula za zbroj i razliku tangenti

Ova tablica prikazuje vrijednosti tangensa i kotangenata za neke vrijednosti argumenta.

Izrazi u terminima kompleksnih brojeva

Izrazi u terminima hiperboličkih funkcija

;
;

Derivati

; .

.
Derivacija n-tog reda u odnosu na varijablu x funkcije:
.
Izvođenje formula za tangentu >>>; za kotangens >>>

Integrali

Proširenja u serije

Da biste dobili ekspanziju tangente u potencije od x, morate uzeti nekoliko članova ekspanzije u niz potencija za funkcije grijeh x i cos x i podijeliti te polinome jedan na drugi, . To rezultira sljedećim formulama.

U .

u .
gdje B n- Bernoullijevi brojevi. Oni se određuju ili iz relacije ponavljanja:
;
;
gdje .
Ili prema Laplaceovoj formuli:

Inverzne funkcije

Inverzne funkcije tangensu i kotangensu su arktangens i arkotangens.

Arktangens, arctg

, gdje n- cijeli.

Arkus tangenta, arcctg

, gdje n- cijeli.

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente visokoškolskih ustanova, Lan, 2009.
G. Korn, Priručnik iz matematike za istraživače i inženjere, 2012.

U petom stoljeću prije Krista starogrčki filozof Zenon iz Eleje formulirao je svoje poznate aporije od kojih je najpoznatija aporija "Ahilej i kornjača". Evo kako to zvuči:

Recimo da Ahilej trči deset puta brže od kornjače i da je tisuću koraka iza nje. Za vrijeme dok Ahil pretrči ovu udaljenost, kornjača otpuže stotinu koraka u istom smjeru. Kad Ahil pretrči stotinu koraka, kornjača će puzati još deset koraka, i tako dalje. Proces će se nastaviti unedogled, Ahil nikada neće sustići kornjaču.

Ovo razmišljanje postalo je logičan šok za sve naredne generacije. Aristotel, Diogen, Kant, Hegel, Gilbert... Svi su oni, na ovaj ili onaj način, razmatrali Zenonove aporije. Šok je bio toliko jak da je " ... rasprave se nastavljaju i danas, znanstvena zajednica još nije uspjela doći do zajedničkog mišljenja o biti paradoksa ... u proučavanje problematike uključeni su matematička analiza, teorija skupova, novi fizikalni i filozofski pristupi ; nijedan od njih nije postao općeprihvaćeno rješenje problema ..."[Wikipedia," Zenonove aporije "]. Svi shvaćaju da su prevareni, ali nitko ne shvaća u čemu je prijevara.

S gledišta matematike, Zenon je u svojim aporijama jasno pokazao prijelaz s vrijednosti na. Ovaj prijelaz podrazumijeva primjenu umjesto konstanti. Koliko ja razumijem, matematički aparat za primjenu promjenjivih mjernih jedinica ili još nije razvijen, ili nije primijenjen na Zenonove aporije. Primjena naše uobičajene logike vodi nas u zamku. Mi, inercijom mišljenja, primjenjujemo konstantne jedinice vremena na recipročne. S fizičke strane to izgleda kao da se vrijeme usporava do potpunog zaustavljanja u trenutku kada Ahilej sustigne kornjaču. Ako vrijeme stane, Ahilej više ne može prestići kornjaču.

Okrenemo li logikom na koju smo navikli, sve dolazi na svoje mjesto. Ahilej trči konstantnom brzinom. Svaki sljedeći segment puta je deset puta kraći od prethodnog. Sukladno tome, vrijeme utrošeno na njegovo prevladavanje je deset puta manje od prethodnog. Ako primijenimo koncept "beskonačnosti" u ovoj situaciji, tada bi bilo ispravno reći "Ahilej će beskrajno brzo prestići kornjaču."

Kako izbjeći ovu logičku zamku? Ostanite u konstantnim jedinicama vremena i ne prelazite na recipročne vrijednosti. Zenonovim jezikom to izgleda ovako:

U vremenu koje je potrebno Ahilu da pretrči tisuću koraka, kornjača otpuže stotinu koraka u istom smjeru. Tijekom sljedećeg vremenskog intervala, jednakog prvom, Ahil će pretrčati još tisuću koraka, a kornjača puzati sto koraka. Sada je Ahilej osam stotina koraka ispred kornjače.

Ovaj pristup adekvatno opisuje stvarnost bez ikakvih logičkih paradoksa. Ali to nije potpuno rješenje problema. Einsteinova izjava o nesavladivosti brzine svjetlosti vrlo je slična Zenonovoj aporiji "Ahilej i kornjača". Taj problem tek trebamo proučiti, promisliti i riješiti. A rješenje se ne mora tražiti u beskonačno velikim brojevima, već u mjernim jedinicama.

Još jedna zanimljiva Zenonova aporija govori o letećoj strijeli:

Strijela koja leti je nepomična, budući da u svakom trenutku miruje, a budući da miruje u svakom trenutku, uvijek miruje.

U ovoj se aporiji logički paradoks prevladava vrlo jednostavno – dovoljno je pojasniti da u svakom trenutku leteća strijela miruje na različitim točkama u prostoru, što je, zapravo, kretanje. Ovdje treba napomenuti još jednu stvar. Iz jedne fotografije automobila na cesti nemoguće je utvrditi ni činjenicu njegovog kretanja ni udaljenost do njega. Da bi se utvrdila činjenica kretanja automobila, potrebne su dvije fotografije snimljene s iste točke u različitim vremenskim točkama, ali se ne mogu koristiti za određivanje udaljenosti. Da biste odredili udaljenost do automobila, potrebne su vam dvije fotografije snimljene s različitih točaka u prostoru u isto vrijeme, ali iz njih ne možete utvrditi činjenicu kretanja (naravno, još uvijek su vam potrebni dodatni podaci za izračune, trigonometrija će vam pomoći). Ono što želim posebno istaknuti je da su dvije točke u vremenu i dvije točke u prostoru dvije različite stvari koje ne treba miješati jer pružaju različite mogućnosti za istraživanje.

Srijeda, 4. srpnja 2018

Vrlo dobro su razlike između skupa i multiskupa opisane u Wikipediji. Mi gledamo.

Kao što vidite, "skup ne može imati dva identična elementa", ali ako postoje identični elementi u skupu, takav skup se naziva "multiskup". Razumna bića nikada neće shvatiti takvu logiku apsurda. Ovo je razina papiga koje govore i dresiranih majmuna, kod kojih je um odsutan od riječi "potpuno". Matematičari se ponašaju kao obični treneri, propovijedajući nam svoje apsurdne ideje.

Jednom davno, inženjeri koji su gradili most bili su u čamcu ispod mosta za vrijeme ispitivanja mosta. Ako se most sruši, osrednji inženjer umro je ispod ruševina svoje kreacije. Ako je most mogao izdržati opterećenje, talentirani inženjer izgradio je druge mostove.

Koliko god se matematičari skrivali iza fraze "pamte me, ja sam u kući", odnosno "matematika proučava apstraktne pojmove", postoji jedna pupčana vrpca koja ih neraskidivo povezuje sa stvarnošću. Ova pupčana vrpca je novac. Primijenimo matematičku teoriju skupova na same matematičare.

Odlično smo učili matematiku i sada sjedimo za blagajnom i isplaćujemo plaće. Ovdje nam dolazi matematičar po svoj novac. Prebrojimo mu cijeli iznos i rasporedimo ga na stolu u različite hrpe u koje stavimo novčanice istog apoena. Zatim sa svake hrpe uzmemo po jednu novčanicu i damo matematičaru njegovu "matematičku plaću". Objašnjavamo matematiku da će ostatak računa dobiti tek kada dokaže da skup bez istovrsnih elemenata nije jednak skupu s istovrsnim elementima. Ovdje počinje zabava.

Prije svega, proradit će zastupnička logika: "možete na druge, ali ne na mene!" Dalje će početi uvjeravanja da na novčanicama istog apoena postoje različiti brojevi novčanica, što znači da se ne mogu smatrati identičnim elementima. Pa mi računamo plaću u kovanicama - na kovanicama nema brojeva. Ovdje će se matematičar izbezumljeno prisjetiti fizike: različiti novčići imaju različite količine prljavštine, kristalna struktura i raspored atoma za svaki je novčić jedinstven...

I sad imam najzanimljivije pitanje: gdje je granica iza koje se elementi multiskupa pretvaraju u elemente skupa i obrnuto? Takva linija ne postoji – o svemu odlučuju šamani, znanost ovdje nije ni blizu.

Pogledaj ovdje. Odabiremo nogometne stadione s istom površinom terena. Površina polja je ista, što znači da imamo multiset. Ali ako uzmemo u obzir nazive istih stadiona, dobivamo puno, jer su nazivi različiti. Kao što vidite, isti skup elemenata je i skup i multiskup u isto vrijeme. Kako u redu? I tu matematičar-šaman-šuler vadi adutskog asa iz rukava i počinje nam pričati ili o skupu ili o multiskupu. U svakom slučaju, on će nas uvjeriti da je u pravu.

Da bismo razumjeli kako moderni šamani operiraju s teorijom skupova, povezujući je sa stvarnošću, dovoljno je odgovoriti na jedno pitanje: po čemu se elementi jednog skupa razlikuju od elemenata drugog skupa? Pokazat ću vam, bez ikakvih "zamislivo kao nejedna cjelina" ili "nezamislivo kao jedinstvena cjelina".

Nedjelja, 18.03.2018

Zbroj znamenki broja je ples šamana s tamburom, koji nema veze s matematikom. Da, na satovima matematike nas uče pronaći zbroj znamenki broja i koristiti ga, ali oni su šamani za to, da bi svoje potomke naučili svojim vještinama i mudrosti, inače će šamani jednostavno izumrijeti.

Trebate li dokaz? Otvorite Wikipediju i pokušajte pronaći stranicu "Zbroj znamenki broja". Ona ne postoji. U matematici ne postoji formula po kojoj možete pronaći zbroj znamenki bilo kojeg broja. Uostalom, brojevi su grafički simboli kojima zapisujemo brojeve, a jezikom matematike zadatak zvuči ovako: "Nađi zbroj grafičkih simbola koji predstavljaju bilo koji broj." Matematičari ne mogu riješiti ovaj problem, ali šamani to elementarno mogu.

Shvatimo što i kako radimo da bismo pronašli zbroj znamenki zadanog broja. I tako, recimo da imamo broj 12345. Što treba učiniti da bismo pronašli zbroj znamenki tog broja? Razmotrimo sve korake redom.

1. Zapišite broj na komad papira. Što smo učinili? Broj smo pretvorili u brojčani grafički simbol. Ovo nije matematička operacija.

2. Jednu primljenu sliku režemo na više slika koje sadrže zasebne brojeve. Rezanje slike nije matematička operacija.

3. Pretvorite pojedinačne grafičke znakove u brojeve. Ovo nije matematička operacija.

4. Dobivene brojeve zbrojite. E sad, to je matematika.

Zbroj znamenki broja 12345 je 15. Ovo su "tečajevi krojenja i šivanja" od šamana koje koriste matematičari. Ali to nije sve.

Sa stajališta matematike nije svejedno u kojem brojevnom sustavu zapisujemo broj. Dakle, u različitim sustavima brojeva zbroj znamenki istog broja bit će različit. U matematici se brojevni sustav označava kao indeks s desne strane broja. S velikim brojem 12345, ne želim zavarati glavu, razmislite o broju 26 iz članka o. Zapišimo ovaj broj u binarnom, oktalnom, decimalnom i heksadecimalnom brojevnom sustavu. Nećemo svaki korak razmatrati pod mikroskopom, već smo to učinili. Pogledajmo rezultat.

Kao što vidite, u različitim brojevnim sustavima zbroj znamenki istog broja je različit. Ovaj rezultat nema nikakve veze s matematikom. To je kao da bi pronalaženje površine pravokutnika u metrima i centimetrima dalo potpuno drugačije rezultate.

Nula u svim brojevnim sustavima izgleda isto i nema zbroj znamenki. To je još jedan argument u prilog činjenici da . Pitanje za matematičare: kako se u matematici označava ono što nije broj? Što, za matematičare ne postoji ništa osim brojeva? Za šamane to mogu dopustiti, ali za znanstvenike ne. Stvarnost nisu samo brojke.

Dobiveni rezultat treba smatrati dokazom da su brojevni sustavi mjerne jedinice brojeva. Uostalom, ne možemo uspoređivati brojeve s različitim mjernim jedinicama. Ako iste radnje s različitim mjernim jedinicama iste veličine dovode do različitih rezultata nakon njihove usporedbe, onda to nema nikakve veze s matematikom.

Što je prava matematika? To je kada rezultat matematičke radnje ne ovisi o vrijednosti broja, korištenoj mjernoj jedinici i o tome tko izvodi tu radnju.

Znak na vratima Otvara vrata i kaže:

Joj! Nije li ovo ženski WC?
- Mlada žena! Ovo je laboratorij za proučavanje neograničene svetosti duša nakon uzašašća na nebo! Nimbus na vrhu i strelica prema gore. Koji drugi WC?

Žensko... Aureola na vrhu i strelica prema dolje je muško.

Ako vam takvo dizajnersko djelo bljesne pred očima nekoliko puta dnevno,

Onda ne čudi da iznenada nađete čudnu ikonu u svom automobilu:

Osobno se trudim vidjeti minus četiri stupnja kod osobe koja kaki (jedna slika) (kompozicija više slika: znak minus, broj četiri, oznaka stupnjeva). I ne smatram ovu djevojku budalom koja ne zna fiziku. Ona samo ima lučni stereotip percepcije grafičkih slika. A matematičari nas tome stalno uče. Evo primjera.

1A nije "minus četiri stupnja" ili "jedan a". Ovo je "čovjek koji kaki" ili broj "dvadeset šest" u heksadecimalnom brojevnom sustavu. Oni ljudi koji stalno rade u ovom sustavu brojeva automatski percipiraju broj i slovo kao jedan grafički simbol.

U članku ćemo u potpunosti razumjeti kako to izgleda tablica trigonometrijskih vrijednosti, sinus, kosinus, tangens i kotangens. Razmotrimo osnovnu vrijednost trigonometrijskih funkcija, pod kutom od 0,30,45,60,90,...,360 stupnjeva. I da vidimo kako koristiti ove tablice u izračunavanju vrijednosti trigonometrijskih funkcija.
Prvo razmislite tablica kosinusa, sinusa, tangensa i kotangensa pod kutom od 0, 30, 45, 60, 90,.. stupnjeva. Definicija ovih veličina omogućuje određivanje vrijednosti funkcija kutova od 0 i 90 stupnjeva:

sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, kotangens od 00 bit će nedefiniran
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, tangens od 90 0 bit će nedefiniran

Ako uzmemo pravokutne trokute čiji su kutovi od 30 do 90 stupnjeva. Dobivamo:

sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3

Sve dobivene vrijednosti predstavljamo u obrascu trigonometrijska tablica:

Tablica sinusa, kosinusa, tangensa i kotangensa!

Ako koristimo formulu cast, naša će se tablica povećati, dodat će se vrijednosti za kutove do 360 stupnjeva. Izgledat će ovako:

Također, na temelju svojstava periodičnosti, tablica se može povećati ako kutove zamijenimo sa 0 0 +360 0 *z .... 330 0 +360 0 *z, u kojem je z cijeli broj. U ovoj tablici moguće je izračunati vrijednost svih kutova koji odgovaraju točkama u jednoj kružnici.

Pogledajmo jasno kako koristiti tablicu u rješenju.
Sve je vrlo jednostavno. Budući da se vrijednost koju trebamo nalazi na sjecištu ćelija koje su nam potrebne. Na primjer, uzmimo kut od 60 stupnjeva, u tablici će izgledati ovako:

U konačnoj tablici glavnih vrijednosti trigonometrijskih funkcija djelujemo na isti način. Ali u ovoj tablici moguće je saznati kolika će biti tangensa iz kuta od 1020 stupnjeva, to je = -√3 Provjerimo 1020 0 = 300 0 +360 0 *2. Pronađimo stol.

Bradis stol. Za sinus, kosinus, tangens i kotangens.

Bradyjeve tablice su podijeljene u nekoliko dijelova, sastoje se od tablica kosinusa i sinusa, tangensa i kotangensa - koji je podijeljen na dva dijela (tg kuta do 90 stupnjeva i ctg malih kutova).

Sinus i kosinus

kut tg od 00 do 760, kut ctg od 140 do 900.

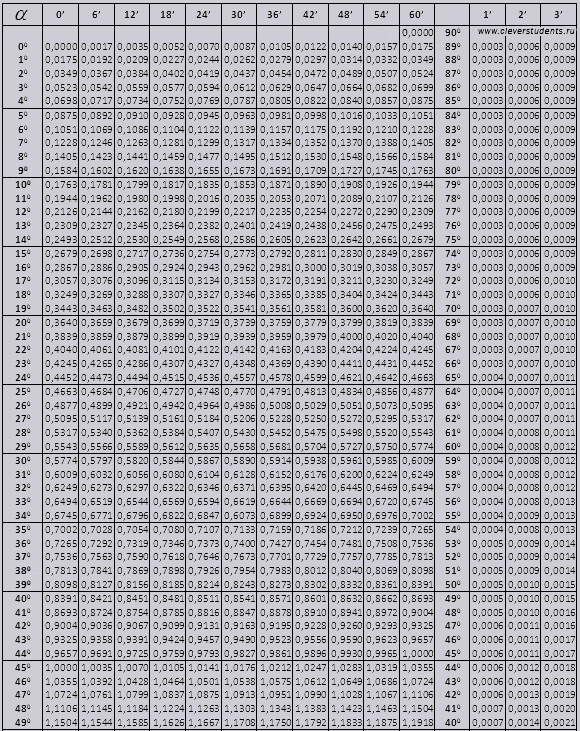
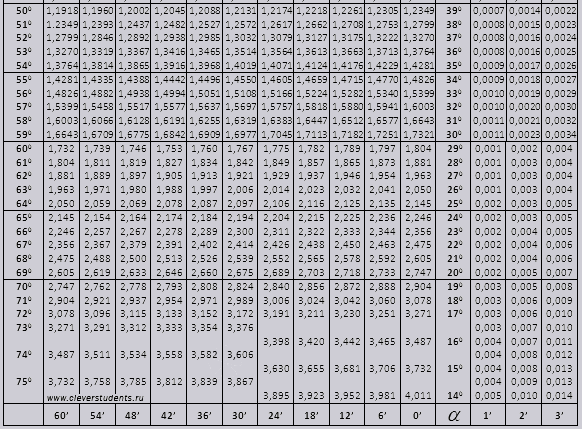
tg do 900 i ctg malih kutova.

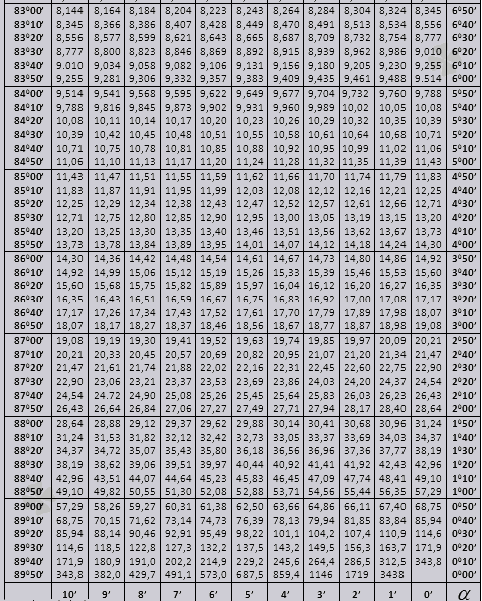
Hajde da shvatimo kako koristiti Bradisove tablice u rješavanju problema.

Pronađimo oznaku sin (oznaka u stupcu s lijevog ruba) 42 minute (oznaka je u gornjem retku). Križanjem tražimo oznaku, to je = 0,3040.

Vrijednosti minuta su naznačene s intervalom od šest minuta, što ako vrijednost koja nam je potrebna spada unutar ovog intervala. Uzmimo 44 minute, au tablici ih je samo 42. Uzimamo 42 kao osnovu i koristimo dodatne stupce s desne strane, uzimamo 2. ispravak i zbrajamo 0,3040 + 0,0006 i dobivamo 0,3046.

Uz sin 47 min, uzimamo 48 min kao osnovu i od njega oduzimamo 1 korekciju, tj. 0,3057 - 0,0003 = 0,3054

Pri izračunavanju cos radimo slično kao i sin, samo što za osnovu uzimamo donji red tablice. Na primjer cos 20 0 = 0,9397

Vrijednosti tg kuta do 90 0 i cot malog kuta su ispravne i u njima nema korekcija. Na primjer, pronađite tg 78 0 37min = 4,967

i ctg 20 0 13 min = 25,83

Pa, ovdje smo razmotrili glavne trigonometrijske tablice. Nadamo se da su vam ove informacije bile izuzetno korisne. Vaša pitanja o stolovima, ako ih ima, svakako napišite u komentarima!

Napomena: Zidni bokobrani - bokobranska ploča za zaštitu zidova. Slijedite vezu bokobrani bez okvira bez zidova (http://www.spi-polymer.ru/otboyniki/) i saznajte više.

1. Trigonometrijske funkcije su elementarne funkcije čiji je argument kutak. Trigonometrijske funkcije opisuju odnose između stranica i oštrih kutova u pravokutnom trokutu. Područja primjene trigonometrijskih funkcija iznimno su raznolika. Tako se, primjerice, svaki periodički proces može prikazati kao zbroj trigonometrijskih funkcija (Fourierov red). Te se funkcije često pojavljuju pri rješavanju diferencijalnih i funkcionalnih jednadžbi.

2. Trigonometrijske funkcije uključuju sljedećih 6 funkcija: sinus, kosinus, tangens,kotangens, sječna i kosekant. Za svaku od ovih funkcija postoji inverzna trigonometrijska funkcija.

3. Pogodno je uvesti geometrijsku definiciju trigonometrijskih funkcija pomoću jedinični krug. Slika ispod prikazuje kružnicu radijusa r=1. Na kružnici je označena točka M(x,y). Kut između radijus vektora OM i pozitivnog smjera osi Ox je α.

4. sinus kut α je omjer ordinate y točke M(x,y) i polumjera r:
sinα=y/r.
Kako je r=1, onda je sinus jednak ordinati točke M(x,y).

5. kosinus kut α je omjer apscise x točke M(x,y) i polumjera r:
cosα=x/r

6. tangens kut α je omjer ordinate y točke M(x,y) i njene apscise x:
tanα=y/x,x≠0

7. Kotangens kut α je omjer apscise x točke M(x,y) i njene ordinate y:
cotα=x/y,y≠0

8. Sjekant kut α je omjer polumjera r i apscise x točke M(x,y):
secα=r/x=1/x,x≠0

9. Kosekant kut α je omjer polumjera r i ordinate y točke M(x,y):
cscα=r/y=1/y,y≠0

10. U jediničnoj kružnici projekcije x, y točke M(x, y) i polumjer r tvore pravokutni trokut u kojemu su x, y katete, a r hipotenuza. Stoga su gornje definicije trigonometrijskih funkcija primijenjene na pravokutni trokut formulirane na sljedeći način:
sinus kut α je omjer suprotnog kraka i hipotenuze.
kosinus kut α je omjer susjedne katete i hipotenuze.
tangens kut α naziva se suprotni krak susjednom.
Kotangens kut α naziva se susjedni krak suprotnom.
Sjekant kut α je omjer hipotenuze i susjednog kraka.
Kosekant kut α je omjer hipotenuze i suprotnog kraka.

11. graf sinusne funkcije
y=sinx, domena: x∈R, domena: −1≤sinx≤1

12. Graf kosinusne funkcije
y=cosx, domena: x∈R, raspon: −1≤cosx≤1

13. graf funkcije tangente
y=tanx, domena: x∈R,x≠(2k+1)π/2, domena: −∞

14. Graf kotangens funkcije
y=cotx, domena: x∈R,x≠kπ, domena: −∞

15. Graf funkcije sekante
y=secx, domena: x∈R,x≠(2k+1)π/2, domena: secx∈(−∞,−1]∪∪)