Zašto trebate uspoređivati brojeve po modulu? Rješavanje usporedbi prvog stupnja
Projekt iz matematike na temu
"Usporedbe po modulu"
Zaripova Aisylu
Sovjetski okrug Kazana
MBOU "Srednja škola br. 166", 7a razred
Znanstveni voditelj: Antonova N.A.
Sadržaj
Uvod________________________________________________________________3
Što su usporedbe_________________________________________________4
Pojam usporedbi po modulu__________________________4
Povijest nastanka pojma usporedbe po modulu_____4
Svojstva usporedbi______________________________________________4
Najjednostavnija uporaba modulo usporedbi je određivanje djeljivosti brojeva___________________________6
Jedan zadatak za usporedbu_______________________________8
Korištenje modulo usporedbi u profesionalnim aktivnostima________________________________________________9
Primjena usporedbi u rješavanju problema_________________________________6
Zaključak_________________________________________________10
Popis korištene literature_______________________________________11
Uvod.
Tema: Modulo usporedbe.
Problem: Mnogi se učenici prilikom priprema za olimpijade susreću s problemima čije se rješavanje temelji na poznavanju ostataka dijeljenja cijelih brojeva prirodnim brojem. Zanimali su nas ovakvi problemi i mogući načini njihovog rješavanja. Ispostavilo se da se oni mogu riješiti korištenjem modulo usporedbi.
Cilj: Saznati bit modulo usporedbi, glavne metode rada s modulo usporedbama.
Ciljevi: pronaći teoretski materijal o ovoj temi, razmotriti probleme koji se rješavaju pomoću modulo usporedbi, pokazati najčešće metode za rješavanje takvih problema, izvući zaključke.
Predmet proučavanja: teorija brojeva.
Predmet istraživanja: teorija modulo usporedbi.
Rad se odnosi na teorijska istraživanja i može se koristiti u pripremama za matematičke olimpijade. Njegov sadržaj otkriva osnovne pojmove modulo usporedbi i njihova glavna svojstva te daje primjere rješavanja zadataka na ovu temu.
ja . Što su usporedbe?
Pojam modulo usporedbi.
Kaže se da su brojevi i usporedivi po modulu ako su djeljivi s, drugim riječima, a i b imaju iste ostatke kada se dijele s.
Oznaka
Primjeri:
12 i 32 su usporedivi po modulu 5, budući da 12 kada se podijeli s 5 ima ostatak 2, a 32 kada se podijeli s 2 ima ostatak 2. Zapisano je12 ;
101 i 17 su usporedivi po modulu 21;
Povijest nastanka pojma modulo usporedbe.
Teoriju djeljivosti većim je dijelom stvorio Euler. Definicija usporedbe formulirana je u knjizi K.F.Gaussa “Aritmetičke studije”. Ovo djelo, napisano na latinskom jeziku, počelo se tiskati 1797. godine, ali je knjiga objavljena tek 1801. godine zbog činjenice da je tiskarski proces u to vrijeme bio izuzetno naporan i dugotrajan. Prvi dio Gaussove knjige zove se: “O usporedbi brojeva”. Gauss je bio taj koji je predložio simboliku modulo usporedbi koja se ustalila u matematici.
Svojstva usporedbi.
Ako
Dokaz:
Ako prvoj jednakosti dodamo drugu, dobivamo
je zbroj dva cijela broja, stoga je cijeli broj, dakle.
Ako od prve jednakosti oduzmemo drugu, dobivamo
ovo je razlika dva cijela broja, što znači da je cijeli broj, dakle.
Razmotrite izraz:
Ovo je razlika umnožaka cijelih brojeva, što znači da je, dakle, cijeli broj.
To je posljedica trećeg svojstva usporedbi.
Q.E.D.
5) Ako.
Dokaz: Nađimo zbroj ova dva izraza:
je zbroj dva cijela broja, stoga je cijeli broj, dakle .
Q.E.D.
6) Ako je cijeli broj, onda
Dokaz: , gdjestr– cijeli broj, pomnožimo ovu jednakost s, dobivamo: . Budući da je umnožak cijelih brojeva, to je trebalo dokazati.
7) Ako
Dokaz: Obrazloženje je slično dokazu svojstva 6.
8) Ako - međusobno prosti brojevi, dakle
Dokaz: , podijelimo ovaj izraz s, dobivamo: - međusobno prosti brojevi, što znači da su djeljivi cijelim brojem, tj. =. A to znači da je ono što je trebalo dokazati.
II . Primjena usporedbi u rješavanju problema.
2.1. Najjednostavnija uporaba modulo usporedbi je određivanje djeljivosti brojeva.
Primjer. Pronađite ostatak od 2 2009 u 7.
Rješenje: Razmotrimo potencije broja 2:
dizanjem usporedbe na potenciju 668 i množenjem s dobivamo: .
Odgovor: 4.
Primjer. Dokažite da je 7+7 2 +7 3 +…+7 4 n je djeljiv sa 100 za bilo kojiniz skupa cijelih brojeva.
Rješenje: Razmotrite usporedbe
itd. Cikličnost ostataka objašnjava se pravilima množenja brojeva u stupcu. Zbrajanjem prve četiri usporedbe dobivamo:
To znači da se taj iznos dijeli sa 100 bez ostatka. Slično, zbrajanjem sljedećih usporedbi oko četiri, dobivamo da je svaki takav zbroj djeljiv sa 100 bez ostatka. To znači da cijeli zbroj koji se sastoji od 4npojmova je djeljiv sa 100 bez ostatka. Q.E.D.
Primjer. Odredite po kojoj vrijednostinizraz je djeljiv s 19 bez ostatka.
Rješenje: .
Pomnožimo ovu usporedbu s 20. Dobivamo.
Zbrojimo onda usporedbe. . Dakle, desna strana usporedbe uvijek je djeljiva s 19 za bilo koji prirodni brojn, što znači da je izvorni izraz djeljiv s 19 s prirodnimn.
Odgovor n – bilo koji prirodni broj.
Primjer. Kojom znamenkom završava broj?
Otopina. Kako bismo riješili ovaj problem, pratit ćemo samo posljednju znamenku. Razmotrite moći broja 14:
Možete primijetiti da ako je eksponent neparan, vrijednost stupnja završava na 4, a ako je eksponent paran, završava na 6. Tada završava na 6, tj. je paran broj. Dakle, završit će za 6.
Odgovor 6.
2.2. Jedan zadatak za usporedbu.
Članak N. Vilenkina “Usporedbe i klase ostataka” predstavlja problem koji je tijekom studentskih godina riješio slavni engleski fizičar Dirac.
Postoji i kratko rješenje ovog problema koristeći modulo usporedbe. Ali susreli smo se s nizom sličnih problema. Na primjer.
Jedan je prolaznik kraj stabla pronašao hrpu jabuka na kojoj je sjedio majmun. Nakon što ih je prebrojao, shvatio je da ako se 1 jabuka da majmunu, tada će se broj preostalih jabuka podijeliti na n bez traga. Davši dodatnu jabuku majmunu, uzeo je 1/ n preostale jabuke i lijevo. Kasnije je hrpi prišao sljedeći prolaznik, zatim sljedeći itd. Svaki sljedeći prolaznik, nakon što je prebrojao jabuke, primijetio je da je njihov broj podijeljen sa n daje ostatak 1 i dajući dodatnu jabuku majmunu uzeo je 1/ n preostale jabuke i krenuli dalje. Nakon što je posljednji otišao, n prolaznika, broj jabuka preostalih na hrpi podijeljen je s n bez traga. Koliko je jabuka bilo prvo na hrpi?
Provodeći isto razmišljanje kao Dirac, dobili smo opću formulu za rješavanje klase sličnih problema: , gdjen– prirodni broj.
2.3. Primjena usporedbi modula u profesionalnim aktivnostima.
Teorija usporedbe primjenjuje se na teoriju kodiranja, tako da će svi ljudi koji izaberu profesiju vezanu uz računala studirati, a možda i primijeniti usporedbe u svojim profesionalnim aktivnostima. Na primjer, brojni koncepti teorije brojeva, uključujući modulo usporedbe, koriste se za razvoj algoritama šifriranja s javnim ključem.
Zaključak.
U radu se iznose osnovni pojmovi i svojstva modulo usporedbi te se na primjerima ilustrira uporaba modulo usporedbi. Materijal se može koristiti u pripremi za olimpijade iz matematike i Jedinstveni državni ispit.
Navedeni popis literature omogućuje, ako je potrebno, razmatranje nekih složenijih aspekata teorije modulo usporedbi i njezinih primjena.
Popis korištene literature.
Alfutova N.B. Algebra i teorija brojeva./N.B.Alfutova, A.V.Ustinov. M.:MCNMO, 2002, 466 str.
Bukhshtab A.A. Teorija brojeva. /A.A.Bukhshtab. M.: Obrazovanje, 1960.
Vilenkin N. Usporedbe i klase ostataka./N.Vilenkin.//Quantum. – 1978.- 10.
Fedorova N.E. Studij algebre i matematičke analize. 10. razred.http:// www. prosv. ru/ e-knjige/ Fedorova_ Algebra_10 kl/1/ xht
ru. wikipedija. org/ wiki/Modul_usporedbe.
Pri n daju iste ostatke.
Ekvivalentne formulacije: a i b usporedivi po modulu n ako njihova razlika a - b je djeljiv s n, ili ako se a može predstaviti kao a = b + kn , Gdje k- neki cijeli broj. Na primjer: 32 i −10 su usporedivi po modulu 7, jer
Izjava "a i b su usporedivi mod n" napisana je kao:
Svojstva jednakosti modula
Relacija modulo usporedbe ima svojstva
Bilo koja dva cijela broja a I b usporedivo po modulu 1.
Kako bi brojke a I b bili usporedivi po modulu n, potrebno je i dovoljno da je njihova razlika djeljiva sa n.
Ako su brojevi i u paru usporedivi po modulu n, zatim njihovi zbrojevi i , kao i umnošci i također su usporedivi po modulu n.
Ako brojevi a I b usporedivi po modulu n, zatim njihove diplome a k I b k također su usporedivi po modulu n pod bilo kojim prirodnim k.
Ako brojevi a I b usporedivi po modulu n, I n podijeljeno sa m, To a I b usporedivi po modulu m.
Kako bi brojke a I b bili usporedivi po modulu n, prikazan u obliku svoje kanonske dekompozicije na jednostavne faktore str ja
potrebno i dovoljno da se
Odnos usporedbe je odnos ekvivalencije i ima mnoga svojstva običnih jednakosti. Na primjer, mogu se zbrajati i množiti: ako
Usporedbe se, međutim, općenito govoreći, ne mogu dijeliti jedna s drugom ili s drugim brojevima. Primjer: , ali smanjenjem za 2 dobivamo pogrešnu usporedbu: . Pravila kratica za usporedbe su sljedeća.
Također ne možete izvoditi operacije na usporedbama ako se njihovi moduli ne podudaraju.
Ostala svojstva:
Povezane definicije
Dedukcijski razredi
Skup svih brojeva usporedivih s a modulo n nazvao razred odbitka a modulo n , a obično se označava [ a] n ili . Dakle, usporedba je ekvivalentna jednakosti klasa ostataka [a] n = [b] n .
Od modulo usporedbe n je relacija ekvivalencije na skupu cijelih brojeva, tada su klase ostataka modulo n predstavljaju klase ekvivalencije; njihov broj je jednak n. Skup svih klasa ostataka po modulu n označen sa ili.
Operacije zbrajanja i množenja induciraju odgovarajuće operacije na skupu:
[a] n + [b] n = [a + b] nS obzirom na te operacije skup je konačan prsten, a ako n jednostavno – konačno polje.
Sustavi odbitka
Sustav ostataka omogućuje izvođenje aritmetičkih operacija na konačnom skupu brojeva bez odlaska izvan njegovih granica. Potpuni sustav odbitaka modulo n je bilo koji skup od n cijelih brojeva koji su neusporedivi po modulu n. Obično se najmanji nenegativni ostaci uzimaju kao potpuni sustav ostataka modulo n
0,1,...,n − 1ili apsolutno najmanji odbici koji se sastoje od brojeva
,u slučaju ak n i brojevima
u slučaju čak n .
Rješavanje usporedbi
Usporedbe prvoga stupnja
U teoriji brojeva, kriptografiji i drugim područjima znanosti često se javlja problem pronalaženja rješenja za usporedbe oblika prvog stupnja:
Rješavanje takve usporedbe započinje izračunavanjem GCD-a (a, m)=d. U ovom slučaju moguća su 2 slučaja:
- Ako b ne višestruka d, tada usporedba nema rješenja.
- Ako b višestruki d, tada usporedba ima jedinstveno rješenje modulo m / d, ili, što je isto, d modulo rješenja m. U ovom slučaju, kao rezultat smanjenja izvorne usporedbe za d usporedba je:
Gdje a 1 = a / d , b 1 = b / d I m 1 = m / d su cijeli brojevi, i a 1 i m 1 su relativno prosti. Stoga broj a 1 se može obrnuti modulo m 1, odnosno pronađite takav broj c, to (drugim riječima, ). Sada se rješenje nalazi množenjem dobivene usporedbe s c:
Praktični izračun vrijednosti c može se implementirati na različite načine: korištenjem Eulerovog teorema, Euklidovog algoritma, teorije kontinuiranih razlomaka (vidi algoritam), itd. Konkretno, Eulerov teorem omogućuje vam da zapišete vrijednost c u obliku:
Primjer
Za usporedbu imamo d= 2, tako da po modulu 22 usporedba ima dva rješenja. Zamijenimo 26 s 4, usporedivo s njim po modulu 22, a zatim smanjimo sva 3 broja za 2:
Budući da je 2 koprost s modulom 11, možemo smanjiti lijevu i desnu stranu za 2. Kao rezultat, dobivamo jedno rješenje po modulu 11: , ekvivalentno dvama rješenjima po modulu 22: .
Usporedbe drugog stupnja
Rješavanje usporedbi drugog stupnja svodi se na pronalaženje je li dati broj kvadratni ostatak (koristeći kvadratni zakon reciprociteta) i zatim izračunavanje kvadratnog korijena po modulu.
Priča
Kineski teorem o ostatku, poznat već stoljećima, tvrdi (na modernom matematičkom jeziku) da je prsten ostataka modulo umnožak nekoliko međusobno prostih brojeva
Razmotrite usporedbu oblika x 2 ≡a(mod strα), gdje str– jednostavan neparan broj. Kao što je pokazano u stavku 4. §4., rješenje ove usporedbe može se pronaći rješavanjem usporedbe x 2 ≡a(mod str). Štoviše, usporedba x 2 ≡a(mod strα) će imati dva rješenja ako a je kvadratni ostatak po modulu str.
Primjer:
Riješite kvadratnu usporedbu x 2 ≡86 (mod 125).
125 = 5 3, 5 je prost broj. Provjerimo je li 86 kvadrat po modulu 5.
Izvorna usporedba ima 2 rješenja.
Nađimo rješenje za usporedbu x 2 ≡86 (mod 5).
x 2 ≡1(mod 5).
Ova se usporedba može riješiti na način naveden u prethodnom paragrafu, ali ćemo koristiti činjenicu da je kvadratni korijen iz 1 modulo ±1, a usporedba ima točno dva rješenja. Dakle, rješenje za usporedbu po modulu 5 je
x≡±1(mod 5) ili, inače, x=±(1+5 t 1).
Zamijenimo dobiveno rješenje u usporedbu po modulu 5 2 =25:
x 2 ≡86 (mod 25)
x 2 ≡11 (mod 25)
(1+5t 1) 2 ≡11 (mod 25)
1+10t 1 +25t 1 2 ≡11 (mod 25)
10t 1 ≡10 (mod 25)
2t 1 ≡2 (mod 5)
t 1 ≡1(mod 5), ili, što je isto, t 1 =1+5t 2 .
Tada je rješenje usporedbe po modulu 25 x=±(1+5(1+5 t 2))=±(6+25 t 2). Zamijenimo dobiveno rješenje u usporedbu po modulu 5 3 =125:
x 2 ≡86 (mod 125)
(6+25t 2) 2 ≡86 (mod 125)
36+12·25 t 2 +625t 2 2 ≡86 (mod 125)
12·25 t 2 ≡50 (mod 125)
12t 2 ≡2 (mod 5)
2t 2 ≡2 (mod 5)
t 2 ≡1(mod 5), ili t 2 =1+5t 3 .
Tada je rješenje usporedbe po modulu 125 x=±(6+25(1+5 t 3))=±(31+125 t 3).
Odgovor: x≡±31 (mod 125).
Razmotrimo sada usporedbu oblika x 2 ≡a(mod 2 α). Takva usporedba nema uvijek dva rješenja. Za takav modul mogući su sljedeći slučajevi:
1) α=1. Tada usporedba ima rješenje samo kada a≡1(mod 2), a rješenje je x≡1(mod 2) (jedno rješenje).
2) α=2. Usporedba ima rješenja samo kada a≡1(mod 4), a rješenje je x≡±1(mod 4) (dva rješenja).
3) α≥3. Usporedba ima rješenja samo kada a≡1(mod 8), a bit će četiri takva rješenja. Usporedba x 2 ≡a(mod 2 α) za α≥3 rješava se na isti način kao usporedbe oblika x 2 ≡a(mod strα), kao početno rješenje djeluju samo rješenja po modulu 8: x≡±1(mod 8) i x≡±3 (mod 8). Treba ih uspoređivati po modulu 16, zatim po modulu 32 itd. do modula 2 α.
Primjer:
Riješite usporedbu x 2 ≡33 (mod 64)
64=2 6 . Provjerimo ima li izvorna usporedba rješenje. 33≡1(mod 8), što znači da usporedba ima 4 rješenja.
Modulo 8 ova će rješenja biti: x≡±1(mod 8) i x≡±3(mod 8), što se može predstaviti kao x=±(1+4 t 1). Zamijenimo ovaj izraz za usporedbu po modulu 16
x 2 ≡33 (mod 16)
(1+4t 1) 2 ≡1 (mod 16)
1+8t 1 +16t 1 2 ≡1 (mod 16)
8t 1 ≡0 (mod 16)
t 1 ≡0 (mod 2)
Tada će rješenje poprimiti oblik x=±(1+4 t 1)=±(1+4(0+2 t 2))=±(1+8 t 2). Zamijenimo dobiveno rješenje u usporedbu po modulu 32:
x 2 ≡33 (mod 32)
(1+8t 2) 2 ≡1 (mod 32)
1+16t 2 +64t 2 2 ≡1 (mod 32)
16t 2 ≡0 (mod 32)
t 2 ≡0 (mod 2)
Tada će rješenje poprimiti oblik x=±(1+8 t 2) =±(1+8(0+2t 3)) =±(1+16 t 3). Zamijenimo dobiveno rješenje u usporedbu po modulu 64:
x 2 ≡33 (mod 64)
(1+16t 3) 2 ≡33 (mod 64)
1+32t 3 +256t 3 2 ≡33 (mod 64)
32t 3 ≡32 (mod 64)
t 3 ≡1 (mod 2)
Tada će rješenje poprimiti oblik x=±(1+16 t 3) =±(1+16(1+2t 4)) =±(17+32 t 4). Dakle, po modulu 64, originalna usporedba ima četiri rješenja: x≡±17(mod 64)i x≡±49 (mod 64).
Sada pogledajmo opću usporedbu: x 2 ≡a(mod m), (a,m)=1, ![]() - kanonsko proširenje modula m. Prema teoremu iz paragrafa 4 §4, ova usporedba je ekvivalentna sustavu
- kanonsko proširenje modula m. Prema teoremu iz paragrafa 4 §4, ova usporedba je ekvivalentna sustavu

Ako je svaka usporedba ovog sustava rješiva, onda je cijeli sustav rješiv. Pronašavši rješenje svake usporedbe ovog sustava, dobit ćemo sustav usporedbi prvog stupnja, čijim rješavanjem uz pomoć kineskog teorema o ostatku ćemo dobiti rješenje izvorne usporedbe. Štoviše, broj različitih rješenja izvorne usporedbe (ako je rješiva) je 2 k, ako je α=1, 2 k+1 ako je α=2, 2 k+2 ako je α≥3.
Primjer:
Riješite usporedbu x 2 ≡4(mod 21).
Usporedba s jednom nepoznatom x izgleda kao
Gdje . Ako a n nije djeljiv sa m, tako se zove stupanj usporedbe.
Odlukom usporedba je bilo koji cijeli broj x 0 , za koje
Ako X 0 zadovoljava usporedbu, tada, prema svojstvu 9 usporedbi, svi cijeli brojevi usporedivi s x 0 modulo m. Stoga sve usporedne otopine koje pripadaju istoj klasi ostataka modulo T, smatrat ćemo ga jednim rješenjem. Dakle, usporedba ima onoliko rješenja koliko ima elemenata cjelovitog sustava ostataka koji je zadovoljavaju.
Usporedbe čiji se skupovi rješenja podudaraju nazivaju se ekvivalent.
2.2.1 Usporedbe prvog stupnja
Usporedba prvog stupnja s jednom nepoznatom X izgleda kao
![]() (2.2)
(2.2)
Teorem 2.4. Da bi usporedba imala barem jedno rješenje, potrebno je i dovoljno da broj b podijeljeno s GCD( a, m).
Dokaz. Prvo dokazujemo nužnost. Neka d
=
GCD( a,
m)
I X 0
- rješenje usporedbe. Zatim ![]() , odnosno razlika Oh 0
−
b
podijeljeno sa T. Dakle, postoji takav cijeli broj q,
Što Oh 0
−
b
=
qm.
Odavde b= ah 0
−
qm.
I budući da d,
kao zajednički djelitelj, dijeli brojeve A I T, tada se minuend i subtrahend dijele sa d,
i prema tome b
podijeljeno sa d.
, odnosno razlika Oh 0
−
b
podijeljeno sa T. Dakle, postoji takav cijeli broj q,
Što Oh 0
−
b
=
qm.
Odavde b= ah 0
−
qm.
I budući da d,
kao zajednički djelitelj, dijeli brojeve A I T, tada se minuend i subtrahend dijele sa d,
i prema tome b
podijeljeno sa d.
Sada dokažimo dostatnost. Neka d- najveći zajednički djelitelj brojeva A I T, I b podijeljeno sa d. Zatim, po definiciji djeljivosti, postoje cijeli brojevi kao npr a 1 , b 1 ,T 1 , Što .
Koristeći prošireni Euklidov algoritam, nalazimo linearni prikaz broja 1 = gcd( a 1 , m 1 ):
![]()
za neke x 0 , g 0 . Pomnožimo obje strane posljednje jednakosti s b 1 d:
ili, što je isto,
,
odnosno i rješenje je usporedbe. □
Primjer 2.10. Usporedba 9 X= 6 (mod 12) ima rješenje budući da je gcd(9, 12) = 3 i 6 djeljivo s 3. □
Primjer 2.11. Usporedba 6x= 9 (mod 12) nema rješenja, budući da je gcd(6, 12) = 6, a 9 nije djeljivo sa 6. □
Teorem 2.5. Neka je usporedba (2.2) rješiva i d = GCD( a, m). Tada se skup usporednih rješenja (2.2) sastoji od d modulo klase ostataka T, naime ako X 0 - jedno od rješenja, onda su sva ostala rješenja
Dokaz. Neka X 0
- rješenje usporedbe (2.2), tj ![]() I ,
.
Dakle, postoji takva stvar q, Što Oh 0
−
b
=
qm.
Sada zamjenjujemo u posljednju jednakost umjesto X 0
proizvoljno rješenje oblika, gdje, dobivamo izraz
I ,
.
Dakle, postoji takva stvar q, Što Oh 0
−
b
=
qm.
Sada zamjenjujemo u posljednju jednakost umjesto X 0
proizvoljno rješenje oblika, gdje, dobivamo izraz
, djeljiv sa m. □
Primjer 2.12. Usporedba 9 X=6 (mod 12) ima točno tri rješenja, jer gcd(9, 12)=3. Ova rješenja: X 0 = 2, x 0 + 4 = 6, X 0 + 2∙4=10.□
Primjer 2.13. Usporedba 11 X=2 (mod 15) ima jedinstveno rješenje X 0 = 7, jer GCD(11,15)=1.□
Pokazat ćemo vam kako riješiti usporedbe prvog stupnja. Bez gubitka općenitosti, pretpostavit ćemo da je GCD( a, t) = 1. Tada se rješenje usporedbe (2.2) može tražiti, na primjer, pomoću Euklidovog algoritma. Doista, koristeći prošireni Euklidski algoritam, predstavljamo broj 1 kao linearnu kombinaciju brojeva a I T:
Pomnožimo obje strane ove jednakosti s b, dobivamo: b = abq + mrb, gdje abq - b = - mrb, odnosno a ∙ (bq) = b(mod m) I bq- rješenje usporedbe (2.2).
Drugo rješenje je korištenje Eulerovog teorema. Opet vjerujemo da GCD(a, T)= 1. Primjenjujemo Eulerov teorem: ![]() . Pomnožite obje strane usporedbe s b:
. Pomnožite obje strane usporedbe s b:
![]() .
Prepisivanje posljednjeg izraza kao
.
Prepisivanje posljednjeg izraza kao  , dobivamo da je to rješenje usporedbe (2.2).
, dobivamo da je to rješenje usporedbe (2.2).
Neka sada GCD( a, m) = d>1. Zatim a = atd, m = mtd, gdje je GCD( A 1 , m 1) = 1. Osim toga potrebno je b = b 1 d, kako bi usporedba bila razrješiva. Ako X 0 - rješenje usporedbe A 1 x = b 1 (mod m 1), i jedini, od GCD( A 1 , m 1) = 1, dakle X 0 bit će rješenje i usporedba A 1 xd = db 1 (mod m 1), odnosno izvorna usporedba (2.2). Odmor d- 1 rješenja se nalaze prema teoremu 2.5.
 Rješavanje usporedbi prvog stupnja
Rješavanje usporedbi prvog stupnja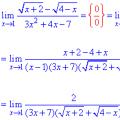 Limit sekvence i funkcije
Limit sekvence i funkcije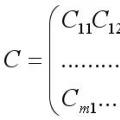 Označavanje elemenata matrice
Označavanje elemenata matrice