Binomial pengedaran. Taburan kebarangkalian pembolehubah rawak diskret

Teori kebarangkalian tidak dapat dilihat dalam kehidupan kita. Kita tidak mempedulikannya, tetapi setiap kejadian dalam hidup kita mempunyai satu atau lain kebarangkalian. Beri perhatian kepada jumlah yang besar senario, menjadi perlu bagi kita untuk menentukan yang paling berkemungkinan dan paling kecil kemungkinannya. Ia adalah paling mudah untuk menganalisis data kebarangkalian sedemikian secara grafik. Pengedaran boleh membantu kami dengan ini. Binomial adalah salah satu yang paling mudah dan paling tepat.

Sebelum beralih terus ke matematik dan teori kebarangkalian, mari kita fikirkan siapa yang pertama menghasilkan pengedaran jenis ini dan apakah sejarah pembangunan radas matematik untuk konsep ini.

cerita

Konsep kebarangkalian telah diketahui sejak zaman dahulu. Walau bagaimanapun, ahli matematik purba tidak begitu mementingkannya dan hanya mampu meletakkan asas bagi teori yang kemudiannya menjadi teori kebarangkalian. Mereka mencipta beberapa kaedah gabungan, yang banyak membantu mereka yang kemudiannya mencipta dan mengembangkan teori itu sendiri.

Pada separuh kedua abad ketujuh belas, pembentukan konsep asas dan kaedah teori kebarangkalian bermula. Takrifan pembolehubah rawak telah diperkenalkan, kaedah untuk mengira kebarangkalian mudah dan beberapa kompleks bebas dan peristiwa bergantung. Kepentingan sedemikian dalam pembolehubah rawak dan kebarangkalian ditentukan oleh perjudian: Setiap orang ingin tahu apakah peluangnya untuk memenangi permainan itu.

Langkah seterusnya ialah aplikasi kaedah analisis matematik dalam teori kebarangkalian. Ahli matematik terkenal seperti Laplace, Gauss, Poisson dan Bernoulli mengambil tugas ini. Merekalah yang memajukan bidang matematik ini tahap baru. James Bernoullilah yang menemui undang-undang pengedaran binomial. Dengan cara ini, seperti yang akan kita ketahui kemudian, berdasarkan penemuan ini, beberapa lagi telah dibuat, yang memungkinkan untuk mewujudkan undang-undang taburan normal dan banyak lagi.

Sekarang, sebelum kita mula menerangkan taburan binomial, kita akan menyegarkan sedikit dalam ingatan konsep teori kebarangkalian, mungkin sudah terlupa dari bangku sekolah.

Asas Teori Kebarangkalian

Kami akan mempertimbangkan sistem sedemikian, akibatnya hanya dua hasil yang mungkin: "kejayaan" dan "kegagalan". Ini mudah difahami dengan contoh: kami melemparkan syiling, meneka bahawa ekor akan jatuh. Kebarangkalian bagi setiap peristiwa yang mungkin (ekor jatuh - "berjaya", kepala jatuh - "tidak berjaya") adalah bersamaan dengan 50 peratus jika syiling seimbang dengan sempurna dan tiada faktor lain yang boleh menjejaskan eksperimen.

Ia adalah acara yang paling mudah. Tetapi ada juga sistem yang kompleks, di mana tindakan berurutan dilakukan, dan kebarangkalian hasil tindakan ini akan berbeza. Sebagai contoh, pertimbangkan sistem berikut: dalam kotak yang kandungannya tidak dapat kita lihat, terdapat enam bola yang sama sekali, tiga pasang biru, merah dan bunga putih. Kami perlu mendapatkan beberapa bola secara rawak. Oleh itu, dengan menarik keluar salah satu bola putih terlebih dahulu, kita akan mengurangkan beberapa kali ganda kebarangkalian bahawa yang seterusnya kita juga akan mendapat bola putih. Ini berlaku kerana bilangan objek dalam sistem berubah.

AT bahagian seterusnya menganggap lebih kompleks konsep matematik, mendekatkan kita dengan perkataan " taburan normal"," taburan binomial "dan seumpamanya.

Elemen statistik matematik

Dalam statistik, yang merupakan salah satu bidang aplikasi teori kebarangkalian, terdapat banyak contoh di mana data untuk analisis tidak diberikan secara eksplisit. Maksudnya, bukan dalam angka, tetapi dalam bentuk pembahagian mengikut ciri, contohnya mengikut jantina. Untuk mengaplikasikan radas matematik kepada data tersebut dan membuat beberapa kesimpulan daripada keputusan yang diperolehi, adalah diperlukan untuk menukar data awal kepada format nombor. Sebagai peraturan, untuk melaksanakan ini, hasil positif diberikan nilai 1, dan negatif diberikan nilai 0. Oleh itu, kami memperoleh data statistik yang boleh dianalisis menggunakan kaedah matematik.

Langkah seterusnya dalam memahami apa itu taburan binomial pembolehubah rawak adalah untuk menentukan varians pembolehubah rawak dan jangkaan matematik. Kita akan bercakap tentang ini dalam bahagian seterusnya.

Nilai yang dijangkakan

Sebenarnya, memahami apa itu jangkaan matematik tidaklah sukar. Pertimbangkan sistem di mana terdapat banyak peristiwa yang berbeza dengan mereka kebarangkalian yang berbeza. Jangkaan matematik akan dipanggil nilai, sama dengan jumlah produk daripada nilai peristiwa ini (dan bentuk matematik, yang kami bincangkan dalam bahagian sebelumnya) mengenai kebarangkalian pelaksanaannya.

Jangkaan matematik bagi taburan binomial dikira mengikut skema yang sama: kita mengambil nilai pembolehubah rawak, mendarabnya dengan kebarangkalian hasil positif, dan kemudian meringkaskan data yang diperolehi untuk semua pembolehubah. Adalah sangat mudah untuk membentangkan data ini secara grafik - dengan cara ini perbezaan antara jangkaan matematik nilai yang berbeza dapat dilihat dengan lebih baik.

Dalam bahagian seterusnya, kami akan memberitahu anda sedikit tentang konsep yang berbeza - varians pembolehubah rawak. Ia juga berkait rapat dengan konsep seperti taburan kebarangkalian binomial, dan merupakan cirinya.

Varian taburan binomial

Nilai ini berkait rapat dengan yang sebelumnya dan juga mencirikan taburan data statistik. Dia mewakili persegi tengah penyimpangan nilai daripada jangkaan matematik mereka. Iaitu, varians pembolehubah rawak ialah jumlah perbezaan kuasa dua antara nilai pembolehubah rawak dan jangkaan matematiknya, didarab dengan kebarangkalian peristiwa ini.

Secara umum, ini sahaja yang perlu kita ketahui tentang varians untuk memahami apa itu taburan kebarangkalian binomial. Sekarang mari kita beralih kepada topik utama kita. Iaitu, apa yang ada di sebalik ini nampaknya cukup frasa kompleks"undang-undang pengedaran binomial".

Taburan binomial

Mari kita fahami dahulu mengapa taburan ini binomial. Ia berasal dari perkataan "binom". Anda mungkin pernah mendengar tentang binomial Newton - formula yang boleh digunakan untuk mengembangkan hasil tambah mana-mana dua nombor a dan b kepada sebarang kuasa bukan negatif n.

Seperti yang anda mungkin sudah meneka, formula binomial Newton dan formula taburan binomial adalah formula yang hampir sama. Dengan satu-satunya pengecualian yang kedua mempunyai nilai yang digunakan untuk kuantiti tertentu, dan yang pertama hanyalah alat matematik umum, aplikasi yang dalam amalan boleh berbeza.

Formula pengedaran

Fungsi taburan binomial boleh ditulis sebagai hasil tambah bagi istilah berikut:

(n!/(n-k)!k!)*p k *q n-k

Di sini n ialah bilangan eksperimen rawak bebas, p ialah bilangan hasil yang berjaya, q ialah bilangan hasil yang tidak berjaya, k ialah bilangan eksperimen (ia boleh mengambil nilai dari 0 hingga n),! - penetapan faktorial, fungsi nombor sedemikian, yang nilainya sama dengan hasil darab semua nombor yang naik kepadanya (contohnya, untuk nombor 4: 4!=1*2*3*4= 24).

Selain itu, fungsi taburan binomial boleh ditulis sebagai fungsi beta yang tidak lengkap. Walau bagaimanapun, ini sudah menjadi definisi yang lebih kompleks, yang digunakan hanya apabila menyelesaikan masalah statistik yang kompleks.

Taburan binomial, contoh yang kami periksa di atas, adalah salah satu yang paling banyak spesies mudah taburan dalam teori kebarangkalian. Terdapat juga taburan normal, iaitu jenis taburan binomial. Ia adalah yang paling biasa digunakan, dan paling mudah untuk dikira. Terdapat juga pengedaran Bernoulli, pengedaran Poisson, pengedaran bersyarat. Kesemuanya mencirikan secara grafik kawasan kebarangkalian proses tertentu di bawah keadaan yang berbeza.

Dalam bahagian seterusnya, kita akan mempertimbangkan aspek-aspek yang berkaitan dengan aplikasi radas matematik ini dalam kehidupan sebenar. Pada pandangan pertama, sudah tentu, nampaknya ini adalah satu lagi perkara matematik, yang, seperti biasa, tidak menemui aplikasi dalam kehidupan sebenar, dan secara amnya tidak diperlukan oleh sesiapa kecuali ahli matematik sendiri. Walau bagaimanapun, ini tidak berlaku. Lagipun, semua jenis pengedaran dan mereka perwakilan grafik dicipta secara eksklusif untuk matlamat praktikal, dan bukan sebagai kehendak saintis.

Permohonan

Setakat ini aplikasi pengedaran yang paling penting ditemui dalam statistik, kerana ia memerlukan analisis yang kompleks banyak data. Seperti yang ditunjukkan oleh amalan, sangat banyak tatasusunan data mempunyai pengagihan nilai yang lebih kurang sama: kawasan kritikal dengan nilai yang sangat rendah dan sangat tinggi, sebagai peraturan, mengandungi lebih sedikit elemen daripada nilai purata.

Analisis tatasusunan data yang besar diperlukan bukan sahaja dalam statistik. Ia amat diperlukan, sebagai contoh, dalam kimia fizikal. Dalam sains ini, ia digunakan untuk menentukan banyak kuantiti yang dikaitkan dengan getaran rawak dan pergerakan atom dan molekul.

Dalam bahagian seterusnya, kita akan membincangkan betapa pentingnya penggunaan sedemikian konsep statistik, sebagai binomial taburan pembolehubah rawak dalam Kehidupan seharian untuk awak dan saya.

Mengapa saya memerlukannya?

Ramai orang bertanya kepada diri sendiri soalan ini apabila ia datang kepada matematik. Dan dengan cara itu, matematik tidak sia-sia dipanggil ratu sains. Ia adalah asas fizik, kimia, biologi, ekonomi, dan dalam setiap sains ini, beberapa jenis pengedaran juga digunakan: sama ada taburan binomial diskret atau taburan normal, tidak mengapa. Dan jika kita melihat dengan lebih dekat dunia di sekeliling kita, kita akan melihat bahawa matematik digunakan di mana-mana: dalam kehidupan seharian, di tempat kerja, dan juga perhubungan manusia boleh dibentangkan dalam bentuk data statistik dan dianalisis (ini, dengan cara ini, dilakukan oleh mereka yang bekerja di organisasi khas mengumpul maklumat).

Sekarang mari kita bercakap sedikit tentang apa yang perlu dilakukan jika anda perlu mengetahui lebih banyak tentang topik ini daripada apa yang telah kami gariskan dalam artikel ini.

Maklumat yang kami berikan dalam artikel ini masih jauh dari lengkap. Terdapat banyak nuansa tentang bentuk pengedaran yang mungkin berlaku. Taburan binomial, seperti yang telah kita ketahui, adalah salah satu jenis utama di mana keseluruhannya statistik matematik dan teori kebarangkalian.

Jika anda berminat, atau berkaitan dengan kerja anda, anda perlu mengetahui lebih lanjut mengenai topik ini, anda perlu mempelajari kesusasteraan khusus. Mulakan dengan kursus universiti analisis matematik dan sampai ke bahagian teori kebarangkalian. Juga pengetahuan dalam bidang siri akan berguna, kerana taburan kebarangkalian binomial tidak lebih daripada satu siri istilah berturut-turut.

Kesimpulan

Sebelum menamatkan artikel, kami ingin memberitahu anda satu lagi perkara yang menarik. Ia melibatkan secara langsung topik artikel kami dan semua matematik secara umum.

Ramai orang mengatakan bahawa matematik adalah sains yang tidak berguna, dan tiada apa yang mereka pelajari di sekolah berguna untuk mereka. Tetapi pengetahuan tidak pernah berlebihan, dan jika sesuatu tidak berguna kepada anda dalam hidup, ini bermakna anda tidak mengingatinya. Jika anda mempunyai ilmu, mereka boleh membantu anda, tetapi jika anda tidak mempunyainya, maka anda tidak boleh mengharapkan bantuan daripada mereka.

Jadi, kami meneliti konsep taburan binomial dan semua definisi yang berkaitan dengannya dan bercakap tentang bagaimana ia digunakan dalam kehidupan kita.

Pertimbangkan taburan Binomial, hitung jangkaan matematiknya, varians, mod. Menggunakan fungsi MS EXCEL BINOM.DIST(), kami akan memplotkan fungsi taburan dan graf ketumpatan kebarangkalian. Mari kita anggarkan parameter taburan p, jangkaan matematik taburan, dan sisihan piawai. Pertimbangkan juga taburan Bernoulli.

Definisi. Biarlah mereka ditahan n ujian, di mana setiap satu hanya 2 peristiwa boleh berlaku: peristiwa "berjaya" dengan kebarangkalian hlm atau peristiwa "gagal" dengan kebarangkalian q =1-p (yang dipanggil Skim Bernoulli,Bernoullipercubaan).

Kebarangkalian mendapat tepat x kejayaan dalam hal ini n ujian adalah sama dengan:

Bilangan kejayaan dalam sampel x ialah pembolehubah rawak yang mempunyai Taburan binomial(Bahasa Inggeris) binomialpengedaran) hlm dan n– adalah parameter taburan ini.

Ingat bahawa untuk memohon Skim Bernoulli dan sepadan taburan binomial, syarat-syarat berikut mesti dipenuhi:

setiap percubaan mesti mempunyai dua keputusan, secara bersyarat dipanggil "kejayaan" dan "kegagalan".
keputusan setiap ujian tidak harus bergantung kepada keputusan ujian sebelumnya (kebebasan ujian).
kadar kejayaan hlm hendaklah tetap untuk semua ujian.

Pengedaran binomial dalam MS EXCEL

Dalam MS EXCEL, bermula dari versi 2010, untuk Taburan binomial terdapat fungsi BINOM.DIST() , tajuk bahasa Inggeris- BINOM.DIST(), yang membolehkan anda mengira kebarangkalian sampel itu tepat X"berjaya" (iaitu fungsi ketumpatan kebarangkalian p(x), lihat formula di atas), dan fungsi taburan integral(kebarangkalian bahawa sampel akan mempunyai x atau kurang "berjaya", termasuk 0).

Sebelum MS EXCEL 2010, EXCEL mempunyai fungsi BINOMDIST(), yang juga membolehkan anda mengira fungsi pengagihan dan ketumpatan kebarangkalian p(x). BINOMDIST() ditinggalkan dalam MS EXCEL 2010 untuk keserasian.

Fail contoh mengandungi graf ketumpatan taburan kebarangkalian dan .

Taburan binomial mempunyai sebutan B(n; hlm) .

Catatan: Untuk bangunan fungsi taburan integral jenis carta yang sesuai Jadual, untuk ketumpatan pengedaran – Histogram dengan kumpulan. Untuk maklumat lanjut tentang membina carta, baca artikel Jenis carta utama.

Catatan: Untuk kemudahan menulis formula dalam fail contoh, Nama untuk parameter telah dicipta Taburan binomial: n dan p.

Fail contoh menunjukkan pelbagai pengiraan kebarangkalian menggunakan fungsi MS EXCEL:

Seperti yang dilihat dalam gambar di atas, diandaikan bahawa:

Populasi tak terhingga dari mana sampel dibuat mengandungi 10% (atau 0.1) unsur yang baik (parameter hlm, argumen fungsi ketiga =BINOM.DIST() )
Untuk mengira kebarangkalian bahawa dalam sampel 10 elemen (parameter n, hujah kedua fungsi) akan ada tepat 5 elemen yang sah (hujah pertama), anda perlu menulis formula: =BINOM.DIST(5, 10, 0.1, SALAH)
Elemen terakhir, keempat ditetapkan = SALAH, i.e. nilai fungsi dikembalikan ketumpatan pengedaran.

Jika nilai argumen keempat = TRUE, maka fungsi BINOM.DIST() mengembalikan nilai fungsi taburan integral atau secara ringkas fungsi pengagihan. Dalam kes ini, kita boleh mengira kebarangkalian bahawa bilangan unsur yang baik dalam sampel akan datang julat tertentu, sebagai contoh, 2 atau kurang (termasuk 0).

Untuk melakukan ini, anda perlu menulis formula:
= BINOM.DIST(2, 10, 0.1, BENAR)

Catatan: Untuk nilai bukan integer bagi x, . Sebagai contoh, formula berikut akan mengembalikan nilai yang sama:
=BINOM.DIST( 2 ; sepuluh; 0.1; BENAR)
=BINOM.DIST( 2,9 ; sepuluh; 0.1; BENAR)

Catatan: Dalam fail contoh ketumpatan kebarangkalian dan fungsi pengagihan juga dikira menggunakan definisi dan fungsi COMBIN().

Penunjuk pengedaran

AT contoh fail pada helaian Contoh terdapat formula untuk mengira beberapa petunjuk pengedaran:

=n*p;
(sisihan piawai kuasa dua) = n*p*(1-p);
= (n+1)*p;
=(1-2*p)*ROOT(n*p*(1-p)).

Kami memperoleh formula jangkaan matematik Taburan binomial menggunakan Skim Bernoulli.

Mengikut takrifan nilai rawak X masuk Skim Bernoulli(pembolehubah rawak Bernoulli) mempunyai fungsi pengagihan:

Pengagihan ini dipanggil Pengagihan Bernoulli.

Catatan: Pengagihan Bernoulli – kes istimewa Taburan binomial dengan parameter n=1.

Mari kita hasilkan 3 tatasusunan 100 nombor dengan kebarangkalian kejayaan yang berbeza: 0.1; 0.5 dan 0.9. Untuk melakukan ini, dalam tetingkap Generasi nombor rawak ditetapkan pilihan berikut bagi setiap kebarangkalian p:

Catatan: Jika anda menetapkan pilihan Taburan rawak (Benih rawak), maka anda boleh memilih yang khusus set rawak nombor yang dijana. Contohnya, dengan menetapkan pilihan ini =25, anda boleh menjana set nombor rawak yang sama pada komputer yang berbeza (jika, sudah tentu, parameter pengedaran lain adalah sama). Nilai pilihan boleh mengambil nilai integer dari 1 hingga 32,767. Nama pilihan Taburan rawak boleh mengelirukan. Adalah lebih baik untuk menterjemahkannya sebagai Tetapkan nombor dengan nombor rawak.

Akibatnya, kita akan mempunyai 3 lajur 100 nombor, berdasarkan yang, sebagai contoh, kita boleh menganggarkan kebarangkalian kejayaan hlm mengikut formula: Bilangan kejayaan/100(cm. contoh helaian fail Menjana Bernoulli).

Catatan: Untuk Pengagihan Bernoulli dengan p=0.5, anda boleh menggunakan formula =RANDBETWEEN(0;1) , yang sepadan dengan .

Penjanaan nombor rawak. Taburan binomial

Katakan terdapat 7 item yang rosak dalam sampel. Ini bermakna "kemungkinan besar" bahagian produk yang rosak telah berubah. hlm, yang merupakan ciri proses pengeluaran kami. Walaupun situasi ini "sangat berkemungkinan", terdapat kemungkinan (risiko alfa, ralat jenis 1, "penggera palsu") yang hlm kekal tidak berubah, dan peningkatan bilangan produk yang rosak adalah disebabkan oleh pensampelan rawak.

Seperti yang dapat dilihat dalam rajah di bawah, 7 ialah bilangan produk yang rosak yang boleh diterima untuk proses dengan p=0.21 pada nilai yang sama Alfa. Ini menggambarkan bahawa apabila ambang item yang rosak dalam sampel melebihi, hlm"mungkin" meningkat. Frasa "kemungkinan besar" bermaksud hanya terdapat 10% peluang (100%-90%) bahawa sisihan peratusan produk yang rosak di atas ambang hanya disebabkan oleh sebab rawak.

Oleh itu, melebihi bilangan ambang produk yang rosak dalam sampel boleh berfungsi sebagai isyarat bahawa proses telah menjadi terganggu dan mula menghasilkan b kira-kira peratusan produk yang rosak yang lebih tinggi.

Catatan: Sebelum MS EXCEL 2010, EXCEL mempunyai fungsi CRITBINOM() , yang bersamaan dengan BINOM.INV() . CRITBINOM() ditinggalkan dalam MS EXCEL 2010 dan lebih tinggi untuk keserasian.

Kaitan taburan Binomial dengan taburan lain

Jika parameter n Taburan binomial cenderung kepada infiniti dan hlm cenderung kepada 0, maka dalam kes ini Taburan binomial boleh dianggarkan.
Ia adalah mungkin untuk merumuskan keadaan apabila anggaran Pengagihan Poisson berfungsi dengan baik:

hlm<0,1 (lebih kurang hlm dan banyak lagi n, lebih tepat anggaran);
hlm>0,9 (mempertimbangkan itu q=1- hlm, pengiraan dalam kes ini mesti dilakukan menggunakan q(a X perlu diganti dengan n- x). Oleh itu, semakin kurang q dan banyak lagi n, lebih tepat anggarannya).

Pada 0.1<=p<=0,9 и n*p>10 Taburan binomial boleh dianggarkan.

Pada gilirannya, Taburan binomial boleh berfungsi sebagai anggaran yang baik apabila saiz populasi ialah N Taburan hipergeometrik jauh lebih besar daripada saiz sampel n (iaitu, N>>n atau n/N<<1).

Anda boleh membaca lebih lanjut tentang hubungan pengedaran di atas dalam artikel. Contoh penghampiran juga diberikan di sana, dan syarat diterangkan apabila mungkin dan dengan ketepatan apa.

NASIHAT: Anda boleh membaca tentang pengedaran lain MS EXCEL dalam artikel.

Taburan binomial adalah salah satu taburan kebarangkalian yang paling penting untuk pembolehubah rawak yang berubah-ubah secara diskret. Taburan binomial ialah taburan kebarangkalian bagi suatu nombor m peristiwa TAPI dalam n pemerhatian yang saling bebas. Selalunya acara TAPI dipanggil "kejayaan" pemerhatian, dan peristiwa yang bertentangan - "kegagalan", tetapi penunjukan ini sangat bersyarat.

Syarat taburan binomial:

dijalankan secara keseluruhan n percubaan di mana peristiwa itu TAPI mungkin atau mungkin tidak berlaku;
peristiwa TAPI dalam setiap percubaan boleh berlaku dengan kebarangkalian yang sama hlm;
ujian adalah saling bebas.

Kebarangkalian bahawa dalam n acara ujian TAPI betul-betul m kali, boleh dikira menggunakan formula Bernoulli:

di mana hlm- kebarangkalian kejadian itu berlaku TAPI;

q = 1 - hlm ialah kebarangkalian kejadian yang bertentangan berlaku.

Mari kita fikirkan mengapa taburan binomial berkaitan dengan formula Bernoulli dengan cara yang diterangkan di atas . Acara - bilangan kejayaan di n ujian dibahagikan kepada beberapa pilihan, di mana setiap satu kejayaan dicapai dalam m percubaan, dan kegagalan - dalam n - m ujian. Pertimbangkan salah satu daripada pilihan ini - B1 . Mengikut peraturan penambahan kebarangkalian, kita mendarabkan kebarangkalian kejadian berlawanan:

dan jika kita nyatakan q = 1 - hlm, kemudian

Kebarangkalian yang sama akan mempunyai pilihan lain di mana m kejayaan dan n - m kegagalan. Bilangan pilihan tersebut adalah sama dengan bilangan cara yang boleh dilakukan n ujian dapat m kejayaan.

Jumlah kebarangkalian semua m nombor acara TAPI(nombor dari 0 hingga n) adalah sama dengan satu:

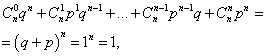
di mana setiap sebutan ialah sebutan bagi binomial Newton. Oleh itu, taburan yang dipertimbangkan dipanggil taburan binomial.

Dalam amalan, selalunya perlu untuk mengira kebarangkalian "paling banyak m kejayaan dalam n ujian" atau "sekurang-kurangnya m kejayaan dalam n ujian". Untuk ini, formula berikut digunakan.

Fungsi integral, iaitu kebarangkalian F(m) bahawa dalam n peristiwa pemerhatian TAPI tidak akan datang lagi m sekali, boleh dikira menggunakan formula:

Pada gilirannya kebarangkalian F(≥m) bahawa dalam n peristiwa pemerhatian TAPI datang sekurang-kurangnya m sekali, dikira dengan formula:

Kadangkala adalah lebih mudah untuk mengira kebarangkalian bahawa dalam n peristiwa pemerhatian TAPI tidak akan datang lagi m kali, melalui kebarangkalian kejadian yang bertentangan:

Mana antara formula yang hendak digunakan bergantung pada formula yang mengandungi lebih sedikit istilah.

Ciri-ciri taburan binomial dikira menggunakan formula berikut .

Nilai jangkaan: .

serakan: .

Sisihan piawai: .

Pengedaran dan pengiraan binomial dalam MS Excel

Kebarangkalian Taburan Binomial P n ( m) dan nilai fungsi kamiran F(m) boleh dikira menggunakan fungsi MS Excel BINOM.DIST. Tetingkap untuk pengiraan yang sepadan ditunjukkan di bawah (klik butang kiri tetikus untuk membesarkan).

MS Excel memerlukan anda memasukkan data berikut:

bilangan kejayaan;
bilangan ujian;
kebarangkalian kejayaan;
integral - nilai logik: 0 - jika anda perlu mengira kebarangkalian P n ( m) dan 1 - jika kebarangkalian F(m).

Contoh 1 Pengurus syarikat itu meringkaskan maklumat tentang bilangan kamera yang dijual sepanjang 100 hari yang lalu. Jadual meringkaskan maklumat dan mengira kebarangkalian bahawa bilangan kamera tertentu akan dijual setiap hari.

Hari ini berakhir dengan keuntungan jika 13 atau lebih kamera dijual. Kebarangkalian bahawa hari itu akan diuruskan dengan keuntungan:

Kebarangkalian bahawa hari itu akan bekerja tanpa keuntungan:

Biarkan kebarangkalian bahawa hari itu diuruskan dengan keuntungan adalah tetap dan sama dengan 0.61, dan bilangan kamera yang dijual setiap hari tidak bergantung pada hari tersebut. Kemudian anda boleh menggunakan taburan binomial, di mana acara itu TAPI- hari itu akan diusahakan dengan keuntungan, - tanpa keuntungan.

Kebarangkalian bahawa daripada 6 hari semua akan diuruskan dengan keuntungan:

Kami mendapat hasil yang sama menggunakan fungsi MS Excel BINOM.DIST (nilai nilai kamiran ialah 0):

P 6 (6 ) = BINOM.DIST(6; 6; 0.61; 0) = 0.052.

Kebarangkalian bahawa daripada 6 hari 4 atau lebih hari akan diusahakan dengan keuntungan:

di mana ,

Menggunakan fungsi MS Excel BINOM.DIST, kami mengira kebarangkalian bahawa daripada 6 hari tidak lebih daripada 3 hari akan dilengkapkan dengan keuntungan (nilai nilai kamiran ialah 1):

P 6 (≤3 ) = BINOM.DIST(3, 6, 0.61, 1) = 0.435.

Kebarangkalian bahawa daripada 6 hari semua akan diselesaikan dengan kerugian:

Kami mengira penunjuk yang sama menggunakan fungsi MS Excel BINOM.DIST:

P 6 (0 ) = BINOM.DIST(0; 6; 0.61; 0) = 0.0035.

Selesaikan masalah itu sendiri dan kemudian lihat penyelesaiannya

Contoh 2 Sebuah guci mengandungi 2 bola putih dan 3 bola hitam. Sebiji bola dikeluarkan dari balang, warna ditetapkan dan diletakkan semula. Percubaan diulang 5 kali. Bilangan kemunculan bola putih ialah pembolehubah rawak diskret X, diedarkan mengikut undang-undang binomial. Susun hukum taburan pembolehubah rawak. Tentukan mod, jangkaan matematik dan varians.

Kami terus menyelesaikan masalah bersama

Contoh 3 Dari perkhidmatan kurier pergi ke objek n= 5 kurier. Setiap kurier dengan kebarangkalian hlm= 0.3 lewat untuk objek tanpa mengira yang lain. Pembolehubah rawak diskret X- bilangan kurier lewat. Bina satu siri taburan pembolehubah rawak ini. Cari jangkaan matematiknya, varians, sisihan piawai. Cari kebarangkalian bahawa sekurang-kurangnya dua kurier akan terlambat untuk objek.

Taburan binomial

taburan kebarangkalian bilangan kejadian beberapa peristiwa dalam percubaan bebas berulang. Jika, bagi setiap percubaan, kebarangkalian sesuatu peristiwa berlaku ialah R, dan 0 ≤ hlm≤ 1, maka bilangan μ kejadian peristiwa ini untuk n percubaan bebas, terdapat pembolehubah rawak yang mengambil nilai m = 1, 2,.., n dengan kebarangkalian

di mana q= 1 - p, a - pekali binomial (oleh itu dinamakan B. r.). Formula di atas kadangkala dipanggil formula Bernoulli. Jangkaan matematik dan varians kuantiti μ, yang mempunyai B. R., adalah sama dengan M(μ) = np dan D(μ) = npq, masing-masing. Pada umumnya n, berdasarkan teorem Laplace (Lihat teorem Laplace), B. r. hampir dengan taburan normal (Lihat taburan normal), iaitu apa yang digunakan dalam amalan. Pada kecil n adalah perlu untuk menggunakan jadual B. r.

Lit.: Bolshev L. N., Smirnov N. V., Jadual statistik matematik, M., 1965.

Ensiklopedia Soviet yang Hebat. - M.: Ensiklopedia Soviet. 1969-1978 .

Lihat apakah "Taburan binomial" dalam kamus lain:

Fungsi kebarangkalian ... Wikipedia

- (taburan binomial) Taburan yang membolehkan anda mengira kebarangkalian berlakunya sebarang peristiwa rawak yang diperoleh hasil daripada memerhati beberapa peristiwa bebas, jika kebarangkalian berlakunya unsur unsur konstituennya ... ... Kamus ekonomi

- (Taburan Bernoulli) taburan kebarangkalian bilangan kejadian beberapa peristiwa dalam percubaan bebas berulang, jika kebarangkalian kejadian ini berlaku dalam setiap percubaan adalah sama dengan p(0 p 1). Betul, nombornya? terdapat kejadian peristiwa ini ... ... Kamus Ensiklopedia Besar

taburan binomial- - Topik telekomunikasi, konsep asas EN taburan binomial ...

- (Taburan Bernoulli), taburan kebarangkalian bilangan kejadian beberapa peristiwa dalam percubaan bebas berulang, jika kebarangkalian kejadian ini berlaku dalam setiap percubaan ialah p (0≤p≤1). Iaitu, bilangan μ kejadian peristiwa ini… … Kamus ensiklopedia

taburan binomial- 1.49. taburan binomial Taburan kebarangkalian pembolehubah rawak diskret X, mengambil sebarang nilai integer dari 0 hingga n, supaya untuk x = 0, 1, 2, ..., n dan parameter n = 1, 2, ... dan 0< p < 1, где Источник … Buku rujukan kamus istilah dokumentasi normatif dan teknikal

Taburan Bernoulli, taburan kebarangkalian pembolehubah rawak X, yang mengambil nilai integer dengan kebarangkalian, masing-masing (pekali binomial; parameter p B. R., dipanggil kebarangkalian hasil positif, yang mengambil nilai ... Ensiklopedia Matematik

- (Taburan Bernoulli), taburan kebarangkalian bilangan kejadian peristiwa tertentu dalam percubaan bebas berulang, jika kebarangkalian kejadian ini berlaku dalam setiap percubaan ialah p (0<или = p < или = 1). Именно, число м появлений … Sains semula jadi. Kamus ensiklopedia

Taburan kebarangkalian binomial- (taburan binomial) Taburan yang diperhatikan dalam kes di mana keputusan setiap eksperimen bebas (pemerhatian statistik) mengambil satu daripada dua nilai yang mungkin: kemenangan atau kekalahan, kemasukan atau pengecualian, tambah atau ... Kamus Ekonomi dan Matematik

taburan kebarangkalian binomial- Taburan yang diperhatikan dalam kes di mana hasil setiap eksperimen bebas (pemerhatian statistik) mengambil satu daripada dua nilai yang mungkin: kemenangan atau kekalahan, kemasukan atau pengecualian, tambah atau tolak, 0 atau 1. Iaitu ... ... Buku Panduan Penterjemah Teknikal

Buku

Teori Kebarangkalian dan Statistik Matematik dalam Masalah. Lebih daripada 360 tugas dan latihan, D. A. Borzykh. Manual yang dicadangkan mengandungi tugas pelbagai peringkat kerumitan. Walau bagaimanapun, penekanan utama diberikan pada tugas yang sederhana kompleks. Ini sengaja dilakukan untuk menggalakkan pelajar…
Teori Kebarangkalian dan Statistik Matematik dalam Masalah: Lebih daripada 360 Masalah dan Latihan, Borzykh D. Manual yang dicadangkan mengandungi masalah pelbagai peringkat kerumitan. Walau bagaimanapun, penekanan utama diberikan pada tugas yang sederhana kompleks. Ini sengaja dilakukan untuk menggalakkan pelajar…

Bab 7

Undang-undang khusus taburan pembolehubah rawak

Jenis-jenis hukum taburan pembolehubah rawak diskret

Biarkan pembolehubah rawak diskret mengambil nilainya X 1 , X 2 , …, x n, … . Kebarangkalian nilai ini boleh dikira menggunakan pelbagai formula, contohnya, menggunakan teorem asas teori kebarangkalian, formula Bernoulli, atau beberapa formula lain. Bagi sesetengah formula ini, undang-undang pengedaran mempunyai namanya sendiri.

Hukum taburan yang paling biasa bagi pembolehubah rawak diskret ialah binomial, geometri, hipergeometrik, hukum taburan Poisson.

Undang-undang pengedaran binomial

Biar terhasil n percubaan bebas, di mana setiap satu peristiwa mungkin atau mungkin tidak berlaku TAPI. Kebarangkalian berlakunya peristiwa ini dalam setiap percubaan tunggal adalah malar, tidak bergantung pada nombor percubaan dan sama dengan R=R(TAPI). Oleh itu kebarangkalian bahawa peristiwa itu tidak akan berlaku TAPI dalam setiap ujian juga adalah tetap dan sama dengan q=1–R. Pertimbangkan pembolehubah rawak X sama dengan bilangan kejadian kejadian TAPI dalam n ujian. Adalah jelas bahawa nilai kuantiti ini adalah sama dengan

X 1 =0 - peristiwa TAPI dalam n ujian tidak muncul;

X 2 =1 – peristiwa TAPI dalam n percubaan muncul sekali;

X 3 =2 - peristiwa TAPI dalam n percubaan muncul dua kali;

…………………………………………………………..

x n +1 = n- acara TAPI dalam n ujian muncul segala-galanya n sekali.

Kebarangkalian nilai ini boleh dikira menggunakan formula Bernoulli (4.1):

di mana kepada=0, 1, 2, …,n .

Undang-undang pengedaran binomial X sama dengan bilangan kejayaan dalam n Percubaan Bernoulli, dengan kebarangkalian berjaya R.

Jadi, pembolehubah rawak diskret mempunyai taburan binomial (atau diedarkan mengikut undang-undang binomial) jika kemungkinan nilainya ialah 0, 1, 2, …, n, dan kebarangkalian yang sepadan dikira dengan formula (7.1).

Taburan binomial bergantung kepada dua parameter R dan n.

Siri taburan pembolehubah rawak yang diedarkan mengikut hukum binomial mempunyai bentuk:

X			…	k	…	n
R			…		…

Contoh 7.1 . Tiga tembakan bebas dilepaskan ke sasaran. Kebarangkalian untuk memukul setiap pukulan ialah 0.4. Nilai rawak X- bilangan pukulan pada sasaran. Bina siri pengedarannya.

Penyelesaian. Kemungkinan nilai pembolehubah rawak X adalah X 1 =0; X 2 =1; X 3 =2; X 4=3. Cari kebarangkalian yang sepadan menggunakan formula Bernoulli. Adalah mudah untuk menunjukkan bahawa penggunaan formula ini di sini adalah wajar sepenuhnya. Ambil perhatian bahawa kebarangkalian untuk tidak mencapai sasaran dengan satu pukulan akan bersamaan dengan 1-0.4=0.6. Dapatkan

Siri pengedaran mempunyai bentuk berikut:

X
R	0,216	0,432	0,288	0,064

Adalah mudah untuk menyemak bahawa jumlah semua kebarangkalian adalah sama dengan 1. Pembolehubah rawak itu sendiri X diedarkan mengikut hukum binomial. ■

Mari kita cari jangkaan dan varians matematik bagi pembolehubah rawak yang diedarkan mengikut hukum binomial.

Apabila menyelesaikan contoh 6.5, telah ditunjukkan bahawa jangkaan matematik bilangan kejadian sesuatu peristiwa TAPI dalam n ujian bebas, jika kebarangkalian berlaku TAPI dalam setiap ujian adalah malar dan sama R, sama n· R

Dalam contoh ini, pembolehubah rawak telah digunakan, diedarkan mengikut hukum binomial. Oleh itu, penyelesaian Contoh 6.5 adalah, sebenarnya, bukti teorem berikut.

Teorem 7.1. Jangkaan matematik bagi pembolehubah rawak diskret yang diedarkan mengikut hukum binomial adalah sama dengan hasil darab bilangan percubaan dan kebarangkalian "berjaya", i.e. M(X)=n· R.

Teorem 7.2. Varians pembolehubah rawak diskret yang diedarkan mengikut hukum binomial adalah sama dengan hasil darab bilangan percubaan dengan kebarangkalian "berjaya" dan kebarangkalian "gagal", i.e. D(X)=npq.

Kecondongan dan kurtosis pembolehubah rawak yang diedarkan mengikut hukum binomial ditentukan oleh formula

Rumus ini boleh diperoleh menggunakan konsep momen awal dan momen pusat.

Undang-undang pengedaran binomial mendasari banyak situasi sebenar. Untuk nilai yang besar n taburan binomial boleh dianggarkan oleh taburan lain, khususnya taburan Poisson.

Pengagihan Poisson

Biarlah ada n Percubaan Bernoulli, dengan bilangan percubaan n cukup besar. Sebelum ini, ditunjukkan bahawa dalam kes ini (jika, sebagai tambahan, kebarangkalian R perkembangan TAPI sangat kecil) untuk mencari kebarangkalian bahawa sesuatu peristiwa TAPI untuk hadir t sekali dalam ujian, anda boleh menggunakan formula Poisson (4.9). Jika pembolehubah rawak X bermakna bilangan kejadian kejadian TAPI dalam n Bernoulli percubaan, maka kebarangkalian itu X akan mengambil makna k boleh dikira dengan formula

, (7.2)

di mana λ = no.

Undang-undang pengedaran Poisson dipanggil taburan pembolehubah rawak diskret X, yang mana nilai yang mungkin adalah integer bukan negatif, dan kebarangkalian p t nilai ini didapati dengan formula (7.2).

Nilai λ = no dipanggil parameter Pengagihan Poisson.

Pembolehubah rawak yang diedarkan mengikut hukum Poisson boleh mengambil bilangan nilai yang tidak terhingga. Oleh kerana untuk taburan ini kebarangkalian R Kejadian sesuatu peristiwa dalam setiap percubaan adalah kecil, maka taburan ini kadang-kadang dipanggil hukum fenomena jarang.

Siri taburan pembolehubah rawak yang diedarkan mengikut hukum Poisson mempunyai bentuk

X					…	t	…
R					…		…

Adalah mudah untuk mengesahkan bahawa jumlah kebarangkalian baris kedua adalah sama dengan 1. Untuk melakukan ini, kita perlu ingat bahawa fungsi itu boleh dikembangkan dalam siri Maclaurin, yang menumpu untuk sebarang X. Dalam kes ini kita ada

. (7.3)

Seperti yang dinyatakan, undang-undang Poisson dalam kes mengehadkan tertentu menggantikan undang-undang binomial. Contohnya ialah pembolehubah rawak X, nilai yang sama dengan bilangan kegagalan untuk tempoh masa tertentu dengan penggunaan berulang peranti teknikal. Diandaikan bahawa peranti ini mempunyai kebolehpercayaan yang tinggi, i.e. kebarangkalian kegagalan dalam satu aplikasi adalah sangat kecil.

Sebagai tambahan kepada kes pengehadan tersebut, dalam amalan terdapat pembolehubah rawak yang diedarkan mengikut undang-undang Poisson, tidak berkaitan dengan taburan binomial. Sebagai contoh, pengedaran Poisson sering digunakan apabila berurusan dengan bilangan peristiwa yang berlaku dalam tempoh masa (bilangan panggilan ke pertukaran telefon pada waktu itu, bilangan kereta yang tiba di tempat cuci kereta pada siang hari, bilangan mesin berhenti setiap minggu, dsb.). Semua peristiwa ini mesti membentuk apa yang dipanggil aliran peristiwa, yang merupakan salah satu konsep asas teori beratur. Parameter λ mencirikan keamatan purata aliran peristiwa.