Mengkaji pergerakan jasad yang dilontar pada sudut ke arah mengufuk. Pergerakan jasad yang dilontar pada sudut ke ufuk Pengiraan jarak penerbangan
Arahan
Biarkan sebuah jasad dilontar pada sudut α ke ufuk dengan kelajuan awal v0. Biarkan koordinat awal badan ialah sifar: x(0)=0, y(0)=0. Dalam unjuran pada paksi koordinat, halaju awal akan diuraikan kepada dua komponen: v0(x) dan v0(y). Kelajuan yang sama secara umum. Sepanjang paksi Lembu, kelajuan secara konvensional dianggap malar, manakala sepanjang paksi Oy ia berubah di bawah pengaruh . Pecutan graviti g boleh diambil kira-kira 10 m/s².
Sudut α di mana badan dibaling tidak diberikan secara kebetulan. Melaluinya anda boleh menerangkan kelajuan awal dalam paksi koordinat. Oleh itu, v0(x)=v0·cos(α), v0(y)=v0·sin(α). Sekarang kita boleh mendapatkan fungsi komponen koordinat halaju: v(x)=const=v0(x)=v0·cos(α), v(y)=v0(y)-g·t=v0·sin( α)-g· t.
Koordinat x dan y badan bergantung pada masa t. Oleh itu, kita boleh mencipta dua persamaan pergantungan: x=x0+v0(x) t+a(x) t²/2, y=y0+v0(y) t+a(y) t²/2. Oleh kerana x0=0, a(x)=0, maka x=v0(x) t=v0 cos(α) t. Juga diketahui bahawa y0=0, a(y)=-g (tanda “ ” muncul kerana arah pecutan graviti g dan arah positif paksi Oy adalah bertentangan). Oleh itu y=v0·sin(α)·t-g·t²/2.
Masa penerbangan boleh dinyatakan daripada formula kelajuan, mengetahui bahawa pada titik maksimum badan berhenti seketika (v = 0), dan tempoh "naik" dan "turun" adalah sama. Jadi, apabila menggantikan v(y)=0 ke dalam persamaan v(y)=v0·sin(α)-g·t ternyata: 0=v0·sin(α)-g·t(p), dengan t (p) – masa puncak, “t vertex”. Oleh itu t(p)=v0·sin(α)/g. Jumlah masa penerbangan kemudiannya akan dinyatakan sebagai t=2·v0·sin(α)/g.
Formula yang sama boleh diperolehi dengan cara lain, secara matematik, daripada persamaan untuk koordinat y=v0·sin(α)·t-g·t²/2. Persamaan ini boleh ditulis semula dalam bentuk yang diubah suai sedikit: y=-g/2·t²+v0·sin(α)·t. Ia boleh dilihat bahawa ini adalah pergantungan kuadratik, di mana y ialah fungsi, t ialah hujah. Puncak parabola yang menerangkan trajektori ialah titik t(p)=[-v0·sin(α)]/[-2g/2]. Tolak dan dua batal, jadi t(p)=v0·sin(α)/g. Jika kita menyatakan ketinggian maksimum sebagai H dan ingat bahawa titik puncak ialah puncak parabola di mana badan bergerak, maka H=y(t(p))=v0²sin²(α)/2g. Iaitu, untuk mendapatkan ketinggian, anda perlu menggantikan "t vertex" ke dalam persamaan untuk koordinat y.
Jadi, masa penerbangan ditulis sebagai t=2·v0·sin(α)/g. Untuk menukarnya, anda perlu menukar kelajuan awal dan sudut kecenderungan dengan sewajarnya. Semakin tinggi kelajuan, semakin lama badan itu terbang. Dengan sudut ia agak lebih rumit, kerana masa tidak bergantung pada sudut itu sendiri, tetapi pada sinusnya. Nilai sinus maksimum yang mungkin - perpaduan - dicapai pada sudut kecondongan 90°. Ini bermakna bahawa badan terbang paling lama apabila ia dilemparkan secara menegak ke atas.
Julat penerbangan ialah koordinat x akhir. Jika kita menggantikan masa penerbangan yang telah dijumpai ke dalam persamaan x=v0·cos(α)·t, maka adalah mudah untuk mencari bahawa L=2v0²sin(α)cos(α)/g. Di sini kita boleh menggunakan formula sudut dwi trigonometri 2sin(α)cos(α)=sin(2α), kemudian L=v0²sin(2α)/g. Sinus dua alfa adalah sama dengan satu apabila 2α=n/2, α=n/4. Oleh itu, jarak penerbangan adalah maksimum jika badan dibaling pada sudut 45°.
Jika jasad dilemparkan pada sudut ke ufuk, maka dalam penerbangan ia digerakkan oleh daya graviti dan daya rintangan udara. Jika daya rintangan diabaikan, maka satu-satunya daya yang tinggal ialah graviti. Oleh itu, disebabkan oleh undang-undang ke-2 Newton, jasad bergerak dengan pecutan sama dengan pecutan graviti; unjuran pecutan pada paksi koordinat ax = 0, ay = - g.
Rajah 1. Ciri-ciri kinematik jasad yang dilontar pada sudut ke arah mengufuk
Sebarang pergerakan kompleks titik material boleh diwakili sebagai superposisi pergerakan bebas di sepanjang paksi koordinat, dan ke arah paksi yang berbeza jenis pergerakan mungkin berbeza. Dalam kes kami, gerakan badan terbang boleh diwakili sebagai superposisi dua gerakan bebas: gerakan seragam sepanjang paksi mendatar (paksi-X) dan gerakan dipercepatkan seragam sepanjang paksi menegak (paksi-Y) (Rajah 1). .
Oleh itu, unjuran halaju badan berubah mengikut masa seperti berikut:
![]()
dengan $v_0$ ialah kelajuan awal, $(\mathbf \alpha )$ ialah sudut lontaran.
Dengan pilihan asal kami, koordinat awal (Rajah 1) ialah $x_0=y_0=0$. Kemudian kita dapat:
 (1)
(1)
Mari analisa formula (1). Mari kita tentukan masa pergerakan badan yang dilemparkan. Untuk melakukan ini, mari kita tetapkan koordinat y sama dengan sifar, kerana pada saat mendarat ketinggian badan adalah sifar. Dari sini kami mendapat masa penerbangan:
Nilai masa kedua di mana ketinggian sifar ialah sifar, yang sepadan dengan momen lontaran, i.e. nilai ini juga mempunyai makna fizikal.
Kami memperoleh julat penerbangan daripada formula pertama (1). Julat penerbangan ialah nilai koordinat x pada penghujung penerbangan, i.e. pada masa bersamaan dengan $t_0$. Menggantikan nilai (2) ke dalam formula pertama (1), kita dapat:
Daripada formula ini dapat dilihat bahawa jarak penerbangan terhebat dicapai pada sudut lontaran 45 darjah.
Ketinggian angkat maksimum badan yang dibaling boleh didapati daripada formula kedua (1). Untuk melakukan ini, anda perlu menggantikan nilai masa yang sama dengan separuh masa penerbangan (2) ke dalam formula ini, kerana Ia adalah di titik tengah trajektori bahawa ketinggian penerbangan adalah maksimum. Menjalankan pengiraan, kita dapat
Daripada persamaan (1) seseorang boleh mendapatkan persamaan trajektori badan, i.e. persamaan yang mengaitkan koordinat x dan y suatu jasad semasa pergerakan. Untuk melakukan ini, anda perlu menyatakan masa dari persamaan pertama (1):
dan gantikannya ke dalam persamaan kedua. Kemudian kita dapat:
![]()
Persamaan ini ialah persamaan trajektori gerakan. Dapat dilihat bahawa ini adalah persamaan parabola dengan cabangnya ke bawah, seperti yang ditunjukkan oleh tanda "-" di hadapan istilah kuadratik. Perlu diingat bahawa sudut lontaran $\alpha $ dan fungsinya hanyalah pemalar di sini, i.e. nombor tetap.
Sebuah jasad dilontar dengan kelajuan v0 pada sudut $(\mathbf \alpha )$ ke ufuk. Masa penerbangan $t = 2 s$. Ketinggian Hmax badan akan meningkat?
$$t_B = 2 s$$ $$H_maks - ?$$

Hukum pergerakan badan mempunyai bentuk:
$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $
Vektor halaju awal membentuk sudut $(\mathbf \alpha )$ dengan paksi OX. Oleh itu,
\ \ \
Sebiji batu dilemparkan dari puncak gunung pada sudut = 30$()^\circ$ ke ufuk dengan kelajuan awal $v_0 = 6 m/s$. Sudut satah condong = 30$()^\circ$. Pada jarak manakah dari tempat melontar batu itu akan jatuh?
$$ \alfa =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Mari letakkan asal koordinat pada titik lontaran, OX - sepanjang satah condong ke bawah, OY - berserenjang dengan satah condong ke atas. Ciri-ciri kinematik pergerakan:
Undang-undang pergerakan:
$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \kanan.$$ \
Menggantikan nilai yang terhasil $t_В$, kita dapati $S$:
Ini adalah tugas kreatif untuk kelas induk dalam sains komputer untuk pelajar sekolah di FEFU.
Tujuan tugasan adalah untuk mengetahui bagaimana trajektori badan akan berubah jika rintangan udara diambil kira. Ia juga perlu untuk menjawab soalan sama ada jarak penerbangan masih akan mencapai nilai maksimum pada sudut lontaran 45°, jika rintangan udara diambil kira.
Bahagian "Penyelidikan Analitik" menggariskan teori. Bahagian ini boleh dilangkau, tetapi bahagian ini sepatutnya jelas kepada anda kerana... O Kebanyakan ini anda pelajari di sekolah.
Bahagian "Kajian Berangka" mengandungi penerangan tentang algoritma yang mesti dilaksanakan pada komputer. Algoritma ini mudah dan ringkas, jadi semua orang sepatutnya dapat melakukannya.
Penyelidikan analisis
Mari kita perkenalkan sistem koordinat segi empat tepat seperti yang ditunjukkan dalam rajah. Pada saat awal suatu badan berjisim m terletak di tempat asal. Vektor pecutan jatuh bebas diarahkan menegak ke bawah dan mempunyai koordinat (0, - g).- vektor halaju awal. Mari kembangkan vektor ini menjadi asasnya:
Mari kita tuliskan hukum kedua Newton: .
Pecutan pada setiap saat masa ialah kadar perubahan kelajuan (semerta), iaitu terbitan kelajuan berkenaan dengan masa: .
Oleh itu, hukum ke-2 Newton boleh ditulis semula seperti berikut:
, di manakah paduan semua daya yang bertindak ke atas badan.
Oleh kerana daya graviti dan daya rintangan udara bertindak ke atas badan, maka  .
.
Kami akan mempertimbangkan tiga kes:
1) Daya rintangan udara ialah 0: .
2) Daya rintangan udara diarahkan secara bertentangan dengan vektor halaju, dan magnitudnya adalah berkadar dengan kelajuan: ![]() .
.
3) Daya rintangan udara diarahkan secara bertentangan dengan vektor halaju, dan magnitudnya adalah berkadar dengan kuasa dua halaju: ![]() .
.
Mari kita pertimbangkan kes pertama.
Dalam kes ini  , atau .
, atau . 
Ia berikutan itu ![]() (gerakan dipercepatkan secara seragam).
(gerakan dipercepatkan secara seragam).
Kerana ( r- vektor jejari), kemudian  .
.
Dari sini  .
.
Formula ini tidak lebih daripada formula biasa untuk hukum pergerakan suatu jasad semasa gerakan dipercepatkan secara seragam.
Sejak itu  .
.
Memandangkan kedua-duanya ![]() , kita memperoleh kesamaan skalar daripada kesamaan vektor terakhir:
, kita memperoleh kesamaan skalar daripada kesamaan vektor terakhir:

Marilah kita menganalisis formula yang terhasil.
Jom cari masa penerbangan badan. Menyamakan y kepada sifar, kita dapat


Daripada formula ini, julat penerbangan maksimum dicapai pada .
Sekarang mari kita cari persamaan traktor badan. Untuk melakukan ini, mari kita nyatakan t melalui x

Dan mari kita gantikan ungkapan yang terhasil untuk t ke dalam persamaan untuk y.

Fungsi terhasil y(x) ialah fungsi kuadratik, grafnya ialah parabola, cabang-cabangnya diarahkan ke bawah.
Pergerakan badan yang dilemparkan pada sudut ke ufuk (tanpa mengambil kira rintangan udara) diterangkan dalam video ini.
Sekarang pertimbangkan kes kedua: ![]() .
.
Undang-undang kedua mengambil bentuk  ,
,
dari sini  .
.
Mari kita tulis kesamaan ini dalam bentuk skalar:

Kami dapat dua persamaan pembezaan linear.
Persamaan pertama mempunyai penyelesaian
![]()
Ini boleh disahkan dengan menggantikan fungsi ini ke dalam persamaan untuk v x dan kepada keadaan awal ![]() .
.
Di sini e = 2.718281828459... ialah nombor Euler.
Persamaan kedua mempunyai penyelesaian
Kerana ![]() ,
,
![]() , maka dengan adanya rintangan udara pergerakan badan cenderung seragam, berbeza dengan kes 1, apabila kelajuan meningkat tanpa had.
, maka dengan adanya rintangan udara pergerakan badan cenderung seragam, berbeza dengan kes 1, apabila kelajuan meningkat tanpa had.
Video berikut mengatakan bahawa penerjun langit mula-mula bergerak pada kadar yang dipercepatkan, dan kemudian mula bergerak secara sekata (walaupun sebelum payung terjun dibuka).
Mari cari ungkapan untuk x Dan y.
Kerana x(0) = 0, y(0) = 0, maka


Tinggal untuk kita mempertimbangkan kes 3, apabila
Hukum kedua Newton mempunyai bentuk
 , atau
, atau  .
.Dalam bentuk skalar, persamaan ini kelihatan seperti:

ini sistem persamaan pembezaan tak linear. Sistem ini tidak boleh diselesaikan secara eksplisit, jadi perlu menggunakan simulasi berangka.
Kajian berangka
Dalam bahagian sebelumnya kita melihat bahawa dalam dua kes pertama undang-undang pergerakan badan boleh diperolehi dalam bentuk yang jelas. Walau bagaimanapun, dalam kes ketiga adalah perlu untuk menyelesaikan masalah secara berangka. Menggunakan kaedah berangka kami hanya akan memperoleh penyelesaian anggaran, tetapi kami akan berpuas hati dengan ketepatan yang kecil. (Nombor π atau punca kuasa dua 2, dengan cara ini, tidak boleh ditulis dengan tepat, jadi apabila mengira, mereka mengambil bilangan digit yang terhingga, dan ini sudah cukup.)Kami akan mempertimbangkan kes kedua, apabila daya rintangan udara ditentukan oleh formula ![]() . Perhatikan bahawa apabila k= 0 kita mendapat kes pertama.
. Perhatikan bahawa apabila k= 0 kita mendapat kes pertama.
Kelajuan badan ![]() mematuhi persamaan berikut:
mematuhi persamaan berikut:

Komponen pecutan ditulis di sebelah kiri persamaan ini  .
.
Ingat bahawa pecutan ialah kadar perubahan halaju (semerta), iaitu terbitan halaju berkenaan dengan masa.
Bahagian sebelah kanan persamaan mengandungi komponen halaju. Oleh itu, persamaan ini menunjukkan bagaimana kadar perubahan halaju berkaitan dengan kelajuan.
Mari kita cuba mencari penyelesaian kepada persamaan ini menggunakan kaedah berangka. Untuk melakukan ini, kami memperkenalkan pada paksi masa mesh: mari pilih nombor dan pertimbangkan detik masa borang: .
Tugas kami adalah untuk mengira nilai lebih kurang ![]() pada nod grid.
pada nod grid.
Mari kita gantikan pecutan dalam persamaan ( kelajuan serta merta perubahan kelajuan) oleh kelajuan purata perubahan dalam kelajuan, mempertimbangkan pergerakan badan dalam tempoh masa:

Sekarang mari kita gantikan anggaran yang diperoleh ke dalam persamaan kita.


Formula yang terhasil membolehkan kita mengira nilai fungsi ![]() pada nod grid seterusnya, jika nilai fungsi ini pada nod grid sebelumnya diketahui.
pada nod grid seterusnya, jika nilai fungsi ini pada nod grid sebelumnya diketahui.
Menggunakan kaedah yang diterangkan, kita boleh mendapatkan jadual nilai anggaran komponen halaju.
Bagaimana untuk mencari hukum pergerakan badan, i.e. jadual nilai koordinat anggaran x(t), y(t)? Begitu juga!
Kami ada
Nilai vx[j] adalah sama dengan nilai fungsi, dan sama untuk tatasusunan lain.
Sekarang yang tinggal hanyalah menulis gelung, di dalamnya kita akan mengira vx menggunakan nilai yang telah dikira vx[j], dan sama dengan tatasusunan yang lain. Kitaran akan menjadi j dari 1 hingga N.
Jangan lupa untuk memulakan nilai awal vx, vy, x, y mengikut formula, x 0 = 0, y 0 = 0.
Dalam Pascal dan C, terdapat fungsi sin(x) dan cos(x) untuk mengira sinus dan kosinus. Perhatikan bahawa fungsi ini mengambil hujah dalam radian.
Anda perlu membina graf pergerakan badan semasa k= 0 dan k> 0 dan bandingkan graf yang terhasil. Graf boleh dibuat dalam Excel.
Ambil perhatian bahawa formula pengiraan adalah sangat mudah sehingga anda boleh menggunakan Excel sahaja untuk pengiraan dan tidak menggunakan bahasa pengaturcaraan.
Walau bagaimanapun, pada masa hadapan anda perlu menyelesaikan masalah dalam CATS, di mana anda perlu mengira masa dan julat penerbangan badan, di mana anda tidak boleh melakukannya tanpa bahasa pengaturcaraan.
Sila ambil perhatian bahawa anda boleh ujian atur cara anda dan semak graf anda dengan membandingkan keputusan pengiraan apabila k= 0 dengan formula tepat yang diberikan dalam bahagian "Kajian analitikal".
Eksperimen dengan program anda. Pastikan bahawa jika tiada rintangan udara ( k= 0) julat penerbangan maksimum pada kelajuan awal tetap dicapai pada sudut 45°.
Bagaimana dengan rintangan udara? Pada sudut manakah julat penerbangan maksimum dicapai?
Rajah menunjukkan trajektori badan di v 0 = 10 m/s, α = 45°, g= 9.8 m/s 2, m= 1 kg, k= 0 dan 1 diperoleh melalui simulasi berangka pada Δ t = 0,01.

Anda boleh membiasakan diri dengan kerja hebat pelajar gred 10 dari Troitsk, yang dibentangkan pada persidangan "Start in Science" pada tahun 2011. Kerja ini dikhaskan untuk memodelkan pergerakan bola tenis yang dilemparkan pada sudut ke ufuk (dengan mengambil kira udara rintangan). Kedua-dua pemodelan berangka dan percubaan skala penuh digunakan.
Oleh itu, tugas kreatif ini membolehkan anda membiasakan diri dengan kaedah pemodelan matematik dan berangka, yang digunakan secara aktif dalam amalan, tetapi sedikit dipelajari di sekolah. Sebagai contoh, kaedah ini digunakan dalam pelaksanaan projek nuklear dan angkasa lepas di USSR pada pertengahan abad ke-20.
 Persamaan logaritma
Persamaan logaritma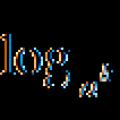 Teknik untuk menyelesaikan persamaan logaritma
Teknik untuk menyelesaikan persamaan logaritma Analisis kendiri guru terapi pertuturan
Analisis kendiri guru terapi pertuturan