Bagaimana untuk mencari pusat graviti rajah yang berbentuk tidak sekata. Kedudukan pusat graviti beberapa rajah

segi empat tepat. Oleh kerana segi empat tepat mempunyai dua paksi simetri, pusat gravitinya terletak di persimpangan paksi simetri, i.e. pada titik persilangan pepenjuru segi empat tepat.

Segi tiga. Pusat graviti terletak pada titik persilangan mediannya. Dari geometri diketahui bahawa median segitiga bersilang pada satu titik dan membahagi dalam nisbah 1:2 dari tapak.

Bulat. Oleh kerana bulatan mempunyai dua paksi simetri, pusat gravitinya berada di persimpangan paksi simetri.

Separuh bulatan. Separuh bulatan mempunyai satu paksi simetri, maka pusat graviti terletak pada paksi ini. Satu lagi koordinat pusat graviti dikira dengan formula: .

Banyak elemen struktur dibuat daripada produk bergulung standard - sudut, rasuk I, saluran dan lain-lain. Semua dimensi, serta ciri geometri profil bergulung, adalah data jadual yang boleh didapati dalam kesusasteraan rujukan dalam jadual pelbagai standard (GOST 8239-89, GOST 8240-89).

Contoh 1 Tentukan kedudukan pusat graviti rajah yang ditunjukkan dalam rajah.

Penyelesaian:

Kami memilih paksi koordinat supaya paksi Lembu melepasi sepanjang dimensi keseluruhan bawah yang melampau, dan paksi Oy - sepanjang dimensi keseluruhan kiri yang melampau.

Kami memecahkan angka kompleks kepada bilangan minimum angka mudah:

segi empat tepat 20x10;

segi tiga 15x10;

bulatan R=3 cm.

Kami mengira luas setiap angka mudah, koordinat pusat gravitinya. Keputusan pengiraan dimasukkan ke dalam jadual

Rajah No.	Luas rajah A	Koordinat pusat graviti

Jawapan: C(14.5; 4.5)

Contoh 2 . Tentukan koordinat pusat graviti bahagian komposit yang terdiri daripada kepingan dan profil bergulung.

Penyelesaian.

Kami memilih paksi koordinat, seperti yang ditunjukkan dalam rajah.

Kami menandakan angka dengan nombor dan menulis data yang diperlukan dari jadual:

Rajah No.	Luas rajah A	Koordinat pusat graviti

Kami mengira koordinat pusat graviti rajah menggunakan formula:

Jawapan: C(0; 10)

Kerja makmal No. 1 "Menentukan pusat graviti angka rata komposit"

Sasaran: Tentukan pusat graviti bagi rajah kompleks rata yang diberi dengan kaedah eksperimen dan analisis dan bandingkan keputusannya.

Arahan kerja

Lukiskan dalam buku nota saiz rata anda, menunjukkan paksi koordinat.

Tentukan pusat graviti secara analitikal.

1. Pecahkan angka itu kepada bilangan angka minimum, yang pusat gravitinya, kita tahu bagaimana untuk menentukannya.

   Nyatakan bilangan kawasan dan koordinat pusat graviti setiap rajah.

   Kira koordinat pusat graviti setiap rajah.

   Kira luas setiap rajah.

   Kira koordinat pusat graviti keseluruhan rajah menggunakan formula (letakkan kedudukan pusat graviti pada lukisan rajah):

Pemasangan untuk penentuan eksperimen koordinat pusat graviti dengan ampaian terdiri daripada rak menegak 1 (lihat rajah) di mana jarum dipasang 2 . angka rata 3 Diperbuat daripada kadbod, yang mudah ditembusi lubang. lubang-lubang TAPI dan AT ditebuk pada titik yang terletak secara rawak (sebaik-baiknya pada jarak paling jauh antara satu sama lain). Satu angka rata digantung pada jarum, pertama pada satu titik TAPI , dan kemudian pada titik itu AT . Dengan bantuan paip 4 , ditetapkan pada jarum yang sama, garis menegak dilukis pada rajah dengan pensil yang sepadan dengan garis paip. Pusat graviti DARI rajah akan terletak di persimpangan garis menegak yang dilukis semasa menggantung rajah pada titik TAPI dan AT .

Pusat graviti Jasad tegar ialah titik geometri yang bersambung tegar dengan jasad ini dan merupakan pusat daya graviti selari yang digunakan pada zarah asas individu badan (Rajah 1.6).

Vektor jejari titik ini

Rajah 1.6

Bagi jasad homogen, kedudukan pusat graviti badan tidak bergantung pada bahan, tetapi ditentukan oleh bentuk geometri badan.

Jika graviti tentu jasad homogen γ , berat zarah asas badan

P k = γΔV k (P = γV ) gantikan ke dalam formula untuk menentukan r C , kita ada

Dari mana, mengunjurkan ke paksi dan melepasi had, kita memperoleh koordinat pusat graviti isipadu homogen

Begitu juga, untuk koordinat pusat graviti permukaan homogen dengan kawasan S (Rajah 1.7, a)

Rajah 1.7

Untuk koordinat pusat graviti garis homogen panjang L (Rajah 1.7, b)

Kaedah untuk menentukan koordinat pusat graviti

Berdasarkan formula umum yang diperoleh sebelum ini, adalah mungkin untuk menunjukkan kaedah untuk menentukan koordinat pusat graviti badan pepejal:

1 Analitikal(secara integrasi).

2 Kaedah simetri. Jika jasad mempunyai satah, paksi atau pusat simetri, maka pusat gravitinya masing-masing terletak pada satah simetri, paksi simetri atau di pusat simetri.

3 Percubaan(kaedah penggantungan badan).

4 membelah. Badan dibahagikan kepada beberapa bahagian yang terhingga, untuk setiap satunya kedudukan pusat graviti C dan kawasan S diketahui. Contohnya, unjuran jasad ke atas satah xOy (Rajah 1.8) boleh diwakili sebagai dua angka rata dengan luas S 1 dan S 2 (S=S 1 +S 2 ). Pusat graviti angka ini berada pada titik C 1 (x 1 ,y 1 ) dan C 2 (x 2 ,y 2 ) . Kemudian koordinat pusat graviti badan ialah

Rajah 1.8

5Penambahan(kaedah kawasan atau isipadu negatif). Kes khas kaedah pembahagian. Ia terpakai kepada badan dengan potongan jika pusat graviti badan tanpa potongan dan potongan diketahui. Sebagai contoh, anda perlu mencari koordinat pusat graviti suatu rajah rata (Rajah 1.9):

Rajah 1.9

Pusat graviti bagi angka termudah

Rajah 1.10

1 segi tiga

Pusat graviti kawasan segi tiga bertepatan dengan titik persilangan mediannya (Rajah 1.10, a).

DM=MB , CM= (1/3)pagi .

2 Lengkok bulatan

Arka mempunyai paksi simetri (Rajah 1.10, b). Pusat graviti terletak pada paksi ini, i.e. y C = 0 .

dl - elemen arka, dl = Rdφ , R ialah jejari bulatan, x = Rcosφ , L= 2aR ,

Akibatnya:

x C = R(sinα/α) .

3 Sektor pekeliling

Sektor jejari R dengan sudut pusat 2 α mempunyai paksi simetri lembu , di mana pusat graviti terletak (Rajah 1.10, c).

Kami membahagikan sektor kepada sektor asas, yang boleh dianggap sebagai segi tiga. Pusat graviti sektor asas terletak pada lengkok bulatan jejari (2/3) R .

Pusat graviti sektor bertepatan dengan pusat graviti arka AB :

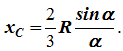
14. Kaedah untuk menentukan pergerakan sesuatu titik.

Dengan kaedah vektor untuk menentukan gerakan, kedudukan sesuatu titik ditentukan oleh vektor jejari yang diambil dari titik tetap dalam sistem rujukan yang dipilih.

Dengan kaedah koordinat untuk menentukan gerakan, koordinat titik ditentukan sebagai fungsi masa:

Ini ialah persamaan parametrik trajektori titik bergerak, di mana masa memainkan peranan parameter t . Untuk menuliskan persamaannya dalam bentuk yang jelas, adalah perlu untuk mengecualikan daripadanya t .

Dengan kaedah semula jadi untuk menentukan pergerakan, trajektori titik, asal pada trajektori dengan petunjuk arah positif rujukan, undang-undang perubahan koordinat arka ditetapkan: s=s(t) . Kaedah ini mudah digunakan jika trajektori titik diketahui lebih awal.

15. 1.2 Kelajuan mata

Pertimbangkan pergerakan titik dalam tempoh masa yang kecil Δt :

kelajuan purata sesuatu titik dalam satu tempoh masa Dt . Kelajuan sesuatu titik pada masa tertentu

Kelajuan mata ialah ukuran kinematik pergerakannya, sama dengan terbitan masa bagi vektor jejari titik ini dalam rangka rujukan yang sedang dipertimbangkan. Vektor halaju diarahkan secara tangen ke trajektori titik dalam arah gerakan.

Pengarang: Jom ambil bentuk badan sewenang-wenangnya. Adakah mungkin untuk menggantungnya pada benang supaya selepas digantung ia mengekalkan kedudukannya (iaitu tidak mula berpusing) apabila mana-mana orientasi awal (rajah 27.1)?

Dalam erti kata lain, adakah terdapat titik sedemikian, berbanding dengan jumlah momen daya graviti yang bertindak pada bahagian badan yang berlainan, akan sama dengan sifar pada mana-mana orientasi badan di angkasa?

Pembaca: Ya saya rasa begitu. Perkara sedemikian dipanggil pusat graviti badan.

Bukti. Untuk kesederhanaan, pertimbangkan badan dalam bentuk plat rata bentuk sewenang-wenangnya berorientasikan sewenang-wenangnya di angkasa (Gamb. 27.2). Ambil sistem koordinat X 0di dengan asalan di pusat jisim - titik DARI, kemudian x C = 0, di C = 0.

Kami mewakili badan ini sebagai koleksi sejumlah besar jisim titik m i, kedudukan setiap satunya diberikan oleh vektor jejari .

Mengikut takrifan pusat jisim , dan koordinat x C = .

Sejak dalam sistem koordinat kami x C= 0, maka . Mari kita darabkan persamaan ini dengan g dan dapat

Seperti yang dapat dilihat dari rajah. 27.2, | x i| adalah bahu kekuatan. Dan jika x i> 0, maka momen daya M i> 0, dan jika x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i momen daya akan M i = m i gx i . Kemudian kesamaan (1) adalah bersamaan dengan , di mana M i ialah momen graviti. Dan ini bermakna bahawa dengan orientasi badan yang sewenang-wenangnya, jumlah momen daya graviti yang bertindak ke atas jasad akan sama dengan sifar berbanding dengan pusat jisimnya.

Agar badan yang kita sedang mempertimbangkan untuk berada dalam keseimbangan, adalah perlu untuk memohon kepadanya pada satu titik DARI kekuatan T = mg menunjuk secara menegak ke atas. Momen kekuatan ini tentang titik DARI sama dengan sifar.

Memandangkan penaakulan kami tidak bergantung dalam apa-apa cara pada bagaimana tepatnya badan berorientasikan di angkasa, kami membuktikan bahawa pusat graviti bertepatan dengan pusat jisim, yang merupakan perkara yang perlu dibuktikan.

Masalah 27.1. Cari pusat graviti bagi rod tanpa berat yang panjangnya l, di hujungnya dua jisim titik ditetapkan t 1 dan t 2 .

t 1 t 2 l	Penyelesaian. Kami tidak akan mencari pusat graviti, tetapi untuk pusat jisim (kerana mereka adalah satu dan sama). Mari kita perkenalkan paksi X(Gamb. 27.3). nasi. 27.3
x C =?

Jawab: jauh dari jisim t 1 .

BERHENTI! Tentukan sendiri: B1-B3.

Pernyataan 1 . Jika jasad rata homogen mempunyai paksi simetri, pusat graviti berada pada paksi ini.

Sesungguhnya, untuk sebarang jisim titik m i, terletak di sebelah kanan paksi simetri, terdapat jisim titik yang sama terletak secara simetri berkenaan dengan yang pertama (Rajah 27.4). Dalam kes ini, jumlah momen daya .

Oleh kerana seluruh badan boleh diwakili sebagai dibahagikan kepada pasangan mata yang serupa, jumlah momen graviti berbanding mana-mana titik yang terletak pada paksi simetri adalah sifar, yang bermaksud pusat graviti badan juga terletak pada paksi ini. Ini membawa kepada kesimpulan penting: jika badan mempunyai beberapa paksi simetri, maka pusat graviti terletak di persimpangan paksi ini(Gamb. 27.5).

nasi. 27.5

Kenyataan 2. Jika dua badan berjisim t 1 dan t 2 disambungkan menjadi satu, maka pusat graviti jasad tersebut akan terletak pada garis lurus yang menghubungkan pusat graviti jasad pertama dan kedua (Rajah 27.6).

nasi. 27.6 nasi. 27.7

Bukti. Mari kita susun badan komposit supaya segmen yang menghubungkan pusat graviti jasad adalah menegak. Kemudian jumlah momen graviti jasad pertama berkenaan dengan titik DARI 1 adalah sama dengan sifar, dan jumlah momen graviti jasad kedua tentang titik itu DARI 2 ialah sifar (Rajah 27.7).

perasan, itu bahu graviti mana-mana jisim titik t i yang sama berkenaan dengan mana-mana titik pada segmen DARI 1 DARI 2 , dan dengan itu momen graviti berbanding mana-mana titik yang terletak pada ruas itu DARI 1 DARI 2 adalah sama. Oleh itu, graviti seluruh badan adalah sifar berkenaan dengan mana-mana titik pada segmen DARI 1 DARI 2. Oleh itu, pusat graviti badan komposit terletak pada segmen DARI 1 DARI 2 .

Pernyataan 2 membayangkan kesimpulan praktikal yang penting, yang dirumus dengan jelas dalam bentuk arahan.

arahan,

bagaimana untuk mencari pusat graviti badan tegar jika ia boleh dipecahkan

kepada bahagian-bahagian, kedudukan pusat graviti setiap satunya diketahui

1. Gantikan setiap bahagian dengan jisim yang terletak di pusat graviti bahagian tersebut.

2. Cari Pusat graviti(dan ini adalah sama dengan pusat graviti) sistem jisim titik yang terhasil, memilih sistem koordinat yang mudah X 0di, mengikut formula:

Sesungguhnya, marilah kita meletakkan badan majmuk sedemikian rupa sehingga segmen DARI 1 DARI 2 adalah mendatar, dan kami akan menggantungnya pada benang pada titik DARI 1 dan DARI 2 (Gamb. 27.8, a). Adalah jelas bahawa badan akan berada dalam keseimbangan. Dan keseimbangan ini tidak akan terganggu jika kita menggantikan setiap badan dengan jisim titik t 1 dan t 2 (Gamb. 27.8, b).

nasi. 27.8

BERHENTI! Tentukan sendiri: C3.

Masalah 27.2. Bola berjisim diletakkan pada dua bucu segitiga sama sisi t setiap satu. Bucu ketiga mengandungi sebiji bola berjisim 2 t(Gamb. 27.9, a). Sebelah segi tiga a. Tentukan pusat graviti sistem ini.

t 2t a	nasi. 27.9
x C = ? di C = ?

Penyelesaian. Kami memperkenalkan sistem koordinat X 0di(Gamb. 27.9, b). Kemudian

,

.

Jawab: x C = a/2; ; pusat graviti terletak pada separuh ketinggian AD.

Keupayaan untuk kekal seimbang tanpa berusaha adalah sangat penting untuk meditasi yang berkesan, yoga, qigong, dan juga untuk tarian perut. Ini adalah keperluan pertama yang dihadapi oleh pemula dalam jenis aktiviti ini dan salah satu sebab mengapa sukar untuk mengambil langkah pertama tanpa pengajar. Soalan yang menunjukkan bahawa seseorang tidak mengetahui pusat gravitinya mungkin kelihatan agak berbeza. Dalam qigong, sebagai contoh, seseorang akan bertanya bagaimana untuk menjadi santai dan masih melakukan pergerakan sambil berdiri, seorang penari oriental pemula tidak akan memahami bagaimana untuk memisahkan dan menyelaraskan pergerakan bahagian bawah dan atas badan, dan dalam kedua-dua kes orang. akan menjadi terlalu tegang dan sering kehilangan keseimbangan. Pergerakan mereka akan menjadi tidak menentu, kekok.

Oleh itu, adalah penting untuk memahami cara mencari pusat graviti anda sendiri, ia memerlukan kerja mental dan kemahiran, tetapi dari masa ke masa kemahiran itu bergerak ke tahap naluri.

Apa yang perlu dilakukan supaya tidak menegangkan otot dan pada masa yang sama tidak menggunakan sokongan luaran. Jawapannya jelas, anda perlu menggerakkan sokongan ke dalam. Lebih tepat lagi, bergantung pada paksi dalaman bersyarat. Ke mana perginya gandar ini? Konsep pusat graviti adalah bersyarat, tetapi ia digunakan dalam fizik. Di sana adalah kebiasaan untuk mentakrifkannya sebagai titik penggunaan daya paduan graviti. Daya paduan graviti ialah keseluruhan semua daya graviti, dengan mengambil kira arah tindakannya.

Adakah sukar setakat ini? Bekalkan kesabaran.

Iaitu, kita sedang mencari titik dalam badan kita yang akan membolehkan kita tidak jatuh, tanpa sedar melawan graviti. Ini bermakna bahawa graviti bumi mesti diarahkan supaya ia menumpu dengan seluruh daya bertindak di suatu tempat di tengah-tengah badan kita.

Arah daya sedemikian mewujudkan paksi bersyarat di tengah-tengah badan kita, permukaan menegak, ini adalah menegak pusat graviti. Bahagian badan di mana kita bersandar pada tanah ialah tapak kaki kita (kita bersandar pada tanah dengan kaki kita). Di tempat menegak ini bersandar pada permukaan tempat kita berdiri, iaitu kita bersandar pada tanah, ini ialah titik pusat graviti di dalam tapak kaki. Jika menegak beralih dari tempat ini, kita akan kehilangan keseimbangan dan jatuh. Lebih besar kawasan sokongan itu sendiri, lebih mudah untuk kita kekal dekat dengan pusatnya, dan oleh itu kita semua secara naluri akan mengambil langkah yang panjang sambil berdiri di atas permukaan yang tidak stabil. Iaitu, kawasan sokongan bukan sahaja kaki itu sendiri, tetapi juga ruang di antara mereka.

Ia juga penting untuk mengetahui bahawa lebar kawasan kawasan sokongan mempengaruhi lebih daripada panjang. Dalam kes manusia, ini bermakna kita lebih cenderung untuk jatuh di sebelah kita daripada ke belakang, dan lebih-lebih lagi ke hadapan. Oleh itu, apabila berlari, lebih sukar bagi kita untuk mengekalkan keseimbangan, perkara yang sama boleh dikatakan mengenai tumit. Tetapi dalam kasut yang luas dan stabil, sebaliknya, lebih mudah untuk ditentang, malah lebih mudah daripada berkaki ayam sepenuhnya. Walau bagaimanapun, aktiviti yang disebutkan pada mulanya memerlukan kasut yang sangat lembut, ringan atau tidak sama sekali. Oleh itu, kita tidak boleh membantu diri kita dengan kasut.

Jadi, adalah sangat penting untuk mencari titik tengah garis menegak pada kaki anda. Biasanya ia tidak terletak di tengah-tengah kaki, seperti yang diandaikan secara automatik, tetapi lebih dekat dengan tumit, di suatu tempat separuh dari tengah kaki, ke tumit.
Tetapi bukan itu sahaja.

Sebagai tambahan kepada garis menegak pusat graviti, terdapat juga yang mendatar, serta yang berasingan untuk anggota badan.
Garis mendatar untuk wanita dan lelaki berjalan sedikit berbeza.

Di hadapan, pada wanita, ia melepasi lebih rendah, dan pada lelaki, lebih tinggi. Pada lelaki, ia berjalan di suatu tempat 4-5 jari di bawah pusar, dan pada wanita, 10, kira-kira. Di belakang garis wanita berjalan hampir koopchik, dan garis lelaki adalah kira-kira lima jari lebih tinggi daripada itu. Di samping itu, untuk kestabilan pada masa meditasi, adalah penting untuk memberi perhatian kepada garisan semata-mata pusat graviti lutut. Ia terletak sedikit di atas tulang (kaki bawah), tetapi dua atau tiga jari di bawah tulang rawan.

Semasa meditasi, dan juga semasa tarian perut, ia tidak begitu baik untuk menyebarkan kaki lebar, lebar maksimum biasanya sepadan dengan lebar bahu.

Oleh itu, anda perlu membantu diri anda sedikit dengan lutut anda, cuba membina paksi menegak selurus mungkin. Berdiri di hadapan cermin, cari semua titik yang diterangkan pada diri anda. Jarakkan kaki anda seluas bahu. Rehatkan otot di kaki dan badan anda. Kemudian, luruskan punggung anda tanpa membebankan badan anda, rilekskan kaki anda dengan sedikit bengkok di lutut anda. Bayangkan tiga garis menegak, masing-masing berjalan pada titik yang sepadan di belakang batang tubuh, di hadapannya, dan di sekeliling lutut. Cuba susun titik supaya paksi hadapan batang tubuh adalah kira-kira separuh antara paksi belakang dan lutut. Dalam kes ini, lutut tidak boleh dibengkokkan supaya mereka melampaui jari kaki, mereka hanya perlu sedikit bengkok dan santai. Sebaiknya di atas pusat graviti di dalam kawasan sokongan yang kami temui di kaki. Pada masa yang sama, tangan boleh diletakkan secara bebas pada tuhan atau meletakkan telapak tangan di pinggul.

Bagaimanakah anda tahu bahawa anda telah menemui pusat graviti anda?

Anda akan berasa sedikit bergoyang, tetapi pada masa yang sama anda pasti akan tahu bahawa anda tidak akan jatuh.

Kuliah 4. Pusat graviti.

Syarahan ini merangkumi soalan-soalan berikut

1. Pusat graviti jasad tegar.

2. Koordinat pusat graviti badan tidak homogen.

3. Koordinat pusat graviti badan homogen.

4. Kaedah untuk menentukan koordinat pusat graviti.

5. Pusat graviti beberapa jasad homogen.

Kajian isu-isu ini adalah perlu pada masa hadapan untuk mengkaji dinamik pergerakan badan, dengan mengambil kira geseran gelongsor dan geseran bergolek, dinamik pusat jisim sistem mekanikal, momen kinetik, untuk menyelesaikan masalah dalam disiplin. "Kekuatan bahan".

Membawa daya selari.

Selepas kita mempertimbangkan pengurangan kepada pusat sistem rata dan sistem spatial kuasa sewenang-wenangnya, kita sekali lagi kembali kepada pertimbangan kes tertentu sistem daya selari.

Membawa dua daya selari.

Semasa mempertimbangkan sistem kuasa sedemikian, tiga kes pengurangan berikut adalah mungkin.

1. Sistem dua daya kolinear. Pertimbangkan sistem dua daya selari dan terarah pada arah yang sama P dan Q, digunakan pada titik TAPI dan AT. Kami akan menganggap bahawa daya adalah berserenjang dengan segmen ini (Rajah 1, a).

DARI, kepunyaan segmen AB dan memenuhi syarat:

AC/SW = Q/P.(1)

Vektor sistem utama RC = P + Q modulo adalah sama dengan jumlah daya ini: RC = P + Q.

DARI mengambil kira (1) adalah sama dengan sifar:MC = P ∙ AC- Q∙ SW = 0.

Oleh itu, sebagai hasil pelakon, kami mendapat: RC ≠ 0, MC= 0. Ini bermakna bahawa vektor utama adalah bersamaan dengan paduan yang melalui pusat pengurangan, iaitu:

Hasil daya kolinear adalah sama dalam nilai mutlak dengan jumlahnya, dan garis tindakannya membahagikan segmen yang menghubungkan titik-titik penggunaannya, berkadar songsang dengan modul daya ini secara dalaman.

Perhatikan bahawa kedudukan titik DARI tidak akan berubah jika kuasa R dan Q pusing satu sudutα . titik DARI, yang mempunyai sifat ini dipanggil pusat daya selari.

2. Sistem dua antikolinear dan tidak sama dalam modulus daya. Semoga angkatan P dan Q, digunakan pada titik TAPI dan AT, selari, diarahkan ke arah yang bertentangan dan tidak sama dalam modulus (Rajah 1, b).

Marilah kita memilih titik sebagai pusat rujukan DARI, yang masih memenuhi hubungan (1) dan terletak pada garis lurus yang sama, tetapi di luar segmen AB.

Vektor utama sistem ini RC = P + Q modulo kini akan sama dengan perbezaan antara modul vektor: RC = Q - P.

Momen utama mengenai pusat DARI masih sifar:MC = P ∙ AC- Q∙ SW= 0, jadi

terhasil antikolinear dan daya yang tidak sama dalam nilai mutlak adalah sama dengan perbezaannya, diarahkan ke arah daya yang lebih besar, dan garis tindakannya membahagikan segmen yang menghubungkan titik-titik penggunaannya, berkadar songsang dengan modul daya ini secara luaran.

Rajah 1

3. Sistem dua antikolinear dan daya yang sama dalam modulus. Mari kita ambil kes pengurangan sebelumnya sebagai yang awal. Mari kita betulkan kuasa R, dan paksaan Q mari kita berusaha modulo untuk memaksa R.

Kemudian pada Q → R dalam formula (1) nisbah AC/SW → 1. Ini bermakna AC → SW, iaitu jarak AC →∞ .

Dalam kes ini, modul vektor utama RC → 0, dan modul momen utama tidak bergantung pada kedudukan pusat pengurangan dan kekal sama dengan nilai asal:

MC = P ∙ AC- Q∙ SW = P ∙ ( AC- SW) =P ∙ TAPIB.

Oleh itu, dalam had, kami telah memperoleh sistem kuasa yang RC = 0, MC≠ 0, dan pusat pengurangan dialihkan kepada infiniti, yang tidak boleh digantikan oleh paduan. Dalam sistem ini, tidak sukar untuk mengetahui sepasang daya, jadi sepasang daya tidak mempunyai paduan.

Pusat sistem daya selari.

Pertimbangkan sistem n angkatan Pi, digunakan pada titikA i (x i , y i , z i) dan selari dengan paksiOv dengan vektor l(Gamb. 2).

Jika kita mengecualikan terlebih dahulu kes sistem yang setara dengan sepasang daya, tidaklah sukar untuk membuktikan, berdasarkan perenggan sebelumnya, kewujudan paduannya.R.

Tentukan koordinat pusatC(x c, y c, z c) daya selari, iaitu, koordinat titik aplikasi paduan sistem ini.

Untuk tujuan ini, kami menggunakan teorem Varignon, berdasarkannya:

M0 (R) = Σ M0(Pi).

Rajah.2

Vektor-momen daya boleh diwakili sebagai hasil silang, oleh itu:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r i× Pi ).

Memandangkan itu R = R v ∙ l, a Pi = P vi ∙ l dan menggunakan sifat produk vektor, kita dapat:

rc × R v ∙ l = Σ ( r i × P vi ∙ l),

rc ∙ R v × l = Σ ( r i ∙ P vi × l) = Σ ( r i ∙ P vi ) × l,

atau:

[ r c R v - Σ ( r i P vi )] × l= 0.

Ungkapan terakhir sah hanya jika ungkapan dalam kurungan segi empat sama adalah sifar. Oleh itu, meninggalkan indeksvdan memandangkan yang terhasilR = Σ Pi , dari sini kita dapat:

rc = (Σ Pi r i )/(Σ Pi ).

Mengunjurkan kesamaan vektor terakhir pada paksi koordinat, kami memperoleh yang dikehendaki ungkapan koordinat pusat daya selari:

x c = (Σ Pi x i)/(Σ Pi );

yc = (Σ Pi y i )/(Σ Pi );(2)

z c = (Σ Pi z i )/(Σ Pi ).

Pusat graviti badan

Koordinat pusat graviti badan homogen.

Pertimbangkan berat badan yang tegar P dan kelantangan V dalam sistem koordinat Oxyz, di mana kapak x dan y dihubungkan dengan permukaan bumi, dan paksi z diarahkan ke zenith.

Jika kita memecahkan badan kepada bahagian asas dengan isipadu∆ V i , maka daya tarikan akan bertindak pada setiap bahagiannya∆ Pidiarahkan ke pusat bumi. Mari kita anggap bahawa dimensi badan jauh lebih kecil daripada dimensi Bumi, maka sistem daya yang digunakan pada bahagian asas badan boleh dianggap tidak menumpu, tetapi selari (Rajah 3), dan semua kesimpulan daripada bab sebelumnya boleh digunakan untuknya.

Rajah.3

Definisi . Pusat graviti jasad tegar ialah pusat daya graviti selari bahagian asas badan ini.

Ingat itu graviti tertentu bahagian asas badan dipanggil nisbah beratnya∆ Pi kepada isipadu ∆ V i : γ i = ∆ Pi/ ∆ V i . Untuk badan homogen, nilai ini adalah tetap:γ i = γ = P/ V.

Menggantikan kepada (2) ∆ Pi = γ i ∙∆ V i bukannya Pi, dengan mengambil kira ucapan terakhir dan mengurangkan pengangka dan penyebut dengang, kita mendapatkan ungkapan untuk koordinat pusat graviti jasad homogen:

x c = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

yc = (Σ ∆ Vi∙ y i )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Beberapa teorem berguna dalam menentukan pusat graviti.

1) Jika jasad homogen mempunyai satah simetri, maka pusat gravitinya berada dalam satah ini.

Jika kapak X dan di diletakkan dalam satah simetri ini, kemudian untuk setiap titik dengan koordinat. dan menyelaras mengikut (3), akan sama dengan sifar, kerana dalam jumlah semua istilah dengan tanda yang bertentangan dihapuskan secara berpasangan. Jadi pusat graviti ialah dalam satah simetri.

2) Jika jasad homogen mempunyai paksi simetri, maka pusat graviti jasad terletak pada paksi ini.

Sesungguhnya, dalam kes ini, jika paksizlukis sepanjang paksi simetri, untuk setiap titik dengan koordinatanda boleh mencari titik dengan koordinat dan koordinat dan dikira dengan formula (3) akan sama dengan sifar.

Teorem ketiga dibuktikan dengan cara yang sama.

3) Jika jasad homogen mempunyai pusat simetri, maka pusat graviti jasad terletak pada titik ini.

Dan beberapa teguran lagi.

Pertama. Jika badan boleh dibahagikan kepada bahagian yang diketahui berat dan kedudukan pusat graviti, maka tidak perlu mempertimbangkan setiap titik, tetapi dalam formula (3) Pi – untuk ditentukan sebagai berat bahagian yang berkaitan dansebagai koordinat pusat gravitinya.

Kedua. Sekiranya badan itu homogen, maka berat bahagian yang berasingan daripadanya, di mana ialah graviti tentu bahan dari mana badan itu dibuat, dan Vi - isipadu bahagian badan ini. Dan formula (3) akan mengambil bentuk yang lebih mudah. Sebagai contoh,

Dan begitu juga, di mana - isipadu seluruh badan.

Nota ketiga. Biarkan badan kelihatan seperti pinggan nipis dengan kawasan F dan ketebalan t terbaring di dalam kapal terbang Oxy. Menggantikan kepada (3)∆ V i =t ∙ ∆F i , kita memperoleh koordinat pusat graviti plat homogen:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

yc = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z i ) / (Σ ∆ F i).

di mana – koordinat pusat graviti plat individu;ialah jumlah kawasan badan.

Nota keempat. Untuk badan dalam bentuk batang lengkung nipis dengan panjang L dengan luas keratan rentas a isipadu asas∆ V i = a ∙∆ L i , sebab tu koordinat pusat graviti rod lengkung nipis akan sama:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

yc = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

di mana – koordinat pusat gravitii-bahagian ke-; .

Perhatikan bahawa mengikut definisi, pusat graviti ialah titik geometri; ia juga boleh terletak di luar had badan tertentu (contohnya, untuk cincin).

Catatan.

Dalam bahagian kursus ini, kami tidak membezakan antara graviti, graviti dan berat badan. Pada hakikatnya, graviti ialah perbezaan antara graviti Bumi dan daya emparan yang disebabkan oleh putarannya.

Koordinat pusat graviti badan tidak homogen.

Koordinat pusat graviti pepejal tidak homogen(Gamb. 4) dalam sistem rujukan yang dipilih ditakrifkan seperti berikut:

Rajah.4

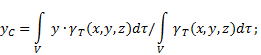
di mana - berat per unit isipadu badan (graviti tentu)

- berat badan keseluruhan.

permukaan tidak rata(Rajah 5), maka koordinat pusat graviti dalam sistem rujukan yang dipilih ditentukan seperti berikut:

Rajah.5

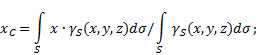
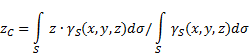
di mana - berat per unit luas badan

- berat badan keseluruhan.

Jika pepejal adalah garis heterogen(Rajah 6), maka koordinat pusat graviti dalam sistem rujukan yang dipilih ditentukan seperti berikut:

Rajah.6

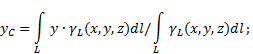
di mana - berat unit panjang badan,

Berat badan keseluruhan.

Kaedah untuk menentukan koordinat pusat graviti.

Berdasarkan formula umum yang diperoleh di atas, adalah mungkin untuk menunjukkan kaedah khusus menentukan koordinat pusat graviti jasad.

1. simetri. Jika jasad homogen mempunyai satah, paksi atau pusat simetri (Rajah 7), maka pusat gravitinya masing-masing terletak pada satah simetri, paksi simetri atau di pusat simetri.

Rajah.7

2. Perpecahan. Badan dibahagikan kepada bilangan bahagian yang terhingga (Rajah 8), yang mana setiap satunya kedudukan pusat graviti dan kawasan diketahui.

Rajah 8

S \u003d S 1 + S 2.

3.Kaedah kawasan negatif. Kes khas kaedah pembahagian (Rajah 9). Ia terpakai kepada badan dengan potongan jika pusat graviti badan tanpa potongan dan potongan diketahui. Badan dalam bentuk plat dengan potongan diwakili oleh gabungan plat pepejal (tanpa potongan) dengan luas S1 dan luas bahagian yang dipotong S2.

Rajah.9

S \u003d S 1 - S 2.

4.kaedah kumpulan. Ia adalah tambahan yang baik kepada dua kaedah terakhir. Selepas memecah angka itu kepada unsur konstituennya, adalah mudah untuk menggabungkan beberapa daripadanya semula, untuk kemudian memudahkan penyelesaian dengan mengambil kira simetri kumpulan ini.

Pusat graviti beberapa jasad homogen.

1) Pusat graviti lengkok bulat. Pertimbangkan arka AB jejariR dengan sudut pusat. Oleh kerana simetri, pusat graviti arka ini terletak pada paksilembu(Gamb. 10).

Rajah.10

Mari cari koordinat mengikut formula . Untuk melakukan ini, pilih pada arka AB unsur MM ’ panjang, yang kedudukannya ditentukan oleh sudut. koordinat X unsur MM' akan jadi. Menggantikan nilai-nilai ini X dan d l dan dengan mengambil kira bahawa kamiran mesti dilanjutkan ke atas keseluruhan panjang lengkok, kita dapat:

di mana L ialah panjang lengkok AB sama dengan .

Dari sini akhirnya kita dapati bahawa pusat graviti lengkok bulat terletak pada paksi simetrinya pada jarak dari pusat Oh sama

mana sudutnya diukur dalam radian.

2) Pusat graviti kawasan segitiga. Pertimbangkan segitiga terletak di dalam satah Oxy, yang koordinat puncaknya diketahui: A i (x i,y i ), (i= 1,2,3). Memecahkan segitiga kepada jalur sempit selari dengan sisi TAPI 1 TAPI 2 , kita sampai pada kesimpulan bahawa pusat graviti segitiga mestilah tergolong dalam median TAPI 3 M 3 (rajah 11) .

Rajah 11

Memecahkan segitiga kepada jalur selari dengan sisi TAPI 2 TAPI 3 , anda boleh memastikan bahawa ia mesti terletak pada median TAPI 1 M satu. Dengan cara ini, pusat graviti segitiga terletak pada titik persilangan mediannya, yang, seperti yang anda ketahui, memisahkan bahagian ketiga daripada setiap median, mengira dari sisi yang sepadan.

Khususnya, untuk median TAPI 1 M 1 kita dapat, memandangkan koordinat titik itu M 1 - ialah min aritmetik bagi koordinat bucu TAPI 2 dan TAPI 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Oleh itu, koordinat pusat graviti segitiga ialah min aritmetik bagi koordinat bucunya:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

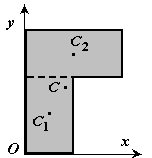
3) Pusat graviti kawasan sektor bulatan. Pertimbangkan sektor bulatan jejari R dengan sudut pusat 2α , terletak secara simetri pada paksi lembu (Gamb. 12) .

Ia adalah jelas bahawa y c = 0, dan jarak dari pusat bulatan dari mana sektor ini dipotong ke pusat gravitinya boleh ditentukan dengan formula:

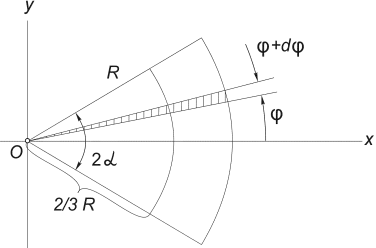
Rajah 12

Cara termudah untuk mengira kamiran ini ialah dengan membahagikan domain penyepaduan kepada sektor asas dengan sudut dφ . Sehingga infinitesimal tertib pertama, sektor sedemikian boleh digantikan dengan segi tiga dengan tapak yang sama dengan R × dφ dan ketinggian R. Luas segi tiga sedemikian dF =(1/2)R 2 ∙ dφ , dan pusat gravitinya ialah 2/3 R dari atas, jadi dalam (5) kita letak x = (2/3)R∙ cos. Menggantikan kepada (5) F= α R 2, kita dapat:

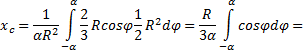
Menggunakan formula terakhir, kami mengira, khususnya, jarak ke pusat graviti separuh bulatan.

Menggantikan dalam (2) α = π /2, kita dapat: x c = (4 R)/(3 π ) ≅ 0.4 R .

Contoh 1Mari kita tentukan pusat graviti jasad homogen yang ditunjukkan dalam Rajah. 13.

Rajah.13

Penyelesaian.Badan adalah homogen, terdiri daripada dua bahagian yang mempunyai bentuk simetri. Koordinat pusat graviti mereka:

Jumlah mereka:

Oleh itu, koordinat pusat graviti badan

Contoh 2 Cari pusat graviti plat yang dibengkokkan pada sudut tepat. Dimensi - pada lukisan (Rajah 14).

Rajah 14

Penyelesaian. Koordinat pusat graviti:

0.

Petak:

Itulah sebabnya:

Contoh 3 Pada helaian persegi cm potong lubang persegi lihat (Gamb. 15). Cari pusat graviti helaian itu. Contoh 4 Cari kedudukan pusat graviti plat yang ditunjukkan dalam rajah. 16. Dimensi diberikan dalam sentimeter.

Rajah.16

Penyelesaian. Kami membahagikan plat kepada angka (Rajah 17), pusat-pusat yang keparahannya diketahui.

Kawasan bagi rajah ini dan koordinat pusat gravitinya:

1) segi empat tepat dengan sisi 30 dan 40 cm,S 1 =30 ∙ 40=1200 sm 2 ; x 1=15 sm; di 1 \u003d 20 cm.

2) segi tiga tegak dengan tapak 50 cm dan tinggi 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; X 2 \u003d 30 + 50 / 3 \u003d 46.7 cm; y 2 =40/3 =13.3 sm;

3) jejari setengah bulatan bulatan r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; X 3 =4 R /3 π =8.5 sm; di

Penyelesaian. Ingat bahawa dalam fizik ketumpatan badanρ dan graviti tentunyagberkaitan dengan nisbah:γ = ρ g , di manag - pecutan graviti. Untuk mencari jisim badan homogen sedemikian, anda perlu mendarabkan ketumpatan dengan isipadunya.

Rajah.19

Istilah "linear" atau "linear" bermaksud untuk menentukan jisim rod kekuda, ketumpatan linear mesti didarab dengan panjang rod ini.

Untuk menyelesaikan masalah, anda boleh menggunakan kaedah pembahagian. Mewakili kekuda yang diberikan sebagai jumlah 6 batang individu, kita dapat:

di manaL i panjangi -th rod ladang, danx i , y i - koordinat pusat gravitinya.

Penyelesaian masalah ini boleh dipermudahkan dengan mengumpulkan 5 batang kekuda yang terakhir. Adalah mudah untuk melihat bahawa mereka membentuk angka dengan pusat simetri yang terletak di tengah-tengah rod keempat, di mana pusat graviti kumpulan rod ini terletak.

Oleh itu, kekuda yang diberikan boleh diwakili oleh gabungan dua kumpulan rod sahaja.

Kumpulan pertama terdiri daripada batang pertama, untuknyaL 1 = 4 m,x 1 = 0 m,y 1 = 2 m Kumpulan kedua rod terdiri daripada lima batang, yang manaL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

Koordinat pusat graviti ladang didapati dengan formula:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Perhatikan bahawa pusat DARI terletak pada talian yang menghubungkan DARI 1 dan DARI 2 dan membahagikan segmen DARI 1 DARI 2 mengenai: DARI 1 DARI/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.

Soalan untuk pemeriksaan diri

Apakah pusat daya selari?

- Bagaimanakah koordinat pusat daya selari ditentukan?

- Bagaimana untuk menentukan pusat daya selari, yang paduannya ialah sifar?

Apakah sifat pusat daya selari?

- Apakah formula yang digunakan untuk mengira koordinat pusat daya selari?

Apakah pusat graviti jasad?

- Mengapakah daya tarikan Bumi, bertindak pada titik jasad, boleh dianggap sebagai sistem daya selari?

- Tuliskan formula untuk menentukan kedudukan pusat graviti badan tidak homogen dan homogen, formula untuk menentukan kedudukan pusat graviti bahagian rata?

- Tuliskan formula untuk menentukan kedudukan pusat graviti bentuk geometri mudah: segi empat tepat, segi tiga, trapezium dan setengah bulatan?

Apakah yang dipanggil momen statik bagi kawasan itu?

- Berikan contoh jasad yang pusat gravitinya terletak di luar jasad.

- Bagaimanakah sifat simetri digunakan untuk menentukan pusat graviti jasad?

- Apakah intipati kaedah pemberat negatif?

Di manakah terletaknya pusat graviti lengkok bulat?

Bagaimanakah anda boleh mencari secara grafik pusat graviti segitiga?

- Tuliskan formula yang menentukan pusat graviti sektor bulatan.

- Menggunakan formula yang menentukan pusat graviti bagi segi tiga dan sektor bulat, terbitkan formula yang serupa untuk segmen bulat.

- Apakah formula yang digunakan untuk mengira koordinat pusat graviti badan homogen, angka rata dan garis?

- Apakah yang dipanggil momen statik kawasan angka rata berbanding paksi, bagaimana ia dikira dan apakah dimensi yang ada padanya?

- Bagaimana untuk menentukan kedudukan pusat graviti kawasan, jika kedudukan pusat graviti bahagian individunya diketahui?

- Apakah teorem bantu yang digunakan dalam menentukan kedudukan pusat graviti?