Bagaimana untuk menentukan fungsi apa yang akan menjadi graf. Fungsi dan Graf

fungsi ialah korespondensi antara elemen dua set, ditubuhkan mengikut peraturan sedemikian bahawa setiap elemen satu set dikaitkan dengan beberapa elemen dari set lain.

graf bagi suatu fungsi ialah lokus titik dalam satah yang absis (x) dan ordinat (y) disambungkan oleh fungsi yang ditentukan:

titik terletak (atau terletak) pada graf fungsi jika dan hanya jika .

Oleh itu, fungsi boleh diterangkan dengan secukupnya oleh grafnya.

cara jadual. Agak biasa, ia terdiri daripada menetapkan jadual nilai hujah individu dan nilai fungsi yang sepadan. Kaedah mentakrifkan fungsi ini digunakan apabila domain fungsi ialah set terhingga diskret.

Dengan kaedah jadual untuk menentukan fungsi, adalah mungkin untuk mengira nilai fungsi yang tidak terkandung dalam jadual, sepadan dengan nilai perantaraan hujah. Untuk melakukan ini, gunakan kaedah interpolasi.

Kelebihan kaedah jadual menetapkan fungsi ialah ia memungkinkan untuk menentukan nilai tertentu tertentu sekali gus, tanpa pengukuran atau pengiraan tambahan. Walau bagaimanapun, dalam beberapa kes, jadual tidak mentakrifkan fungsi sepenuhnya, tetapi hanya untuk beberapa nilai hujah dan tidak memberikan gambaran visual tentang sifat perubahan dalam fungsi bergantung kepada perubahan dalam hujah.

Cara grafik. Graf bagi fungsi y = f(x) ialah set semua titik dalam satah yang koordinatnya memenuhi persamaan yang diberikan.

Cara grafik untuk menentukan fungsi tidak selalu memungkinkan untuk menentukan nilai berangka hujah dengan tepat. Walau bagaimanapun, ia mempunyai kelebihan besar berbanding kaedah lain - keterlihatan. Dalam kejuruteraan dan fizik, kaedah grafik untuk menetapkan fungsi sering digunakan, dan graf adalah satu-satunya cara yang tersedia untuk ini.

Agar tugasan grafik sesuatu fungsi menjadi agak betul dari sudut pandangan matematik, adalah perlu untuk menunjukkan pembinaan geometri tepat graf, yang, selalunya, diberikan oleh persamaan. Ini membawa kepada cara berikut untuk menentukan fungsi.

cara analitikal. Selalunya, undang-undang yang mewujudkan hubungan antara hujah dan fungsi ditentukan melalui formula. Cara mentakrifkan fungsi ini dipanggil analitikal.

Kaedah ini membolehkan setiap nilai berangka hujah x mencari nilai berangka yang sepadan bagi fungsi y dengan tepat atau dengan sedikit ketepatan.

Jika hubungan antara x dan y diberikan oleh formula yang diselesaikan berkenaan dengan y, i.e. mempunyai bentuk y = f(x), maka kita katakan bahawa fungsi x diberikan secara eksplisit.

Jika nilai x dan y dikaitkan dengan beberapa persamaan dalam bentuk F(x,y) = 0, i.e. formula tidak dibenarkan berkenaan dengan y, yang bermaksud bahawa fungsi y = f(x) ditakrifkan secara tersirat.

Sesuatu fungsi boleh ditakrifkan oleh formula yang berbeza di bahagian berlainan kawasan tugasnya.

Kaedah analisis adalah cara yang paling biasa untuk menentukan fungsi. Kekompakan, ketepatan, keupayaan untuk mengira nilai fungsi untuk nilai arbitrari hujah dari domain definisi, keupayaan untuk menggunakan radas analisis matematik untuk fungsi tertentu adalah kelebihan utama kaedah analisis untuk mentakrifkan fungsi. Kelemahannya termasuk kekurangan keterlihatan, yang diimbangi oleh keupayaan untuk membina graf dan keperluan untuk melakukan pengiraan yang kadangkala sangat menyusahkan.

cara lisan. Kaedah ini terdiri daripada fakta bahawa pergantungan fungsi dinyatakan dalam kata-kata.

Contoh 1: fungsi E(x) ialah bahagian integer bagi nombor x. Secara umum, E(x) = [x] menandakan integer terbesar yang tidak melebihi x. Dalam erti kata lain, jika x = r + q, di mana r ialah integer (mungkin negatif) dan q tergolong dalam selang = r. Fungsi E(x) = [x] adalah malar pada selang = r.

Contoh 2: fungsi y = (x) - bahagian pecahan nombor. Lebih tepat lagi, y =(x) = x - [x], dengan [x] ialah bahagian integer bagi nombor x. Fungsi ini ditakrifkan untuk semua x. Jika x ialah nombor arbitrari, maka mewakilinya sebagai x = r + q (r = [x]), dengan r ialah integer dan q terletak pada selang .
Kami melihat bahawa menambah n pada hujah x tidak mengubah nilai fungsi.
Nombor bukan sifar terkecil dalam n ialah , maka tempohnya ialah sin 2x .

Nilai hujah yang fungsinya sama dengan 0 dipanggil sifar (akar) fungsi.

Fungsi boleh mempunyai berbilang sifar.

Sebagai contoh, fungsi y=x(x+1)(x-3) mempunyai tiga sifar: x=0, x=-1, x=3.

Secara geometri, sifar fungsi ialah absis titik persilangan graf fungsi dengan paksi X .

Rajah 7 menunjukkan graf fungsi dengan sifar: x = a, x = b dan x = c .

Jika graf fungsi menghampiri garis lurus tertentu selama-lamanya semasa ia bergerak menjauhi asalan, maka garis lurus ini dipanggil asimtot.

Fungsi songsang

Biarkan fungsi y=ƒ(x) diberikan dengan domain definisi D dan set nilai E. Jika setiap nilai yєE sepadan dengan nilai tunggal xєD, maka fungsi x=φ(y) ditakrifkan dengan domain definisi E dan set nilai D (lihat Rajah 102).

Fungsi φ(y) sedemikian dipanggil songsang bagi fungsi ƒ(x) dan ditulis dalam bentuk berikut: x=j(y)=f -1 (y) Mengenai fungsi y=ƒ(x) dan x=φ(y) mereka mengatakan bahawa mereka saling songsang. Untuk mencari fungsi x=φ(y) songsang kepada fungsi y=ƒ(x), adalah memadai untuk menyelesaikan persamaan ƒ(x)=y berkenaan dengan x (jika boleh).

1. Untuk fungsi y \u003d 2x, fungsi songsang ialah fungsi x \u003d y / 2;

2. Untuk fungsi y \u003d x2 xє, fungsi songsang ialah x \u003d √y; ambil perhatian bahawa untuk fungsi y \u003d x 2, diberikan pada segmen [-1; 1], tiada songsang, kerana satu nilai y sepadan dengan dua nilai x (contohnya, jika y=1/4, maka x1=1/2, x2=-1/2).

Ia berikutan daripada takrifan fungsi songsang bahawa fungsi y=ƒ(x) mempunyai songsang jika dan hanya jika fungsi ƒ(x) mentakrifkan padanan satu-dengan-satu antara set D dan E. Ia berikutan bahawa sebarang fungsi monotonik tegas mempunyai songsang. Lebih-lebih lagi, jika fungsi bertambah (berkurang), maka fungsi songsang juga bertambah (berkurang).

Perhatikan bahawa fungsi y \u003d ƒ (x) dan songsangnya x \u003d φ (y) digambarkan oleh lengkung yang sama, iaitu, grafnya bertepatan. Jika kita bersetuju bahawa, seperti biasa, pembolehubah bebas (iaitu, argumen) dilambangkan dengan x, dan pembolehubah bersandar oleh y, maka fungsi songsang bagi fungsi y \u003d ƒ (x) akan ditulis sebagai y \u003d φ (x).

Ini bermakna titik M 1 (x o; y o) bagi lengkung y=ƒ(x) menjadi titik M 2 (y o; x o) bagi lengkung y=φ(x). Tetapi titik M 1 dan M 2 adalah simetri mengenai garis lurus y \u003d x (lihat Rajah 103). Oleh itu, graf bagi fungsi songsang bersama y=ƒ(x) dan y=φ(x) adalah simetri berkenaan dengan pembahagi dua sudut koordinat pertama dan ketiga.

Fungsi kompleks

Biarkan fungsi y=ƒ(u) ditakrifkan pada set D, dan fungsi u= φ(x) pada set D 1 , dan untuk  x D 1 nilai yang sepadan u=φ(x) є D. Kemudian pada set D 1 ditakrifkan fungsi u=ƒ(φ(x)), yang dipanggil fungsi kompleks bagi x (atau superposisi fungsi yang diberikan, atau fungsi fungsi).

Pembolehubah u=φ(x) dipanggil hujah perantaraan bagi fungsi kompleks.

Sebagai contoh, fungsi y=sin2x ialah superposisi dua fungsi y=sinu dan u=2x. Fungsi kompleks boleh mempunyai berbilang argumen perantaraan.

4. Fungsi asas asas dan grafnya.

Fungsi berikut dipanggil fungsi asas asas.

1) Fungsi eksponen y \u003d a x, a> 0, a ≠ 1. Dalam rajah. 104 menunjukkan graf fungsi eksponen sepadan dengan pelbagai asas eksponen.

2) Fungsi kuasa y=x α , αєR. Contoh graf fungsi kuasa yang sepadan dengan pelbagai eksponen disediakan dalam rajah

3) Fungsi logaritma y=log a x, a>0,a≠1; Graf bagi fungsi logaritma sepadan dengan asas yang berbeza ditunjukkan dalam rajah. 106.

4) Fungsi trigonometri y=sinx, y=cosx, y=tgx, y=ctgx; Graf fungsi trigonometri mempunyai bentuk yang ditunjukkan dalam rajah. 107.

5) Fungsi trigonometri songsang y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Pada rajah. 108 menunjukkan graf bagi fungsi trigonometri songsang.

Fungsi yang diberikan oleh satu formula, yang terdiri daripada fungsi asas asas dan pemalar menggunakan bilangan terhingga operasi aritmetik (tambah, tolak, darab, bahagi) dan operasi mengambil fungsi daripada fungsi, dipanggil fungsi asas.

Contoh fungsi asas ialah fungsi

Contoh fungsi bukan asas ialah fungsi

5. Konsep had jujukan dan fungsi. Hadkan hartanah.

Had fungsi (had fungsi) pada titik tertentu, mengehadkan domain definisi fungsi, ialah nilai yang nilai fungsi yang sedang dipertimbangkan cenderung apabila hujahnya cenderung kepada titik tertentu.

Dalam matematik had urutan unsur ruang metrik atau ruang topologi ialah unsur ruang yang sama yang mempunyai sifat "menarik" unsur urutan tertentu. Had jujukan unsur ruang topologi ialah titik sedemikian, setiap kejiranan yang mengandungi semua unsur jujukan, bermula dari beberapa nombor. Dalam ruang metrik, kejiranan ditakrifkan dari segi fungsi jarak, jadi konsep had dirumuskan dalam bahasa jarak. Dari segi sejarah, yang pertama ialah konsep had jujukan berangka, yang timbul dalam analisis matematik, di mana ia berfungsi sebagai asas untuk sistem penghampiran dan digunakan secara meluas dalam pembinaan kalkulus pembezaan dan kamiran.

Jawatan:

(baca: had bagi jujukan ke-x sebagai en cenderung kepada infiniti ialah a)

Sifat urutan untuk mempunyai had dipanggil penumpuan: jika suatu jujukan mempunyai had, maka jujukan yang diberikan itu dikatakan menumpu; sebaliknya (jika jujukan tiada had) jujukan itu dikatakan menyimpang. Dalam ruang Hausdorff, dan khususnya ruang metrik, setiap jujukan jujukan penumpu menumpu, dan hadnya adalah sama dengan had jujukan asal. Dengan kata lain, urutan unsur dalam ruang Hausdorff tidak boleh mempunyai dua had yang berbeza. Walau bagaimanapun, mungkin ternyata urutan itu tidak mempunyai had, tetapi terdapat urutan (dari urutan yang diberikan) yang mempunyai had. Jika jujukan penumpuan boleh dibezakan daripada sebarang jujukan titik dalam ruang, maka ruang itu dikatakan mempunyai sifat kekompakan jujukan (atau, ringkasnya, kekompakan jika kekompakan ditakrifkan secara eksklusif dari segi jujukan).

Konsep had jujukan secara langsung berkaitan dengan konsep titik had (set): jika set mempunyai titik had, maka terdapat jujukan unsur set yang diberikan menumpu ke titik yang diberikan.

Definisi

Biarkan ruang topologi dan jujukan diberikan Kemudian, jika wujud unsur sedemikian

di mana set terbuka mengandungi , maka ia dipanggil had jujukan . Jika ruang ialah metrik, maka had boleh ditakrifkan menggunakan metrik: jika wujud unsur sedemikian

di mana metrik, maka dipanggil had.

· Jika ruang dilengkapi dengan topologi antidiscrete, maka had sebarang jujukan ialah sebarang unsur ruang.

6. Had fungsi pada satu titik. Had unilateral.

Fungsi satu pembolehubah. Menentukan had fungsi pada satu titik mengikut Cauchy. Nombor b dipanggil had fungsi di = f(x) pada X berusaha untuk a(atau pada titik a) jika bagi sebarang nombor positif  terdapat nombor positif  supaya bagi semua x ≠ a, supaya | x – a | < , выполняется неравенство
| f(x) – a | <  .

Menentukan had fungsi pada satu titik mengikut Heine. Nombor b dipanggil had fungsi di = f(x) pada X berusaha untuk a(atau pada titik a) jika untuk sebarang urutan ( x n ) menumpu kepada a(bercita-cita untuk a, yang mempunyai nombor had a), dan untuk sebarang nilai n x n≠ a, susulan ( y n= f(x n)) menumpu kepada b.

Takrifan ini menganggap bahawa fungsi di = f(x) ditakrifkan dalam beberapa kejiranan titik a, kecuali mungkin untuk perkara yang sangat penting a.

Takrifan had fungsi pada satu titik mengikut Cauchy dan menurut Heine adalah setara: jika nombor b berfungsi sebagai had dalam salah satu daripada mereka, maka perkara yang sama berlaku dalam yang kedua.

Had yang ditentukan ditunjukkan seperti berikut:

Secara geometri, kewujudan had fungsi pada satu titik mengikut Cauchy bermakna bagi sebarang nombor  > 0, seseorang boleh menunjukkan segi empat tepat sedemikian pada satah koordinat dengan tapak 2 > 0, ketinggian 2 dan pusat di bahagian titik ( a; b) bahawa semua titik graf fungsi ini pada selang ( a– ; a+ ), dengan kemungkinan pengecualian titik M(a; f(a)), terletak di segi empat tepat ini

Had berat sebelah dalam analisis matematik, had fungsi berangka, membayangkan "mendekati" titik had dari satu sisi. Had sedemikian dipanggil masing-masing had sebelah kiri(atau had kiri) dan had sebelah kanan (had di sebelah kanan). Biarkan fungsi berangka diberikan pada beberapa set berangka dan nombor itu adalah titik had domain definisi. Terdapat pelbagai takrifan untuk had sebelah satu fungsi pada satu titik, tetapi semuanya adalah setara.

1) Skop fungsi dan julat fungsi.

Skop fungsi ialah set semua nilai sah argumen yang sah x(pembolehubah x) yang mana fungsinya y = f(x) ditakrifkan. Julat fungsi ialah set semua nilai sebenar y bahawa fungsi menerima.

Dalam matematik asas, fungsi dikaji hanya pada set nombor nyata.

2) Fungsi sifar.

Sifar fungsi ialah nilai hujah di mana nilai fungsi adalah sama dengan sifar.

3) Selang ketekalan tanda bagi sesuatu fungsi.

Selang tanda malar bagi sesuatu fungsi ialah set nilai hujah yang mana nilai fungsi itu hanya positif atau negatif sahaja.

4) Kemonotonan fungsi.

Fungsi yang meningkat (dalam selang tertentu) ialah fungsi di mana nilai argumen yang lebih besar daripada selang ini sepadan dengan nilai fungsi yang lebih besar.

Mengurangkan fungsi (dalam beberapa selang) - fungsi di mana nilai argumen yang lebih besar daripada selang ini sepadan dengan nilai fungsi yang lebih kecil.

5) Fungsi genap (ganjil)..

Fungsi genap ialah fungsi yang domain definisinya adalah simetri berkenaan dengan asalan dan untuk sebarang X daripada domain takrifan persamaan f(-x) = f(x). Graf bagi fungsi genap adalah simetri tentang paksi-y.

Fungsi ganjil ialah fungsi yang domain definisinya adalah simetri berkenaan dengan asalan dan untuk mana-mana X daripada domain takrifan persamaan f(-x) = - f(x). Graf bagi fungsi ganjil adalah simetri tentang asalan.

6) Fungsi terhad dan tidak terhad.

Sesuatu fungsi dipanggil bersempadan jika wujud nombor positif M sehingga |f(x)| ≤ M untuk semua nilai x . Jika tiada nombor sedemikian, maka fungsi itu tidak terhad.

7) Keberkalaan fungsi.

Fungsi f(x) adalah berkala jika wujud bukan sifar nombor T supaya bagi mana-mana x daripada domain fungsi itu, f(x+T) = f(x). Nombor terkecil ini dipanggil tempoh fungsi. Semua fungsi trigonometri adalah berkala. (Rumus trigonometri).

19. Fungsi asas asas, sifat dan grafnya. Aplikasi fungsi dalam ekonomi.

Fungsi asas asas. Sifat dan graf mereka

1. Fungsi linear.

Fungsi linear dipanggil fungsi bentuk , di mana x ialah pembolehubah, dan dan b ialah nombor nyata.

Nombor a dipanggil kecerunan garis lurus, ia adalah sama dengan tangen sudut kecondongan garis lurus ini ke arah positif paksi-x. Graf fungsi linear ialah garis lurus. Ia ditakrifkan oleh dua mata.

Sifat Fungsi Linear

1. Domain definisi - set semua nombor nyata: D (y) \u003d R

2. Set nilai ialah set semua nombor nyata: E(y)=R

3. Fungsi mengambil nilai sifar untuk atau.

4. Fungsi bertambah (menurun) ke atas keseluruhan domain definisi.

5. Fungsi linear adalah berterusan pada keseluruhan domain definisi, boleh dibezakan dan .

2. Fungsi kuadratik.

Satu fungsi bentuk, di mana x ialah pembolehubah, pekali a, b, c ialah nombor nyata, dipanggil kuadratik.

Fungsi kuasa. Ini adalah fungsinya: y = kapak n, di mana a,n- kekal. Pada n= 1 kita dapat perkadaran langsung: y = kapak; di n = 2 - parabola segi empat sama ; di n = - 1 - perkadaran songsang atau hiperbola. Oleh itu, fungsi ini adalah kes khas bagi fungsi kuasa. Kita tahu bahawa kuasa sifar mana-mana nombor bukan sifar ialah 1, oleh itu, pada n= 0 fungsi kuasa menjadi pemalar:y = a, iaitu e. jadual dia garis lurus selari dengan paksiX, tidak termasuk asal (sila jelaskan, kenapa? ). Semua kes ini (dengan a= 1 ) ditunjukkan dalam Rajah.13 (n 0 ) dan Rajah 14 ( n < 0). Отрицательные значения xtidak dipertimbangkan di sini seperti kemudian beberapa fungsi:

Sekiranya n– keseluruhan, fungsi kuasa masuk akal walaupun ketikax< 0, но их графики имеют различный вид в зависимости от того, является ли nnombor genap atau nombor ganjil. Rajah 15 menunjukkan dua fungsi kuasa sedemikian: untuk n= 2 dan n = 3.


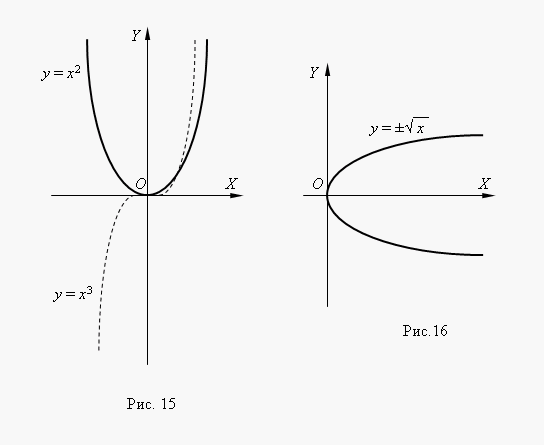
Pada n= 2 fungsi genap dangrafnya adalah simetri tentang paksi Y. Pada n= 3 fungsi adalah ganjil dan grafnya adalah simetri berkenaan dengan asalan koordinat. Fungsiy = x 3 dipanggil parabola padu.

Rajah 16 menunjukkan fungsi . ini fungsi ialah parabola songsang kepada segi empat sama y = x 2 , grafnya diperoleh dengan memutarkan graf parabola segi empat sama mengelilingi pembahagi dua sudut koordinat pertama. Ini ialah satu cara untuk mendapatkan graf sebarang fungsi songsang daripada graf fungsi asalnya. Kita boleh melihat daripada graf bahawa ini ialah fungsi dua nilai (ini juga ditunjukkan oleh tanda ± di hadapan punca kuasa dua). Fungsi sedemikian tidak dipelajari dalam matematik asas, oleh itu, sebagai fungsi, kita biasanya menganggap salah satu cabangnya: atas atau bawah.

Apakah maksud perkataan tersebut "fungsi set"? Mereka bermaksud: untuk menerangkan kepada semua orang, tentang apa fungsi tertentu sedang bercakap. Selain itu, terangkan dengan jelas dan jelas!

Bagaimana saya boleh melakukannya? Bagaimana tetapkan fungsi?

Anda boleh menulis formula. Anda boleh melukis graf. Anda boleh membuat meja. Apa-apa cara pun beberapa peraturan yang membolehkan anda mengetahui nilai pemain untuk nilai x yang telah kami pilih. Itu. "fungsi tetapkan", ini bermakna - untuk menunjukkan undang-undang, peraturan yang mengikutnya x bertukar menjadi y.

Biasanya, dalam pelbagai tugas ada sedia fungsi. Mereka memberi kita sudah ditetapkan. Tentukan sendiri, tetapi buat keputusan.) Tetapi ... Selalunya, pelajar sekolah (dan pelajar) bekerja dengan formula. Mereka terbiasa dengannya, anda faham... Mereka sudah terbiasa dengannya sehinggakan sebarang soalan asas yang berkaitan dengan cara berbeza untuk menentukan fungsi serta-merta mengganggu seseorang...)

Untuk mengelakkan kes sedemikian, masuk akal untuk memahami cara yang berbeza untuk mentakrifkan fungsi. Dan, sudah tentu, gunakan pengetahuan ini untuk soalan "licik". Ia cukup mudah. Jika anda tahu apa itu fungsi...)

Pergi?)

Cara analitik untuk mentakrifkan fungsi.

Cara yang paling serba boleh dan berkuasa. Fungsi ditakrifkan secara analitikal, ini adalah fungsi yang diberikan formula. Sebenarnya, ini adalah penjelasan keseluruhannya.) Fungsi yang biasa kepada semua orang (saya mahu percaya!)), contohnya: y=2x atau y=x2 dan lain-lain. dan lain-lain. diberikan secara analitikal.

By the way, tidak setiap formula boleh menentukan fungsi. Tidak setiap formula mengikut syarat ketat definisi fungsi. Iaitu - untuk setiap x ada sahaja satu permainan. Sebagai contoh, dalam formula y = ±x, untuk satu nilai x=2, ternyata dua nilai y: +2 dan -2. Adalah mustahil untuk menentukan fungsi nilai tunggal dengan formula ini. Dan dengan fungsi berbilang nilai dalam bahagian matematik ini, dalam analisis matematik, ia tidak berfungsi, sebagai peraturan.

Mengapakah cara analisis untuk mentakrifkan fungsi adalah baik? Hakikat bahawa jika anda mempunyai formula - anda tahu tentang fungsi semua! Anda boleh membuat meja. Bina graf. Terokai ciri ini sepenuhnya. Ramalkan dengan tepat di mana dan bagaimana fungsi ini akan berfungsi. Semua analisis matematik bergantung pada kaedah mentakrifkan fungsi ini. Katakan amat sukar untuk mengambil terbitan jadual...)

Kaedah analisis agak biasa dan tidak menimbulkan masalah. Kecuali mungkin beberapa jenis kaedah ini yang dihadapi oleh pelajar. Saya bercakap tentang penetapan fungsi parametrik dan tersirat.) Tetapi fungsi tersebut adalah dalam pelajaran khas.

Mari kita beralih kepada cara yang kurang biasa untuk mentakrifkan fungsi.

Cara jadual mentakrifkan fungsi.

Seperti namanya, kaedah ini adalah plat mudah. Dalam jadual ini, setiap x sepadan dengan ( adalah sejajar) beberapa nilai pemain. Baris pertama mengandungi nilai hujah. Baris kedua mengandungi nilai fungsi yang sepadan, contohnya:

Jadual 1.

x	- 3	- 1	0	2	3	4
y	5	2	- 4	- 1	6	5

Sila ambil perhatian! Dalam contoh ini, y bergantung kepada x bagaimanapun. Saya datang dengan ini dengan sengaja.) Tiada corak. Tidak mengapa, ia berlaku. Bermaksud, betul-betul Saya menetapkan fungsi khusus ini. Tepat sekali Saya menyediakan peraturan yang x bertukar menjadi y.

Boleh disusun yang lain pinggan dengan corak. Pinggan ini akan ditetapkan yang lain fungsi, contohnya:

Jadual 2.

x	- 3	- 1	0	2	3	4
y	- 6	- 2	0	4	6	8

Adakah anda menangkap coraknya? Di sini, semua nilai y diperoleh dengan mendarab x dengan dua. Berikut ialah soalan "licik" pertama: bolehkah fungsi yang dinyatakan menggunakan Jadual 2 dianggap sebagai fungsi y = 2x? Fikir sejenak, jawapannya akan ada di bawah, secara grafik. Ia sangat jelas di sana.)

Apa yang baik cara jadual menetapkan fungsi? Ya, anda tidak perlu mengira apa-apa. Semuanya telah dikira dan ditulis dalam jadual.) Dan tidak ada yang lebih baik. Kita tidak tahu nilai fungsi untuk x, yang tiada dalam jadual. Dalam kaedah ini, nilai x seperti itu hanyalah semata-mata tidak wujud. Ngomong-ngomong, ini adalah petunjuk kepada soalan rumit.) Kami tidak dapat mengetahui bagaimana fungsi berfungsi di luar jadual. Kami tidak boleh berbuat apa-apa. Ya, dan keterlihatan dalam kaedah ini meninggalkan banyak yang diingini ... Untuk kejelasan, kaedah grafik adalah baik.

Cara grafik untuk menentukan fungsi.

Dalam kaedah ini, fungsi diwakili oleh graf. Hujah (x) diplot di sepanjang absis, dan nilai fungsi (y) diplot di sepanjang ordinat. Mengikut jadual, anda juga boleh memilih mana-mana X dan cari nilai yang sepadan di. Jadual boleh menjadi apa-apa, tetapi... bukan sebarang.) Kami hanya berfungsi dengan fungsi bernilai tunggal. Takrifan fungsi tersebut dengan jelas menyatakan: setiap X adalah sejajar hanya satu di. satu satu, bukan dua, atau tiga... Contohnya, mari kita lihat graf bulatan:

Bulatan adalah seperti bulatan... Mengapa ia tidak sepatutnya menjadi graf fungsi? Dan mari kita cari y yang manakah akan sepadan dengan nilai x, sebagai contoh, 6? Kami menggerakkan kursor ke atas carta (atau sentuh gambar pada tablet), dan ... kami melihat bahawa X ini sepadan dengannya dua nilai pemain: y=2 dan y=6.

Dua dan enam! Oleh itu, graf sedemikian tidak akan menjadi tugasan grafik bagi sesuatu fungsi. Pada satu x dikira dua permainan. Graf ini tidak sepadan dengan definisi fungsi.

Tetapi jika syarat keunikan dipenuhi, graf boleh menjadi apa-apa sahaja. Sebagai contoh:

Ini sangat krivulina - dan terdapat undang-undang yang mana anda boleh menterjemah x ke dalam y. Tidak jelas. Kami ingin mengetahui nilai fungsi untuk x = 4, sebagai contoh. Kita perlu mencari empat pada paksi-x dan lihat yang mana y sepadan dengan x ini. Tuding tetikus di atas rajah dan lihat bahawa nilai fungsi di untuk x=4 sama dengan lima. Kita tidak tahu dengan formula apakah transformasi X menjadi Y diberikan. Dan ia tidak perlu. Semuanya ditetapkan mengikut jadual.

Sekarang kita boleh kembali kepada soalan "susah" tentang y=2x. Mari kita plot fungsi ini. Inilah dia:

Sudah tentu, semasa melukis graf ini, kami tidak mengambil bilangan nilai yang tidak terhingga X. Kami mengambil beberapa nilai, dikira y, membuat pinggan - dan anda sudah selesai! Yang paling celik biasanya hanya mengambil dua nilai X! Dan memang betul. Untuk garis lurus, anda tidak memerlukan lebih banyak lagi. Kenapa kerja tambahan?

Tetapi kita tahu betul-betul apa x boleh sesiapa. Keseluruhan, pecahan, negatif... Mana-mana. Ini mengikut formula y=2x ia dilihat. Oleh itu, kami dengan berani menyambungkan titik-titik pada graf dengan garis pepejal.

Jika fungsi itu diberikan kepada kita oleh Jadual 2, maka kita perlu mengambil nilai-x hanya dari meja. Untuk X lain (dan Y) tidak diberikan kepada kami, dan tiada tempat untuk membawanya. Tidak ada, nilai-nilai ini, dalam fungsi ini. Jadual akan berubah daripada mata. Kami menghalakan tetikus pada gambar dan melihat graf fungsi yang diberikan oleh Jadual 2. Saya tidak menulis nilai x-y pada paksi, adakah anda akan memikirkannya, pergi, dengan sel?)

Inilah jawapan kepada soalan rumit itu. Fungsi yang diberikan oleh Jadual 2 dan fungsi y=2x - pelbagai.

Kaedah grafik adalah baik untuk kejelasannya. Anda boleh melihat dengan serta-merta bagaimana fungsi berfungsi apabila ia meningkat. di mana ia berkurangan. Daripada graf, anda boleh segera mengetahui beberapa ciri penting fungsi tersebut. Dan dalam topik dengan terbitan, tugasan dengan graf - sepanjang masa!

Secara umum, cara analisis dan grafik untuk mentakrifkan fungsi berjalan seiring. Bekerja dengan formula membantu membina graf. Dan graf sering mencadangkan penyelesaian yang anda tidak akan perasan dalam formula ... Kami akan berkawan dengan graf.)

Hampir mana-mana pelajar mengetahui tiga cara untuk mentakrifkan fungsi yang baru sahaja kami bincangkan. Tetapi kepada soalan: "Dan yang keempat!?" - membeku dengan sempurna.)

Ada cara sedemikian.

Penerangan lisan tentang fungsi.

Ya Ya! Fungsi boleh ditakrifkan dengan jelas dalam perkataan. Bahasa Rusia yang hebat dan hebat mampu berbuat banyak!) Contohnya, fungsi y=2x boleh diberikan penerangan lisan berikut: setiap nilai sebenar argumen x diberikan nilai dua kali gandanya. Macam ni! Peraturan ditetapkan, fungsi ditetapkan.

Selain itu, adalah mungkin untuk menentukan fungsi secara lisan, yang sangat sukar, jika tidak mustahil, untuk ditentukan dengan formula. Sebagai contoh: setiap nilai hujah asli x diberikan jumlah digit yang membentuk nilai x. Sebagai contoh, jika x=3, kemudian y=3. Sekiranya x=257, kemudian y=2+5+7=14. Dan sebagainya. Sukar untuk menulis ini dalam formula. Tetapi meja itu mudah dibuat. Dan bina carta. Dengan cara ini, jadual ternyata lucu ...) Cubalah.

Kaedah penerangan lisan adalah kaedah yang agak eksotik. Tetapi kadang-kadang ia berlaku. Di sini saya membawanya untuk memberi anda keyakinan dalam situasi yang tidak dijangka dan tidak standard. Anda hanya perlu memahami maksud perkataan "set fungsi..." Inilah maksudnya:

Sekiranya terdapat undang-undang surat menyurat satu dengan satu antara X dan di bermakna ada fungsi. Undang-undang apa, dalam bentuk apa ia dinyatakan - dengan formula, tablet, graf, perkataan, lagu, tarian - tidak mengubah intipati perkara itu. Undang-undang ini membenarkan anda menentukan nilai y yang sepadan dengan nilai x. Semuanya.

Sekarang kita akan menggunakan pengetahuan yang mendalam ini untuk beberapa tugas yang tidak standard.) Seperti yang dijanjikan pada permulaan pelajaran.

Latihan 1:

Fungsi y = f(x) diberikan dalam Jadual 1:

Jadual 1.

Cari nilai fungsi p(4) jika p(x)= f(x) - g(x)

Jika anda tidak dapat mengetahui apa itu sama sekali - baca pelajaran sebelumnya "Apakah itu fungsi?" Di sana, ia ditulis dengan sangat jelas tentang huruf dan kurungan sedemikian.) Dan jika hanya bentuk jadual yang mengelirukan anda, maka kami akan memikirkannya di sini.

Jelas daripada pelajaran lepas bahawa jika, p(x) = f(x) - g(x), kemudian p(4) = f(4) - g(4). surat f dan g bermaksud peraturan mengikut mana setiap X diberikan Y sendiri. Bagi setiap huruf ( f dan g) - sendiri peraturan. Yang diberikan oleh jadual yang sepadan.

Nilai fungsi f(4) ditentukan daripada Jadual 1. Ini akan menjadi 5. Nilai fungsi g(4) ditentukan oleh Jadual 2. Ini akan menjadi 8. Yang paling sukar kekal.)

p(4) = 5 - 8 = -3

Ini adalah jawapan yang betul.

Selesaikan ketaksamaan f(x) > 2

Itu sahaja! Ia adalah perlu untuk menyelesaikan ketidaksamaan, yang (dalam bentuk biasa) tidak hadir dengan cemerlang! Ia kekal sama ada berhenti tugas, atau menghidupkan kepala. Kami memilih yang kedua dan berhujah.)

Apakah yang dimaksudkan untuk menyelesaikan ketidaksamaan? Ini bermakna untuk mencari semua nilai x yang mana syarat yang diberikan kepada kita dipenuhi f(x) > 2. Itu. semua nilai fungsi ( di) mestilah lebih besar daripada dua. Dan kita mempunyai setiap y pada carta... Dan terdapat lebih daripada dua, dan kurang... Dan mari, untuk kejelasan, lukis garis pada dua ini! Kami menggerakkan kursor ke atas gambar dan melihat sempadan ini.

Tegasnya, sempadan ini ialah graf fungsi y=2, tetapi bukan itu maksudnya. Adalah penting bahawa sekarang pada graf ia boleh dilihat dengan jelas di mana, pada apa x, nilai fungsi, i.e. y, lebih daripada dua. Mereka lebih X > 3. Pada X > 3 keseluruhan fungsi kami berlalu di atas sempadan y=2. Itulah penyelesaian keseluruhan. Tetapi masih terlalu awal untuk menutup kepala anda!) Kami masih perlu menulis jawapan ...

Graf menunjukkan bahawa fungsi kami tidak memanjang ke kiri dan kanan ke infiniti. Titik di hujung graf bercakap tentang perkara ini. Fungsi itu berakhir di sana. Oleh itu, dalam ketaksamaan kita, semua x yang melampaui had fungsi tidak mempunyai makna. Untuk fungsi x ini tidak wujud. Dan kami, sebenarnya, menyelesaikan ketidaksamaan untuk fungsi ...

Jawapan yang betul ialah:

3 < X ≤ 6

Atau, dalam bentuk lain:

X ∈ (3; 6]

Sekarang semuanya seperti yang sepatutnya. Rangkap tiga tidak termasuk dalam jawapan, kerana ketidaksamaan asal adalah ketat. Dan enam bertukar, kerana dan fungsi pada enam wujud, dan keadaan ketaksamaan dipenuhi. Kami telah berjaya menyelesaikan ketidaksamaan yang (dalam bentuk biasa) tidak wujud...

Inilah cara beberapa pengetahuan dan logik asas menyimpan dalam kes bukan standard.)

Panjang segmen pada paksi koordinat didapati dengan formula:

Panjang segmen pada satah koordinat dicari dengan formula:

Untuk mencari panjang segmen dalam sistem koordinat tiga dimensi, formula berikut digunakan:

Koordinat tengah segmen (untuk paksi koordinat hanya formula pertama digunakan, untuk satah koordinat - dua formula pertama, untuk sistem koordinat tiga dimensi - ketiga-tiga formula) dikira oleh formula:

Fungsi ialah surat-menyurat borang y= f(x) antara pembolehubah, kerana setiap satunya menganggap nilai beberapa pembolehubah x(argumen atau pembolehubah bebas) sepadan dengan nilai tertentu pembolehubah lain, y(pembolehubah bersandar, kadangkala nilai ini hanya dipanggil nilai fungsi). Ambil perhatian bahawa fungsi menganggap bahawa satu nilai hujah X hanya terdapat satu nilai pembolehubah bersandar di. Namun, nilai yang sama di boleh diperolehi dengan pelbagai X.

Skop fungsi adalah semua nilai pembolehubah bebas (hujah fungsi, biasanya X) yang mana fungsi itu ditakrifkan, i.e. maknanya wujud. Domain definisi ditunjukkan D(y). Pada umumnya, anda sudah biasa dengan konsep ini. Skop fungsi sebaliknya dipanggil domain nilai sah, atau ODZ, yang anda dapat cari untuk masa yang lama.

Julat fungsi adalah semua nilai yang mungkin bagi pembolehubah bersandar bagi fungsi ini. Ditandakan E(di).

Fungsi meningkat pada selang di mana nilai argumen yang lebih besar sepadan dengan nilai fungsi yang lebih besar. Fungsi Menurun pada selang di mana nilai argumen yang lebih besar sepadan dengan nilai fungsi yang lebih kecil.

Selang fungsi ialah selang pembolehubah bebas di mana pembolehubah bersandar mengekalkan tanda positif atau negatifnya.

Fungsi sifar ialah nilai hujah yang nilai fungsinya sama dengan sifar. Pada titik ini, graf fungsi bersilang dengan paksi absis (paksi OX). Selalunya, keperluan untuk mencari sifar fungsi bermakna hanya menyelesaikan persamaan. Juga, selalunya keperluan untuk mencari selang tanda malar bermakna keperluan untuk menyelesaikan ketaksamaan sahaja.

Fungsi y = f(x) dipanggil malah X

Ini bermakna bahawa untuk mana-mana nilai yang bertentangan dengan hujah, nilai fungsi genap adalah sama. Graf bagi fungsi genap sentiasa simetri tentang paksi-y bagi op-amp.

Fungsi y = f(x) dipanggil ganjil, jika ia ditakrifkan pada set simetri dan untuk mana-mana X dari domain definisi kesaksamaan dipenuhi:

Ini bermakna bahawa untuk mana-mana nilai yang bertentangan dengan hujah, nilai fungsi ganjil juga bertentangan. Graf bagi fungsi ganjil sentiasa simetri tentang asalan.

Jumlah punca bagi fungsi genap dan ganjil (titik persilangan paksi absis OX) sentiasa sama dengan sifar, kerana untuk setiap akar positif X mempunyai akar negatif X.

Adalah penting untuk ambil perhatian bahawa sesetengah fungsi tidak semestinya genap atau ganjil. Terdapat banyak fungsi yang tidak genap dan tidak ganjil. Fungsi sedemikian dipanggil fungsi umum, dan tiada kesamaan atau sifat di atas berlaku untuk mereka.

Fungsi linear dipanggil fungsi yang boleh diberikan oleh formula:

Graf fungsi linear ialah garis lurus dan dalam kes umum kelihatan seperti ini (contoh diberikan untuk kes apabila k> 0, dalam kes ini fungsi semakin meningkat; untuk kes itu k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

Graf Fungsi Kuadratik (Parabola)

Graf parabola diberikan oleh fungsi kuadratik:

Fungsi kuadratik, seperti fungsi lain, memotong paksi OX pada titik yang menjadi puncanya: ( x satu ; 0) dan ( x 2; 0). Jika tiada punca, maka fungsi kuadratik tidak bersilang dengan paksi OX, jika terdapat satu punca, maka pada titik ini ( x 0; 0) fungsi kuadratik hanya menyentuh paksi OX, tetapi tidak memotongnya. Fungsi kuadratik sentiasa bersilang dengan paksi OY pada satu titik dengan koordinat: (0; c). Graf fungsi kuadratik (parabola) mungkin kelihatan seperti ini (rajah menunjukkan contoh yang jauh daripada ekzos semua jenis parabola yang mungkin):

Di mana:

• jika pekali a> 0, dalam fungsi y = kapak 2 + bx + c, maka cabang parabola diarahkan ke atas;
• jika a < 0, то ветви параболы направлены вниз.

Koordinat puncak parabola boleh dikira menggunakan formula berikut. X puncak (hlm- dalam rajah di atas) parabola (atau titik di mana trinomial segi empat sama mencapai nilai maksimum atau minimum):

Y puncak (q- dalam rajah di atas) parabola atau maksimum jika cabang parabola diarahkan ke bawah ( a < 0), либо минимальное, если ветви параболы направлены вверх (a> 0), nilai trinomial segi empat sama:

Graf fungsi lain

fungsi kuasa

Berikut ialah beberapa contoh graf fungsi kuasa:

Pergantungan berkadar songsang panggil fungsi yang diberikan oleh formula:

Bergantung pada tanda nombor k Graf berkadar songsang boleh mempunyai dua pilihan asas:

Asimtot ialah garis yang menghampiri garis graf fungsi yang hampir tak terhingga, tetapi tidak bersilang. Asimtot untuk graf perkadaran songsang yang ditunjukkan dalam rajah di atas ialah paksi koordinat, yang mana graf fungsi menghampiri hampir tak terhingga, tetapi tidak bersilang.

fungsi eksponen dengan asas a panggil fungsi yang diberikan oleh formula:

a graf fungsi eksponen boleh mempunyai dua pilihan asas (kami juga akan memberikan contoh, lihat di bawah):

fungsi logaritma panggil fungsi yang diberikan oleh formula:

Bergantung kepada sama ada bilangannya lebih besar atau kurang daripada satu a Graf fungsi logaritma boleh mempunyai dua pilihan asas:

Graf Fungsi y = |x| seperti berikut:

Graf fungsi berkala (trigonometrik).

Fungsi di = f(x) dipanggil berkala, jika wujud nombor bukan sifar sedemikian T, apa f(x + T) = f(x), untuk sesiapa X di luar skop fungsi f(x). Jika fungsi f(x) adalah berkala dengan tempoh T, maka fungsinya:

di mana: A, k, b ialah nombor tetap, dan k tidak sama dengan sifar, juga berkala dengan tempoh T 1 , yang ditentukan oleh formula:

Kebanyakan contoh fungsi berkala ialah fungsi trigonometri. Berikut ialah graf bagi fungsi trigonometri utama. Rajah berikut menunjukkan sebahagian daripada graf fungsi y= dosa x(keseluruhan graf diteruskan tanpa had ke kiri dan kanan), graf fungsi y= dosa x dipanggil sinusoid:

Graf Fungsi y= cos x dipanggil gelombang kosinus. Graf ini ditunjukkan dalam rajah berikut. Sejak graf sinus, ia berterusan sepanjang paksi OX ke kiri dan ke kanan:

Graf Fungsi y=tg x dipanggil tangentoid. Graf ini ditunjukkan dalam rajah berikut. Seperti graf fungsi berkala yang lain, graf ini berulang tanpa had sepanjang paksi OX ke kiri dan ke kanan.

Dan akhirnya, graf fungsi y=ctg x dipanggil kotangentoid. Graf ini ditunjukkan dalam rajah berikut. Seperti graf fungsi berkala dan trigonometri yang lain, graf ini berulang tanpa had sepanjang paksi OX ke kiri dan ke kanan.

Pelajari semua formula dan undang-undang dalam fizik, dan formula dan kaedah dalam matematik. Malah, ia juga sangat mudah untuk melakukan ini, hanya terdapat kira-kira 200 formula yang diperlukan dalam fizik, dan bahkan kurang sedikit dalam matematik. Dalam setiap mata pelajaran ini terdapat kira-kira sedozen kaedah standard untuk menyelesaikan masalah tahap kerumitan asas, yang juga boleh dipelajari, dan dengan itu, sepenuhnya secara automatik dan tanpa kesukaran, menyelesaikan kebanyakan transformasi digital pada masa yang tepat. Selepas itu, anda hanya perlu memikirkan tugas yang paling sukar.

Hadiri ketiga-tiga peringkat ujian latih tubi dalam fizik dan matematik. Setiap RT boleh dilawati dua kali untuk menyelesaikan kedua-dua pilihan. Sekali lagi, pada CT, sebagai tambahan kepada keupayaan untuk menyelesaikan masalah dengan cepat dan cekap, dan pengetahuan tentang formula dan kaedah, ia juga perlu untuk dapat merancang masa dengan betul, mengagihkan kuasa, dan yang paling penting mengisi borang jawapan dengan betul , tanpa mengelirukan sama ada bilangan jawapan dan tugasan, atau nama anda sendiri. Selain itu, semasa RT, adalah penting untuk membiasakan diri dengan gaya mengemukakan soalan dalam tugasan, yang mungkin kelihatan sangat luar biasa bagi orang yang tidak bersedia di DT.

Pelaksanaan ketiga-tiga perkara ini yang berjaya, tekun dan bertanggungjawab akan membolehkan anda menunjukkan hasil yang cemerlang pada CT, maksimum yang anda mampu.

Menjumpai ralat?

Jika anda, seperti yang anda fikirkan, mendapati ralat dalam bahan latihan, maka sila tulis mengenainya melalui mel. Anda juga boleh menulis tentang ralat pada rangkaian sosial (). Dalam surat itu, nyatakan subjek (fizik atau matematik), nama atau nombor topik atau ujian, nombor tugasan, atau tempat dalam teks (halaman) di mana, pada pendapat anda, terdapat ralat. Terangkan juga apakah ralat yang didakwa itu. Surat anda tidak akan disedari, kesilapan sama ada akan dibetulkan, atau anda akan dijelaskan mengapa ia bukan kesilapan.