Kosinus sudut antara dua satah. Mencari sudut antara satah (sudut dihedral)

Matlamat:

membangunkan keupayaan untuk mempertimbangkan pelbagai pendekatan untuk menyelesaikan masalah dan menganalisis "kesan" menggunakan kaedah penyelesaian ini;
membangunkan keupayaan pelajar untuk memilih kaedah untuk menyelesaikan masalah mengikut keutamaan matematik mereka, berdasarkan pengetahuan yang lebih mantap dan kemahiran yakin;
membangunkan keupayaan untuk merangka pelan peringkat berturut-turut untuk mencapai keputusan;
membangunkan keupayaan untuk mewajarkan semua langkah dan pengiraan yang diambil;
ulang dan betulkan pelbagai tema dan isu stereometri dan planimetri, struktur stereometrik biasa yang berkaitan dengan penyelesaian masalah semasa;
mengembangkan pemikiran spatial.

analisis pelbagai kaedah penyelesaian masalah: kaedah vektor koordinat, penggunaan teorem kosinus, penggunaan teorem tiga serenjang;
membandingkan kelebihan dan kekurangan setiap kaedah;
pengulangan sifat kubus, prisma segi tiga, heksagon sekata;
persediaan untuk lulus peperiksaan;
pembangunan kemerdekaan dalam membuat keputusan.

Rangka pelajaran

kiub ABCDA 1 B 1 C 1 D 1 dengan tepi 1 titik O - tengah muka ABCD.

a) sudut antara garisan A 1 D dan BO;

b) jarak dari titik B ke tengah potong A 1 D.

Titik keputusan a).

Mari kita masukkan kiub kita sistem segi empat tepat koordinat seperti yang ditunjukkan dalam rajah, bucu A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Vektor arah garisan A 1 D dan B1O:

(0; 1; -1) dan (½; ½; -1);

sudut φ yang dikehendaki di antara mereka didapati dengan formula:

cos∠φ = ,
dari mana ∠φ = 30°.

2 cara. Kami menggunakan teorem kosinus.

1) Lukiskan garis lurus Pada 1 C selari dengan garis lurus A 1 D. Sudut CB1O akan diingini.

2) Dari segi tiga tepat BB 1 O mengikut teorem Pythagoras:

3) Dengan hukum kosinus daripada segi tiga CB1O mengira sudut CB1O:

cos CB 1 O = , sudut yang dikehendaki ialah 30°.

Komen. Apabila menyelesaikan masalah dengan cara ke-2, dapat dilihat bahawa, menurut teorem pada tiga serenjang COB 1 = 90°, jadi daripada segi empat tepat ∆ CB1O ia juga mudah untuk mengira kosinus sudut yang dikehendaki.

Titik keputusan b).

1 cara. Mari kita gunakan formula untuk jarak antara dua titik

Biarkan titik E- tengah A 1 D, kemudian koordinat E (1; 1/2; ½), B (0; 0; 0).

B.E.= .

2 cara. Mengikut teorem Pythagoras

Daripada segi empat tepat ∆ BAE dengan langsung BAE cari JADILAH = .

Di sebelah kanan Prisma segi tiga ABCA 1 B 1 C 1 semua tepi adalah sama a. Cari sudut antara garis AB dan A 1 C.

1 cara. Kaedah vektor koordinat

Koordinat bucu prisma dalam sistem segi empat tepat apabila prisma itu terletak, seperti dalam rajah: A (0; 0; 0), B (a; ; 0), A 1 (0; 0; a), C (0; a; 0).

Vektor arah garisan A 1 C dan AB:

(0; a; -a) dan (a; ; 0} ;

cos φ = ;

2 cara. Kami menggunakan hukum kosinus

Kami menganggap ∆ A 1 B 1 C, di mana A 1 B 1 || AB. Kami ada

cos φ = .

(Daripada koleksi Peperiksaan Negeri Bersepadu-2012. Matematik: tipikal pilihan peperiksaan ed. A.L. Semenova, I.V. Yashchenko)

Dalam prisma heksagon sekata ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, semua tepinya sama dengan 1, cari jarak dari titik itu E kepada lurus B 1 C 1.

1 cara. Kaedah vektor koordinat

1) Letakkan prisma dalam sistem koordinat segi empat tepat, letakkan paksi koordinat seperti yang ditunjukkan dalam rajah. SS 1, SW dan CE adalah serenjang berpasangan, jadi paksi koordinat boleh diarahkan di sepanjangnya. Kami mendapat koordinat:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) Cari koordinat bagi vektor arah untuk garisan Dari 1 hingga 1 dan C 1 E:

(0;1;0), (;0;-1).

3) Cari kosinus sudut antara Dari 1 hingga 1 dan C 1 E menggunakan produk skalar vektor dan:

cos β = = 0 => β = 90° => C 1 E ialah jarak yang dikehendaki.

4)C 1 E \u003d \u003d 2.

Kesimpulan: pengetahuan pendekatan yang berbeza untuk menyelesaikan masalah stereometrik membolehkan anda memilih kaedah pilihan untuk mana-mana pelajar, i.e. satu yang pelajar yakin, membantu mengelakkan kesilapan, membawa kepada penyelesaian masalah yang berjaya dan mendapat markah yang baik dalam peperiksaan. kaedah koordinat mempunyai kelebihan berbanding kaedah lain kerana ia memerlukan kurang pertimbangan dan penglihatan stereometrik, dan berdasarkan penggunaan formula yang mempunyai banyak analogi planimetrik dan algebra yang lebih biasa kepada pelajar.

Bentuk pelajaran adalah gabungan penerangan guru dengan kerja kolektif frontal murid.

Polihedron yang sedang dipertimbangkan ditunjukkan pada skrin menggunakan projektor video, yang memungkinkan untuk membandingkan pelbagai cara penyelesaian.

Kerja rumah: selesaikan masalah 3 dengan cara yang berbeza, contohnya, menggunakan teorem tiga serenjang .

kesusasteraan

1. Ershova A.P., Goloborodko V.V. Berdikari dan kertas ujian dalam geometri untuk gred 11. - M .: ILEKSA, - 2010. - 208 p.

2. Geometri, 10-11: buku teks untuk institusi pendidikan: tahap asas dan profil / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev dan lain-lain - M .: Pendidikan, 2007. - 256 p.

3. KEGUNAAN-2012. Matematik: pilihan peperiksaan biasa: 10 pilihan / ed. A.L. Semenova, I.V. Yashchenko. – M.: pendidikan negara, 2011. - 112 p. - (USE-2012. FIPI - sekolah).

Artikel itu membincangkan tentang mencari sudut antara satah. Selepas membawa definisi, kami akan menetapkan ilustrasi grafik, pertimbangkan cara bertele-tele mencari dengan kaedah koordinat. Kami memperoleh formula untuk satah bersilang, yang termasuk koordinat vektor biasa.

Yandex.RTB R-A-339285-1

Bahan tersebut akan menggunakan data dan konsep yang telah dikaji sebelum ini dalam artikel tentang satah dan garisan di angkasa. Sebagai permulaan, adalah perlu untuk beralih kepada penaakulan yang membolehkan seseorang mempunyai pendekatan tertentu untuk menentukan sudut antara dua satah bersilang.

Dua satah bersilang γ 1 dan γ 2 diberi. Persimpangan mereka akan mengambil sebutan c . Pembinaan satah χ disambungkan dengan persilangan satah ini. Satah χ melalui titik M sebagai garis lurus c. Satah γ 1 dan γ 2 akan bersilang menggunakan satah χ. Kami menerima penetapan garis yang bersilang γ 1 dan χ untuk garis a, dan bersilang γ 2 dan χ untuk garis b. Kami mendapat bahawa persilangan garis a dan b memberikan titik M .

Lokasi titik M tidak menjejaskan sudut antara garis bersilang a dan b, dan titik M terletak pada garis c yang melalui satah χ.

Ia adalah perlu untuk membina satah χ 1 berserenjang dengan garis c dan berbeza daripada satah χ . Persilangan satah γ 1 dan γ 2 dengan bantuan χ 1 akan mengambil penetapan garis a 1 dan b 1 .

Dapat dilihat bahawa apabila membina χ dan χ 1, garis a dan b berserenjang dengan garis c, kemudian a 1, b 1 berserenjang dengan garis c. Mencari garis a dan a 1 dalam satah γ 1 dengan serenjang dengan garis c, maka ia boleh dianggap selari. Dengan cara yang sama, lokasi b dan b 1 dalam satah γ 2 dengan keserenjangan garis c menunjukkan keselariannya. Ini bermakna bahawa adalah perlu untuk membuat pemindahan selari satah χ 1 kepada χ, di mana kita mendapat dua garis bertepatan a dan a 1 , b dan b 1 . Kami mendapat bahawa sudut antara garis bersilang a dan b 1 sama dengan sudut garis bersilang a dan b.

Pertimbangkan rajah di bawah.

Penghakiman ini dibuktikan dengan fakta bahawa antara garis bersilang a dan b terdapat sudut yang tidak bergantung pada lokasi titik M, iaitu titik persilangan. Garisan ini terletak pada satah γ 1 dan γ 2 . Malah, sudut yang terhasil boleh dianggap sebagai sudut antara dua satah bersilang.

Mari kita teruskan untuk menentukan sudut antara satah bersilang sedia ada γ 1 dan γ 2 .

Definisi 1

Sudut antara dua satah bersilang γ 1 dan γ 2 panggil sudut yang dibentuk oleh persilangan garis a dan b, di mana satah γ 1 dan γ 2 bersilang dengan satah χ berserenjang dengan garis c.

Pertimbangkan rajah di bawah.

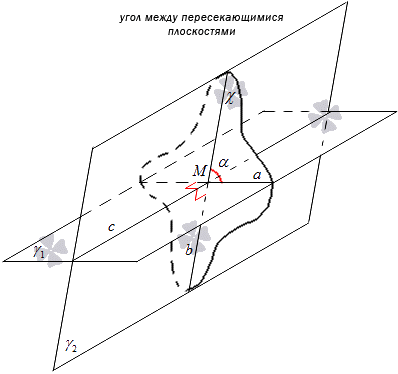
Takrifan boleh dikemukakan dalam bentuk lain. Di persilangan satah γ 1 dan γ 2, di mana c ialah garis di mana ia bersilang, tandakan titik M, yang melaluinya lukis garis a dan b, berserenjang dengan garis c dan terletak pada satah γ 1 dan γ 2, maka sudut antara garis a dan b akan menjadi sudut antara satah. Dalam amalan, ini boleh digunakan untuk membina sudut antara satah.

Di persimpangan, sudut terbentuk yang nilainya kurang daripada 90 darjah, iaitu, ukuran darjah sudut itu sah pada selang jenis ini (0, 90] . Pada masa yang sama, satah ini dipanggil serenjang jika sudut tegak terbentuk di persimpangan. Sudut antara satah selari dianggap sebagai sifar.

Cara biasa untuk mencari sudut antara satah bersilang adalah dengan melakukan pembinaan tambahan. Ini membantu untuk menentukannya dengan ketepatan, dan ini boleh dilakukan dengan menggunakan tanda-tanda kesamaan atau persamaan segi tiga, sinus, kosinus sudut.

Pertimbangkan untuk menyelesaikan masalah menggunakan contoh daripada GUNAKAN tugas blok C 2 .

Contoh 1

Ditanya kuboid A B C D A 1 B 1 C 1 D 1, di mana sisi A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, titik E memisahkan sisi A A 1 dalam nisbah 4: 3. Cari sudut antara satah A B C dan B E D 1 .

Penyelesaian

Untuk kejelasan, anda perlu membuat lukisan. Kami dapat itu

Perwakilan visual diperlukan untuk menjadikannya lebih mudah untuk bekerja dengan sudut antara satah.

Kami membuat definisi garis lurus di mana satah A B C dan B E D 1 bersilang. Titik B ialah titik biasa. Kena cari yang lain titik biasa persimpangan. Pertimbangkan garis D A dan D 1 E , yang terletak dalam satah yang sama A D D 1 . Lokasi mereka tidak menunjukkan keselarian, yang bermaksud mereka mempunyai titik persimpangan yang sama.

Walau bagaimanapun, garisan D A terletak dalam satah A B C, dan D 1 E dalam B E D 1 . Oleh itu kita mendapat bahawa baris D A dan D 1 E mempunyai titik persilangan yang sama, yang juga biasa bagi satah A B C dan B E D 1 . Menunjukkan titik persilangan garis D A dan D 1 E huruf F. Dari sini kita dapati bahawa B F ialah garis lurus sepanjang satah A B C dan B E D 1 bersilang.

Pertimbangkan rajah di bawah.

Untuk mendapatkan jawapan, adalah perlu untuk membina garis lurus yang terletak pada satah A B C dan B E D 1 dengan laluan melalui titik yang terletak pada garis B F dan berserenjang dengannya. Kemudian sudut yang terhasil di antara garis-garis ini dianggap sudut yang dikehendaki antara satah A B C dan B E D 1.

Daripada ini dapat dilihat bahawa titik A ialah unjuran titik E ke atas satah A B C. Adalah perlu untuk melukis garis yang bersilang dengan garis B F pada sudut tegak di titik M. Dapat dilihat bahawa garis A M ialah unjuran garis E M ke atas satah A B C, berdasarkan teorem tentang serenjang tersebut A M ⊥ B F . Pertimbangkan rajah di bawah.

∠ A M E ialah sudut yang dikehendaki dibentuk oleh satah A B C dan B E D 1 . Daripada segi tiga A E M yang terhasil kita boleh mencari sinus, kosinus atau tangen sudut, selepas itu sudut itu sendiri, hanya dengan dua sisi yang diketahui. Dengan syarat, kita mempunyai bahawa panjang A E didapati dengan cara ini: garis A A 1 dibahagikan dengan titik E dalam nisbah 4: 3, yang bermaksud jumlah panjang garis ialah 7 bahagian, kemudian A E \u003d 4 bahagian. Kami dapati A.M.

Perlu dipertimbangkan segi tiga tepat A B F . Kami mempunyai sudut tegak A dengan ketinggian A M. Dari keadaan A B \u003d 2, maka kita boleh mencari panjang A F dengan persamaan segitiga D D 1 F dan A E F. Kami mendapat bahawa A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Ia adalah perlu untuk mencari panjang sisi B F daripada segi tiga A B F menggunakan teorem Pythagoras. Kami mendapat bahawa B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Panjang sisi A M didapati melalui luas segi tiga A B F. Kami mempunyai bahawa luas boleh sama dengan kedua-dua S A B C = 1 2 · A B · A F , dan S A B C = 1 2 · B F · A M .

Kami mendapat bahawa A M = A B A F B F = 2 4 2 5 = 4 5 5

Kemudian kita boleh mencari nilai tangen sudut segitiga A E M. Kita dapat:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Sudut yang dikehendaki diperolehi oleh persilangan satah A B C dan B E D 1 adalah sama dengan a r c t g 5, maka, apabila dipermudahkan, kita mendapat a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Jawapan: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Beberapa kes mencari sudut antara garis bersilang diberikan menggunakan satah koordinat Mengenai x y z dan kaedah koordinat. Mari kita pertimbangkan dengan lebih terperinci.

Jika masalah diberikan di mana ia perlu untuk mencari sudut antara satah bersilang γ 1 dan γ 2, kita menandakan sudut yang dikehendaki dengan α.

Kemudian sistem yang diberikan koordinat menunjukkan bahawa kita mempunyai koordinat bagi vektor normal bagi satah bersilang γ 1 dan γ 2 . Kemudian kita menyatakan bahawa n 1 → = n 1 x , n 1 y , n 1 z ialah vektor normal satah γ 1 , dan n 2 → = (n 2 x , n 2 y , n 2 z) - untuk satah γ 2 . Pertimbangkan penemuan terperinci sudut yang terletak di antara satah ini mengikut koordinat vektor.

Adalah perlu untuk menetapkan garis lurus di sepanjang satah γ 1 dan γ 2 bersilang dengan huruf c. Pada garis dengan kita mempunyai titik M, di mana kita melukis satah χ, berserenjang dengan c. Satah χ di sepanjang garis a dan b bersilang dengan satah γ 1 dan γ 2 pada titik M . ia mengikuti daripada takrifan bahawa sudut antara satah bersilang γ 1 dan γ 2 adalah sama dengan sudut garis bersilang a dan b kepunyaan satah ini, masing-masing.

Dalam satah χ, kita mengetepikan vektor normal dari titik M dan menandakannya n 1 → dan n 2 →. Vektor n 1 → terletak pada garis berserenjang dengan garis a, dan vektor n 2 → pada garis berserenjang dengan garis b. Oleh itu kita mendapat itu kapal terbang yang diberiχ mempunyai vektor normal garis a sama dengan n 1 → dan untuk garis lurus b sama dengan n 2 → . Pertimbangkan rajah di bawah.

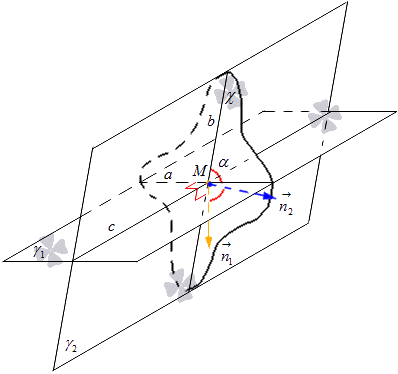
Dari sini kita memperoleh formula yang mana kita boleh mengira sinus sudut garis bersilang menggunakan koordinat vektor. Kami mendapati bahawa kosinus sudut antara garis a dan b adalah sama dengan kosinus antara satah bersilang γ 1 dan γ 2 diperoleh daripada formula cosα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , di mana kita mempunyai bahawa n 1 → = (n 1 x , n 1 y , n 1 z) dan n 2 → = (n 2 x , n 2 y , n 2 z) ialah koordinat bagi vektor satah yang diwakili.

Sudut antara garis bersilang dikira menggunakan formula

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Contoh 2

Mengikut keadaan, paip selari А В С D A 1 B 1 C 1 D 1 diberi , di mana A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, dan titik E memisahkan sisi A A 1 4: 3. Cari sudut antara satah A B C dan B E D 1 .

Penyelesaian

Ia boleh dilihat daripada keadaan sisinya berserenjang berpasangan. Ini bermakna perlu memperkenalkan sistem koordinat O x y z dengan bucu pada titik C dan paksi koordinat O x, O y, O z. Ia adalah perlu untuk meletakkan arah pada sisi yang sesuai. Pertimbangkan rajah di bawah.

Pesawat bersilang A B C dan B E D 1 membentuk sudut, yang boleh didapati dengan formula 2 x 2 + n 2 y 2 + n 2 z 2 , di mana n 1 → = (n 1 x , n 1 y , n 1 z) dan n 2 → = (n 2 x , n 2 y , n 2 z ) ialah vektor normal bagi satah ini. Ia adalah perlu untuk menentukan koordinat. Daripada rajah itu kita lihat paksi koordinat Kira-kira x y bertepatan dalam satah A B C, yang bermaksud bahawa koordinat vektor normal k → sama dengan nilai n 1 → = k → = (0, 0, 1) .

Vektor normal satah B E D 1 ialah hasil vektor B E → dan B D 1 → , di mana koordinatnya ditemui oleh koordinat titik melampau B, E, D 1 , yang ditentukan berdasarkan keadaan masalah.

Kami mendapat bahawa B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Kerana A E E A 1 = 4 3 , daripada koordinat titik A 2 , 3 , 0 , A 1 2 , 3 , 7 kita dapati E 2 , 3 , 4 . Kami mendapat bahawa B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Ia adalah perlu untuk menggantikan koordinat yang ditemui ke dalam formula untuk mengira sudut melalui kosinus arka. Kita mendapatkan

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Kaedah koordinat memberikan hasil yang sama.

Jawapan: a r c cos 6 6 .

Masalah terakhir dipertimbangkan untuk mencari sudut antara satah bersilang dengan persamaan satah yang diketahui tersedia.

Contoh 3

Hitung sinus, kosinus sudut, dan nilai sudut yang dibentuk oleh dua garis bersilang, yang ditakrifkan dalam sistem koordinat O x y z dan diberikan oleh persamaan 2 x - 4 y + z + 1 = 0 dan 3 y - z - 1 = 0 .

Penyelesaian

Apabila mempelajari sesuatu topik persamaan am garisan bentuk A x + B y + C z + D = 0 mendedahkan bahawa A, B, C adalah pekali yang sama dengan koordinat vektor normal. Oleh itu, n 1 → = 2 , - 4 , 1 dan n 2 → = 0 , 3 , - 1 ialah vektor normal bagi garisan yang diberi.

Ia adalah perlu untuk menggantikan koordinat vektor biasa satah ke dalam formula untuk mengira sudut yang dikehendaki bagi satah bersilang. Kemudian kita dapat itu

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Oleh itu kita mempunyai bahawa kosinus sudut mengambil bentuk cos α = 13 210 . Kemudian sudut garis bersilang tidak tumpul. Menggantikan dalam identiti trigonometri, kita mendapat bahawa nilai sinus sudut adalah sama dengan ungkapan. Kami mengira dan mendapatkannya

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Jawapan: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Jika anda melihat kesilapan dalam teks, sila serlahkannya dan tekan Ctrl+Enter

Dalam tugasan C2 dalam matematik, selalunya anda perlu menyelesaikan masalah yang anda perlukan untuk menentukan:

Jarak antara dua titik
Jarak dari titik ke garisan
Jarak dari titik ke satah
Jarak antara garis bersilang
Sudut antara dua garis
Sudut antara garis dan satah
Sudut antara satah

Tugas-tugas adalah asas, jika anda mengikuti algoritma untuk menyelesaikan C2 dan ingat yang utama sifat trigonometri, seperti sifat pepenjuru atau luas permukaan polihedron. Tugas sokongan akan membantu anda mengingati sifat asas ini.

Sekarang mari kita beralih kepada algoritma.

1. Untuk menentukan jarak antara dua titik A dan B, kami menggunakan salah satu daripada dua kaedah:

Kami memasukkan AB dalam beberapa segi tiga dan cari panjangnya sebagai sisi segi tiga
Mengikut formula

Selain itu, kaedah koordinat, pada pendapat saya, adalah yang paling mudah, hanya perlu menentukan koordinat setiap titik dengan tepat.

2. Untuk menentukan jarak dari titik ke garis, hitung

sebagai panjang segmen berserenjang, jika mungkin untuk memasukkan segmen ini dalam beberapa segi tiga sebagai salah satu ketinggian

menggunakan kaedah koordinat menggunakan formula untuk mengira kawasan, di mana jarak yang diperlukan ialah ketinggian dan

3. Jarak dari titik ke satah ialah

panjang serenjang jatuh dari titik ini ke satah. Untuk melakukan ini, berhati-hati bina bahagian yang berserenjang dengan satah dan melaluinya titik yang diberikan. Jarak yang diingini akan sama dengan ketinggian polihedron baharu yang terhasil.
Menggunakan kaedah koordinat

Persamaan ditemui dengan menggantikan koordinat tiga titik kepunyaan satah ini

Menggunakan kaedah vektor

Untuk melakukan ini, anda perlu mengingati peraturan untuk menambah dan menolak vektor, bahawa produk vektor serenjang sama dengan sifar.

Menggunakan kaedah isipadu, jika terdapat piramid ABCM, maka jarak dari titik M ke satah yang mengandungi segitiga ABC dikira dengan formula

Dengan kaedah masalah rujukan, yang boleh dilihat

4. Jarak antara garisan lintasan boleh diselesaikan menggunakan

4.1. Kaedah pengiraan langkah demi langkah:

bina serenjang sepunya dua garis bersilang dan cari panjangnya;
bina satah yang mengandungi satu daripada garisan dan selari dengan yang lain. Kemudian jarak yang dikehendaki akan sama dengan jarak dari titik ke garis lurus yang dibina dalam satah;
sertakan garisan yang diberi dalam satah selari yang melalui garis condong yang diberi, cari jarak antara satah ini
bina satah berserenjang dengan salah satu garis ini dan bina unjuran ortogon bagi garisan kedua

4.2. Kaedah vektor-koordinat

Cari koordinat hujung segmen yang serenjang sepunya bagi dua garis bersilang
Mencari jarak antara dua titik

4.3. kaedah vektor
Kami mengurangkan masalah untuk menentukan panjang vektor kepunyaan serenjang yang merupakan serenjang biasa dua garis bersilang

6. Sudut antara garis dan satah ditentukan dengan memasukkannya dalam segi tiga tepat sebagai salah satu sudut akut, atau dengan kaedah penyelaras vektor

Ataupun

Bagaimana sudut antara satah ditentukan akan dipertimbangkan dalam pelajaran seterusnya. Algoritma ini untuk menyelesaikan C2 menyumbang kepada pemahaman yang menyeluruh tentang kaedah untuk menyelesaikan masalah. "Untuk membantu majalah pelajar untuk pelajar dan ibu bapa mereka." Baca lebih lanjut: http://education-club.ru/#ixzz2IXf5GOJU

7. Sudut antara satah(kaedah geometri)

1. Cari garis di sepanjang satah bersilang.
2. Pilih satu titik pada garis ini dan lukis dua serenjang padanya, terletak dalam satah ini. Atau lukis satah berserenjang dengan garis persilangan satah.
3. Cari fungsi trigonometri bagi sudut yang dibentuk oleh serenjang dengan garis persilangan satah. Sebagai peraturan, kami melakukan ini melalui segi tiga, yang termasuk sudut yang dikehendaki.
4. Dalam jawapan, tulis nilai sudut, atau fungsi trigonometri sudut.

Sudut antara satah. kaedah koordinat. Tugasan C2

Dua satah bersilang membentuk dua pasang sudut dihedral yang sama:

Nilai sudut dihedral diukur dengan nilai sudut linear yang sepadan.

Untuk membina sudut linear sudut dihedral, anda perlu mengambil garis persilangan satah. titik sewenang-wenangnya, dan dalam setiap satah lukiskan sinar ke titik ini berserenjang dengan garis persilangan satah itu. Sudut yang dibentuk oleh sinar ini ialah sudut linear sudut dihedral:

Nilai sudut antara satah ialah nilai sudut dihedral kurang daripada satu tahun.

Biarkan satah kita dan diberikan oleh persamaan:

Kosinus sudut antara satah didapati dengan formula berikut:

Dalam jawapannya, kita tulis , kerana nilai sudut antara satah ialah nilai sudut dihedral yang lebih kecil.

Dalam prisma segi empat sekata dengan sisi tapak 12 dan ketinggian 21, satu titik M diambil pada tepi supaya . Titik K diambil di tepi supaya . Cari sudut antara satah dan satah.

Jom buat lukisan. Oleh kerana kami akan menggunakan kaedah koordinat, kami akan segera memperkenalkan sistem koordinat: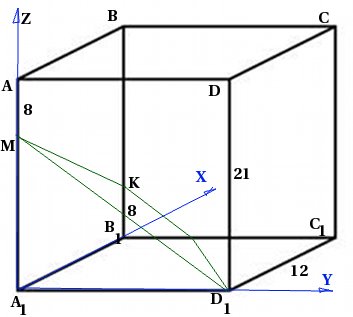

Sekarang kita berhadapan dengan tugas menulis persamaan satah dan satah.

Saya menerangkan algoritma terperinci untuk mencari persamaan satah menggunakan tiga titik.

Selepas kita mencari pekali dalam persamaan satah dan satah, kita menggantikannya ke dalam formula untuk mencari kosinus sudut antara satah, dan mencari sudut.

Saya cadangkan anda menonton penyelesaian video terperinci untuk masalah ini:

Satu lagi tugas dari Inna Vladimirovna Feldman

Pelajaran video "Kaedah koordinat untuk menyelesaikan masalah c-2"

Pelajaran 2 http://youtu.be/dKQWG8OZRGo
pelajaran 3 http://youtu.be/ddgr0PnbFno
pelajaran 4 http://youtu.be/n6yx2pQC0Lo
pelajaran 5 http://youtu.be/JkWbxAw1YLI
pelajaran 6 http://youtu.be/gybIqCMKBiI
pelajaran 7 http://youtu.be/_LpARpYxp5g
pelajaran 8 http://youtu.be/XJhyZQoofD8

Sudut antara dua satah yang berbeza boleh ditentukan untuk mana-mana kedudukan relatif kapal terbang.

Kes remeh adalah jika pesawat selari. Kemudian sudut di antara mereka dianggap sama dengan sifar.

Kes bukan remeh jika pesawat bersilang. Kes ini menjadi bahan perbincangan lanjut. Mula-mula kita memerlukan konsep sudut dihedral.

9.1 Sudut dihedral

Sudut dihedral ialah dua separuh satah dengan garis lurus sepunya (yang dipanggil tepi sudut dihedral). Pada rajah. 50 menunjukkan sudut dihedral yang dibentuk oleh separuh satah dan; tepi sudut dihedral ini ialah garis biasa kepada separuh satah yang diberikan.

nasi. 50. Sudut dihedral

Sudut dihedral boleh diukur dalam darjah atau radian dalam perkataan, masukkan nilai sudut sudut dihedral. Ini dilakukan dengan cara berikut.

Di tepi sudut dihedral yang dibentuk oleh separuh satah dan, kita ambil titik sewenang-wenangnya M. Mari kita lukis sinar MA dan MB, masing-masing terletak dalam separuh satah ini dan berserenjang dengan tepi (Rajah 51).

nasi. 51. Sudut linear Sudut dihedral

Sudut AMB yang terhasil ialah sudut linear bagi sudut dihedral. Sudut " = \AMB adalah tepat nilai sudut sudut dihedral kami.

Definisi. Magnitud sudut sudut dihedral ialah magnitud sudut linear sudut dihedral tertentu.

Semua sudut linear sudut dihedral adalah sama antara satu sama lain (selepas semua, ia diperoleh daripada satu sama lain dengan anjakan selari). sebab tu takrifan ini betul: nilai "tidak bergantung pada pilihan tertentu titik M pada tepi sudut dihedral.

9.2 Menentukan sudut antara satah

Apabila dua satah bersilang, empat sudut dihedral diperolehi. Jika mereka semua ada nilai yang sama(dengan 90), maka satah itu dipanggil serenjang; sudut antara satah itu ialah 90 .

Jika tidak semua sudut dihedral adalah sama (iaitu, terdapat dua akut dan dua tumpul), maka sudut antara satah ialah nilai sudut dihedral akut (Rajah 52).

nasi. 52. Sudut antara satah

9.3 Contoh penyelesaian masalah

Mari kita pertimbangkan tiga tugasan. Yang pertama adalah mudah, yang kedua dan ketiga adalah lebih kurang pada tahap C2 pada peperiksaan dalam matematik.

Tugasan 1. Cari sudut antara dua muka tetrahedron sekata.

Penyelesaian. Biarkan ABCD menjadi tetrahedron biasa. Mari kita lukis median AM dan DM bagi muka yang sepadan, serta ketinggian tetrahedron DH (Rajah 53).

nasi. 53. Kepada masalah 1

Sebagai median, AM dan DM juga adalah ketinggian sama sisi segi tiga ABC dan DBC. Oleh itu, sudut " = \AMD ialah sudut linear bagi sudut dihedral yang dibentuk oleh muka ABC dan DBC. Kita dapati dari segi tiga DHM:

			1 PAGI

Jawapan: arccos 1 3 .

Masalah 2. Dalam piramid segi empat biasa biasa SABCD (dengan bucu S), tepi sisi adalah sama dengan sisi tapak. Titik K ialah titik tengah tepi SA. Cari sudut antara satah

Penyelesaian. Garisan BC adalah selari dengan AD dan dengan itu selari dengan satah ADS. Oleh itu, satah KBC bersilang dengan satah ADS di sepanjang garis lurus KL selari dengan BC (Rajah 54).

nasi. 54. Kepada masalah 2

Dalam kes ini, KL juga akan selari dengan garis AD; maka KL garisan tengah segi tiga ADS, dan titik L ialah titik tengah DS.

Lukiskan ketinggian piramid SO. Biarkan N ialah titik tengah DO. Maka LN ialah garis tengah bagi segi tiga DOS, dan oleh itu LN k SO. Jadi LN adalah berserenjang dengan satah ABC.

Dari titik N kita jatuhkan NM berserenjang ke garis BC. Garis lurus NM akan menjadi unjuran LM serong pada satah ABC. Ia kemudiannya mengikuti daripada teorem tiga serenjang bahawa LM juga berserenjang dengan BC.

Oleh itu, sudut " = \LMN ialah sudut linear bagi sudut dihedral yang dibentuk oleh separuh satah KBC dan ABC. Kita akan mencari sudut ini dari segi tiga tepat LMN.

Biarkan tepi piramid itu ialah a. Pertama, cari ketinggian piramid:

SO=p

Penyelesaian. Biarkan L ialah titik persilangan garis A1 K dan AB. Kemudian satah A1 KC bersilang dengan satah ABC sepanjang garis lurus CL (Gamb.55).

A C

nasi. 55. Masalah 3

Segitiga A1 B1 K dan KBL adalah sama di kaki dan sudut lancip. Oleh itu, kaki yang lain juga sama: A1 B1 = BL.

Pertimbangkan segi tiga ACL. Di dalamnya BA = BC = BL. Sudut CBL ialah 120 ; jadi \BCL = 30 . Juga, \BCA = 60 . Oleh itu \ACL = \BCA + \BCL = 90 .

Jadi LC? AC. Tetapi garis AC ialah unjuran garis A1 C ke atas satah ABC. Dengan teorem tiga serenjang, kita kemudian membuat kesimpulan bahawa LC? A1C.

Oleh itu, sudut A1 CA ialah sudut linear bagi sudut dihedral yang dibentuk oleh separuh satah A1 KC dan ABC. Ini adalah sudut yang diperlukan. Daripada segi tiga tegak sama kaki A1 AC kita lihat bahawa ia adalah sama dengan 45 .

\(\blacktriangleright\) Sudut dihedral ialah sudut yang dibentuk oleh dua satah separuh dan garis lurus \(a\) , yang merupakan sempadan sepunya mereka.

\(\blacktriangleright\) Untuk mencari sudut antara satah \(\xi\) dan \(\pi\) , anda perlu mencari sudut linear pedas atau lurus) bagi sudut dihedral yang dibentuk oleh satah \(\xi\) dan \(\pi\) :

Langkah 1: biarkan \(\xi\cap\pi=a\) (garisan persilangan satah). Dalam satah \(\xi\) kita menandakan titik sembarangan \(F\) dan lukis \(FA\perp a\) ;

Langkah 2: lukis \(FG\perp \pi\) ;

Langkah 3: mengikut TTP (\(FG\) - berserenjang, \(FA\) - serong, \(AG\) - unjuran) kita ada: \(AG\perp a\) ;

Langkah 4: Sudut \(\angle FAG\) dipanggil sudut linear bagi sudut dihedral yang dibentuk oleh satah \(\xi\) dan \(\pi\) .

Perhatikan bahawa segitiga \(AG\) ialah segi tiga tegak.
Perhatikan juga bahawa satah \(AFG\) yang dibina dengan cara ini adalah berserenjang dengan kedua-dua satah \(\xi\) dan \(\pi\) . Oleh itu, ia boleh dikatakan dengan cara lain: sudut antara satah\(\xi\) dan \(\pi\) ialah sudut antara dua garis bersilang \(c\in \xi\) dan \(b\in\pi\) , membentuk satah berserenjang dengan \(\xi\ ), dan \(\pi\) .

Tugasan 1 #2875

Tahap tugas: Lebih sukar daripada peperiksaan

Dana piramid segi empat, semua tepinya adalah sama, dan tapaknya ialah segi empat sama. Cari \(6\cos \alpha\) , dengan \(\alpha\) ialah sudut antara muka sisi bersebelahannya.

Biarkan \(SABCD\) ialah piramid yang diberi (\(S\) ialah bucu) yang tepinya sama dengan \(a\) . Oleh itu, semua muka sebelah ialah segi tiga sama sisi. Cari sudut antara muka \(SAD\) dan \(SCD\) .

Mari lukis \(CH\perp SD\) . Kerana \(\segitiga SAD=\segi tiga SCD\), maka \(AH\) juga akan menjadi ketinggian \(\triangle SAD\) . Oleh itu, mengikut takrifan, \(\angle AHC=\alpha\) ialah sudut dihedral linear antara muka \(SAD\) dan \(SCD\) .
Oleh kerana tapaknya ialah segi empat sama, maka \(AC=a\sqrt2\) . Perhatikan juga bahawa \(CH=AH\) ialah ketinggian segi tiga sama sisi dengan sisi \(a\) , maka \(CH=AH=\frac(\sqrt3)2a\) .
Kemudian dengan teorem kosinus daripada \(\segitiga AHC\): \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Jawapan: -2

Tugasan 2 #2876

Tahap tugas: Lebih sukar daripada peperiksaan

Satah \(\pi_1\) dan \(\pi_2\) bersilang pada sudut yang kosinusnya sama dengan \(0,2\) . Satah \(\pi_2\) dan \(\pi_3\) bersilang pada sudut tepat, dan garis persilangan satah \(\pi_1\) dan \(\pi_2\) adalah selari dengan garis persilangan bagi satah \(\pi_2\) dan \(\ pi_3\) . Cari sinus sudut antara satah \(\pi_1\) dan \(\pi_3\) .

Biarkan garis persilangan \(\pi_1\) dan \(\pi_2\) ialah garis \(a\) , garis persilangan \(\pi_2\) dan \(\pi_3\) ialah garis \ (b\) , dan garis persilangan \(\pi_3\) dan \(\pi_1\) ialah garis lurus \(c\) . Oleh kerana \(a\parallel b\) , maka \(c\parallel a\parallel b\) (mengikut teorem dari bahagian rujukan teori "Geometri dalam ruang" \(\rightarrow\) "Pengenalan kepada stereometri, paralelisme”).

Tandakan titik \(A\dalam a, B\dalam b\) supaya \(AB\perp a, AB\perp b\) (ini mungkin kerana \(a\selari b\) ). Perhatikan \(C\in c\) supaya \(BC\perp c\) , maka \(BC\perp b\) . Kemudian \(AC\perp c\) dan \(AC\perp a\) .
Sesungguhnya, oleh kerana \(AB\perp b, BC\perp b\) , maka \(b\) adalah berserenjang dengan satah \(ABC\) . Oleh kerana \(c\parallel a\parallel b\) , maka garis \(a\) dan \(c\) juga berserenjang dengan satah \(ABC\) , dan oleh itu mana-mana garisan dari satah ini, khususnya, baris \ (AC\) .

Oleh itu ia mengikutinya \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\sudut ABC=\sudut (\pi_2, \pi_3)=90^\lingkaran\), \(\sudut BCA=\sudut (\pi_3, \pi_1)\). Ternyata \(\segitiga ABC\) ialah segi empat tepat, yang bermaksud \[\sin \sudut BCA=\cos \sudut BAC=0,2.\]

Jawapan: 0.2

Tugasan 3 #2877

Tahap tugas: Lebih sukar daripada peperiksaan

Diberi garis \(a, b, c\) bersilang pada satu titik, dan sudut antara mana-mana dua daripadanya adalah sama dengan \(60^\circ\) . Cari \(\cos^(-1)\alpha\) , dengan \(\alpha\) ialah sudut antara satah yang dibentuk oleh garis \(a\) dan \(c\) dan satah yang dibentuk oleh garis \(b\ ) dan \(c\) . Berikan jawapan anda dalam darjah.

Biarkan garis bersilang pada titik \(O\) . Oleh kerana sudut antara mana-mana dua daripadanya adalah sama dengan \(60^\circ\) , maka ketiga-tiga garisan tidak boleh terletak dalam satah yang sama. Mari kita tandakan titik \(A\) pada garis \(a\) dan lukis \(AB\perp b\) dan \(AC\perp c\) . Kemudian \(\segitiga AOB=\segi tiga AOC\) sebagai segi empat tepat dalam hipotenus dan sudut lancip. Oleh itu \(OB=OC\) dan \(AB=AC\) .
Mari kita lakukan \(AH\perp (BOC)\) . Kemudian dengan tiga teorem serenjang \(HC\perp c\) , \(HB\perp b\) . Oleh kerana \(AB=AC\) , maka \(\segitiga AHB=\segi tiga AHC\) sebagai segi empat tepat di sepanjang hipotenus dan kaki. Oleh itu, \(HB=HC\) . Oleh itu, \(OH\) ialah pembahagi dua sudut \(BOC\) (memandangkan titik \(H\) adalah sama jarak dari sisi sudut).

Perhatikan bahawa dengan cara ini kita juga telah membina sudut linear sudut dihedral yang dibentuk oleh satah yang dibentuk oleh garis \(a\) dan \(c\) dan satah yang dibentuk oleh garis \(b\) dan \( c\). Ini ialah sudut \(ACH\) .

Jom cari sudut ni. Oleh kerana kita memilih titik \(A\) dengan sewenang-wenangnya, maka marilah kita memilihnya supaya \(OA=2\) . Kemudian dalam segi empat tepat \(\triangle AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Oleh kerana \(OH\) ialah pembahagi dua, maka \(\angle HOC=30^\circ\) , oleh itu, dalam segi empat tepat \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Kemudian dari segi empat tepat \(\triangle ACH\): \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Jawapan: 3

Tugasan 4 #2910

Tahap tugas: Lebih sukar daripada peperiksaan

Satah \(\pi_1\) dan \(\pi_2\) bersilang di sepanjang garis \(l\) , yang mengandungi titik \(M\) dan \(N\) . Segmen \(MA\) dan \(MB\) adalah berserenjang dengan garis \(l\) dan terletak pada satah \(\pi_1\) dan \(\pi_2\), masing-masing, dan \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Cari \(3\cos\alpha\) , dengan \(\alpha\) ialah sudut antara satah \(\pi_1\) dan \(\pi_2\) .

Segitiga \(AMN\) adalah bersudut tegak, \(AN^2 = AM^2 + MN^2\) , dari mana \ Segitiga \(BMN\) adalah bersudut tegak, \(BN^2 = BM^2 + MN^2\) , dari mana \ Kami menulis teorem kosinus untuk segitiga \(AMB\): \ Kemudian \ Oleh kerana sudut \(\alfa\) antara satah ialah sudut tajam, dan \(\angle AMB\) adalah dungu, kemudian \(\cos\alpha=\dfrac5(12)\) . Kemudian \

Jawapan: 1.25

Tugasan 5 #2911

Tahap tugas: Lebih sukar daripada peperiksaan

\(ABCDA_1B_1C_1D_1\) ialah sebuah selari, \(ABCD\) ialah segi empat sama dengan sisi \(a\) , titik \(M\) ialah tapak serenjang yang dijatuhkan dari titik \(A_1\) ke satah \ ((ABCD)\) , selain itu, \(M\) ialah titik persilangan bagi pepenjuru segi empat sama \(ABCD\) . Adalah diketahui bahawa \(A_1M = \dfrac(\sqrt(3))(2)a\). Cari sudut antara satah \((ABCD)\) dan \((AA_1B_1B)\) . Berikan jawapan anda dalam darjah.

Kami membina \(MN\) berserenjang dengan \(AB\) seperti yang ditunjukkan dalam rajah.

Oleh kerana \(ABCD\) ialah segi empat sama dengan sisi \(a\) dan \(MN\perp AB\) dan \(BC\perp AB\) , maka \(MN\parallel BC\) . Oleh kerana \(M\) ialah titik persilangan bagi pepenjuru segi empat sama, maka \(M\) ialah titik tengah bagi \(AC\) , oleh itu, \(MN\) ialah garis tengah dan \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) ialah unjuran \(A_1N\) pada satah \((ABCD)\) , dan \(MN\) berserenjang dengan \(AB\) , kemudian, dengan teorem tiga serenjang, \( A_1N\) berserenjang dengan \(AB \) dan sudut antara satah \((ABCD)\) dan \((AA_1B_1B)\) ialah \(\sudut A_1NM\) .
\[\mathrm(tg)\, \sudut A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\sudut A_1NM = 60^(\circ)\]

Jawapan: 60

Tugasan 6 #1854

Tahap tugas: Lebih sukar daripada peperiksaan

Dalam segi empat sama \(ABCD\): \(O\) ialah titik persilangan pepenjuru; \(S\) bukan dalam satah segi empat sama, \(SO \perp ABC\) . Cari sudut antara satah \(ASD\) dan \(ABC\) jika \(SO = 5\) dan \(AB = 10\) .

Segitiga tepat \(\segitiga SAO\) dan \(\segitiga SDO\) adalah sama dalam dua sisi dan sudut di antara mereka (\(SO \perp ABC\) \(\Rightarrow\) \(\sudut SOA = \sudut SOD = 90^\lingkaran\); \(AO = DO\) , kerana \(O\) ialah titik persilangan pepenjuru segi empat sama, \(SO\) ialah sisi biasa) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) ialah sama kaki. Titik \(K\) ialah titik tengah bagi \(AD\) , kemudian \(SK\) ialah ketinggian dalam segi tiga \(\segitiga ASD\) , dan \(OK\) ialah ketinggian dalam segi tiga \ (AOD\) \(\ Rightarrow\) satah \(SOK\) berserenjang dengan satah \(ASD\) dan \(ABC\) \(\Rightarrow\) \(\angle SKO\) ialah sudut linear yang sama kepada sudut dihedral yang diperlukan.

Dalam \(\segitiga SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) ialah segi tiga sama kaki \(\Rightarrow\) \(\sudut SKO = 45^\circ\) .

Jawapan: 45

Tugasan 7 #1855

Tahap tugas: Lebih sukar daripada peperiksaan

Dalam segi empat sama \(ABCD\): \(O\) ialah titik persilangan pepenjuru; \(S\) bukan dalam satah segi empat sama, \(SO \perp ABC\) . Cari sudut antara satah \(ASD\) dan \(BSC\) jika \(SO = 5\) dan \(AB = 10\) .

Segitiga tepat \(\segitiga SAO\) , \(\segitiga SDO\) , \(\segitiga SOB\) dan \(\segitiga SOC\) adalah sama dalam dua sisi dan sudut di antara mereka (\(SO \perp ABC \) \(\Rightarrow\) \(\sudut SOA = \sudut SOD = \sudut SOB = \sudut SOC = 90^\lingkaran\); \(AO = OD = OB = OC\) , kerana \(O\) ialah titik persilangan pepenjuru segi empat sama, \(SO\) ialah sisi sepunya) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\segitiga ASD\) dan \(\segitiga BSC\) ialah sama kaki. Titik \(K\) ialah titik tengah bagi \(AD\) , kemudian \(SK\) ialah ketinggian dalam segi tiga \(\segitiga ASD\) , dan \(OK\) ialah ketinggian dalam segi tiga \ (AOD\) \(\ Rightarrow\) satah \(SOK\) berserenjang dengan satah \(ASD\) . Titik \(L\) ialah titik tengah bagi \(BC\) , kemudian \(SL\) ialah ketinggian dalam segi tiga \(\segitiga BSC\) , dan \(OL\) ialah ketinggian dalam segi tiga \ (BOC\) \(\ Rightarrow\) satah \(SOL\) (aka satah \(SOK\) ) adalah berserenjang dengan satah \(BSC\) . Oleh itu, kita memperoleh bahawa \(\sudut KSL\) ialah sudut linear sama dengan sudut dihedral yang dikehendaki.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – ketinggian sama segi tiga sama kaki, yang boleh didapati menggunakan teorem Pythagoras: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Ia boleh dilihat bahawa \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) untuk segi tiga \(\triangle KSL\) teorem terbalik Pythagoras \(\Rightarrow\) \(\triangle KSL\) – segi tiga tepat \(\Rightarrow\) \(\sudut KSL = 90^\circ\) .

Jawapan: 90

Menyediakan pelajar untuk peperiksaan dalam matematik, sebagai peraturan, bermula dengan pengulangan formula asas, termasuk yang membolehkan anda menentukan sudut antara satah. Walaupun fakta bahawa bahagian geometri ini diliputi dengan terperinci yang mencukupi dalam rangka kerja kurikulum sekolah, ramai graduan perlu mengulang bahan asas. Memahami cara mencari sudut antara pesawat, pelajar sekolah menengah akan dapat mengira dengan cepat jawapan yang betul semasa menyelesaikan masalah dan bergantung kepada mendapat markah yang baik berdasarkan peperiksaan negeri bersatu.

Nuansa utama

Supaya persoalan bagaimana mencari sudut dihedral tidak menyebabkan kesukaran, kami mengesyorkan agar anda mengikuti algoritma penyelesaian yang akan membantu anda mengatasi tugas peperiksaan.

Mula-mula anda perlu menentukan garis di mana satah bersilang.

Kemudian pada baris ini anda perlu memilih satu titik dan lukis dua serenjang kepadanya.

Langkah seterusnya ialah mencari fungsi trigonometri bagi sudut dihedral, yang dibentuk oleh serenjang. Adalah paling mudah untuk melakukan ini dengan bantuan segitiga yang terhasil, yang mana sudutnya adalah sebahagian.

Jawapannya ialah nilai sudut atau fungsi trigonometrinya.

Persediaan untuk ujian peperiksaan bersama Shkolkovo adalah kunci kejayaan anda

Semasa kelas sehari sebelumnya lulus peperiksaan ramai pelajar berhadapan dengan masalah mencari definisi dan formula yang membolehkan anda mengira sudut antara 2 satah. Buku teks sekolah tidak selalu tersedia tepat pada waktunya. Dan untuk mencari formula yang diperlukan dan contoh aplikasi yang betul, termasuk mencari sudut antara pesawat di Internet dalam talian, kadangkala ia memerlukan banyak masa.

Portal matematik "Shkolkovo" menawarkan pendekatan baru untuk persediaan menghadapi peperiksaan negeri. Kelas di tapak web kami akan membantu pelajar mengenal pasti bahagian yang paling sukar untuk diri mereka sendiri dan mengisi jurang dalam pengetahuan.

Kami telah menyediakan dan membentangkan dengan jelas semua bahan yang diperlukan. Definisi asas dan formula dibentangkan dalam bahagian "Rujukan Teori".

Untuk mengasimilasikan bahan dengan lebih baik, kami juga mencadangkan untuk mempraktikkan latihan yang sepadan. Banyak pilihan tugas darjah yang berbeza-beza kerumitan, sebagai contoh, pada, dibentangkan dalam bahagian "Katalog". Semua tugasan mengandungi algoritma terperinci untuk mencari jawapan yang betul. Senarai latihan di laman web ini sentiasa ditambah dan dikemas kini.

Berlatih dalam menyelesaikan masalah di mana ia diperlukan untuk mencari sudut antara dua satah, pelajar mempunyai peluang untuk menyimpan sebarang tugasan dalam talian ke "Kegemaran". Terima kasih kepada ini, mereka akan dapat kembali kepadanya. jumlah yang diperlukan kali dan membincangkan perjalanan keputusannya dengan Cikgu sekolah atau tutor.