Kebergantungan linear dua vektor. Vektor bersandar linear dan bebas linear

Untuk memeriksa sama ada sistem vektor bergantung secara linear, adalah perlu untuk mengarang gabungan linear vektor ini, dan semak sama ada ia boleh menjadi sifar jika sekurang-kurangnya satu pekali adalah sama dengan sifar.

Kes 1. Sistem vektor diberikan oleh vektor

Membuat gabungan linear

Kami telah memperoleh sistem persamaan homogen. Jika ia mempunyai penyelesaian bukan sifar, maka penentu mestilah sama dengan sifar. Mari kita karang penentu dan cari nilainya.

Penentunya ialah sifar, oleh itu vektor adalah bersandar secara linear.

Kes 2. Sistem vektor ditakrifkan oleh fungsi analisis:

a)
, jika identiti adalah benar, maka sistem adalah bergantung secara linear.

Mari kita buat gabungan linear.

Adalah perlu untuk menyemak sama ada wujud a, b, c (sekurang-kurangnya satu daripadanya tidak sama dengan sifar) yang mana ungkapan ini sama dengan sifar.

Mari kita tulis fungsi hiperbolik

,
, Kemudian

maka gabungan linear vektor akan mengambil bentuk:

di mana
, ambil, sebagai contoh, maka gabungan linear adalah sifar, oleh itu, sistem adalah bergantung secara linear.

Jawapan: sistem bergantung secara linear.

b)
, mari buat gabungan linear

Gabungan linear vektor mestilah sama dengan sifar untuk sebarang nilai x.

Mari semak kes khas.

Gabungan linear vektor adalah sama dengan sifar hanya jika semua pekali adalah sama dengan sifar.

Oleh itu, sistem adalah bebas linear.

Jawapan: sistem adalah bebas linear.

5.3. Cari beberapa asas dan tentukan dimensi ruang penyelesaian linear.

Mari kita bentuk matriks lanjutan dan kurangkan kepada bentuk trapezoid menggunakan kaedah Gaussian.

Untuk mendapatkan beberapa asas, mari kita gantikan nilai arbitrari:

Mari dapatkan koordinat yang lain

Jawapan:

5.4. Cari koordinat vektor X dalam asas, jika ia diberikan dalam asas.

Mencari koordinat vektor dalam asas baharu dikurangkan kepada menyelesaikan sistem persamaan

Kaedah 1. Mencari menggunakan matriks peralihan

Mari buat matriks peralihan

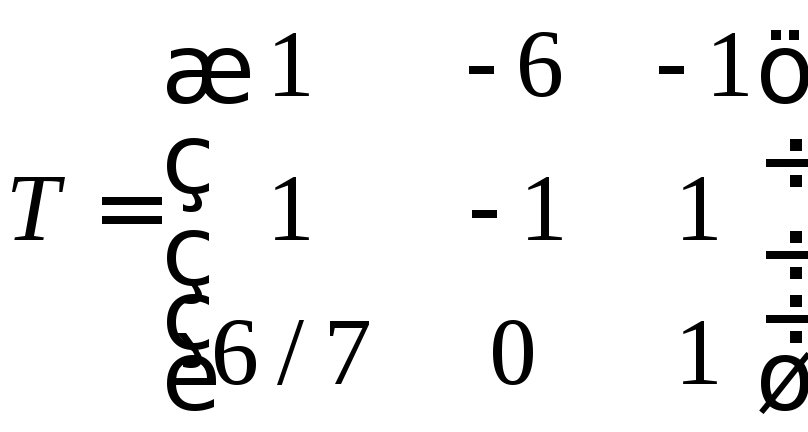
Mari cari vektor dalam asas baharu menggunakan formula

Mari cari matriks songsang dan laksanakan pendaraban

,

Kaedah 2. Mencari dengan mengarang sistem persamaan.

Mari kita susun vektor asas daripada pekali asas

,
,

Mencari vektor dalam asas baharu mempunyai bentuk

, Di mana d ini vektor yang diberi x.

Persamaan yang terhasil boleh diselesaikan dalam apa jua cara, jawapannya akan serupa.

Jawapan: vektor dalam asas baru
.

5.5. Biarkan x = (x 1 , x 2 , x 3 ) . Adakah penjelmaan berikut linear?

Mari kita susun matriks pengendali linear daripada pekali vektor yang diberikan.

Mari kita semak sifat operasi linear untuk setiap matriks operator linear.

Kami mencari bahagian kiri dengan mendarab matriks A kepada vektor

Kami mencari bahagian kanan dengan mendarabkan vektor yang diberikan dengan skalar
.

Kita nampak itu
Ini bermakna bahawa penjelmaan tidak linear.

Mari kita semak vektor lain.

, penjelmaan tidak linear.

, penjelmaan adalah linear.

Jawapan: Oh- Tidak transformasi linear, Dalam- tidak linear, Cx– linear.

Nota. Anda boleh menyelesaikan tugas ini dengan lebih mudah dengan melihat dengan teliti pada vektor yang diberikan. DALAM Oh kita lihat ada istilah yang tidak mengandungi unsur X, yang tidak boleh diperolehi hasil daripada operasi linear. DALAM Dalam ada unsur X kepada kuasa ketiga, yang juga tidak boleh diperolehi dengan mendarab dengan vektor X.

5.6. Diberi x = { x 1 , x 2 , x 3 } , Ax = { x 2 – x 3 , x 1 , x 1 + x 3 } , Bx = { x 2 , 2 x 3 , x 1 } . Lakukan operasi yang ditentukan: ( A ( B – A )) x .

Mari kita tuliskan matriks operator linear.

Mari kita laksanakan operasi pada matriks

Apabila mendarabkan matriks yang terhasil dengan X, kita dapat

Jawapan:

Tugasan 1. Ketahui sama ada sistem vektor bebas linear. Sistem vektor akan ditentukan oleh matriks sistem, lajur yang terdiri daripada koordinat vektor.

.

Penyelesaian. Biarkan gabungan linear sama dengan sifar. Setelah menulis kesamaan ini dalam koordinat, kami memperoleh sistem persamaan berikut:

.

Sistem persamaan sedemikian dipanggil segi tiga. Dia hanya mempunyai satu penyelesaian . Oleh itu, vektor bebas linear.

Tugasan 2. Ketahui sama ada sistem vektor bebas linear.

.

Penyelesaian. vektor adalah bebas secara linear (lihat masalah 1). Mari kita buktikan bahawa vektor ialah gabungan linear bagi vektor . Pekali pengembangan vektor ditentukan daripada sistem persamaan

.

Sistem ini, seperti segi tiga, mempunyai penyelesaian yang unik.

Oleh itu, sistem vektor bergantung secara linear.

Komen. Matriks jenis yang sama seperti dalam Masalah 1 dipanggil segi tiga , dan dalam masalah 2 – melangkah segi tiga . Persoalan pergantungan linear sistem vektor mudah diselesaikan jika matriks yang terdiri daripada koordinat vektor ini adalah segi tiga langkah. Jika matriks tidak mempunyai jenis khas, kemudian menggunakan penukaran rentetan asas , mengekalkan hubungan linear antara lajur, ia boleh dikurangkan kepada bentuk segi tiga langkah.

Transformasi asas garisan matriks (EPS) operasi berikut pada matriks dipanggil:

1) penyusunan semula rentetan;

2) mendarab rentetan dengan nombor bukan sifar;

3) menambah rentetan lain pada rentetan, didarab dengan nombor arbitrari.

Tugasan 3. Cari subsistem bebas linear maksimum dan hitung pangkat sistem vektor

.

Penyelesaian. Mari kita kurangkan matriks sistem menggunakan EPS kepada bentuk segi tiga langkah. Untuk menerangkan prosedur, kami menandakan garis dengan nombor matriks yang akan diubah oleh simbol . Lajur selepas anak panah menunjukkan tindakan pada baris matriks yang sedang ditukar yang mesti dilakukan untuk mendapatkan baris matriks baharu.

.

Jelas sekali, dua lajur pertama bagi matriks yang terhasil adalah bebas secara linear, lajur ketiga ialah gabungan linearnya, dan lajur keempat tidak bergantung pada dua yang pertama. vektor dipanggil asas. Mereka membentuk subsistem bebas linear maksimum sistem , dan pangkat sistem ialah tiga.

Asas, koordinat

Tugasan 4. Cari asas dan koordinat bagi vektor dalam asas ini pada set vektor geometri, yang koordinatnya memenuhi syarat .

Penyelesaian. Set ialah satah yang melalui asalan. Asas sembarangan pada satah terdiri daripada dua vektor bukan kolinear. Koordinat vektor dalam asas yang dipilih ditentukan dengan menyelesaikan sistem persamaan linear yang sepadan.

Terdapat satu lagi cara untuk menyelesaikan masalah ini, apabila anda boleh mencari asas menggunakan koordinat.

Koordinat ruang bukan koordinat pada satah, kerana ia berkaitan dengan hubungan , iaitu mereka tidak berdikari. Pembolehubah bebas dan (ia dipanggil bebas) secara unik mentakrifkan vektor pada satah dan, oleh itu, ia boleh dipilih sebagai koordinat dalam . Kemudian asas terdiri daripada vektor yang terletak di dalam dan sepadan dengan set pembolehubah bebas Dan , iaitu .

Tugasan 5. Cari asas dan koordinat bagi vektor dalam asas ini pada set semua vektor dalam ruang yang koordinat ganjilnya adalah sama antara satu sama lain.

Penyelesaian. Marilah kita memilih, seperti dalam masalah sebelumnya, koordinat dalam ruang.

Kerana , kemudian pembolehubah bebas secara unik menentukan vektor dari dan oleh itu koordinat. Asas yang sepadan terdiri daripada vektor.

Tugasan 6. Cari asas dan koordinat bagi vektor dalam asas ini pada set semua matriks bentuk , Di mana – nombor sewenang-wenangnya.

Penyelesaian. Setiap matriks daripada boleh diwakili secara unik dalam bentuk:

Hubungan ini ialah pengembangan vektor dari berkenaan dengan asas
dengan koordinat .

Tugasan 7. Cari dimensi dan asas badan linear sistem vektor

.

Penyelesaian. Menggunakan EPS, kami menukar matriks daripada koordinat vektor sistem kepada bentuk segi tiga langkah.

.

Lajur matriks terakhir adalah bebas linear, dan lajur dinyatakan secara linear melalui mereka. Oleh itu, vektor membentuk asas , Dan .

Komen. Asas dalam dipilih secara samar-samar. Contohnya, vektor juga membentuk asas .

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Penyelesaian. sedang mencari penyelesaian umum sistem persamaan

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

Kaedah Gauss. Untuk melakukan ini, kami menulis sistem homogen ini dalam koordinat:

Matriks Sistem

Sistem yang dibenarkan mempunyai bentuk: (r A = 2, n= 3). Sistem ini kooperatif dan tidak pasti. Penyelesaian amnya ( x 2 – pembolehubah bebas): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . Kehadiran penyelesaian tertentu bukan sifar, sebagai contoh, menunjukkan bahawa vektor a 1 , a 2 , a 3 bergantung secara linear.

Contoh 2.

Ketahui sama ada sistem ini vektor bersandar linear atau bebas linear:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Penyelesaian. Pertimbangkan sistem persamaan homogen a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

atau dalam bentuk dikembangkan (mengikut koordinat)

Sistem ini adalah homogen. Jika ia tidak merosot, maka ia mempunyai penyelesaian yang unik. Dalam kes sistem homogen– penyelesaian sifar (remeh). Ini bermakna dalam kes ini sistem vektor adalah bebas. Jika sistem merosot, maka ia mempunyai penyelesaian bukan sifar dan, oleh itu, ia bergantung.

Kami menyemak sistem untuk degenerasi:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Sistem ini tidak merosot dan, dengan itu, vektor a 1 , a 2 , a 3 bebas linear.

Tugasan. Ketahui sama ada sistem vektor tertentu adalah bersandar secara linear atau tidak bersandar linear:

1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.

2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.

3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.

6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.

7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.

8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.

9. Buktikan bahawa sistem vektor akan bergantung secara linear jika ia mengandungi:

a) dua vektor yang sama;

b) dua vektor berkadar.

Vektor, sifat dan tindakan mereka dengannya

Vektor, tindakan dengan vektor, ruang vektor linear.

Vektor ialah himpunan tertib bagi bilangan nombor nyata yang terhingga.

Tindakan: 1.Mendarab vektor dengan nombor: lambda*vektor x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. Penambahan vektor (kepunyaan ruang vektor yang sama) vektor x + vektor y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vektor 0=(0,0…0)---n E n – n-dimensi (ruang linear) vektor x + vektor 0 = vektor x

Teorem. Agar sistem n vektor, ruang linear n-dimensi, bergantung secara linear, adalah perlu dan mencukupi bahawa salah satu vektor adalah gabungan linear yang lain.

Teorem. Mana-mana set n+ vektor pertama bagi ruang linear n-dimensi bagi fenomena. bergantung secara linear.

Penambahan vektor, pendaraban vektor dengan nombor. Penolakan vektor.

Jumlah dua vektor ialah vektor yang diarahkan dari permulaan vektor ke penghujung vektor, dengan syarat permulaannya bertepatan dengan penghujung vektor. Jika vektor diberikan oleh pengembangannya dalam vektor unit asas, maka apabila menambah vektor, koordinat sepadannya ditambah.

Mari kita pertimbangkan ini menggunakan contoh sistem koordinat Cartesian. biarlah

Mari kita tunjukkan itu

Daripada Rajah 3 jelas bahawa

Jumlah mana-mana nombor terhingga vektor boleh didapati menggunakan peraturan poligon (Rajah 4): untuk membina jumlah bilangan vektor terhingga, cukup untuk menggabungkan permulaan setiap vektor berikutnya dengan penghujung yang sebelumnya dan membina vektor yang menghubungkan permulaan daripada vektor pertama dengan penghujung yang terakhir.

Sifat operasi penambahan vektor:

Dalam ungkapan ini m, n ialah nombor.

Perbezaan antara vektor dipanggil vektor Sebutan kedua ialah vektor yang bertentangan dengan vektor dalam arah, tetapi sama dengan panjangnya.

Oleh itu, operasi tolak vektor digantikan dengan operasi tambah

Vektor yang permulaannya berada di titik asal dan berakhir di titik A (x1, y1, z1) dipanggil vektor jejari titik A dan dilambangkan secara ringkas. Oleh kerana koordinatnya bertepatan dengan koordinat titik A, pengembangannya dalam vektor unit mempunyai bentuk

Vektor yang bermula pada titik A(x1, y1, z1) dan berakhir di titik B(x2, y2, z2) boleh ditulis sebagai

dengan r 2 ialah vektor jejari titik B; r 1 - vektor jejari titik A.

Oleh itu, pengembangan vektor dalam vektor unit mempunyai bentuk

Panjangnya adalah sama dengan jarak antara titik A dan B

DARAB

Jadi dalam kes itu masalah kapal terbang hasil darab vektor dengan a = (ax; ay) dengan nombor b ditemui oleh formula

a b = (ax b; ay b)

Contoh 1. Cari hasil darab vektor a = (1; 2) dengan 3.

3 a = (3 1; 3 2) = (3; 6)

Jadi dalam kes itu masalah spatial hasil darab vektor a = (ax; ay; az) dengan nombor b ditemui oleh formula

a b = (ax b; ay b; az b)

Contoh 1. Cari hasil darab vektor a = (1; 2; -5) dengan 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Hasil darab titik bagi vektor dan di manakah sudut antara vektor dan ; jika sama ada, maka

Daripada takrifan hasil kali skalar ia mengikutinya

di mana, sebagai contoh, ialah magnitud unjuran vektor ke arah vektor.

Vektor kuasa dua skalar:

Sifat produk titik:

Hasil titik dalam koordinat

Jika Itu

Sudut antara vektor

Sudut antara vektor - sudut antara arah vektor ini (sudut terkecil).

Hasil silang (hasil silang dua vektor.) - ini adalah pseudovector, berserenjang dengan satah, dibina daripada dua faktor, iaitu hasil daripada operasi binari “pendaraban vektor” ke atas vektor dalam ruang Euclidean tiga dimensi. Produk ini bukan komutatif mahupun bersekutu (ia adalah antikomutatif) dan berbeza daripada hasil darab titik vektor. Dalam banyak masalah kejuruteraan dan fizik, anda perlu dapat membina vektor berserenjang dengan dua yang sedia ada - produk vektor menyediakan peluang ini. Hasil silang berguna untuk "mengukur" keserenjangan vektor - panjang hasil silang dua vektor adalah sama dengan hasil darab panjangnya jika ia berserenjang, dan berkurangan kepada sifar jika vektor selari atau antiselari.

Hasil silang ditakrifkan hanya dalam ruang tiga dimensi dan tujuh dimensi. Hasil produk vektor, seperti produk skalar, bergantung pada metrik ruang Euclidean.

Tidak seperti formula untuk mengira koordinat vektor produk titik dalam sistem koordinat segi empat tepat tiga dimensi, formula untuk hasil silang bergantung pada orientasi sistem segi empat tepat koordinat atau, dengan kata lain, "kiraliti"nya

Kolineariti vektor.

Dua vektor bukan sifar (tidak sama dengan 0) dipanggil kolinear jika ia terletak pada garis selari atau pada garis yang sama. Sinonim yang boleh diterima, tetapi tidak disyorkan, ialah vektor "selari". vektor kolinear boleh diarahkan secara sama (“co-directional”) atau berlawanan arah (dalam kes yang terakhir mereka kadang-kadang dipanggil "antikolinear" atau "antiparallel").

hasil campuran vektor( a, b, c)- hasil darab skalar bagi vektor a dan hasil darab vektor bagi vektor b dan c:

(a,b,c)=a ⋅(b ×c)

kadang-kadang dipanggil triple produk skalar vektor, kemungkinan besar disebabkan oleh fakta bahawa hasilnya adalah skalar (lebih tepat, pseudoscalar).

Makna geometri: Modulus hasil campuran adalah secara berangka sama dengan isipadu selari yang dibentuk oleh vektor (a,b,c) .

Hartanah

Produk campuran adalah simetri condong berkenaan dengan semua hujahnya: i.e. e. menyusun semula mana-mana dua faktor mengubah tanda produk. Ia berikutan bahawa produk campuran di sebelah kanan Sistem kartesian koordinat (dalam asas ortonormal) adalah sama dengan penentu matriks yang terdiri daripada vektor dan:

Hasil campuran dalam sistem koordinat Cartes kiri (dalam asas ortonormal) adalah sama dengan penentu matriks yang terdiri daripada vektor dan, diambil dengan tanda tolak:

khususnya,

Jika mana-mana dua vektor adalah selari, maka dengan mana-mana vektor ketiga mereka membentuk hasil bercampur sama dengan sifar.

Jika tiga vektor bersandar secara linear (iaitu, coplanar, terletak dalam satah yang sama), maka hasil campurannya adalah sama dengan sifar.

Deria geometri - Produk campuran oleh nilai mutlak sama dengan isipadu parallelepiped (lihat rajah) yang dibentuk oleh vektor dan; tanda bergantung kepada sama ada tiga vektor ini adalah tangan kanan atau kidal.

Kesamaan vektor.

Tiga vektor (atau bilangan yang lebih besar) dipanggil coplanar jika mereka, dikurangkan kepada permulaan umum, berbaring dalam satah yang sama

Sifat coplanariti

Jika sekurang-kurangnya satu daripada tiga vektor- sifar, maka ketiga-tiga vektor itu juga dianggap koplanar.

Tiga kali ganda vektor yang mengandungi sepasang vektor kolinear ialah koplanar.

Hasil campuran vektor coplanar. Ini adalah kriteria untuk kesetaraan tiga vektor.

Vektor koplanar bergantung secara linear. Ini juga merupakan kriteria untuk keserasian.

Dalam ruang 3 dimensi, 3 vektor bukan koplanar membentuk asas

Vektor bersandar linear dan bebas linear.

Sistem vektor bersandar linear dan bebas.Definisi. Sistem vektor dipanggil bergantung secara linear, jika terdapat sekurang-kurangnya satu kombinasi linear bukan remeh bagi vektor ini bersamaan dengan vektor sifar. Jika tidak, i.e. jika hanya gabungan linear remeh bagi vektor yang diberikan sama dengan vektor nol, vektor dipanggil bebas linear.

Teorem (kriteria pergantungan linear). Agar sistem vektor dalam ruang linear bersandar secara linear, adalah perlu dan mencukupi bahawa sekurang-kurangnya satu daripada vektor ini ialah gabungan linear yang lain.

1) Jika di antara vektor terdapat sekurang-kurangnya satu vektor sifar, maka keseluruhan sistem vektor adalah bergantung secara linear.

Malah, jika, sebagai contoh, , maka, dengan andaian , kita mempunyai gabungan linear bukan remeh .▲

2) Jika di antara vektor ada yang membentuk sistem bersandar linear, maka keseluruhan sistem adalah bergantung secara linear.

Sesungguhnya, biarkan vektor , , bersandar secara linear. Ini bermakna terdapat gabungan linear bukan remeh bersamaan dengan vektor sifar. Tetapi kemudian, andaikan , kita juga memperoleh gabungan linear bukan trivial sama dengan vektor sifar.

2. Asas dan dimensi. Definisi. Sistem vektor bebas linear ruang vektor dipanggil asas ruang ini jika mana-mana vektor daripada boleh diwakili sebagai gabungan linear vektor sistem ini, i.e. untuk setiap vektor ada nombor nyata sehingga kesamaan itu dipegang penguraian vektor mengikut asas, dan nombor dipanggil koordinat vektor berbanding asas(atau dalam asas) .

Teorem (mengenai keunikan pengembangan berkenaan dengan asas). Setiap vektor dalam ruang boleh dikembangkan menjadi asas dengan satu-satunya cara, i.e. koordinat setiap vektor dalam asas ditentukan dengan jelas.

Sistem vektor dipanggil bergantung secara linear, jika terdapat nombor di antaranya sekurang-kurangnya satu berbeza daripada sifar, supaya kesamaan https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src= " >.

Jika kesamaan ini dipenuhi hanya dalam kes apabila semua , maka sistem vektor dipanggil bebas linear.

Teorem. Sistem vektor akan bergantung secara linear jika dan hanya jika sekurang-kurangnya satu daripada vektornya ialah gabungan linear yang lain.

Contoh 1. Polinomial ialah gabungan linear polinomial https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Polinomial membentuk sistem bebas linear, kerana polinomial https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Contoh 2. Sistem matriks, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> adalah bebas linear, kerana gabungan linear adalah sama dengan matriks sifar hanya dalam kes apabila https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" width="40" height="21"> bergantung secara linear.

Penyelesaian.

Mari kita buat gabungan linear vektor ini https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" ketinggian=" 22">.

Menyamakan koordinat dengan nama yang sama vektor yang sama, kami mendapat https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Akhirnya kita dapat

Dan

Sistem ini hanya mempunyai satu penyelesaian remeh, oleh itu gabungan linear vektor ini adalah sama dengan sifar hanya dalam kes apabila semua pekali adalah sama dengan sifar. Oleh itu, sistem vektor ini adalah bebas linear.

Contoh 4. Vektor adalah bebas linear. Bagaimanakah sistem vektor akan menjadi seperti?

a).;

b).?

Penyelesaian.

a). Mari kita buat gabungan linear dan samakannya dengan sifar

Menggunakan sifat operasi dengan vektor dalam ruang linear, kami menulis semula kesamaan terakhir dalam bentuk

Memandangkan vektor adalah bebas linear, pekali untuk mestilah sama dengan sifar, iaitu..gif" width="12" height="23 src=">

Sistem persamaan yang terhasil mempunyai penyelesaian remeh yang unik .

Sejak kesamarataan (*) dilaksanakan hanya apabila https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – bebas linear;

b). Mari kita buat kesamarataan https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Menggunakan alasan yang sama, kami memperoleh

Menyelesaikan sistem persamaan dengan kaedah Gauss, kita perolehi

atau

Sistem yang terakhir mempunyai set tak terhingga penyelesaian https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Oleh itu, terdapat set pekali bukan sifar di mana kesamaan memegang (**) . Oleh itu, sistem vektor – bergantung secara linear.

Contoh 5 Sistem vektor tidak bersandar secara linear dan sistem vektor bersandar secara linear..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

Dalam kesamarataan (***) . Sesungguhnya, pada , sistem akan bergantung secara linear.

Daripada perhubungan (***) kita dapat atau Mari kita nyatakan .

Kami dapat

Tugasan untuk keputusan bebas(dalam penonton)

1. Sistem yang mengandungi vektor sifar adalah bergantung secara linear.

2. Sistem yang terdiri daripada satu vektor A, adalah bergantung secara linear jika dan hanya jika, a=0.

3. Sistem yang terdiri daripada dua vektor adalah bersandar secara linear jika dan hanya jika vektor adalah berkadar (iaitu, satu daripadanya diperoleh daripada yang lain dengan mendarab dengan nombor).

4. Jika k adalah linear sistem bergantung tambah vektor, anda mendapat sistem bergantung secara linear.

5. Jika dari linear sistem bebas keluarkan vektor, maka sistem vektor yang terhasil adalah bebas secara linear.

6. Jika sistem S adalah bebas secara linear, tetapi menjadi bergantung secara linear apabila menambah vektor b, kemudian vektor b dinyatakan secara linear melalui vektor sistem S.

c). Sistem matriks , , dalam ruang matriks tertib kedua.

10. Biarkan sistem vektor a,b,c ruang vektor adalah bebas secara linear. Buktikan kemerdekaan linear sistem berikut vektor:

a).a+b, b, c.

b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– nombor sewenang-wenangnya

c).a+b, a+c, b+c.

11. biarlah a,b,c– tiga vektor pada satah dari mana sebuah segitiga boleh dibentuk. Adakah vektor ini bergantung secara linear?

12. Dua vektor diberikan a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Cari dua lagi vektor empat dimensi a3 dana4 supaya sistem a1,a2,a3,a4 adalah bebas secara linear .