Persamaan perbezaan linear dengan pekali malar. Persamaan pembezaan untuk dummies

Selalunya hanya sebutan persamaan pembezaan memberikan pelajar perasaan yang tidak menyenangkan. Mengapa ini berlaku? Selalunya, kerana apabila mempelajari asas-asas bahan, jurang pengetahuan timbul, yang menyebabkan kajian lanjut mengenai peresap menjadi penyeksaan semata-mata. Tidak jelas apa yang perlu dilakukan, bagaimana untuk membuat keputusan, di mana untuk bermula?

Walau bagaimanapun, kami akan cuba menunjukkan kepada anda bahawa peresap tidak sesukar yang disangka.

Konsep asas teori persamaan pembezaan

Dari sekolah kita tahu persamaan paling mudah di mana kita perlu mencari x yang tidak diketahui. Pada asasnya persamaan pembezaan hanya berbeza sedikit daripada mereka - bukannya pembolehubah X anda perlu mencari fungsi di dalamnya y(x) , yang akan menjadikan persamaan menjadi identiti.

Persamaan pembezaan mempunyai kepentingan praktikal yang besar. Ini bukan matematik abstrak yang tiada kaitan dengan dunia sekeliling kita. Banyak proses semula jadi sebenar diterangkan menggunakan persamaan pembezaan. Contohnya, getaran tali, pergerakan pengayun harmonik, menggunakan persamaan pembezaan dalam masalah mekanik, mencari kelajuan dan pecutan jasad. Juga DU digunakan secara meluas dalam biologi, kimia, ekonomi dan banyak lagi sains lain.

Persamaan pembezaan (DU) ialah persamaan yang mengandungi derivatif bagi fungsi y(x), fungsi itu sendiri, pembolehubah bebas dan parameter lain dalam pelbagai kombinasi.

Terdapat banyak jenis persamaan pembezaan: persamaan pembezaan biasa, linear dan tak linear, homogen dan tidak homogen, persamaan pembezaan tertib pertama dan lebih tinggi, persamaan pembezaan separa, dan sebagainya.

Penyelesaian kepada persamaan pembezaan ialah fungsi yang mengubahnya menjadi identiti. Terdapat penyelesaian umum dan khusus alat kawalan jauh.

Penyelesaian umum kepada persamaan pembezaan ialah set umum penyelesaian yang mengubah persamaan menjadi identiti. Penyelesaian separa bagi persamaan pembezaan ialah penyelesaian yang memenuhi syarat tambahan yang dinyatakan pada mulanya.

Susunan persamaan pembezaan ditentukan oleh susunan tertinggi terbitannya.

Persamaan pembezaan biasa

Persamaan pembezaan biasa adalah persamaan yang mengandungi satu pembolehubah bebas.

Mari kita pertimbangkan persamaan pembezaan biasa termudah bagi susunan pertama. Ia kelihatan seperti:

Persamaan ini boleh diselesaikan dengan hanya menyepadukan sebelah kanannya.

Contoh persamaan tersebut:

Persamaan boleh dipisahkan

Secara umum, persamaan jenis ini kelihatan seperti ini:

Berikut ialah contoh:

Apabila menyelesaikan persamaan sedemikian, anda perlu memisahkan pembolehubah, membawanya ke bentuk:

Selepas ini, ia kekal untuk mengintegrasikan kedua-dua bahagian dan mendapatkan penyelesaian.

Persamaan pembezaan linear bagi urutan pertama

Persamaan sedemikian kelihatan seperti:

Di sini p(x) dan q(x) ialah beberapa fungsi pembolehubah bebas, dan y=y(x) ialah fungsi yang diingini. Berikut adalah contoh persamaan sedemikian:

Apabila menyelesaikan persamaan sedemikian, selalunya mereka menggunakan kaedah mengubah pemalar arbitrari atau mewakili fungsi yang diingini sebagai hasil darab dua fungsi lain y(x)=u(x)v(x).

Untuk menyelesaikan persamaan sedemikian, penyediaan tertentu diperlukan dan agak sukar untuk mengambilnya "sepintas lalu".

Contoh penyelesaian persamaan pembezaan dengan pembolehubah boleh dipisahkan

Jadi kami melihat jenis alat kawalan jauh yang paling mudah. Sekarang mari kita lihat penyelesaian kepada salah satu daripada mereka. Biarkan ini menjadi persamaan dengan pembolehubah boleh dipisahkan.

Mula-mula, mari kita tulis semula derivatif dalam bentuk yang lebih biasa:

Kemudian kami membahagikan pembolehubah, iaitu, dalam satu bahagian persamaan kami mengumpul semua "Saya", dan yang lain - "X":

Kini ia kekal untuk mengintegrasikan kedua-dua bahagian:

Kami menyepadukan dan mendapatkan penyelesaian umum untuk persamaan ini:

Sudah tentu, menyelesaikan persamaan pembezaan adalah sejenis seni. Anda perlu dapat memahami jenis persamaan itu, dan juga belajar untuk melihat transformasi yang perlu dibuat dengannya untuk membawa kepada satu bentuk atau yang lain, apatah lagi hanya keupayaan untuk membezakan dan menyepadukan. Dan untuk berjaya menyelesaikan DE, anda memerlukan latihan (seperti dalam segala-galanya). Dan jika pada masa ini anda tidak mempunyai masa untuk memahami cara persamaan pembezaan diselesaikan, atau masalah Cauchy telah tersekat seperti tulang di kerongkong anda, atau anda tidak tahu cara menyediakan pembentangan dengan betul, hubungi pengarang kami. Dalam masa yang singkat, kami akan memberikan anda penyelesaian siap pakai dan terperinci, butiran yang anda boleh fahami pada bila-bila masa yang sesuai untuk anda. Sementara itu, kami mencadangkan menonton video mengenai topik "Cara menyelesaikan persamaan pembezaan":

Mari kita pertimbangkan persamaan perbezaan urutan ke-n

y(k) = F(k) (92)

Seperti persamaan pembezaan, penyelesaian sentiasa ditentukan untuk persamaan tertib pertama dan secara amnya tidak boleh didapati untuk persamaan tertib tinggi.

Penyelesaian yang berguna.

Pertimbangkan persamaan tertib pertama homogen

a 1 (k)y(k+1) + a 0 (k)y(k) = 0, (93)

di mana 0 (k)≠0 dan 1 (k)≠0. Ia boleh ditulis semula dalam bentuk

y(k+1) = a(k)y(k). (94)

pada k=0,1,2...

y(1)=a(0)y(0),

y(2)=a(1)a(0)y(0)

y(3)=a(2)a(1)a(0)y(0)

atau, secara amnya,

jadi penyelesaian umum kepada persamaan (94) ialah

Had bawah produk adalah sembarangan, kerana sebarang bilangan tetap faktor a(0), a(1), dan a(2), ... boleh digabungkan dengan pemalar arbitrari C.

Penyelesaian persamaan homogen di atas susunan pertama dalam kes umum tidak dinyatakan dalam bentuk fungsi asas, kerana prosedur berdasarkan persamaan (81) dan (82), dengan pekali bergantung pada k, tidak lagi sah. Jika semua kecuali satu penyelesaian bebas kepada persamaan diketahui, maka penyelesaian yang tinggal boleh ditentukan. Seperti persamaan pembezaan, dalam beberapa kes individu adalah mungkin untuk mendapatkan penyelesaian yang jelas. Persamaan bentuk

a n f(k + n)y(k + n) + ... + a 1 f (k + 1)y(k + 1) + a n f(k)y(k) = 0,

di mana pekali a i ialah nilai malar, dengan menggantikan z(k)=f(k)y(k) ia dikurangkan kepada persamaan perbezaan dengan pekali malar. Prosedur ini sebahagiannya serupa dengan yang digunakan untuk persamaan pembezaan Euler, tetapi dalam kes ini pembolehubah bersandar (bukan bebas) tertakluk kepada penggantian. Kaedah ini digunakan secara meluas dalam menyelesaikan persamaan dengan pekali pembolehubah.

Persamaan pembezaan sistem kawalan automatik. Metodologi untuk menyusun persamaan pembezaan untuk sistem kawalan automatik.

Nota am.

Sistem kawalan automatik adalah berbeza dalam tujuan dan reka bentuknya. Tingkah laku ACS boleh diterangkan oleh persamaan pembezaan separa biasa, persamaan perbezaan, dsb.

Mana-mana ACS mewakili satu set elemen individu yang berinteraksi antara satu sama lain, disambungkan melalui sambungan. Langkah pertama dalam menyusun persamaan pembezaan untuk ACS ialah membahagikan sistem kepada elemen individu dan mengarang persamaan pembezaan untuk unsur-unsur ini. Persamaan unsur dan persamaan sambungan antara unsur individu menerangkan proses dalam sistem kawalan, i.e. berubah mengikut masa semua koordinat sistem. Mengetahui persamaan unsur dan persamaan sambungan, adalah mungkin untuk membuat gambarajah blok ACS.

Gambar rajah struktur ACS mencirikan geometri sistem, i.e. menunjukkan unsur-unsur yang terdiri daripada ATS dan bagaimana elemen ini berkaitan antara satu sama lain. Keadaan ACS, serta setiap elemen yang termasuk di dalamnya, dicirikan oleh sebilangan pembolehubah bebas tertentu. Pembolehubah ini boleh sama ada kuantiti elektrik (arus, voltan, dsb.) atau kuantiti mekanikal (kelajuan, sudut putaran, pergerakan, dsb.). Biasanya, untuk mencirikan keadaan sistem atau elemennya, satu koordinat umum dipilih pada input sistem atau elemen (g(t)) dan satu pada output (x(t)). Dalam sesetengah kes, perwakilan sedemikian adalah mustahil, kerana sistem atau elemennya mungkin mempunyai beberapa kuantiti input dan output. Dalam sistem multidimensi, seseorang boleh mempertimbangkan input vektor dan kuantiti output dengan dimensi yang bertepatan, masing-masing, dengan bilangan kuantiti input dan output ACS.

Penyusunan dan linearisasi persamaan pembezaan elemen sistem.

Apabila menyusun persamaan pembezaan untuk ACS, tugas utama adalah untuk menyusun persamaan pembezaan untuk elemen individu sistem. Persamaan unsur-unsur individu disusun berdasarkan undang-undang fizik yang mencirikan kelakuan unsur tersebut.

Apabila merangka persamaan pembezaan untuk elemen ACS, seseorang harus berusaha untuk menerangkan tingkah laku elemen tertentu setepat mungkin. Walau bagaimanapun, kerumitan persamaan yang terhasil menyukarkan untuk mengkaji sifat penyelesaiannya. Oleh itu, apabila mengarang persamaan pembezaan, adalah perlu untuk berusaha untuk kompromi yang munasabah antara penerangan yang paling lengkap tentang kelakuan elemen dan kemungkinan menyemak dan mengkaji persamaan yang terhasil.

Jika dinamik unsur diterangkan oleh persamaan pembezaan linear, maka unsur ini dipanggil linear, jika persamaan pembezaan tidak linear, maka unsur dipanggil tak linear.

Untuk memudahkan analisis, jika boleh, persamaan pembezaan tak linear lebih kurang digantikan dengan persamaan linear yang penyelesaiannya bertepatan dengan penyelesaian persamaan tak linear dengan tahap ketepatan yang mencukupi. Proses menggantikan persamaan pembezaan tak linear dengan persamaan linear dipanggil linearisasi.

Jika persamaan pembezaan unsur adalah tak linear disebabkan oleh ketaklinearan ciri statiknya, maka linearisasi persamaan dikurangkan untuk menggantikan ciri tak linear unsur tersebut. x=φ(g) beberapa fungsi linear x= ag+ b. Secara analitikal, penggantian ini dibuat menggunakan pengembangan siri Taylor bagi fungsi tersebut x=φ(g) di sekitar titik yang sepadan dengan keadaan mantap dan membuang semua istilah yang mengandungi sisihan ∆g nilai input unsur kepada kuasa yang lebih tinggi daripada yang pertama. Secara geometri, ini bermakna menggantikan lengkung x=φ(g) tangen yang dilukis pada lengkung pada titik (x 0, g 0), sepadan dengan keadaan mantap operasi elemen (Rajah 29). Dalam kes lain, linearisasi dijalankan dengan melukis sekan yang menyimpang sedikit daripada fungsi x=φ(g) dalam julat perubahan yang diperlukan dalam nilai input elemen.

Bersama-sama dengan ciri-ciri boleh linearizable, terdapat juga ciri-ciri yang tidak bersetuju dengan linearization tersebut. Ini termasuk, sebagai contoh, ciri yang tidak boleh dikembangkan menjadi siri Taylor di sekitar titik keadaan mantap. Kami akan memanggil ciri sedemikian ketara tidak linear.

Mari kita pertimbangkan proses linearisasi persamaan unsur tak linear menggunakan siri Taylor. Biarkan kelakuan unsur diterangkan oleh persamaan pembezaan tak linear

F(x n , x ’ , x, g) = 0 (1). Kemudian keadaan mantap unsur tersebut dicirikan oleh persamaan F(0, 0, x, g) = 0 (2). biarkan g 0 dan x 0 ialah nilai keadaan mantap. Kemudian koordinat g dan x boleh ditulis sebagai x = x 0 + ∆x, g = g 0 + ∆g, dengan ∆g dan ∆x ialah sisihan koordinat g dan x daripada keadaan mantap. Persamaan (1) dalam sisihan mempunyai bentuk:

F(∆x ’’ , ∆x ’ , x 0 + ∆x, g 0 + ∆g) = 0 (3).

Mari kita kembangkan bahagian kiri persamaan (3) ke dalam siri Taylor berbanding dengan titik keadaan mantap (0, 0, x 0, g 0):

Terbitan separa di sebelah kiri persamaan (4) mewakili beberapa nombor, yang nilainya bergantung pada jenis fungsi F(x '', x ', x, g) dan nilai koordinat x 0 dan g 0.

Memandangkan sisihan ∆g, ∆x daripada keadaan mantap, serta terbitannya berkenaan dengan masa, adalah kecil dan mengandaikan bahawa fungsi F(x '' , x ' , x, g) cukup lancar berkenaan dengan semua hujah di sekitar titik yang sepadan dengan keadaan mantap, kami membuang dalam persamaan (4) semua istilah yang mengandungi sisihan ∆g dan ∆x, serta terbitannya pada tahap yang lebih tinggi daripada yang pertama. Persamaan (5) yang terhasil ialah persamaan pembezaan linear dengan pekali malar ,,,dan merupakan hasil linearisasi persamaan (1).

Jelas sekali, syarat yang perlu untuk linearisasi ialah kemungkinan mengembangkan fungsi F(x ’’ , x ’ , x, g) ke dalam siri Taylor di sekitar titik yang sepadan dengan keadaan mantap.

Proses linearisasi persamaan (1) boleh ditafsirkan secara geometri seperti berikut. Dalam ruang pembolehubah x '' , x ' , x, g, persamaan (1) mentakrifkan permukaan tertentu. Peralihan daripada persamaan (1) kepada persamaan linear (5) bermaksud menggantikan permukaan dengan satah tangen tertentu yang dilukis ke permukaan pada titik yang sepadan dengan keadaan mantap. Sememangnya, semakin kecil perbezaan antara titik permukaan dan titik satah, semakin kecil ralat dalam penggantian tersebut. Ini benar hanya dalam persekitaran kecil keadaan mantap.

Konsep kebolehkawalan dan pemerhatian.

Proses atau objek biasanya dipanggil boleh dikawal sepenuhnya jika ia boleh dipindahkan dari keadaan tertentu x(t 0) kepada keadaan keseimbangan yang dikehendaki x(t 1) dalam selang masa terhingga t 1 – t 0. Dalam erti kata lain, proses itu boleh dikawal sepenuhnya jika terdapat tindakan kawalan m(t), ditakrifkan pada selang masa terhingga t 0 ≤ t ≤ t 1, yang memindahkan proses dari keadaan awal x(t 0) kepada yang dikehendaki. keadaan keseimbangan x(t 1) semasa masa t 1 – t 0 .

Keadaan yang perlu dan mencukupi untuk kebolehkawalan lengkap bagi kes sistem diskret boleh dirumuskan seperti berikut.

Proses diskret linear bagi urutan ke-n boleh dikawal sepenuhnya jika dan hanya jika vektor

s 1 = φ(-T)h(T),

s 2 = φ(-T)h(T),

s n = φ(-T)h(T)

bebas linear.

Vektor ini timbul kerana transformasi berikut.

(t) = Ax(t) + d m(t),

di mana m(t) adalah satu-satunya tindakan kawalan. Kes tindakan kawalan tunggal dianggap untuk memudahkan tafsiran ungkapan yang terhasil. Persamaan keadaan peralihan proses mempunyai bentuk

di mana φ(T) ialah matriks peralihan proses dan
.

Konsep kebolehkawalan juga boleh diberikan tafsiran lain, yang akan menyumbang kepada pemahaman yang lebih baik. Biarkan proses multidimensi linear diterangkan oleh persamaan pembezaan vektor (t) = Ax(t) + D m(t), dengan x ialah vektor keadaan dimensi-n;

m – vektor r-dimensi yang mewakili tindakan kawalan;

A – matriks kuadratik bagi pekali urutan ke-n;

D – matriks kawalan saiz n×r.

Matriks A boleh dikurangkan kepada bentuk pepenjuru

,

di mana λ i ialah nilai eigen matriks A proses linear, yang diandaikan semuanya berbeza.

Dengan menggunakan penggantian x=Tz, kita tulis persamaan dalam bentuk kanonik

(t) = Λz(t) + ∆ m(t),

di mana
. Vectorz akan dipanggil vektor keadaan kanonik.

Proses yang diterangkan oleh persamaan (t) = Ax(t) + D m(t), boleh dikawal jika matriks ∆ tidak mengandungi baris yang elemennya semuanya sifar; koordinat yang sepadan dengan baris bukan sifar ∆ dianggap terkawal.

Contoh:

Terbitkan persamaan pembezaan bandul emparan, yang digunakan sebagai elemen penderiaan dalam beberapa sistem kawalan automatik. Rajah bandul ditunjukkan dalam rajah. Kuantiti input ialah halaju sudut ω, dan kuantiti keluaran ialah sesaran x platform. Apabila kelajuan putaran meningkat, bola menyimpang di bawah pengaruh daya emparan dan menggerakkan platform. Platform juga dipengaruhi oleh daya anjal spring, daya redaman dan daya inersia.

Mari kita perkenalkan tatatanda berikut: c – pekali kekakuan spring; k – pekali geseran likat; m - jisim bola; M – jisim bahagian yang terlibat dalam gerakan translasi sepanjang paksi OX; ω – halaju sudut aci; f 0 – daya pra-mampatan spring.

Untuk menyusun persamaan pembezaan bandul emparan, kami menggunakan persamaan Lagrange jenis kedua:
(I = 1, 2,…, n) (*). Sebagai koordinat umum x i, kita memilih koordinat keluaran - pergerakan platform x. Mari kita cari ungkapan untuk tenaga kinetik T, tenaga keupayaan P dan fungsi pelesapan R bandul emparan. Daripada rajah itu jelas bahawa

ρ = r + l sin α, x = 2a(1 – cos α).

Tenaga kinetik sistem T = T 1 + T 2 + T 3, di mana T 1 ialah tenaga kinetik dalam gerakan putaran mengelilingi paksi OX; T 2 – tenaga kinetik bola dalam gerakan putaran mengelilingi titik A dan A’; Т 3 – tenaga kinetik jisim dalam gerakan translasi sepanjang paksi OX. Kami ada:

,

,
. (*1)

Tenaga keupayaan bandul P = P 1 + P 2 + P 3, di mana P 1 ialah tenaga keupayaan jisim yang bergerak selari dengan paksi OX; P 2 – tenaga keupayaan; P 3 – tenaga keupayaan spring. Untuk kes yang sedang dipertimbangkan kami ada:

,
,
. (*2)

Mari kita cari daya pelesapan umum Q R . Disebabkan kehadiran peredam, daya geseran kering adalah kecil berbanding dengan daya geseran likat dan boleh diabaikan. Mengikut formula
kita akan ada

. (*3)

Mari kita hitung nilai istilah individu yang disertakan dalam persamaan Lagrange (*):

,

,

.

Mari kita gantikan ungkapan yang terhasil ke dalam persamaan Lagrange jenis kedua (*), kemudian

Mari kita perkenalkan notasi berikut:

,
,

; (*5)

. (*6)

Dengan mengambil kira tatatanda yang diterima, persamaan bandul emparan akan ditulis dalam bentuk

Persamaan (*7) ialah persamaan pembezaan tak linear. Keadaan keseimbangan (x 0, ω 0) ialah penyelesaian kepada persamaan

Mari kita pertimbangkan ayunan kecil bandul berbanding keadaan keseimbangan

x = x 0 + ∆x, ω = ω 0 + ∆ω. (*9)

Mari kita kembangkan fungsi f 1 (x), f 2 (x), f 3 (x, ω) menjadi siri Taylor di sekitar keadaan keseimbangan (x 0, ω 0).

di mana fungsi F 1 (∆x), F 2 (∆x), F 3 (∆x, ∆ω) mempunyai susunan kekecilan yang lebih tinggi berbanding ∆x dan ∆ω. Memandangkan x’ = ∆x’ dan x” = ∆x”, dan mengambil kira ungkapan (*8), (*9), (*10), persamaan (*7) boleh ditulis semula sebagai

di mana fungsinya

mempunyai susunan kekecilan yang lebih tinggi berbanding dengan
. Menggugurkan fungsi
, kita memperoleh persamaan linear ayunan bandul berbanding keadaan keseimbangan (x 0, ω 0)

, (*11)

,

(*12)

.

Sistem yang urutan input dan outputnya disambungkan dengan persamaan perbezaan linear dengan pekali malar membentuk subset kelas sistem linear dengan parameter malar. Penerangan sistem LPP mengikut persamaan perbezaan adalah sangat penting, kerana ia sering membolehkan seseorang mencari cara yang berkesan untuk membina sistem sedemikian. Selain itu, daripada persamaan perbezaan adalah mungkin untuk menentukan banyak ciri sistem yang sedang dipertimbangkan, termasuk frekuensi semula jadi dan kepelbagaiannya, susunan sistem, frekuensi yang sepadan dengan keuntungan sifar, dsb.

Dalam kes yang paling umum, persamaan perbezaan linear tertib ke- dengan pekali malar, berkaitan dengan sistem yang boleh direalisasikan secara fizikal, mempunyai bentuk

(2.18)

di mana pekali dan menerangkan sistem tertentu, dan . Tepat bagaimana susunan sistem mencirikan sifat matematik bagi persamaan perbezaan akan ditunjukkan di bawah. Persamaan (2.18) ditulis dalam bentuk yang sesuai untuk diselesaikan dengan kaedah penggantian terus. Mempunyai satu set syarat awal [sebagai contoh, untuk ] dan jujukan input, menggunakan formula (2.18) anda boleh terus mengira jujukan output untuk . Sebagai contoh, persamaan perbezaan

(2.19)

dengan keadaan awal dan boleh diselesaikan dengan penggantian, yang memberi

Walaupun menyelesaikan persamaan perbezaan melalui penggantian langsung berguna dalam beberapa kes, ia adalah lebih berguna untuk mendapatkan penyelesaian eksplisit kepada persamaan itu. Kaedah untuk mencari penyelesaian sedemikian diliputi secara terperinci dalam literatur tentang persamaan perbezaan, dan hanya gambaran ringkas akan diberikan di sini. Idea utama datang untuk mendapatkan dua penyelesaian kepada persamaan perbezaan: homogen dan separa. Penyelesaian homogen diperoleh dengan menggantikan sifar untuk semua istilah yang mengandungi unsur-unsur jujukan input dan menentukan tindak balas apabila jujukan input adalah sifar. Kelas penyelesaian inilah yang menerangkan sifat asas sistem tertentu. Penyelesaian tertentu diperoleh dengan memilih jenis urutan keluaran untuk urutan input yang diberikan. Untuk menentukan pemalar arbitrari penyelesaian homogen, keadaan awal digunakan. Sebagai contoh, mari kita selesaikan persamaan (2.19) menggunakan kaedah ini. Persamaan homogen mempunyai bentuk

(2.20)

Adalah diketahui bahawa penyelesaian ciri persamaan homogen sepadan dengan persamaan perbezaan linear dengan pekali malar ialah penyelesaian dalam bentuk

(2.21)

Mari cuba cari penyelesaian tertentu yang sepadan dengan urutan input dalam borang

(2.22)

Daripada persamaan (2.19) kita perolehi

Oleh kerana pekali bagi darjah yang sama mestilah sama, B, C dan D mestilah sama

(2.24)

Oleh itu, penyelesaian umum mempunyai bentuk

(2.25)

Pekali ditentukan dari keadaan awal, dari mana dan

(2.26)

Semakan terpilih bagi penyelesaian (2.26) at menunjukkan persetujuan lengkapnya dengan penyelesaian langsung yang diberikan di atas. Kelebihan jelas penyelesaian (2.26) ialah ia membolehkan seseorang menentukan dengan mudah untuk mana-mana .

Rajah. 2.7. Skim untuk melaksanakan persamaan perbezaan tertib pertama yang mudah.

Kepentingan persamaan perbezaan ialah ia secara langsung menentukan kaedah membina sistem digital. Oleh itu, persamaan perbezaan tertib pertama daripada bentuk yang paling umum

boleh dilaksanakan menggunakan litar yang ditunjukkan dalam Rajah. 2.7. Blok "kelewatan" melambatkan satu kiraan. Bentuk reka bentuk sistem ini, di mana elemen kelewatan berasingan digunakan untuk urutan input dan output, dipanggil bentuk langsung 1. Di bawah ini kita akan membincangkan pelbagai kaedah untuk membina ini dan sistem digital lain.

Persamaan perbezaan tertib kedua bentuk paling umum

Rajah. 2.8. Skim untuk melaksanakan persamaan perbezaan tertib kedua.

boleh dilaksanakan menggunakan litar yang ditunjukkan dalam Rajah. 2.8. Litar ini juga menggunakan elemen kelewatan yang berasingan untuk urutan input dan output.

Daripada pembentangan seterusnya bahan-bahan dalam bab ini, ia akan menjadi jelas bahawa sistem tertib pertama dan kedua boleh digunakan dalam pelaksanaan sistem tertib lebih tinggi, kerana sistem tertib yang lebih tinggi boleh diwakili dalam bentuk siri atau tersambung selari tertib pertama dan kedua. sistem.

V i r e f e r m o r e l a l i v e n ts dipanggil. persamaan bentuk

mana yang dikehendaki dan F- fungsi yang diberikan. Menggantikan perbezaan terhingga dalam (2) dengan ungkapan mereka melalui nilai fungsi yang dikehendaki mengikut (1) membawa kepada persamaan bentuk

Jika , iaitu persamaan (3) benar-benar mengandungi kedua-duanya , dan , maka persamaan (3) dipanggil. persamaan pembezaan tertib ke-m, atau persamaan pembezaan V o r m e l a l i n g i n g .

(6)

di mana pemalar sewenang-wenangnya.

3) Penyelesaian am bagi persamaan linear tak homogen. (4) dibentangkan sebagai hasil tambah sebarang penyelesaian tertentu dan penyelesaian umum persamaan linear homogen. (5).

Penyelesaian tertentu bagi persamaan tak homogen (5) boleh dibina berdasarkan penyelesaian umum (6) persamaan homogen dengan menggunakan kaedah variasi pemalar arbitrari (lihat, sebagai contoh,). Dalam kes R. u. dengan pekali malar

seseorang boleh terus mencari penyelesaian separa bebas linear. Untuk tujuan ini, ciri ciri dipertimbangkan. persamaan

dan akarnya dicari. Jika semua akar adalah mudah, maka fungsinya

membentuk sistem bebas linear bagi penyelesaian persamaan (7). Dalam kes apabila - punca kepelbagaian r, penyelesaian adalah bebas secara linear

Jika pekali a 0 ,a 1 , . . ., a t nyata dan persamaan (8) mempunyai punca kompleks, contohnya. punca mudah, maka bukannya penyelesaian kompleks, dua penyelesaian nyata bebas linear dibezakan

Biar ada R.u. Tertib ke-2 dengan pekali nyata malar

(9) Ciri persamaan

mempunyai akar

Dalam kes ini, adalah mudah untuk menulis penyelesaian umum persamaan (9) dalam bentuk

(10)

di mana c 1 dan c 2 ialah pemalar arbitrari. Jika dan merupakan akar konjugat kompleks:

maka satu lagi perwakilan penyelesaian am mempunyai bentuk

Dalam kes punca berbilang, penyelesaian umum boleh diperolehi dengan meneruskan ke had dari (10) atau (11). nampak macam

Seperti dalam kes persamaan susunan arbitrari, untuk R. at. Daripada urutan ke-2, seseorang boleh mempertimbangkan masalah Cauchy atau pelbagai masalah nilai sempadan. Sebagai contoh, untuk masalah Cauchy

Menyelesaikan persamaan perbezaan linear biasa

dengan pekali malar

Hubungan antara output dan input sistem diskret linear boleh diterangkan oleh persamaan perbezaan linear biasa dengan pekali malar

,

di mana y[n]- isyarat keluaran pada masa ini n,

x[n]- isyarat input pada masa ini n,

a saya,b k– pekali malar.

Dua kaedah boleh digunakan untuk menyelesaikan persamaan tersebut

• Kaedah langsung
• Kaedah Z – transformasi.

Pertama, mari kita pertimbangkan untuk menyelesaikan persamaan perbezaan linear menggunakan kaedah langsung.

Penyelesaian umum persamaan perbezaan linear tidak homogen (dengan sisi kanan bukan sifar) adalah sama dengan hasil tambah penyelesaian umum persamaan perbezaan homogen linear dan penyelesaian peribadi persamaan tak homogen

Penyelesaian umum persamaan perbezaan homogen ( sifar-inputtindak balas) y h [n]

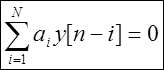
ditakrifkan sebagai

.

Menggantikan penyelesaian ini ke dalam persamaan homogen, kita perolehi

Polinomial sedemikian dipanggil polinomial ciri sistem. Dia ada N akar . Akar boleh menjadi nyata atau kompleks dan beberapa akar boleh bertepatan (berbilang).

Jika akar adalah nyata dan berbeza, maka penyelesaian kepada persamaan homogen mempunyai bentuk

di manakah pekali

Jika beberapa akar, sebagai contoh, λ 1 mempunyai kepelbagaian m, maka istilah penyelesaian yang sepadan mengambil bentuk

Jika semua pekali persamaan homogen dan, oleh itu, polinomial ciri adalah nyata, maka dua sebutan penyelesaian sepadan dengan akar konjugat kompleks ringkas boleh diwakili (ditulis) dalam bentuk , dengan pekali A,B ditentukan oleh syarat awal.

Jenis penyelesaian peribadi y p [n] persamaan bergantung pada sebelah kanan (isyarat input) dan ditentukan mengikut jadual di bawah

Jadual 1. Jenis penyelesaian tertentu untuk sifat berbeza sebelah kanan

Isyarat masukanx[n]	Penyelesaian peribadiy p [n]
A(malar)

Penyelesaian persamaan perbezaan linear dengan kaedah penjelmaan Z- terdiri daripada menggunakan Z– penjelmaan kepada persamaan menggunakan sifat lineariti dan anjakan masa. Hasilnya ialah persamaan algebra linear berkenaan dengan Z- imej fungsi yang diperlukan. terbalik Z– transformasi memberikan penyelesaian yang diingini dalam domain masa. Untuk mendapatkan penjelmaan Z - songsang, penguraian ungkapan rasional kepada pecahan mudah (elemen) paling kerap digunakan, kerana penjelmaan songsang daripada pecahan asas yang berasingan mempunyai bentuk mudah.

Ambil perhatian bahawa untuk beralih ke domain masa, kaedah lain untuk mengira perubahan Z songsang boleh digunakan.

Contoh. Mari kita tentukan tindak balas (isyarat output) sistem yang diterangkan oleh persamaan perbezaan linear kepada isyarat input

Penyelesaian.

1. Kaedah langsung untuk menyelesaikan persamaan.

Persamaan homogen. Polinomial cirinya.

Akar-akar polinomial .

Penyelesaian persamaan homogen.

Oleh kerana, kami mentakrifkan penyelesaian tertentu dalam bentuk .

Kami menggantikannya ke dalam persamaan

Untuk mencari pemalar KEPADA mari terima n=2. Kemudian

Atau, K=2.33

Oleh itu penyelesaian khusus dan penyelesaian umum kepada persamaan perbezaan (1)

Mari cari pemalar C 1 Dan C 2. Untuk melakukan ini, mari letakkan n=0, maka daripada persamaan perbezaan asal kita perolehi . Untuk persamaan yang diberikan

sebab tu . Daripada ungkapan (1)

Oleh itu,

.

Daripada ungkapan (1) untuk n=1 kita ada.
Kami memperoleh dua persamaan berikut untuk C 1 dan C 2

.

Menyelesaikan sistem ini memberikan nilai berikut: C 1 = 0.486 dan C 2 = -0.816.

Oleh itu, penyelesaian umum bagi persamaan ini ialah

2. Penyelesaian menggunakan kaedah transformasi Z.

Mari kita ambil Z - transformasi daripada persamaan perbezaan asal, dengan mengambil kira sifat (teorem) peralihan masa . Kami dapat