Cari kamiran tak tentu: permulaan permulaan, contoh penyelesaian. Kalkulator dalam talian. Kira kamiran tak tentu (antiterbitan)

Mencari kamiran tak tentu (satu set antiderivatif atau "antiderivatif") bermakna memulihkan fungsi daripada terbitan yang diketahui bagi fungsi ini. Set antiderivatif yang dipulihkan F(x) + Dengan untuk fungsi f(x) mengambil kira pemalar pengamiran C. Mengikut kelajuan pergerakan titik material (derivatif), hukum pergerakan titik ini (asal) boleh dipulihkan; mengikut pecutan pergerakan sesuatu titik - kelajuannya dan hukum gerakan. Seperti yang anda lihat, integrasi adalah bidang yang luas untuk aktiviti Sherlock Holmes dari fizik. Ya, dan dalam ekonomi, banyak konsep diwakili melalui fungsi dan derivatifnya, dan oleh itu, sebagai contoh, adalah mungkin untuk memulihkan jumlah output yang dihasilkan pada masa yang sesuai oleh produktiviti buruh pada masa tertentu (derivatif).

Untuk mencari kamiran tak tentu, sejumlah kecil formula pengamiran asas diperlukan. Tetapi proses mencarinya adalah lebih sukar daripada hanya menggunakan formula ini. Semua kerumitan tidak berkaitan dengan penyepaduan, tetapi untuk membawa ungkapan boleh disepadukan kepada bentuk sedemikian yang memungkinkan untuk mencari kamiran tak tentu menggunakan formula asas yang disebutkan di atas. Ini bermakna untuk memulakan amalan penyepaduan, anda perlu mengaktifkan hasil yang diperolehi dalam sekolah Menengah kemahiran transformasi ekspresi.

Kami akan belajar mencari kamiran menggunakan sifat dan jadual kamiran tak tentu daripada pelajaran tentang konsep asas topik ini (dibuka dalam tetingkap baharu).

Terdapat beberapa kaedah untuk mencari kamiran, yang mana kaedah penggantian berubah-ubah dan kaedah integrasi mengikut bahagian- set lelaki wajib untuk semua orang yang telah berjaya lulus matematik yang lebih tinggi. Walau bagaimanapun, adalah lebih berguna dan menyenangkan untuk memulakan pembelajaran integrasi menggunakan kaedah pengembangan berdasarkan dua teorem berikut tentang sifat kamiran tak tentu, yang akan kami ulangi di sini untuk kemudahan.

Teorem 3. Faktor pemalar dalam kamiran dan boleh dikeluarkan daripada tanda kamiran tak tentu, i.e.

Teorem 4. Kamiran tak tentu bagi jumlah algebra nombor terhingga fungsi ialah jumlah algebra kamiran tak tentu bagi fungsi ini, i.e.

(2)

Di samping itu, peraturan berikut mungkin berguna dalam penyepaduan: jika ungkapan kamiran dan mengandungi faktor malar, maka ungkapan antiterbitan didarabkan dengan timbal balik faktor malar, iaitu

(3)

Memandangkan pelajaran ini adalah pengenalan kepada menyelesaikan masalah integrasi, adalah penting untuk mengambil perhatian dua perkara yang sama ada sudah peringkat awal, atau sedikit kemudian mungkin mengejutkan anda. Kejutan adalah disebabkan oleh fakta bahawa kamiran ialah operasi songsang bagi pembezaan dan kamiran tak tentu boleh dipanggil "anti-derivatif".

Perkara pertama yang tidak perlu terkejut apabila mengintegrasikan. Dalam jadual kamiran terdapat formula yang tidak mempunyai analog di antara formula jadual terbitan . Ini adalah formula berikut:

Walau bagaimanapun, seseorang boleh mengesahkan bahawa terbitan ungkapan di sebelah kanan formula ini bertepatan dengan kamiran yang sepadan.

Perkara kedua tidak perlu terkejut apabila menyepadukan. Walaupun terbitan mana-mana fungsi asas juga merupakan fungsi asas, kamiran tak tentu bagi beberapa fungsi asas tidak lagi fungsi asas . Contoh kamiran tersebut ialah:

Kemahiran berikut akan berguna untuk membangunkan teknik kamiran: mengurangkan pecahan, membahagi polinomial dalam pengangka pecahan dengan monomial dalam penyebut (untuk mendapatkan hasil tambah kamiran tak tentu), menukar punca kepada darjah, mendarab monomial dengan polinomial, menaikkan kepada kuasa. Kemahiran ini diperlukan untuk mengubah kamiran, yang sepatutnya menghasilkan jumlah kamiran yang terdapat dalam jadual kamiran.

Mencari kamiran tak tentu bersama-sama

Contoh 1 Cari kamiran tak tentu

Keputusan. Kita lihat dalam penyebut bagi kamiran dan polinomial di mana x adalah kuasa dua. Ini hampir merupakan tanda pasti bahawa kamiran jadual 21 (dengan tangen arka hasil) boleh digunakan. Kami mengeluarkan faktor dua daripada penyebut (terdapat sifat kamiran sedemikian - faktor malar boleh dikeluarkan daripada tanda kamiran, ia telah disebutkan di atas sebagai Teorem 3). Hasil daripada semua ini:

Sekarang penyebutnya ialah jumlah kuasa dua, yang bermaksud bahawa kita boleh menggunakan kamiran jadual yang disebutkan. Akhirnya kita mendapat jawapan:

Contoh 2 Cari kamiran tak tentu

Keputusan. Kami sekali lagi menggunakan Teorem 3 - sifat kamiran, yang berdasarkannya faktor pemalar boleh diambil daripada tanda kamiran:

Kami menggunakan formula 7 daripada jadual kamiran (pembolehubah dalam darjah) kepada kamiran dan:

Kami mengurangkan pecahan yang terhasil dan kami mempunyai jawapan akhir:

Contoh 3 Cari kamiran tak tentu

Keputusan. Menggunakan Teorem 4 dan kemudian Teorem 3 pada sifat, kita dapati kamiran ini sebagai hasil tambah tiga kamiran:

Ketiga-tiga kamiran yang diperoleh adalah jadual. Kami menggunakan formula (7) daripada jadual kamiran untuk n = 1/2, n= 2 dan n= 1/5, dan kemudian

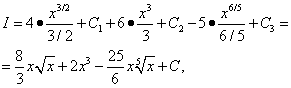
menggabungkan ketiga-tiga pemalar arbitrari yang diperkenalkan apabila mencari tiga kamiran. Oleh itu, dalam situasi yang sama, hanya satu pemalar arbitrari (malar) penyepaduan harus diperkenalkan.

Contoh 4 Cari kamiran tak tentu

Keputusan. Apabila terdapat satu monomial dalam penyebut integrand, kita boleh membahagikan pengangka dengan sebutan penyebut dengan sebutan. Kamiran asal bertukar menjadi hasil tambah dua kamiran:

Untuk menggunakan integral jadual, kami menukar akar kepada kuasa dan inilah jawapan akhir:

Kami terus mencari kamiran tak tentu bersama-sama

Contoh 7 Cari kamiran tak tentu

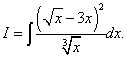
Keputusan. Jika kita menukar kamiran dan dengan mengkuadratkan binomial dan membahagikan pengangka dengan sebutan penyebut dengan sebutan, maka kamiran asal menjadi hasil tambah tiga kamiran.

Fungsi F(x) dipanggil antiterbitan untuk fungsi f(x) pada selang (a; b) jika f(x) untuk semua x (a; b) memenuhi kesamaan F (x) = f(x) . 2

Teorem 1. Jika F(x) ialah antiterbitan untuk f(x) pada (a; b), maka F(x) + C, dengan C ialah nombor, juga merupakan antiterbitan untuk f(x) pada (a; b). Bukti: (F + C) = F + C = f + 0 = f 3

Mari kita buktikan dua teorem tambahan: Jika fungsi g(x) adalah tetap pada (a; b), maka g (x) = 0. Jika g (x) = 0 untuk semua x (a; b), maka g( x) = C pada (a; b). 4

Teorem 2. Jika F(x) ialah antiterbitan bagi f(x) pada selang (a; b), dan G(x) ialah satu lagi antiterbitan bagi f(x) pada (a; b), maka G = F + C, dengan C ialah nombor. lima

Set semua antiterbitan bagi fungsi f(x) pada selang (a; b) dipanggil kamiran tak tentu dan dilambangkan dengan kamiran f(x)dx. dx Pengiraan tidak kamiran pasti daripada fungsi yang diberikan dipanggil integrasi 6

Jika fungsi f(x) adalah selanjar dan fungsi (t) mempunyai terbitan selanjar (t), maka formula berikut berlaku: f((t)) (t) dt = f(x) dx, dengan x = ( t). lapan

Biarkan u(x) dan v(x) menjadi fungsi yang boleh dibezakan pada beberapa selang. Kemudian (uv) = u v + v u Ini membayangkan (uv) dx = (u v + v u)dx = u v dx + v u dx atau uv dx = uv – u v dx. 10

Ini membayangkan formula yang dipanggil formula penyepaduan demi bahagian: penyepaduan demi bahagian u(x)dv(x) = u(x) v(x) – v(x)du(x) 11

Kamiran pasti bagi suatu fungsi sepanjang selang ialah had yang mana jumlah kamiran cenderung dalam proses ini, jika had itu wujud: 13

Nombor a dipanggil had bawah pengamiran, dan nombor b dipanggil had atas pengamiran. Dalam Rajah 2 trapezoid melengkung ditandakan dengan sengkang. Luas S trapezoid ini ditentukan oleh formula 14

Biarkan fungsi f(t) ditakrifkan dan berterusan pada beberapa selang yang mengandungi titik a. Kemudian setiap nombor x daripada selang ini boleh dikaitkan dengan nombor, dengan itu mentakrifkan fungsi I(x) pada selang, yang dipanggil kamiran pasti dengan had atas pembolehubah 17

Terbitan kamiran pasti berkenaan dengan had atas pada titik x adalah sama dengan nilai kamiran dan pada titik x. lapan belas

Biarkan fungsi y = f(x) ditakrifkan dan berterusan pada selang separuh tak terhingga (t) dt

yang, dengan mengambil kira tatatanda yang diperkenalkan, adalah andaian awal. Teorem telah terbukti.

Contoh. Cari kamiran tak tentu
.

Jom buat pengganti t = sinx, dt = cosxdt.

Contoh.

Penggantian
Kita mendapatkan:

Di bawah ini kita akan mempertimbangkan contoh lain menggunakan kaedah penggantian untuk pelbagai jenis fungsi.

Integrasi mengikut bahagian.

Kaedah ini adalah berdasarkan formula yang terkenal untuk terbitan produk:

(uv)=uv+vu

di mana u dan v ialah beberapa fungsi bagi x.

Dalam bentuk pembezaan: d(uv) =udv+vdu

Selepas menyepadukan, kami mendapat:
, dan mengikut sifat kamiran tak tentu di atas:

atau
;

Kami telah memperoleh formula penyepaduan demi bahagian yang membolehkan kami mencari kamiran banyak fungsi asas.

Contoh.

Seperti yang anda lihat, aplikasi konsisten formula penyepaduan demi bahagian membolehkan anda secara beransur-ansur memudahkan fungsi dan membawa kamiran kepada satu jadual.

Contoh.

Dapat dilihat bahawa sebagai hasil daripada aplikasi integrasi yang berulang mengikut bahagian, fungsi itu tidak dapat dipermudahkan kepada bentuk jadual. Walau bagaimanapun, kamiran terakhir yang diperolehi tidak berbeza dengan yang asal. Oleh itu, kami memindahkannya ke sebelah kiri kesamaan.

Oleh itu, kamiran ditemui tanpa menggunakan jadual kamiran sama sekali.

Sebelum mempertimbangkan secara terperinci kaedah mengintegrasikan pelbagai kelas fungsi, kami memberikan beberapa lagi contoh mencari kamiran tak tentu dengan mengurangkannya kepada jadual.

Contoh.

Penyepaduan pecahan asas.

Definisi: peringkat rendah pecahan daripada empat jenis berikut dipanggil:

saya.
III.

II.
IV.

m,n– integer(m2,n2) dan b 2 – 4ac<0.

Dua jenis kamiran pertama bagi pecahan asas dikurangkan dengan mudah kepada penggantian jadual t=ax+b.

Pertimbangkan kaedah untuk menyepadukan pecahan asas bagi bentuk III.

Kamiran pecahan jenis III boleh diwakili sebagai:

Di sini, dalam Pandangan umum pengurangan kamiran pecahan bentuk III kepada dua kamiran jadual ditunjukkan.

Pertimbangkan penggunaan formula di atas dengan contoh.

Contoh.

Secara umumnya, jika kapak trinomial 2 +bx+cexpressionb 2 – 4ac>0, maka pecahan itu bukan asas mengikut takrifan, walau bagaimanapun, ia boleh disepadukan dengan cara di atas.

Contoh.

Sekarang mari kita pertimbangkan kaedah untuk menyepadukan pecahan termudah jenis IV.

Pertama, pertimbangkan kes khas dengan M = 0, N = 1.

Kemudian kamiran bentuk
boleh diwakili dengan menyerlahkan petak penuh dalam penyebut sebagai
. Mari lakukan transformasi berikut:

Kamiran kedua yang termasuk dalam kesamarataan ini akan diambil mengikut bahagian.

Nyatakan:

Untuk integral asal kita dapat:

Formula yang terhasil dipanggil berulang. Jika anda menggunakannya n-1 kali, anda mendapat kamiran jadual
.

Sekarang mari kita kembali kepada kamiran pecahan asas bagi bentuk IV dalam kes am.

Dalam kesamaan yang terhasil, kamiran pertama menggunakan penggantian t = u 2 + s dikurangkan kepada jadual , dan formula berulang yang dipertimbangkan di atas digunakan pada kamiran kedua.

Walaupun kerumitan yang ketara untuk mengintegrasikan pecahan asas jenis IV, dalam praktiknya agak mudah untuk menerapkannya pada pecahan dengan darjah kecil n, dan kesejagatan dan keluasan pendekatan memungkinkan untuk melaksanakan kaedah ini dengan sangat mudah pada komputer.

Contoh:

Integrasi fungsi rasional.

Pengamiran pecahan rasional.

Untuk mengintegrasikan pecahan rasional, adalah perlu untuk menguraikannya kepada pecahan asas.

Teorem: Jika
ialah pecahan rasional wajar yang penyebutnya P(x) diwakili sebagai hasil darab faktor linear dan kuadratik (perhatikan bahawa sebarang polinomial dengan pekali nyata boleh diwakili dalam bentuk ini: P(x) = (x - a)  …(x - b)  (x 2 + px + q)  …(x 2 + rx + s)  ), maka pecahan ini boleh diuraikan menjadi pecahan asas mengikut skema berikut:

di mana A i ,B i ,M i ,N i ,R i ,S i ialah beberapa nilai malar.

Apabila menyepadukan pecahan rasional, seseorang terpaksa menguraikan pecahan asal kepada pecahan asas. Untuk mencari nilai A i ,B i ,M i ,N i ,R i ,S i gunakan apa yang dipanggil kaedah pekali tak tentu, yang intipatinya ialah agar dua polinomial menjadi sama, adalah perlu dan mencukupi bahawa pekali pada kuasa yang sama bagi x adalah sama.

Kami akan mempertimbangkan penggunaan kaedah ini pada contoh tertentu.

Contoh.

Mengurangkan kepada penyebut biasa dan menyamakan pengangka yang sepadan, kita mendapat:

Contoh.

Kerana Jika pecahan itu tidak betul, maka anda harus terlebih dahulu memilih bahagian integer daripadanya:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x– 7 3x 3 – 4x 2 – 17x+ 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x3 + 8x2 - 76x - 7

9x 3 - 12x 2 - 51x +18

20x2-25x-25

Kami menguraikan penyebut pecahan yang terhasil kepada faktor. Ia boleh dilihat bahawa pada x = 3 penyebut pecahan menjadi sifar. Kemudian:

3x 3 – 4x 2 – 17x+ 6x- 3

3x 3 – 9x 2 3x 2 + 5x- 2

Oleh itu 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1). Kemudian:

Untuk mengelakkan apabila mencari pekali yang tidak pasti bagi kurungan pembukaan, mengumpulkan dan menyelesaikan sistem persamaan (yang dalam beberapa kes mungkin menjadi agak besar), apa yang dipanggil kaedah nilai sewenang-wenangnya. Intipati kaedah ini ialah beberapa (mengikut bilangan pekali yang tidak pasti) nilai x sewenang-wenangnya digantikan ke dalam ungkapan yang diperoleh di atas. Untuk memudahkan pengiraan, adalah kebiasaan untuk mengambil sebagai nilai sewenang-wenangnya titik di mana penyebut pecahan adalah sama dengan sifar, i.e. dalam kes kami - 3, -2, 1/3. Kita mendapatkan:

Akhirnya kita dapat:

Contoh.

Mari cari pekali tak tentu:

Kemudian nilai kamiran yang diberikan:

Penyepaduan beberapa trigonometri

fungsi.

Kamiran daripada fungsi trigonometri mungkin ada bilangan yang tidak terhingga. Kebanyakan kamiran ini tidak boleh dikira secara analitik sama sekali, jadi pertimbangkan beberapa jenis utama fungsi yang sentiasa boleh disepadukan.

Kamiran bentuk
.

Di sini R ialah penetapan beberapa fungsi rasional pembolehubah sinx dan cosx.

Kamiran jenis ini dikira menggunakan penggantian
. Penggantian ini membolehkan anda menukar fungsi trigonometri kepada fungsi rasional.

Kemudian

Oleh itu:

Transformasi yang diterangkan di atas dipanggil penggantian trigonometri sejagat.

Contoh.

Kelebihan penggantian ini yang tidak diragukan ialah ia sentiasa boleh digunakan untuk mengubah fungsi trigonometri kepada fungsi rasional dan mengira kamiran yang sepadan. Kelemahannya termasuk hakikat bahawa transformasi boleh menghasilkan fungsi rasional yang agak kompleks, yang penyepaduan akan mengambil banyak masa dan usaha.

Walau bagaimanapun, jika mustahil untuk menggunakan perubahan pembolehubah yang lebih rasional, kaedah ini adalah satu-satunya kaedah yang berkesan.

Contoh.

Kamiran bentuk
jika

fungsiRcosx.

Walaupun terdapat kemungkinan untuk mengira kamiran sedemikian menggunakan penggantian trigonometri universal, adalah lebih rasional untuk menggunakan penggantian itu. t = sinx.

Fungsi
boleh mengandungi cosx hanya kepada kuasa genap, dan oleh itu boleh ditukar kepada fungsi rasional berkenaan dengan sinx.

Contoh.

Secara umumnya, untuk menggunakan kaedah ini, hanya keganjilan fungsi berkenaan dengan kosinus diperlukan, dan darjah sinus yang termasuk dalam fungsi itu boleh menjadi sebarang, kedua-dua integer dan pecahan.

Kamiran bentuk
jika

fungsiRadalah ganjil berkenaan dengansinx.

Dengan analogi dengan kes yang dipertimbangkan di atas, penggantian t = cosx.

Contoh.

Kamiran bentuk

fungsiRmalah secara relatifnyasinxdancosx.

Untuk mengubah fungsi R menjadi satu rasional, penggantian digunakan

t = tgx.

Contoh.

Kamiran hasil darab sinus dan kosinus

pelbagai hujah.

Bergantung pada jenis kerja, satu daripada tiga formula akan digunakan:

Contoh.

Kadangkala, apabila menyepadukan fungsi trigonometri, adalah mudah untuk menggunakan formula trigonometri yang terkenal untuk mengurangkan susunan fungsi.

Contoh.

Kadangkala beberapa helah bukan standard digunakan.

Contoh.

Penyepaduan beberapa fungsi tidak rasional.

Jauh dari setiap fungsi tidak rasional mungkin mempunyai kamiran yang dinyatakan oleh fungsi asas. Untuk mencari kamiran fungsi tak rasional, seseorang harus menggunakan penggantian yang membolehkan seseorang mengubah fungsi itu menjadi satu rasional, kamirannya sentiasa boleh didapati, seperti yang diketahui, sentiasa.

Pertimbangkan beberapa teknik untuk menyepadukan pelbagai jenis fungsi tidak rasional.

Kamiran bentuk
di manan- nombor asli.

Dengan bantuan penggantian
fungsi itu dirasionalkan.

Contoh.

Jika fungsi tidak rasional termasuk punca darjah yang berbeza, maka adalah rasional untuk mengambil sebagai pembolehubah baharu punca darjah yang sama dengan gandaan sepunya terkecil bagi kuasa punca yang termasuk dalam ungkapan.

Mari kita gambarkan ini dengan contoh.

Contoh.

Integrasi pembezaan binomial.

Definisi: Pembezaan binomial disebut ungkapan

x m (a + bx n ) hlm dx

di mana m, n, dan hlm ialah nombor rasional.

Seperti yang dibuktikan oleh Ahli Akademik Chebyshev P.L. (1821-1894), kamiran pembezaan binomial hanya boleh dinyatakan dari segi fungsi asas dalam tiga kes berikut:

Jika R ialah integer, maka kamiran dirasionalkan menggunakan penggantian

, dengan  ialah penyebut sepunya m dan n.

Sebelum ini, untuk fungsi tertentu, berpandukan pelbagai formula dan peraturan, kami mendapati derivatifnya. Derivatif mempunyai banyak aplikasi: ia ialah kelajuan pergerakan (atau, lebih umum, kelajuan sebarang proses); cerun tangen kepada graf fungsi; menggunakan derivatif, anda boleh menyiasat fungsi untuk monotonicity dan extrema; Ia membantu menyelesaikan masalah pengoptimuman.

Tetapi seiring dengan masalah mencari kelajuan mengikut undang-undang gerakan yang diketahui, ada juga masalah songsang- masalah memulihkan hukum gerakan dari kelajuan yang diketahui. Mari kita pertimbangkan salah satu masalah ini.

Contoh 1 Bergerak dalam garis lurus titik material, kelajuan pergerakannya pada masa t diberikan oleh formula v=gt. Cari hukum gerakan.
Keputusan. Biarkan s = s(t) ialah hukum gerakan yang dikehendaki. Adalah diketahui bahawa s"(t) = v(t). Jadi, untuk menyelesaikan masalah, anda perlu memilih fungsi s = s(t), yang terbitannya sama dengan gt. Mudah untuk meneka bahawa $ s(t) = \frac(gt^ 2)(2) $ Sesungguhnya
$s"(t) = \kiri(\frac(gt^2)(2) \kanan)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t=gt$
Jawapan: $s(t) = \frac(gt^2)(2) $

Kami ambil perhatian segera bahawa contoh diselesaikan dengan betul, tetapi tidak lengkap. Kami mendapat $s(t) = \frac(gt^2)(2) $. Sebenarnya, masalah itu mempunyai banyak penyelesaian yang tidak terhingga: sebarang fungsi dalam bentuk $s(t) = \frac(gt^2)(2) + C $, di mana C ialah pemalar arbitrari, boleh berfungsi sebagai hukum bagi gerakan, sejak $\kiri (\frac(gt^2)(2) +C \kanan)" = gt $

Untuk menjadikan masalah lebih spesifik, kami perlu membetulkan keadaan awal: nyatakan koordinat titik bergerak pada satu-satu masa, sebagai contoh, pada t = 0. Jika, katakan, s(0) = s 0 , maka dari kesamaan s(t) = (gt 2)/2 + C kita dapat: s(0) = 0 + C, iaitu C = s 0 . Kini hukum gerakan ditakrifkan secara unik: s(t) = (gt 2)/2 + s 0 .

Dalam matematik, operasi timbal balik diberikan nama yang berbeza, tampilkan dengan tatatanda khas, contohnya: kuasa dua (x 2) dan mengekstrak punca kuasa dua($\sqrt(x) $), sinus (sin x) dan arcsin (arcsin x), dsb. Proses mencari terbitan berkenaan dengan fungsi tertentu dipanggil pembezaan, dan operasi songsang, iaitu proses mencari fungsi oleh terbitan tertentu, - integrasi.

Istilah "derivatif" itu sendiri boleh dibenarkan "dengan cara duniawi": fungsi y \u003d f (x) "menghasilkan ke dunia" ciri baharu y" = f"(x). Fungsi y \u003d f (x) bertindak seolah-olah sebagai "ibu bapa", tetapi ahli matematik, tentu saja, tidak memanggilnya "ibu bapa" atau "pengeluar", mereka mengatakan bahawa ini adalah, berkaitan dengan fungsi y " = f" (x) , imej utama atau antiterbitan.

Definisi. Fungsi y = F(x) dipanggil antiterbitan untuk fungsi y = f(x) pada selang X jika $x \dalam X $ memenuhi kesamaan F"(x) = f(x)

Dalam amalan, selang X biasanya tidak dinyatakan, tetapi tersirat (sebagai domain semula jadi fungsi).

Mari beri contoh.
1) Fungsi y \u003d x 2 ialah antiderivatif untuk fungsi y \u003d 2x, kerana untuk mana-mana x kesamaan (x 2) "\u003d 2x adalah benar
2) Fungsi y \u003d x 3 ialah antiderivatif untuk fungsi y \u003d 3x 2, kerana untuk mana-mana x kesamaan (x 3)" \u003d 3x 2 adalah benar
3) Fungsi y \u003d sin (x) ialah antiterbitan untuk fungsi y \u003d cos (x), kerana untuk mana-mana x kesamaan (sin (x)) "= cos (x) adalah benar

Apabila mencari antiderivatif, serta derivatif, bukan sahaja formula digunakan, tetapi juga beberapa peraturan. Ia berkaitan secara langsung dengan peraturan yang sepadan untuk pengiraan derivatif.

Kita tahu bahawa derivatif jumlah adalah sama dengan jumlah derivatif. Peraturan ini menjana peraturan yang sepadan untuk mencari antiderivatif.

Peraturan 1 Antiterbitan jumlah adalah sama dengan jumlah antiterbitan.

Kita tahu bahawa faktor malar boleh dikeluarkan daripada tanda terbitan. Peraturan ini menjana peraturan yang sepadan untuk mencari antiderivatif.

Peraturan 2 Jika F(x) ialah antiterbitan bagi f(x), maka kF(x) ialah antiterbitan untuk kf(x).

Teorem 1. Jika y = F(x) ialah antiterbitan bagi fungsi y = f(x), maka antiterbitan bagi fungsi y = f(kx + m) ialah fungsi $y=\frac(1)(k)F (kx+m) $

Teorem 2. Jika y = F(x) ialah antiterbitan untuk fungsi y = f(x) pada selang X, maka fungsi y = f(x) mempunyai banyak antiterbitan tak terhingga, dan kesemuanya mempunyai bentuk y = F(x) + C.

Kaedah integrasi

Kaedah penggantian boleh ubah (kaedah penggantian)

Kaedah penyepaduan penggantian terdiri daripada memperkenalkan pembolehubah penyepaduan baharu (iaitu penggantian). Dalam kes ini, kamiran yang diberikan dikurangkan kepada kamiran baharu, yang berbentuk jadual atau boleh dikurangkan kepadanya. Kaedah Umum pemilihan penggantian tidak wujud. Keupayaan untuk menentukan penggantian dengan betul diperoleh melalui latihan.
Biarkan ia diperlukan untuk mengira kamiran $\textstyle \int F(x)dx $. Mari kita buat penggantian $x= \varphi(t) $ dengan $\varphi(t) $ ialah fungsi yang mempunyai terbitan berterusan.
Kemudian $dx = \varphi " (t) \cdot dt $ dan berdasarkan sifat invarian formula kamiran kamiran tak tentu, kami memperoleh formula penyepaduan penggantian:
$\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt $

Penyepaduan ungkapan seperti $\textstyle \int \sin^n x \cos^m x dx $

Jika m ganjil, m > 0, maka lebih mudah untuk membuat penggantian sin x = t.
Jika n ganjil, n > 0, maka lebih mudah untuk membuat penggantian cos x = t.
Jika n dan m genap, maka lebih mudah untuk membuat penggantian tg x = t.

Integrasi mengikut bahagian

Penyepaduan mengikut bahagian - menggunakan formula berikut untuk penyepaduan:
$\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du $
atau:
$\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx $

Jadual kamiran tak tentu (antiterbitan) bagi beberapa fungsi

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch )x+C $$

Adakah mungkin untuk membawa fungsi bukan linear di bawah tanda pembezaan? Ya, jika integrand ialah hasil darab dua faktor: satu faktor ialah fungsi kompleks bagi sesetengahnya fungsi bukan linear, dan faktor lain ialah terbitan bagi fungsi tak linear ini. Mari lihat contoh.

Cari kamiran tak tentu.

Contoh 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+C.

Apakah integrand ini? Kerja fungsi kuasa daripada (x 2 + x + 2) dan faktor (2x + 1), yang sama dengan terbitan asas darjah: (x 2 + x + 2) "= 2x + 1.

Ini membolehkan kami membawa (2x + 1) di bawah tanda pembezaan:

∫u 5 du=u 6 : 6+ C. (Formula 1). )

Peperiksaan. (F (x) + C)" = ((x² + x + 2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

\u003d (x 2 + x + 2) 5 (2x + 1) \u003d (2x + 1) (x 2 + x + 2) 5 \u003d f (x).

Contoh 2∫(3x 2 - 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 - x 2 + 3x + 1) 5 d (x 3 - x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+C

Bagaimanakah contoh ini berbeza daripada contoh 1? tiada apa-apa! Kuasa kelima yang sama dengan tapak (x 3 - x 2 + 3x + 1) didarab dengan trinomial (3x 2 - 2x + 3), iaitu terbitan asas darjah: (x 3 - x 2 + 3x + 1) "= 3x 2 - 2x + 3. Kami membawa asas darjah ini di bawah tanda pembezaan, dari mana nilai integrand tidak berubah, dan kemudian menggunakan formula yang sama 1).( Kamiran)

Contoh 3

Di sini terbitan (2x 3 - 3x) akan memberikan (6x 2 - 3), dan kita mempunyai

terdapat (12x 2 - 6), iaitu ungkapan dalam 2 kali lebih besar, maka mari kita jumlahkan (2x 3 - 3x) di bawah tanda pembezaan, dan letakkan faktor sebelum kamiran 2 . Jom amalkan formula 2) ( lembaran ).

Inilah yang berlaku:

Mari kita semak, memandangkan:

Contoh. Cari kamiran tak tentu.

1. ∫(6x+5) 3 dx. Bagaimana kita akan membuat keputusan? Tengok helaian dan kami berhujah seperti ini: integrand ialah ijazah, dan kami mempunyai formula untuk integral darjah (rumus 1) ), tetapi di dalamnya asas darjah u dan pembolehubah integrasi juga u.

Dan kami mempunyai pembolehubah integrasi X, dan asas darjah (6x+5). Mari kita buat perubahan pembolehubah penyepaduan: bukannya dx kita tulis d (6x+5). Apa yang berubah? Oleh kerana, apa yang datang selepas tanda pembezaan d, secara lalai, dibezakan,

maka d (6x+5)=6dx, i.e. apabila pembolehubah x digantikan dengan pembolehubah (6x + 5), kamiran dan telah meningkat sebanyak 6 kali ganda, jadi kami meletakkan faktor 1/6 di hadapan tanda kamiran. Anda boleh menulis hujah ini seperti ini:

Jadi, kami menyelesaikan contoh ini dengan memperkenalkan pembolehubah baharu (pembolehubah x digantikan dengan pembolehubah 6x+5). Dan di manakah anda menulis pembolehubah baharu (6x + 5)? Di bawah tanda pembezaan. sebab itu, kaedah ini memperkenalkan pembolehubah baru sering dipanggil kaedah ( atau cara ) menjumlahkan(pembolehubah baharu ) di bawah tanda pembezaan.

Dalam contoh kedua, kami mula-mula memperoleh ijazah dengan penunjuk negatif, dan kemudian dibawa ke bawah tanda pembezaan (7x-2) dan menggunakan formula kamiran darjah 1) (Sepadu ).

Mari kita ambil contoh penyelesaian 3.

Kamiran didahului oleh pekali 1/5. kenapa? Oleh kerana d (5x-2)=5dx, maka, dengan memasukkan fungsi u=5x-2 di bawah tanda pembezaan, kami meningkatkan integrand sebanyak 5 kali, oleh itu, agar nilai ungkapan ini tidak berubah, adalah perlu untuk membahagi dengan 5, iaitu. darab dengan 1/5. Seterusnya, formula digunakan 2) (kamiran) .

Semua formula integral yang paling mudah akan kelihatan seperti:

∫f (x) dx=F (x)+C, dan persamaan berikut mesti dipegang:

(F(x)+C)"=f(x).

Rumus penyepaduan boleh diperolehi dengan menyongsangkan formula pembezaan yang sepadan.

sungguh,

Eksponen n mungkin pecahan. Selalunya anda perlu mencari kamiran tak tentu bagi fungsi y=√x. Hitung kamiran bagi fungsi f (x)=√x menggunakan formula 1) .

Mari kita tulis contoh ini sebagai formula 2) .

Oleh kerana (x+C)"=1, maka ∫dx=x+C.

3) ∫dx=x+C.

Menggantikan 1 / x² dengan x -2, kami mengira kamiran 1 / x².

Dan anda boleh mendapatkan jawapan ini dengan merayu formula yang diketahui pembezaan:

Kami menulis penaakulan kami dalam bentuk formula 4).

Mendarab kedua-dua belah kesamaan yang terhasil dengan 2, kita memperoleh formula 5).

Mari kita cari kamiran bagi fungsi trigonometri utama, mengetahui terbitannya: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Kami mendapat formula penyepaduan 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

Selepas meneliti demonstrasi dan fungsi logaritma Mari tambah beberapa lagi formula.

Sifat asas kamiran tak tentu.

saya. Terbitan kamiran tak tentu adalah sama dengan kamiran .

(∫f(x)dx)"=f(x).

II. Pembezaan kamiran tak tentu adalah sama dengan kamiran.

d∫f (x) dx=f (x) dx.

III. Kamiran tak tentu bagi pembezaan (terbitan) bagi sesetengah fungsi adalah sama dengan jumlah fungsi ini dan pemalar arbitrari C.

∫dF(x)=F(x)+C atau ∫F"(x) dx=F(x)+C.

Beri perhatian: dalam sifat I, II dan III, tanda-tanda pembezaan dan integral (integral dan pembezaan) "makan" satu sama lain!

IV. Faktor pemalar bagi kamiran dan boleh dikeluarkan daripada tanda kamiran.

∫kf (x) dx=k ∫f (x) dx, di mana k - tetap, tidak sama dengan sifar.

v. Kamiran bagi hasil tambah algebra bagi fungsi adalah sama dengan hasil tambah algebra bagi kamiran fungsi ini.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Jika F(x) ialah antiterbitan bagi f(x) dan k dan b ialah nilai tetap, dan, k≠0, maka (1/k) F (kx+b) ialah antiterbitan untuk f (kx+b). Sesungguhnya, mengikut peraturan untuk mengira derivatif fungsi kompleks kami ada:

Anda boleh menulis:

Untuk setiap tindakan matematik terdapat tindakan songsang. Untuk tindakan pembezaan (mencari derivatif fungsi), terdapat juga tindakan songsang - integrasi. Dengan cara penyepaduan, fungsi ditemui (dipulihkan) oleh terbitan atau pembezaan yang diberikan. Fungsi yang ditemui dipanggil primitif.

Definisi. Fungsi yang boleh dibezakan F(x) dipanggil antiderivatif untuk fungsi tersebut f(x) pada selang waktu tertentu, jika untuk semua X dari selang ini kesamaan adalah benar: F′(x)=f(x).

Contoh. Cari antiderivatif untuk fungsi: 1) f (x)=2x; 2) f(x)=3cos3x.

1) Oleh kerana (x²)′=2x, maka, mengikut takrifan, fungsi F (x)=x² akan menjadi antiterbitan untuk fungsi f (x)=2x.

2) (sin3x)′=3cos3x. Jika kita menyatakan f (x)=3cos3x dan F (x)=sin3x, maka, dengan takrif antiterbitan, kita mempunyai: F′(x)=f (x), dan, oleh itu, F (x)=sin3x ialah antiterbitan untuk f ( x)=3cos3x.

Perhatikan bahawa dan (sin3x +5 )′= 3cos3x, dan (sin3x -8,2 )′= 3cos3x, ... dalam bentuk umum, kita boleh menulis: (sin3x +C)′= 3cos3x, di mana Dengan adalah beberapa nilai tetap. Contoh-contoh ini bercakap tentang kekaburan tindakan penyepaduan, berbeza dengan tindakan pembezaan, apabila mana-mana fungsi boleh dibezakan mempunyai terbitan tunggal.

Definisi. Jika fungsi F(x) ialah antiterbitan untuk fungsi tersebut f(x) pada beberapa selang, maka set semua antiderivatif fungsi ini mempunyai bentuk:

F(x)+C di mana C ialah sebarang nombor nyata.

Set semua antiterbitan F (x) + C bagi fungsi f (x) pada selang yang dipertimbangkan dipanggil kamiran tak tentu dan dilambangkan dengan simbol ∫ (tanda kamiran). Menulis: ∫f (x) dx=F (x)+C.

Ungkapan ∫f(x)dx baca: "kamiran ef daripada x kepada de x".

f(x)dx ialah integrand,

f(x) ialah integrand,

X ialah pembolehubah integrasi.

F(x) ialah antiterbitan untuk fungsi tersebut f(x),

Dengan adalah beberapa nilai tetap.

Sekarang contoh yang dipertimbangkan boleh ditulis seperti berikut:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Apakah maksud tanda d?

d- tanda pembezaan - mempunyai dua tujuan: pertama, tanda ini memisahkan integrand daripada pembolehubah integrasi; kedua, segala-galanya selepas tanda ini dibezakan secara lalai dan didarab dengan integrand.

Contoh. Cari kamiran: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Selepas ikon pembezaan d kos XX, a R

∫ 2хрdx=px²+С. Bandingkan dengan contoh 1).

Jom buat pemeriksaan. F′(x)=(px²+C)′=p (x²)′+C′=p 2x=2px=f (x).

4) Selepas ikon pembezaan d kos R. Jadi pembolehubah integrasi R, dan pengganda X harus dianggap sebagai nilai tetap.

∫ 2хрdр=р²х+С. Bandingkan dengan contoh 1) dan 3).

Jom buat pemeriksaan. F′(p)=(p²x+C)′=x (p²)′+C′=x 2p=2px=f (p).

Muka surat 1 daripada 1 1