Persamaan pembezaan homogen umum tertib pertama. Persamaan homogen umum Persamaan homogen umum tertib kedua
Persamaan pembezaan dalam fungsi umum
Biar ada persamaan. Jika ialah fungsi biasa, maka penyelesaiannya ialah antiterbitan, iaitu. Biarkan sekarang menjadi fungsi umum.
Definisi. Fungsi umum dipanggil fungsi umum primitif jika. Jika ialah fungsi umum tunggal, maka terdapat kemungkinan kes apabila antiterbitannya ialah fungsi umum biasa. Sebagai contoh, antiderivatif ialah; antiterbitan ialah fungsi, dan penyelesaian kepada persamaan boleh ditulis dalam bentuk: , di mana.
Terdapat persamaan linear bagi tertib ke dengan pekali malar
di mana adalah fungsi umum. Biarkan polinomial pembezaan tertib ke-.
Definisi. Penyelesaian umum bagi persamaan pembezaan (8) ialah fungsi umum yang mana perhubungan berikut dipegang:
Jika ialah fungsi selanjar, maka satu-satunya penyelesaian kepada persamaan (8) ialah penyelesaian klasik.
Definisi. Penyelesaian asas kepada persamaan (8) ialah sebarang fungsi umum sedemikian.
Fungsi Green ialah penyelesaian asas yang memenuhi syarat sempadan, permulaan atau asimptotik.
Teorem. Penyelesaian kepada persamaan (8) wujud dan mempunyai bentuk:
melainkan konvolusi ditakrifkan.
Bukti. Sungguh, . Mengikut sifat lilitan ia berikut: .
Adalah mudah untuk melihat bahawa penyelesaian asas kepada persamaan ini adalah, kerana
Sifat terbitan umum
Operasi pembezaan adalah linear dan berterusan dari kepada:
dalam, jika dalam;

Setiap fungsi umum boleh dibezakan secara tak terhingga. Sesungguhnya, jika, maka; mengikut giliran, dsb.;
Hasil pembezaan tidak bergantung pada susunan pembezaan. Contohnya, ;
Jika dan, maka formula Leibniz untuk pembezaan produk adalah sah. Contohnya, ;
Jika ia adalah fungsi umum, maka;
Jika siri yang terdiri daripada fungsi boleh integrasi setempat menumpu secara seragam pada setiap set padat, maka ia boleh dibezakan sebutan demi sebutan beberapa kali (sebagai fungsi umum), dan siri yang terhasil akan menumpu masuk.
Contoh. biarlah
Fungsi itu dipanggil fungsi Heaviside atau fungsi unit. Ia boleh diintegrasikan secara tempatan dan oleh itu boleh dianggap sebagai fungsi umum. Anda boleh mencari derivatifnya. Mengikut definisi, i.e. .
Fungsi umum sepadan dengan bentuk kuadratik dengan pekali kompleks
Setakat ini, hanya bentuk kuadratik dengan pekali nyata telah dipertimbangkan. Dalam bahagian ini kita mengkaji ruang semua bentuk kuadratik dengan pekali kompleks.
Tugasnya adalah untuk menentukan fungsi umum, di mana adalah nombor kompleks. Walau bagaimanapun, dalam kes umum tidak akan ada fungsi analisis yang unik. Oleh itu, dalam ruang semua bentuk kuadratik, "satah separuh atas" bentuk kuadratik dengan bahagian khayalan pasti positif diasingkan dan satu fungsi ditentukan untuknya. Iaitu, jika bentuk kuadratik tergolong dalam "satah separuh" ini, maka diandaikan di mana. Fungsi sedemikian ialah fungsi analitik yang unik bagi.
Kini kita boleh mengaitkan fungsi dengan fungsi umum:
di mana integrasi dijalankan ke atas seluruh ruang. Kamiran (13) menumpu pada dan merupakan fungsi analisis dalam separuh satah ini. Meneruskan fungsi ini secara analitikal, fungsi untuk nilai lain ditentukan.
Untuk bentuk kuadratik dengan bahagian khayalan pasti positif, titik tunggal bagi fungsi ditemui dan baki fungsi ini pada titik tunggal dikira.
Fungsi umum secara analitik bergantung bukan sahaja pada, tetapi juga pada pekali bentuk kuadratik. Oleh itu, ia adalah fungsi analisis dalam "satah separuh" atas semua bentuk kuadratik bentuk di mana terdapat bentuk pasti positif. Akibatnya, ia ditentukan secara unik oleh nilainya pada "semi-paksi khayalan," iaitu, pada set bentuk kuadratik bentuk, di mana adalah bentuk pasti positif.
.
Persamaan pembezaan.
§ 1. Konsep asas tentang persamaan pembezaan biasa.
Definisi 1. Persamaan pembezaan biasa n– perintah ke- untuk fungsi itu y hujah x dipanggil hubungan bentuk
di mana F– fungsi tertentu bagi hujahnya. Atas nama kelas persamaan matematik ini, istilah "pembezaan" menekankan bahawa ia termasuk derivatif  (fungsi yang terbentuk hasil daripada pembezaan); istilah "biasa" menunjukkan bahawa fungsi yang dikehendaki bergantung pada hanya satu hujah sebenar.
(fungsi yang terbentuk hasil daripada pembezaan); istilah "biasa" menunjukkan bahawa fungsi yang dikehendaki bergantung pada hanya satu hujah sebenar.
Persamaan pembezaan biasa mungkin tidak mengandungi hujah yang jelas x,
fungsi yang diperlukan  dan mana-mana derivatifnya, tetapi terbitan tertinggi
dan mana-mana derivatifnya, tetapi terbitan tertinggi  mesti dimasukkan ke dalam persamaan n-
pesanan ke. Contohnya
mesti dimasukkan ke dalam persamaan n-
pesanan ke. Contohnya
A)  – persamaan tertib pertama;
– persamaan tertib pertama;
b)  – persamaan tertib ketiga.
– persamaan tertib ketiga.
Apabila menulis persamaan pembezaan biasa, notasi untuk terbitan dari segi pembezaan sering digunakan:
V)  – persamaan tertib kedua;
– persamaan tertib kedua;
G)  – persamaan tertib pertama,
– persamaan tertib pertama,
penjana selepas pembahagian oleh dx bentuk setara untuk menyatakan persamaan:  .
.
Fungsi  dipanggil penyelesaian kepada persamaan pembezaan biasa jika, apabila digantikan dengannya, ia bertukar menjadi identiti.
dipanggil penyelesaian kepada persamaan pembezaan biasa jika, apabila digantikan dengannya, ia bertukar menjadi identiti.
Sebagai contoh, persamaan tertib ke-3
Mempunyai penyelesaian  .
.
Mencari dengan satu kaedah atau yang lain, sebagai contoh, pemilihan, satu fungsi yang memenuhi persamaan tidak bermakna menyelesaikannya. Untuk menyelesaikan persamaan pembezaan biasa bermakna mencari Semua fungsi yang membentuk identiti apabila digantikan ke dalam persamaan. Untuk persamaan (1.1), satu keluarga fungsi sedemikian dibentuk menggunakan pemalar arbitrari dan dipanggil penyelesaian umum bagi persamaan pembezaan biasa. n tertib ke-, dan bilangan pemalar bertepatan dengan susunan persamaan: Penyelesaian umum mungkin, tetapi tidak diselesaikan secara eksplisit berkenaan dengan y(x) : Dalam kes ini, penyelesaian biasanya dipanggil kamiran am bagi persamaan (1.1).
Sebagai contoh, penyelesaian umum persamaan pembezaan  ialah ungkapan berikut: , dan sebutan kedua juga boleh ditulis sebagai
ialah ungkapan berikut: , dan sebutan kedua juga boleh ditulis sebagai  , sejak pemalar arbitrari
, sejak pemalar arbitrari  , dibahagikan dengan 2, boleh digantikan dengan pemalar arbitrari baharu
, dibahagikan dengan 2, boleh digantikan dengan pemalar arbitrari baharu  .
.
Dengan memberikan beberapa nilai yang boleh diterima kepada semua pemalar arbitrari dalam penyelesaian am atau dalam kamiran am, kita memperoleh fungsi tertentu yang tidak lagi mengandungi pemalar arbitrari. Fungsi ini dipanggil penyelesaian separa atau kamiran separa persamaan (1.1). Untuk mencari nilai pemalar arbitrari, dan oleh itu penyelesaian tertentu, pelbagai syarat tambahan kepada persamaan (1.1) digunakan. Sebagai contoh, apa yang dipanggil syarat awal boleh dinyatakan pada (1.2)
Di sebelah kanan keadaan awal (1.2) nilai berangka fungsi dan derivatif ditentukan, dan jumlah bilangan keadaan awal adalah sama dengan bilangan pemalar arbitrari yang ditentukan.
Masalah mencari penyelesaian tertentu kepada persamaan (1.1) berdasarkan keadaan awal dipanggil masalah Cauchy.
§ 2. Persamaan pembezaan biasa tertib pertama - konsep asas.
Persamaan pembezaan biasa bagi urutan pertama ( n=1) mempunyai bentuk:  atau, jika ia boleh diselesaikan berkenaan dengan terbitan:
atau, jika ia boleh diselesaikan berkenaan dengan terbitan:  . Penyelesaian umum y=
y(x, DENGAN) atau kamiran am
. Penyelesaian umum y=
y(x, DENGAN) atau kamiran am  Persamaan tertib pertama mengandungi satu pemalar arbitrari. Satu-satunya syarat awal untuk persamaan tertib pertama
Persamaan tertib pertama mengandungi satu pemalar arbitrari. Satu-satunya syarat awal untuk persamaan tertib pertama  membolehkan anda menentukan nilai pemalar daripada penyelesaian am atau daripada kamiran am. Oleh itu, penyelesaian tertentu akan ditemui atau, yang sama, masalah Cauchy akan diselesaikan. Persoalan kewujudan dan keunikan penyelesaian kepada masalah Cauchy adalah salah satu persoalan utama dalam teori umum persamaan pembezaan biasa. Untuk persamaan tertib pertama, khususnya, teorem adalah sah, yang diterima di sini tanpa bukti.
membolehkan anda menentukan nilai pemalar daripada penyelesaian am atau daripada kamiran am. Oleh itu, penyelesaian tertentu akan ditemui atau, yang sama, masalah Cauchy akan diselesaikan. Persoalan kewujudan dan keunikan penyelesaian kepada masalah Cauchy adalah salah satu persoalan utama dalam teori umum persamaan pembezaan biasa. Untuk persamaan tertib pertama, khususnya, teorem adalah sah, yang diterima di sini tanpa bukti.
Teorem 2.1. Jika dalam persamaan fungsi  dan terbitan separanya
dan terbitan separanya  berterusan di beberapa wilayah D kapal terbang XOY, dan dalam kawasan ini satu titik ditentukan
berterusan di beberapa wilayah D kapal terbang XOY, dan dalam kawasan ini satu titik ditentukan  , maka terdapat penyelesaian unik yang memenuhi kedua-dua persamaan dan keadaan awal
, maka terdapat penyelesaian unik yang memenuhi kedua-dua persamaan dan keadaan awal  .
.
Secara geometri, penyelesaian umum bagi persamaan tertib pertama ialah keluarga lengkung pada satah XOY, tidak mempunyai titik sepunya dan berbeza antara satu sama lain dalam satu parameter - nilai pemalar C. Lengkung ini dipanggil lengkung kamiran untuk persamaan tertentu. Lengkung persamaan kamiran mempunyai sifat geometri yang jelas: pada setiap titik, tangen tangen kepada lengkung adalah sama dengan nilai sebelah kanan persamaan pada titik itu:  . Dalam erti kata lain, persamaan diberikan dalam satah XOY medan arah tangen kepada lengkung kamiran. Ulasan: Perlu diingatkan bahawa kepada Pers.
. Dalam erti kata lain, persamaan diberikan dalam satah XOY medan arah tangen kepada lengkung kamiran. Ulasan: Perlu diingatkan bahawa kepada Pers.  persamaan dan persamaan yang dipanggil diberikan dalam bentuk simetri
persamaan dan persamaan yang dipanggil diberikan dalam bentuk simetri  .
.
§ 3. Persamaan pembezaan tertib pertama dengan pembolehubah boleh dipisahkan.
Definisi. Persamaan pembezaan dengan pembolehubah boleh dipisahkan ialah persamaan bentuk  (3.1)
(3.1)
atau persamaan bentuk (3.2)
Untuk memisahkan pembolehubah dalam persamaan (3.1), i.e. kurangkan persamaan ini kepada apa yang dipanggil persamaan pembolehubah dipisahkan, lakukan yang berikut:
 ;
;
Sekarang kita perlu menyelesaikan persamaan g(y)= 0 . Jika ia mempunyai penyelesaian sebenar y= a, Itu y= a juga akan menjadi penyelesaian kepada persamaan (3.1).
Persamaan (3.2) dikurangkan kepada persamaan pembolehubah yang dipisahkan dengan membahagikan dengan hasil  :
:
 , yang membolehkan kita mendapatkan kamiran am persamaan (3.2):
, yang membolehkan kita mendapatkan kamiran am persamaan (3.2):  . (3.3)
. (3.3)
Lengkung kamiran (3.3) akan ditambah dengan penyelesaian  , jika penyelesaian sedemikian wujud.
, jika penyelesaian sedemikian wujud.
Selesaikan persamaan: .
Kami memisahkan pembolehubah:

 .
.
Mengintegrasikan, kita dapat 
Selanjutnya daripada persamaan  Dan
Dan  kita jumpa x=1,
y=-1.
Penyelesaian ini adalah penyelesaian peribadi.
kita jumpa x=1,
y=-1.
Penyelesaian ini adalah penyelesaian peribadi.
§ 4. Persamaan pembezaan homogen tertib pertama.
Definisi 1. Persamaan tertib pertama dipanggil homogen jika untuk bahagian kanannya untuk sebarang  nisbahnya adalah sah
nisbahnya adalah sah  , dipanggil keadaan kehomogenan fungsi dua pembolehubah dimensi sifar.
, dipanggil keadaan kehomogenan fungsi dua pembolehubah dimensi sifar.
Contoh 1. Tunjukkan fungsi itu  - dimensi sifar homogen.
- dimensi sifar homogen.
Penyelesaian.
 ,
,
Q.E.D.
Teorem. Apa-apa fungsi  - homogen dan, sebaliknya, sebarang fungsi homogen
- homogen dan, sebaliknya, sebarang fungsi homogen  dimensi sifar dikurangkan kepada bentuk
dimensi sifar dikurangkan kepada bentuk  .
.
Bukti.
Pernyataan pertama teorem adalah jelas, kerana  . Mari kita buktikan kenyataan kedua. Mari letak
. Mari kita buktikan kenyataan kedua. Mari letak  , kemudian untuk fungsi homogen
, kemudian untuk fungsi homogen  , itulah yang perlu dibuktikan.
, itulah yang perlu dibuktikan.
Definisi 2. Persamaan (4.1)
di mana M Dan N– fungsi homogen darjah yang sama, i.e. mempunyai harta untuk semua  , dipanggil homogen.
, dipanggil homogen.
Jelas sekali, persamaan ini sentiasa boleh dikurangkan kepada bentuk  (4.2), walaupun untuk menyelesaikannya anda tidak perlu melakukan ini.
(4.2), walaupun untuk menyelesaikannya anda tidak perlu melakukan ini.
Persamaan homogen dikurangkan kepada persamaan dengan pembolehubah boleh dipisahkan dengan menggantikan fungsi yang dikehendaki. y mengikut formula y=
zx,
di mana z(x)
– fungsi baru yang diperlukan. Setelah melakukan penggantian ini dalam persamaan (4.2), kami memperoleh:  atau
atau  atau
atau  .
.
Menyepadukan, kita memperoleh kamiran am bagi persamaan berkenaan dengan fungsi z(x)
 , yang selepas penggantian berulang
, yang selepas penggantian berulang  memberikan kamiran am bagi persamaan asal. Lebih-lebih lagi, jika
memberikan kamiran am bagi persamaan asal. Lebih-lebih lagi, jika  - punca persamaan
- punca persamaan  , kemudian fungsi
, kemudian fungsi  - menyelesaikan persamaan homogen yang diberikan. Jika
- menyelesaikan persamaan homogen yang diberikan. Jika  , maka persamaan (4.2) mengambil bentuk
, maka persamaan (4.2) mengambil bentuk
 dan menjadi persamaan dengan pembolehubah boleh dipisahkan. Penyelesaiannya adalah separa langsung:
dan menjadi persamaan dengan pembolehubah boleh dipisahkan. Penyelesaiannya adalah separa langsung:  .
.
Komen. Kadangkala dinasihatkan untuk menggunakan penggantian dan bukannya penggantian di atas x= zy.
§ 5. Persamaan pembezaan dikurangkan kepada persamaan homogen.
Pertimbangkan persamaan bentuk  . (5.1)
. (5.1)
Jika  , maka ini adalah persamaan menggunakan penggantian, di mana
, maka ini adalah persamaan menggunakan penggantian, di mana  Dan
Dan  - pembolehubah baru, dan
- pembolehubah baru, dan  - beberapa nombor tetap ditentukan daripada sistem
- beberapa nombor tetap ditentukan daripada sistem 
Dikurangkan kepada persamaan homogen 
Jika  , maka persamaan (5.1) mengambil bentuk
, maka persamaan (5.1) mengambil bentuk
 .
.
Percaya z= kapak+ oleh, kita sampai pada persamaan yang tidak mengandungi pembolehubah bebas.
Mari lihat contoh.
Contoh 1.
Integrasi Persamaan
dan serlahkan lengkung kamiran yang melalui titik: a) (2;2); b) (1;-1).
Penyelesaian.
Mari letak y= zx. Kemudian dy= xdz+ zdx Dan
Mari kita pendekkan dengan  dan mengumpulkan ahli di dx Dan dz:
dan mengumpulkan ahli di dx Dan dz:
Mari kita pisahkan pembolehubah: 
 .
.
Mengintegrasikan, kita dapat ;
atau  ,
,  .
.
Berganti di sini z pada  , kita memperoleh kamiran am bagi persamaan yang diberikan dalam bentuk (5.2)
, kita memperoleh kamiran am bagi persamaan yang diberikan dalam bentuk (5.2)  atau
atau 
 .
.
Ini adalah keluarga kalangan  , yang pusatnya terletak pada garis lurus y =
x dan yang pada asalan adalah tangen kepada garis y +
x = 0.
baris iniy
= -
x
seterusnya, penyelesaian tertentu persamaan.
, yang pusatnya terletak pada garis lurus y =
x dan yang pada asalan adalah tangen kepada garis y +
x = 0.
baris iniy
= -
x
seterusnya, penyelesaian tertentu persamaan.
Sekarang mod masalah Cauchy:
A) memasukkan kamiran am x=2,
y=2,
kita jumpa C=2, oleh itu penyelesaian yang diperlukan ialah  .
.
B) tiada satu pun bulatan (5.2) melalui titik (1;-1). Tetapi ia separa lurus y = -
x,  melalui titik dan memberikan penyelesaian yang diperlukan.
melalui titik dan memberikan penyelesaian yang diperlukan.
Contoh 2. Selesaikan persamaan: .
Penyelesaian.
Persamaan adalah kes khas persamaan (5.1).
Penentu  dalam contoh ini
dalam contoh ini  , jadi kita perlu menyelesaikan sistem berikut
, jadi kita perlu menyelesaikan sistem berikut 
Menyelesaikan, kita dapat itu  . Dengan melakukan penggantian dalam persamaan yang diberikan
. Dengan melakukan penggantian dalam persamaan yang diberikan  , kita memperoleh persamaan homogen. Mengintegrasikannya menggunakan penggantian
, kita memperoleh persamaan homogen. Mengintegrasikannya menggunakan penggantian  , kami dapati
, kami dapati  .
.
Kembali kepada pembolehubah lama x Dan y mengikut formula  , kita ada .
, kita ada .
§ 6. Persamaan homogen umum.
Persamaan M(x,
y)
dx+
N(x,
y)
dy=0
dipanggil homogen umum jika boleh memilih nombor sedemikian k, bahawa bahagian kiri persamaan ini menjadi fungsi homogen pada tahap tertentu m secara relatifnya x,
y,
dx Dan dy dengan syarat itu x dianggap sebagai nilai dimensi pertama, y – k ukuran ke ,
dx Dan dy –
masing-masing sifar dan (k-1)
ukuran ke. Sebagai contoh, ini akan menjadi persamaan  . (6.1)
. (6.1)
Sah di bawah andaian yang dibuat mengenai ukuran
x,
y,
dx Dan dy anggota sebelah kiri  Dan dy akan mempunyai dimensi -2, 2 masing-masing k Dan k-1. Dengan menyamakan mereka, kita memperoleh syarat yang mesti dipenuhi oleh nombor yang diperlukan k: -2 = 2k=k-1. Syarat ini berpuas hati apabila k= -1 (dengan ini k semua sebutan di sebelah kiri persamaan yang sedang dipertimbangkan akan mempunyai dimensi -2). Oleh itu, persamaan (6.1) digeneralisasikan homogen.
Dan dy akan mempunyai dimensi -2, 2 masing-masing k Dan k-1. Dengan menyamakan mereka, kita memperoleh syarat yang mesti dipenuhi oleh nombor yang diperlukan k: -2 = 2k=k-1. Syarat ini berpuas hati apabila k= -1 (dengan ini k semua sebutan di sebelah kiri persamaan yang sedang dipertimbangkan akan mempunyai dimensi -2). Oleh itu, persamaan (6.1) digeneralisasikan homogen.
Persamaan homogen umum dikurangkan kepada persamaan dengan pembolehubah boleh dipisahkan menggunakan penggantian  , Di mana z– fungsi baru yang tidak diketahui. Mari kita sepadukan persamaan (6.1) menggunakan kaedah yang ditunjukkan. Kerana k= -1, maka
, Di mana z– fungsi baru yang tidak diketahui. Mari kita sepadukan persamaan (6.1) menggunakan kaedah yang ditunjukkan. Kerana k= -1, maka  , selepas itu kita mendapat persamaan .
, selepas itu kita mendapat persamaan .
Mengintegrasikannya, kami dapati  , di mana
, di mana  . Ini adalah penyelesaian umum kepada persamaan (6.1).
. Ini adalah penyelesaian umum kepada persamaan (6.1).
§ 7. Persamaan pembezaan linear tertib pertama.
Persamaan linear tertib pertama ialah persamaan yang linear berkenaan dengan fungsi yang dikehendaki dan terbitannya. Ia kelihatan seperti:
 , (7.1)
, (7.1)
di mana P(x)
Dan Q(x)
– diberi fungsi berterusan bagi x.
Jika fungsi  ,
maka persamaan (7.1) mempunyai bentuk:
,
maka persamaan (7.1) mempunyai bentuk:  (7.2)
(7.2)
dan dipanggil persamaan homogen linear, sebaliknya  ia dipanggil persamaan tak homogen linear.
ia dipanggil persamaan tak homogen linear.
Persamaan pembezaan homogen linear (7.2) ialah persamaan dengan pembolehubah boleh dipisahkan:

 (7.3)
(7.3)
Ungkapan (7.3) ialah penyelesaian umum persamaan (7.2). Untuk mencari penyelesaian umum kepada persamaan (7.1), di mana fungsi P(x) menunjukkan fungsi yang sama seperti dalam persamaan (7.2), kami menggunakan teknik yang dipanggil kaedah variasi pemalar arbitrari dan terdiri daripada yang berikut: kami akan cuba memilih fungsi C=C(x) supaya penyelesaian umum kepada persamaan homogen linear (7.2) akan menjadi penyelesaian kepada persamaan linear tidak homogen (7.1). Kemudian untuk terbitan fungsi (7.3) kita perolehi:
 .
.
Menggantikan terbitan yang ditemui ke dalam persamaan (7.1), kita akan mempunyai:
atau  .
.
di mana  , di mana ialah pemalar arbitrari. Akibatnya, penyelesaian umum kepada persamaan linear tak homogen (7.1) ialah (7.4)
, di mana ialah pemalar arbitrari. Akibatnya, penyelesaian umum kepada persamaan linear tak homogen (7.1) ialah (7.4) 
Sebutan pertama dalam formula ini mewakili penyelesaian umum (7.3) bagi persamaan pembezaan homogen linear (7.2), dan sebutan kedua formula (7.4) ialah penyelesaian tertentu bagi persamaan tidak homogen linear (7.1), yang diperoleh daripada umum ( 7.4) dengan  . Kami menyerlahkan kesimpulan penting ini dalam bentuk teorem.
. Kami menyerlahkan kesimpulan penting ini dalam bentuk teorem.
Teorem. Jika satu penyelesaian tertentu bagi persamaan pembezaan tak homogen linear diketahui  , maka semua penyelesaian lain mempunyai bentuk
, maka semua penyelesaian lain mempunyai bentuk  , Di mana
, Di mana  - penyelesaian umum persamaan pembezaan homogen linear sepadan.
- penyelesaian umum persamaan pembezaan homogen linear sepadan.
Walau bagaimanapun, perlu diingatkan bahawa untuk menyelesaikan persamaan pembezaan tak homogen linear tertib pertama (7.1), kaedah lain lebih kerap digunakan, kadangkala dipanggil kaedah Bernoulli. Kami akan mencari penyelesaian kepada persamaan (7.1) dalam bentuk  . Kemudian
. Kemudian  . Mari kita gantikan terbitan yang ditemui ke dalam persamaan asal:
. Mari kita gantikan terbitan yang ditemui ke dalam persamaan asal:  .
.
Mari kita gabungkan, sebagai contoh, sebutan kedua dan ketiga bagi ungkapan terakhir dan ekstrak fungsi u(x)
di belakang kurungan:  (7.5)
(7.5)
Kami memerlukan kurungan untuk dibatalkan:  .
.
Mari kita selesaikan persamaan ini dengan menetapkan pemalar arbitrari C sama dengan sifar:  . Dengan fungsi yang ditemui v(x)
Mari kita kembali kepada persamaan (7.5):
. Dengan fungsi yang ditemui v(x)
Mari kita kembali kepada persamaan (7.5):  .
.
Menyelesaikannya, kami mendapat:  .
.
Oleh itu, penyelesaian umum kepada persamaan (7.1) mempunyai bentuk:
§ 8. Persamaan Bernoulli.
Definisi.
Persamaan pembezaan bentuk  , Di mana
, Di mana  , dipanggil persamaan Bernoulli.
, dipanggil persamaan Bernoulli.
Andainya  , bahagikan kedua-dua belah persamaan Bernoulli dengan
, bahagikan kedua-dua belah persamaan Bernoulli dengan  . Hasilnya kami mendapat:
. Hasilnya kami mendapat:  (8.1)
(8.1)
Mari perkenalkan fungsi baharu  . Kemudian
. Kemudian  . Mari kita darabkan persamaan (8.1) dengan
. Mari kita darabkan persamaan (8.1) dengan  dan mari pergi ke fungsi z(x)
:
dan mari pergi ke fungsi z(x)
:  , iaitu untuk fungsi z(x)
memperoleh persamaan tak homogen linear tertib pertama. Persamaan ini diselesaikan menggunakan kaedah yang dibincangkan dalam perenggan sebelumnya. Mari kita gantikan ke dalam penyelesaian amnya z(x)
ungkapan
, iaitu untuk fungsi z(x)
memperoleh persamaan tak homogen linear tertib pertama. Persamaan ini diselesaikan menggunakan kaedah yang dibincangkan dalam perenggan sebelumnya. Mari kita gantikan ke dalam penyelesaian amnya z(x)
ungkapan  , kita memperoleh kamiran am bagi persamaan Bernoulli, yang mudah diselesaikan berkenaan dengan y. Pada
, kita memperoleh kamiran am bagi persamaan Bernoulli, yang mudah diselesaikan berkenaan dengan y. Pada  larutan ditambah y(x)=0
. Persamaan Bernoulli juga boleh diselesaikan tanpa membuat peralihan kepada persamaan linear dengan penggantian
larutan ditambah y(x)=0
. Persamaan Bernoulli juga boleh diselesaikan tanpa membuat peralihan kepada persamaan linear dengan penggantian  , dan menggunakan kaedah Bernoulli, dibincangkan secara terperinci dalam § 7. Mari kita pertimbangkan penggunaan kaedah ini untuk menyelesaikan persamaan Bernoulli menggunakan contoh khusus.
, dan menggunakan kaedah Bernoulli, dibincangkan secara terperinci dalam § 7. Mari kita pertimbangkan penggunaan kaedah ini untuk menyelesaikan persamaan Bernoulli menggunakan contoh khusus.
Contoh. Cari penyelesaian umum bagi persamaan:  (8.2)
(8.2)
Penyelesaian.
Oleh itu, penyelesaian umum untuk persamaan ini mempunyai bentuk:  , y(x)=0.
, y(x)=0.
§ 9. Persamaan pembezaan dalam jumlah pembezaan.
Definisi. Jika dalam Persamaan. M(x, y) dx+ N(x, y) dy=0 (9.1) sebelah kiri ialah jumlah pembezaan bagi beberapa fungsi U(x, y) , maka ia dipanggil persamaan pembezaan jumlah. Persamaan ini boleh ditulis semula sebagai du(x, y)=0 , oleh itu, kamiran amnya ialah u(x, y)= c.
Sebagai contoh, persamaan xdy+
ydx=0
terdapat persamaan dalam jumlah pembezaan, kerana ia boleh ditulis semula dalam bentuk d(xy)=0.
Kamiran am ialah xy=
c- fungsi boleh dibezakan sewenang-wenangnya. Mari kita bezakan (9.3) berkenaan dengan u
§ 10. Faktor penyepaduan.
Jika persamaan M(x, y) dx + N(x, y) dy = 0 bukan persamaan pembezaan total dan terdapat fungsi µ = µ(x, y) , supaya selepas mendarab kedua-dua belah persamaan dengannya, kita mendapat persamaan
µ(Mdx + Ndy) = 0 dalam jumlah pembezaan, i.e. µ(Mdx + Ndy)du, kemudian fungsi µ(x, y) dipanggil faktor penyepaduan persamaan. Dalam kes di mana persamaan sudah menjadi persamaan dalam jumlah pembezaan, kita andaikan µ = 1.
Jika faktor penyepaduan didapati µ , maka penyepaduan persamaan ini dikurangkan kepada mendarab kedua-dua belahnya dengan µ dan mencari kamiran am bagi persamaan yang terhasil dalam jumlah pembezaan.
Jika µ
ialah fungsi boleh dibezakan secara berterusan bagi x Dan y, Itu  .
.
Ia berikutan bahawa faktor penyepaduan µ memenuhi persamaan pembezaan separa tertib pertama berikut:
 (10.1).
(10.1).
Jika diketahui terlebih dahulu bahawa µ= µ(ω) , Di mana ω – fungsi yang diberikan daripada x Dan y, maka persamaan (10.1) dikurangkan kepada persamaan biasa (dan, lebih-lebih lagi, linear) dengan fungsi yang tidak diketahui µ pada pembolehubah bebas ω :
 (10.2),
(10.2),
di mana  , iaitu pecahan ialah fungsi sahaja bagi ω
.
, iaitu pecahan ialah fungsi sahaja bagi ω
.
Menyelesaikan persamaan (10.2), kita dapati faktor penyepaduan
 , Dengan = 1.
, Dengan = 1.
Khususnya, persamaan M(x, y) dx + N(x, y) dy = 0 mempunyai faktor penyepaduan yang hanya bergantung pada x(ω = x) atau hanya daripada y(ω = y), jika syarat berikut dipenuhi dengan sewajarnya:
 ,
, 
 ,
,  .
.
Dengan mengklik pada butang "Muat turun arkib", anda akan memuat turun fail yang anda perlukan sepenuhnya secara percuma.
Sebelum memuat turun fail ini, fikirkan tentang esei yang bagus, ujian, kertas penggal, disertasi, artikel dan dokumen lain yang tidak dituntut pada komputer anda. Ini adalah kerja anda, ia harus mengambil bahagian dalam pembangunan masyarakat dan memberi manfaat kepada orang ramai. Cari karya ini dan serahkannya ke pangkalan pengetahuan.
Kami dan semua pelajar, pelajar siswazah, saintis muda yang menggunakan asas pengetahuan dalam pengajian dan kerja mereka akan sangat berterima kasih kepada anda.
Untuk memuat turun arkib dengan dokumen, masukkan nombor lima digit dalam medan di bawah dan klik butang "Muat turun arkib"
Dokumen yang serupa
Masalah Cauchy untuk persamaan pembezaan. Graf penyelesaian kepada persamaan pembezaan tertib pertama. Persamaan dengan pembolehubah boleh dipisahkan dan dikurangkan kepada persamaan homogen. Persamaan linear homogen dan tak homogen bagi urutan pertama. Persamaan Bernoulli.
kuliah, ditambah 08/18/2012
Konsep asas teori persamaan pembezaan biasa. Tanda persamaan dalam jumlah pembezaan, pembinaan kamiran am. Kes paling mudah untuk mencari faktor penyepaduan. Kes pengganda yang hanya bergantung pada X dan hanya pada Y.
kerja kursus, ditambah 24/12/2014
Ciri-ciri persamaan pembezaan sebagai hubungan antara fungsi dan terbitannya. Bukti teorem kewujudan dan keunikan penyelesaian. Contoh dan algoritma untuk menyelesaikan persamaan dalam jumlah pembezaan. Mengintegrasikan faktor dalam contoh.
kerja kursus, ditambah 02/11/2014
Persamaan pembezaan Riccati. Penyelesaian am bagi persamaan linear. Mencari semua penyelesaian yang mungkin untuk persamaan pembezaan Bernoulli. Menyelesaikan persamaan dengan pembolehubah boleh dipisahkan. Penyelesaian am dan khas bagi persamaan pembezaan Clairaut.
kerja kursus, ditambah 26/01/2015
Persamaan dengan pembolehubah boleh dipisahkan. Persamaan pembezaan homogen dan linear. Sifat geometri lengkung kamiran. Pembezaan lengkap fungsi dua pembolehubah. Penentuan kamiran dengan kaedah Bernoulli dan variasi pemalar arbitrari.
abstrak, ditambah 08/24/2015
Konsep dan penyelesaian persamaan pembezaan termudah dan persamaan pembezaan tertib arbitrari, termasuk yang mempunyai pekali analisis malar. Sistem persamaan linear. Tingkah laku asimptotik penyelesaian beberapa sistem linear.
tesis, ditambah 06/10/2010
Kamiran am bagi persamaan, penggunaan kaedah Lagrange untuk menyelesaikan persamaan linear tak homogen dengan fungsi yang tidak diketahui. Menyelesaikan persamaan pembezaan dalam bentuk parametrik. Keadaan Euler, persamaan tertib pertama dalam jumlah pembezaan.
ujian, ditambah 11/02/2011
def 1 jenis DU
dipanggil persamaan pembezaan homogen tertib pertama(ODU).
Th 1 Biarkan syarat berikut dipenuhi untuk fungsi:
1) berterusan di
Kemudian ODE (1) mempunyai kamiran am, yang diberikan oleh formula:
di mana terdapat beberapa antiterbitan bagi fungsi tersebut Dengan adalah pemalar arbitrari.
Nota 1 Jika untuk sesetengah syarat dipenuhi, maka dalam proses menyelesaikan ODE (1) penyelesaian bentuk mungkin hilang kes sedemikian mesti dirawat dengan lebih berhati-hati dan setiap daripada mereka mesti diperiksa secara berasingan.
Oleh itu daripada teorem Th1 sepatutnya algoritma umum untuk menyelesaikan ODE (1):
1) Buat penggantian:
2) Oleh itu, persamaan pembezaan dengan pembolehubah boleh dipisahkan akan diperolehi, yang harus disepadukan;
3) Kembali kepada pembolehubah lama;
4) Semak nilai untuk penglibatan mereka dalam penyelesaian alat kawalan jauh asal, yang mana syaratnya akan dipenuhi
5) Tulis jawapan.
Contoh 1 Selesaikan DE (4).
Penyelesaian: DE (4) ialah persamaan pembezaan homogen, kerana ia mempunyai bentuk (1). Mari kita buat perubahan (3), ini akan membawa persamaan (4) kepada bentuk:
Persamaan (5) ialah kamiran am DE (4).
Ambil perhatian bahawa apabila mengasingkan pembolehubah dan membahagi dengan, penyelesaian boleh hilang, tetapi ini bukan penyelesaian kepada DE (4), yang mudah disahkan melalui penggantian terus kepada kesamaan (4), kerana nilai ini tidak termasuk dalam domain definisi daripada DE asal.
Jawapan:
Nota 2 Kadangkala anda boleh menulis ODE dari segi pembezaan pembolehubah X Dan u. Adalah disyorkan untuk beralih dari tatatanda alat kawalan jauh ini kepada ungkapan melalui terbitan dan hanya kemudian lakukan penggantian (3).
Persamaan pembezaan dikurangkan kepada persamaan homogen.
def 2 Fungsi itu dipanggil fungsi homogen darjah k di kawasan tersebut, yang mana kesaksamaan akan dipenuhi:
Berikut ialah jenis persamaan pembezaan yang paling biasa yang boleh dikurangkan kepada bentuk (1) selepas pelbagai transformasi.
1) di mana fungsinya adalah homogen, darjah sifar, iaitu, kesamaan adalah sah: DE (6) mudah dikurangkan kepada bentuk (1), jika kita meletakkan , yang selanjutnya disepadukan menggunakan penggantian (3).
2) (7), di mana fungsinya adalah homogen pada tahap yang sama k . DE dalam bentuk (7) juga disepadukan menggunakan penggantian (3).
Contoh 2 Selesaikan DE (8).
Penyelesaian: Mari kita tunjukkan bahawa DE (8) adalah homogen. Mari kita bahagikan dengan apa yang mungkin, kerana ia bukan penyelesaian kepada DE (8).
Mari kita buat perubahan (3), ini akan membawa persamaan (9) kepada bentuk:
Persamaan (10) ialah kamiran am DE (8).
Ambil perhatian bahawa apabila mengasingkan pembolehubah dan membahagi dengan, penyelesaian yang sepadan dengan nilai dan boleh hilang. Mari kita semak ungkapan ini. Mari kita gantikannya kepada DE (8):
Jawapan:
Adalah menarik untuk diperhatikan bahawa apabila menyelesaikan contoh ini, fungsi muncul dipanggil "tanda" nombor X(membaca" tanda x"), ditakrifkan oleh ungkapan:
Nota 3 Mengurangkan DE (6) atau (7) kepada bentuk (1) tidak perlu; jika jelas bahawa DE adalah homogen, maka anda boleh membuat penggantian dengan segera
3) DE dalam bentuk (11) disepadukan sebagai ODE jika , dan penggantian dilakukan pada mulanya:
(12), di manakah penyelesaian sistem: (13), dan kemudian gunakan penggantian (3) untuk fungsi Selepas menerima kamiran am, mereka kembali kepada pembolehubah X Dan di.
Jika , maka, dengan mengandaikan dalam persamaan (11), kita memperoleh persamaan pembezaan dengan pembolehubah boleh dipisahkan.
Contoh 3 Selesaikan masalah Cauchy (14).
Penyelesaian: Mari kita tunjukkan bahawa DE (14) dikurangkan kepada DE homogen dan disepadukan mengikut skema di atas:
Mari kita selesaikan sistem tak homogen bagi persamaan algebra linear (15) menggunakan kaedah Cramer:
Mari kita buat perubahan pembolehubah dan sepadukan persamaan yang terhasil:
(16) – Kamiran am DE (14). Apabila mengasingkan pembolehubah, penyelesaian boleh hilang apabila membahagi dengan ungkapan, yang boleh diperolehi secara eksplisit selepas menyelesaikan persamaan kuadratik. Walau bagaimanapun, ia diambil kira dalam kamiran am (16) di
Mari cari penyelesaian kepada masalah Cauchy: gantikan nilai dan ke dalam kamiran am (16) dan cari Dengan.
Oleh itu, kamiran separa akan diberikan oleh formula:
Jawapan:
4) Adalah mungkin untuk mengurangkan beberapa DE kepada yang homogen untuk fungsi baharu yang belum diketahui jika kita menggunakan penggantian borang:
Dalam kes ini, nombor m dipilih daripada syarat bahawa persamaan yang terhasil, jika boleh, menjadi homogen pada tahap tertentu. Walau bagaimanapun, jika ini tidak dapat dilakukan, maka DE yang dimaksudkan tidak boleh dikurangkan kepada yang homogen dengan cara ini.
Contoh 4 Selesaikan DE. (18)
Penyelesaian: Mari kita tunjukkan bahawa DE (18) dikurangkan kepada DE homogen menggunakan penggantian (17) dan disepadukan lagi menggunakan penggantian (3):
Jom cari Dengan:
Oleh itu, penyelesaian tertentu DE (24) mempunyai bentuk
Ia ditunjukkan bagaimana untuk mengenali persamaan pembezaan homogen umum. Satu kaedah untuk menyelesaikan persamaan pembezaan homogen umum tertib pertama dipertimbangkan. Contoh penyelesaian terperinci bagi persamaan sedemikian diberikan.
kandunganDefinisi
Persamaan pembezaan homogen umum tertib pertama ialah persamaan bentuk:, di mana α ≠ 0 , α ≠ 1 , f - fungsi.
Cara Menentukan Sama ada Persamaan Pembezaan Digeneralisasikan Homogen
Untuk menentukan sama ada persamaan pembezaan digeneralisasikan homogen, anda perlu memperkenalkan t pemalar dan membuat penggantian:
y → t α · y , x → t · x .
Jika ada kemungkinan untuk memilih nilai α di mana pemalar t dikurangkan, maka ini ialah - persamaan pembezaan homogen umum. Perubahan dalam derivatif y′ dengan penggantian ini mempunyai bentuk:
.
Contoh
Tentukan sama ada persamaan yang diberi adalah homogen umum:
.
Kami membuat penggantian y → t α y, x → t x, y′ → t α- 1 th:
;
.
Bahagikan dengan t α+ 5
:
;
.
Persamaan tidak akan mengandungi t jika
4 α - 6 = 0,
α = 3/2
.
Sejak bila α = 3/2
, t telah berkurangan, maka ini adalah persamaan homogen umum.
Kaedah penyelesaian
Pertimbangkan persamaan pembezaan homogen umum bagi urutan pertama:
(1)
.
Mari kita tunjukkan bahawa ia dikurangkan kepada persamaan homogen menggunakan penggantian:
t = xα.
sungguh,
.
Dari sini
;
.
(1)
:
;
.
Ini adalah persamaan homogen. Ia boleh diselesaikan dengan penggantian:
y = z t,
di mana z ialah fungsi t.
Apabila menyelesaikan masalah, lebih mudah untuk segera menggunakan penggantian:
y = z x α,
di mana z ialah fungsi bagi x.
Contoh penyelesaian persamaan pembezaan homogen umum tertib pertama
Selesaikan persamaan pembezaan
(H.1) .
Mari kita semak sama ada persamaan ini adalah homogen umum. Untuk tujuan ini dalam (H.1) buat pengganti:
y → t α y , x → t x , y′ → t α- 1 th.
.
Bahagikan dengan t α:
.
t akan membatalkan jika kita menetapkan α = - 1
.
Ini bermakna bahawa ini adalah persamaan homogen umum.
Mari buat penggantian: 1
,
di mana z ialah fungsi bagi x.
.
y = z x α = z x - (H.1):
(H.1) ;
;
.
Gantikan ke dalam persamaan asal
;
;
.
Darab dengan x dan buka kurungan: 2
Kami memisahkan pembolehubah - darab dengan dx dan bahagi dengan x z 0
.
.
Apabila z ≠
;
;
;
.
kami ada:
.
Kami menyepadukan menggunakan jadual kamiran:
.
Mari kuatkan:
.
Marilah kita menggantikan pemalar e C → C dan keluarkan tanda modulus, kerana pilihan tanda yang dikehendaki ditentukan oleh pilihan tanda pemalar C:
Mari kembali kepada pembolehubah y. .
Gantikan z = xy: 2
Bahagikan dengan x: 0
(H.2) 0
Apabila kita bahagi dengan z 0
.
, kami mengandaikan bahawa z ≠ 0
. Mari kembali kepada pembolehubah y. Sekarang pertimbangkan penyelesaian z = xy = 0
.
;
.
, atau y =
Sejak bila y =
 tidak ditakrifkan, maka kepada kamiran am yang terhasil kita tambahkan penyelesaian y =
tidak ditakrifkan, maka kepada kamiran am yang terhasil kita tambahkan penyelesaian y =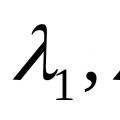 Sastera terpakai:
Sastera terpakai: N.M. Gunter, R.O. Kuzmin, Koleksi masalah dalam matematik yang lebih tinggi, "Lan", 2003.
N.M. Gunter, R.O. Kuzmin, Koleksi masalah dalam matematik yang lebih tinggi, "Lan", 2003.