Matriks songsang dan sifatnya. matriks songsang

Mencari matriks songsang- masalah yang paling kerap diselesaikan dengan dua kaedah:

kaedah penambahan algebra, di mana ia diperlukan untuk mencari penentu dan transpos matriks;
kaedah penyingkiran gauss tidak diketahui, di mana ia diperlukan untuk melakukan transformasi asas matriks (tambah baris, darab baris dengan nombor yang sama, dsb.).

Bagi mereka yang sangat ingin tahu, terdapat kaedah lain, contohnya, kaedah transformasi linear. Dalam pelajaran ini, kita akan menganalisis tiga kaedah yang disebutkan dan algoritma untuk mencari matriks songsang dengan kaedah ini.

matriks songsang DAN, matriks sedemikian dipanggil

DAN
. (1)

matriks songsang , yang diperlukan untuk didapati untuk matriks segi empat sama tertentu DAN, matriks sedemikian dipanggil

hasil darab yang menggunakan matriks DAN di sebelah kanan ialah matriks identiti, iaitu,
. (1)

Matriks identiti ialah matriks pepenjuru di mana semua entri pepenjuru adalah sama dengan satu.

Teorem.Bagi setiap matriks persegi bukan tunggal (bukan tunggal, bukan tunggal), seseorang boleh mencari matriks songsang, dan lebih-lebih lagi, hanya satu. Untuk matriks segi empat tepat (merosot, tunggal), matriks songsang tidak wujud.

Matriks segi empat sama dipanggil tidak istimewa(atau tidak merosot, bukan tunggal) jika penentunya tidak sama dengan sifar, dan istimewa(atau merosot, tunggal) jika penentunya ialah sifar.

matriks songsang hanya boleh didapati untuk matriks segi empat sama. Sememangnya, matriks songsang juga akan menjadi segi empat sama dan susunan yang sama dengan matriks yang diberikan. Matriks yang mana matriks songsang boleh didapati dipanggil matriks boleh terbalik.

Untuk matriks songsang terdapat analogi yang sesuai dengan salingan nombor. Untuk setiap nombor a, yang tidak sama dengan sifar, wujud nombor b bahawa kerja itu a dan b sama dengan satu: ab= 1 . Nombor b dipanggil salingan nombor b. Sebagai contoh, untuk nombor 7, songsang ialah nombor 1/7, kerana 7*1/7=1.

Mencari matriks songsang dengan kaedah penambahan algebra (matriks kesatuan)

Untuk matriks persegi bukan tunggal DAN songsangan ialah matriks

di manakah penentu matriks DAN, а ialah matriks yang dikaitkan dengan matriks DAN.

Bersekutu dengan matriks segi empat sama A ialah matriks tertib yang sama yang unsur-unsurnya penambahan algebra unsur-unsur yang sepadan bagi penentu matriks yang dialihkan berkenaan dengan matriks A. Oleh itu, jika

kemudian

dan

Algoritma untuk mencari matriks songsang dengan kaedah penambahan algebra

1. Cari penentu bagi matriks ini A. Jika penentu adalah sama dengan sifar, mencari matriks songsang berhenti, kerana matriks merosot dan tidak ada songsang untuknya.

2. Cari matriks yang ditukarkan berkenaan dengan A.

3. Kira unsur matriks kesatuan sebagai pelengkap algebra bagi marita yang terdapat dalam langkah 2.

4. Guna formula (2): darab nombor, penentu songsang matriks A, kepada matriks kesatuan yang terdapat dalam langkah 4.

5. Semak hasil yang diperoleh dalam langkah 4 dengan mendarab matriks ini A kepada matriks songsang. Jika hasil darab matriks ini sama dengan matriks identiti, maka matriks songsang didapati dengan betul. Jika tidak, mulakan proses penyelesaian semula.

Contoh 1 Untuk matriks

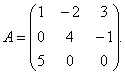
cari matriks songsang.

Keputusan. Untuk mencari matriks songsang, adalah perlu untuk mencari penentu matriks itu DAN. Kami dapati dengan peraturan segitiga:

Oleh itu, matriks DAN adalah bukan tunggal (tidak merosot, tidak tunggal) dan terdapat songsang untuknya.

Mari cari matriks yang dikaitkan dengan matriks yang diberikan DAN.

Mari kita cari matriks yang ditransposkan berkenaan dengan matriks A:

Kami mengira unsur-unsur matriks kesatuan sebagai pelengkap algebra bagi matriks yang dialihkan berkenaan dengan matriks A:

Oleh itu, matriks terkonjugasi dengan matriks A, mempunyai borang

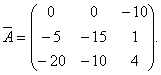
Komen. Susunan pengiraan unsur dan transposisi matriks mungkin berbeza. Pertama sekali, seseorang boleh mengira pelengkap algebra matriks A, dan kemudian alihkan matriks pelengkap algebra. Hasilnya mestilah elemen yang sama bagi matriks kesatuan.

Menggunakan formula (2), kita dapati matriks songsang kepada matriks DAN:

Mencari Matriks Songsang oleh Gaussian Elimination of Unknowns

Langkah pertama untuk mencari matriks songsang dengan penyingkiran Gaussian adalah untuk menetapkan kepada matriks A matriks identiti daripada susunan yang sama, memisahkannya dengan bar menegak. Kami mendapat matriks dwi. Darab kedua-dua bahagian matriks ini dengan , maka kita dapat

Algoritma untuk mencari matriks songsang dengan penghapusan Gaussian yang tidak diketahui

1. Kepada matriks A tetapkan matriks identiti dengan susunan yang sama.

2. Ubah matriks dwi yang terhasil supaya matriks identiti diperoleh di bahagian kirinya, maka matriks songsang secara automatik akan diperolehi di bahagian kanan menggantikan matriks identiti. Matriks A di sebelah kiri ditukar kepada matriks identiti oleh transformasi asas matriks.

2. Jika dalam proses penjelmaan matriks A ke dalam matriks identiti dalam mana-mana baris atau dalam mana-mana lajur hanya akan ada sifar, maka penentu matriks adalah sama dengan sifar, dan, oleh itu, matriks A akan merosot, dan ia tidak mempunyai matriks songsang. Dalam kes ini, penemuan selanjutnya bagi matriks songsang berhenti.

Contoh 2 Untuk matriks

cari matriks songsang.

dan kami akan mengubahnya supaya matriks identiti diperoleh di sebelah kiri. Mari kita mulakan transformasi.

Darab baris pertama matriks kiri dan kanan dengan (-3) dan tambahkannya ke baris kedua, dan kemudian darab baris pertama dengan (-4) dan tambahkannya ke baris ketiga, maka kita dapat

Untuk mengelakkan, jika boleh nombor pecahan dalam penjelmaan seterusnya, kita akan mula-mula mencipta unit dalam baris kedua di sebelah kiri matriks dwi. Untuk melakukan ini, darabkan baris kedua dengan 2 dan tolak baris ketiga daripadanya, maka kita dapat

Mari tambahkan baris pertama pada baris kedua, dan kemudian darab baris kedua dengan (-9) dan tambahkannya pada baris ketiga. Kemudian kita dapat

Bahagikan baris ketiga dengan 8, kemudian

Darab baris ketiga dengan 2 dan tambahkannya pada baris kedua. Kesudahannya:

Menukar tempat baris kedua dan ketiga, maka akhirnya kita dapat:

Kami melihat bahawa matriks identiti diperoleh di sebelah kiri, oleh itu, matriks songsang diperoleh di sebelah kanan. Oleh itu:

Anda boleh menyemak ketepatan pengiraan dengan mendarab matriks asal dengan matriks songsang yang ditemui:

Hasilnya mestilah matriks songsang.

Contoh 3 Untuk matriks

cari matriks songsang.

Keputusan. Menyusun matriks dwi

dan kami akan mengubahnya.

Kami mendarabkan baris pertama dengan 3, dan yang kedua dengan 2, dan menolak dari yang kedua, dan kemudian kami mendarabkan baris pertama dengan 5, dan yang ketiga dengan 2 dan menolak dari baris ketiga, maka kami mendapat

Kami mendarabkan baris pertama dengan 2 dan menambahnya pada baris kedua, dan kemudian menolak baris kedua dari baris ketiga, kemudian kami mendapat

Kami melihat bahawa dalam baris ketiga di sebelah kiri, semua elemen ternyata sama dengan sifar. Oleh itu, matriks merosot dan tidak mempunyai matriks songsang. Kami berhenti mencari lagi maria terbalik.

Topik ini antara yang paling dibenci oleh pelajar. Lebih teruk, mungkin, hanya penentu.

Caranya ialah konsep unsur songsang (dan saya bukan hanya bercakap tentang matriks sekarang) merujuk kita kepada operasi pendaraban. Walaupun dalam kurikulum sekolah pendaraban dipertimbangkan operasi yang rumit, dan pendaraban matriks secara amnya merupakan topik yang berasingan, yang mana saya mempunyai satu perenggan keseluruhan dan tutorial video yang dikhaskan untuknya.

Hari ini kita tidak akan pergi ke butiran pengiraan matriks. Ingatlah: bagaimana matriks dilambangkan, bagaimana ia didarab dan apa yang berikut daripada ini.

Semakan: Pendaraban Matriks

Pertama sekali, mari kita bersetuju dengan notasi. Matriks $A$ bersaiz $\left[ m\times n \right]$ hanyalah jadual nombor dengan tepat $m$ baris dan $n$ lajur:

\=\underbrace(\left[ \begin(matriks) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & (a)_(mn)) \\\end(matriks) \kanan])_(n)\]

Agar tidak mengelirukan baris dan lajur secara tidak sengaja di tempat (percayalah, dalam peperiksaan anda boleh mengelirukan satu dengan deuce - apa yang boleh kita katakan tentang beberapa baris di sana), lihat sahaja gambar:

Penentuan indeks untuk sel matriks

Apa yang sedang berlaku? Jika kita meletakkan sistem koordinat piawai $OXY$ di sebelah kiri sudut atas dan arahkan paksi supaya ia meliputi keseluruhan matriks, maka setiap sel matriks ini boleh dikaitkan secara unik dengan koordinat $\left(x;y \right)$ - ini akan menjadi nombor baris dan nombor lajur.

Mengapakah sistem koordinat diletakkan tepat di sudut kiri atas? Ya, kerana dari situlah kita mula membaca mana-mana teks. Ia sangat mudah untuk diingati.

Mengapakah paksi $x$ menghala ke bawah dan bukan ke kanan? Sekali lagi, ia mudah: ambil sistem koordinat piawai (paksi $x$ pergi ke kanan, paksi $y$ naik) dan putarkannya supaya ia melampirkan matriks. Ini ialah putaran 90 darjah mengikut arah jam - kita lihat hasilnya dalam gambar.

Secara umum, kami mengetahui cara menentukan indeks unsur matriks. Sekarang mari kita berurusan dengan pendaraban.

Definisi. Matriks $A=\left[ m\times n \right]$ dan $B=\left[ n\times k \right]$, apabila bilangan lajur dalam yang pertama sepadan dengan bilangan baris dalam yang kedua, adalah dipanggil konsisten.

Ia dalam susunan itu. Seseorang boleh menjadi samar-samar dan mengatakan bahawa matriks $A$ dan $B$ membentuk pasangan tertib $\left(A;B \kanan)$: jika ia konsisten dalam susunan ini, maka ia tidak perlu sama sekali $B $ dan $A$, itu. pasangan $\left(B;A \right)$ juga konsisten.

Hanya matriks yang konsisten boleh didarab.

Definisi. Hasil darab matriks tekal $A=\kiri[ m\kali n \kanan]$ dan $B=\kiri[ n\kali k \kanan]$ ialah matriks baharu $C=\kiri[ m\kali k \kanan ]$ , yang unsur $((c)_(ij))$ dikira dengan formula:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Dengan kata lain: untuk mendapatkan elemen $((c)_(ij))$ matriks $C=A\cdot B$, anda perlu mengambil $i$-baris matriks pertama, $j$ -lajur ke- matriks kedua, dan kemudian darab dalam pasangan elemen daripada baris dan lajur ini. Tambah hasilnya.

Ya, itu definisi yang keras. Beberapa fakta serta-merta mengikuti daripadanya:

Pendaraban matriks, secara amnya, tidak komutatif: $A\cdot B\ne B\cdot A$;
Walau bagaimanapun, pendaraban adalah bersekutu: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
Dan juga pengedaran: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
Dan pengedaran sekali lagi: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Pengagihan pendaraban terpaksa diterangkan secara berasingan untuk jumlah pengganda kiri dan kanan hanya kerana operasi pendaraban tidak komutatif.

Jika, bagaimanapun, ternyata $A\cdot B=B\cdot A$, matriks sedemikian dipanggil boleh ubah.

Di antara semua matriks yang didarab dengan sesuatu di sana, terdapat yang istimewa - yang, apabila didarab dengan mana-mana matriks $A$, sekali lagi memberikan $A$:

Definisi. Matriks $E$ dipanggil identiti jika $A\cdot E=A$ atau $E\cdot A=A$. Dalam kes matriks segi empat sama $A$ kita boleh menulis:

Matriks identiti adalah tetamu yang kerap dalam penyelesaian persamaan matriks. Dan secara umum, tetamu yang kerap dalam dunia matriks. :)

Dan kerana $E$ ini, seseorang telah menghasilkan semua permainan yang akan ditulis seterusnya.

Apakah itu matriks songsang

Memandangkan pendaraban matriks adalah operasi yang sangat memakan masa (anda perlu mendarab sekumpulan baris dan lajur), konsep matriks songsang juga bukanlah yang paling remeh. Dan ia memerlukan beberapa penjelasan.

Definisi Utama

Nah, sudah tiba masanya untuk mengetahui kebenaran.

Definisi. Matriks $B$ dipanggil songsang bagi matriks $A$ jika

Matriks songsang dilambangkan dengan $((A)^(-1))$ (jangan dikelirukan dengan darjah!), jadi takrifan boleh ditulis semula seperti ini:

Nampaknya semuanya sangat mudah dan jelas. Tetapi apabila menganalisis definisi sedemikian, beberapa soalan segera timbul:

Adakah matriks songsang sentiasa wujud? Dan jika tidak selalu, maka bagaimana untuk menentukan: bila ia wujud dan bila ia tidak?
Dan siapa yang mengatakan bahawa matriks sedemikian adalah tepat? Bagaimana jika bagi sesetengah matriks asal $A$ terdapat sekumpulan songsang?
Apakah rupa semua "terbalikan" ini? Dan bagaimana anda sebenarnya mengira mereka?

Bagi algoritma pengiraan - kita akan membincangkannya sedikit kemudian. Tetapi kami akan menjawab soalan yang lain sekarang. Marilah kita menyusunnya dalam bentuk pernyataan-lemmas yang berasingan.

Sifat asas

Mari kita mulakan dengan bagaimana matriks $A$ sepatutnya kelihatan supaya ia mempunyai $((A)^(-1))$. Sekarang kita akan memastikan bahawa kedua-dua matriks ini mestilah segi empat sama, dan saiz yang sama: $\left[ n\times n \right]$.

Lema 1. Diberi matriks $A$ dan songsangannya $((A)^(-1))$. Maka kedua-dua matriks ini adalah segi empat sama dan mempunyai susunan yang sama $n$.

Bukti. Semuanya mudah. Biarkan matriks $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Oleh kerana hasil darab $A\cdot ((A)^(-1))=E$ wujud mengikut takrifan, matriks $A$ dan $((A)^(-1))$ adalah konsisten dalam susunan itu:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( selaraskan)\]

Ini adalah akibat langsung daripada algoritma pendaraban matriks: pekali $n$ dan $a$ ialah "transit" dan mestilah sama.

Pada masa yang sama, pendaraban songsang juga ditakrifkan: $((A)^(-1))\cdot A=E$, jadi matriks $((A)^(-1))$ dan $A$ ialah juga konsisten dalam susunan ini:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( selaraskan)\]

Oleh itu, tanpa kehilangan keluasan, kita boleh menganggap bahawa $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Walau bagaimanapun, mengikut takrifan $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, jadi dimensi matriks adalah sama:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Jadi ternyata ketiga-tiga matriks - $A$, $((A)^(-1))$ dan $E$ - adalah saiz persegi$\left[ n\times n \right]$. Lemma terbukti.

Nah, itu sudah bagus. Kami melihat bahawa hanya matriks segi empat sama boleh terbalik. Sekarang mari kita pastikan bahawa matriks songsang sentiasa sama.

Lemma 2. Diberi matriks $A$ dan songsangannya $((A)^(-1))$. Kemudian matriks songsang ini adalah unik.

Bukti. Mari kita mulakan dari sebaliknya: biarkan matriks $A$ mempunyai sekurang-kurangnya dua kejadian songsang — $B$ dan $C$. Kemudian, mengikut definisi, persamaan berikut adalah benar:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(align)\]

Daripada Lemma 1 kami menyimpulkan bahawa keempat-empat matriks $A$, $B$, $C$ dan $E$ ialah segi empat sama dengan susunan yang sama: $\left[ n\times n \right]$. Oleh itu, produk ditakrifkan:

Oleh kerana pendaraban matriks adalah bersekutu (tetapi bukan komutatif!), kita boleh menulis:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(align)\]

Diterima sahaja varian yang mungkin: dua kejadian matriks songsang adalah sama. Lemma terbukti.

Alasan di atas hampir verbatim mengulangi bukti keunikan unsur songsang untuk semua nombor nyata$b\ne 0$. Satu-satunya penambahan yang ketara ialah mengambil kira dimensi matriks.

Walau bagaimanapun, kami masih tidak tahu apa-apa tentang sama ada ada matriks segi empat sama boleh diterbalikkan. Di sini penentu datang untuk membantu kami - ini adalah ciri utama untuk semua matriks persegi.

Lemma 3 . Diberi matriks $A$. Jika matriks $((A)^(-1))$ songsang kepadanya wujud, maka penentu matriks asal ialah bukan sifar:

\[\kiri| A \right|\ne 0\]

Bukti. Kita sudah tahu bahawa $A$ dan $((A)^(-1))$ ialah matriks segi empat sama bersaiz $\left[ n\times n \right]$. Oleh itu, bagi setiap daripada mereka adalah mungkin untuk mengira penentu: $\left| A \kanan|$ dan $\kiri| ((A)^(-1)) \kanan|$. Walau bagaimanapun, penentu produk adalah sama dengan produk penentu:

\[\kiri| A\cdot B \kanan|=\kiri| A \kanan|\cdot \kiri| B \kanan|\Anak panah kanan \kiri| A\cdot ((A)^(-1)) \kanan|=\kiri| A \kanan|\cdot \kiri| ((A)^(-1)) \kanan|\]

Tetapi menurut takrifan $A\cdot ((A)^(-1))=E$, dan penentu $E$ sentiasa sama dengan 1, jadi

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \kiri| A\cdot ((A)^(-1)) \kanan|=\kiri| E\kanan|; \\ & \kiri| A \kanan|\cdot \kiri| ((A)^(-1)) \kanan|=1. \\ \end(align)\]

Hasil darab dua nombor adalah sama dengan satu hanya jika setiap nombor ini berbeza daripada sifar:

\[\kiri| A \kanan|\ne 0;\quad \kiri| ((A)^(-1)) \kanan|\ne 0.\]

Jadi ternyata $\left| A \kanan|\ne 0$. Lemma terbukti.

Malah, keperluan ini agak logik. Sekarang kita akan menganalisis algoritma untuk mencari matriks songsang - dan ia akan menjadi jelas sepenuhnya mengapa, pada dasarnya, tiada matriks songsang boleh wujud dengan penentu sifar.

Tetapi pertama, mari kita rumuskan definisi "bantu":

Definisi. Matriks merosot ialah matriks segi empat sama bersaiz $\left[ n\times n \right]$ yang penentunya ialah sifar.

Oleh itu, kita boleh menegaskan bahawa mana-mana matriks boleh terbalik adalah tidak merosot.

Bagaimana untuk mencari matriks songsang

Sekarang kita akan mempertimbangkan algoritma universal untuk mencari matriks songsang. Secara umum, terdapat dua algoritma yang diterima umum, dan kami juga akan mempertimbangkan yang kedua hari ini.

Yang akan dipertimbangkan sekarang adalah sangat cekap untuk matriks bersaiz $\left[ 2\times 2 \right]$ dan - sebahagiannya - daripada saiz $\left[ 3\times 3 \right]$. Tetapi bermula dari saiz $\left[ 4\times 4 \right]$ adalah lebih baik untuk tidak menggunakannya. Mengapa - sekarang anda akan memahami segala-galanya.

Penambahan algebra

Bersedia. Sekarang akan ada rasa sakit. Tidak, jangan risau: seorang jururawat cantik dalam skirt, stoking dengan renda tidak datang kepada anda dan tidak akan memberi anda suntikan di punggung. Segala-galanya lebih prosaik: penambahan algebra dan Kebawah Duli Yang Maha Mulia "Matriks Kesatuan" akan datang kepada anda.

Mari kita mulakan dengan yang utama. Biarkan terdapat matriks segi empat sama bersaiz $A=\left[ n\times n \right]$ yang unsur-unsurnya dinamakan $((a)_(ij))$. Kemudian, untuk setiap elemen tersebut, seseorang boleh menentukan pelengkap algebra:

Definisi. Pelengkap algebra $((A)_(ij))$ kepada unsur $((a)_(ij))$ dalam baris $i$-ke dan $j$-lajur matriks $A=\kiri [ n \times n \right]$ ialah binaan borang

\[((A)_(ij))=((\kiri(-1 \kanan))^(i+j))\cdot M_(ij)^(*)\]

Di mana $M_(ij)^(*)$ ialah penentu matriks yang diperolehi daripada $A$ asal dengan memotong baris $i$-th dan lajur $j$-th yang sama.

sekali lagi. Pelengkap algebra kepada elemen matriks dengan koordinat $\left(i;j \right)$ dilambangkan sebagai $((A)_(ij))$ dan dikira mengikut skema:

Mula-mula, kami memadamkan $i$-row dan lajur $j$-th daripada matriks asal. Kami mendapat matriks segi empat sama baharu, dan kami menyatakan penentunya sebagai $M_(ij)^(*)$.
Kemudian kita darabkan penentu ini dengan $((\left(-1 \right))^(i+j))$ - pada mulanya ungkapan ini mungkin kelihatan menarik, tetapi sebenarnya kita hanya mengetahui tanda di hadapan $ M_(ij)^(*) $.
Kami mengira - kami dapat nombor tertentu. Itu. penambahan algebra hanyalah nombor, bukan beberapa matriks baru, dan sebagainya.

Matriks $M_(ij)^(*)$ itu sendiri dipanggil minor pelengkap kepada unsur $((a)_(ij))$. Dan dalam pengertian ini, takrifan pelengkap algebra di atas ialah kes khas bagi lebih definisi kompleks- apa yang kita pertimbangkan dalam pelajaran tentang penentu.

Nota PENTING. Sebenarnya, dalam matematik "dewasa", penambahan algebra ditakrifkan seperti berikut:

Kami mengambil $k$ baris dan $k$ lajur dalam matriks segi empat sama. Di persimpangan mereka, kita mendapat matriks bersaiz $\left[ k\times k \right]$ — penentunya dipanggil minor of order $k$ dan dilambangkan dengan $((M)_(k))$.

Kemudian kami memotong baris $k$ dan lajur $k$ yang "dipilih" ini. Sekali lagi, kita mendapat matriks segi empat sama - penentunya dipanggil minor pelengkap dan dilambangkan dengan $M_(k)^(*)$.

Darabkan $M_(k)^(*)$ dengan $((\kiri(-1 \kanan))^(t))$, dengan $t$ ialah (perhatian sekarang!) jumlah nombor semua baris yang dipilih dan lajur. Ini akan menjadi penambahan algebra.

Lihatlah langkah ketiga: sebenarnya terdapat sejumlah $2k$ terma! Perkara lain ialah untuk $k=1$ kita hanya mendapat 2 sebutan - ini akan menjadi $i+j$ yang sama - "koordinat" unsur $((a)_(ij))$, yang mana kita mencari pelengkap algebra.

Jadi hari ini kita menggunakan definisi yang sedikit dipermudahkan. Tetapi seperti yang akan kita lihat nanti, ia akan lebih daripada mencukupi. Yang lebih penting ialah perkara berikut:

Definisi. Matriks kesatuan $S$ kepada matriks segi empat sama $A=\left[ n\times n \right]$ ialah matriks baharu bersaiz $\left[ n\times n \right]$, yang diperoleh daripada $A$ dengan menggantikan $(( a)_(ij))$ dengan pelengkap algebra $((A)_(ij))$:

\\Anak panah kanan S=\kiri[ \mulakan(matriks) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ ((( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matriks) \kanan]\]

Pemikiran pertama yang timbul pada saat merealisasikan definisi ini ialah "inilah jumlah yang anda perlu kira!" Bersantai: anda perlu mengira, tetapi tidak terlalu banyak. :)

Nah, semua ini sangat bagus, tetapi mengapa ia perlu? Tapi kenapa.

Teorem utama

Jom balik sikit. Ingat, Lemma 3 menyatakan bahawa matriks boleh terbalik $A$ sentiasa bukan tunggal (iaitu, penentunya bukan sifar: $\left| A \right|\ne 0$).

Jadi, sebaliknya juga benar: jika matriks $A$ tidak merosot, maka ia sentiasa boleh terbalik. Malah terdapat skim carian $((A)^(-1))$. Semak ia:

Teorem matriks songsang. Biarkan matriks segi empat sama $A=\left[ n\times n \right]$ diberikan, dan penentunya ialah bukan sifar: $\left| A \kanan|\ne 0$. Kemudian matriks songsang $((A)^(-1))$ wujud dan dikira dengan formula:

\[((A)^(-1))=\frac(1)(\kiri| A \kanan|)\cdot ((S)^(T))\]

Dan sekarang - semuanya sama, tetapi dalam tulisan tangan yang boleh dibaca. Untuk mencari matriks songsang, anda memerlukan:

Kira penentu $\left| A \right|$ dan pastikan ia bukan sifar.
Susun matriks kesatuan $S$, i.e. kira 100500 penambahan algebra $((A)_(ij))$ dan letakkan pada tempatnya $((a)_(ij))$.
Ubah matriks ini $S$ dan kemudian darabkannya dengan beberapa nombor $q=(1)/(\kiri| A \kanan|)\;$.

Dan itu sahaja! Matriks songsang $((A)^(-1))$ ditemui. Mari lihat contoh:

\[\kiri[ \begin(matriks) 3 & 1 \\ 5 & 2 \\\end(matriks) \kanan]\]

Keputusan. Mari kita semak kebolehterbalikan. Mari kita hitung penentu:

\[\kiri| A \kanan|=\kiri| \begin(matriks) 3 & 1 \\ 5 & 2 \\\end(matriks) \kanan|=3\cdot 2-1\cdot 5=6-5=1\]

Penentu berbeza daripada sifar. Jadi matriks boleh terbalik. Mari buat matriks kesatuan:

Mari kita hitung penambahan algebra:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\kanan|=2; \\ & ((A)_(12))=((\kiri(-1 \kanan))^(1+2))\cdot \kiri| 5\kanan|=-5; \\ & ((A)_(21))=((\kiri(-1 \kanan))^(2+1))\cdot \kiri| 1 \kanan|=-1; \\ & ((A)_(22))=((\kiri(-1 \kanan))^(2+2))\cdot \kiri| 3\kanan|=3. \\ \end(align)\]

Beri perhatian: penentu |2|, |5|, |1| dan |3| ialah penentu bagi matriks bersaiz $\left[ 1\times 1 \right]$, bukan modul. Itu. jika penentunya nombor negatif, tidak perlu mengeluarkan "tolak".

Secara keseluruhan, matriks kesatuan kami kelihatan seperti ini:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \kanan]\]

Itu sahaja. Masalah selesai.

Jawab. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Satu tugas. Cari matriks songsang:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Keputusan. Sekali lagi, kami mempertimbangkan penentu:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matriks ) \kiri(1\cdot 2\cdot 1+\kiri(-1 \kanan)\cdot \kiri(-1 \kanan)\cdot 1+2\cdot 0\cdot 0 \kanan)- \\ -\kiri (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matriks)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Penentu berbeza daripada sifar - matriks boleh terbalik. Tetapi sekarang ia akan menjadi yang paling kecil: anda perlu mengira sebanyak 9 (sembilan, sial!) Penambahan algebra. Dan setiap satu daripadanya akan mengandungi kelayakan $\left[ 2\times 2 \right]$. Terbang:

\[\begin(matriks) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matriks) 2 & -1 \\ 0 & 1 \\\end(matriks) \kanan|=2; \\ ((A)_(12))=((\kiri(-1 \kanan))^(1+2))\cdot \kiri| \begin(matriks) 0 & -1 \\ 1 & 1 \\\end(matriks) \kanan|=-1; \\ ((A)_(13))=((\kiri(-1 \kanan))^(1+3))\cdot \kiri| \begin(matriks) 0 & 2 \\ 1 & 0 \\\end(matriks) \kanan|=-2; \\ ... \\ ((A)_(33))=((\kiri(-1 \kanan))^(3+3))\cdot \kiri| \begin(matriks) 1 & -1 \\ 0 & 2 \\\end(matriks) \right|=2; \\ \end(matriks)\]

Ringkasnya, matriks kesatuan akan kelihatan seperti ini:

Oleh itu, matriks songsang ialah:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matriks) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matriks) \kanan]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(array) \right]\]

Nah, itu sahaja. Inilah jawapannya.

Jawab. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Seperti yang anda lihat, pada akhir setiap contoh, kami melakukan pemeriksaan. Dalam hal ini, satu nota penting:

Jangan malas nak semak. Darabkan matriks asal dengan songsang yang ditemui - anda sepatutnya mendapat $E$.

Adalah lebih mudah dan cepat untuk melakukan semakan ini daripada mencari ralat dalam pengiraan selanjutnya, apabila, sebagai contoh, anda menyelesaikan persamaan matriks.

Cara alternatif

Seperti yang saya katakan, teorem matriks songsang berfungsi dengan baik untuk saiz $\left[ 2\times 2 \right]$ dan $\left[ 3\times 3 \right]$ (dalam kes terakhir- ia tidak begitu "sempurna" lagi), tetapi untuk matriks bersaiz besar, kesedihan bermula.

Tetapi jangan risau: terdapat algoritma alternatif yang boleh digunakan untuk mencari songsang dengan tenang walaupun untuk matriks $\left[ 10\times 10 \right]$. Tetapi, seperti yang sering berlaku, untuk mempertimbangkan algoritma ini, kita memerlukan sedikit latar belakang teori.

Transformasi asas

Di antara pelbagai transformasi matriks, terdapat beberapa yang istimewa - ia dipanggil asas. Terdapat betul-betul tiga transformasi sedemikian:

Pendaraban. Anda boleh mengambil baris $i$-th (lajur) dan darabkannya dengan sebarang nombor $k\ne 0$;
Penambahan. Tambahkan pada baris $i$-th (lajur) mana-mana baris (lajur) $j$-th lain yang didarab dengan sebarang nombor $k\ne 0$ (sudah tentu, $k=0$ juga boleh, tetapi apa gunanya daripada itu??Tiada apa yang akan berubah walaupun).
Permutasi. Ambil baris $i$-th dan $j$-th (lajur) dan tukarkannya.

Mengapa penjelmaan ini dipanggil asas (untuk matriks besar ia tidak kelihatan begitu asas) dan mengapa hanya terdapat tiga daripadanya - soalan ini berada di luar skop pelajaran hari ini. Oleh itu, kami tidak akan pergi ke butiran.

Perkara lain yang penting: kita perlu melakukan semua penyelewengan ini pada matriks yang berkaitan. Ya, ya, anda dengar betul. Sekarang akan ada satu lagi definisi - yang terakhir dalam pelajaran hari ini.

Matriks yang dilampirkan

Sudah tentu di sekolah anda menyelesaikan sistem persamaan menggunakan kaedah penambahan. Nah, di sana, tolak satu lagi dari satu baris, darab beberapa baris dengan nombor - itu sahaja.

Jadi: kini semuanya akan sama, tetapi sudah "dengan cara dewasa". sedia?

Definisi. Biarkan matriks $A=\left[ n\times n \right]$ dan matriks identiti $E$ yang sama saiz $n$ diberikan. Kemudian matriks yang berkaitan $\left[ A\left| E\betul. \right]$ ialah matriks $\left[ n\times 2n \right]$ baharu yang kelihatan seperti ini:

\[\left[ A\left| E\betul. \kanan]=\kiri[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \kanan]\]

Ringkasnya, kami mengambil matriks $A$, di sebelah kanan kami menetapkan padanya matriks identiti $E$ daripada saiz yang diperlukan, kami memisahkannya dengan bar menegak untuk kecantikan - inilah yang dilampirkan. :)

Apa tangkapannya? Dan inilah yang:

Teorem. Biarkan matriks $A$ boleh terbalik. Pertimbangkan matriks bersebelahan $\left[ A\left| E\betul. \kanan]$. Jika menggunakan transformasi rentetan asas bawa ke borang $\left[ E\left| B\betul. \kanan]$, i.e. dengan mendarab, menolak dan menyusun semula baris untuk mendapatkan daripada $A$ matriks $E$ di sebelah kanan, maka matriks $B$ yang diperoleh di sebelah kiri ialah songsang bagi $A$:

\[\left[ A\left| E\betul. \kanan]\ke \kiri[ E\kiri| B\betul. \kanan]\Anak panah kanan B=((A)^(-1))\]

Semudah itu! Ringkasnya, algoritma untuk mencari matriks songsang kelihatan seperti ini:

Tulis matriks yang berkaitan $\left[ A\left| E\betul. \kanan]$;
Lakukan penukaran rentetan asas sehingga kanan bukannya $A$ muncul $E$;
Sudah tentu, sesuatu juga akan muncul di sebelah kiri - matriks tertentu $B$. Ini akan menjadi sebaliknya;
KEUNTUNGAN! :)

Sudah tentu, lebih mudah diucapkan daripada dilakukan. Jadi mari kita lihat beberapa contoh: untuk saiz $\left[ 3\times 3 \right]$ dan $\left[ 4\times 4 \right]$.

Satu tugas. Cari matriks songsang:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Keputusan. Kami menyusun matriks yang dilampirkan:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Oleh kerana lajur terakhir matriks asal diisi dengan yang, tolak baris pertama daripada yang lain:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \kanan]\begin(matriks) \downarrow \\ -1 \\ -1 \\\end(matriks)\to \\ & \to \left [ \mulakan(susun)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Tiada unit lagi, kecuali baris pertama. Tetapi kami tidak menyentuhnya, jika tidak, unit yang baru dikeluarkan akan mula "membiak" di lajur ketiga.

Tetapi kita boleh menolak baris kedua dua kali daripada yang terakhir - kita mendapat satu unit di sudut kiri bawah:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \kanan]\begin(matriks) \ \\ \downarrow \\ -2 \\\end(matriks)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Sekarang kita boleh menolak baris terakhir dari yang pertama dan dua kali dari yang kedua - dengan cara ini kita akan "sifar" lajur pertama:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matriks) -1 \\ -2 \\ \uparrow \\\end(matriks)\to \\ & \ ke \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Darab baris kedua dengan −1 dan kemudian tolaknya 6 kali daripada yang pertama dan tambah 1 kali kepada yang terakhir:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan]\begin(matriks) \ \\ \left| \cdot \kiri(-1 \kanan) \kanan. \\ \ \\\tamat(matriks)\ke \\ & \ke \kiri[ \mulakan(tatasusunan)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan]\begin(matriks) -6 \\ \updownarrow \\ +1 \\\end (matriks)\ke \\ & \ke \kiri[ \mulakan(tatasusunan)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(align)\]

Ia kekal hanya untuk menukar baris 1 dan 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(array) \right]\]

sedia! Di sebelah kanan ialah matriks songsang yang diperlukan.

Jawab. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Satu tugas. Cari matriks songsang:

\[\kiri[ \mulakan(matriks) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matriks) \kanan]\]

Keputusan. Sekali lagi kami menyusun yang dilampirkan:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Mari kita pinjam sedikit, bimbang tentang berapa banyak yang perlu kita kira sekarang ... dan mula mengira. Sebagai permulaan, kita "sifarkan" lajur pertama dengan menolak baris 1 daripada baris 2 dan 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \kanan]\mulakan(matriks) \anak panah ke bawah \\ -1 \\ -1 \\ \ \\\tamat(matriks)\ke \\ & \ke \kiri[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Kami melihat terlalu banyak "tolak" dalam baris 2-4. Darab ketiga-tiga baris dengan −1, dan kemudian bakar lajur ketiga dengan menolak baris 3 daripada yang lain:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matriks) \ \\ \left| \cdot \kiri(-1 \kanan) \kanan. \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\\end(matriks)\ke \\ & \ke \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (array) \right]\begin(matriks) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matriks)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Kini tiba masanya untuk "menggoreng" lajur terakhir matriks asal: tolak baris 4 daripada yang lain:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array ) \kanan]\begin(matriks) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matriks)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Gulungan akhir: "burn out" lajur kedua dengan menolak baris 2 daripada baris 1 dan 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( tatasusunan) \kanan]\mulakan(matriks) 6 \\ \anak panah ke bawah \\ -5 \\ \ \\\tamat(matriks)\ke \\ & \ke \kiri[ \mulakan(tatasusunan)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Dan sekali lagi, matriks identiti di sebelah kiri, jadi songsang di sebelah kanan. :)

Jawab. $\left[ \begin(matriks) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matriks) \kanan]$

Definisi 1: Matriks dipanggil degenerate jika penentunya adalah sifar.

Definisi 2: Matriks dipanggil bukan tunggal jika penentunya tidak sama dengan sifar.

Matriks "A" dipanggil matriks songsang, jika syarat A*A-1 = A-1 *A = E (matriks identiti) dipenuhi.

Matriks segi empat sama boleh terbalik hanya jika ia bukan tunggal.

Skim untuk mengira matriks songsang:

1) Kirakan penentu bagi matriks "A" jika ∆ A = 0, maka matriks songsang tidak wujud.

2) Cari semua pelengkap algebra bagi matriks "A".

3) Susun matriks penambahan algebra (Aij )

4) Ubah matriks pelengkap algebra (Aij )T

5) Darab matriks terpindah dengan salingan penentu matriks ini.

6) Jalankan semakan:

Pada pandangan pertama ia mungkin kelihatan sukar, tetapi sebenarnya semuanya sangat mudah. Semua penyelesaian adalah berdasarkan mudah operasi aritmetik, perkara utama semasa menyelesaikan adalah untuk tidak keliru dengan tanda "-" dan "+", dan tidak kehilangannya.

Sekarang mari kita putuskan bersama tugas praktikal, mengira matriks songsang.

Tugas: cari matriks songsang "A", ditunjukkan dalam gambar di bawah:

Kami menyelesaikan segala-galanya tepat seperti yang ditunjukkan dalam rancangan untuk mengira matriks songsang.

1. Perkara pertama yang perlu dilakukan ialah mencari penentu bagi matriks "A":

Penjelasan:

Kami telah memudahkan penentu kami dengan menggunakan fungsi utamanya. Pertama, kami menambah pada baris ke-2 dan ke-3 unsur-unsur baris pertama, didarab dengan satu nombor.

Kedua, kami menukar lajur ke-2 dan ke-3 penentu, dan mengikut sifatnya, kami menukar tanda di hadapannya.

Ketiga, kami mengeluarkan faktor sepunya (-1) baris kedua, dengan itu menukar tanda itu semula, dan ia menjadi positif. Kami juga memudahkan baris 3 dengan cara yang sama seperti pada permulaan contoh.

Kami mempunyai penentu segi tiga, di mana unsur-unsur di bawah pepenjuru adalah sama dengan sifar, dan oleh sifat 7 ia adalah sama dengan hasil darab unsur pepenjuru. Hasilnya, kami mendapat ∆ A = 26, maka wujudlah matriks songsang.

A11 = 1*(3+1) = 4

A12 \u003d -1 * (9 + 2) \u003d -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Langkah seterusnya ialah menyusun matriks daripada penambahan yang terhasil:

5. Kami mendarabkan matriks ini dengan salingan penentu, iaitu, dengan 1/26:

6. Nah, sekarang kita hanya perlu menyemak:

Semasa pengesahan, kami menerima matriks identiti, oleh itu, keputusan dibuat dengan betul.

2 cara untuk mengira matriks songsang.

1. Penjelmaan asas bagi matriks

2. Matriks songsang melalui penukar asas.

Transformasi matriks asas termasuk:

1. Mendarab rentetan dengan nombor bukan sifar.

2. Menambah pada mana-mana baris baris lain, didarab dengan nombor.

3. Menukar baris matriks.

4. Menggunakan rantaian transformasi asas, kami memperoleh matriks lain.

DAN -1 = ?

1. (A|E) ~ (E|A -1 )

2. A -1*A=E

Pertimbangkan ia contoh praktikal dengan nombor nyata.

Tugas: Cari matriks songsang.

Keputusan:

Mari semak:

Sedikit penjelasan mengenai penyelesaian:

Kami mula-mula menukar baris 1 dan 2 matriks, kemudian kami mendarabkan baris pertama dengan (-1).

Selepas itu, baris pertama didarab dengan (-2) dan ditambah pada baris kedua matriks. Kemudian kami mendarabkan baris ke-2 dengan 1/4.

peringkat akhir penjelmaan ialah pendaraban baris kedua dengan 2 dan penambahan daripada baris pertama. Akibatnya, kita mempunyai matriks identiti di sebelah kiri, oleh itu, matriks songsang ialah matriks di sebelah kanan.

Selepas menyemak, kami yakin dengan ketepatan keputusan itu.

Seperti yang anda lihat, mengira matriks songsang adalah sangat mudah.

Sebagai mengakhiri kuliah ini, saya juga ingin menumpukan sedikit masa kepada sifat-sifat matriks tersebut.

Kaedah mencari matriks songsang, . Pertimbangkan matriks segi empat sama

Nyatakan Δ = det A.

Matriks persegi A dipanggil tidak merosot, atau tidak istimewa jika penentunya bukan sifar, dan merosot, atau istimewa, jikaΔ = 0.

Matriks segi empat sama B wujud untuk matriks segi empat sama A dengan susunan yang sama jika hasil darabnya A B = B A = E, dengan E ialah matriks identiti susunan yang sama dengan matriks A dan B.

Teorem . Untuk membolehkan matriks A mempunyai matriks songsang, adalah perlu dan mencukupi bahawa penentunya adalah bukan sifar.

Matriks songsang kepada matriks A, dilambangkan dengan A- 1 jadi B = A - 1 dan dikira dengan formula

, (1)

di mana А i j - pelengkap algebra bagi unsur a i j bagi matriks A..

Pengiraan A -1 dengan formula (1) untuk matriks perintah tinggi sangat susah payah, jadi dalam praktiknya adalah mudah untuk mencari A -1 menggunakan kaedah transformasi asas (EP). Mana-mana matriks bukan tunggal A boleh dikurangkan dengan EP bagi lajur sahaja (atau baris sahaja) kepada matriks identiti E. Jika EP yang dilakukan pada matriks A digunakan dalam susunan yang sama kepada matriks identiti E, maka hasilnya ialah matriks songsang. Adalah mudah untuk melakukan EP pada matriks A dan E secara serentak, menulis kedua-dua matriks sebelah menyebelah melalui garisan. Kami perhatikan sekali lagi bahawa apabila mencari bentuk kanonik matriks, untuk mencarinya, seseorang boleh menggunakan transformasi baris dan lajur. Jika anda perlu mencari matriks songsang, anda harus menggunakan hanya baris atau lajur sahaja dalam proses transformasi.

Contoh 2.10. Untuk matriks cari A -1 .

Keputusan.Mula-mula kita cari penentu bagi matriks A
jadi matriks songsang wujud dan kita boleh mencarinya dengan formula: , dengan A i j (i,j=1,2,3) - pelengkap algebra bagi unsur a i j bagi matriks asal.

di mana .

Contoh 2.11. Dengan menggunakan kaedah penjelmaan asas, cari A -1 untuk matriks: A=.

Keputusan.Kami menetapkan matriks identiti dengan susunan yang sama kepada matriks asal di sebelah kanan: . Dengan bantuan transformasi lajur asas, kami mengurangkan "separuh" kiri kepada identiti satu, pada masa yang sama melakukan transformasi sedemikian pada matriks kanan.
Untuk melakukan ini, tukar lajur pertama dan kedua: ~ . Kami menambah yang pertama ke lajur ketiga, dan yang pertama didarab dengan -2 kepada yang kedua: . Dari lajur pertama kita tolak kedua dua kali ganda, dan dari yang ketiga - yang kedua didarab dengan 6; . Mari tambahkan lajur ketiga pada lajur pertama dan kedua: . Darab lajur terakhir dengan -1: . Matriks segi empat sama yang diperoleh di sebelah kanan bar menegak ialah matriks songsang kepada matriks A yang diberi. Jadi,
.

Bagi apa apa matriks tidak merosot Dan wujud dan, lebih-lebih lagi, matriks unik A -1 seperti itu

A*A -1 =A -1 *A = E,

di mana E ialah matriks identiti bagi susunan yang sama seperti A. Matriks A -1 dipanggil songsang bagi matriks A.

Jika seseorang terlupa, dalam matriks identiti, kecuali pepenjuru yang diisi dengan satu, semua kedudukan lain diisi dengan sifar, contoh matriks identiti:

Mencari matriks songsang dengan kaedah matriks bersebelahan

Matriks songsang ditakrifkan oleh formula:

di mana A ij - unsur a ij .

Itu. Untuk mengira songsangan matriks, anda perlu mengira penentu matriks ini. Kemudian cari penambahan algebra untuk semua elemennya dan buat matriks baharu daripadanya. Seterusnya, anda perlu mengangkut matriks ini. Dan bahagikan setiap elemen matriks baharu dengan penentu matriks asal.

Mari lihat beberapa contoh.

Cari A -1 untuk matriks

Penyelesaian. Cari A -1 dengan kaedah matriks bersebelahan. Kami mempunyai det A = 2. Cari pelengkap algebra bagi unsur-unsur matriks A. Dalam kes ini pelengkap algebra bagi unsur matriks akan menjadi unsur yang sepadan bagi matriks itu sendiri, diambil dengan tanda mengikut formula

Kami mempunyai A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Kami membentuk matriks bersebelahan

Kami mengangkut matriks A*:

Kami mencari matriks songsang dengan formula:

Kita mendapatkan:

Gunakan kaedah matriks bersebelahan untuk mencari A -1 jika

Penyelesaian Pertama sekali, kita mengira matriks yang diberikan untuk memastikan bahawa matriks songsang wujud. Kami ada

Di sini kami telah menambah elemen baris kedua pada elemen baris ketiga, didarab sebelum ini dengan (-1), dan kemudian mengembangkan penentu dengan baris kedua. Oleh kerana takrifan matriks ini berbeza daripada sifar, maka matriks songsang kepadanya wujud. Untuk membina matriks bersebelahan, kita dapati pelengkap algebra bagi unsur-unsur matriks ini. Kami ada

Mengikut formula

kami mengangkut matriks A*:

Kemudian mengikut formula

Mencari matriks songsang dengan kaedah penjelmaan asas

Sebagai tambahan kepada kaedah mencari matriks songsang, yang mengikuti dari formula (kaedah matriks yang berkaitan), terdapat kaedah untuk mencari matriks songsang, yang dipanggil kaedah transformasi asas.

Transformasi matriks asas

Penjelmaan berikut dipanggil penjelmaan matriks asas:

1) pilih atur baris (lajur);

2) mendarab baris (lajur) dengan nombor bukan sifar;

3) menambah kepada elemen baris (lajur) elemen yang sepadan dengan baris lain (lajur), yang sebelum ini didarab dengan nombor tertentu.

Untuk mencari matriks A -1, kita bina matriks segi empat tepat B = (A|E) pesanan (n; 2n), memberikan kepada matriks A di sebelah kanan matriks identiti E melalui garis pembahagi:

Pertimbangkan satu contoh.

Dengan menggunakan kaedah penjelmaan asas, cari A -1 jika

Penyelesaian. Kami membentuk matriks B:

Nyatakan baris matriks B hingga α 1 , α 2 , α 3 . Mari kita lakukan penjelmaan berikut pada baris matriks B.