Teorem asas dinamik. Teorem umum dinamik

Kuliah 3. Teorem umum dinamik

Dinamik sistem titik material merupakan cabang penting dalam mekanik teori. Di sini kita terutamanya mempertimbangkan masalah tentang gerakan sistem mekanikal (sistem mata bahan) dengan nombor terhingga darjah kebebasan – bilangan maksimum parameter bebas yang menentukan kedudukan sistem. Tugas utama dinamik sistem - kajian tentang undang-undang pergerakan badan tegar dan sistem mekanikal.

Pendekatan paling mudah untuk mengkaji gerakan sistem, yang terdiri daripada N mata material, turun untuk mempertimbangkan pergerakan setiap titik individu sistem. Dalam kes ini, semua daya yang bertindak pada setiap titik sistem, termasuk daya interaksi antara titik, mesti ditentukan.

Menentukan pecutan setiap titik mengikut undang-undang kedua Newton (1.2), kita memperoleh bagi setiap titik tiga hukum pembezaan skalar bagi gerakan tertib kedua, i.e. 3 N hukum pembezaan pergerakan untuk keseluruhan sistem.

Untuk mencari persamaan gerakan sistem mekanikal untuk daya yang diberikan dan keadaan awal untuk setiap titik sistem, diperolehi undang-undang pembezaan perlu disepadukan. Masalah ini sukar walaupun dalam kes dua titik material yang bergerak hanya di bawah pengaruh daya interaksi mengikut undang-undang tarikan sejagat (masalah dua badan), dan amat sukar dalam kes tiga titik berinteraksi (masalah tiga badan ).

Oleh itu, adalah perlu untuk mencari kaedah untuk menyelesaikan masalah yang akan membawa kepada persamaan yang boleh diselesaikan dan memberi gambaran tentang pergerakan sistem mekanikal. Teorem umum dinamik, sebagai akibat daripada undang-undang pembezaan gerakan, membolehkan kita mengelakkan kerumitan yang timbul semasa penyepaduan dan mendapatkan keputusan yang diperlukan.

3. 1. Nota am

Kami akan menomborkan titik sistem mekanikal dengan indeks i, j, k dll., yang dijalankan melalui semua nilai 1, 2, 3… N, Di mana N – bilangan titik sistem. Kuantiti fizik yang berkaitan dengan k titik ke-th ditetapkan oleh indeks yang sama dengan titik. Sebagai contoh, nyatakan vektor jejari dan kelajuan, masing-masing k titik ke.

Setiap titik sistem digerakkan oleh kuasa dua asal: pertama, daya yang sumbernya terletak di luar sistem, dipanggil luaran pasukan dan ditetapkan; kedua, daya dari titik lain sistem tertentu, dipanggil dalaman pasukan dan ditetapkan . Daya dalaman memenuhi undang-undang ketiga Newton. Mari kita pertimbangkan sifat termudah bagi daya dalaman yang bertindak ke atas keseluruhan sistem mekanikal di mana-mana keadaan.

Harta pertama. Jumlah geometri semua daya dalaman sistem (vektor utama daya dalaman) adalah sama dengan sifar.

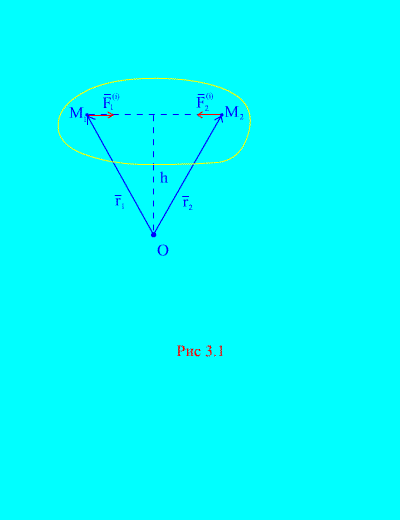
Sesungguhnya, jika kita mempertimbangkan mana-mana dua titik sewenang-wenangnya sistem, contohnya dan (Gamb. 3.1), kemudian untuk mereka , kerana daya tindakan dan tindak balas sentiasa sama dalam magnitud, bertindak sepanjang satu garis tindakan dalam arah yang bertentangan, yang menghubungkan titik-titik yang berinteraksi. Vektor utama daya dalaman terdiri daripada pasangan daya titik berinteraksi, oleh itu

(3.1)

Harta kedua. Jumlah geometri momen semua daya dalaman berbanding dengan titik arbitrari dalam ruang adalah sama dengan sifar.

Mari kita pertimbangkan sistem momen daya dan relatif kepada titik TENTANG(Gamb. 3.1). daripada (Gamb. 3.1). itu jelas

,

kerana kedua-dua daya mempunyai lengan yang sama dan bertentangan arah momen vektor. Momen utama daya dalaman relatif kepada satu titik TENTANG terdiri daripada jumlah vektor bagi ungkapan tersebut dan bersamaan dengan sifar. Oleh itu,

Biarkan luaran dan kuasa dalaman, bertindak ke atas sistem mekanikal yang terdiri daripada N mata (Gamb. 3.2). Jika paduan daya luaran dan paduan semua daya dalaman digunakan pada setiap titik sistem, maka bagi mana-mana k titik ke-1 sistem, persamaan pembezaan gerakan boleh dibuat. Akan ada sejumlah persamaan sedemikian N:

dan dalam unjuran pada paksi koordinat tetap 3 N:

(3.4)

Persamaan vektor (3.3) atau persamaan skalar setara (3.4) mewakili hukum pembezaan pergerakan titik bahan bagi keseluruhan sistem. Jika semua titik bergerak selari dengan satu satah atau satu garis lurus, maka bilangan persamaan (3.4) dalam kes pertama ialah 2 N, pada yang kedua N.

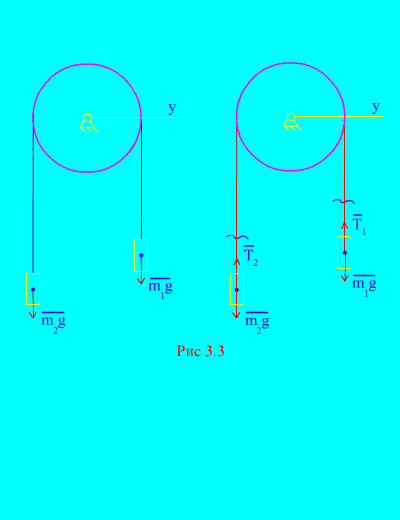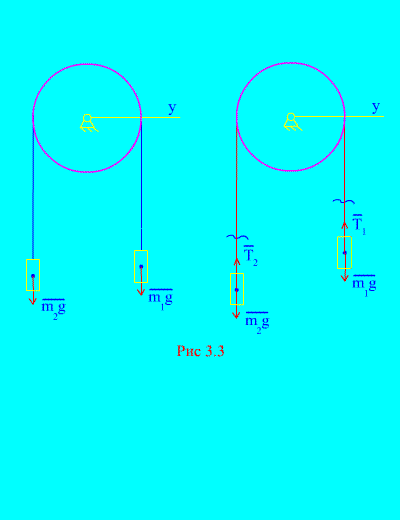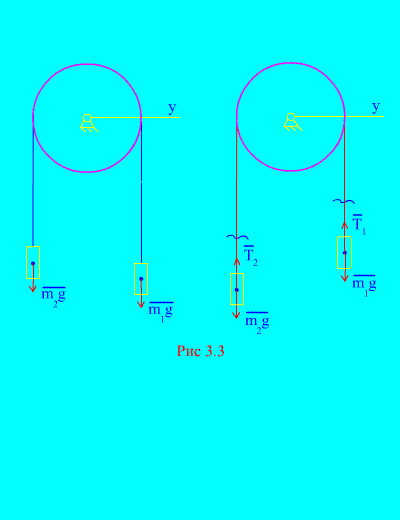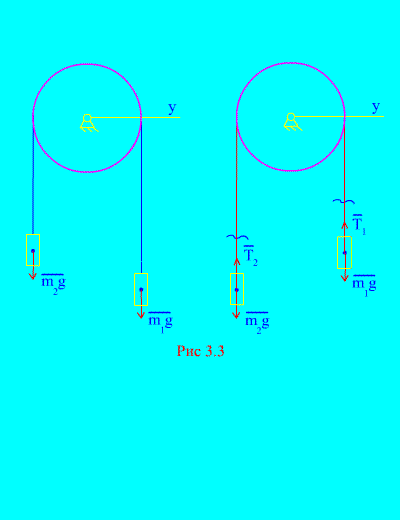
Contoh 1. Dua jisim disambungkan antara satu sama lain dengan kabel yang tidak dapat dipanjangkan yang dilemparkan ke atas bongkah (Gamb. 3.3). Mengabaikan daya geseran, serta jisim blok dan kabel, menentukan hukum pergerakan beban dan ketegangan kabel.

Penyelesaian. Sistem ini terdiri daripada dua badan bahan (disambungkan dengan kabel yang tidak boleh dipanjangkan) yang bergerak selari dengan paksi yang sama X. Mari kita tuliskan hukum pembezaan gerakan dalam unjuran pada paksi X untuk setiap badan.

Biarkan berat kanan turun dengan pecutan, maka berat kiri akan naik dengan pecutan. Kami secara mental membebaskan diri daripada sambungan (kabel) dan menggantikannya dengan reaksi dan (Gamb. 3.3). Memandangkan badan itu bebas, mari kita lukiskan undang-undang pembezaan pergerakan dalam unjuran ke paksi X(bermaksud bahawa ketegangan benang adalah daya dalaman, dan berat beban adalah luaran):

Oleh kerana dan (badan disambungkan dengan tali yang tidak dapat dipanjangkan), kami memperoleh

Menyelesaikan persamaan ini untuk pecutan dan ketegangan kabel T, kita dapat

.

Perhatikan bahawa ketegangan dalam kabel tidak sama dengan daya graviti beban yang sepadan.

3. 2. Teorem tentang gerakan pusat jisim

Adalah diketahui bahawa badan tegar dan sistem mekanikal dalam pesawat boleh bergerak dengan agak kompleks. Teorem pertama tentang gerakan jasad dan sistem mekanikal boleh didapati seperti berikut: baling k.-l. objek yang terdiri daripada banyak jasad pepejal yang diikat bersama. Jelas bahawa dia akan terbang dalam parabola. Ini didedahkan ketika mengkaji pergerakan titik. Walau bagaimanapun, kini objek itu bukan titik. Ia berpusing dan bergoyang semasa penerbangannya mengelilingi beberapa pusat berkesan yang bergerak dalam parabola. Teorem gerakan pertama mata pelajaran yang kompleks mengatakan bahawa pusat berkesan tertentu ialah pusat jisim objek yang bergerak. Pusat jisim tidak semestinya terletak di dalam badan itu sendiri; ia boleh terletak di luarnya.

Teorem. Pusat jisim sistem mekanikal bergerak seperti titik bahan dengan jisim jisim yang sama keseluruhan sistem di mana semua daya luaran yang bertindak ke atas sistem digunakan.

Untuk membuktikan teorem, kita menulis semula hukum pembezaan gerakan (3.3) ke dalam borang berikut:

(3.5)

di mana N – bilangan titik sistem.

Mari tambahkan persamaan bersama-sama sebutan demi sebutan:

(A)

Kedudukan pusat jisim sistem mekanikal relatif kepada sistem koordinat yang dipilih ditentukan oleh formula (2.1): di mana M– jisim sistem. Kemudian bahagian kiri kesamaan (a) akan ditulis

Jumlah pertama di sebelah kanan kesamaan (a) adalah sama dengan vektor utama daya luaran, dan yang terakhir, dengan sifat daya dalaman, adalah sama dengan sifar. Kemudian kesamaan (a), dengan mengambil kira (b), akan ditulis semula

, (3.6)

mereka. hasil darab jisim sistem dan pecutan pusat jisimnya adalah sama dengan jumlah geometri semua kuasa luar yang bertindak ke atas sistem.

Daripada persamaan (3.6) ia menunjukkan bahawa daya dalaman tidak secara langsung mempengaruhi pergerakan pusat jisim. Walau bagaimanapun, dalam beberapa kes ia adalah punca kemunculan daya luaran yang digunakan pada sistem. Oleh itu, daya dalaman yang menggerakkan roda pemanduan kereta ke dalam putaran menyebabkan daya lekatan luaran dikenakan pada rim roda untuk bertindak ke atasnya.

Contoh 2. Mekanisme, terletak dalam satah menegak, dipasang pada satah licin mendatar dan dilekatkan padanya dengan bar yang dipasang tegar ke permukaan KEPADA Dan L (Gamb. 3.4).

Jejari cakera 1 R tidak bergerak. Jisim cakera 2 m dan jejari r dilekatkan pada engkol, panjang R+ r pada titik C 2. Engkol berputar pada pemalar

kelajuan sudut. DALAM detik permulaan engkol menduduki kedudukan mendatar yang betul. Mengabaikan jisim engkol, tentukan daya mendatar dan menegak maksimum yang bertindak pada bar jika jumlah jisim katil dan roda 1 adalah sama M. Juga pertimbangkan kelakuan mekanisme jika tiada bar.

Penyelesaian. Sistem ini terdiri daripada dua jisim ( N=2 ): cakera tetap 1 dengan bingkai dan cakera boleh alih 2. Arahkan paksi di melalui pusat graviti cakera pegun secara menegak ke atas, paksi X- bersama satah mendatar.

Mari kita tulis teorem tentang gerakan pusat jisim (3.6) dalam bentuk koordinat

Daya luaran sistem ini ialah: berat bingkai dan cakera tetap - Mg, berat cakera bergerak - mg, - jumlah tindak balas mendatar bolt, - jumlah tindak balas normal satah. Oleh itu,

Kemudian undang-undang gerakan (b) akan ditulis semula

Mari kita hitung koordinat pusat jisim sistem mekanikal:

; (G)

seperti yang dapat dilihat daripada (Gamb. 3.4), , , (sudut engkol), . Menggantikan ungkapan ini kepada (d) dan mengira terbitan kedua berkenaan dengan masa t daripada , , kita dapat itu

(e)

Menggantikan (c) dan (e) kepada (b), kita dapati

Tekanan mendatar yang bertindak pada bar adalah paling besar dan nilai terkecil, Bila cos = 1 sewajarnya, i.e.

Tekanan mekanisme pada satah mendatar mempunyai nilai tertinggi dan terendah apabila dosa sewajarnya, i.e.

Malah, masalah pertama dinamik telah diselesaikan: mengikut persamaan gerakan yang diketahui pusat jisim sistem (d), daya yang terlibat dalam pergerakan itu dipulihkan.

Dengan ketiadaan bar K Dan L (Gamb. 3.4), mekanisme mungkin mula melantun di atas satah mendatar. Ini akan berlaku apabila, i.e. apabila , ia berikutan bahawa halaju sudut putaran engkol, di mana mekanisme melantun, mesti memenuhi kesamaan

.

3. 3. Hukum kekekalan gerakan pusat jisim

Jika vektor utama daya luaran yang bertindak pada sistem adalah sama dengan sifar, i.e. , kemudian dari(3.6)ia berikutan bahawa pecutan pusat jisim adalah sifar, oleh itu, kelajuan pusat jisim adalah malar dalam magnitud dan arah. Jika, khususnya, pada saat awal pusat jisim berada dalam keadaan pegun, maka ia berada dalam keadaan pegun untuk sepanjang masa manakala vektor utama daya luaran adalah sama dengan sifar.

Beberapa akibat daripada teorem ini.

· Daya dalaman sahaja tidak boleh mengubah sifat pergerakan pusat jisim sistem.

· Jika vektor utama daya luaran yang bertindak ke atas sistem adalah sifar, maka pusat jisim berada dalam keadaan rehat atau bergerak secara seragam dan lurus.

· Jika unjuran vektor utama daya luaran sistem pada beberapa paksi tetap adalah sama dengan sifar, maka unjuran halaju pusat jisim sistem pada paksi ini tidak berubah.

· Sepasang daya yang dikenakan pada jasad tegar tidak boleh mengubah pergerakan pusat jisimnya (ia hanya boleh menyebabkan badan berputar mengelilingi pusat jisim).

Mari kita pertimbangkan contoh yang menggambarkan undang-undang pemuliharaan gerakan pusat jisim.

Contoh 3. Dua jisim disambungkan oleh benang yang tidak dapat dipanjangkan yang dilemparkan melalui bongkah (Gamb. 3.5), ditetapkan pada baji dengan jisim M. Baji terletak pada satah mendatar yang licin. Pada saat awal sistem berada dalam keadaan rehat. Cari anjakan baji di sepanjang satah apabila beban pertama diturunkan ke ketinggian N. Abaikan jisim blok dan benang.

Penyelesaian. Daya luaran yang bertindak pada baji bersama-sama dengan beban ialah graviti, dan Mg, dan juga tindak balas biasa permukaan mendatar licin N. Oleh itu,

Memandangkan pada mulanya sistem berada dalam keadaan rehat, kami mempunyai .

Mari kita mengira koordinat pusat jisim sistem pada dan pada masa ini t 1 apabila beban berat g akan turun ke ketinggian H.

Buat masa ini:

,

di mana , , X– masing-masing, koordinat pusat jisim beban seberat g, g dan seberat baji Mg.

Mari kita andaikan bahawa baji pada saat masa bergerak ke arah positif paksi lembu mengikut jumlah L, jika berat beban jatuh ke ketinggian N. Kemudian, buat masa ini

kerana beban bersama baji akan bergerak ke L ke kanan, dan beban akan bergerak ke atas sepanjang baji. Sejak , kemudian selepas pengiraan kita dapat

.

3.4. Kuantiti pergerakan sistem

3.4.1. Pengiraan momentum sistem

Kuantiti pergerakan titik bahan dipanggil kuantiti vektor, sama dengan produk jisim titik dengan vektor halajunya

Unit ukuran momentum -

Momentum sistem mekanikal ialah jumlah vektor momentum titik individu sistem, i.e.

di mana N – bilangan titik sistem.

Momentum sistem mekanikal boleh dinyatakan dalam sebutan jisim sistem M dan kelajuan pusat jisim. sungguh,

mereka. Momentum sistem adalah sama dengan hasil darab jisim keseluruhan sistem dan kelajuan pusat jisimnya. Hala tuju sama dengan arah (Gamb. 3.6)

Dalam unjuran ke paksi segi empat tepat yang kita ada

di mana , , ialah unjuran halaju pusat jisim sistem.

Di sini M– jisim sistem mekanikal; tidak berubah apabila sistem bergerak.

Keputusan ini amat mudah digunakan apabila mengira kuantiti pergerakan jasad tegar.

Daripada formula (3.7) adalah jelas bahawa jika sistem mekanikal bergerak sedemikian rupa sehingga pusat jisimnya kekal pegun, maka momentum sistem itu kekal sama dengan sifar.

3.4.2. Dorongan daya asas dan penuh

Tindakan daya pada titik material dari semasa ke semasa dt boleh dicirikan oleh impuls asas. Jumlah impuls daya dari semasa ke semasa t, atau dorongan daya, ditentukan oleh formula

atau dalam unjuran ke koordinat paksi

(3.8a)

Unit impuls daya ialah .

3.4.3. Teorem tentang perubahan momentum sistem

Biarkan daya luaran dan dalaman digunakan pada titik-titik sistem. Kemudian untuk setiap titik sistem kita boleh menggunakan hukum pembezaan gerakan (3.3), dengan mengingati bahawa :

.

Menjumlahkan semua mata sistem, kami memperoleh

Dengan harta kuasa dalaman dan dengan definisi kita ada

(3.9)

Mendarab kedua-dua belah persamaan ini dengan dt, kita memperoleh teorem tentang perubahan momentum dalam bentuk pembezaan:

, (3.10)

mereka. momentum pembezaan sistem mekanikal adalah sama dengan jumlah vektor bagi impuls asas semua daya luaran yang bertindak pada titik sistem mekanikal.

Mengira kamiran kedua-dua belah (3.10) sepanjang masa dari 0 hingga t, kita memperoleh teorem dalam bentuk terhingga atau kamiran

(3.11)

Dalam unjuran ke paksi koordinat yang kita akan ada

Perubahan momentum sistem mekanikal dari semasa ke semasat, adalah sama dengan jumlah vektor semua impuls daya luar yang bertindak pada titik sistem mekanikal pada masa yang sama.

Contoh 4. Muatkan berat m turun ke bawah satah condong daripada keadaan rehat di bawah pengaruh daya F, berkadar dengan masa: , di mana (Gamb. 3.7). Apakah kelajuan yang akan diperolehi oleh badan selepas itu t saat selepas permulaan pergerakan, jika pekali geseran gelongsor beban pada satah condong adalah sama dengan f.

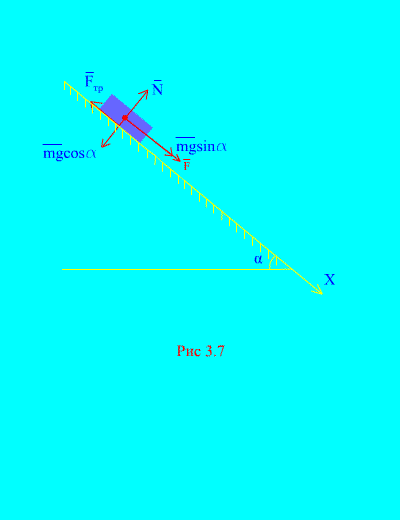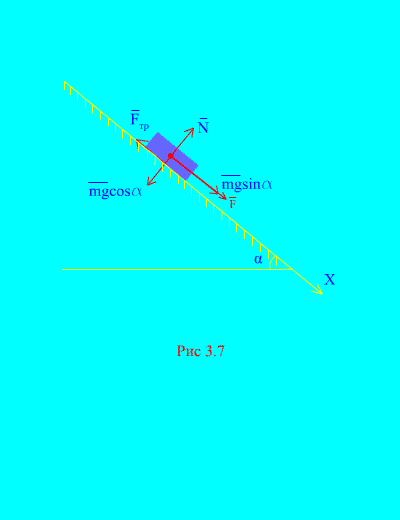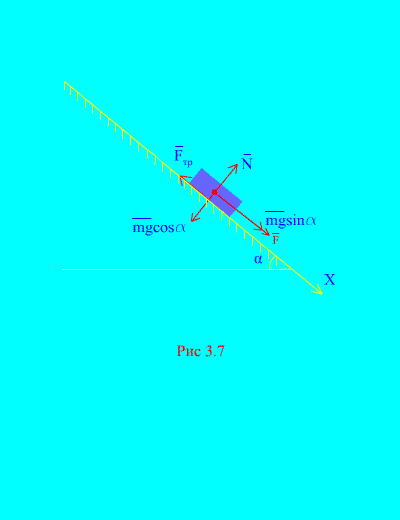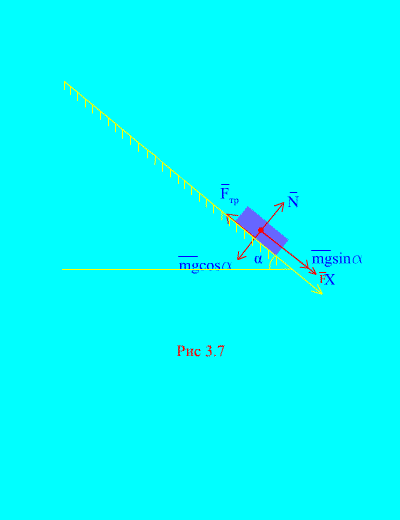
Penyelesaian. Mari kita gambarkan daya yang dikenakan pada beban: mg - daya graviti beban, N ialah tindak balas normal satah, ialah daya geseran gelongsor beban pada satah, dan . Arah semua daya ditunjukkan dalam (Gamb. 3.7).

Mari kita arahkan paksi X sepanjang satah condong ke bawah. Mari kita tulis teorem tentang perubahan momentum (3.11) dalam unjuran pada paksi X:

(A)

Mengikut syarat, kerana pada saat awal masa beban berada dalam keadaan rehat. Jumlah unjuran impuls semua daya pada paksi x adalah sama dengan

Oleh itu,

,

.

3.4.4. Undang-undang pengekalan momentum

Undang-undang pemuliharaan diperoleh sebagai kes khas teorem mengenai perubahan momentum. Dua kes khas mungkin.

· Jika jumlah vektor semua daya luar yang digunakan pada sistem adalah sama dengan sifar, i.e. , maka daripada teorem ia mengikuti (3.9) , Apa ,

mereka. jika vektor utama daya luaran sistem adalah sifar, maka jumlah gerakan sistem adalah malar dalam magnitud dan arah.

· Jika unjuran vektor utama daya luaran ke mana-mana paksi koordinat sama dengan sifar, contohnya Oh, i.e. , maka unjuran momentum pada paksi ini ialah nilai malar.

Mari kita pertimbangkan contoh penggunaan undang-undang pengekalan momentum.

Contoh 5. Bandul balistik ialah jasad dengan jisim yang digantung pada benang panjang (Gamb. 3.8).

Sebutir peluru berjisim, bergerak dengan laju V dan memukul badan yang tidak bergerak, tersangkut di dalamnya, dan badan itu menyimpang. Berapakah kelajuan peluru itu jika badan naik ke ketinggian h ?

Penyelesaian. Biarkan badan dengan peluru yang tersangkut memperoleh kelajuan. Kemudian, menggunakan undang-undang pemuliharaan momentum semasa interaksi dua jasad, kita boleh menulis .

Kelajuan boleh dikira menggunakan undang-undang pemuliharaan tenaga mekanikal . lepas tu . Hasilnya kita dapati

.

Contoh 6. Air memasuki saluran pegun (Gamb. 3.9) keratan rentas berubah-ubah dengan kelajuan pada sudut ke mendatar; segi empat sama keratan rentas saluran di pintu masuk; kelajuan air di pintu keluar dari saluran membuat sudut dengan ufuk.

Tentukan komponen mendatar bagi tindak balas yang terdapat pada air pada dinding saluran. Ketumpatan air .

Penyelesaian. Kami akan menentukan komponen mendatar tindak balas yang dikenakan oleh dinding saluran pada air. Daya ini sama besarnya dan bertentangan dengan tanda dengan daya yang dikehendaki. Kami mempunyai, menurut (3.11a),

. (A)

Kami mengira jisim isipadu cecair yang memasuki saluran semasa masa t:

Kuantiti rAV 0 dipanggil jisim kedua - jisim cecair yang mengalir melalui mana-mana bahagian paip per unit masa.

Jumlah air yang sama meninggalkan terusan pada masa yang sama. Kelajuan awal dan akhir diberikan dalam keadaan.

Jom kira sebelah kanan kesamaan (a) yang menentukan jumlah unjuran pada paksi mendatar bagi daya luar yang digunakan pada sistem (air). Satu-satunya daya mendatar ialah komponen mendatar bagi tindak balas dinding yang terhasil Rx. Daya ini malar semasa pergerakan air mantap. sebab tu

. (V)

Menggantikan (b) dan (c) kepada (a), kita dapat

3.5. Momen kinetik sistem

3.5.1. Momen momentum utama sistem

Biarkan vektor jejari titik dengan jisim sistem berbanding beberapa titik A, dipanggil pusat (Gamb. 3.10).

Momentum momentum (momen kinetik) sesuatu titik berbanding pusat A dipanggil vektor , ditentukan oleh formula

. (3.12)

Dalam kes ini, vektor diarahkan berserenjang dengan satah yang melalui pusat A dan vektor .

Momentum momentum (momen kinetik) sesuatu titik berbanding paksi dipanggil unjuran pada paksi ini bagi momen momentum titik relatif kepada mana-mana pusat yang dipilih pada paksi ini.

Momen utama momentum (momen kinetik) sistem berbanding pusat A dipanggil kuantiti

(3.13)

Momen utama momentum (momen kinetik) sistem berbanding paksi dipanggil unjuran pada paksi ini bagi momen momentum utama sistem berbanding mana-mana yang dipilih pada ini paksi tengah.

3.5.2. Momen kinetik jasad tegar berputar tentang paksi putaran

Mari kita selaraskan titik tetap TENTANG badan berbaring pada paksi putaran TENTANGz, dengan asal usul sistem koordinat Ohooz, yang paksinya akan berputar dengan badan (Gamb. 3.11). Biarkan vektor jejari sesuatu titik badan berbanding dengan asal koordinat; Unjuran vektor halaju sudut jasad pada paksi yang sama kita nyatakan 0, 0, ().

Selalunya adalah mungkin untuk mengenal pasti ciri penting gerakan sistem mekanikal tanpa menggunakan penyepaduan sistem persamaan pembezaan gerakan. Ini dicapai dengan menggunakan teorem umum dinamik.

5.1. Konsep dan definisi asas

Kekuatan luaran dan dalaman. Sebarang daya yang bertindak pada titik dalam sistem mekanikal semestinya sama ada daya aktif, atau tindak balas komunikasi. Seluruh set daya yang bertindak pada titik sistem boleh dibahagikan kepada dua kelas secara berbeza: daya luaran dan daya dalaman (indeks e dan i - dari perkataan Latin externus - luaran dan internus - dalaman). Daya luaran ialah daya yang bertindak pada titik sistem dari titik dan badan yang bukan sebahagian daripada sistem yang sedang dipertimbangkan. Daya interaksi antara titik dan badan sistem yang sedang dipertimbangkan dipanggil dalaman.

Pembahagian ini bergantung pada mata dan badan bahan mana yang dimasukkan oleh penyelidik dalam sistem mekanikal yang sedang dipertimbangkan. Jika anda mengembangkan komposisi sistem dengan memasukkan titik dan badan tambahan, maka beberapa daya yang berada di luar untuk sistem sebelumnya boleh menjadi dalaman untuk sistem yang dikembangkan.

Sifat kuasa dalaman. Oleh kerana daya ini adalah daya interaksi antara bahagian sistem, mereka memasuki sistem lengkap daya dalaman dalam "dua", disusun mengikut aksiom tindakan-tindak balas. Setiap "dua" itu mempunyai kekuatan

vektor utama dan perkara utama relatif kepada pusat sewenang-wenangnya adalah sama dengan sifar. Oleh kerana sistem lengkap kuasa dalaman hanya terdiri daripada "dua", maka

1) vektor utama sistem daya dalaman adalah sifar,

2) momen utama sistem daya dalaman berbanding dengan titik sewenang-wenangnya adalah sama dengan sifar.

Jisim sistem dipanggil jumlah aritmetik jisim tk semua titik dan jasad yang membentuk sistem:

Pusat jisim(pusat inersia) sistem mekanikal dipanggil titik geometri C, vektor jejari dan koordinat yang ditentukan oleh formula

di manakah vektor jejari dan koordinat titik-titik yang membentuk sistem.

Untuk jasad tegar yang terletak dalam medan graviti seragam, kedudukan pusat jisim dan pusat graviti bertepatan dalam kes lain, ini adalah titik geometri yang berbeza.

Bersama-sama dengan sistem rujukan inersia, sistem rujukan bukan inersia yang bergerak secara translasi sering dianggap serentak. Paksi koordinatnya (paksi König) dipilih supaya asal C sentiasa bertepatan dengan pusat jisim sistem mekanikal. Selaras dengan definisi, pusat jisim tidak bergerak dalam paksi Koenig dan terletak pada asal koordinat.

Momen inersia sistem relatif kepada paksi dipanggil kuantiti skalar sama dengan jumlah hasil darab jisim mk semua titik sistem dengan kuasa dua jaraknya ke paksi:

Jika sistem mekanikal adalah badan tegar, untuk mencari 12 anda boleh menggunakan formula

di manakah ketumpatan, isipadu yang diduduki oleh badan.

Mari kita pertimbangkan pergerakan sistem objek material tertentu berbanding sistem koordinat tetap Apabila sistem itu tidak bebas, maka ia boleh dianggap sebagai bebas jika kita membuang sambungan yang dikenakan pada sistem dan menggantikan tindakannya dengan tindak balas yang sepadan.

Marilah kita membahagikan semua daya yang digunakan pada sistem kepada luaran dan dalaman; kedua-duanya mungkin termasuk tindak balas yang dibuang

sambungan. Biarkan dan nyatakan vektor utama dan momen utama daya luar berbanding titik A.

1. Teorem tentang perubahan momentum. Jika ialah jumlah pergerakan sistem, maka (lihat)

iaitu teorem adalah sah: terbitan masa bagi momentum sistem adalah sama dengan vektor utama semua daya luaran.

Menggantikan vektor melalui ungkapannya di mana jisim sistem, ialah halaju pusat jisim, persamaan (4.1) boleh diberikan bentuk yang berbeza:

Kesamaan ini bermakna bahawa pusat jisim sistem bergerak seperti titik bahan yang jisimnya sama dengan jisim sistem dan yang dikenakan daya yang secara geometri sama dengan vektor utama semua daya luaran sistem. Pernyataan terakhir dipanggil teorem mengenai gerakan pusat jisim (pusat inersia) sistem.

Jika kemudian daripada (4.1) ia mengikuti bahawa vektor momentum adalah malar dalam magnitud dan arah. Mengunjurkannya pada paksi koordinat, kami memperoleh tiga kamiran pertama skalar, persamaan pembezaan penutup berganda sistem:

Kamiran ini dipanggil kamiran momentum. Apabila kelajuan pusat jisim adalah malar, iaitu, ia bergerak secara seragam dan selari.

Jika unjuran vektor utama daya luaran pada mana-mana satu paksi, contohnya pada paksi, adalah sama dengan sifar, maka kita mempunyai satu kamiran pertama, atau jika dua unjuran vektor utama adalah sama dengan sifar, maka terdapat dua kamiran momentum.

2. Teorem tentang perubahan momentum sudut. Biarkan A adalah beberapa titik sewenang-wenang dalam ruang (bergerak atau pegun), yang tidak semestinya bertepatan dengan mana-mana titik material tertentu sistem sepanjang masa pergerakan. Kami menandakan kelajuannya dalam sistem koordinat tetap dengan Teorem pada perubahan momentum sudut sistem bahan relatif kepada titik A mempunyai bentuk

Jika titik A ditetapkan, maka kesamaan (4.3) mengambil bentuk yang lebih mudah:

Kesamaan ini menyatakan teorem tentang perubahan momentum sudut sistem berbanding dengan titik tetap: terbitan masa bagi momentum sudut sistem, dikira relatif kepada beberapa titik tetap, adalah sama dengan momen utama semua daya luaran berbanding dengan titik ini.

Jika kemudian mengikut (4.4) vektor momentum sudut adalah malar dalam magnitud dan arah. Mengunjurkannya pada paksi koordinat, kami memperoleh kamiran pertama skalar bagi persamaan pembezaan sistem berganda:

Kamiran ini dipanggil kamiran momentum atau kamiran luas.

Jika titik A bertepatan dengan pusat jisim sistem, maka sebutan pertama di sebelah kanan kesamaan (4.3) hilang dan teorem pada perubahan momentum sudut mempunyai bentuk tulisan yang sama (4.4) seperti dalam kes titik tetap A. Perhatikan (lihat ms 4 § 3), bahawa dalam kes yang sedang dipertimbangkan, momentum sudut mutlak sistem di sebelah kiri kesamaan (4.4) boleh digantikan dengan momentum sudut yang sama sistem dalam pergerakannya berbanding dengan pusat jisim.

Biarkan beberapa paksi malar atau paksi arah malar yang melalui pusat jisim sistem, dan jadikan momen kinetik sistem berbanding paksi ini. Daripada (4.4) ia mengikutinya

di mana adalah momen daya luar berbanding paksi. Jika semasa keseluruhan pergerakan kita mempunyai kamiran pertama

Dalam karya S.A. Chaplygin, beberapa generalisasi teorem mengenai perubahan momentum kinetik telah diperoleh, yang kemudiannya digunakan dalam menyelesaikan beberapa masalah pada bola bergolek. Generalisasi lanjut teorem mengenai perubahan momen mekanikal dan aplikasinya dalam masalah dinamik badan tegar terkandung dalam karya. Hasil utama kerja-kerja ini berkaitan dengan teorem tentang perubahan momentum kinetik berbanding dengan yang bergerak, sentiasa melalui beberapa titik bergerak A. Biarkan - vektor unit, diarahkan sepanjang paksi ini. Mendarab secara skalar dengan kedua-dua belah kesamaan (4.3) dan menambah istilah kepada dua bahagiannya yang kita dapat

Apabila keadaan kinematik dipenuhi

Persamaan (4.5) mengikuti daripada (4.7). Dan jika keadaan (4.8) dipenuhi semasa keseluruhan pergerakan, maka kamiran pertama (4.6) wujud.

Jika sambungan sistem adalah ideal dan membenarkan, antara anjakan maya, putaran sistem sebagai badan tegar di sekeliling paksi dan, maka momen utama tindak balas relatif kepada paksi dan sama dengan sifar, dan kemudian nilai pada sebelah kanan persamaan (4.5) mewakili momen utama semua daya aktif luaran berbanding paksi dan . Kesamaan momen ini kepada sifar dan kesahihan hubungan (4.8) akan berada dalam kes yang sedang dipertimbangkan syarat yang mencukupi untuk kewujudan kamiran (4.6).

Jika arah paksi dan malar, maka keadaan (4.8) akan ditulis dalam bentuk

Kesamaan ini bermakna unjuran halaju pusat jisim dan halaju titik A pada paksi dan pada satah berserenjang dengan ini adalah selari. Dalam karya S.A. Chaplygin, bukannya (4.9), kurang daripada keadaan umum di mana X ialah nilai pemalar arbitrari.

Perhatikan bahawa keadaan (4.8) tidak bergantung pada pilihan titik pada . Sesungguhnya, biarkan P ialah titik arbitrari pada paksi. Kemudian

dan oleh itu

Sebagai kesimpulan, kita perhatikan tafsiran geometri Rézal bagi persamaan (4.1) dan (4.4): vektor kelajuan mutlak hujung vektor dan adalah sama, masing-masing, dengan vektor utama dan momen utama semua daya luaran berbanding dengan titik A.

KEMENTERIAN PERTANIAN DAN MAKANAN REPUBLIK BELARUS

Institusi pendidikan "PERTANIAN NEGERI BELARUSIA

UNIVERSITI TEKNIKAL"

Jabatan Mekanik Teori dan Teori Mekanisme dan Mesin

MEKANIK TEORI

kompleks metodologi untuk pelajar kepakaran

74 06 Kejuruteraan Tani

Dalam 2 bahagian Bahagian 1

UDC 531.3(07) BBK 22.213ya7 T 33

Disusun oleh:

Calon Sains Fizikal dan Matematik, Profesor Madya Yu. S. Biza, calon sains teknikal, profesor madya N. L. Rakova, pensyarah kanan. A. Tarasevich

Pengulas:

Jabatan Mekanik Teori Institusi Pendidikan "Belarus National universiti teknikal"(pengurus

Jabatan Mekanik Teori BNTU Doktor Sains Fizikal dan Matematik, Profesor A. V. Chigarev);

Penyelidik Utama Makmal Perlindungan Getaran Sistem Mekanikal Institusi Saintifik Negeri United Institute of Mechanical Engineering

NAS of Belarus", calon sains teknikal, profesor bersekutu A. M. Goman

Mekanik teori. Bahagian "Dinamik": pendidikan

kaedah T33. kompleks. Dalam 2 bahagian. Bahagian 1 / disusun oleh: Yu S. Biza, N. L. Rakova, I. A. Tarasevich. – Minsk: BGATU, 2013. – 120 p.

ISBN 978-985-519-616-8.

DALAM kompleks pendidikan dan metodologi bahan mengenai kajian bahagian "Dinamik", bahagian 1, yang merupakan sebahagian daripada disiplin "Mekanik Teori", dibentangkan. Termasuk kursus kuliah, bahan asas untuk membuat persembahan kelas amali, tugasan dan sampel tugasan untuk kerja dan kawalan bebas aktiviti pendidikan sepenuh masa dan borang surat menyurat latihan.

UDC 531.3(07) BBK 22.213ya7

PENGENALAN................................................ ....... .........................................
1. KANDUNGAN SAINTIFIK DAN TEORI PENDIDIKAN
KOMPLEKS METODOLOGI................................................ .... ..
1.1. Glosari................................................. ................................
1.2. Tajuk syarahan dan kandungannya............................................ .......... ..
Bab 1. Pengenalan kepada dinamik. Konsep Asas
mekanik klasik................................................. ........ ....................
Topik 1. Dinamik titik material............................................ ..........
1.1. Undang-undang dinamik titik material
(Hukum Galileo – Newton) ............................................ ..... ..........
1.2. Persamaan pembezaan pergerakan
1.3. Dua masalah utama dinamik............................................ ............
Topik 2. Dinamik gerakan relatif
titik bahan................................................ ... ..............................
Soalan untuk semakan................................................ .......... .............
Topik 3. Dinamik sistem mekanikal............................................ ..........
3.1. Geometri jisim Pusat jisim sistem mekanikal......
3.2. Kuasa dalaman................................................ ........ ...............
Soalan untuk semakan................................................ .......... .............
Topik 4. Momen inersia jasad tegar............................................ ............
4.1. Detik inersia badan tegar
relatif kepada paksi dan kutub................................................ ....... ......
4.2. Teorem mengenai momen inersia jasad tegar
relatif kepada paksi selari
(Teorem Huygens – Steiner) ............................................ ...... ....
4.3. Momen inersia emparan................................................ ......
Soalan untuk semakan................................................ .......... ............
Bab 2. Teorem am kedinamikan titik material

Topik 5. Teorem tentang gerakan pusat jisim sistem................................... .
Soalan untuk semakan................................................ .......... .............
Tugasan belajar kendiri................................................ ....
Topik 6. Momentum titik material
dan sistem mekanikal .............................................. ......... ...................
6.1. Momentum titik material 43
6.2. Daya impuls................................................ ... .......................
6.3. Teorem perubahan momentum
titik bahan................................................ ... ....................
6.4. Teorem perubahan vektor utama
momentum sistem mekanikal.........................
Soalan untuk semakan................................................ .......... .............
Tugasan belajar kendiri................................................ ....
Topik 7. Momentum titik material
dan sistem mekanikal berbanding pusat dan paksi......
7.1. Momentum titik material
relatif kepada pusat dan paksi................................................ ....... ..........
7.2. Teorem tentang perubahan momentum sudut
titik bahan relatif kepada pusat dan paksi......................
7.3. Teorem tentang perubahan momentum sudut
sistem mekanikal relatif kepada pusat dan paksi.................
Soalan untuk semakan................................................ .......... .............
Tugasan belajar kendiri................................................ ....
Topik 8. Kerja dan kuasa kuasa.......................................... .......... ............
Soalan untuk semakan................................................ .......... .............
Tugasan belajar kendiri................................................ ....
Topik 9. Tenaga kinetik titik bahan
dan sistem mekanikal .............................................. ......... ...................
9.1. Tenaga kinetik titik bahan
dan sistem mekanikal. Teorem König...................................
9.2. Tenaga kinetik pepejal
dengan pergerakan yang berbeza................................................. ......... ............
9.3. Tukar teorem tenaga kinetik
titik bahan................................................ ... ....................

9.4. Teorem tentang perubahan tenaga kinetik
sistem mekanikal................................................ ........ ................
Soalan untuk semakan................................................ .......... .............
Tugasan belajar kendiri................................................ ....
Topik 10. Medan daya berpotensi
dan tenaga keupayaan ................................................. .... ..............
Soalan untuk semakan................................................ .......... .............
Topik 11. Dinamik jasad tegar............................................ .......... .......
Soalan untuk semakan................................................ .......... .............
2. BAHAN UNTUK KAWALAN
MENGIKUT MODUL................................................ ... ...................................
KERJA BEBAS PELAJAR....................................
4. KEPERLUAN UNTUK PENDAFTARAN KAWALAN
BEKERJA UNTUK PELAJAR SEPENUH MASA DAN SURAT MENYURAT
BENTUK LATIHAN................................................ .... ........................
5. SENARAI SOALAN UNTUK PERSEDIAAN
UNTUK PEPERIKSAAN (UJIAN) PELAJAR
BENTUK PENGAJIAN SEPENUH MASA DAN SURAT MENYURAT.....................................
6. RUJUKAN.............................................. ..... ............

PENGENALAN

Mekanik teori - sains undang-undang am pergerakan mekanikal, keseimbangan dan interaksi badan material.

Ini adalah salah satu disiplin fiziko-matematik saintifik am asas. Ia adalah asas teori teknologi moden.

Kajian mekanik teori, bersama-sama dengan disiplin fizikal dan matematik yang lain, membantu mengembangkan ufuk saintifik, membangunkan kebolehan untuk khusus dan pemikiran abstrak dan membantu meningkatkan budaya teknikal umum pakar masa depan.

Mekanik teori, menjadi asas saintifik semua disiplin teknikal, menggalakkan pembangunan kemahiran keputusan yang rasional masalah kejuruteraan berkaitan dengan pengendalian, pembaikan dan reka bentuk mesin dan peralatan tebus guna pertanian dan tanah.

Berdasarkan sifat masalah yang sedang dipertimbangkan, mekanik dibahagikan kepada statik, kinematik dan dinamik. Dinamik ialah cabang mekanik teori yang mengkaji pergerakan badan material di bawah tindakan daya gunaan.

DALAM pendidikan dan metodologi kompleks (UMK) membentangkan bahan untuk mengkaji bahagian "Dinamik", yang merangkumi kursus kuliah, bahan asas untuk mengendalikan kerja amali, tugasan dan contoh pelaksanaan untuk kerja bebas dan memantau aktiviti pendidikan pelajar sepenuh masa dan separuh masa.

DALAM Hasil daripada mempelajari bahagian "Dinamik", pelajar mesti belajar asas teori dinamik dan kuasai kaedah asas untuk menyelesaikan masalah dinamik:

Mengetahui kaedah untuk menyelesaikan masalah dinamik, teorem am dinamik, prinsip mekanik;

Dapat menentukan undang-undang pergerakan badan bergantung kepada daya yang bertindak ke atasnya; menggunakan undang-undang dan teorem mekanik untuk menyelesaikan masalah; tentukan tindak balas statik dan dinamik sambungan yang mengehadkan pergerakan jasad.

Kurikulum disiplin "Mekanik Teori" menyediakan jumlah jam bilik darjah - 136, termasuk 36 jam untuk mempelajari bahagian "Dinamik".

1. KANDUNGAN SAINTIFIK DAN TEORI KOMPLEKS PENDIDIKAN DAN METODOLOGI

1.1. Glosari

Statik ialah bahagian mekanik yang menetapkan doktrin umum tentang pengurangan daya dan kajian sistem yang kompleks daya kepada bentuk termudah dan keadaan keseimbangan diwujudkan pelbagai sistem kekuatan

Kinematik ialah cabang mekanik teori yang mengkaji pergerakan objek material tanpa mengira sebab yang menyebabkan pergerakan ini, iaitu, tanpa mengira daya yang bertindak ke atas objek ini.

Dinamik ialah cabang mekanik teori yang mengkaji pergerakan jasad material (titik) di bawah tindakan daya gunaan.

Titik bahan– badan material, perbezaan dalam pergerakan mata yang tidak ketara.

Jisim badan ialah kuantiti positif skalar yang bergantung kepada jumlah bahan yang terkandung dalam badan tertentu dan menentukan ukuran inersianya pada pergerakan ke hadapan.

Sistem rujukan ialah sistem koordinat yang dikaitkan dengan badan yang berkaitan dengan pergerakan badan lain dikaji.

Sistem inersia– sistem di mana undang-undang dinamik pertama dan kedua dipenuhi.

Impuls daya ialah ukuran vektor bagi tindakan daya selama beberapa waktu.

Momentum titik material – ukuran vektor bagi gerakannya, sama dengan hasil darab jisim titik dan vektor halajunya.

Tenaga kinetik– ukuran skalar gerakan mekanikal.

Kerja daya asas ialah kuantiti skalar tak terhingga sama dengan produk skalar vektor daya kepada vektor anjakan kecil tak terhingga titik penggunaan daya.

Tenaga kinetik– ukuran skalar bagi gerakan mekanikal.

Tenaga kinetik titik bahan ialah tenaga skalar

kuantiti positif sama dengan separuh hasil darab jisim suatu titik dan kuasa dua halajunya.

Tenaga kinetik sistem mekanikal - aritme-

jumlah tik tenaga kinetik semua titik bahan sistem ini.

Daya ialah ukuran interaksi mekanikal badan, mencirikan keamatan dan arahnya.

1.2. Topik dan kandungan kuliah

Bahagian 1. Pengenalan kepada dinamik. Konsep Asas

mekanik klasik

Topik 1. Dinamik titik material

Undang-undang dinamik titik material (hukum Galileo – Newton). Persamaan pembezaan pergerakan titik bahan. Dua masalah utama dinamik untuk titik material. Penyelesaian masalah kedua dinamik; pemalar kamiran dan penentuannya mengikut keadaan awal.

Sastera:, ms 180-196, , ms 12-26.

Topik 2. Dinamik pergerakan relatif bahan

Pergerakan relatif bagi titik material. Persamaan pembezaan bagi gerakan relatif suatu titik; daya inersia mudah alih dan Coriolis. Prinsip relativiti dalam mekanik klasik. Kes keamanan relatif.

Sastera: , ms 180-196, , ms 127-155.

Topik 3. Geometri jisim. Pusat jisim sistem mekanikal

Jisim sistem. Pusat jisim sistem dan koordinatnya.

Sastera:, ms 86-93, ms 264-265

Topik 4. Momen inersia jasad tegar

Momen inersia jasad tegar berbanding paksi dan kutub. Jejari inersia. Teorem tentang momen inersia tentang paksi selari. Momen paksi inersia sesetengah jasad.

Momen inersia sentrifugal sebagai ciri asimetri badan.

Sastera: , ms 265-271, , ms 155-173.

Bahagian 2. Teorem am mengenai dinamik titik material

dan sistem mekanikal

Topik 5. Teorem tentang gerakan pusat jisim sistem

Teorem tentang gerakan pusat jisim sistem. Akibat daripada teorem mengenai gerakan pusat jisim sistem.

Sastera: , ms 274-277, , ms 175-192.

Topik 6. Momentum titik material

dan sistem mekanikal

Jumlah pergerakan titik bahan dan sistem mekanikal. Impuls asas dan impuls daya dalam tempoh masa yang terhad. Teorem tentang perubahan momentum titik dan sistem dalam bentuk pembezaan dan kamiran. Hukum kekekalan momentum.

Sastera: , ms 280-284, , ms 192-207.

Topik 7. Momentum titik material

dan sistem mekanikal berbanding pusat dan paksi

Momen momentum sesuatu titik relatif kepada pusat dan paksi. Teorem tentang perubahan momentum sudut suatu titik. Momen kinetik sistem mekanikal berbanding pusat dan paksi.

Momen kinetik jasad tegar berputar tentang paksi putaran. Teorem tentang perubahan momentum sudut sistem. Hukum kekekalan momentum sudut.

Sastera: , ms 292-298, , ms 207-258.

Topik 8. Kerja dan kuasa kuasa

Kerja daya asas, ungkapan analitikalnya. Kerja yang dilakukan secara paksa jalan akhir. Kerja graviti, daya kenyal. Jumlah kerja yang dilakukan oleh daya dalaman yang bertindak dalam jasad pepejal adalah sama dengan sifar. Kerja daya yang dikenakan pada jasad tegar yang berputar mengelilingi paksi tetap. kuasa. Kecekapan.

Sastera: , ms 208-213, , ms 280-290.

Topik 9. Tenaga kinetik titik bahan

dan sistem mekanikal

Tenaga kinetik titik bahan dan sistem mekanikal. Pengiraan tenaga kinetik jasad tegar dalam pelbagai kes pergerakannya. Teorem Koenig. Teorem tentang perubahan tenaga kinetik suatu titik dalam bentuk pembezaan dan kamiran. Teorem tentang perubahan tenaga kinetik sistem mekanikal dalam bentuk pembezaan dan kamiran.

Sastera: , ms 301-310, , ms 290-344.

Topik 10. Medan daya potensi dan potensi

Konsep medan daya. Medan daya berpotensi dan fungsi daya. Kerja daya pada anjakan akhir titik dalam medan daya berpotensi. Tenaga berpotensi.

Sastera: , ms 317-320, , ms 344-347.

Topik 11. Dinamik badan tegar

Persamaan pembezaan gerakan translasi bagi jasad tegar. Persamaan pembezaan pergerakan putaran jasad tegar mengelilingi paksi tetap. Bandul fizikal. Persamaan pembezaan gerakan satah jasad tegar.

Sastera: , ms 323-334, , ms 157-173.

Bahagian 1. Pengenalan kepada dinamik. Konsep Asas

mekanik klasik

Dinamik ialah cabang mekanik teori yang mengkaji pergerakan jasad material (titik) di bawah tindakan daya gunaan.

badan material- badan yang mempunyai jisim.

Titik bahan– badan material, perbezaan dalam pergerakan mata yang tidak ketara. Ini boleh sama ada jasad yang dimensinya semasa pergerakannya boleh diabaikan, atau jasad dengan dimensi terhingga jika ia bergerak secara translasi.

Titik bahan juga dipanggil zarah di mana badan pepejal dipecahkan secara mental apabila menentukan beberapa ciri dinamiknya. Contoh titik material (Rajah 1): a – pergerakan Bumi mengelilingi Matahari. Bumi ialah titik material b – gerakan translasi jasad tegar. Padat- ibu-

titik al, kerana V B = V A ; a B = a A ; c – putaran badan mengelilingi paksi.

Zarah jasad ialah titik material.

Inersia ialah sifat badan material untuk menukar kelajuan pergerakannya lebih cepat atau lebih perlahan di bawah pengaruh daya yang dikenakan.

Jisim jasad ialah kuantiti positif skalar yang bergantung kepada jumlah bahan yang terkandung dalam jasad tertentu dan menentukan ukuran inersianya semasa gerakan translasi. Dalam mekanik klasik, jisim ialah kuantiti tetap.

Kekuatan - ukuran kuantitatif interaksi mekanikal antara jasad atau antara jasad (titik) dan medan (elektrik, magnet, dll.).

Daya ialah kuantiti vektor yang dicirikan oleh magnitud, titik aplikasi dan arah (garis tindakan) (Rajah 2: A - titik aplikasi; AB - garis tindakan daya).

nasi. 2

Dalam dinamik, bersama-sama dengan daya malar, terdapat juga daya berubah, yang boleh bergantung pada masa t, kelajuanϑ, jarak, atau pada gabungan kuantiti ini, i.e.

F = const;

F = F(t) ;

F = F(ϑ ) ;

F = F(r) ;

F = F(t, r, ϑ) .

	Contoh daya sedemikian ditunjukkan dalam Rajah. 3: a −										– berat badan;
			(ϑ) – daya rintangan udara;		T =						– daya tarikan

lokomotif elektrik; c − F = F (r) – daya tolakan dari pusat O atau tarikan kepadanya.

Sistem rujukan ialah sistem koordinat yang dikaitkan dengan badan yang berkaitan dengan pergerakan badan lain dikaji.

Sistem inersia ialah sistem di mana hukum dinamik pertama dan kedua dipenuhi. Ini ialah sistem koordinat tetap atau sistem yang bergerak secara seragam dan linear.

Pergerakan dalam mekanik ialah perubahan kedudukan sesuatu jasad dalam ruang dan masa dalam hubungannya dengan jasad lain.

Ruang dalam mekanik klasik adalah tiga dimensi, mematuhi geometri Euclidean.

Masa ialah kuantiti skalar yang mengalir sama rata dalam mana-mana sistem rujukan.

Sistem unit ialah himpunan unit ukuran kuantiti fizik. Untuk mengukur semua kuantiti mekanikal, tiga unit asas adalah mencukupi: unit panjang, masa, jisim atau daya.

mekanikal	Dimensi		Jawatan	Dimensi	Jawatan
magnitud
				sentimeter
	kilogram-

Semua unit pengukuran kuantiti mekanikal yang lain diperoleh daripada ini. Dua jenis sistem unit digunakan: sistem antarabangsa Unit SI (atau lebih kecil - GHS) dan sistem teknikal unit - MKGSS.

Topik 1. Dinamik titik material

1.1. Undang-undang dinamik titik material (hukum Galileo–Newton)

Undang-undang pertama (hukum inersia).

Terpencil daripada pengaruh luar titik material mengekalkan keadaan rehatnya atau bergerak secara seragam dan lurus sehingga daya yang dikenakan memaksanya mengubah keadaan ini.

Pergerakan yang dilakukan oleh titik tanpa ketiadaan daya atau di bawah tindakan sistem daya yang seimbang dipanggil pergerakan oleh inersia.

Sebagai contoh, pergerakan badan sepanjang licin (daya geseran adalah sifar)

permukaan mendatar (Rajah 4: G – berat badan; N – tindak balas satah biasa).

Oleh kerana G = − N, maka G + N = 0.

Apabila ϑ 0 ≠ 0 badan bergerak pada kelajuan yang sama; apabila ϑ 0 = 0 badan berada dalam keadaan rehat (ϑ 0 ialah kelajuan awal).

Undang-undang kedua (undang-undang asas dinamik).

Hasil darab jisim titik dan pecutan yang diterimanya di bawah pengaruh daya tertentu adalah sama besarnya dengan daya ini, dan arahnya bertepatan dengan arah pecutan.

a b

Secara matematik, undang-undang ini dinyatakan oleh kesamaan vektor

Apabila F = const,

a = const – gerakan titik berubah secara seragam. EU-

sama ada ≠ const, α

– gerakan perlahan (Rajah 5, a);

a ≠ const,

a –

– pergerakan dipercepatkan (Rajah 5, b);

vektor pecutan;

– vektor daya; ϑ 0 – vektor halaju).

Apabila F = 0,a 0 = 0 = ϑ 0 = const – titik bergerak secara seragam dan rectilinearly atau pada ϑ 0 = 0 – ia berada dalam keadaan pegun (hukum inersia). Kedua

undang-undang membenarkan kita mewujudkan hubungan antara jisim m jasad yang terletak berhampiran permukaan bumi, dan beratnyaG .G = mg, dimanag –

pecutan graviti.

Undang-undang ketiga (undang-undang kesamaan tindakan dan tindak balas). Dua titik material bertindak antara satu sama lain dengan daya yang sama besarnya dan diarahkan sepanjang garis lurus yang bersambung

titik ini dalam arah yang bertentangan.

Oleh kerana daya F 1 = − F 2 dikenakan pada titik yang berbeza, maka sistem daya (F 1, F 2) tidak seimbang, iaitu (F 1, F 2)≈ 0 (Rajah 6).

Seterusnya

m a = m a

- sikap

jisim titik yang berinteraksi adalah berkadar songsang dengan pecutannya.

Undang-undang keempat (undang-undang kebebasan tindakan kuasa). Pecutan yang diterima oleh titik apabila bertindak padanya pada masa yang sama

tetapi beberapa daya, sama dengan jumlah geometri bagi pecutan tersebut yang akan diterima oleh titik jika setiap daya dikenakan padanya secara berasingan.

Penjelasan (Rajah 7).

t a n

a 1 a kF n

Daya terhasil R (F 1 ,...F k ,...F n ) .

Oleh kerana ma = R,F 1 = ma 1, ...,F k = ma k, ...,F n = lelaki, maka

a = a 1 + ...+ a k + ...+ a n = ∑ a k, iaitu hukum keempat adalah setara

k = 1

peraturan penambahan daya.

1.2. Persamaan pembezaan pergerakan titik bahan

Biarkan beberapa daya bertindak serentak pada titik material, di antaranya terdapat kedua-dua malar dan berubah-ubah.

Mari kita tulis hukum dinamik kedua dalam bentuk

= ∑

(t,

k = 1

, ϑ=

r – vektor jejari bagi yang bergerak

titik, maka (1.2) mengandungi terbitan r dan merupakan persamaan pembezaan pergerakan titik bahan dalam bentuk vektor atau persamaan asas dinamik bagi titik bahan.

Unjuran kesamaan vektor (1.2): - pada paksi koordinat Cartesan (Rajah 8, a)

maks = md
					= ∑ F kx;
					k = 1
boleh = md
					= ∑ F ky;	(1.3)
					k = 1
maz = m					= ∑ F kz;
					k = 1

Pada paksi semula jadi (Rajah 8, b)

maτ				= ∑ F k τ ,
				k = 1
				= ∑ F k n ;
				k = 1

mab = m0 = ∑ Fk b

k = 1

M t oM oa

b pada o

Persamaan (1.3) dan (1.4) ialah persamaan pembezaan pergerakan titik material, masing-masing, dalam paksi koordinat Cartesian dan paksi semula jadi, iaitu, persamaan pembezaan semula jadi yang biasanya digunakan untuk gerakan lengkung titik, jika trajektori bagi titik dan jejari kelengkungannya diketahui.

1.3. Dua masalah utama dinamik untuk titik material dan penyelesaiannya

Tugas pertama (langsung).

Mengetahui hukum gerakan dan jisim titik, tentukan daya yang bertindak ke atas titik itu.

Untuk menyelesaikan masalah ini, anda perlu mengetahui pecutan titik. Dalam masalah jenis ini, ia boleh dinyatakan secara langsung atau undang-undang pergerakan sesuatu titik boleh ditentukan, mengikut mana ia boleh ditentukan.

1. Jadi, jika gerakan sesuatu titik dinyatakan dalam koordinat Cartesan

x = f 1 (t), y = f 2 (t) dan z = f 3 (t), maka unjuran pecutan ditentukan

tion pada paksi koordinat x =		d 2 x			d 2 y			d 2 z		Dan kemudian - projek itu
daya F x , F y dan F z pada paksi ini:
				,k ) = F F z . (1.6) 2. Jika titik melakukan pergerakan melengkung dan hukum gerakan s = f (t), trajektori titik dan jejari kelengkungannya ρ diketahui, maka Ia adalah mudah untuk menggunakan paksi semula jadi, dan unjuran pecutan pada paksi ini ditentukan menggunakan formula yang terkenal: Paksi tangen a τ = d ϑ = d 2 2 s – pecutan tangen;dt dt Homenormal ds 2 a n = ϑ 2 = dt – pecutan normal. Unjuran pecutan ke binormal ialah sifar. Kemudian unjuran daya pada paksi semula jadi F = m F = m Modul dan arah daya ditentukan oleh formula: F =F τ 2 +F n 2 ; cos( ; cos( Masalah kedua ( songsang). Mengetahui daya yang bertindak pada titik, jisimnya dan syarat awal pergerakan, tentukan hukum pergerakan suatu titik atau mana-mana ciri kinematiknya yang lain. Keadaan awal untuk pergerakan titik dalam paksi Cartes ialah koordinat titik x 0, y 0, z 0 dan unjuran halaju awal ϑ 0 ke atas ini. paksi ϑ 0 x = x 0, ϑ 0 y = y 0 dan ϑ 0 z = z 0 pada masa yang sepadan dengan sepadan dengan permulaan gerakan titik dan diambil sama dengan sifar. Menyelesaikan masalah jenis ini datang kepada membuat pembezaan persamaan nyata (atau satu persamaan) gerakan titik material dan penyelesaiannya yang berikutnya dengan integrasi langsung atau menggunakan teori persamaan pembezaan. Ulangkaji soalan 1. Apakah kajian dinamik? 2. Apakah jenis gerakan yang dipanggil gerakan inersia? 3. Dalam keadaan apakah titik material akan berada dalam keadaan diam atau bergerak secara seragam dan lurus? 4. Apakah intipati masalah utama pertama bagi dinamik titik material? Tugasan kedua? 5. Tuliskan persamaan pembezaan semula jadi bagi gerakan suatu titik bahan. Tugasan belajar sendiri 1. Titik dengan jisim m = 4 kg bergerak sepanjang garis lurus mengufuk dengan pecutan a = 0.3 t. Tentukan magnitud daya yang bertindak pada titik itu mengikut arah pergerakannya pada masa t = 3 s. 2. Bahagian berjisim m = 0.5 kg meluncur ke bawah dulang. Pada sudut yang manakah kepada satah mengufuk dulang harus diletakkan supaya bahagian itu bergerak dengan pecutan a = 2 m/s 2? Ekspres sudut dalam darjah. 3. Satu titik berjisim m = 14 kg bergerak di sepanjang paksi Ox dengan pecutan x = 2 t. Tentukan modulus daya yang bertindak pada satu titik dalam arah gerakan pada masa t = 5 s.

(SISTEM MEKANIKAL) – Pilihan IV

1. Persamaan asas bagi dinamik titik material, seperti yang diketahui, dinyatakan oleh persamaan. Persamaan pembezaan gerakan mata sewenang-wenangnya sistem mekanikal bukan bebas mengikut dua kaedah pembahagian daya boleh ditulis dalam dua bentuk:

(1) , dengan k=1, 2, 3, … , n – bilangan titik sistem bahan.

(2)

di manakah jisim titik k; - vektor jejari titik k-th, - daya (aktif) tertentu yang bertindak pada titik k-th atau paduan semua daya aktif yang bertindak pada titik k-th. - terhasil daripada daya tindak balas ikatan yang bertindak pada titik k; - terhasil daripada daya dalaman yang bertindak pada titik k; - terhasil daripada daya luar yang bertindak pada titik k.

Menggunakan persamaan (1) dan (2), seseorang boleh berusaha untuk menyelesaikan kedua-dua masalah pertama dan kedua dinamik. Walau bagaimanapun, menyelesaikan masalah kedua dinamik untuk sistem menjadi sangat rumit bukan sahaja dengan titik matematik penglihatan, tetapi juga kerana kita berhadapan dengan kesukaran asas. Mereka terdiri daripada fakta bahawa kedua-dua untuk sistem (1) dan untuk sistem (2) bilangan persamaan adalah penting kurang bilangan tidak diketahui.

Jadi, jika kita menggunakan (1), maka dinamik yang diketahui untuk masalah kedua (songsang) ialah dan , dan yang tidak diketahui akan menjadi dan . Persamaan vektor akan menjadi " n”, dan yang tidak diketahui - “2n”.

Jika kita meneruskan dari sistem persamaan (2), maka beberapa daya luar diketahui. Mengapa berpisah? Hakikatnya ialah kuasa luar termasuk tindak balas luaran sambungan yang tidak diketahui. Selain itu, .

Oleh itu, kedua-dua sistem (1) dan sistem (2) TIDAK DITUTUP. Ia adalah perlu untuk menambah persamaan, dengan mengambil kira persamaan sambungan, dan mungkin juga perlu untuk mengenakan beberapa sekatan pada sambungan itu sendiri. Apa yang perlu dilakukan?

Jika kita bermula dari (1), maka kita boleh mengikuti laluan mengarang persamaan Lagrange jenis pertama. Tetapi jalan ini tidak rasional kerana tugas yang lebih mudah(sedikit darjah kebebasan), semakin sukar untuk diselesaikan dari sudut matematik.

Kemudian mari kita perhatikan sistem (2), di mana - sentiasa tidak diketahui. Langkah pertama dalam menyelesaikan sistem adalah untuk menghapuskan yang tidak diketahui ini. Perlu diingat bahawa, sebagai peraturan, kita tidak berminat dengan daya dalaman apabila sistem bergerak, iaitu, apabila sistem bergerak, tidak perlu mengetahui bagaimana setiap titik sistem bergerak, tetapi ia sudah cukup. untuk mengetahui bagaimana sistem bergerak secara keseluruhan.

Justeru, jika dalam pelbagai cara kecualikan daripada sistem (2) kuasa yang tidak diketahui, maka kita memperoleh beberapa hubungan, iaitu, beberapa muncul ciri umum untuk sistem, pengetahuan yang membolehkan kita menilai bagaimana sistem bergerak secara umum. Ciri-ciri ini diperkenalkan menggunakan apa yang dipanggil teorem umum dinamik. Terdapat empat teorem sedemikian:

1. Teorem tentang pergerakan pusat jisim sistem mekanikal;

2. Teorem tentang perubahan dalam momentum sistem mekanikal;

3. Teorem tentang perubahan dalam momen kinetik sistem mekanikal;

4. Teorem tentang perubahan tenaga kinetik sistem mekanikal.