Penggunaan sifat sempadan bagi sesuatu fungsi. aplikasi sifat fungsi untuk menyelesaikan persamaan dan ketaksamaan kerja ditumpukan kepada salah satu kaedah bukan piawai

Disediakan dan dikendalikan oleh guru matematik

MCOU "Sekolah Menengah No. 1" Povorino

Wilayah Voronezh

Kartashova S. A.

2014

Topik pelajaran:"Menyelesaikan persamaan menggunakan kaedah bukan piawai menggunakan sifat fungsi"

Bentuk pengajaran ialah syarahan diikuti dengan pengukuhan. Direka untuk 2 pelajaran

(Slaid No. 1)

Objektif pelajaran:

Ulang dan umumkan pengetahuan tentang topik: "Sifat fungsi"

Belajar menggunakan kaedah berfungsi untuk menyelesaikan persamaan

Membangunkan pemikiran logik, pemerhatian

Memupuk aktiviti dan inisiatif kreatif.

(slaid No. 2)

peralatan: papan putih interaktif, komputer dengan pembentangan.

Rancangan pengajaran:

Detik organisasi.

Motivasi aktiviti pendidikan(mesej topik, matlamat pelajaran).

Pengemaskinian pengetahuan asas (pengulangan sifat fungsi asas).

Mempelajari bahan baru (kaedah berfungsi untuk menyelesaikan persamaan).

Pemantapan pengetahuan (latihan penyelesaian).

Merumuskan. Penilaian.

Kemajuan pelajaran.

cikgu:

Untuk menyelesaikan kebanyakan persamaan yang dihadapi dalam peperiksaan, sudah cukup untuk mengetahui kursus sekolah matematik, tetapi pada masa yang sama adalah perlu untuk dapat menyelesaikan bukan sahaja menggunakan teknik standard yang dimaksudkan untuk jenis persamaan yang sangat spesifik, tetapi juga kaedah "tidak standard", yang akan kita bicarakan hari ini di dalam kelas. Salah satu kaedah untuk menyelesaikan persamaan ini adalah berfungsi, berdasarkan penggunaan sifat-sifat fungsi. Tidak seperti kaedah grafik, pengetahuan tentang sifat fungsi membolehkan anda mencari punca sebenar persamaan, tanpa perlu membina graf fungsi. Menggunakan sifat fungsi membantu merasionalkan penyelesaian persamaan.

(slaid No. 3)

Jom jawab soalan:

Apakah persamaan yang dipanggil?

Apakah punca persamaan?

Apakah yang dimaksudkan untuk menyelesaikan persamaan?

Apakah fungsi yang dipanggil?

Apakah domain fungsi?

Apakah julat sesuatu fungsi?

(slaid No. 4)

Mari kita pertimbangkan(slaid No. 5)

CONTOH 1. Selesaikan persamaan:

Penyelesaian: ODZ:

Jawapan: tiada penyelesaian.

(slaid No. 6)

CONTOH 2. Selesaikan persamaan:

Penyelesaian: ODZ:

ODZ terdiri daripada satu titik x=1. Ia kekal untuk menyemak sama ada x=1 ialah punca persamaan. Menggantikan, kita melihat bahawa x=1 ialah punca persamaan.

Jawapan: x=1.

cikgu:

Kadang-kadang ternyata cukup untuk mempertimbangkan bukan keseluruhan domain definisi fungsi, tetapi hanya subsetnya, di mana fungsi mengambil nilai yang memenuhi syarat tertentu (contohnya, hanya nilai bukan negatif)

(slaid no. 7 )

CONTOH 3.

Penyelesaian. Mari cari persilangan domain definisi fungsi di sebelah kanan dan kiri persamaan:

D 1

Mari kita hadkan setD, dengan mengambil kira bahawa bahagian kiri persamaan adalah bukan negatif, dan, oleh itu, ia sepatutnya sama sebelah kanan Untuk melakukan ini, kita perlu mempertimbangkan persimpangan setDdengan banyak penyelesaian kepada ketidaksamaan , iaitu dengan banyak . Oleh itu, sudah cukup untuk mempertimbangkan persamaan pada set .

Dengan penggantian kita memastikan bahawa kedua-dua elemen berfungsi sebagai penyelesaian kepada persamaan.

Jawapan: -3; 2.

(slaid no. 8 )

CONTOH 4.

Penyelesaian.

Memandangkan itu punca persamaan ialah x=4.

Jawapan: 4.

cikgu:

Mari kita beralih kepada menyelesaikan persamaan menggunakan konsep julat nilai fungsi.

(slaid No. 9-No. 10)

(slaid No. 11)

CONTOH 1.

Penyelesaian. Kerana , maka persamaan tidak mempunyai penyelesaian.

Jawapan: tiada penyelesaian.

CONTOH 2.

Penyelesaian. ODZ:

Jawapan: tiada penyelesaian.

cikgu:

Jika fungsi f ( x ) pada selang X dibatasi dari atas, dan fungsi g ( x ) bersempadan di bawah, kemudian persamaan f ( x ) = g ( x ) adalah bersamaan dengan sistem

(slaid No. 12)

CONTOH 3.

Penyelesaian. Mengikut definisi,

Kesaksamaan tercapai jika

Mari kita selesaikan persamaan pertama sistem:

arccos (x-1) =π, x-1 = -1, x=0.

Apabila x=0, persamaan kedua bertukar menjadi kesamaan berangka sebenar.

Oleh itu, penyelesaian kepada sistem dan persamaan ini ialah x=0.

Jawapan: 0.

(slaid No. 13-14)

CONTOH 4.

Penyelesaian.

Mari kita cari maksimum fungsi ini pada selang (2;4) menggunakan terbitan.

= 0,

g’ + -

g 2 3 4 x

Maks

g(3)=2.Kami ada

Kemudian persamaan yang diberikan setara dengan sistem

Setelah menyelesaikan persamaan pertama sistem, kita mendapat x=3, dengan menyemak, menggantikannya ke dalam persamaan kedua, kita akan memastikan bahawa x=3 ialah penyelesaian kepada sistem dan persamaan ini.

Jawapan: 3.

(slaid No. 15)

cikgu:

Kaedah ini sering dijumpai pada Peperiksaan Negeri Bersepadu dalam matematik. Kaedah ini terletak pada fakta bahawa satu bahagian persamaan dihadkan dari atas oleh nombor M tertentu, dan bahagian lain persamaan dihadkan dari bawah oleh nombor yang sama M. Nombor M biasanya dipanggilmajorante , dan kaedah ini ialahkaedah major . Dalam kaedah majorant, seperti yang anda mungkin telah meneka, anda perlu mempunyai pemahaman yang baik tentang apa itu fungsi dan dapat mengkaji sifat-sifat fungsi.

(slaid No. 16)

Latihan untuk penyatuan, pembangunan kemahiran.

Kelas dibahagikan kepada 2 kumpulan mengikut pilihan.

Pilihan 1.

Buktikan bahawa persamaan tidak mempunyai punca.

Selesaikan persamaan: Jawapan: 2.6.

Jawapan: 2.

cikgu:

Hari ini kita melihat kaedah bukan standard untuk menyelesaikan persamaan menggunakan sifat fungsi, yang juga boleh digunakan untuk menyelesaikan ketaksamaan, tetapi kita akan membincangkannya dalam beberapa pelajaran seterusnya.

Kesimpulannya, penilaian.

(slaid No. 17)

Kerja rumah:

Bahagian I. Matematik dan Fizik

UDC 372.8 BBK 74.262.21

TIDAK. Lyakhova, A.I. Grishina, I.V. Yakovenko

MENGGUNAKAN FUNGSI TERHAD DALAM KURSUS MATEMATIK SEKOLAH

Anotasi. Artikel itu membentangkan metodologi untuk mengkaji kaedah untuk menyelesaikan persamaan "bukan piawai" matematik asas menggunakan keterbatasan fungsi.

Kata kunci: menyelesaikan persamaan, menggunakan sempadan fungsi.

N.E. Lyakhova, A.I Grishina, I.V. Yakovenko

PENGGUNAAN HAD FUNGSI DALAM KURSUS MATEMATIK SEKOLAH

Abstrak. Kertas kerja ini membentangkan metodologi untuk mengkaji kaedah untuk menyelesaikan persamaan "tidak piawai" matematik asas dengan fungsi terhad. Kata kunci: penyelesaian persamaan, menggunakan fungsi terhad.

Fungsi terhad membolehkan menyelesaikan banyak persamaan bukan piawai dan ketidaksamaan yang pada masa yang sama mengandungi pelbagai fungsi, yang tidak membenarkan menggunakan kaedah standard untuk menyelesaikan masalah kepada mereka jenis tertentu. Menggunakan keterbatasan fungsi, kaedah sedemikian untuk menyelesaikan persamaan dan ketaksamaan sebagai kaedah mini-maks dan akibatnya dibina. Nama kaedah - kaedah mini-max - mungkin kontroversi, tetapi ia membolehkan anda mengingati dengan cepat intipati kaedah dan berfungsi sebagai titik rujukan untuk pelajar. Perhatikan bahawa mempelajari kaedah ini berguna untuk seorang lepasan sekolah baik dari sudut memperluaskan kebolehannya untuk menyelesaikan masalah "tidak standard", dan dari sudut mengembangkan kemahiran dalam mengkaji fungsi (terutamanya menggunakan kaedah matematik asas ). Kedua-duanya penting untuk menyediakan graduan untuk Peperiksaan Negeri Bersepadu dalam matematik, sejak ujian itu bahan pengukur secara tradisinya mengandungi tugasan sedemikian, manakala dalam buku teks sekolah mereka jelas tidak cukup mewakili atau tidak dibentangkan sama sekali.

Intipati kaedah mini-max ialah pernyataan berikut.

Pernyataan 1. Jika pada domain takrifan X persamaan

dan fungsi

maka persamaan ini adalah bersamaan dengan sistem

f (*) = a g(*) = a "

Sesungguhnya, di bawah syarat-syarat yang ditetapkan kesaksamaan

adalah mungkin jika dan hanya jika fungsi f (*) dan g (*) mengambil nilai a untuk nilai yang sama *. Dalam kes ini, nombor a adalah untuk fungsi f (*) dan g (*), masing-masing, nilai terbesar dan terkecil pada set X. Perhatikan bahawa jika sekurang-kurangnya satu daripada fungsi f (*) atau g (*) pada set X tidak mengambil nilai a, maka persamaan

tidak mempunyai akar. Tetapi dalam kes ini, sistem juga tidak mempunyai penyelesaian dan, oleh itu, kesetaraan persamaan dan sistem tidak dilanggar. Oleh itu, apabila mendapatkan anggaran yang diperlukan, tidak perlu memastikan bahawa a adalah pada set X nilai tertinggi fungsi f(*) dan nilai terendah fungsi g(*) .

Menggunakan Pernyataan 1 dan Sifat ketaksamaan berangka, tidak sukar untuk membuktikan dua lagi kenyataan, yang merupakan akibat daripada kaedah mini-max.

Pernyataan 2. Biarkan set X ialah persilangan bagi domain takrif bagi fungsi f (x) dan g (x), dan ketaksamaan dipegang pada set ini

kemudian ketidaksamaan

f (x) + g (x) > a + b,

adalah bersamaan dengan persamaan

f (x) + g (x) = a + b, yang, seterusnya, adalah bersamaan dengan sistem:

/ (x) = a, e (x) = b.

Pernyataan 3. Biarkan set X ialah persilangan bagi domain takrif bagi fungsi f (x) dan е (x), dan ketaksamaan dipegang pada set ini

0 < f (х) < а

e (x)< Ь, где а >0, b > 0

kemudian ketidaksamaan

f (x) e (x) > a b

akan bersamaan dengan persamaan

f (x) e (x) = a b, yang, seterusnya, adalah bersamaan dengan sistem

/ (x) = a, e(x) = b.

Seperti yang dapat dilihat daripada kata-kata kenyataan, untuk melaksanakan kaedah mini-max (atau akibatnya), adalah perlu untuk menganggarkan fungsi yang termasuk dalam persamaan atau ketaksamaan. Malah, penilaian fungsi adalah aktiviti utama dalam pelaksanaan kaedah. Oleh itu, pengajaran kaedah mestilah berdasarkan membangunkan kemahiran untuk menilai pelbagai fungsi. Pada pendapat kami, kaedah penilaian berikut akan menjadi yang paling relevan untuk pelajar sekolah.

1. Teknik paling mudah- penilaian fungsi dalam bentuk f (x) = A ± a(x), dengan a(x) ialah beberapa fungsi bukan negatif.

5. Penilaian fungsi kompleks.

Marilah kita memikirkan lebih terperinci mengenai setiap teknik, menggambarkannya dengan contoh dan menyediakan satu set latihan latihan untuk membangunkan kemahiran dalam menyelesaikan persamaan menggunakan teknik ini.

1. Kaedah paling mudah untuk menganggar fungsi. Biarkan a(x) ialah beberapa fungsi bukan negatif, maka:

Jika f (x) = A + a (x), maka f (x) > A;

Jika f (x) = A - a (x), maka f (x)< А.

Kami memanggil kaedah pertama sebagai paling mudah, kerana anggaran dalam kes ini boleh dikatakan jelas dengan syarat pelajar mengetahui set fungsi bukan negatif: 24x, x2", x~2", xa (di mana-), |x|, |x| -x, arccosx, arc^x, ax, dsb. Di samping itu, nilai bukan negatif akan mengambil fungsi yang kompleks, yang merupakan hasil gubahan fungsi jika fungsi terakhir gubahan itu bukan negatif. Oleh itu, senarai fungsi bukan negatif boleh

umumkan: 2^u(x), (u(x))2", (m(x))-2i, ageo8u(x), agccyoi(x), |u(x)|, |u(x) - u(x), a"(x), (u(x))a (di mana k).

Mari kita berikan contoh penggunaan kaedah mini-maks, dalam penyelesaian yang mana teknik anggaran yang dipertimbangkan digunakan.

Contoh 1. Selesaikan persamaan 2 + |x(x -1)| = 2 - ^(x -1)(x + 2) . Penyelesaian. Fungsi

/ (x) = |x(x -1)|, I (x) = 7 (x -1)(x + 2)

bukan negatif. Oleh itu, kami mempunyai anggaran berikut untuk sisi kiri dan kanan persamaan

2 + | x(x -1)| > 2,

2-y/(x-1)(x + 2)< 2 "

Kemudian, menurut Pernyataan 1, persamaan asal adalah bersamaan dengan sistem

Kemudian:

Jika fungsi f (u) bertambah pada selang masa maka ketaksamaan itu kekal

f(a)< f (u(x)) < f (b);

Jika fungsi f (u) berkurangan pada selang, maka ketaksamaan kekal

f(b)< f (u(x)) < f (a) .

Contoh 7. Selesaikan persamaan log2 (x2 - 6x+11) = cos((x - 3) sin x).

Penyelesaian. Menyerlahkan segi empat tepat dalam trinomial kuadratik di bawah tanda logaritma, kita memperoleh persamaan

log2 (2+(x - 3)2) = cos((x - 3) sin x). Marilah kita menilai fungsi di sebelah kiri dan bahagian yang betul persamaan ini.

f (x) = log2 (2+(x - 3)2) > 1. Sesungguhnya, 2 + (x - 3)2 > 2, fungsi log2 u bertambah, oleh itu,

log2 (2+(x - 3)2) > log2 2 = 1. Fungsi u2 meningkat secara monoton.

"Aplikasi Kesinambungan" - Maksud Ungkapan. Makna geometri terbitan. Kaedah selang waktu. Tulis persamaan untuk tangen kepada graf fungsi itu. Tangen kepada graf fungsi. Graf adalah hampir dengan tangen. Formula. Mari kita mengira menggunakan formula. Tangen kepada lengkung pada titik M tertentu ialah kedudukan mengehadkan NM sekan. Hiperbola.

"Fungsi melampau" - Pergantungan tekanan gas pada suhu. Topik pelajaran: “Tanda-tanda peningkatan dan penurunan fungsi. Ujian. Tukar kekuatan arus apabila litar dibuka. Penyiasatan fungsi ke ekstrem". Berubah AC. Pelan: Kebergantungan arus pada voltan. Pergantungan tekanan gas pada isipadu. Topik: “Tanda-tanda peningkatan dan penurunan fungsi.

"Fungsi dan sifatnya" - Pembolehubah bebas dipanggil argumen. Meningkatkan fungsi. Definisi fungsi. Malah dan fungsi ganjil. Kemonotonan fungsi. Nilai-nilai pembolehubah bersandar dipanggil nilai-nilai fungsi. Semua nilai pembolehubah bebas membentuk domain takrifan fungsi -D (f). 1. Nilai fungsi adalah positif.

Terdapat sejumlah 23 pembentangan dalam topik tersebut

Topik: Kaedah untuk menggunakan fungsi terhad.
Hidup ini baik kerana apa yang ada di dalamnya awak boleh buat matematik. (Leonard Euler)Matlamat: pembangunan pemikiran baru yang tidak konvensional yang boleh berjaya diterapkan dalam bidang lain aktiviti manusia(sibernetik, teknologi komputer, ekonomi, radiofizik, kimia, dll.).
Tugasan: - latihan dalam menilai kesukaran objektif dan subjektif tugasan dan bijak memilih tugasan ini dalam peperiksaan;

Mencipta "piggy bank" dengan alasan yang tidak konvensional dan luar biasa.

Kemajuan pelajaran:

Org. seketika. Pelajar merumus topik pelajaran dengan menyiapkan tugasan Peperiksaan Negeri Bersepadu bahagian A dan B dan mentafsir topik mengikut tertib menurun bagi jawapan yang diterima. (Sulitkan 12 kad bernombor dari -2 hingga 10 sebagai perkataan yang sepatutnya) (Lampiran 1 dan 2)

batasan

2. Bahagikan pelajar kepada 2 kumpulan, berikan mereka set "Teori + 10 tugasan" (Lampiran 3 dan 4), minta mereka memilih tugasan yang boleh diselesaikan untuk bahagian teori ini, dan mewajarkan pilihan mereka.3. Tunjukkan kemajuan tugas-tugas ini di papan tulis oleh pelajar: Noskova K., Dedevshin I., Veselov I.4. Bahagikan tugasan daripada kad kepada 2 kumpulan untuk menyelesaikannya, diikuti dengan ujian kendiri pada helaian penyelesaian siap sedia. (Lampiran 5)5. Edarkan helaian kepada kumpulan yang menerangkan kaedah bukan piawai baharu untuk menyelesaikan persamaan dan ketaksamaan untuk pemilihan topik seterusnya(sebagai tugasan kerja rumah, cari dalam koleksi Tugas Peperiksaan Negeri Bersatu, yang boleh diselesaikan dengan kaedah ini (Lampiran 6)6. Refleksi pelajar (mengisi jadual) F.I. pelajar

Lampiran 1.
Selesaikan tugasan ini dan susun jawapan dalam susunan menurun, kumpulkan topik pelajaran kami berdasarkan jawapan.

Cari absis titik dalam graf fungsi y=3x 2 -7x+7, di mana tangen sudut tangen adalah sama dengan -1.

Lampiran 2.
9 2 0 7Kajian fungsi menggunakan derivatif. 10 5 1 -1Kaedah menggunakan fungsi terhad. 4 -2 8 12Menyelesaikan ketaksamaan secara grafik.
3 11 6Penyelesaian persamaan fungsian.
Belajar

Lampiran 3.

Salah satu daripada kaedah yang berkesan menyelesaikan persamaan atau ketaksamaan ialah kaedah berdasarkan penggunaan fungsi terikat. Kepada yang paling terkenal fungsi terhad termasuk, sebagai contoh, beberapa trigonometri; terbalik fungsi trigonometri; fungsi yang mengandungi modulus, darjah, punca c walaupun ijazah dan lain-lain.

Ketaksamaan yang paling biasa adalah seperti berikut:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

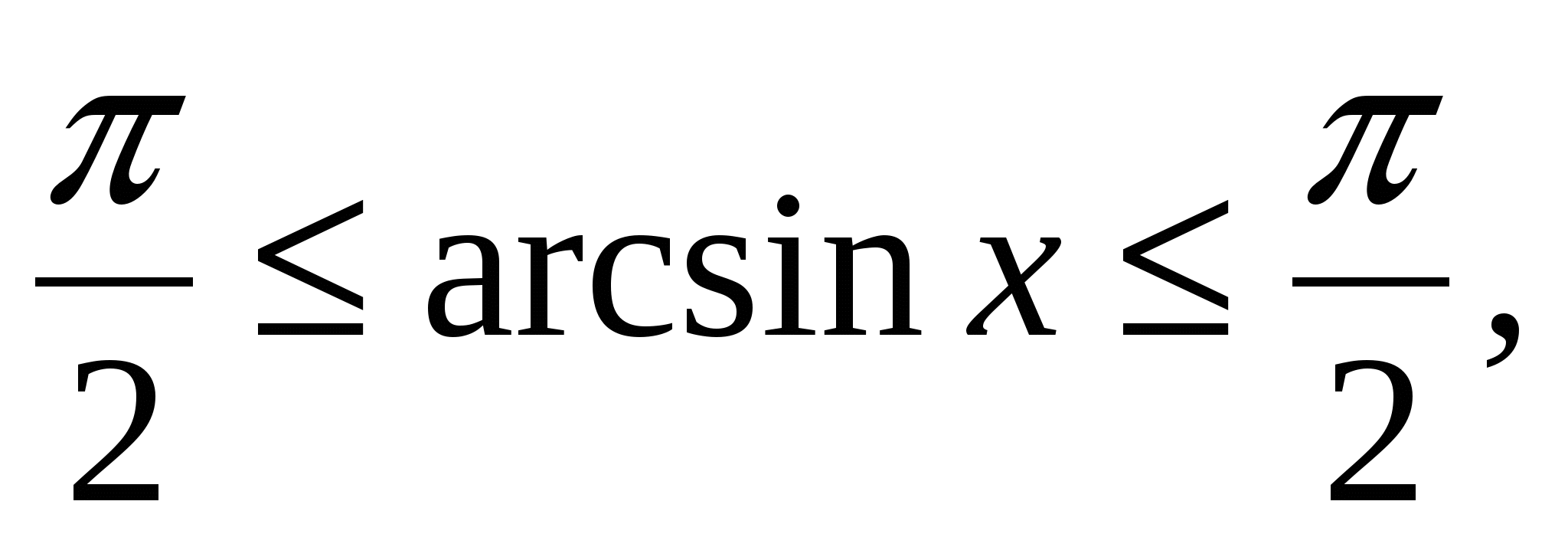
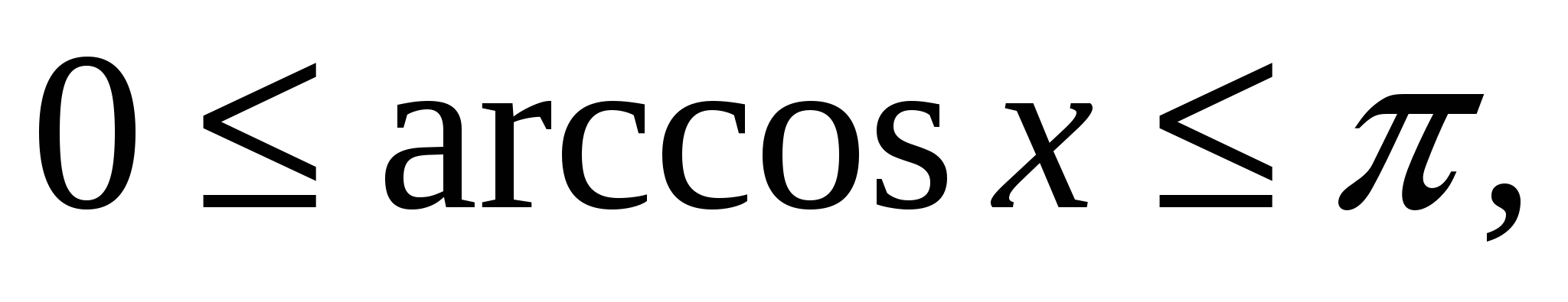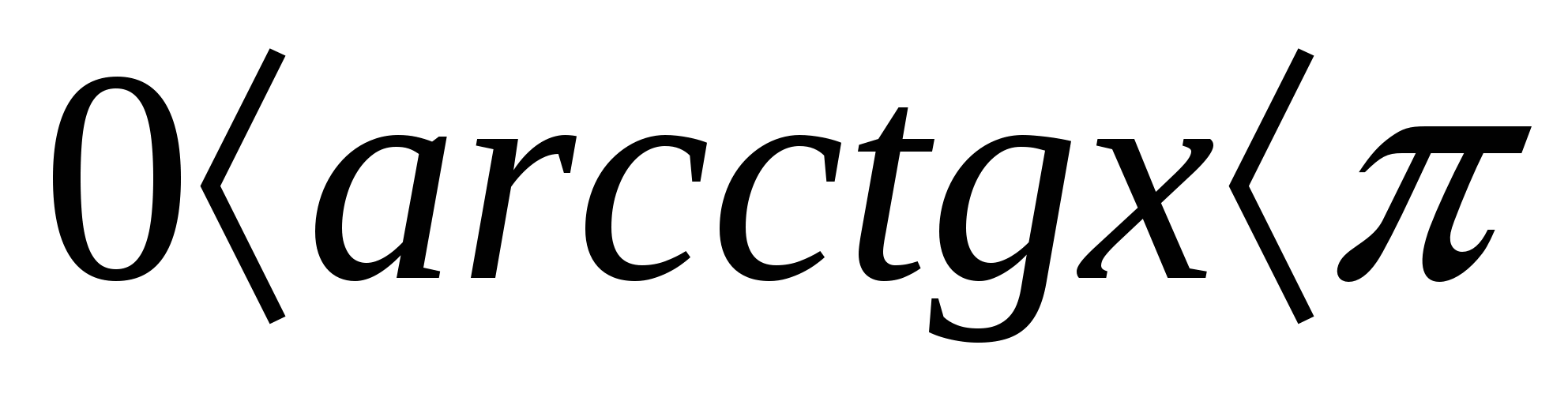, a f ( x ) >0, (f(x) ± g(x)) 2 n ≥ 0,
, a+ ≥ 2, b+ ≤ -2 dan lain-lain lagi. Di sini n - nombor asli, h(x) ≥ 0, a>0, b 0.

Sebagai tambahan kepada ketaksamaan paling mudah yang diberikan di atas, terdapat juga yang lebih kompleks, khususnya, ketaksamaan trigonometri -,

,

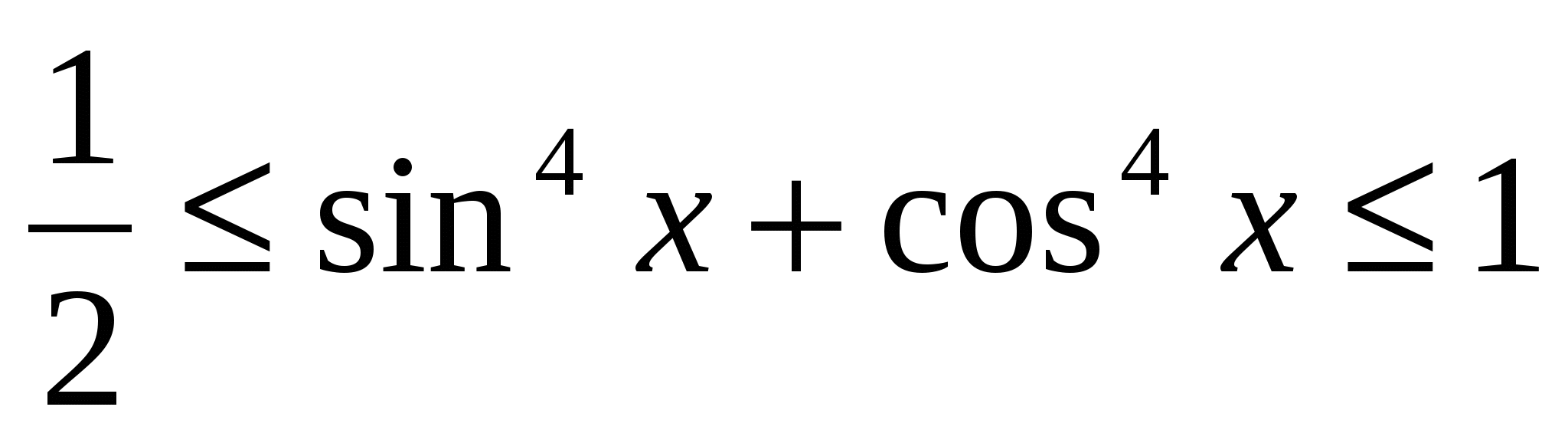dan ketidaksamaan dengan modul borang
.

Contoh 1.Selesaikan persamaan:

Penyelesaian: Mari kita pilih segi empat sama lengkap di sebelah kanan persamaan, i.e. . Ia berikutan itu
. Sejak dalam kes ini dosaπ x ≤ 1, maka kita memperoleh sistem persamaan

Menyelesaikan persamaan kedua sistem, kita mendapat bahawa x=. Dengan menggantikan persamaan pertama, kami memastikan bahawa nilai x yang ditemui ialah penyelesaian kepada sistem, dan oleh itu ialah penyelesaian kepada persamaan asal.

Jawapan: x=.

Contoh 2.Selesaikan persamaan:

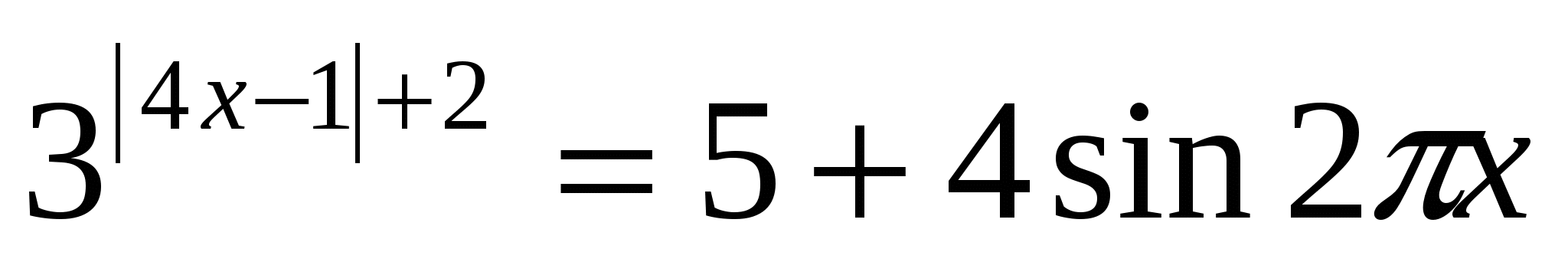
Penyelesaian: sejak Walau bagaimanapun sin2 π x ≤ 1. Oleh itu, 5+4 sin2 π x ≤ 9. Oleh itu, kita memperoleh sistem persamaan:

Dari sini kita memperoleh sistem persamaan
, daripada persamaan pertama kita dapati x=. Mari kita gantikannya ke dalam persamaan kedua sistem dan pastikan bahawa x = ialah penyelesaian kepada sistem, dan oleh itu ialah penyelesaian kepada persamaan asal.

Jawapan: x=

Lampiran 4. Daripada senarai tugasan yang dicadangkan, pilih tugasan yang boleh diselesaikan menggunakan kaedah fungsi terhad. 1. Selesaikan persamaan x 2 -4 x=(2-kos
2. Cari kuantiti penyelesaian integer ketidaksamaan x 2ctg 2
3. Selesaikan persamaan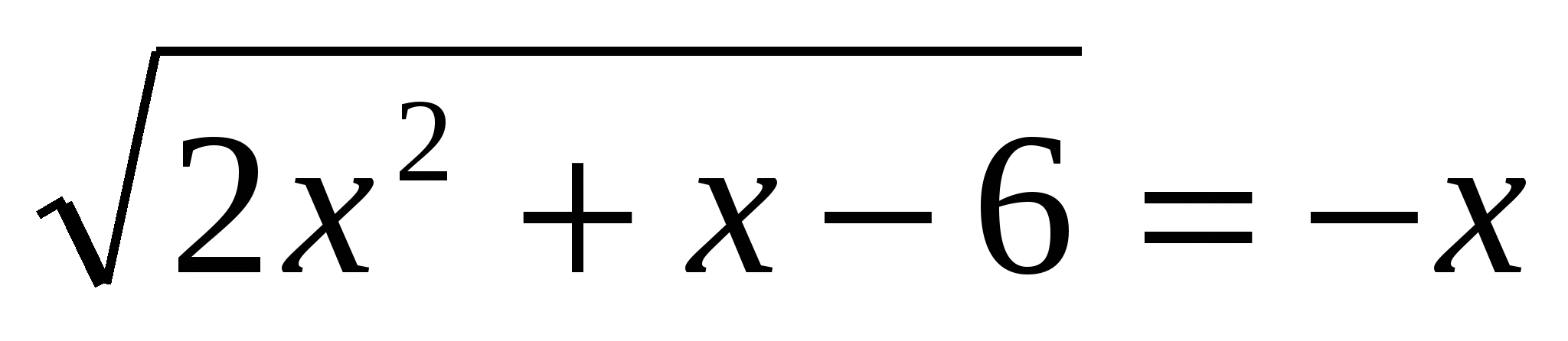
4. Selesaikan persamaan 3-(5. Cari bilangan penyelesaian integer kepada ketaksamaan 16's 2 ≥0 yang memenuhi syarat 3 tg 2
6. Selesaikan persamaan
7. Selesaikan persamaan -25x 2 +40x-23=( cos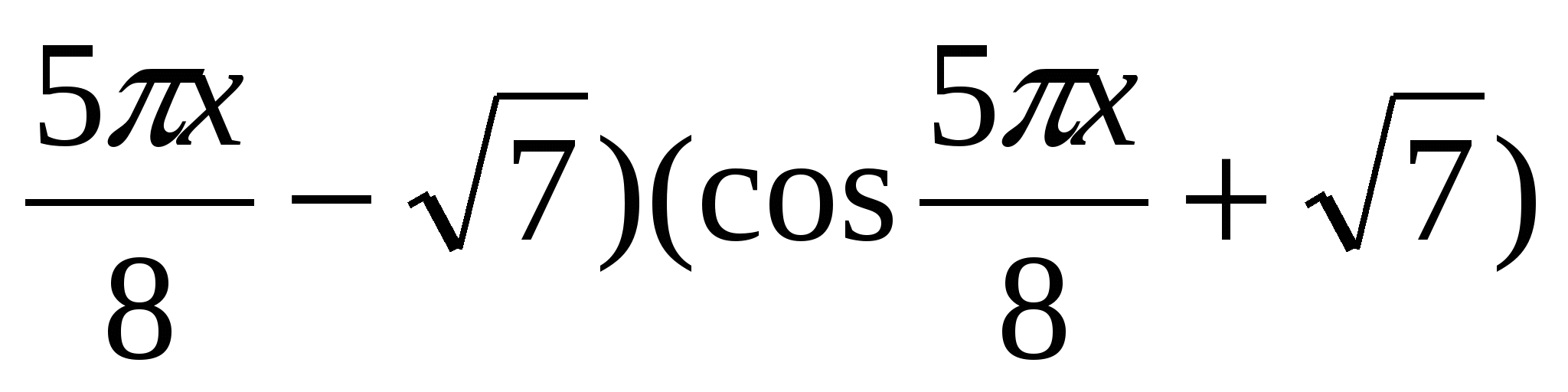
8. Cari hasil darab punca-punca persamaan x
9. Selesaikan persamaan
10. Selesaikan persamaan 3- cos 2

Lembaran ujian kendiri. Lampiran 5. 1. Selesaikan persamaan Penyelesaian: kerana , maka kerana dan kemudian
kita mendapat sistem persamaan

selesaikan persamaan pertama, dapatkan x=, gantikan nilai ini ke dalam persamaan kedua

2 . Selesaikan persamaan 3- cos 2 Penyelesaian: kerana , maka kerana dan kemudian
kita mendapat sistem persamaan

selesaikan persamaan kedua, dapatkan x=, gantikan nilai ini ke dalam persamaan pertama

ini bermakna x= ialah penyelesaian kepada persamaan asal. Jawapan: x=
3. Cari bilangan penyelesaian integer kepada ketaksamaan x 2 +7x-8≤0, memenuhi syarat ctg 2 Penyelesaian: kerana dan kemudian untuk mana-mana nilai x yang dibenarkan kita akan menemui sifar trinomial kuadratik, mengikut teorem Vieta, kita menyelesaikan ketaksamaan menggunakan kaedah selang
Itu. kita tahu itu
nilai integer x ialah nombor yang dihapuskan Jawapan: 8 penyelesaian integer 4. Cari bilangan penyelesaian integer kepada ketaksamaan 16's 2 ≥0 yang memenuhi syarat 3 tg 2 Penyelesaian: kerana dan kemudian untuk sebarang nilai x yang dibenarkan, kita dapati sifar bagi ungkapan, x = dan x = Selesaikan ketaksamaan menggunakan kaedah selang
Itu. kita tahu itu

nilai integer x ialah nombor yang dihapuskan Jawapan: 7 penyelesaian integer
Lampiran 6.

Kaedah menggunakan fungsi yang monotoni. Apabila menyelesaikan persamaan seperti f(x)=g(x) dalam sesetengah kes, kaedah yang berkesan ialah menggunakan kemonotonan fungsi y= f(x) dan y= g(x) Jika fungsi y= f(x) adalah selanjar dan meningkat (menurun) pada segmen a≤ x ≤ b, dan fungsi у= g(x) adalah berterusan dan berkurang (meningkat) pada segmen yang sama, maka persamaan f(x)=g(x) pada segmen a≤ x ≤ b boleh mempunyai tidak lebih daripada satu punca, yang bermaksud sama ada perlu cuba mencari satu-satunya punca persamaan melalui pemilihan, atau menunjukkan bahawa punca tersebut tidak wujud. Kaedah ini amat berkesan dalam kes apabila kedua-dua belah persamaan f(x) = g(x) adalah fungsi "menyusahkan" untuk kajian bersama. Ulasan: Jika fungsi y= f(x) bertambah, dan fungsi y= g(x) berkurang untuk a≤ x ≤ b Dan pada masa yang sama f(a)>g(A), maka punca-punca persamaan adalah antara a≤ x ≤ b Tidak.

Contoh: Selesaikan persamaanPenyelesaian: Wilayah nilai yang boleh diterima persamaannya ialah x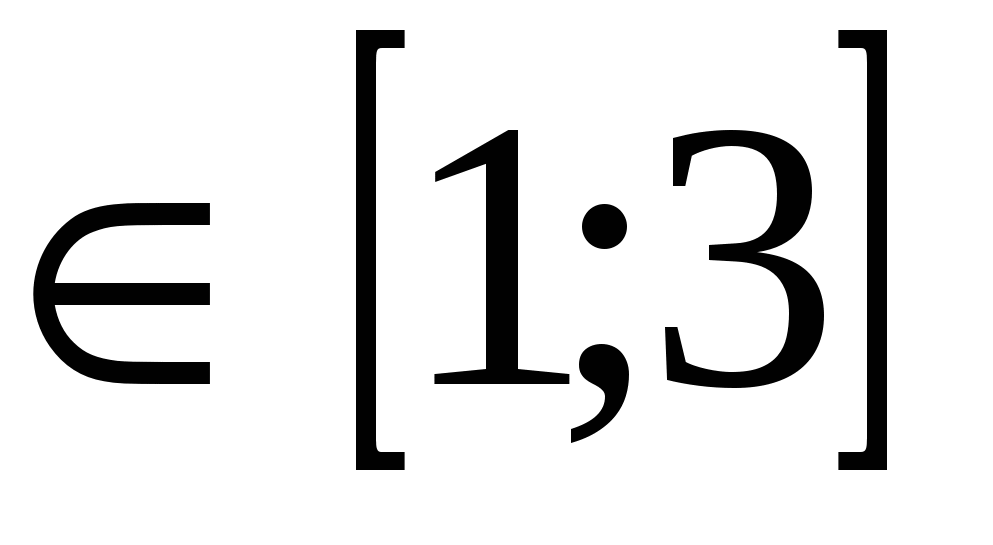
. Adalah mudah untuk melihat bahawa di rantau ini bahagian kiri persamaan meningkat, dan bahagian kanan berkurangan, i.e. fungsif(x)=
semakin meningkat, dan fungsig(x)=
- berkurangan. Dalam hal ini, persamaan asal hanya boleh mempunyai satu punca (jika ada). Dengan pemilihan kita dapati punca persamaan x = 2.Jawab: x=2
Kaedah untuk menyelesaikan persamaan fungsi. Antara yang paling banyak tugasan yang kompleks Peperiksaan Negeri Bersepadu termasuk masalah yang penyelesaiannya bermuara kepada pertimbangan persamaan fungsi bentuk f(f(….f(x)…))=x atau f(g(x))=f(h(x)), dengan f(x),g(x),h(x) ialah beberapa fungsi dan n≥ 2
Kaedah untuk menyelesaikan persamaan fungsi ini adalah berdasarkan penggunaan banyak teorem, mari kita pertimbangkan salah satu daripadanya.
Teorem 1. Punca-punca persamaan f(x)=0 ialah punca-punca persamaan f(f(….f(x)…))=x
Contoh: Selesaikan persamaan x=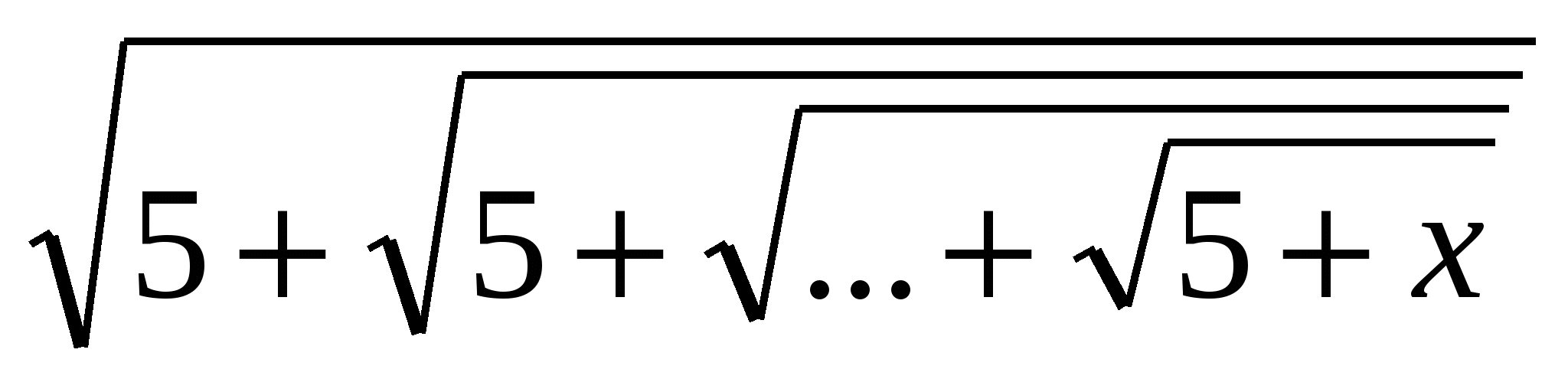
, di mana punca kuasa dua diambilnsekali dann≥ 1 Penyelesaian: Daripada keadaan masalah ia mengikuti bahawa x> 0. Biarkanf(x)=
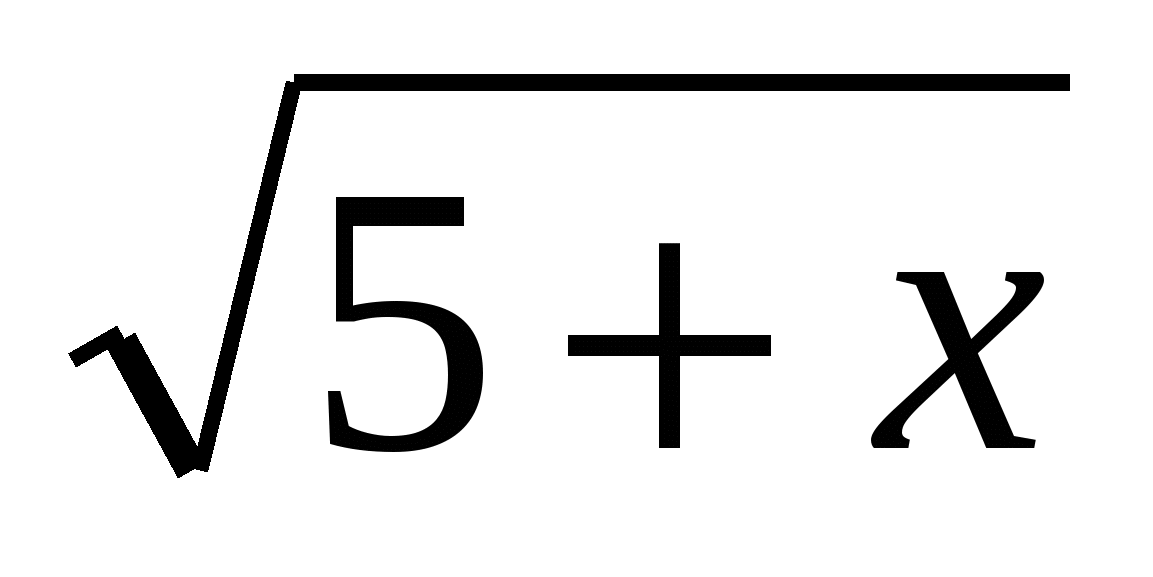, maka persamaan kita boleh diwakili sebagai fungsi f( f(…. f( x)…))= x. Sejak pada x> 0 fungsif(x)= meningkat danf(x) > 0, maka persamaan x= adalah bersamaan dengan persamaanf(x)= x, iaitu =x, penyelesaian positifnya ialah x=
Jawapan: x=