Penguraian nombor kepada faktor perdana, kaedah dan contoh penguraian. Dapatkan penguraian kanonik suatu nombor kepada faktor perdana

Kuliah 14 Proses rawak Pengembangan kanonik proses rawak. Penguraian spektrum pegun proses rawak. SluLecture 14
Proses rawak
Pengembangan kanonik proses rawak.
Penguraian spektrum rawak pegun
proses. Proses rawak dengan bebas
bahagian. Proses Markov dan rantai Markov.
Proses rawak biasa. Secara berkala
proses rawak tidak pegun
(Akhmetov S.K.)

Pengembangan kanonik proses rawak

Mana-mana SP X(t) m.b. dibentangkan dalam
bentuk penguraiannya, i.e. sebagai jumlah
proses asas:
Vk – pembolehubah rawak
φk(t) – fungsi bukan rawak (sinusoid, eksponen, kuasa
fungsi, dsb.)
Kes khas penguraian sedemikian ialah Canonical
penguraian
SP X(t), yang mempunyai bentuk
mx(t) = M – jangkaan matematik SP X(t)
V1, V2…Vk – SV tidak berkorelasi dan berpusat
D1, D2…Dk- SW penyebaran V1, V2…Vk
φk(t) – fungsi bukan rawak bagi hujah t
Pembolehubah rawak V1, V2…Vk dipanggil pekali bagi kanonik
penguraian,
dan fungsi bukan rawak φ1(t), φ2(t) φk(t) - fungsi koordinat
pengembangan kanonik

Ciri-ciri utama SP yang ditakrifkan oleh penguraian kanonik

M – jangkaan matematik SP X(t)
Kx(t,t’) – fungsi korelasi SP X(t)
Ungkapan
- pengembangan kanonik korelasi
fungsi
Jika t=t’, maka mengikut yang pertama
sifat fungsi korelasi
Ungkapan
Dk(t) –
penyebaran
pengembangan kanonik varians SP X(t)

Penguraian spektrum SP pegun

Usahasama pegun m.b. diwakili oleh penguraian kanonik
Vk dan Uk – SV tidak berkorelasi dan berpusat dengan serakan
D = D = Dk
ω – nilai bukan rawak (kekerapan)
Dalam kes ini, pengembangan kanonik fungsi korelasi
ditentukan oleh ungkapan
diserahkan
berkanun
penguraian
JV
X(t)
dipanggil
penguraian spektrum SP dan
dinyatakan sebagai
Θk - fasa getaran harmonik SP pegun asas,
menjadi SW teragih seragam dalam selang (0, 2π);
Zk – SV, iaitu amplitud ayunan harmonik
pegun asas SP

Penguraian spektrum SP pegun (2)

Pembolehubah rawak Θk dan Zk adalah bergantung dan yang berikut berlaku untuknya:
Vk = Zk cos Θk
Uk = Zk sin Θk
Usahasama pegun m.b. dibentangkan sebagai jumlah harmonik
ayunan dengan amplitud rawak Zk dan fasa rawak Θk pada
pelbagai frekuensi bukan rawak ωk
Fungsi korelasi SP X(t) pegun ialah genap
fungsi hujahnya, i.e. kx(τ) = kx(-τ). Oleh itu, pada selang (-T,
T) boleh dikembangkan menjadi siri Fourier dalam harmonik genap (kosinus):
Varians bagi SP X(t) pegun adalah sama dengan
jumlah
kelainan
semua orang
harmonik
miliknya
penguraian spektrum
Kebergantungan Dk = f(wk) dipanggil spektrum penyebaran diskret atau
spektrum diskret bagi SP pegun.

Penguraian spektrum SP pegun (3)

Pada ∆ω
→ 0 akan berlaku peralihan kepada spektrum berterusan
Sx(ω) - ketumpatan spektrum
Oleh itu, fungsi korelasi dan ketumpatan spektrum
dikaitkan dengan kosinus – transformasi Fourier. Oleh itu, spektrum
ketumpatan usaha sama pegun m.b. dinyatakan melalui korelasi
fungsi mengikut formula

Proses rawak dengan keratan rentas bebas

Dalam hidrologi, dipercayai bahawa siri ini sepadan dengan model rawak
nilai, jika tiada korelasi yang signifikan antara ahli siri ini
untuk sebarang anjakan τ.
Proses rawak dengan keratan rentas bebas ialah SP yang mana
pada nilai t dan t
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx untuk τ = 0 dan 0 untuk τ ≠ 0)
Proses sedemikian adalah pegun dan mempunyai ergodik
harta benda
Untuk proses sedemikian, ciri-ciri undang-undang pengedaran satu dimensi
boleh dinilai untuk mana-mana bahagian dan untuk mana-mana (cukup
jangka panjang) pelaksanaan
Proses sedemikian tidak mempunyai korelasi antara ahli dalam mana-mana
pelaksanaan
Menerima model sedemikian, diandaikan bahawa beberapa kuantiti hidrologi
mewakili satu pelaksanaan usaha sama
Proses rawak dengan keratan rentas bebas kadangkala dipanggil
"bunyi putih" dengan analogi dengan cahaya putih

Proses Markov dan rantai Markov

Proses rawak
dipanggil Markovian jika ada
pada masa t kebarangkalian setiap keadaan sistem pada masa hadapan
(pada t > t0) hanya bergantung pada keadaannya pada masa sekarang (pada t = t0) dan tidak
bergantung pada keadaannya pada masa lalu (pada t< t0)
rantai Markov atau ringkas rantai Markov dipanggil
Proses Markov dengan keadaan diskret dan masa diskret
Markov SP diterangkan sepenuhnya oleh undang-undang dua dimensi
pengagihan. Jika proses Markov adalah pegun dan
ergodik, maka ciri-cirinya boleh dianggarkan berdasarkan satu
pelaksanaan.
Litar di mana kebarangkalian bersyarat negeri pada masa hadapan bergantung
dari keadaannya dalam beberapa langkah sebelumnya dipanggil kompleks
rantai Markov.

Proses rawak biasa (Gaussian).

Proses rawak biasa (Gaussian) X(t) dipanggil
SP, di mana dalam semua bahagian SP X(ti) mempunyai normal
pengedaran
Usahasama bukan pegun secara berkala
Apabila belajar tahunan, bulanan, harian, dll. proses biasanya
diperhatikan setiap tahun, dsb. turun naik. Dalam kes ini, sebagai
model matematik, anda boleh menggunakan model secara berkala
proses rawak tidak pegun (NSRP)
Proses rawak dipanggil secara berkala tidak pegun jika
ciri kebarangkaliannya adalah invarian berkenaan dengan anjakan oleh
nombor positif T. Contohnya, dengan langkah diskret satu bulan
invarian hendaklah dikekalkan pada syif 12, 24, 36, dsb.

Artikel ini memberikan jawapan kepada soalan pemfaktoran nombor pada helaian. Mari kita pertimbangkan idea umum tentang penguraian dengan contoh. Mari kita selesaikan bentuk kanonik penguraian dan algoritmanya. Semua kaedah alternatif akan dipertimbangkan menggunakan tanda boleh bahagi dan jadual pendaraban.

Yandex.RTB R-A-339285-1

Apakah yang dimaksudkan dengan memfaktorkan nombor ke dalam faktor perdana?

Mari kita lihat konsepnya faktor utama. Adalah diketahui bahawa setiap faktor perdana ialah nombor perdana. Dalam produk dalam bentuk 2 · 7 · 7 · 23 kita mempunyai 4 faktor perdana dalam bentuk 2, 7, 7, 23.

Pemfaktoran melibatkan perwakilannya dalam bentuk hasil darab perdana. Jika kita perlu menguraikan nombor 30, maka kita mendapat 2, 3, 5. Penyertaan akan menggunakan borang 30 = 2 · 3 · 5. Ada kemungkinan bahawa pengganda boleh diulang. Nombor seperti 144 mempunyai 144 = 2 2 2 2 3 3.

Tidak semua nombor terdedah kepada pereputan. Nombor yang lebih besar daripada 1 dan integer boleh difaktorkan. Nombor perdana, apabila difaktorkan, hanya boleh dibahagi dengan 1 dan mereka sendiri, jadi adalah mustahil untuk mewakili nombor ini sebagai hasil darab.

Apabila z merujuk kepada integer, ia diwakili sebagai hasil darab a dan b, di mana z dibahagikan dengan a dan b. Nombor komposit difaktorkan ke dalam faktor perdana menggunakan teorem asas aritmetik. Jika nombornya lebih besar daripada 1, maka pemfaktorannya p 1, p 2, ..., p n mengambil bentuk a = p 1 , p 2 , … , p n . Penguraian diandaikan dalam satu varian.

Pemfaktoran kanonik nombor menjadi faktor perdana

Semasa pengembangan, faktor boleh diulang. Ia ditulis padat menggunakan darjah. Jika, apabila menguraikan nombor a, kita mempunyai faktor p 1, yang berlaku s 1 kali dan seterusnya p n – s n kali. Oleh itu pengembangan akan mengambil bentuk a=p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n. Catatan ini dipanggil pemfaktoran kanonik nombor menjadi faktor perdana.

Apabila mengembangkan nombor 609840, kita mendapat bahawa 609 840 = 2 2 2 2 3 3 5 7 11 11, bentuk kanoniknya ialah 609 840 = 2 4 3 2 5 7 11 2. Menggunakan pengembangan kanonik, anda boleh mencari semua pembahagi nombor dan nombornya.

Untuk memfaktorkan dengan betul, anda perlu mempunyai pemahaman tentang nombor perdana dan komposit. Intinya adalah untuk mendapatkan nombor pembahagi berurutan dalam bentuk p 1, p 2, ..., p n nombor a , a 1 , a 2 , … , a n - 1, ini memungkinkan untuk mendapatkan a = p 1 a 1, dengan a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , dengan a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · a n , di mana a n = a n - 1: p n. Setelah diterima a n = 1, kemudian kesamarataan a = p 1 · p 2 · … · p n kita memperoleh penguraian nombor a yang diperlukan kepada faktor perdana. Perhatikan bahawa p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Untuk mencari yang terkecil pembahagi biasa anda perlu menggunakan jadual nombor perdana. Ini dilakukan dengan menggunakan contoh mencari pembahagi perdana terkecil bagi nombor z. Apabila mengambil nombor perdana 2, 3, 5, 11 dan seterusnya, dan membahagikan nombor z dengannya. Oleh kerana z tidak nombor perdana, ia harus diambil kira bahawa pembahagi perdana terkecil tidak akan lebih besar daripada z. Dapat dilihat bahawa tiada pembahagi z, maka jelaslah bahawa z ialah nombor perdana.

Contoh 1

Mari kita lihat contoh nombor 87. Apabila ia dibahagikan dengan 2, kita mempunyai 87: 2 = 43 dengan baki 1. Ia berikutan bahawa 2 tidak boleh menjadi pembahagi mesti dilakukan sepenuhnya. Apabila dibahagikan dengan 3, kita mendapat 87: 3 = 29. Oleh itu kesimpulannya ialah 3 ialah pembahagi perdana terkecil bagi nombor 87.

Apabila memfaktorkan kepada faktor perdana, anda mesti menggunakan jadual nombor perdana, di mana a. Apabila memfaktorkan 95, anda harus menggunakan kira-kira 10 nombor perdana, dan apabila memfaktorkan 846653, kira-kira 1000.

Mari kita pertimbangkan algoritma penguraian menjadi faktor utama:

mencari faktor terkecil pembahagi p 1 bagi suatu nombor a dengan formula a 1 = a: p 1, apabila a 1 = 1, maka a ialah nombor perdana dan termasuk dalam pemfaktoran, apabila tidak sama dengan 1, maka a = p 1 · a 1 dan ikuti ke titik di bawah;
mencari pembahagi perdana p 2 bagi nombor a 1 dengan membilang nombor perdana secara berurutan menggunakan a 2 = a 1: p 2 , apabila 2 = 1 , maka pengembangan akan mengambil bentuk a = p 1 p 2 , apabila a 2 = 1, maka a = p 1 p 2 a 2 , dan kita teruskan ke langkah seterusnya;
mencari melalui nombor perdana dan mencari pembahagi perdana p 3 nombor a 2 mengikut formula a 3 = a 2: p 3 apabila a 3 = 1 , maka kita dapati bahawa a = p 1 p 2 p 3 , apabila tidak sama dengan 1, maka a = p 1 p 2 p 3 a 3 dan teruskan ke langkah seterusnya;
pembahagi utama ditemui p n nombor a n - 1 dengan menghitung nombor perdana dengan pn - 1, dan juga a n = a n - 1: p n, di mana a n = 1, langkahnya adalah muktamad, hasilnya kita mendapat bahawa a = p 1 · p 2 · … · p n .

Hasil algoritma ditulis dalam bentuk jadual dengan faktor terurai dengan bar menegak secara berurutan dalam lajur. Pertimbangkan rajah di bawah.

Algoritma yang terhasil boleh digunakan dengan menguraikan nombor menjadi faktor perdana.

Apabila memfaktorkan faktor utama, algoritma asas harus diikuti.

Contoh 2

Faktorkan nombor 78 kepada faktor perdana.

Penyelesaian

Untuk mencari pembahagi perdana terkecil, anda perlu melalui semua nombor perdana dalam 78. Iaitu 78: 2 = 39. Pembahagian tanpa baki bermakna ini ialah pembahagi mudah pertama, yang kami nyatakan sebagai p 1. Kami mendapat bahawa a 1 = a: p 1 = 78: 2 = 39. Kami tiba pada kesamaan bentuk a = p 1 · a 1 , di mana 78 = 2 39. Kemudian 1 = 39, iaitu, kita harus meneruskan ke langkah seterusnya.

Mari fokus untuk mencari pembahagi utama p2 nombor a 1 = 39. Anda harus melalui nombor perdana, iaitu, 39: 2 = 19 (baki 1). Oleh kerana pembahagian dengan baki, 2 bukan pembahagi. Apabila memilih nombor 3, kita mendapat bahawa 39: 3 = 13. Ini bermakna p 2 = 3 ialah pembahagi perdana terkecil 39 dengan a 2 = a 1: p 2 = 39: 3 = 13. Kami memperoleh kesamaan bentuk a = p 1 p 2 a 2 dalam bentuk 78 = 2 3 13. Kami mempunyai bahawa 2 = 13 tidak sama dengan 1, maka kita harus meneruskan.

Pembahagi perdana terkecil bagi nombor a 2 = 13 didapati dengan mencari melalui nombor, bermula dengan 3. Kami mendapat bahawa 13: 3 = 4 (baki 1). Daripada ini kita dapat melihat bahawa 13 tidak boleh dibahagikan dengan 5, 7, 11, kerana 13: 5 = 2 (rehat. 3), 13: 7 = 1 (rehat. 6) dan 13: 11 = 1 (rehat. 2) . Dapat dilihat bahawa 13 ialah nombor perdana. Mengikut formula ia kelihatan seperti ini: a 3 = a 2: p 3 = 13: 13 = 1. Kami mendapati bahawa 3 = 1, yang bermaksud penyelesaian algoritma. Sekarang faktor ditulis sebagai 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Jawapan: 78 = 2 3 13.

Contoh 3

Faktorkan nombor 83,006 kepada faktor perdana.

Penyelesaian

Langkah pertama melibatkan pemfaktoran p 1 = 2 Dan a 1 = a: p 1 = 83,006: 2 = 41,503, di mana 83,006 = 2 · 41,503.

Langkah kedua menganggap bahawa 2, 3 dan 5 bukanlah pembahagi utama untuk nombor a 1 = 41,503, tetapi 7 ialah pembahagi utama, kerana 41,503: 7 = 5,929. Kami mendapat bahawa p 2 = 7, a 2 = a 1: p 2 = 41,503: 7 = 5,929. Jelas sekali, 83,006 = 2 7 5 929.

Mencari pembahagi perdana terkecil p 4 kepada nombor a 3 = 847 ialah 7. Dapat dilihat bahawa a 4 = a 3: p 4 = 847: 7 = 121, jadi 83 006 = 2 7 7 7 121.

Untuk mencari pembahagi utama nombor a 4 = 121, kita menggunakan nombor 11, iaitu, p 5 = 11. Kemudian kita mendapat ungkapan bentuk a 5 = a 4: p 5 = 121: 11 = 11, dan 83,006 = 2 7 7 7 11 11.

Untuk nombor a 5 = 11 nombor p 6 = 11 ialah pembahagi perdana terkecil. Oleh itu a 6 = a 5: p 6 = 11: 11 = 1. Kemudian 6 = 1. Ini menunjukkan penyelesaian algoritma. Faktor akan ditulis sebagai 83 006 = 2 · 7 · 7 · 7 · 11 · 11.

Notasi kanonik jawapan akan berbentuk 83 006 = 2 · 7 3 · 11 2.

Jawapan: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2.

Contoh 4

Faktorkan nombor 897,924,289.

Penyelesaian

Untuk mencari faktor perdana pertama, cari melalui nombor perdana, bermula dengan 2. Penghujung carian berlaku pada nombor 937. Kemudian p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 dan 897 924 289 = 937 958 297.

Langkah kedua algoritma adalah untuk mengulangi nombor perdana yang lebih kecil. Iaitu, kita mulakan dengan nombor 937. Nombor 967 boleh dianggap perdana kerana ia merupakan pembahagi utama bagi nombor a 1 = 958,297. Dari sini kita dapat p 2 = 967, kemudian a 2 = a 1: p 1 = 958 297: 967 = 991 dan 897 924 289 = 937 967 991.

Langkah ketiga mengatakan bahawa 991 ialah nombor perdana, kerana ia tidak mempunyai faktor perdana tunggal yang tidak melebihi 991. Nilai anggaran ungkapan radikal ialah 991< 40 2 . Иначе запишем как 991 < 40 2 . Ini menunjukkan bahawa p 3 = 991 dan a 3 = a 2: p 3 = 991: 991 = 1. Kami mendapati bahawa penguraian nombor 897 924 289 kepada faktor perdana diperoleh sebagai 897 924 289 = 937 967 991.

Jawapan: 897 924 289 = 937 967 991.

Menggunakan ujian kebolehbahagi untuk pemfaktoran perdana

Untuk memfaktorkan nombor ke dalam faktor perdana, anda perlu mengikuti algoritma. Apabila terdapat bilangan kecil, adalah dibenarkan menggunakan jadual pendaraban dan tanda bahagi. Mari kita lihat ini dengan contoh.

Contoh 5

Jika perlu memfaktorkan 10, maka jadual menunjukkan: 2 · 5 = 10. Nombor 2 dan 5 yang terhasil adalah nombor perdana, jadi ia adalah faktor perdana untuk nombor 10.

Contoh 6

Sekiranya perlu untuk menguraikan nombor 48, maka jadual menunjukkan: 48 = 6 8. Tetapi 6 dan 8 bukanlah faktor utama, kerana ia juga boleh dikembangkan sebagai 6 = 2 3 dan 8 = 2 4. Kemudian penguraian lengkap maka ternyata 48 = 6 8 = 2 3 2 4. Notasi kanonik akan mengambil bentuk 48 = 2 4 · 3.

Contoh 7

Apabila menguraikan nombor 3400, anda boleh menggunakan tanda-tanda pembahagian. DALAM dalam kes ini Kriteria bagi pembahagian dengan 10 dan 100 adalah relevan. Dari sini kita mendapat bahawa 3,400 = 34 · 100, di mana 100 boleh dibahagikan dengan 10, iaitu, ditulis sebagai 100 = 10 · 10, yang bermaksud bahawa 3,400 = 34 · 10 · 10. Berdasarkan ujian boleh bahagi, kita dapati bahawa 3 400 = 34 10 10 = 2 17 2 5 2 5. Semua faktor adalah utama. Pengembangan kanonik mengambil bentuk 3 400 = 2 3 5 2 17.

Apabila kita mencari faktor perdana, kita perlu menggunakan ujian kebolehbahagi dan jadual pendaraban. Jika anda membayangkan nombor 75 sebagai hasil daripada faktor, maka anda perlu mengambil kira peraturan pembahagian sebanyak 5. Kami mendapat bahawa 75 = 5 15, dan 15 = 3 5. Iaitu, pengembangan yang dikehendaki adalah contoh bentuk produk 75 = 5 · 3 · 5.

Jika anda melihat ralat dalam teks, sila serlahkannya dan tekan Ctrl+Enter

Pembolehubah rawak V dipanggil berpusat , jika jangkaan matematiknya adalah sama dengan 0. Proses rawak berpusat asas ialah hasil darab pembolehubah rawak berpusat V dan fungsi bukan rawak φ(t):X(t)=Vφ(t). Proses rawak berpusat asas mempunyai ciri-ciri berikut:

Ungkapan bentuk
, di mana φ k ( t ), k =1;2;…-fungsi bukan rawak; , k =1;2;…-pembolehubah rawak berpusat tidak berkorelasi, dipanggil pengembangan kanonik proses rawakX ( t ), manakala pembolehubah rawak dipanggil pekali pengembangan kanonik; dan fungsi bukan rawak φ k ( t ) - menyelaraskan fungsi pengembangan kanonik.

Mari kita pertimbangkan ciri-ciri proses rawak

Sejak dengan syarat
Itu

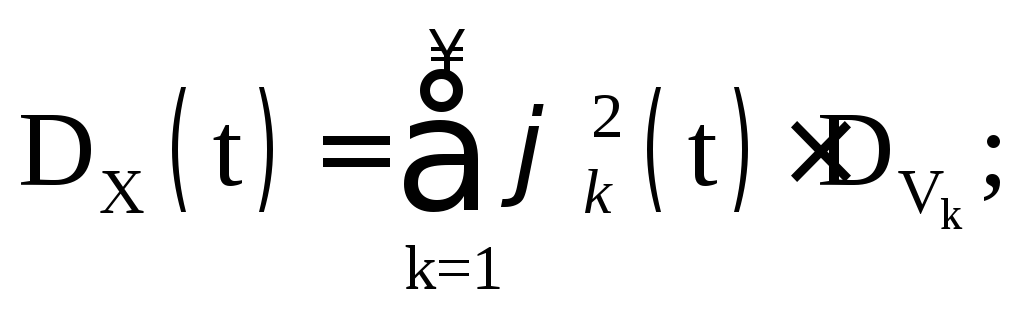
Jelas sekali, proses rawak yang sama mempunyai pelbagai jenis pengembangan kanonik bergantung pada pilihan fungsi koordinat. Selain itu, walaupun dengan pilihan fungsi koordinat, terdapat kesewenang-wenangan dalam pengagihan pembolehubah rawak V k Dalam amalan, berdasarkan keputusan eksperimen, anggaran diperolehi untuk jangkaan matematik dan fungsi korelasi:
.
Selepas penguraian

menjadi siri Fourier berganda dalam fungsi koordinat φ hingga (t):
mendapatkan nilai varians

4.2. Konsep fungsi umum. Fungsi delta Dirac. Perwakilan kanonik bersepadu bagi proses rawak.

Fungsi umum dipanggil had jujukan keluarga satu parameter bagi fungsi berterusan.

Fungsi delta Dirac
- ini adalah fungsi umum yang terhasil daripada lulus ke had di
dalam keluarga fungsi

Antara harta -fungsi kami perhatikan perkara berikut:

3. Jika f(t)- fungsi berterusan, Itu

Proses rawak X( t ), fungsi korelasi yang mempunyai bentuk yang dipanggil "bunyi putih" tidak pegun. Jika W ( t 1 )= W - const , kemudian X( t )-pegun "bunyi putih".

Seperti berikut dari definisi, tidak ada dua, tidak kira seberapa dekat, bahagian "bunyi putih" dikaitkan. Ungkapan W(t) dipanggil

keamatan "bunyi putih". t Perwakilan kanonik kamiran bagi proses rawak X(
) dipanggil ungkapan bentuk
di mana
- fungsi berpusat rawak;

- fungsi bukan rawak bagi hujah berterusan

Fungsi korelasi proses rawak sedemikian mempunyai bentuk:

Ia boleh ditunjukkan bahawa terdapat fungsi bukan rawak G(λ) seperti itu

di mana G(λ 1) ialah ketumpatan serakan; δ(x) ialah fungsi delta Dirac.

Kami dapat

Oleh itu, varians proses rawak X(t):

4.3. Transformasi linear dan bukan linear bagi proses rawak

Masalah berikut dipertimbangkan: "isyarat input" yang mempunyai sifat proses rawak X(t) dibekalkan kepada input sistem (peranti, penukar) S. Sistem menukarnya kepada "isyarat output" Y(t):

Secara formal, penjelmaan proses rawak X(t) kepada Y(t) boleh diterangkan menggunakan apa yang dipanggil pengendali sistem A t:

Y(t)=A t (X(t)). Indeks t menunjukkan bahawa operator ini melakukan penukaran masa. Rumusan masalah berikut untuk mengubah proses rawak adalah mungkin. Undang-undang pengedaran diketahui atau

ciri umum

proses rawak X(t) pada input kepada sistem S, operator A t sistem S diberikan, adalah perlu untuk menentukan undang-undang taburan atau ciri umum proses rawak Y(t) pada output sistem S.

Undang-undang taburan (ciri am) bagi proses rawak X(t) dan keperluan bagi proses rawak Y(t) diketahui; adalah perlu untuk menentukan jenis operator A t sistem S yang paling memenuhi keperluan yang diberikan kY(t). Undang-undang taburan (ciri umum) bagi proses rawak Y(t) diketahui dan operator A t sistem S diberikan; ia diperlukan untuk menentukan hukum taburan atau ciri umum proses rawak X(t). pengendali A t sistem S:

Operator Sistem

Linear LNonlinearN

Linear homogeneous L 0 Linear inhomogenous L n

Mari kita pertimbangkan kesan sistem tidak homogen linear

L n (...)=L 0 (...)+φ(t)

kepada proses rawak X(t) yang mempunyai pengembangan kanonik berikut:

Kami mendapat:

mari kita perkenalkan notasi

maka pengembangan kanonik Y(t) mengambil bentuk:

Jangkaan matematik bagi proses rawak Y(t):

fungsi korelasi proses rawak Y(t):

oleh itu,

Di seberang sana

Varians proses rawak Y(t):

Sebagai kesimpulan perenggan ini, kami perhatikan bahawa pengendali pembezaan dan penyepaduan proses rawak adalah homogen linear.

2. Penjelmaan kuadratik dianggap:

Y(t)=(X(t)) 2 ,

V k -pembolehubah rawak berpusat yang mempunyai simetri taburan kira-kira sifar; mana-mana empat daripada mereka adalah bebas bersama.

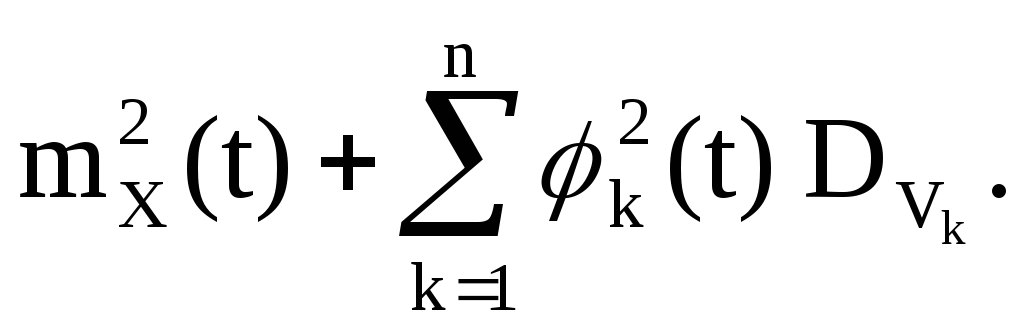
Kemudian

Mari perkenalkan fungsi bukan rawak

dan pembolehubah rawak

maka proses rawak Y(t) mengambil bentuk

Pengembangan kanonik bagi proses rawak Y(t) diperolehi. Fungsi korelasiY(t): Formulasi. Diberinombor asli n(

n > 1) . Dapatkan penguraian kanoniknya kepada faktor mudah, iaitu, tunjukkan ia sebagai hasil daripada faktor mudah. Dalam kes ini, adalah dibenarkan untuk menunjukkan faktor 1 dalam pengembangan Contohnya, 264 = 2 * 2 * 2 * 3 * 11 (program boleh menghasilkan jawapan 264 = 1 * 2 * 2 * 2 * 3 *. 11). Penyelesaian.

tugasan ini mempunyai penyelesaian yang cukup bagus. daripada

teorem asas aritmetik diketahui bahawa untuk sebarang nombor asli yang lebih besar daripada 1 terdapat penguraian kanonik kepada faktor perdana, dan penguraian ini adalah unik mengikut susunan faktor. Iaitu, sebagai contoh, 12 = 2 * 2 * 2 dan 12 = 3 * 2 * 2 adalah pengembangan yang sama. Pertimbangkan bentuk kanonik sebarang nombor pada contoh khusus. Contohnya, 264 = 2 * 2 * 2 * 3 * 11. Bagaimanakah struktur ini boleh dikenal pasti? Untuk menjawab soalan ini, marilah kita mengingati apa yang dinyatakan dalam mana-mana

Iaitu, jika kita membahagikan 264 dengan 2, maka dalam pengembangan kanoniknya akan ada satu dua. Kemudian kita boleh menyemak sama ada hasil bahagi yang terhasil sekali lagi boleh dibahagikan dengan 2. Jawapannya adalah ya, tetapi kali ketiga pembahagian akan memberikan baki. Kemudian anda perlu mengambil nombor asli 3 seterusnya untuk pertimbangan - hasil bagi akan dibahagikan dengannya sekali. Akibatnya, melepasi garis nombor ke arah positif, kita akan mencapai nombor 11, dan selepas membahagikan dengan 11 n akan menjadi sama dengan 1, yang akan menunjukkan keperluan untuk menyelesaikan prosedur.

Mengapa, dengan "menyilang" faktor-faktor yang ditemui, kita tidak mendapat pembahagian kepada nombor komposit? Sebenarnya, semuanya mudah di sini - sebarang nombor komposit adalah hasil darab faktor perdana yang lebih kecil daripadanya. Akibatnya, ternyata kita akan mencoret n semua faktor bagi sebarang nombor komposit, sehingga kita mencapainya sendiri dalam rantaian pembahagian. Contohnya, dengan carian yang begitu menyeluruh n tidak akan dibahagikan dengan 4, kerana "dalam perjalanan" ke nombor ini kami akan padamkan daripada n semua faktor adalah dua.

Algoritma dalam bahasa semula jadi:

1) Input n;

2) Tugasan kepada pembolehubah hlm nombor 2;

3) Keluarkan nombor n, tanda dan unit yang sama untuk merasmikan pengembangan;

4) Memulakan gelung dengan prasyarat n< > 1 . Dalam gelung:

Jika mmodp = 0, kemudian paparkan tanda darab dan pembolehubah p, kemudian bahagikan n pada hlm, jika tidak, tingkatkan nilai i oleh 1;

program PrimeFactors;
n, p: perkataan;
bermula
p:= 2;
readln(n);
tulis(n, ‘= 1’);
manakala n<>1 bermula
jika (n mod p) = 0 maka mulakan
tulis(‘ * ‘, p);
n:= n div p
lain bermula
inc(p)