Perbezaan contoh janjang aritmetik. Janjang aritmetik dengan contoh
Kalkulator dalam talian.
Menyelesaikan janjang aritmetik.
Diberi: a n , d, n
Cari: a 1
Atur cara matematik ini mencari \(a_1\) janjang aritmetik berdasarkan nombor yang ditentukan pengguna \(a_n, d\) dan \(n\).
Nombor \(a_n\) dan \(d\) boleh ditentukan bukan sahaja sebagai integer, tetapi juga sebagai pecahan. Lebih-lebih lagi, nombor pecahan boleh dimasukkan sebagai pecahan perpuluhan (\(2.5\)) dan sebagai pecahan sepunya(\(-5\frac(2)(7)\)).
Program ini bukan sahaja memberikan jawapan kepada masalah, tetapi juga memaparkan proses mencari penyelesaian.
Kalkulator dalam talian ini mungkin berguna untuk pelajar sekolah menengah sekolah menengah sebagai persediaan untuk ujian dan peperiksaan, apabila menguji pengetahuan sebelum Peperiksaan Negeri Bersepadu, untuk ibu bapa mengawal penyelesaian banyak masalah dalam matematik dan algebra. Atau mungkin terlalu mahal untuk anda mengupah tutor atau membeli buku teks baharu? Atau adakah anda hanya mahu menyelesaikannya secepat mungkin? kerja rumah
dalam matematik atau algebra? Dalam kes ini, anda juga boleh menggunakan program kami dengan penyelesaian terperinci. Dengan cara ini anda boleh membelanjakan anda latihan sendiri dan/atau melatih mereka adik-adik lelaki
atau saudara perempuan, manakala tahap pendidikan dalam bidang masalah yang diselesaikan meningkat.
Jika anda tidak biasa dengan peraturan untuk memasukkan nombor, kami mengesyorkan agar anda membiasakan diri dengannya.
Peraturan untuk memasukkan nombor
Nombor \(a_n\) dan \(d\) boleh ditentukan bukan sahaja sebagai integer, tetapi juga sebagai pecahan.
Nombor \(n\) hanya boleh menjadi integer positif.
Peraturan untuk memasukkan pecahan perpuluhan.
Bahagian integer dan pecahan dalam pecahan perpuluhan boleh dipisahkan sama ada dengan noktah atau koma. Sebagai contoh, anda boleh masuk perpuluhan
jadi 2.5 atau lebih 2.5
Peraturan untuk memasukkan pecahan biasa.
Hanya nombor bulat boleh bertindak sebagai pengangka, penyebut dan bahagian integer pecahan.
Penyebut tidak boleh negatif. Apabila masuk pecahan berangka /
Pengangka dipisahkan dari penyebut dengan tanda bahagi:
Input:
Keputusan: \(-\frac(2)(3)\) Seluruh bahagian &
Pengangka dipisahkan dari penyebut dengan tanda bahagi:
dipisahkan daripada pecahan dengan ampersand:
Cari 1
Telah didapati bahawa beberapa skrip yang diperlukan untuk menyelesaikan masalah ini tidak dimuatkan, dan program mungkin tidak berfungsi.
Anda mungkin telah mendayakan AdBlock.
Untuk penyelesaian muncul, anda perlu mendayakan JavaScript.
Berikut ialah arahan tentang cara mendayakan JavaScript dalam penyemak imbas anda.
Kerana Terdapat ramai orang yang bersedia untuk menyelesaikan masalah, permintaan anda telah beratur.
Dalam beberapa saat penyelesaian akan muncul di bawah.
Sila tunggu sek...
jika anda perasan ralat dalam penyelesaian, maka anda boleh menulis tentang perkara ini dalam Borang Maklum Balas.
jangan lupa nyatakan tugasan yang mana anda tentukan apa masuk dalam ladang.
Permainan, teka-teki, emulator kami:
Sedikit teori.
Urutan nombor
Penomboran sering digunakan dalam amalan harian pelbagai barangan untuk menunjukkan susunan yang muncul. Sebagai contoh, rumah di setiap jalan bernombor. Di perpustakaan, langganan pembaca dinomborkan dan kemudian disusun mengikut susunan nombor yang ditetapkan dalam fail kad khas.
Dalam bank simpanan, menggunakan nombor akaun peribadi pendeposit, anda boleh mencari akaun ini dengan mudah dan melihat deposit yang ada padanya. Biarkan akaun No. 1 mengandungi deposit a1 rubel, akaun No. 2 mengandungi deposit a2 rubel, dll. Ternyata urutan nombor
a 1 , a 2 , a 3 , ..., a N
di mana N ialah nombor semua akaun. Di sini, setiap nombor asli n dari 1 hingga N dikaitkan dengan nombor a n.
Juga belajar dalam matematik urutan nombor tak terhingga:
a 1 , a 2 , a 3 , ..., a n , ... .
Nombor a 1 dipanggil sebutan pertama bagi urutan itu, nombor a 2 - sebutan kedua bagi urutan itu, nombor a 3 - sebutan ketiga bagi urutan itu dll.
Nombor a n dipanggil ahli ke- (nth) bagi jujukan, dan nombor asli n ialahnya nombor.
Contohnya, dalam urutan segi empat sama nombor asli 1, 4, 9, 16, 25, ..., n 2, (n + 1) 2, ... dan 1 = 1 ialah sebutan pertama bagi jujukan; dan n = n 2 ialah penggal ke- urutan; a n+1 = (n + 1) 2 ialah sebutan (n + 1)th (n tambah pertama) bagi jujukan. Selalunya urutan boleh ditentukan oleh formula sebutan ke-nnya. Sebagai contoh, formula \(a_n=\frac(1)(n), \; n \in \mathbb(N) \) mentakrifkan jujukan \(1, \; \frac(1)(2) , \; \frac( 1)(3) , \; \frac(1)(4) , \dots,\frac(1)(n) , \dots \)
Janjang aritmetik
Panjang tahun adalah kira-kira 365 hari. Nilai yang lebih tepat ialah \(365\frac(1)(4)\) hari, jadi setiap empat tahun ralat satu hari terkumpul.
Untuk mengambil kira ralat ini, satu hari ditambahkan pada setiap tahun keempat, dan tahun lanjutan dipanggil tahun lompat.
Sebagai contoh, pada alaf ketiga tahun lompat ialah tahun 2004, 2008, 2012, 2016, ... .
Dalam urutan ini, setiap ahli, bermula dari yang kedua, adalah sama dengan yang sebelumnya, ditambah dengan nombor 4 yang sama. Urutan sedemikian dipanggil janjang aritmetik.
Definisi.
Urutan nombor a 1, a 2, a 3, ..., a n, ... dipanggil janjang aritmetik, jika untuk semua semula jadi n kesamarataan
\(a_(n+1) = a_n+d, \)
di mana d ialah beberapa nombor.
Daripada formula ini ia mengikuti bahawa a n+1 - a n = d. Nombor d dipanggil perbezaan janjang aritmetik.
Mengikut takrifan janjang aritmetik kita mempunyai:
\(a_(n+1)=a_n+d, \quad a_(n-1)=a_n-d, \)
di mana
\(a_n= \frac(a_(n-1) +a_(n+1))(2) \), di mana \(n>1 \)
Oleh itu, setiap sebutan janjang aritmetik, bermula dari yang kedua, adalah sama dengan min aritmetik bagi dua sebutan yang bersebelahan. Ini menerangkan nama janjang "aritmetik".
Ambil perhatian bahawa jika a 1 dan d diberikan, maka baki sebutan janjang aritmetik boleh dikira menggunakan formula berulang a n+1 = a n + d. Dengan cara ini, tidak sukar untuk mengira beberapa sebutan pertama janjang, bagaimanapun, sebagai contoh, 100 sudah memerlukan banyak pengiraan. Biasanya, formula istilah ke-n digunakan untuk ini. Mengikut takrifan janjang aritmetik
\(a_2=a_1+d, \)
\(a_3=a_2+d=a_1+2d, \)
\(a_4=a_3+d=a_1+3d \)
dll.
sama sekali,
\(a_n=a_1+(n-1)d, \)
kerana penggal ke- janjang aritmetik diperoleh daripada sebutan pertama dengan menambah (n-1) kali nombor d.
Formula ini dipanggil formula bagi sebutan ke-n suatu janjang aritmetik.
Jumlah n sebutan pertama suatu janjang aritmetik
Cari hasil tambah semua nombor asli dari 1 hingga 100.
Mari tulis jumlah ini dalam dua cara:
S = l + 2 + 3 + ... + 99 + 100,
S = 100 + 99 + 98 + ... + 2 + 1.
Mari tambah istilah kesamaan ini mengikut istilah:
2S = 101 + 101 + 101 + ... + 101 + 101.
Jumlah ini mempunyai 100 istilah
Oleh itu, 2S = 101 * 100, maka S = 101 * 50 = 5050.
Sekarang mari kita pertimbangkan janjang aritmetik sewenang-wenangnya
a 1 , a 2 , a 3 , ..., a n , ...
Biarkan S n ialah hasil tambah n sebutan pertama janjang ini:
S n = a 1 , a 2 , a 3 , ..., a n
Kemudian hasil tambah n sebutan pertama suatu janjang aritmetik adalah sama dengan
\(S_n = n \cdot \frac(a_1+a_n)(2) \)
Oleh kerana \(a_n=a_1+(n-1)d\), kemudian menggantikan a n dalam formula ini kita mendapat formula lain untuk mencari hasil tambah n sebutan pertama suatu janjang aritmetik:
\(S_n = n \cdot \frac(2a_1+(n-1)d)(2) \)
Tahap kemasukan
Janjang aritmetik. Teori terperinci dengan contoh (2019)
Urutan nombor
Jadi, mari kita duduk dan mula menulis beberapa nombor. Contohnya:
Anda boleh menulis sebarang nombor, dan boleh ada seberapa banyak nombor yang anda suka (dalam kes kami, ada mereka). Tidak kira berapa banyak nombor yang kita tulis, kita sentiasa boleh menyebut yang mana satu pertama, yang mana satu kedua, dan seterusnya sehingga yang terakhir, iaitu, kita boleh menomborkannya. Ini adalah contoh urutan nombor:
Urutan nombor
Sebagai contoh, untuk urutan kami:
Nombor yang diberikan adalah khusus untuk hanya satu nombor dalam urutan. Dalam erti kata lain, tiada tiga nombor saat dalam urutan itu. Nombor kedua (seperti nombor ke) sentiasa sama.
Nombor dengan nombor dipanggil sebutan ke-jujukan.
Kami biasanya memanggil keseluruhan jujukan dengan beberapa huruf (contohnya,), dan setiap ahli jujukan ini adalah huruf yang sama dengan indeks yang sama dengan nombor ahli ini: .
Dalam kes kami: 
Katakan kita mempunyai urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama.
Contohnya: 
dll.
Urutan nombor ini dipanggil janjang aritmetik.
Istilah "kemajuan" diperkenalkan oleh pengarang Rom Boethius pada abad ke-6 dan difahami lebih banyak lagi. dalam erti kata yang luas, seperti urutan nombor tak terhingga. Nama "aritmetik" dipindahkan dari teori perkadaran berterusan, yang dikaji oleh orang Yunani kuno.
Ini ialah urutan nombor, setiap ahlinya adalah sama dengan yang sebelumnya ditambah kepada nombor yang sama. Nombor ini dipanggil perbezaan janjang aritmetik dan ditetapkan.
Cuba tentukan urutan nombor yang merupakan janjang aritmetik dan yang bukan:
a)
b)
c)
d)
faham? Mari bandingkan jawapan kami:
Adakah janjang aritmetik - b, c.
bukan janjang aritmetik - a, d.
Mari kita kembali ke perkembangan yang diberikan() dan cuba cari nilai ahli ke-nya. wujud dua cara untuk mencarinya.
1. Kaedah
Kita boleh menambah nombor janjang kepada nilai sebelumnya sehingga kita mencapai sebutan ke-janjang itu. Ada baiknya kita tidak mempunyai banyak perkara untuk diringkaskan - hanya tiga nilai:
Jadi, sebutan ke janjang aritmetik yang diterangkan adalah sama dengan.
2. Kaedah
Bagaimana jika kita perlu mencari nilai sebutan ke-kemajuan itu? Penjumlahan akan mengambil masa lebih daripada satu jam, dan bukan fakta bahawa kita tidak akan membuat kesilapan semasa menambah nombor.
Sudah tentu, ahli matematik telah menghasilkan satu cara yang tidak perlu menambah perbezaan janjang aritmetik kepada nilai sebelumnya. Perhatikan gambar yang dilukis dengan lebih dekat... Pasti anda sudah perasan corak tertentu iaitu:
Sebagai contoh, mari kita lihat apakah nilai sebutan ke-dalam janjang aritmetik ini terdiri daripada: 
Dengan kata lain:
Cuba cari sendiri nilai ahli janjang aritmetik tertentu dengan cara ini.
Adakah anda mengira? Bandingkan nota anda dengan jawapan:
Sila ambil perhatian bahawa anda mendapat nombor yang sama seperti dalam kaedah sebelumnya, apabila kami secara berurutan menambah istilah janjang aritmetik kepada nilai sebelumnya.
Mari cuba "menyahpersonalisasi" formula ini- mari kita bawa dia ke pandangan umum dan kita dapat:
|
Persamaan janjang aritmetik. |
Janjang aritmetik boleh meningkat atau menurun.
Bertambah- janjang di mana setiap nilai terma berikutnya adalah lebih besar daripada yang sebelumnya.
Contohnya:
Menurun- janjang di mana setiap nilai terma berikutnya adalah kurang daripada yang sebelumnya.
Contohnya:
Formula terbitan digunakan dalam pengiraan sebutan dalam kedua-dua sebutan meningkat dan menurun bagi janjang aritmetik.
Mari kita semak ini dalam amalan.
Kami diberi janjang aritmetik yang terdiri daripada nombor berikut: Mari kita semak apakah nombor ke janjang aritmetik ini jika kita menggunakan formula kita untuk mengiranya:

Sejak itu:
Oleh itu, kami yakin bahawa formula beroperasi dalam kedua-dua janjang aritmetik yang menurun dan meningkat.
Cuba cari sendiri sebutan ke dan ke bagi janjang aritmetik ini.
Mari bandingkan hasilnya:
Sifat janjang aritmetik
Mari kita rumitkan masalah - kita akan memperoleh sifat janjang aritmetik.
Katakan kita diberi syarat berikut:
- janjang aritmetik, cari nilai.
Mudah, anda katakan dan mula mengira mengikut formula yang anda sudah tahu:
Mari, ah, kemudian:
benar sekali. Ternyata kita mula-mula mencari, kemudian menambahnya pada nombor pertama dan mendapatkan apa yang kita cari. Jika perkembangan diwakili oleh nilai kecil, maka tidak ada yang rumit mengenainya, tetapi bagaimana jika kita diberi nombor dalam keadaan? Setuju, terdapat kemungkinan membuat kesilapan dalam pengiraan.
Sekarang fikirkan sama ada mungkin untuk menyelesaikan masalah ini dalam satu langkah menggunakan sebarang formula? Sudah tentu ya, dan itulah yang akan kami cuba kemukakan sekarang.
Mari kita nyatakan istilah yang diperlukan bagi janjang aritmetik sebagai, formula untuk mencarinya diketahui oleh kita - ini adalah formula yang sama yang kita perolehi pada mulanya:
, Kemudian:
- istilah janjang sebelumnya ialah:
- istilah janjang seterusnya ialah:
Mari kita rumuskan istilah janjang sebelumnya dan seterusnya:
Ternyata jumlah terma janjang sebelumnya dan seterusnya ialah nilai berganda bagi istilah janjang yang terletak di antara mereka. Dalam erti kata lain, untuk mencari nilai istilah janjang yang diberikan sebelumnya dan diketahui nilai berturut-turut, anda perlu menambahnya dan membahagikannya dengan.
Betul, kami mendapat nombor yang sama. Mari selamatkan bahan. Kira nilai untuk kemajuan itu sendiri, ia sama sekali tidak sukar.
Syabas! Anda tahu hampir segala-galanya tentang kemajuan! Tinggal untuk mengetahui hanya satu formula, yang, menurut legenda, mudah disimpulkan oleh salah seorang ahli matematik terhebat sepanjang masa, "raja ahli matematik" - Karl Gauss...
Apabila Carl Gauss berumur 9 tahun, seorang guru, sibuk memeriksa kerja pelajar di kelas lain, bertanya tugas berikut di dalam kelas: "Kira jumlah semua nombor asli dari hingga (mengikut sumber lain hingga) termasuk." Bayangkan guru terkejut apabila salah seorang pelajarnya (ialah Karl Gauss) seminit kemudian memberikan jawapan yang betul untuk tugas itu, manakala kebanyakan rakan sekelas daredevil, selepas pengiraan yang panjang, menerima keputusan yang salah...
Carl Gauss muda melihat corak tertentu yang anda juga boleh perasan dengan mudah.
Katakan kita mempunyai janjang aritmetik yang terdiri daripada sebutan -th: Kita perlu mencari jumlah sebutan janjang aritmetik ini. Sudah tentu, kita boleh menjumlahkan semua nilai secara manual, tetapi bagaimana jika tugas itu memerlukan mencari jumlah istilahnya, seperti yang dicari oleh Gauss?
Mari kita gambarkan perkembangan yang diberikan kepada kita. Lihat dengan teliti nombor yang diserlahkan dan cuba lakukan pelbagai operasi matematik dengan mereka. 
Sudahkah anda mencubanya? Apa yang awak perasan? Betul! Jumlah mereka adalah sama

Sekarang beritahu saya, berapakah jumlah pasangan sebegitu yang terdapat dalam janjang yang diberikan kepada kita? Sudah tentu, tepat separuh daripada semua nombor, iaitu.
Berdasarkan fakta bahawa jumlah dua sebutan janjang aritmetik adalah sama, dan pasangan yang serupa adalah sama, kita memperoleh bahawa jumlah keseluruhan adalah sama dengan:
.
Oleh itu, formula untuk jumlah sebutan pertama mana-mana janjang aritmetik ialah:
Dalam sesetengah masalah kita tidak tahu istilah ke-, tetapi kita tahu perbezaan perkembangannya. Cuba gantikan formula sebutan ke dalam formula jumlah.
Apa yang awak dapat?
Syabas! Sekarang mari kita kembali kepada masalah yang ditanyakan kepada Carl Gauss: hitung sendiri apakah jumlah nombor yang bermula dari th sama dengan dan jumlah nombor bermula dari th.
Berapa banyak yang anda dapat?
Gauss mendapati bahawa jumlah istilah adalah sama, dan jumlah istilah. Adakah itu yang anda putuskan?
Malah, formula untuk jumlah sebutan bagi janjang aritmetik telah dibuktikan oleh saintis Yunani purba Diophantus pada abad ke-3, dan sepanjang masa ini orang yang cerdik menggunakan sepenuhnya sifat janjang aritmetik.
Sebagai contoh, bayangkan Mesir Purba dan projek pembinaan terbesar pada masa itu - pembinaan piramid... Gambar menunjukkan sebelahnya. 
Di manakah perkembangan di sini, anda katakan? Lihat dengan teliti dan cari corak dalam bilangan blok pasir dalam setiap baris dinding piramid. 
Mengapa tidak janjang aritmetik? Kira berapa banyak blok yang diperlukan untuk membina satu dinding jika bata blok diletakkan di pangkalan. Saya harap anda tidak akan mengira semasa menggerakkan jari anda pada monitor, anda masih ingat formula terakhir dan semua yang kami katakan tentang janjang aritmetik?
DALAM dalam kes ini Perkembangannya kelihatan seperti ini: .
Perbezaan janjang aritmetik.
Bilangan sebutan bagi suatu janjang aritmetik.
Mari kita gantikan data kita ke dalam formula terakhir (kira bilangan blok dalam 2 cara).
Kaedah 1.
Kaedah 2.
Dan kini anda boleh mengira pada monitor: bandingkan nilai yang diperoleh dengan bilangan blok yang ada dalam piramid kami. faham? Syabas, anda telah menguasai jumlah sebutan ke-n suatu janjang aritmetik.
Sudah tentu, anda tidak boleh membina piramid dari blok di pangkalan, tetapi dari? Cuba kira berapa banyak bata pasir yang diperlukan untuk membina dinding dengan keadaan ini.
Adakah anda berjaya?
Jawapan yang betul ialah blok:
Latihan
Tugasan:
- Masha semakin sihat untuk musim panas. Setiap hari dia menambah bilangan cangkung. Berapa kali Masha akan melakukan squats dalam seminggu jika dia melakukan squats pada sesi latihan pertama?
- Apakah hasil tambah semua nombor ganjil yang terkandung dalam.
- Apabila menyimpan log, pembalak menyusunnya sedemikian rupa sehingga setiap lapisan atas mengandungi satu log kurang daripada yang sebelumnya. Berapa banyak kayu balak dalam satu batu, jika asas batu itu ialah kayu balak?
Jawapan:
- Mari kita tentukan parameter janjang aritmetik. Dalam kes ini
(minggu = hari).Jawapan: Dalam dua minggu, Masha perlu melakukan squat sekali sehari.
- Nombor ganjil pertama, nombor terakhir.
Perbezaan janjang aritmetik.
Bilangan nombor ganjil dalam ialah separuh, bagaimanapun, mari kita semak fakta ini menggunakan formula untuk mencari sebutan ke satu janjang aritmetik:Nombor memang mengandungi nombor ganjil.
Mari kita gantikan data yang tersedia ke dalam formula:Jawapan: Jumlah semua nombor ganjil yang terkandung dalam adalah sama.
- Mari kita ingat masalah tentang piramid. Untuk kes kami, a , kerana setiap lapisan atas dikurangkan dengan satu log, maka secara keseluruhan terdapat sekumpulan lapisan, iaitu.
Mari kita gantikan data ke dalam formula:Jawapan: Terdapat kayu balak di dalam batu.
Mari kita ringkaskan
- - urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama. Ia boleh meningkat atau menurun.
- Mencari formula Sebutan ke-1 bagi suatu janjang aritmetik ditulis dengan formula - , di mana ialah bilangan nombor dalam janjang itu.
- Harta ahli sesuatu janjang aritmetik- - di manakah bilangan nombor dalam kemajuan.
- Jumlah sebutan bagi suatu janjang aritmetik boleh didapati dalam dua cara:
, di manakah bilangan nilai.
PERKEMBANGAN AITMETIK. PERINGKAT TENGAH
Urutan nombor
Mari duduk dan mula menulis beberapa nombor. Contohnya:
Anda boleh menulis sebarang nombor, dan boleh ada seberapa banyak nombor yang anda suka. Tetapi kita sentiasa boleh mengatakan yang mana satu pertama, yang mana satu kedua, dan seterusnya, iaitu, kita boleh menomborkannya. Ini adalah contoh urutan nombor.
Urutan nombor ialah satu set nombor, setiap satunya boleh diberikan nombor unik.
Dalam erti kata lain, setiap nombor boleh dikaitkan dengan nombor asli tertentu, dan nombor unik. Dan kami tidak akan memberikan nombor ini kepada mana-mana nombor lain daripada set ini.
Nombor dengan nombor dipanggil ahli urutan ke-.
Kami biasanya memanggil keseluruhan jujukan dengan beberapa huruf (contohnya,), dan setiap ahli jujukan ini adalah huruf yang sama dengan indeks yang sama dengan nombor ahli ini: .
Ia adalah sangat mudah jika sebutan ke-jujukan boleh ditentukan oleh beberapa formula. Sebagai contoh, formula
menetapkan urutan:
Dan formulanya adalah urutan berikut:
Sebagai contoh, janjang aritmetik ialah jujukan (istilah pertama di sini adalah sama, dan perbezaannya ialah). Atau (, perbezaan).
formula penggal ke-n
Kami memanggil formula berulang di mana, untuk mengetahui istilah ke, anda perlu mengetahui yang sebelumnya atau beberapa yang sebelumnya:
Untuk mencari, sebagai contoh, sebutan ke-janjang menggunakan formula ini, kita perlu mengira sembilan sebelumnya. Contohnya, biarkan. Kemudian:
Nah, adakah ia jelas sekarang apakah formulanya?
Dalam setiap baris yang kita tambah, didarab dengan beberapa nombor. yang mana satu? Sangat mudah: ini ialah bilangan ahli semasa tolak:
Jauh lebih mudah sekarang, bukan? Kami menyemak:
Tentukan sendiri:
Dalam janjang aritmetik, cari formula bagi sebutan ke-n dan cari sebutan keseratus.
Penyelesaian:
Sebutan pertama adalah sama. Apa bezanya? Inilah yang:
(Inilah sebabnya ia dipanggil perbezaan kerana ia sama dengan perbezaan sebutan berturut-turut janjang).
Jadi, formulanya:
Maka sebutan keseratus adalah sama dengan:
Apakah hasil tambah semua nombor asli dari hingga?
Menurut legenda, ahli matematik yang hebat Karl Gauss, sebagai budak lelaki berusia 9 tahun, mengira jumlah ini dalam beberapa minit. Dia perasan bahawa jumlah nombor pertama dan terakhir adalah sama, jumlah kedua dan kedua terakhir adalah sama, jumlah ketiga dan ke-3 dari hujung adalah sama, dan seterusnya. Berapakah jumlah pasangan sedemikian? Betul, tepat separuh daripada bilangan semua nombor, iaitu. Jadi,
Formula umum untuk jumlah sebutan pertama mana-mana janjang aritmetik ialah:
Contoh:
Cari jumlah semua nombor dua digit, gandaan.
Penyelesaian:
Nombor yang pertama ialah ini. Setiap yang berikutnya diperoleh dengan menambah tarikh sebelumnya. Oleh itu, nombor yang kita minati membentuk janjang aritmetik dengan sebutan pertama dan perbezaannya.
Formula istilah ke-1 untuk janjang ini:
Berapakah bilangan yang terdapat dalam janjang jika kesemuanya mestilah dua digit?
Sangat mudah: .
Penggal terakhir janjang adalah sama. Kemudian jumlahnya:
Jawapan: .
Sekarang tentukan sendiri:
- Setiap hari atlet berlari lebih meter daripada hari sebelumnya. Berapakah jumlah kilometer yang dia akan lari dalam seminggu, jika pada hari pertama dia berlari km m?
- Seorang penunggang basikal menempuh lebih banyak kilometer setiap hari berbanding hari sebelumnya. Pada hari pertama dia mengembara km. Berapa hari dia perlu menempuh perjalanan sejauh satu kilometer? Berapa kilometer yang akan dia tempuh pada hari terakhir perjalanannya?
- Harga peti sejuk di kedai menurun dengan jumlah yang sama setiap tahun. Tentukan berapa banyak harga peti sejuk menurun setiap tahun jika, dijual untuk rubel, enam tahun kemudian ia dijual untuk rubel.
Jawapan:
- Perkara yang paling penting di sini ialah mengenali janjang aritmetik dan menentukan parameternya. Dalam kes ini, (minggu = hari). Anda perlu menentukan jumlah sebutan pertama janjang ini:
.
Jawapan: - Di sini diberikan: , mesti dijumpai.
Jelas sekali, anda perlu menggunakan formula jumlah yang sama seperti dalam masalah sebelumnya:
.
Gantikan nilai:Akarnya jelas tidak sesuai, jadi jawapannya adalah.
Mari kita mengira laluan yang dilalui pada hari terakhir menggunakan formula istilah ke-:
(km).
Jawapan: - Diberi: . Cari: .
Ia tidak boleh menjadi lebih mudah:
(gosok).
Jawapan:
PERKEMBANGAN AITMETIK. SECARA RINGKAS TENTANG PERKARA UTAMA
Ini ialah urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama.
Janjang aritmetik boleh meningkat () dan menurun ().
Contohnya:
Formula untuk mencari sebutan ke-n suatu janjang aritmetik
ditulis oleh formula, di mana bilangan nombor dalam janjang.
Harta ahli sesuatu janjang aritmetik
Ia membolehkan anda mencari istilah janjang dengan mudah jika istilah jirannya diketahui - di manakah bilangan nombor dalam janjang itu.
Jumlah sebutan bagi suatu janjang aritmetik
Terdapat dua cara untuk mencari jumlah:
Di manakah bilangan nilai.
Di manakah bilangan nilai.
Jenis pelajaran: mempelajari bahan baharu.
Objektif pelajaran:
- mengembangkan dan mendalami pemahaman pelajar tentang masalah yang diselesaikan menggunakan janjang aritmetik; mengatur aktiviti pencarian pelajar apabila memperoleh formula bagi hasil tambah n sebutan pertama suatu janjang aritmetik;
- membangunkan keupayaan untuk memperoleh pengetahuan baharu secara bebas dan menggunakan pengetahuan yang telah diperoleh untuk mencapai tugas yang diberikan;
- mengembangkan keinginan dan keperluan untuk menyamaratakan fakta yang diperoleh, mengembangkan kemerdekaan.
Tugasan:
- meringkaskan dan sistematikkan pengetahuan sedia ada mengenai topik "Janjang aritmetik";
- terbitkan formula untuk mengira hasil tambah n sebutan pertama suatu janjang aritmetik;
- mengajar cara menggunakan formula yang diperolehi semasa menyelesaikan pelbagai masalah;
- menarik perhatian pelajar kepada prosedur mencari nilai ungkapan berangka.
peralatan:
- kad dengan tugas untuk bekerja dalam kumpulan dan berpasangan;
- lembaran markah;
- pembentangan"Janjang aritmetik."
I. Pengemaskinian pengetahuan asas.
1. Kerja bebas secara berpasangan.
Pilihan pertama:
Tentukan janjang aritmetik. Tuliskannya formula berulang, yang digunakan untuk menentukan janjang aritmetik. Sila berikan contoh janjang aritmetik dan nyatakan perbezaannya.
pilihan ke-2:
Tuliskan formula bagi sebutan ke-n suatu janjang aritmetik. Cari sebutan ke-100 janjang aritmetik ( a n}: 2, 5, 8 …
Pada masa ini, dua orang pelajar bahagian belakang papan sedang menyediakan jawapan kepada soalan yang sama ini.
Pelajar menilai hasil kerja pasangan mereka dengan menyemaknya di papan tulis. (Helaian dengan jawapan diserahkan.)
2. Detik permainan.
Tugasan 1.
cikgu. Saya memikirkan beberapa janjang aritmetik. Tanya saya hanya dua soalan supaya selepas jawapan anda boleh menamakan penggal ke-7 janjang ini dengan cepat. (1, 3, 5, 7, 9, 11, 13, 15…)
Soalan daripada pelajar.
- Apakah sebutan keenam janjang itu dan apakah perbezaannya?
- Apakah sebutan kelapan janjang itu dan apakah perbezaannya?
Sekiranya tidak ada lagi soalan, guru boleh merangsang mereka - "larangan" pada d (perbezaan), iaitu, tidak dibenarkan bertanya apakah perbezaan itu sama. Anda boleh bertanya soalan: apakah sebutan ke-6 bagi janjang itu bersamaan dan apakah sebutan ke-8 janjang itu sama dengan?
Tugasan 2.
Terdapat 20 nombor yang tertulis di papan tulis: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.
Guru berdiri membelakangi papan. Pelajar memanggil nombor, dan guru serta-merta memanggil nombor itu sendiri. Terangkan bagaimana saya boleh melakukan ini?
Guru mengingati rumus penggal ke-n a n = 3n – 2 dan, menggantikan nilai yang ditentukan n, mencari nilai yang sepadan a n.
II. Menetapkan tugas pembelajaran.
Saya bercadang untuk menyelesaikan masalah purba sejak alaf ke-2 SM, yang ditemui dalam papirus Mesir.
Tugasan:“Hendaklah dikatakan kepadamu: Bagilah 10 takar barli kepada 10 orang, selisih antara setiap orang dengan jirannya ialah 1/8 dari takaran”.
- Bagaimanakah masalah ini berkaitan dengan janjang aritmetik topik? (Setiap orang seterusnya menerima 1/8 daripada ukuran lebih, yang bermaksud perbezaannya ialah d=1/8, 10 orang, yang bermaksud n=10.)
- Pada pendapat anda, apakah maksud ukuran nombor 10? (Jumlah semua sebutan janjang.)
- Apa lagi yang anda perlu tahu untuk memudahkan dan mudah membahagikan barli mengikut keadaan masalah? (Penggal pertama kemajuan.)
Objektif Pelajaran– mendapatkan pergantungan jumlah syarat janjang pada bilangannya, sebutan pertama dan perbezaannya, dan menyemak sama ada masalah itu telah diselesaikan dengan betul pada zaman dahulu.
Sebelum kita menyimpulkan formula, mari kita lihat bagaimana orang Mesir kuno menyelesaikan masalah itu.
Dan mereka menyelesaikannya seperti berikut:
1) 10 ukuran: 10 = 1 ukuran – bahagian purata;
2) 1 sukatan ∙ = 2 sukatan – digandakan purata kongsi.
Berganda purata syer ialah jumlah syer orang ke-5 dan ke-6.
3) 2 sukatan – 1/8 sukatan = 1 7/8 sukatan – dua kali ganda bahagian orang kelima.
4) 1 7/8: 2 = 5/16 – pecahan seperlima; dan seterusnya, anda boleh mencari bahagian setiap orang sebelumnya dan seterusnya.
Kami mendapat urutan:
III. Menyelesaikan masalah.
1. Bekerja dalam kumpulan
Kumpulan I: Cari hasil tambah 20 nombor asli berturut-turut: S 20 =(20+1)∙10 =210.
Secara amnya ![]()
Kumpulan II: Cari jumlah nombor asli dari 1 hingga 100 (The Legend of Little Gauss).
S 100 = (1+100)∙50 = 5050
Kesimpulan: ![]()
Kumpulan III: Cari hasil tambah nombor asli dari 1 hingga 21.
Penyelesaian: 1+21=2+20=3+19=4+18…
![]()
Kesimpulan: ![]()
Kumpulan IV: Cari hasil tambah nombor asli dari 1 hingga 101.
![]()
Kesimpulan: ![]()
Kaedah menyelesaikan masalah yang dipertimbangkan ini dipanggil "Kaedah Gauss".
2. Setiap kumpulan membentangkan penyelesaian masalah di papan tulis.
3. Generalisasi penyelesaian yang dicadangkan untuk janjang aritmetik arbitrari:
a 1, a 2, a 3,…, a n-2, a n-1, a n.
S n =a 1 + a 2 + a 3 + a 4 +…+ a n-3 + a n-2 + a n-1 + a n.
Mari cari jumlah ini menggunakan alasan yang sama:

4. Adakah kita telah menyelesaikan masalah tersebut?(Ya.)
IV. Pemahaman utama dan penggunaan formula yang diperoleh semasa menyelesaikan masalah.
1. Menyemak penyelesaian kepada masalah purba menggunakan formula.

2. Aplikasi formula dalam menyelesaikan pelbagai masalah.
3. Latihan untuk mengembangkan kebolehan menggunakan formula semasa menyelesaikan masalah.
A) No. 613
Diberi: ( a n) - janjang aritmetik;
(a n): 1, 2, 3, …, 1500
Cari: S 1500
Penyelesaian: ![]() , a 1 = 1, dan 1500 = 1500,
, a 1 = 1, dan 1500 = 1500,
B) Diberi: ( a n) - janjang aritmetik;
(a n): 1, 2, 3, …
S n = 210
Cari: n
Penyelesaian:

V. Kerja bebas dengan pengesahan bersama.
Denis mula bekerja sebagai kurier. Pada bulan pertama gajinya ialah 200 rubel, pada setiap bulan berikutnya ia meningkat sebanyak 30 rubel. Berapakah jumlah pendapatannya dalam setahun?
Diberi: ( a n) - janjang aritmetik;
a 1 = 200, d=30, n=12
Cari: S 12
Penyelesaian:

Jawapan: Denis menerima 4380 rubel untuk tahun ini.
VI. Arahan kerja rumah.
- Bahagian 4.3 – pelajari terbitan formula.
- №№ 585, 623 .
- Cipta satu masalah yang boleh diselesaikan menggunakan formula bagi hasil tambah n sebutan pertama suatu janjang aritmetik.
VII. Merumuskan pelajaran.
1. Lembaran markah
2. Sambung ayat
- Hari ini dalam kelas saya belajar...
- Formula yang dipelajari...
- Saya percaya bahawa...
3. Bolehkah anda mencari jumlah nombor dari 1 hingga 500? Apakah kaedah yang akan anda gunakan untuk menyelesaikan masalah ini?
Rujukan.
1. Algebra, darjah 9. Tutorial untuk institusi pendidikan. Ed. G.V. Dorofeeva. M.: "Pencerahan", 2009.
Tahap kemasukan
Janjang aritmetik. Teori terperinci dengan contoh (2019)
Urutan nombor
Jadi, mari kita duduk dan mula menulis beberapa nombor. Contohnya:
Anda boleh menulis sebarang nombor, dan boleh ada seberapa banyak nombor yang anda suka (dalam kes kami, ada mereka). Tidak kira berapa banyak nombor yang kita tulis, kita sentiasa boleh menyebut yang mana satu pertama, yang mana satu kedua, dan seterusnya sehingga yang terakhir, iaitu, kita boleh menomborkannya. Ini adalah contoh urutan nombor:
Urutan nombor
Sebagai contoh, untuk urutan kami:
Nombor yang diberikan adalah khusus untuk hanya satu nombor dalam urutan. Dalam erti kata lain, tiada tiga nombor saat dalam urutan itu. Nombor kedua (seperti nombor ke) sentiasa sama.
Nombor dengan nombor dipanggil sebutan ke-jujukan.
Kami biasanya memanggil keseluruhan jujukan dengan beberapa huruf (contohnya,), dan setiap ahli jujukan ini adalah huruf yang sama dengan indeks yang sama dengan nombor ahli ini: .
Dalam kes kami: 
Katakan kita mempunyai urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama.
Contohnya: 
dll.
Urutan nombor ini dipanggil janjang aritmetik.
Istilah "kemajuan" diperkenalkan oleh pengarang Rom Boethius pada abad ke-6 dan difahami dalam erti kata yang lebih luas sebagai urutan berangka yang tidak terhingga. Nama "aritmetik" dipindahkan dari teori perkadaran berterusan, yang dikaji oleh orang Yunani kuno.
Ini ialah urutan nombor, setiap ahlinya adalah sama dengan yang sebelumnya ditambah kepada nombor yang sama. Nombor ini dipanggil perbezaan janjang aritmetik dan ditetapkan.
Cuba tentukan urutan nombor yang merupakan janjang aritmetik dan yang bukan:
a)
b)
c)
d)
faham? Mari bandingkan jawapan kami:
Adakah janjang aritmetik - b, c.
bukan janjang aritmetik - a, d.
Mari kembali ke janjang yang diberikan () dan cuba cari nilai sebutan ke-nya. wujud dua cara untuk mencarinya.
1. Kaedah
Kita boleh menambah nombor janjang kepada nilai sebelumnya sehingga kita mencapai sebutan ke-janjang itu. Ada baiknya kita tidak mempunyai banyak perkara untuk diringkaskan - hanya tiga nilai:
Jadi, sebutan ke janjang aritmetik yang diterangkan adalah sama dengan.
2. Kaedah
Bagaimana jika kita perlu mencari nilai sebutan ke-kemajuan itu? Penjumlahan akan mengambil masa lebih daripada satu jam, dan bukan fakta bahawa kita tidak akan membuat kesilapan semasa menambah nombor.
Sudah tentu, ahli matematik telah menghasilkan satu cara yang tidak perlu menambah perbezaan janjang aritmetik kepada nilai sebelumnya. Perhatikan gambar yang dilukis dengan lebih dekat... Pasti anda sudah perasan corak tertentu iaitu:
Sebagai contoh, mari kita lihat apakah nilai sebutan ke-dalam janjang aritmetik ini terdiri daripada: 
Dengan kata lain:
Cuba cari sendiri nilai ahli janjang aritmetik tertentu dengan cara ini.
Adakah anda mengira? Bandingkan nota anda dengan jawapan:
Sila ambil perhatian bahawa anda mendapat nombor yang sama seperti dalam kaedah sebelumnya, apabila kami secara berurutan menambah istilah janjang aritmetik kepada nilai sebelumnya.
Mari cuba "menyahpersonalisasi" formula ini - mari letakkannya dalam bentuk umum dan dapatkan:
|
Persamaan janjang aritmetik. |
Janjang aritmetik boleh meningkat atau menurun.
Bertambah- janjang di mana setiap nilai terma berikutnya adalah lebih besar daripada yang sebelumnya.
Contohnya:
Menurun- janjang di mana setiap nilai terma berikutnya adalah kurang daripada yang sebelumnya.
Contohnya:
Formula terbitan digunakan dalam pengiraan sebutan dalam kedua-dua sebutan meningkat dan menurun bagi janjang aritmetik.
Mari kita semak ini dalam amalan.
Kami diberi janjang aritmetik yang terdiri daripada nombor berikut: Mari kita semak apakah nombor ke janjang aritmetik ini jika kita menggunakan formula kita untuk mengiranya:

Sejak itu:
Oleh itu, kami yakin bahawa formula beroperasi dalam kedua-dua janjang aritmetik yang menurun dan meningkat.
Cuba cari sendiri sebutan ke dan ke bagi janjang aritmetik ini.
Mari bandingkan hasilnya:
Sifat janjang aritmetik
Mari kita rumitkan masalah - kita akan memperoleh sifat janjang aritmetik.
Katakan kita diberi syarat berikut:
- janjang aritmetik, cari nilai.
Mudah, anda katakan dan mula mengira mengikut formula yang anda sudah tahu:
Mari, ah, kemudian:
benar sekali. Ternyata kita mula-mula mencari, kemudian menambahnya pada nombor pertama dan mendapatkan apa yang kita cari. Jika perkembangan diwakili oleh nilai kecil, maka tidak ada yang rumit mengenainya, tetapi bagaimana jika kita diberi nombor dalam keadaan? Setuju, terdapat kemungkinan membuat kesilapan dalam pengiraan.
Sekarang fikirkan sama ada mungkin untuk menyelesaikan masalah ini dalam satu langkah menggunakan sebarang formula? Sudah tentu ya, dan itulah yang akan kami cuba kemukakan sekarang.
Mari kita nyatakan istilah yang diperlukan bagi janjang aritmetik sebagai, formula untuk mencarinya diketahui oleh kita - ini adalah formula yang sama yang kita perolehi pada mulanya:
, Kemudian:
- istilah janjang sebelumnya ialah:
- istilah janjang seterusnya ialah:
Mari kita rumuskan istilah janjang sebelumnya dan seterusnya:
Ternyata jumlah terma janjang sebelumnya dan seterusnya ialah nilai berganda bagi istilah janjang yang terletak di antara mereka. Dalam erti kata lain, untuk mencari nilai istilah janjang dengan nilai sebelumnya dan berturut-turut yang diketahui, anda perlu menambahnya dan membahagikannya dengan.
Betul, kami mendapat nombor yang sama. Mari selamatkan bahan. Kira nilai untuk kemajuan itu sendiri, ia sama sekali tidak sukar.
Syabas! Anda tahu hampir segala-galanya tentang kemajuan! Tinggal untuk mengetahui hanya satu formula, yang, menurut legenda, mudah disimpulkan oleh salah seorang ahli matematik terhebat sepanjang masa, "raja ahli matematik" - Karl Gauss...
Apabila Carl Gauss berumur 9 tahun, seorang guru, sibuk memeriksa kerja pelajar di kelas lain, bertanya tugas berikut di dalam kelas: "Kira jumlah semua nombor asli dari hingga (mengikut sumber lain hingga) termasuk." Bayangkan guru terkejut apabila salah seorang pelajarnya (ialah Karl Gauss) seminit kemudian memberikan jawapan yang betul untuk tugas itu, manakala kebanyakan rakan sekelas daredevil, selepas pengiraan yang panjang, menerima keputusan yang salah...
Carl Gauss muda melihat corak tertentu yang anda juga boleh perasan dengan mudah.
Katakan kita mempunyai janjang aritmetik yang terdiri daripada sebutan -th: Kita perlu mencari jumlah sebutan janjang aritmetik ini. Sudah tentu, kita boleh menjumlahkan semua nilai secara manual, tetapi bagaimana jika tugas itu memerlukan mencari jumlah istilahnya, seperti yang dicari oleh Gauss?
Mari kita gambarkan perkembangan yang diberikan kepada kita. Lihat dengan teliti nombor yang diserlahkan dan cuba lakukan pelbagai operasi matematik dengan mereka. 
Sudahkah anda mencubanya? Apa yang awak perasan? Betul! Jumlah mereka adalah sama

Sekarang beritahu saya, berapakah jumlah pasangan sebegitu yang terdapat dalam janjang yang diberikan kepada kita? Sudah tentu, tepat separuh daripada semua nombor, iaitu.
Berdasarkan fakta bahawa jumlah dua sebutan janjang aritmetik adalah sama, dan pasangan yang serupa adalah sama, kita memperoleh bahawa jumlah keseluruhan adalah sama dengan:
.
Oleh itu, formula untuk jumlah sebutan pertama mana-mana janjang aritmetik ialah:
Dalam sesetengah masalah kita tidak tahu istilah ke-, tetapi kita tahu perbezaan perkembangannya. Cuba gantikan formula sebutan ke dalam formula jumlah.
Apa yang awak dapat?
Syabas! Sekarang mari kita kembali kepada masalah yang ditanyakan kepada Carl Gauss: hitung sendiri apakah jumlah nombor yang bermula dari th sama dengan dan jumlah nombor bermula dari th.
Berapa banyak yang anda dapat?
Gauss mendapati bahawa jumlah istilah adalah sama, dan jumlah istilah. Adakah itu yang anda putuskan?
Malah, formula untuk jumlah sebutan janjang aritmetik telah dibuktikan oleh saintis Yunani purba Diophantus pada abad ke-3, dan sepanjang masa ini, orang cerdik menggunakan sepenuhnya sifat janjang aritmetik.
Sebagai contoh, bayangkan Mesir Purba dan projek pembinaan terbesar pada masa itu - pembinaan piramid... Gambar menunjukkan sebelahnya. 
Di manakah perkembangan di sini, anda katakan? Lihat dengan teliti dan cari corak dalam bilangan blok pasir dalam setiap baris dinding piramid. 
Mengapa tidak janjang aritmetik? Kira berapa banyak blok yang diperlukan untuk membina satu dinding jika bata blok diletakkan di pangkalan. Saya harap anda tidak akan mengira semasa menggerakkan jari anda pada monitor, anda masih ingat formula terakhir dan semua yang kami katakan tentang janjang aritmetik?
Dalam kes ini, perkembangannya kelihatan seperti ini: .
Perbezaan janjang aritmetik.
Bilangan sebutan bagi suatu janjang aritmetik.
Mari kita gantikan data kita ke dalam formula terakhir (kira bilangan blok dalam 2 cara).
Kaedah 1.
Kaedah 2.
Dan kini anda boleh mengira pada monitor: bandingkan nilai yang diperoleh dengan bilangan blok yang ada dalam piramid kami. faham? Syabas, anda telah menguasai jumlah sebutan ke-n suatu janjang aritmetik.
Sudah tentu, anda tidak boleh membina piramid dari blok di pangkalan, tetapi dari? Cuba kira berapa banyak bata pasir yang diperlukan untuk membina dinding dengan keadaan ini.
Adakah anda berjaya?
Jawapan yang betul ialah blok:
Latihan
Tugasan:
- Masha semakin sihat untuk musim panas. Setiap hari dia menambah bilangan cangkung. Berapa kali Masha akan melakukan squats dalam seminggu jika dia melakukan squats pada sesi latihan pertama?
- Apakah hasil tambah semua nombor ganjil yang terkandung dalam.
- Apabila menyimpan log, pembalak menyusunnya sedemikian rupa sehingga setiap lapisan atas mengandungi satu log kurang daripada yang sebelumnya. Berapa banyak kayu balak dalam satu batu, jika asas batu itu ialah kayu balak?
Jawapan:
- Mari kita tentukan parameter janjang aritmetik. Dalam kes ini
(minggu = hari).Jawapan: Dalam dua minggu, Masha perlu melakukan squat sekali sehari.
- Nombor ganjil pertama, nombor terakhir.
Perbezaan janjang aritmetik.
Bilangan nombor ganjil dalam ialah separuh, bagaimanapun, mari kita semak fakta ini menggunakan formula untuk mencari sebutan ke satu janjang aritmetik:Nombor memang mengandungi nombor ganjil.
Mari kita gantikan data yang tersedia ke dalam formula:Jawapan: Jumlah semua nombor ganjil yang terkandung dalam adalah sama.
- Mari kita ingat masalah tentang piramid. Untuk kes kami, a , kerana setiap lapisan atas dikurangkan dengan satu log, maka secara keseluruhan terdapat sekumpulan lapisan, iaitu.
Mari kita gantikan data ke dalam formula:Jawapan: Terdapat kayu balak di dalam batu.
Mari kita ringkaskan
- - urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama. Ia boleh meningkat atau menurun.
- Mencari formula Sebutan ke-1 bagi suatu janjang aritmetik ditulis dengan formula - , di mana ialah bilangan nombor dalam janjang itu.
- Harta ahli sesuatu janjang aritmetik- - di manakah bilangan nombor dalam kemajuan.
- Jumlah sebutan bagi suatu janjang aritmetik boleh didapati dalam dua cara:
, di manakah bilangan nilai.
PERKEMBANGAN AITMETIK. PERINGKAT TENGAH
Urutan nombor
Mari duduk dan mula menulis beberapa nombor. Contohnya:
Anda boleh menulis sebarang nombor, dan boleh ada seberapa banyak nombor yang anda suka. Tetapi kita sentiasa boleh mengatakan yang mana satu pertama, yang mana satu kedua, dan seterusnya, iaitu, kita boleh menomborkannya. Ini adalah contoh urutan nombor.
Urutan nombor ialah satu set nombor, setiap satunya boleh diberikan nombor unik.
Dalam erti kata lain, setiap nombor boleh dikaitkan dengan nombor asli tertentu, dan nombor unik. Dan kami tidak akan memberikan nombor ini kepada mana-mana nombor lain daripada set ini.
Nombor dengan nombor dipanggil ahli urutan ke-.
Kami biasanya memanggil keseluruhan jujukan dengan beberapa huruf (contohnya,), dan setiap ahli jujukan ini adalah huruf yang sama dengan indeks yang sama dengan nombor ahli ini: .
Ia adalah sangat mudah jika sebutan ke-jujukan boleh ditentukan oleh beberapa formula. Sebagai contoh, formula
menetapkan urutan:
Dan formulanya adalah urutan berikut:
Sebagai contoh, janjang aritmetik ialah jujukan (istilah pertama di sini adalah sama, dan perbezaannya ialah). Atau (, perbezaan).
formula penggal ke-n
Kami memanggil formula berulang di mana, untuk mengetahui istilah ke, anda perlu mengetahui yang sebelumnya atau beberapa yang sebelumnya:
Untuk mencari, sebagai contoh, sebutan ke-janjang menggunakan formula ini, kita perlu mengira sembilan sebelumnya. Contohnya, biarkan. Kemudian:
Nah, adakah ia jelas sekarang apakah formulanya?
Dalam setiap baris yang kita tambah, didarab dengan beberapa nombor. yang mana satu? Sangat mudah: ini ialah bilangan ahli semasa tolak:
Jauh lebih mudah sekarang, bukan? Kami menyemak:
Tentukan sendiri:
Dalam janjang aritmetik, cari formula bagi sebutan ke-n dan cari sebutan keseratus.
Penyelesaian:
Sebutan pertama adalah sama. Apa bezanya? Inilah yang:
(Inilah sebabnya ia dipanggil perbezaan kerana ia sama dengan perbezaan sebutan berturut-turut janjang).
Jadi, formulanya:
Maka sebutan keseratus adalah sama dengan:
Apakah hasil tambah semua nombor asli dari hingga?
Menurut legenda, ahli matematik hebat Carl Gauss, sebagai budak lelaki berusia 9 tahun, mengira jumlah ini dalam beberapa minit. Dia perasan bahawa jumlah nombor pertama dan terakhir adalah sama, jumlah kedua dan kedua terakhir adalah sama, jumlah ketiga dan ke-3 dari hujung adalah sama, dan seterusnya. Berapakah jumlah pasangan sedemikian? Betul, tepat separuh daripada bilangan semua nombor, iaitu. Jadi,
Formula umum untuk jumlah sebutan pertama mana-mana janjang aritmetik ialah:
Contoh:
Cari hasil tambah semua gandaan dua digit.
Penyelesaian:
Nombor yang pertama ialah ini. Setiap nombor berikutnya diperoleh dengan menambah nombor sebelumnya. Oleh itu, nombor yang kita minati membentuk janjang aritmetik dengan sebutan pertama dan perbezaannya.
Formula istilah ke-1 untuk janjang ini:
Berapakah bilangan yang terdapat dalam janjang jika kesemuanya mestilah dua digit?
Sangat mudah: .
Penggal terakhir janjang adalah sama. Kemudian jumlahnya:
Jawapan: .
Sekarang tentukan sendiri:
- Setiap hari atlet berlari lebih meter daripada hari sebelumnya. Berapakah jumlah kilometer yang dia akan lari dalam seminggu, jika pada hari pertama dia berlari km m?
- Seorang penunggang basikal menempuh lebih banyak kilometer setiap hari berbanding hari sebelumnya. Pada hari pertama dia mengembara km. Berapa hari dia perlu menempuh perjalanan sejauh satu kilometer? Berapa kilometer yang akan dia tempuh pada hari terakhir perjalanannya?
- Harga peti sejuk di kedai menurun dengan jumlah yang sama setiap tahun. Tentukan berapa banyak harga peti sejuk menurun setiap tahun jika, dijual untuk rubel, enam tahun kemudian ia dijual untuk rubel.
Jawapan:
- Perkara yang paling penting di sini ialah mengenali janjang aritmetik dan menentukan parameternya. Dalam kes ini, (minggu = hari). Anda perlu menentukan jumlah sebutan pertama janjang ini:
.
Jawapan: - Di sini diberikan: , mesti dijumpai.
Jelas sekali, anda perlu menggunakan formula jumlah yang sama seperti dalam masalah sebelumnya:
.
Gantikan nilai:Akarnya jelas tidak sesuai, jadi jawapannya adalah.
Mari kita mengira laluan yang dilalui pada hari terakhir menggunakan formula istilah ke-:
(km).
Jawapan: - Diberi: . Cari: .
Ia tidak boleh menjadi lebih mudah:
(gosok).
Jawapan:
PERKEMBANGAN AITMETIK. SECARA RINGKAS TENTANG PERKARA UTAMA
Ini ialah urutan nombor di mana perbezaan antara nombor bersebelahan adalah sama dan sama.
Janjang aritmetik boleh meningkat () dan menurun ().
Contohnya:
Formula untuk mencari sebutan ke-n suatu janjang aritmetik
ditulis oleh formula, di mana bilangan nombor dalam janjang.
Harta ahli sesuatu janjang aritmetik
Ia membolehkan anda mencari istilah janjang dengan mudah jika istilah jirannya diketahui - di manakah bilangan nombor dalam janjang itu.
Jumlah sebutan bagi suatu janjang aritmetik
Terdapat dua cara untuk mencari jumlah:
Di manakah bilangan nilai.
Di manakah bilangan nilai.
Sebagai contoh, urutan \(2\); \(5\); \(8\); \(11\); \(14\)... ialah janjang aritmetik, kerana setiap elemen berikutnya berbeza daripada yang sebelumnya dengan tiga (boleh diperoleh daripada yang sebelumnya dengan menambah tiga):
Dalam janjang ini, perbezaan \(d\) adalah positif (sama dengan \(3\)), dan oleh itu setiap sebutan seterusnya adalah lebih besar daripada yang sebelumnya. Perkembangan sedemikian dipanggil semakin meningkat.
Walau bagaimanapun, \(d\) juga boleh nombor negatif. Contohnya, dalam janjang aritmetik \(16\); \(10\); \(4\); \(-2\); \(-8\)... perbezaan janjang \(d\) adalah sama dengan tolak enam.
Dan dalam kes ini, setiap elemen seterusnya akan menjadi lebih kecil daripada yang sebelumnya. Perkembangan ini dipanggil semakin berkurangan.
tatatanda janjang aritmetik
Kemajuan ditunjukkan oleh huruf Latin kecil.
Nombor yang membentuk janjang dipanggil ahli(atau unsur-unsur).
Mereka dilambangkan dengan huruf yang sama dengan janjang aritmetik, tetapi dengan indeks berangka yang sama dengan bilangan elemen dalam susunan.
Sebagai contoh, janjang aritmetik \(a_n = \left\( 2; 5; 8; 11; 14...\right\)\) terdiri daripada unsur \(a_1=2\); \(a_2=5\); \(a_3=8\) dan seterusnya.
Dalam erti kata lain, untuk janjang \(a_n = \left\(2; 5; 8; 11; 14…\right\)\)
Menyelesaikan masalah janjang aritmetik
Pada dasarnya, maklumat yang dibentangkan di atas sudah cukup untuk menyelesaikan hampir semua masalah janjang aritmetik (termasuk yang ditawarkan di OGE).
Contoh (OGE).
Janjang aritmetik ditentukan oleh keadaan \(b_1=7; d=4\). Cari \(b_5\).
Penyelesaian:
Jawapan: \(b_5=23\)
Contoh (OGE).
Tiga sebutan pertama suatu janjang aritmetik diberikan: \(62; 49; 36…\) Cari nilai sebutan negatif pertama janjang ini..
Penyelesaian:
|
Kami diberi elemen pertama jujukan dan mengetahui bahawa ia adalah janjang aritmetik. Iaitu, setiap elemen berbeza daripada jirannya dengan nombor yang sama. Mari kita ketahui yang mana satu dengan menolak yang sebelumnya daripada elemen seterusnya: \(d=49-62=-13\). |
|
|
Sekarang kita boleh memulihkan perkembangan kita kepada elemen (negatif pertama) yang kita perlukan. |
|
|
sedia. Anda boleh menulis jawapan. |
Jawapan: \(-3\)
Contoh (OGE).
Diberi beberapa unsur berturutan bagi janjang aritmetik: \(…5; x; 10; 12.5...\) Cari nilai unsur yang ditetapkan oleh huruf \(x\).
Penyelesaian:
|
|
Untuk mencari \(x\), kita perlu tahu berapa banyak perbezaan elemen seterusnya daripada yang sebelumnya, dengan kata lain, perbezaan janjang. Mari cari daripada dua unsur jiran yang diketahui: \(d=12.5-10=2.5\). |
|
|
Dan kini kita boleh mencari dengan mudah apa yang kita cari: \(x=5+2.5=7.5\). |
|
|
sedia. Anda boleh menulis jawapan. |
Jawapan: \(7,5\).
Contoh (OGE).
Janjang aritmetik diberikan syarat berikut: \(a_1=-11\); \(a_(n+1)=a_n+5\) Cari hasil tambah enam sebutan pertama janjang ini.
Penyelesaian:
|
Kita perlu mencari jumlah enam sebutan pertama janjang itu. Tetapi kita tidak tahu maksudnya; kita hanya diberikan unsur pertama. Oleh itu, kita mula-mula mengira nilai satu demi satu, menggunakan apa yang diberikan kepada kita: \(n=1\); \(a_(1+1)=a_1+5=-11+5=-6\) |
|
|
\(S_6=a_1+a_2+a_3+a_4+a_5+a_6=\) |
Jumlah yang diperlukan telah ditemui. |
Jawapan: \(S_6=9\).
Contoh (OGE).
Dalam janjang aritmetik \(a_(12)=23\); \(a_(16)=51\). Cari perbezaan janjang ini.
Penyelesaian:
Jawapan: \(d=7\).
Formula penting untuk janjang aritmetik
Seperti yang anda lihat, banyak masalah mengenai janjang aritmetik boleh diselesaikan hanya dengan memahami perkara utama - bahawa janjang aritmetik ialah rantai nombor, dan setiap elemen berikutnya dalam rantai ini diperoleh dengan menambah nombor yang sama kepada yang sebelumnya ( perbezaan perkembangan).
Walau bagaimanapun, kadangkala terdapat situasi apabila membuat keputusan "head-on" adalah sangat menyusahkan. Sebagai contoh, bayangkan bahawa dalam contoh pertama kita perlu mencari bukan elemen kelima \(b_5\), tetapi tiga ratus lapan puluh enam \(b_(386)\). Patutkah kita menambah empat \(385\) kali? Atau bayangkan bahawa dalam contoh terakhir anda perlu mencari jumlah tujuh puluh tiga elemen pertama. Anda akan penat mengira...
Oleh itu, dalam kes sebegini mereka tidak menyelesaikan perkara secara "head-on", tetapi menggunakan formula khas yang diperoleh untuk janjang aritmetik. Dan yang utama ialah formula untuk sebutan ke-n bagi janjang dan formula untuk jumlah \(n\) sebutan pertama.
Formula bagi \(n\) sebutan ke: \(a_n=a_1+(n-1)d\), dengan \(a_1\) ialah sebutan pertama janjang;
\(n\) – nombor elemen yang diperlukan;
\(a_n\) – sebutan janjang dengan nombor \(n\).
Formula ini membolehkan kita mencari dengan cepat walaupun unsur tiga ratus atau sejuta, hanya mengetahui yang pertama dan perbezaan janjang.
Contoh.
Janjang aritmetik ditentukan oleh syarat: \(b_1=-159\); \(d=8.2\). Cari \(b_(246)\).
Penyelesaian:
Jawapan: \(b_(246)=1850\).
Formula untuk jumlah n sebutan pertama: \(S_n=\frac(a_1+a_n)(2) \cdot n\), di mana
\(a_n\) – sebutan terakhir yang dijumlahkan;
Contoh (OGE).
Janjang aritmetik ditentukan oleh keadaan \(a_n=3.4n-0.6\). Cari hasil tambah bagi sebutan \(25\) pertama bagi janjang ini.
Penyelesaian:
|
\(S_(25)=\)\(\frac(a_1+a_(25))(2 )\) \(\cdot 25\) |
Untuk mengira jumlah bagi dua puluh lima sebutan pertama, kita perlu mengetahui nilai sebutan pertama dan dua puluh lima. |
|
|
\(n=1;\) \(a_1=3.4·1-0.6=2.8\) |
Sekarang mari kita cari sebutan kedua puluh lima dengan menggantikan dua puluh lima bukannya \(n\). |
|
|
\(n=25;\) \(a_(25)=3.4·25-0.6=84.4\) |
Nah, sekarang kita boleh mengira jumlah yang diperlukan dengan mudah. |
|
|
\(S_(25)=\)\(\frac(a_1+a_(25))(2)\) \(\cdot 25=\) |
Jawapannya sudah sedia. |
Jawapan: \(S_(25)=1090\).
Untuk jumlah \(n\) sebutan pertama, anda boleh mendapatkan formula lain: anda hanya perlu \(S_(25)=\)\(\frac(a_1+a_(25))(2)\) \ (\cdot 25\ ) bukannya \(a_n\) gantikan formula untuknya \(a_n=a_1+(n-1)d\). Kami mendapat:
Formula untuk hasil tambah n sebutan pertama: \(S_n=\)\(\frac(2a_1+(n-1)d)(2)\) \(\cdot n\), di mana
\(S_n\) – jumlah yang diperlukan bagi \(n\) elemen pertama;
\(a_1\) – sebutan penjumlahan pertama;
\(d\) – perbezaan janjang;
\(n\) – bilangan elemen secara keseluruhan.
Contoh.
Cari hasil tambah bagi sebutan \(33\)-ex pertama bagi janjang aritmetik: \(17\); \(15.5\); \(14\)…
Penyelesaian:
Jawapan: \(S_(33)=-231\).
Masalah janjang aritmetik yang lebih kompleks
Sekarang anda mempunyai segala-galanya maklumat yang diperlukan untuk menyelesaikan hampir semua masalah janjang aritmetik. Mari kita selesaikan topik dengan mempertimbangkan masalah di mana anda bukan sahaja perlu menggunakan formula, tetapi juga berfikir sedikit (dalam matematik ini boleh berguna ☺)
Contoh (OGE).
Cari hasil tambah semua sebutan negatif janjang itu: \(-19.3\); \(-19\); \(-18.7\)…
Penyelesaian:
|
\(S_n=\)\(\frac(2a_1+(n-1)d)(2)\) \(\cdot n\) |
Tugas ini sangat serupa dengan yang sebelumnya. Kita mula menyelesaikan perkara yang sama: mula-mula kita dapati \(d\). |
|
|
\(d=a_2-a_1=-19-(-19.3)=0.3\) |
Sekarang saya ingin menggantikan \(d\) ke dalam formula untuk jumlah... dan di sini satu nuansa kecil muncul - kita tidak tahu \(n\). Dalam erti kata lain, kita tidak tahu berapa banyak istilah yang perlu ditambah. Bagaimana untuk mengetahui? Mari kita fikirkan. Kami akan berhenti menambah elemen apabila kami mencapai elemen positif pertama. Iaitu, anda perlu mengetahui bilangan elemen ini. Bagaimana? Mari tuliskan formula untuk mengira mana-mana unsur janjang aritmetik: \(a_n=a_1+(n-1)d\) untuk kes kami. |
|
|
\(a_n=a_1+(n-1)d\) |
||
|
\(a_n=-19.3+(n-1)·0.3\) |
Kita perlu \(a_n\) untuk menjadi lebih besar daripada sifar. Mari kita ketahui apa \(n\) ini akan berlaku. |
|
|
\(-19.3+(n-1)·0.3>0\) |
||
|
\((n-1)·0.3>19.3\) \(|:0.3\) |
Kami membahagikan kedua-dua belah ketaksamaan dengan \(0.3\). |
|
|
\(n-1>\)\(\frac(19.3)(0.3)\) |
Kami memindahkan tolak satu, tidak lupa untuk menukar tanda-tanda |
|
|
\(n>\)\(\frac(19.3)(0.3)\) \(+1\) |
Jom kira... |
|
|
\(n>65,333…\) |
...dan ternyata unsur positif pertama akan mempunyai nombor \(66\). Oleh itu, yang terakhir negatif mempunyai \(n=65\). Untuk berjaga-jaga, mari kita semak ini. |
|
|
\(n=65;\) \(a_(65)=-19.3+(65-1)·0.3=-0.1\) |
Jadi kita perlu menambah elemen \(65\) pertama. |
|
|
\(S_(65)=\) \(\frac(2 \cdot (-19.3)+(65-1)0.3)(2)\)\(\cdot 65\) |
Jawapannya sudah sedia. |
Jawapan: \(S_(65)=-630.5\).
Contoh (OGE).
Janjang aritmetik ditentukan oleh syarat: \(a_1=-33\); \(a_(n+1)=a_n+4\). Cari jumlah dari \(26\)th hingga \(42\) elemen inklusif.
Penyelesaian:
|
\(a_1=-33;\) \(a_(n+1)=a_n+4\) |
Dalam masalah ini anda juga perlu mencari jumlah elemen, tetapi bukan bermula dari yang pertama, tetapi dari \(26\)th. Untuk kes sedemikian kami tidak mempunyai formula. Bagaimana untuk membuat keputusan? |
|
|
Untuk perkembangan kami \(a_1=-33\), dan perbezaan \(d=4\) (lagipun, kami menambah empat pada elemen sebelumnya untuk mencari yang seterusnya). Mengetahui ini, kita dapati jumlah unsur \(42\)-y yang pertama. |
|
\(S_(42)=\) \(\frac(2 \cdot (-33)+(42-1)4)(2)\)\(\cdot 42=\) |
Sekarang jumlah unsur \(25\) pertama. |
|
\(S_(25)=\) \(\frac(2 \cdot (-33)+(25-1)4)(2)\)\(\cdot 25=\) |
Dan akhirnya, kami mengira jawapannya. |
|
\(S=S_(42)-S_(25)=2058-375=1683\) |
Jawapan: \(S=1683\).
Untuk janjang aritmetik, terdapat beberapa lagi formula yang tidak kami pertimbangkan dalam artikel ini kerana kegunaan praktikalnya yang rendah. Walau bagaimanapun, anda boleh mencari mereka dengan mudah.




 Persamaan logaritma
Persamaan logaritma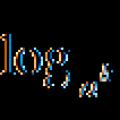 Teknik untuk menyelesaikan persamaan logaritma
Teknik untuk menyelesaikan persamaan logaritma Analisis kendiri guru terapi pertuturan
Analisis kendiri guru terapi pertuturan