Нестандартные задания. Нестандартные задачи, как средство формирования интереса к математике у учащихся
НЕСТАНДАРТНЫЕ ЗАДАНИЯ НА УРОКАХ МАТЕМАТИКИ
Учитель начальных классов Шамалова С. В.
Каждое поколение людей предъявляет свои требования к школе. Древняя римская пословица гласит: «Не для школы, а для жизни мы учимся». Смысл этой пословицы актуален и сегодня. Современное общество диктует системе образования заказ на воспитание личности, готовой к жизни в постоянно меняющихся условиях, к продолжению образования, способной учиться на протяжении всей своей жизни.
Среди духовных способностей человека есть такая, которая на протяжении многих столетий была предметом пристального внимания ученых и которая вместе с тем до сих пор является труднейшим и загадочным предметом науки. Это способность мыслить. С ней мы постоянно сталкиваемся в труде, в учении, в быту.
Любая деятельность рабочего, школьника и ученого неотделима от мыслительной работы. Во всяком настоящем деле необходимо поломать голову, пораскинуть умом, т.е., говоря языком науки, нужно осуществить мыслительное действие, интеллектуальную работу. Известно, что задача может быть решена, и не решена, один справится с нею быстро, другой думает долго. Есть задачи посильные и ребенку, а над некоторыми бьются годами целые коллективы ученых. Значит, есть умение мыслить. Одни им владеют лучше, другие хуже. Что это за умение? Какими путями оно возникает? Как его приобрести?
Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать, мы, учителя, не всегда знаем. Нередко это приводит к тому, что развитие логического мышления в значительной мере идет стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приемами логического мышления (анализ, сравнение, синтез, абстрагирование и др.).
По мнению экспертов, уровень логической культуры школьников на сегодняшний день нельзя признать удовлетворительным. Специалисты считают, что причина этого кроется в отсутствии работы по целенаправленному логическому развитию учащихся на ранних этапах обучения. Большинство современных пособий для дошкольников и младших школьников содержит набор всевозможных задач, останавливающихся на таких приемах мыслительной деятельности, как анализ, синтез, аналогия, обобщение, классификация, гибкость и вариативность мышления. Иначе говоря, развитие логического мышления происходит в значительной степени стихийно, поэтому большинство учеников не овладевают приемами мышления даже в старших классах, а этим приемам необходимо учить младших школьников.
В своей практике использую современные образовательные технологии, различные формы организации учебного процесса, систему развивающих заданий. Эти задания должны носить развивающий характер (учить определенным мыслительным приемам), они должны учитывать возрастные особенности учащихся.
В процессе решения учебных задач у детей формируется такое умение, как отвлекаться от несущественных деталей. Это действие даётся младшим школьникам с не меньшим трудом, чем выделение существенного. Младшие школьники в результате обучения в школе, когда необходимо регулярно выполнять задания в обязательном порядке, учатся управлять своим мышлением, думать тогда, когда надо. Сначала вводятся доступные детям логические упражнения, направленные на совершенствование мыслительных операций.
В процессе выполнения таких логических упражнений ученики практически учатся сравнивать различные объекты, в том числе и математические, строить правильные суждения на доступном и на их жизненном опыте проводить несложные доказательства. Логические упражнения постепенно усложняются.
Использую в своей практике и нестандартные развивающие логические задачи. Существует значительное множество такого рода задач; особенно много подобной специализированной литературы было выпущено в последние годы.
В методической литературе за развивающими задачами закрепились такие названия: задачи на сообразительность, задачи на смекалку, задачи с «изюминкой». Во всём многообразии можно выделить в особый класс такие задачи, которые называют задачами – ловушками, провоцирующими задачами. В условиях таких задач содержаться различного рода упоминания, указания, намёки, подталкивающие к выбору ошибочного пути решения или неверного ответа. Приведу примеры таких заданий.
Задачи, навязывающие один, вполне определенный ответ.
Какое из чисел 333, 555, 666, 999 не делиться на 3?
Задачи, побуждающие сделать неправильный выбор ответа из предложенных верных и неверных ответов.
Один ослик везёт 10 кг сахара, а другой – 10 кг поп-корна. У кого поклажа была тяжелее?
Задачи, условия которых подталкивают к тому, чтобы выполнить какое-либо действие с заданными числами, тогда как выполнять это действие вовсе не нужно.
Автомобиль «Мерседес» проехал 100 км. Сколько км проехало каждое его колесо?
Петя сказал однажды друзьям: "Позавчера мне было 9 лет, а в будущем году мне исполнится 12 лет". Какого числа родился Петя?
Решение логических задач с помощью рассуждений.
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский, арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом утверждении только одно утверждение верно. Какой язык изучает каждый из них?
Коротышки из Цветочного города посадили арбуз. Для его полива требуется ровно 1 литр воды. У них есть только два пустых бидона ёмкостью 3 л. И 5 л. Как пользуясь этими бидонами. Набрать из реки ровно 1 л. воды?
Сколько лет сиднем просидел на печи Илья Муромец? Известно, что если бы он просидел ещё 2 раза по столько, то его возраст составил бы наибольшее двузначное число.
Барон Мюнхгаузен пересчитал число волшебных волос в бороде старика Хоттабыча. Оно оказалось равным сумме наименьшего трёхзначного числа и наибольшего двузначного. Что это за число?
При обучении решению нестандартных задач соблюдаю следующие условия: в о-первых , задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся; в о-вторых , необходимо предоставлять ученикам максимальную самостоятельность при поиске решения задач, дать им возможность пройти до конца по неверному пути, чтобы убедиться в ошибке, вернуться к началу и искать другой, верный путь решения; в-третьих , нужно помочь учащимся осознать некоторые способы, приемы и общие подходы к решению нестандартных арифметических задач. Чаще всего предлагаемые логические упражнения не требуют вычислений, а лишь заставляют детей выполнять правильные суждения и приводить несложные доказательства. Сами же упражнения носят занимательный характер, поэтому они содействуют возникновению интереса у детей к процессу мыслительной деятельности. А это одна из кардинальных задач учебно-воспитательного процесса в школе.
Примеры заданий, используемых в моей практике.
Найди закономерность и продолжи гирлянды
Найдите закономерность и продолжите ряд
а, б, в, г, д, е, …
1, 2, 4, 8, 16,…
Работа началась с развития у детей умения подмечать закономерности, сходства и различия при постепенном усложнении заданий. С этой целью я подбирала задания на выявление закономерностей, зависимостей и формулировку обобщения с постепенным повышением уровня трудности заданий. Работа по развитию логического мышления должна стать объектом серьезного внимания учителя и систематически проводиться на уроках математики. С этой целью в устную работу на уроке постоянно должны включаться упражнения на логику. Например:
Найди результат, пользуясь данным равенством:
3+5=8
3+6=
3+7=
3+8=
Сравни выражения, найди общее в полученных неравенствах, сформулируй вывод:
2+3*2x3
4+4*3x4
4+5*4x5
5+6*5x6
Продолжи ряд чисел.
3. 5, 7, 9, 11…
1, 4, 7, 10…
Придумай к каждому данному примеру похожий пример.
12+6=18
16-4=12
Что общего в записи чисел каждой строки?
12 24 20 22
30 37 13 83
Даны числа:
23 74 41 14
40 17 60 50
Какое число лишнее в каждой строке?
В начальной школе на уроках математики я часто использую упражнения со счетными палочками. Это задачи геометрического характера, так как в ходе решения, как правило, идет трансфигурация, преобразование одних фигур в другие, а не только изменение их количества. Их нельзя решать каким-либо усвоенным ранее способом. В ходе решения каждой новой задачи ребенок включается в активный поиск пути решения, стремясь при этом к конечной цели, требуемому видоизменению фигуры.
Упражнения со счетными палочками можно объединить в 3 группы: задачи на составление заданной фигуры из определенного количества палочек; задачи на изменение фигур, для решения которых надо убрать или добавить указанное количество палочек; задачи, решение которых состоит в перекладывании палочек с целью видоизменения, преобразования заданною фигуры.
Упражнения со счетными палочками.
Задачи на составление фигур из определенного количества палочек.
Составь два разных квадрата из 7 палочек.

Задачи на изменение фигуры, где нужно убрать или добавить указанное количество палочек.
Дана фигура из 6 квадратов. Надо убрать 2 палочки так, чтобы осталось 4 квадрата"

Задачи на перекладывание палочек с целью преобразования.
Переложи две палочки так, чтобы получилось 3 треугольника.
Регулярные упражнения - одно из условий успешного развития учащихся. Прежде всего из урока в урок нужно развивать у ребенка способности к анализу и синтезу, кратковременное обучение логическим понятиям не дает эффекта.
Решение нестандартных задач формирует у учащихся умение высказывать предположения, проверять их достоверность, логически их обосновывать. Проговаривание с целью доказательств, способствует развитию речи, выработке умений делать выводы, строить умозаключения. В процессе использования этих упражнений на уроках и во внеклассной работе по математике появилась положительная динамика влияния этих упражнений на уровень развития логического мышления учеников.
Тесты и опросники 3 класс.
Известно, что решение текстовых задач представляет большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап - анализ текста задачи. Учащиеся плохо ориентируются в тексте задачи, в ее условиях и требовании. Текст задачи - это рассказ о некоторых жизненных фактах: «Маша пробежала 100 м, а навстречу ей…»,
«Ученики первого класса купили 12 гвоздик, а ученики второго …», «Мастер сделал за смену 20 деталей, а его ученик…».
В тексте важно все; и действующие лица, и их действия, и числовые характеристики. При работе с математической моделью задачи (числовым выражением или уравнением) часть этих деталей опускается. Но мы именно и учим умению абстрагироваться от некоторых свойств и использовать другие.
Умение ориентироваться в тексте математической задачи - важный результат и важное условие общего развития ученика. И заниматься этим нужно не только на уроках математики, но и на уроках чтения и изобразительного искусства. Некоторые задачи - хорошие темы для рисунков. И любая задача - хорошая тема для пересказа. А если в классе есть уроки театра, то некоторые математические задачи можно инсценировать. Разумеется, все эти приемы: пересказ, рисунок, инсценировка - могут иметь место и на самих уроках математики. Итак, работа над текстами математических задач - важный элемент общего развития ребенка, элемент развивающего обучения.
Но достаточно ли для этого тех задач, которые имеются в ныне действующих учебниках и решение которых входит в обязательный минимум? Нет, недостаточно. В обязательный минимум входит умение решать задачи определенных типов:
о числе элементов некоторого множества;
о движении, его скорости, пути и времени;
о цене и стоимости;
о работе, ее времени, объеме и производительности труда.
 Указанные четыре темы являются стандартными. Считается, что умение решать задачи на эти темы может научить решать задачи вообще. К сожалению, это не так. Хорошие ученики, умеющие решить практически
Указанные четыре темы являются стандартными. Считается, что умение решать задачи на эти темы может научить решать задачи вообще. К сожалению, это не так. Хорошие ученики, умеющие решить практически
любую задачу из учебника на перечисленные темы, часто бывают не в состоянии понять условие задачи на другую тему.
Выход заключается в том, чтобы не ограничиваться какой-либо тематикой текстовых задач, а решать и нестандартные задачи, то есть задачи, тематика которых не является сама по себе объектом изучения. Ведь не ограничиваем мы сюжеты рассказов на уроках чтения!
Нестандартные задачи нужно решать в классе ежедневно. Их можно черпать в учебниках математики для 5-6-го классов и в журналах «Начальная школа», «Математика в школе» и даже «Квант».
Число задач таково, что можно выбрать из них задачи для каждого урока: по одной на урок. Задачи решаются дома. Но очень часто нужно разбирать их и в классе. Среди предлагаемых задач есть такие, которые сильный ученик решает моментально. Тем не менее нужно требовать и от сильных детей достаточной аргументации, объясняя, что на легких задачах человек учится способам рассуждения, которые понадобятся при решении трудных задач. Нужно воспитывать в детях любовь к красоте логичных рассуждений. В крайнем случае, можно добиваться от сильных учеников таких рассуждений, требуя построить объяснение, понятное для других - для тех, кто не понимает быстрого решения.
Среди задач есть совершенно однотипные в математическом отношении. Если дети увидят это, - замечательно. Учитель может и сам показывать это. Однако недопустимо говорить: решаем эту задачу, как ту, и ответ будет такой же. Дело в том, что, во-первых, не все учащиеся способны к таким аналогиям. А во-вторых, в нестандартных задачах фабула не менее важна, чем математическое содержание. Поэтому лучше подчеркивать связи между задачами со сходной фабулой.
Не все задачи нужно обязательно решать (их здесь больше, чем уроков математики в учебном году). Возможно, Вам захочется поменять порядок следования задач или добавить задачу, которой здесь нет.
Лябина Т.И.
Учитель математики высшей категории
МОУ «Мошокская средняя общеобразовательная школа»
Нестандартные задачи как средство развития логического мышления
Какая задача по математике может называться нестандартной? Хорошее определение приведено в книге
Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Не следует путать их с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого – решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 5 классе нестандартна, а в 6 классе она является обычной, и даже не повышенной сложности.
Итак, если решение задачи учащийся не знает, на какой теоретический материал ему опираться, он тоже не знает, то в этом случае задачу по математике можно назвать нестандартной на данный период времени.
Каковы же методы обучения решению задач по математике, которые мы считаем на данный момент нестандартными? Универсального рецепта, к сожалению, никто не придумал, учитывая уникальность данных задач. Некоторые учителя, что называется, натаскивают в шаблонных упражнениях. Происходит это следующим образом: учитель показывает способ решения, а затем ученик повторяет это при решении задач многократно. При этом убивается интерес учащихся к математике, что, по меньшей мере, печально.
Научить ребят решению задач нестандартного вида можно, если вызвать интерес, другими словами, предложить задачи, интересные и содержательные для современного ученика. Или же заменять формулировку вопроса, используя проблемные жизненные ситуации. Например, вместо задания «решить Диафантово уравнение», предложить решить следующую задачу. Может ли
ученик расплатиться за покупку стоимостью 19 р., если у него только трехрублевые купюры, а у продавца – десятирублевые?
Также действенен метод подбора вспомогательных задач. Это средство обучения решению задач говорит об определенном уровне достижения в решении задач. Обычно в таких случаях думающий ученик пытается самостоятельно, без помощи учителя находить вспомогательные задачи или упрощать и видоизменять условия данных задач.
Умение решать нестандартные задачи приобретается практикой. Не зря говорят, что математике нельзя научиться, глядя, как это делает сосед. Самостоятельная работа и помощь учителя – вот залог плодотворной учебы.
1.Нестандартные задачи и их характеристики.
Наблюдения показывают, что математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решать задачи, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.
Нестандартные задачи способствуют развитию логического мышления в еще большей степени. Кроме того, они являются мощным средством активизациипознавательной деятельности, т. е. вызывают у детей огромный интерес и желание работать. Приведем пример нестандартных задач.
I. Задачи на смекалку .
1. Масса цапли, стоящей на одной ноге 12 кг. Сколько будет весить цапля, если встанет на 2 ноги?
2. Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?
3. У семи братьев по одной сестре. Сколько всего детей в семье?
4. Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы за сто минут съесть сто мышей?
5. Стоят 6 стаканов, 3 с водой, 3 пустых. Как расставить их, чтобы стаканы с водой и пустые чередовались? Разрешается переставить только один стакан.
6. Геологи нашли 7 камней. Масса каждого камня: 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг и 7 кг. Эти камни разложили в 4 рюкзака так,
что в каждом рюкзаке масса камней оказалась одинаковой.
Как это сделали?
7. В классе причесанных девочек столько же, сколько непричесанных мальчиков. Кого в классе больше, девочек или непричесанных учеников?
8. Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток?
9. Миша говорит: «Позавчера мне было10 лет, а в следующем году мне исполнится 13 лет». Возможно ли это?
10. У Андрея и Бори 11 конфет, у Бори и Вовы 13 конфет, а у Андрея и Вовы – 12. Сколько всего конфет у мальчиков?
11.Отец с двумя сыновьями катались на велосипедах: двухколесных и трехколесных. Всего у них было 7 колес. Сколько было велосипедов, и каких?
12. Во дворе куры и поросята. У них у всех 5 голов и 14 ног. Сколько кур и сколько поросят?
13. По двору гуляют куры и кролики. Всего у них 12 ног. Сколько кур и сколько кроликов?
14.У каждого марсианина по 3 руки. Могут ли 13 марсиан взяться за руки так, чтобы не оставалось свободных рук?
15. Играя, каждая из трех девочек – Катя, Галя, Оля – спрятали одну из игрушек – медведя, зайца и слона. Катя не прятала зайца, Оля не прятала ни зайца, ни медведя. Кто какую игрушку спрятал?
II. Занимательные задачи.
1. Как расставить 6 стульев у 4 стен, чтобы у каждой стены было по 2 стула.
2. Папа с двумя сыновьями отправился в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде одного папу или двух сыновей. Как переправиться на другой берег папе с сыновьями?
3. Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?
4. Четыре утенка и пять гусят весят 4кг100г, а пять утят и четыре гусенка весят 4кг. Сколько весят один утенок?
5. У мальчика было 22 монеты – пятирублевые и десятирублевые, всего на сумму 150 рублей. Сколько было пятирублевых и десятирублевых монет?
6. В квартире № 1, 2, 3 живут три котенка: белый, черный и рыжий. В квартире № 1 и 2 жил не черный котенок. Белый котенок жил не в квартире № 1. В какой квартире жил каждый из котят?
7.За пять недель пират Ерема способен выпить бочку рома. А у пирата Емели ушло б на это две недели. За сколько дней прикончат ром пираты, действуя вдвоем?
8.Лошадь съедает воз сена за месяц, коза - за два месяца, овца – за три месяца. За какое время лошадь, коза, овца вместе съедят такой же воз сена?
9.Двое очистили 400 картофелин; один очищал 3 штуки в минуту, другой -2. Второй работал на 25 минут больше, чем первый. Сколько времени работал каждый?
10. Среди футбольных мячей красный мяч тяжелее коричневого, а коричневый тяжелее зеленого. Какой мяч тяжелее: зеленый или красный?
11.Три кренделя, пять коврижек и шесть баранок стоят вместе 24 рубля. Что дороже: крендель или баранка?
12. Как тремя взвешиваниями на чашечных весах без гирь найти одну фальшивую (более легкую) монету из 20 монет?
13.Из верхнего угла комнаты вниз по стене поползли две мухи. Спустившись до полу, они поползли обратно. Первая муха ползла в оба конца с одинаковой скоростью, а вторая, хоть и поднималась вдвое медленнее первой, но зато спускалась вдвое быстрее ее. Какая из мух раньше приползет обратно?
14.В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?
15. Говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четвертая часть изучает природу, седьмая часть проводит время в молчаливом размышлении, остальная часть составляют 3 девы» Сколько учеников было у Пифагора?
III. Геометрические задачи .
1. Раздели пирог прямоугольной формы двумя разрезами на части так, чтобы они имели треугольную форму. Сколько получилось частей?

2. Нарисуй фигуру, не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.

3.Разрежь квадрат на 4 части и сложи из них 2 квадрата. Как это сделать?

4.Убери 4 палочки так, чтобы осталось 5 квадратов.
5.Разрежьте треугольник на два треугольника, четырехугольник и пятиугольник, проведя две прямые линии.
6.Можно ли квадрат разделить на 5 частей и собрать восьмиугольник?
IV. Логические квадраты .
1. Заполни квадрат (4 х 4) числами 1, 2, 3, 6 так, чтобы сумма чисел по всем строкам, столбцами и диагоналям была одинаковой. Числа в строках, столбцах и диагоналях не должны повторяться.
2. Раскрась квадрат красным, зеленым, желтым и синим цветами так, чтобы цвета в строках, столбцах и по диагоналям не повторялись.
3.В квадрате нужно разместить еще числа 2,2,2,3,3,3 так, чтобы по всем линиям получить в сумме число 6.
5.В клетках квадрата поставить числа 4,6,7,9,10,11,12 так, чтобы в столбцах, в строчках и по диагоналям получить сумму 24.
V. Комбинаторные задачи .
1. У Даши 2 юбки: красная и синяя, и 2 блузки: в полоску и в горошек. Сколько разных нарядов у Даши?
2. Сколько существует двузначных чисел, у которых все цифры нечетные?
3. Родители приобрели путевку в Грецию. До Греции можно добраться, используя один из трех видов транспорта: самолет, теплоход или автобус. Составьте все возможные варианты использования данных видов транспорта.
4. Сколько разных слов можно образовать при помощи букв слова «соединение»?
5. Из цифр 1, 3, 5 составить различные трехзначные числа так, чтобы в числе не было одинаковых цифр.
6. Встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас блондин, другой брюнет, а третий рыжеволосый. Но ни у одного нет волос того цвета, на который указывает его фамилия», - заметил брюнет. «Ты прав», - сказал Белов. Какой цвет волос у художника?
7. Три подруги вышли погулять в белом, зеленом и синем платьях и туфлях таких же цветов. Известно, что только у Ани цвет платья и цвет туфель совпадают. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель на каждой из подруг.
8. В отделении банка работают кассир, контролер и заведующий. Их фамилии Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролера. Назовите фамилии контролера и заведующего.
9. Для пикника сладкоежка Маша взяла в трех одинаковых коробках конфеты, печенье и торт. На коробках были этикетки: «Конфеты», «Печенье», и «Торт». Но Маша знала, что мама любит шутить и всегда кладет продукты в
коробки, надписи на которых не соответствуют их содержимому. Маша была уверена, что конфеты не лежат в коробке, на которой написано «Торт». В какой же коробке торт?
10. По кругу сидят Иванов, Петров, Марков, Карпов. Их имена Андрей, Сергей, Тимофей, Алексей. Известно, Иванов не Андрей и не Алексей. Сергей сидит между Марковым и Тимофеем. Петров сидит между Карповым и Андреем. Как зовут Иванова, Петрова, Маркова и Карпова?
VI. Задачи на переливание.
1. Можно ли, имея лишь два сосуда емкостью 3 и 5л, набрать из водопроводного крана 4 л воды?
2. Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?
3.Как, имея два сосуда емкостью 9л и 5л, набрать из водоема ровно 3 литра воды?
4.Бидон, емкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?
5. Имеются два сосуда. Емкость одного из них 9л, а другого 4л. Как с помощью этих сосудов набрать из бака 6 литров некоторой жидкости? (Жидкость можно сливать обратно в бак).
Анализ предложенных текстовых задач показывает, что решение их не укладывается в рамки той или иной системы типовых задач. Такие задачи называют нетиповыми (И. К. Андронов, А. С. Пчелко и др.) или нестандартными (Ю. М. Колягин, К. И. Нешков, Д. Пойа и др.)
Обобщая различные подходы методистов в понимании стандартных и нестандартных задач (Д. Пойа, Я. М. Фридман и др.), под нестандартной задачей понимаем такую задачу, алгоритм которой не знаком учащемуся и в дальнейшем не формируется как программное требование.
Анализ учебников и учебных пособий по математике показывает, что каждая текстовая задача в определенных условиях может быть нестандартной, а в других – обычной, стандартной. Стандартная задача одного курса математики может быть нестандартной в другом курсе.
Например. «На аэродроме было 57 самолетов и 79 вертолетов, 60 машин поднялось в воздух. Можно ли утверждать, что в воздухе находится: а) хотя бы 1 самолет; б) хотя бы 1 вертолет?»
Такие задачи были необязательными для всех учащихся, они предназначались для наиболее способных к математике.
«Если хотите научиться решать задачи, то решайте их!» - советует Д. Пойа.
Главное при этом – сформировать такой общий подход к решению задач, когда задача рассматривается как объект для исследования, а ее решение – как конструирование и изобретение способа решения.
Естественно, что такой подход требует не бездумного решения огромного числа задач, а неторопливого, внимательного и обстоятельного решения значительно меньшего числа задач, но с последующим анализом проведенного решения.
Итак, общих правил решения нестандартных задач нет (поэтому – то эти задачи и называются нестандартными). Однако выдающиеся математики и педагоги (С.А. Яновская, Л.М. Фридман,
Э.Н. Балаян) нашли ряд общих указаний и рекомендаций, которыми можно руководствоваться при решении нестандартных задач. Эти указания обычно называют эвристическими правилами или, просто, эвристиками. Слово «эвристика» греческого происхождения и означает «искусство нахождения истины».
В отличие от математических правил эвристики носят характер необязательных рекомендаций, советов, следование которым может привести (а может и не привести) к решению задачи.
Процесс решения любой нестандартной задачи (по мнению
С.А. Яновской) состоит в последовательном применении двух операций:
1.сведение путем преобразований нестандартной задачи к другой, ей сходной, но уже стандартной задаче;
2. разбиение нестандартной задачи на несколько стандартных подзадач.
Для сведения нестандартной задачи к стандартной не существует определенных правил. Однако если внимательно, вдумчиво анализировать, решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами были решены задачи, то вырабатывается умение в таком сведении.
Рассмотрим на примере задачи:
По тропинке, вдоль кустов, шел десяточек хвостов,
Ну а мой вопрос таков – сколько было петухов?
И узнать я был бы рад - сколько было поросят?
Если не удается решить данную задачу, попытаемся свести ее к сходной.
Переформулируем:
1.Придумаем и решим похожую, но более простую.
2. Используем её решение для решения данной.
Трудность в том, что в задаче два типа зверей. Пусть все будут поросятами, тогда ног будет 40.
Составим похожую задачу:
По тропинке, вдоль кустов, шел десяточек хвостов.
Это вместе шли куда – то петухи и поросята.
Ну а мой вопрос таков - сколько было петухов?
И узнать я был бы рад – сколько было поросят?
Ясно, что если ног в 4 раза больше, чем хвостов, то все животные – поросята.
В похожей задаче взяли 40 ног, а в основной их было 30. Как уменьшить число ног? Заменить поросенка петушком.
Решение основной задачи: если бы все животные были поросятами, то у них было 40 ног. Когда заменяем поросенка петушком, число ног уменьшается на два. Всего надо сделать пять замен, чтобы получить 30 ног. Значит, шагало 5 петушков и 5 поросят.
Как придумать «похожую» задачу?
2 способ решения задачи.
В данной задаче можно применить принцип уравнивания.
Пусть все поросята встанут на задние ноги.
10*2 =20 столько ног шагает по тропинке
30 – 20 =10 столько передних ног у поросят
10:2 = 5 поросенка шло по тропинке
Ну а петушков 10 -5 =5.
Сформулируем несколько правил решения нестандартных задач.
1. «Простое» правило: не пропустите самую простую задачу.
Обычно простую задачу не замечают. А начинать надо именно с неё.
2. «Очередное» правило: условия по возможности надо менять по очереди. Количество условий - конечное число, так что до всех рано или поздно дойдет очередь.
3. «Неизвестное» правило: изменив одно условие, другое, связанное с ним обозначьте х, а потом подберите его так, чтобы вспомогательная задача решалась при данном значении и не решалась при увеличении х на единицу.
3. «Интересное » правило: делайте условия задачи более интересными.
4. «Временное» правило: если в задаче идет какой-то процесс и конечное состояние более определенно, чем начальное, стоит запустить время в обратную сторону: рассмотреть последний шаг процесса, потом предпоследний и т.д.
Рассмотрим применение этих правил.
Задача№1. Пять мальчиков нашли девять грибов. Докажите, что хотя бы двое из них нашли грибов поровну.
1шаг. Мальчиков очень много. Пусть их будет на 2 меньше в следующей задаче.
«Трое мальчиков нашли х грибов. Докажите, что хотя бы двое из них нашли грибов поровну».
Для доказательства установим, при каких х задача имеет решение.
При х=0, х=1, х=2 задача имеет решение, при х=3 задача не имеет решение.
Сформулируем похожую задачу.
Трое мальчиков нашли 2 гриба. Докажите, что хотя бы двое из них нашли грибов поровну.
Пусть все трое мальчиков нашли разное число грибов. Тогда минимальное число грибов равно 3, поскольку 3=0+1+2. Но по условию число грибов меньше 3, поэтому два мальчика из трех нашли одинаковое число грибов.
При решении исходной задачи рассуждения точно такие же. Пусть все, пять мальчиков, нашли разное число грибов. Минимальное число грибов тогда должно равняться 10. (10 =0+1+2+3+4). Но по условию число грибов меньше 10, поэтому двое мальчиков нашли одинаковое число грибов.
При решении использовали «неизвестное» правило.
Задача№2. Над озерами летели лебеди. На каждом садилась половина лебедей и еще пол-лебедя, остальные летели дальше. Все сели на семи озерах. Сколько было лебедей?
1шаг. Идет процесс, начальное состояние не определено, конечное – нулевое, т.е. не стало летящих лебедей.
Запускаем время в обратную сторону, придумав такую задачу:
Над озерами летели лебеди. На каждом взлетало пол-лебедя и еще столько, сколько теперь летело. Все взлетали с семи озер. Сколько было лебедей?
2шаг. Начинаем с нуля:
(((((((0+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2+1/2)2 =127.
Задача №3.
У моста через речку встретились лодырь и черт. Лодырь пожаловался на свою бедность. В ответ черт предложил:
Я могу помочь тебе. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки. Три раза переходил мост лодырь, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
(((0+24):2+24):2+24):2= 21
При решении задач № 2и № 3 использовали «временное» правило.
Задача №4. Кузнец подковывает одно копыто за 15 минут. Сколько времени потребуется 8 кузнецам, чтобы подковать 10 лошадей. (Лошадь не умеет стоять на двух ногах).
1шаг. Лошадей и кузнецов слишком много, уменьшим пропорционально их количество, составив задачу.
Кузнец подковывает одно копыто за пять минут. Сколько времени потребуется четверым кузнецам, чтобы подковать пять лошадей?
Ясно, что минимально возможное время 25 минут, но может ли оно быть достигнуто? Необходимо организовать работу кузнецов без простоев. Будем действовать, не нарушая симметрии. Расположим пять лошадей по кругу. После того как четверо кузнецов подкуют каждый одно копыто лошади, кузнецы сдвинутся на одну лошадь по кругу. Чтобы обойти полный круг, потребуется пять тактов работы по пять минут. Во время 4 тактов каждая лошадь будет подковываться, а один такт отдыхать. В итоге все лошади будут подкованы за 25 минут.
2 шаг. Возвращаясь к исходной задаче, заметим, что 8=2* 4, а 10=2*5. Тогда 8 кузнецов нужно разбить на две бригады
по 4 человека в каждой, а лошадей – на два табуна по 5 лошадей в каждом.
За 25 минут первая бригада кузнецов подкует первый табун, а вторая – второй.
При решении использовалось «очередное» правило.
Конечно, может встретиться задача, к которой не удастся применить ни одного из перечисленных правил. Тогда нужно изобрести особый метод решения этой задачи.
Необходимо помнить, что решение нестандартных задач есть искусство, которым можно овладеть лишь в результате постоянного самоанализа действий по решению задач.
2. Образовательные функции нестандартных задач.
Роль нестандартных задач в формировании логического мышления.
На современном этапе обучения наметилась тенденция использования задач как необходимого компонента обучения учащихся математике. Объясняется это, прежде всего, возрастающими требованиями, направленными на усиление развивающих функций обучений.
Понятие «нестандартная задача» используется многими методистами. Так, Ю. М. Колягин раскрывает это понятие следующим образом: «Под нестандартной понимается задача , при предъявлении которой учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение».
Опираясь на анализ теории и практики использования нестандартных задач в обучении математике, установлена их общая и специфическая роль.
Нестандартные задачи :
Учат детей использовать не только готовые алгоритмы, но и самостоятельно находить новые способы решения задач, т. е. способствуют умению находить оригинальные способы решения задач;
Оказывают влияние на развитие смекалки, сообразительности учащихся;
препятствуют выработке вредных штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся, предполагают не столько усвоение алгоритмических приемов, сколько нахождение новых связей в знаниях, к переносу
знаний в новые условия, к овладению разнообразными приемами умственной деятельности;
Создают благоприятные условия для повышения прочности и глубины знаний учащихся, обеспечивают сознательное усвоение математических понятий.
Нестандартные задачи :
Не должны иметь уже готовых, заученных детьми алгоритмов;
Должны быть доступны по содержанию всем учащимся;
Должны быть интересными по содержанию;
Для решения нестандартных задач учащимся должно хватать знаний, усвоенных ими по программе.
3.Методика формирования умения решать нестандартные задачи.
Задача№1.
По пустыне медленно идет караван верблюдов, всего их 40. Если пересчитать все горбы у этих верблюдов, то получится 57 горбов. Сколько в этом караване одногорбых верблюдов?
Сколько горбов может быть у верблюдов?
(их может быть два или один)
Давайте каждому верблюду на один горб прикрепим цветок.
Сколько цветков потребуется? (40 верблюдов – 40 цветов)
Сколько верблюдов останется без цветов?
(Таких будет 57-40=17. Это вторые горбы двугорбых верблюдов).
Сколько двугорбых верблюдов? (17)
Сколько одногорбых верблюдов? (40-17=23)
Каков же ответ задачи? (17 и 23 верблюдов).
Задача № 2.
В гараже стояли легковые машины и мотоциклы с колясками, всех вместе 18. У машин и мотоциклов – 65 колес. Сколько мотоциклов с колясками стояло в гараже, если у машин 4 колеса, а у мотоцикла – 3 колеса?
Переформулируем задачу. Грабители, пришедшие в гараж, где стояли 18 машин и мотоциклов с колясками, сняли с каждой машины и каждого мотоцикла по три колеса и унесли. Сколько колес осталось в гараже, если их было 65? Машине или мотоциклу они принадлежат?
Сколько колес унесли грабители? (3*18=54колес)
Сколько осталось колес? (65-54=11)
Сколько машин было в гараже?
В гараже стояли 18 легковых машин и мотоциклов с коляской. У машин и мотоциклов 65 колес. Сколько в гараже мотоциклов, если в каждую коляску положили запасное колесо?
Сколько стало колес у машин и мотоциклов вместе? (4*18=72)
Сколько запасных колес положили в каждую коляску? (72-65= 7)
Сколько машин в гараже? (18-7=1)
Задача №3.
Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35 кг сена. Сколько сена выдают одной лошади и сколько одной корове?
Запишем краткое условие задачи:
1 лошади и 2 коров -34кг.
2 лошадей и 1 коров -35кг.
Можно ли узнать, сколько сена потребуется для 3 лошадей и 3 коров? (для 3 лошадей и 3 коров – 34+35=69 кг)
Можно ли узнать, сколько сена потребуется для одной лошади и одной коровы? (69: 3 – 23кг)
Сколько сена потребуется для одной лошади? (35-23=12кг)
Сколько сена потребуется для одной коровы? (23 -13 =11кг)
Ответ: 12кг и 11 кг
Задача№4.
-Летели гуси: 2 впереди, 1 позади, 1 впереди, 2 позади.
Сколько гусей летело?
Сколько летело гусей, как сказано в условии? (2 впереди, 1 позади)
Изобразите это точками.
Изобразите точками.
Посчитайте то, что у вас получилось (2 впереди, 1, 1, 2 позади)
Так говорится в условии? (нет)
Значит, вы нарисовали гусей лишних. По вашему рисунку можно сказать, что 2 впереди и 4 позади, или 4 впереди, а 2 позади. А это не по условию. Что же нужно сделать? (убрать 3 последние точки)
Что получится?
Так сколько же гусей летело? (3)
Задачи № 5.
Четыре утенка и пять гусят весят 4кг 100г, пять утят и четыре гусенка весят 4 кг. Сколько весит один утенок?
Переформулируем задачу.
Четыре утенка и пять гусят весят 4кг 100г, пять утят и четыре гусенка весят 4 кг.
Сколько весят один утенок и один гусенок вместе?
Сколько весят 9 утят и 9 гусят вместе?
Примените решение вспомогательной задачи для решения основной, зная сколько весят 3 утенка и 3 гусенка вместе?
Задачи с элементами комбинаторики и на смекалку .
Задача № 6.
Марина решила позавтракать в школьном буфете. Изучи меню и ответь, сколькими способами она может выбрать напиток и кондитерское изделие?
Давайте предположим, что из напитков Марина выберет чай. Какое кондитерское изделие она может подобрать к чаю? (чай – ватрушка, чай – печенье, чай – булка)
Сколько способов? (3)
А если компот? (тоже 3)
Как же узнать, сколько способов может Марина использовать, чтобы выбрать себе обед? (3+3+3=9)
Да, вы правы. Но чтобы нам было легче решать такую задачу, мы будем использовать графы. Обозначим напитки и кондитерские изделия точками и соединим пары тех блюд, которые выберет Марина.
чай молоко компот

ватрушка печенье булочка
Теперь сосчитаем количество линий. Их 9. Значит, существует 9 способов выбора блюд.
Задача № 7.
Три богатыря – Илья Муромец, Алеша Попович и Добрыня Никитич, защищая от нашествия родную землю, срубили Змею Горынычу все 13 голов. Больше всех голов срубил Илья Муромец, а меньше всех – Алеша Попович. Сколько голов мог срубить каждый из них?
Кто может ответить на этот вопрос?
(учитель спрашивает несколько человек – ответы у всех разные)
Почему получились разные ответы? (потому что не сказано конкретно, сколько голов срубил хотя бы один из богатырей)
Давайте попробуем найти все возможные варианты решения этой задачи. Поможет нам в этом таблица.
Какое условие мы обязательно должны соблюдать, решая эту задачу? (Все богатыри срубили разное количество голов, и у Алеши – меньше всех, у Ильи – больше всех)
Сколько же вариантов решения имеет данная задача? (8)
Такие задачи называют – задачи с многовариантными решениями.
Составьте свою задачу с многовариантным решением.
Задача № 8.
-В битве с трехглавым и треххвостым Змеем Горынычем
Иван-Царевич одним ударом меча может срубить либо одну голову, либо две головы, либо один хвост, либо два хвоста. Если срубить одну голову – новая вырастет, если срубить один хвост – два новых вырастут, если срубить два хвоста – голова вырастет, если срубить две головы – ничего не вырастет. Посоветуйте Ивану-Царевичу, как поступить, чтобы он мог срубить Змею все головы и хвосты.
Что же произойдет, если Иван-Царевич отрубит одну голову? (вырастет новая голова)
Есть смысл отрубать одну голову? (нет, ничего не изменится)
Значит, отрубание одной головы исключаем - лишняя трата сил и времени.
Что произойдет, если отрубить один хвост? (вырастут два новых хвоста)
А если отрубить два хвоста? (вырастет голова)
А две головы? (ничего не вырастет)
Итак, мы не можем срубить одну голову, т. к. при этом ничего не изменится, опять вырастет голова. Надо добиться такого положения, чтобы голов было четное число, а хвостов – ни одного. Но для этого нужно, чтобы и хвостов было четное число.
Как же можно добиться нужного результата?
1). 1-ый удар: срубить 2 хвоста – станет 4 головы и 1 хвост;
2-ой удар: срубить 1 хвост – станет 4 головы и 2 хвоста;
3-ий удар: срубить 1 хвост – станет 4 головы и 3 хвоста;
4-ый удар: срубить 1 хвост – станет 4 головы и 4 хвоста;
5-ый удар: срубить 2 хвоста – станет 5 голов и 2 хвоста;
6-ой удар: срубить 2 хвоста – станет 6 голов и 0 хвостов;
7-ой удар: срубить 2 головы – станет 4 головы;
2). 1-ый удар: срубить 2 головы – станет 1 голова и 3 хвоста;
2-ой удар: срубить 1 хвост – станет 1 голова и 4 хвоста;
3-ий удар: срубить 1 хвост – станет 1 голова и 5 хвостов;
4-ый удар: срубить 1 хвост – станет 1 голова и 6 хвостов;
5-ый удар: срубить 2 хвоста – станет 2 головы и 4 хвоста;
6-ой удар: срубить 2 хвоста – станет 3 головы и 2 хвоста;
7-ой удар: срубить 2 хвоста – станет 4 головы;
8-ой удар: срубить 2 головы – станет 2 головы;
9-ый удар: срубить 2 головы – станет 0 голов.
Задача № 9.
В семье четверо детей: Сережа, Ира, Витя и Галя. Им 5, 7, 9 и 11 лет. Сколько лет каждому из них, если один из мальчиков ходит в детский сад, Ира моложе Сережи, а сумма лет девочек делится на 3?
Повторите условие задачи.
Чтобы не запутаться в процессе рассуждений начертим таблицу.
Что мы знаем про одного из мальчиков? (ходит в детский сад)
Сколько лет этому мальчику? (5)
Этого мальчика могут звать Сережа? (нет, Сережа старше Иры, значит, его зовут Витя)
Поставим в строке «Витя», столбце «5» знак «+». Значит, самого младшего ребенка зовут Витя и ему 5 лет.
Что знаем про Иру? (она младше Сережи, и если к ее возрасту прибавить возраст другой сестры, то эта сумма будет делиться на 3)
Попробуем вычислить все суммы чисел 7, 9 и 11.
16 и 20 на 3 не делится, а 18 на 3 делится.
Значит, возраст девочек 7 и 11 лет.
Сколько лет Сереже? (9)
А Ире? (7, т. к. она младше Сережи)
А Гале? (11 лет)
Заносим данные в таблицу:
Какой же ответ на вопрос задачи? (Вите 5 лет, Ире 7 лет, Сереже 9 лет, а Гале 11 лет)
Задача №10.
Катя, Соня, Галя и Тома родились 2 марта, 17 мая, 2 июня, 20 марта. Соня и Галя родились в одном месяце, а у Гали и Кати день рождения обозначился одинаковыми числами. Кто, какого числа, и в каком месяце родился?
Прочитайте задачу.
Что знаем? (что Соня и Галя родились в одном месяце, а Галя и Катя – в одно число)
Значит, в каком месяце день рождения у Сони и Гали? (в марте)
А что можно сказать про Галю, зная, что она родилась в марте, да еще ее число совпадает с числом Кати? (Галя родилась 2 марта)
Понятие «нестандартная задача» используется многими методистами. Так, Ю. М. Колягин раскрывает это понятие следующим образом: «Под нестандартной понимается задача , при предъявлении которой учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение» .
Определение нестандартной задачи приведено также в книге «Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого: «Нестандартные задачи - это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения» .
Не следует путать нестандартные задачи с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого - решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 5 классе нестандартна, а в 6 классе она является обычной, и даже не повышенной сложности.
Анализ учебников и учебных пособий по математике показывает, что каждая текстовая задача в определенных условиях может быть нестандартной, а в других - обычной, стандартной. Стандартная задача одного курса математики может быть нестандартной в другом курсе.
Опираясь на анализ теории и практики использования нестандартных задач в обучении математике, можно установить их общую и специфическую роль. Нестандартные задачи:
- · учат детей использовать не только готовые алгоритмы, но и самостоятельно находить новые способы решения задач, т.е. способствуют умению находить оригинальные способы решения задач;
- · оказывают влияние на развитие смекалки, сообразительности учащихся;
- · препятствуют выработке вредных штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся, предполагают не столько усвоение алгоритмических приемов, сколько нахождение новых связей в знаниях, к переносу знаний в новые условия, к овладению разнообразными приемами умственной деятельности;
- · создают благоприятные условия для повышения прочности и глубины знаний учащихся, обеспечивают сознательное усвоение математических понятий.
Нестандартные задачи:
- · не должны иметь уже готовых, заученных детьми алгоритмов;
- · должны быть доступны по содержанию всем учащимся;
- · должны быть интересными по содержанию;
- · для решения нестандартных задач учащимся должно хватать знаний, усвоенных ими по программе.
Решение нестандартных задач активизирует деятельность учащихся. Учащиеся учатся сравнивать, классифицировать, обобщать, анализировать, а это способствует более прочному и сознательному усвоению знаний.
Как показала практика, нестандартные задачи весьма полезны не только для уроков, но и для внеклассных занятий, для олимпиадных заданий, так как при этом открывается возможность по-настоящему дифференцировать результаты каждого участника. Такие задачи могут с успехом использоваться и в качестве индивидуальных заданий для тех учеников, которые легко и быстро справляются с основной частью самостоятельной работы на уроке, или для желающих в качестве дополнительных заданий. В результате учащиеся получают интеллектуальное развитие и подготовку к активной практической деятельности.
Общепринятой классификации нестандартных задач нет, но Б.А. Кордемский выделяет следующие виды таких задач:
- · Задачи, примыкающие к школьному курсу математики, но повышенной трудности - типа задач математических олимпиад. Предназначаются в основном для школьников с определившимся интересом к математике; тематически эти задачи обычно связаны с тем или иным определённым разделом школьной программы. Относящиеся сюда упражнения углубляют учебный материал, дополняют и обобщают отдельные положения школьного курса, расширяют математический кругозор, развивают навыки в решении трудных задач.
- · Задачи типа математических развлечений. Прямого отношения к школьной программе не имеют и, как правило, не предполагают большой математической подготовки. Это не значит, однако, что во вторую категорию задач входят только лёгкие упражнения. Здесь есть задачи с очень трудным решением и такие задачи, решение которых до сих пор не получено. «Нестандартные задачи, поданные в увлекательной форме, вносят эмоциональный момент в умственные занятия. Не связанные с необходимостью всякий раз применять для их решения заученные правила и приёмы, они требуют мобилизации всех накопленных знаний, приучают к поискам своеобразных, не шаблонных способов решения, обогащают искусство решения красивыми примерами, заставляют восхищаться силой разума» .
К этому виду задач относятся:
разнообразные числовые ребусы («… примеры, в которых все или некоторые цифры заменены звездочками или буквами. Одинаковые буквы заменяют одинаковые цифры, разные буквы - разные цифры» .) и головоломки на смекалку;
логические задачи, решение которых не требует вычислений, но основывается на построении цепочки точных рассуждений;
задачи, решение которых основывается на соединении математического развития и практической смекалки: взвешивание и переливания при затруднительных условиях;
математические софизмы - это умышленное, ложное умозаключение, которое имеет видимость правильного. (Софизм - доказательство ложного утверждения, причём ошибка в доказательстве искусно замаскирована. Софизм в переводе с греческого означает хитроумную выдумку, ухищрение, головоломку);
задачи-шутки;
комбинаторные задачи, в которых рассматриваются различные комбинации из заданных объектов, удовлетворяющие определённым условиям (Б.А. Кордемский, 1958).
Не менее интересна классификация нестандартных задач, приведённая И.В. Егорченко:
- · задачи, направленные на поиск взаимосвязей между заданными объектами, процессами или явлениями;
- · задачи, неразрешимые или не решаемые средствами школьного курса на данном уровне знаний учащихся;
- · задачи, в которых необходимо:
проведение и использование аналогий, определение различий заданных объектов, процессов или явлений, установление противоположности заданных явлений и процессов или их антиподов;
осуществление практической демонстрации, абстрагирование от тех или иных свойств объекта, процесса, явления или конкретизации той или иной стороны данного явления;
установка причинно-следственных отношений между заданными объектами, процессами или явлениями;
построение аналитическим или синтетическим путем причинно-следственных цепочек с последующим анализом получившихся вариантов;
правильное осуществление последовательности определенных действий, избегая ошибок-«ловушек»;
осуществление перехода от плоскостного к пространственному варианту заданного процесса, объекта, явления или наоборот (И.В. Егорченко, 2003).
Итак, единой классификации нестандартных задач нет. Их существует несколько, но автор работы использовал в исследовании классификацию, предложенную И.В. Егорченко.
В сборнике представлены материалы по формированию умений учащихся решать нестандартные задачи.Умение решать нестандартные задачи, т. е. такие, алгоритм решения которых не известен заранее, – важный компонент школьного обучения. Как же научить школьников решать нестандартные задачи? Об одном из возможных вариантов такого обучения – постоянном конкурсе решения задач рассказывалось на страницах приложения «Математика» (№ 28-29, 38-40/96). Предлагаемый Вашему вниманию набор задач может быть использован и во внеклассной работе . Материал подготовлен по заявкам педагогов города Костромы.
Умение решать задачи – важнейшая (и легче всего контролируемая) составляющая математического развития учащихся. Речь идет не о типовых заданиях (упражнениях), а о задачах нестандартных, алгоритм решения которых заранее не известен (граница между этими видами задач условна, и то, что является нестандартным для шестиклассника, может быть привычным для ученика седьмого класса!. Предлагаемые ниже 150 задач (непосредственное продолжение нестандартных задач для пятиклассников) предназначены для проведения годового конкурса в 6-м классе. Эти задачи также могут быть использованы и во внеклассной работе.
Комментарий к задачам
Все задачи можно условно разделить на три группы:
1.Задачи на смекалку . Для решения таких задач, как правило, не требуется глубоких знаний, необходимы лишь сообразительность и желание преодолеть трудности, встречающиеся на пути к решению. Кроме всего прочего – это шанс заинтересовать учеников, которые не проявляют особого рвения к учению, и, в частности, к математике.
2.Задачи на закрепление материала . Время от времени, необходимо решать задачи, предназначенные исключительно для закрепления усвоенных идей. Заметим, что проверять степень усвоения нового материала желательно через некоторое время после его изучения.
3.Задачи на пропедевтику новых идей . Задачи этого типа подготавливают учеников к систематическому изучению программного материала, а содержащиеся в них идеи и факты получают в дальнейшем естественное и простое обобщение. Так, например, вычисление различных числовых сумм поможет ученикам понять вывод формулы суммы арифметической прогрессии, а идеи и факты, содержащиеся в некоторых текстовых задачах данного набора, готовят к изучению тем: Системы линейных уравнений», «Равномерное движение» и т. Д. Как показывает опыт, чем дольше изучается материал, тем легче его усвоить.
О решении задач
Отметим принципиально важные моменты:
1. Мы приводим «чисто арифметические» решения текстовых задач, где это представляется возможным, даже если школьники могут легко решать их с помощью уравнений. Это объясняется тем, что воспроизведение материала в словесной форме требует значительно больших логических усилий и поэтому наиболее эффективно развивает мышление учащихся. Умение излагать материал в словесной форме – важнейший показатель уровня математического мышления.
2. Изученный материал лучше усваивается, если в сознании учащихся он связан с другим материалом, поэтому, как правило, мы ссылаемся на уже решенные задачи (такие ссылки набраны курсивом).
3. Задачи полезно решать разными способами (положительная оценка ставится за любой способ решения). Поэтому для всех текстовых задач кроме арифметического рассматривается алгебраическое решение (уравнение). Учителю рекомендуется провести сравнительный анализ предложенных решений.
Условия задач
▼ 1.1. На какое однозначное число надо умножить, чтобы в результате получилось новое число, записанное одними единицами?
1.2. Если Аня идет в школу пешком, а обратно едет на автобусе, то всего на дорогу она затрачивает 1,5 ч. Если же она едет в оба конца на автобусе, то весь путь занимает у нее 30 мин. Сколько времени потратит Аня на дорогу, если и в школу, и из школы она будет идти пешком?
1.3. Картофель подешевел на 20%. На сколько процентов больше можно купить картофеля на ту же сумму?
1.4. В шестилитровом ведре содержится 4 л кваса, а в семилитровом – 6 л. Как разделить весь имеющийся квас пополам, используя эти ведра и пустую трехлитровую банку?
1.5. Можно ли ходом шахматного коня попасть из левого нижнего угла доски в правый верхний, побывав на каждом поле ровно один раз? Если можно, то укажите маршрут, если же нет, то объясните, почему.
▼ 2.1. Верно ли утверждение: если к отрицательному числу прибавить квадрат этого же числа, то всегда получится положительное число?
2.2. Я иду от дома до школы 30 мин, а мой брат – 40 мин. Через сколько минут я догоню брата, если он вышел из дома на 5 мин раньше меня?
2.3.
Ученик написал на доске пример на умножение двузначных чисел. Затем он стер все цифры и заменил их буквами. Получилось равенство: ![]() .
Докажите, что ученик ошибся.
.
Докажите, что ученик ошибся.
 2.4.
Кувшин уравновешивает графин и стакан, два кувшина весят столько же, сколько три чашки, а стакан и чашка уравновешивают графин. Сколько стаканов уравновешивают графин?
2.4.
Кувшин уравновешивает графин и стакан, два кувшина весят столько же, сколько три чашки, а стакан и чашка уравновешивают графин. Сколько стаканов уравновешивают графин?

▼ 3.1. Пассажир, проехав половину всего пути, лег спать и спал до тех пор, пока не осталось ехать половину того пути, что он проехал спящим. Какую часть пути он проехал спящим?
3.2. Какое слово зашифровано в записи числа, если каждая буква заменена её номером в алфавите ?
3.3. Даны 173 числа, каждое из которых равно 1 или -1. Можно ли разбить их на две группы так, чтобы суммы чисел в группах были равны?
3.4. Школьник прочитал книгу за 3 дня. В первый день он прочитал 0,2 всей книги и еще 16 страниц, во второй день – 0,3 остатка и еще 20 страниц, а в третий день – 0,75 нового остатка и последние 30 страниц. Сколько страниц в книге?
3.5. Окрашенный куб с ребром 10 см распилили на кубики с ребром, равным 1 см. Сколько среди них окажется кубиков с одной окрашенной гранью? С двумя окрашенными гранями?
▼ 4.1. Из чисел 21, 19, 30, 25, 3, 12, 9, 15, 6, 27 выбрать три такие числа, сумма которых равна 50.
4.2. Машина едет со скоростью 60 км/ч. На сколько надо увеличить скорость, чтобы километр пути проезжать на одну минуту быстрее?
4.3. К доске для игры в крестики-нолики добавлена одна клетка (см. рисунок). Как нужно играть первому игроку, чтобы наверняка обеспечить себе выигрыш?
4.4. В шахматном турнире участвовало 7 человек. Каждый шахматист сыграл с каждым по одной партии. Сколько партий было сыграно?
4.5. Можно ли разрезать шахматную доску на прямоугольники размером 3x1?
▼5.1. За книгу заплатили 5000 р. И осталось заплатить столько, сколько осталось бы заплатить, если бы за нее заплатили столько, сколько осталось заплатить. Сколько стоит книга?
5.2. Племянник спросил дядю, сколько тому лет. Дядя ответил: «Если к половине моих лет прибавить 7, то узнаешь мой возраст 13 лет назад». Сколько лет дяде?
5.3. Если между цифрами некоторого двузначного числа вписать 0, то полученное трехзначное число в 9 раз больше первоначального. Найдите это двузначное число.
5.4. Найдите сумму чисел 1 + 2 + … + 870 + 871.
5.5. Имеется 6 палочек, каждая длиной по 1 см, 3 палочки – по 2 см, 6 палочек – по 3 см, 5 палочек – по 4 см. Можно ли из этого набора составить квадрат, используя при этом все палочки, не ломая их и не накладывая одна на другую?
▼ 6.1. Множимое увеличили на 10%, а множитель уменьшили на 10%. Как при этом изменилось произведение?
 6.2.
Три бегуна А
, Б
и В
соревновались в беге на 100 м. Когда А
добежал до конца дистанции, Б
отставал от него на 10 м, Когда Б
добежал до финиша, В
отставал от него на 10 м. На сколько метров отставал В
от А
, когда А
финишировал?
6.2.
Три бегуна А
, Б
и В
соревновались в беге на 100 м. Когда А
добежал до конца дистанции, Б
отставал от него на 10 м, Когда Б
добежал до финиша, В
отставал от него на 10 м. На сколько метров отставал В
от А
, когда А
финишировал?
 6.3.
Количество отсутствующих учеников в классе составляет числа присутствующих. После того, как из класса вышел один ученик, число отсутствующих стало равно числа присутствующих. Сколько учеников в классе?
6.3.
Количество отсутствующих учеников в классе составляет числа присутствующих. После того, как из класса вышел один ученик, число отсутствующих стало равно числа присутствующих. Сколько учеников в классе?
6.4 . Арбуз уравновешивает дыню и свеклу. Дыня уравновешивает капусту и свеклу. Два арбуза весят столько же, сколько три кочана капусты. Во сколько раз дыня тяжелее свеклы?
6.5. Можно ли прямоугольник размером 4x8 разрезать на 9 квадратов?
▼ 7.1. Цену товара уменьшили на 10%, а затем еще раз на 10%. Станет ли товар дешевле, если его цену сразу снизить на 20%?
7.2. Гребец, плывя по реке, потерял под мостом шляпу. Через 15 мин он заметил пропажу, вернулся и поймал шляпу в 1 км от моста. Какова скорость течения реки?

7.3. Известно, что одна из монет фальшивая и она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно монета фальшивая?
7.4. Можно ли по правилам игры выложить в цепь все 28 костей домино так, чтобы на одном конце оказалась «шестерка», а на другом - «пятерка»?
7.5. Имеется 19 телефонов. Можно ли соединить их попарно так, чтобы каждый был соединен ровно с тринадцатью из них?
▼ 8.1. В соревнованиях по олимпийской системе (проигравший выбывает) участвует 47 боксеров. Сколько боев надо провести, чтобы определить победителя?
8.2. В саду растут яблони и вишни . Если взять всех вишен и всех яблонь, то и тех, и других деревьев останется поровну, а всего в саду 360 деревьев. Сколько яблонь и вишен было в саду?
8.3. Коля, Боря, Вова и Юра заняли в соревновании первые четыре места, причем никакие два мальчика не делили между собой какие-нибудь места. На вопрос, кто какое место завял, Коля ответил: «Ни первое, ни четвертое».Боря сказал: «Второе», а Вова заметил, что он не был последним. Какое место занял каждый из мальчиков, если все они сказали правду?
8.4. Делится ли числона 9?
8.5. Разрежьте прямоугольник, длина которого равна 9 см, а ширина 4 см, на две равные части так, чтобы из них было можно сложить квадрат.
▼ 9.1. Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность
снизилась до 98%. Какой стала масса грибов после подсушивания?
9.2. Можно ли из чисел 1, 2, 3, …, 11, 12 составить таблицу из 3 строк и 4 столбцов такую, чтобы сумма чисел в каждом из столбцов была одной и той же?
9.3. Какой цифрой оканчивается сумма135x + 31y + 56x+y, если x и y – натуральные числа?
9.4. Пятеро мальчиков Андрей, Боря, Володя, Гена и Дима имеют разный возраст: одному 1 год, другому 2 года, остальным 3, 4 и 5 лет. Володя – самый маленький, Диме столько лет, сколько Андрею и Гене вместе. Сколько лет Боре? Чей еще возраст можно определить?
9.5. У шахматной доски отпилены два поля: левое нижнее и правое верхнее. Можно ли покрыть такую шахматную доску «костями» домино размером 2x1?
▼ 10.1. Можно ли из чисел 1,2,3,…. 11,12 составить таблицу из 3 строк и 4 столбцов такую, чтобы сумма чисел в каждой из трех строк была одной и той же?
10.2. Директор завода обычно приезжает поездом в город в 8 ч. Точно к этому времени подъезжает автомобиль и отвозит его на завод. Однажды директор приехал на вокзал в 7 ч и пошел на завод пешком. Встретив машину, он сел в нее и приехал на завод на 20 мин раньше обычного. Какое время показывали часы в момент встречи директора с машиной?
10.3 . В двух мешках 140 кг муки. Если из первого мешка переложить во второй 1/8 часть муки, находящейся в первом мешке, то в обоих мешках муки будет поровну. Сколько муки было первоначально в каждом мешке?
10.4. В одном месяце три среды пришлись на четные числа. Какого числа в этом месяце будет второе воскресенье?
10.5. После 7 стирок длина, ширина и толщина куска мыла уменьшились вдвое. На сколько таких же стирок хватит оставшегося мыла?
▼ 11.1. Продолжите ряд чисел: 10, 8, 11, 9, 12, 10 до восьмого числа. По какому правилу он составлен?
11.2. Из дома в школу Юра вышел на 5 мин позже Лены, но шел в два раза быстрее, чем она. Через сколько минут после выхода Юра догонит Лену?
11.3. 2100?
11.4. Ученики двух шестых классов купили 737 учебников, причем каждый купил одинаковое количество учебников. Сколько было шестиклассников, и сколько каждый из них купил учебников?
11.5 . Найдите площадь изображенного на рисунке треугольника (площадь каждой клетки 1 кв. см).

▼ 12.1. Влажность свежескошенной травы 60%, а сена 15%. Сколько сена получится из одной тонны свежескошенной травы?
12.2. Пять учеников купила 100 тетрадей. Коля и Вася купили 52 тетради, Вася и Юра – 43, Юра и Саша – 34, Саша и Сережа – 30. Сколько тетрадей купил каждый из них?
12.3. Сколько шахматистов играло в круговом турнире, если всего было сыграно 190 партий?
12.4. На какую цифру заканчивается число З100?
12.5. Известно, что длины сторон треугольника – целые числа, причем одна сторона равна 5, а другая 1. Чему равна длина третьей стороны?
▼ 13.1. Билет стоилруб. После снижения платы за проезд число пассажиров увеличилось на 50%, а выручка при этом выросла на 25%. Сколько стал стоить билет после снижения?
13.2. От Нижнего Новгорода до Астрахани теплоход идет 5 суток, а обратно – 7 суток. Сколько времени будут плыть плоты от Нижнего Новгорода до Астрахани?
13.3. Юра взял книгу на 3 дня. В первый день он прочитал половину книги, во второй – треть оставшихся страниц, а количество страниц, прочитанных в третий день, равно половине страниц, прочитанных за первые два дня. Успел ли Юра прочитать книгу за 3 дня?
13.4. Алеша, Боря и Витя учатся в одном классе. Один из них ездит домой из школы на автобусе, другой – на трамвае, третий – на троллейбусе. Однажды после уроков Алеша пошел проводить друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадь!» На каком виде транспорта каждый ездит домой?
13.5. Мне сейчас вдвое больше лет, чем вам было тогда, когда мне было столько лет, сколько вам сейчас. Сейчас нам вместе 35 лет. Сколько лет каждому из вас?
▼ 14.1. Дано 2001 число. Известно, что сумма любых четырех из них положительна. Верно ли, что сумма всех чисел положительна?
14.2. Когда велосипедист проехал пути, лопнула шина. Оставшийся путь он прошел пешком и затратил на это в 2 раза больше времени, чем на езду на велосипеде. Во сколько раз велосипедист ехал быстрее, чем шел?
14.3. Имеются двух чашечные весы и гири массой 1, 3, 9, 27 и 81 г. На одну чашку весов кладут груз, гири разрешается класть на обе чашки. Докажите что весы можно уравновесить, если масса груза равна: а) 13 г; б) 19 г; в) 23 г; г) 31 г.
14.4.
Ученик написал на доске пример на умножение двузначных чисел. Затем он стер все цифры и заменил их буквами: одинаковые цифры – одинаковыми буквами, а разные – разными. Получилось равенство: ![]() .
Докажите, что ученик ошибся.
.
Докажите, что ученик ошибся.
14.5. Среди музыкантов каждый седьмой – шахматист, а среди шахматистов каждый девятый – музыкант. Кого больше: музыкантов или шахматистов? Почему?
▼ 15.1. Длину прямоугольного участка увеличили на 35%, а ширину уменьшили на 14%. На сколько процентов изменилась площадь участка?
15.2. Вычислили сумму цифр числа 109! Затем вычислили сумму цифр вновь полученного числа и так продолжали до тех пор, пока не было получено однозначное число. Что это за число?
15.3. Три пятницы некоторого месяца пришлись на четные даты. Какой день недели был 18 числа этого месяца?
15.4. Разбирается дело Браун, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления:
Браун: 1. Я не преступник. 2. Джонс тоже.
Джонс: 1, Это не Браун. 2. Это Смит.
Сжит: 1. Преступник Браун. 2. Это не я.
Было установлено, что один из них дважды солгал, другой дважды сказал правду, а третий один раз солгал и один раз сказал правду. Кто совершил преступление?
15.5. На часах 19 ч 15 мин. Чему равен угол между минутной и часовой стрелками?
▼ 16.1. Если человек, стоящий в очереди перед Вами, был выше человека, стоящего после того человека, который стоял перед вами, то был ли человек, стоящий перед Вами, Выше вас?
16.2. В классе учатся менее 50 школьников. За контрольную работу седьмая часть учеников получила оценку «5», третья часть – «4», а половина – «3». Остальные получили «2». Сколько было таких работ?
16.3. Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу и встретились в 70 км от А. Продолжая двигаться с теми же скоростями, они достигли конечных пунктов и, отдохнув равное время, вернулись назад. Вторая встреча произошла в 90 км от В. Найдите расстояние от А до В.
16.4. Делится ли число 111…111 (999 единиц) на 37?
16.5. Разделите прямоугольник размером 18x8 на части так, чтобы из этих частей можно было сложить квадрат.
▼ 17.1. Когда Ваню спросили, сколько ему лет, он подумал и сказал: «Я втрое моложе папы, но зато втрое старше Сережи». Тут подбежал маленький Се режа и сообщил, что папа старше его на 40 лет. Сколько лет Ване?
17.2. На три склада доставлен груз. На первый и второй склады было доставлено 400 т, на второй и третий вместе 300 т, а на первый и третий – 440 т. Сколько тонн груза было доставлено на каждый склад в отдельности?
17.3. От потолка комнаты вертикально вниз по стене поползли две мухи. Спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая, хотя и поднималась в два раза медленней первой, но зато спускалась вдвое быстрее. Какая из мух раньше приползет обратно?
17.4. В магазин привезли 25 ящиков яблок трех сортов, причем в каждом из ящиков лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
17.5. Найдите два простых числа, сумма и разность которых также является простым числом.
▼ 18.1. Задумано трехзначное число, у которого с любым из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?
18.2. На балу каждый кавалер танцевал с тремя дамами, а каждая дама – с тремя кавалерами. Докажите, что на балу число дам было равно числу кавалеров.
18.3. В школе, 33 класса, 1150 учеников. Найдется ли в этой школе класс, в котором не менее 35 учеников?
18.4. В одном районе города более 94% домов имеют больше 5 этажей. Какое наименьшее число домов возможно в данном районе?
18.5. Найдите все треугольники, длины сторон которых целые числа сантиметров и длина каждой из них не превышает 2 см.
▼ 19.1. Докажите, что если сумма двух натуральных чисел меньше 13, то их произведение не больше 36.
19.2. Из 75 одинаковых по виду колец одно по весу отличается от других. Как за два взвешивания на чашечных весах определить, легче или тяжелее это кольцо, чем остальные?
19.3. Самолет летел из А в В сначала со скоростью 180 км/ч, но когда ему осталось лететь на 320 км меньше, чем он уже пролетел, он увеличил скорость до 250 км/ч. Оказалось, что средняя скорость самолета на всем пути 200 км/ч. Определите расстояние от А до В.
19.4. Милиционер обернулся на звук бьющегося стекла и увидел четырех подростков, убегающих от разбитой витрины . Через 5 мин они были в отделении милиции. Андрей заявил, что стекло разбил Виктор, Виктор же утверждал, что виноват Сергей. Сергей заверял, что Виктор лжет, а Юрий твердил, что это сделал не он. Из дальнейшего разговора выяснилось, что лишь один из ребят говорил правду. Кто разбил стекло?
19.5. На доске выписаны все натуральные числа от 1 до 99. Каких цифр на доске больше - четных или нечетных?
▼ 20.1. Два крестьянина вышли из деревни в город. Пройдя пути, они сели отдохнуть. «Сколько еще осталось идти?» - спросил один другого. «Нам осталось пройти на 12 км больше, чем мы уже прошли», - был ответ. Чему равно расстояние между городом и деревней?
20.2. Докажите, что число 7777 + 1 не делится на 5.
20.3. В семье четверо детей, им 5, 8, 13 и 15 лет. Детей зовут Аня, Боря, Вера и Галя. Сколько лет каждому ребенку, если одна из девочек ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на 3?
20.4. В темной комнате 10 арбузов и 8 дынь (дыни и арбузы не различимы на ощупь). Сколько нужно взять фруктов, чтобы среди них было не менее двух арбузов?
20.5. Пришкольный участок прямоугольной формы имеет периметр 160 м. Как изменится его площадь, если длину каждой стороны увеличить на 10 м?
▼ 21.1. Найти сумму 1 + 5 + … + 97 + 101.
21.2. Вчера число учеников, присутствующих в классе, было в 8 раз больше отсутствующих. Сегодня не пришло еще 2 ученика и оказалось, что отсутствуют 20% от числа учеников, присутствующих в классе. Сколько всего учеников в классе?
21.3. Что больше 3200 или 2300?
21.4. Сколько диагоналей у тридцатичетырехугольника?
21.5. Посередине участка квадратной формы устроена цветочная клумба, которая также имеет форму квадрата. Площадь участка равна 100 м2. Сторона клумбы в два раза меньше стороны участка. Чему равна площадь клумбы?
▼ 22.1. Сократите дробь
22.2. Кусок проволоки длиной 102 см нужно разрезать на части длиной 15 и 12 см так, чтобы не было обрезков. Как это сделать? Сколько решений имеет задача?
22.3. В коробке лежат 7 красных и 5 синих карандашей. Из коробки в темноте берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее двух красных и трех синих?
22.4. В одном сосуде 2а литров воды, а другой пустой. Из 1-го сосуда переливают половину воды во 2-й,
затем из 2-го переливают воды в 1-й, затем из 1-го переливают воды во 2-й и т. Д. Сколько литров воды будет в первом сосуде после 1995 переливания?
8. Из числа …5960 вычеркнуть сто цифр так, чтобы полученное число было наибольшим.
▼ 23.1. Сначала отпили чашки черного кофе и долили ее молоком. Затем выпили чашки и снова долили ее молоком. Потом выпили еще полчашки и опять долили ее молоком. Наконец, выпили всю чашку. Чего выпили больше: кофе или молока?
23.2. К трехзначному числу слева приписали 3 и оно увеличилось в 9 раз. Что это за число?
23.3. Из пункта А в пункт В ползут два жука и возвращаются обратно. Первый жук полз в обе стороны с одинаковой скоростью. Второй полз в В в 1,5 раза быстрее, а обратно в 1,5 раза медленнее, чем первый. Какой жук вернулся в А раньше?
23.4. Какое число больше: 2 379∙23 или 2 378∙23 ?
23.5. Площадь квадрата равна 16 м2. Чему будет равна площадь квадрата, если:
а) сторону квадрата увеличить, в 2 раза?
Б) сторону квадрата увеличить в 3 раза?
В) сторону квадрата увеличить на 2 дм?
▼ 24.1. На какое число нужно умножить, чтобы получить число, которое записывается с помощью одних пятерок?
24.2. Верно ли, что число 1 является квадратом некоторого натурального числа?
24.3. Автомобиль из А в В ехал со средней скоростью 50 км/ч, а обратно возвращался со скоростью 30 км/ч. Какова его средняя скорость?
24.4. Докажите, что любую сумму из целого числа рублей, большую семи, можно уплатить без сдачи денежными купюрами в 3 и 5 руб.?
24.5. На завод привезли бревна двух видов: длиной 6 и 7 м. Их нужно распилить на метровые чурбаки. Какие бревна выгоднее пилить?
▼ 25.1. Сумма нескольких чисел равна 1. Может ли сумма их квадратов быть меньше 0,01?
25.2. Имеется 10 мешков монет. В девяти мешках монеты настоящие (весят по 10 г), а в одном – фальшивые (весят по 11 г). Одним взвешиванием на электронных весах определить, в каком мешке фальшивые монеты.
25.3. Докажите, что сумма любых четырех последовательных натуральных чисел не делится на 4.
25.3. Из числа …5960 вычеркните сто цифр так, чтобы полученное число было наименьшим.
25.4. Купили несколько одинаковых книг и одинаковых альбомов. За книги заплатили 10 руб. 56 коп. Сколько купили книг, если цена одной книги более чем на рубль превышает цену альбома, а книг купили на 6 больше, чем альбомов.
▼ 26.1. Две противоположные стороны прямоугольника увеличили на их часть, а две другие уменьшили на часть. Как изменилась площадь прямоугольника?
26.2. Десять команд участвуют в турнире по футболу. Доказать, что при любом расписании игр всегда найдутся две команды, сыгравшие одинаковое количество матчей.
26.3. Самолет летит по прямой из города А в В, а затем обратно. Его собственная скорость постоянна. Когда самолет пролетит весь путь быстрее: при отсутствии ветра или при ветре, постоянно дующем в на правлении из А в В?
26.4. Числа 100 и 90 разделили на одно я то же число. В первом случае получили в остатке 4, а во втором – 18. На какое число выполнялось деление?
26.5.
 Шесть прозрачных колб с водой расставлены в два параллельных ряда по 3 колбы в каждом. На рис. 1 видны три передние колбы, а на рис. 2 – две правые боковые. Через прозрачные стенки колб видны уровни воды в каждой видимой колбе и во всех колбах, стоящих за ними. Определите, в каком порядке стоят колбы и какой уровень воды в каждой из них.
Шесть прозрачных колб с водой расставлены в два параллельных ряда по 3 колбы в каждом. На рис. 1 видны три передние колбы, а на рис. 2 – две правые боковые. Через прозрачные стенки колб видны уровни воды в каждой видимой колбе и во всех колбах, стоящих за ними. Определите, в каком порядке стоят колбы и какой уровень воды в каждой из них.
▼ 27.1. Бригада косцов в первый день скосила половину луга и еще 2 га, а во второй – 25% оставшейся части и последние 6 га. Найдите площадь луга.
27.2. Имеется 11 мешков монет. В десяти мешках монеты настоящие (весят по 10 г), а в одном – фальшивые (весят по 11 г). Одним взвешиванием определить, в каком мешке фальшивые монеты.
27.3. В ящике лежат 10 красных, 8 синих и 4 желтых карандаша. Из ящика в темноте берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было: а) не менее 4 карандашей одного цвета? Б) не менее 6 карандашей одного цвета? В) хотя бы 1 карандаш каждого цвета?
Г) не менее 6 синих карандашей?
27.4. Вася сказал, что знает решение уравнения ху 8 + х 8у = 1995 в натуральных числах. Докажите, что Вася ошибся.
 27.5.
Нарисуйте такой многоугольник и точку внутри него, чтобы ни одна сторона многоугольника не была видна из этой точки полностью (на рис. 3 из точки О не полностью видна сторона АВ).
27.5.
Нарисуйте такой многоугольник и точку внутри него, чтобы ни одна сторона многоугольника не была видна из этой точки полностью (на рис. 3 из точки О не полностью видна сторона АВ).
▼ 28.1. Гриша с папой пошли в тир. Уговор был такой: Гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать еще 2 выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз он попал в цель?
28.2. Лист бумаги разрезали на 4 части, затем некоторые (быть может, все) из этих частей тоже разрезали на 4 части и т. Д. Могло ли в результате получиться ровно 50 кусочков бумаги?
28.3. Первую половину пути всадник скакал со скоростью 20 км/ч, а вторую – со скоростью 12 км/ч. Найти среднюю скорость всадника.
28.4. Имеется 4 арбуза различной массы. Как, используя чашечные весы без гирь, не более чем за пять взвешиваний расположить их по возрастанию массы?
28.5. Доказать, что нельзя провести прямую так, чтобы она пересекла все стороны 1001-угольника (не проходя при этом через его вершины).
▼ 29.1. Простое ля число 1 ?
29.2. В одной бутылке белое вино, а в другой – красное. Капнем одну каплю красного вина в белое, а затем из полученной смеси вернем одну каплю в красное вино. Чего больше – белого вина в красном или красного вина в белом?
29.3. Курьеры равномерно, но с разными скоростями двигаются из А в В навстречу друг другу. После встречи для прибытия к месту назначения одному нужно было затратить еще 16 ч, а другому -9 ч. Сколько времени требуется каждому из них для прохождения всего пути от А до В?
29.4. Что больше 3111 или 1714?
29.5. а) Сумма сторон квадрата равна 40 дм. Чему равна площадь квадрата?
б) Площадь квадрата 64. Чему равен его периметр?
▼ 30.1. Можно ли число 203 представать в виде суммы нескольких слагаемых, произведение которых также равно 203?
30.2. Сто городов соединено авиалиниями . Доказать, что среди них имеется два города, через которые проходит одинаковое количество авиалиний.
30.3. Из четырех внешне одинаковых деталей одна отличается по массе от трех остальных, однако неизвестно, больше ее масса или меньше. Как выявить эту деталь двумя взвешиваниями на чашечных весах без гирь?
30.4. На какую цифру оканчивается число
13 + 23 + … + 9993?
30.5. Проведите 3 прямые так, чтобы тетрадный лист разделился на наибольшее число частей. Сколько получится частей? Проведите 4 прямые с тем же условием. Сколько теперь получилось частей?
РЕШЕНИЯ ЗАДАЧ
1.1. Проверкой убеждаемся: если числоумножить на 9,то в результате получится Вопрос учащимся: почему «проверять» следует только число 9?)
1.2. Если Аня едет в оба конца на автобусе, то весь путь занимает у нее 30 мин, следовательно, в один конец на автобусе она добирается за 15 мин. Если Аня идет в школу пешком, а обратно – на автобусе, то всего на дорогу она затрачивает 1,5 часа, значит, в один конец пешком она добирается за 1 ч 15 мин. Если же Аня и в школу, и из школы идет пешком, то на дорогу она тратит 2 ч 30 мин.
1.3. Так как картофель подешевел на 20%, то на весь купленный ранее картофель теперь надо истратить 80% имевшихся денег, а на оставшиеся 20% купить еще 1/4 часть картофеля, что составляет 25% . 4
1.4. Ход решения виден из таблицы:
|
в шаг |
1-й шаг |
2-й шаг |
3-й ими |
4-й шаг |
5-й шаг |
|
1.5. Для того чтобы обойти все 64 клетки шахматной доски, побывав на каждом поле ровно один раз. Конь должен сделать 63 хода. При каждом ходе конь переходит с белого поля на черное (или с черного поля на белое), поэтому после ходов с четными номерами конь будет попадать на поля того же цвета, что и исходное, а после «нечетных» ходов – на поля, имеющие противоположный цвет. Поэтому конь не может на 63-м ходу попасть в правый верхний угол доски, так как он одинакового цвета с правым верхним.
 Корпускулярные и волновые свойства частиц
Корпускулярные и волновые свойства частиц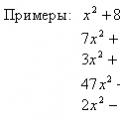 Уравнения онлайн X 5 0 решение
Уравнения онлайн X 5 0 решение Предельные монокарбоновые кислоты
Предельные монокарбоновые кислоты