7 oppgaveprofilnivå. Unified State Examination-oppgaver i spesialisert matematikk - hva du bør være oppmerksom på
I oppgave nr. 7 i profilen Unified State Exam-nivå i matematikk er det nødvendig å demonstrere kunnskap om funksjonene deriverte og antideriverte. I de fleste tilfeller er det tilstrekkelig å bare definere begrepene og forstå betydningen av derivatet.
Analyse av typiske alternativer for oppgave nr. 7 i Unified State Examination i matematikk på profilnivå
Første versjon av oppgaven (demoversjon 2018)
Figuren viser grafen til den differensierbare funksjonen y = f(x). Ni punkter er markert på abscisseaksen: x 1, x 2, ..., x 9. Blant disse punktene, finn alle punktene der den deriverte av funksjonen y = f(x) er negativ. I svaret ditt angir du antall poeng funnet.
Løsningsalgoritme:
- La oss se på grafen til funksjonen.
- Vi ser etter punkter der funksjonen avtar.
- La oss telle tallet deres.
- Vi skriver ned svaret.
Løsning:
1. På grafen øker og minker funksjonen periodisk.
2. I de intervallene hvor funksjonen avtar, har den deriverte negative verdier.
3. Disse intervallene inneholder poeng x 3 , x 4 , x 5 , x 9. Det er 4 slike punkter.
Andre versjon av oppgaven (fra Yashchenko, nr. 4)
Figuren viser en graf av funksjonen y = f(x). Punktene -2, -1, 2, 4 er markert på abscisseaksen Ved hvilket av disse punktene er verdien av den deriverte størst? Vennligst angi dette punktet i svaret ditt.

Løsningsalgoritme:
- La oss se på grafen til funksjonen.
- Vi vurderer oppførselen til funksjonen ved hvert av punktene og tegnet til den deriverte ved dem.
- Vi finner poengene ved den største verdien av den deriverte.
- Vi skriver ned svaret.
Løsning:
1. Funksjonen har flere intervaller med avtagende og økende.
2. Hvor funksjonen avtar. Den deriverte har et minustegn. Slike punkter er blant de som er angitt. Men det er punkter på grafen hvor funksjonen øker. I dem er den deriverte positiv. Dette er punktene med abscisse -2 og 2.
3. Betrakt grafen ved punkter med x=-2 og x=2. I punktet x=2 går funksjonen brattere opp, noe som betyr at tangenten på dette punktet har en større helning. Derfor, på punktet med abscisse 2. Den deriverte har høyeste verdi.
Tredje versjon av oppgaven (fra Yashchenko, nr. 21)
Linjen er tangent til grafen til funksjonen ![]() . Finn en.
. Finn en.
Løsningsalgoritme:
- La oss sette likhetstegn mellom tangent- og funksjonslikningene.
- La oss forenkle den resulterende likheten.
- Vi finner diskriminanten.
- Definere parameteren EN, som det bare finnes én løsning for.
- Vi skriver ned svaret.
Løsning:
1. Koordinatene til tangentpunktet tilfredsstiller begge ligningene: tangent og funksjon. Derfor kan vi sette likhetstegn mellom likningene. Vi får:
2. Vi forenkler likheten ved å flytte alle termer til én side:
![]()
3. Det må være én løsning ved tangenspunktet, så diskriminanten til den resulterende ligningen må være lik null. Dette er betingelsen for rotens unikhet andregradsligning.
4. Vi får:

Det er ingen endringer ved Unified State Exam i matematikk på profilnivå i 2019 – eksamensprogrammet er som tidligere år satt sammen av materialer fra de matematiske hoveddisiplinene. Billettene vil inneholde matematiske, geometriske og algebraiske problemer.
Det er ingen endringer i KIM Unified State Exam 2019 i matematikk på profilnivå.
Funksjoner ved Unified State Examination-oppgaver i matematikk 2019
- Når du forbereder deg til Unified State Exam i matematikk (profil), vær oppmerksom på de grunnleggende kravene til eksamensprogrammet. Den er designet for å teste kunnskap om et dybdeprogram: vektor og matematiske modeller, funksjoner og logaritmer, algebraiske ligninger og ulikheter.
- Separat, tren på å løse problemer i .
- Det er viktig å vise nytenkning.
Eksamensstruktur
Unified State Exam-oppgaver spesialisert matematikk delt i to blokker.
- Del - korte svar, inkluderer 8 oppgaver som tester grunnleggende matematisk forberedelse og evnen til å anvende matematikkkunnskaper i hverdagen.
- Del - kort og detaljerte svar. Den består av 11 oppgaver, hvorav 4 krever et kort svar, og 7 - en detaljert med argumenter for utførte handlinger.
- Avansert vanskelighetsgrad- oppgave 9-17 i andre del av KIM.
- Høy vanskelighetsgrad- oppgaver 18-19 –. Denne delen eksamensoppgaver kontrollerer ikke bare nivået på matematisk kunnskap, men også tilstedeværelse eller fravær kreativ tilnærming til å løse tørre «tall»-oppgaver, samt effektiviteten av evnen til å bruke kunnskap og ferdigheter som et profesjonelt verktøy.
Viktig! Derfor, som forberedelse til Unified State Exam-teori I matematikk, støtt dem alltid ved å løse praktiske problemer.
Hvordan vil poeng fordeles?
Oppgavene til første del av KIM i matematikk ligger tett på Unified State Exam tester grunnleggende nivå, Det er derfor høy poengsum Det er umulig å ringe på dem.
Poengene for hver oppgave i matematikk på profilnivå ble fordelt slik:
- for riktige svar på oppgave nr. 1-12 - 1 poeng;
- nr. 13-15 – 2 stk;
- nr. 16-17 – 3 stk;
- nr. 18-19 – 4 stk.
Varighet av eksamen og oppførselsregler for Unified State Exam
For å fullføre eksamensoppgaven -2019 eleven er tildelt 3 timer 55 minutter(235 minutter).
I løpet av denne tiden skal studenten ikke:
- oppføre seg støyende;
- bruke dingser og annet tekniske midler;
- avskrive;
- prøv å hjelpe andre, eller be om hjelp for deg selv.
For slike handlinger kan eksaminanden bli bortvist fra klasserommet.
På statlig eksamen i matematikk lov å ta med Ta bare med deg en linjal; resten av materialet vil bli gitt til deg rett før Unified State-eksamenen. utstedes på stedet.
Effektiv forberedelse– dette er løsningen online tester i matematikk 2019. Velg og få maksimal poengsum!
Lær å oppdage grammatiske feil. Hvis du lærer å gjenkjenne dem trygt i en oppgave, vil du ikke miste poeng i essayet. (Kriterium 9 - "Overholdelse språknormer".) I tillegg krever en oppgave som du kan få 5 poeng for en spesiell holdning!
Oppgave 7 Unified State-eksamen på russisk
Oppgaveformulering: Etabler en samsvar mellom grammatiske feil og setningene de ble laget i: for hver posisjon i den første kolonnen, velg den tilsvarende posisjonen fra den andre kolonnen.
| Grammatikkfeil | tilbud |
| A) brudd i konstruksjonen av en setning med en deltakende setning B) feil i konstruksjonen av en kompleks setning C) krenkelse i konstruksjonen av en setning med en inkonsekvent anvendelse D) forstyrrelse av forbindelsen mellom subjekt og predikat D) brudd på aspektuell-tidsmessig korrelasjon av verbformer |
1) I.S. Turgenev utsetter Bazarov for den vanskeligste testen - "kjærlighetens prøve" - og avslørte dermed den sanne essensen av helten hans.2) Alle som besøkte Krim tok ham med seg etter å ha skilt seg med ham levende inntrykk om hav, fjell, sørlandsurter og blomster. 3) Verket «The Tale of a Real Man» er basert på virkelige hendelser det skjedde med Alexey Maresyev. 4) S. Mikhalkov hevdet at verden til kjøpmannen Zamoskvorechye kan sees på scenen til Maly Theatre takket være den utmerkede skuespillet til skuespillerne. 5) I 1885 V.D. Polenov stilte ut nittisju skisser hentet fra en reise til østen på en vandreutstilling. 6) Teori om veltalenhet for alle kjønn poetiske verk skrevet av A.I. Galich, som underviste i russisk og latinsk litteratur ved Tsarskoye Selo Lyceum. 7) I I. Mashkovs landskap "Utsikt over Moskva" er det en følelse av den klingende skjønnheten til en bygate. 8) Lykkelige er de som er ute etter lang reise med kulde og slaps ser han et kjent hus og hører stemmene til slektninger. 9) Lesing klassisk litteratur, legger du merke til hvor annerledes "byen Petrov" er avbildet i verkene til A.S. Pushkina, N.V. Gogol, F.M. Dostojevskij. |
Skriv ned de valgte tallene i tabellen under de tilsvarende bokstavene.
Hvordan fullføre en slik oppgave? Det er bedre å starte fra venstre side. Finn det navngitte syntaktiske fenomenet (partisipiell frase, subjekt og predikat osv.) i setningene til høyre og se etter en grammatisk feil. Start med de som er lettere å finne og identifisere.
La oss se på typiske grammatiske feil i den rekkefølgen de skal sjekkes på eksamen.
Inkonsekvent applikasjon
Et inkonsekvent vedlegg er tittelen på en bok, et blad, en film, et bilde, etc., omgitt av anførselstegn.
Endringer etter store og små bokstaver i en setning generisk ord, og inkonsekvent applikasjon koster inn innledende form og endres ikke: V roman"Krig og fred"; bilde Levitan "Golden Autumn" på stasjonen Tverskaya t-banestasjon.
Hvis det ikke er noe generisk ord i setningen, endres selve applikasjonen fra tilfelle: helter fra "Krig og fred"; jeg ser på " Gylden høst» Levitan, møt meg på Tverskaya.
grammatisk feil : i romanen "Krig og fred"; i maleriet "Golden Autumn", på Tverskoy metrostasjon.
I oppgaven oppsto en slik feil i setning 3.
Direkte og indirekte tale.
Tilby med indirekte tale er en kompleks setning. Sammenligne:
Konduktøren sa: "Jeg skal bringe deg te" - Konduktøren sa at han ville gi oss te. Grammatikkfeil: Konduktøren sa at jeg skal gi deg te.(Det personlige pronomenet må endres.)
Passasjeren spurte: "Kan jeg åpne vinduet?" - Passasjeren spurte om han kunne åpne vinduet. grammatisk feil : Passasjeren spurte om han kunne åpne vinduet.(Setningen inneholder LI som en konjunksjon; konjunksjonen THAT er ikke tillatt i en setning.)
Deltakende setning
Vi finner setninger med en delsetningsfrase og ser om det er noen feil i konstruksjonen.
1. Inne deltakende setning Det definerte (hoved)ordet kan ikke inkluderes, det kan komme før eller etter det. Grammatikkfeil: de som kom tilskuere til et møte med direktøren. Høyre: tilskuere som kom for å møte regissøren eller tilskuere som kom for å møte regissøren.
2. Partisippet må i kjønn, tall og kasus stemme overens med hovedordet, som er bestemt av betydning og etter spørsmål: innbyggere fjell (hvilke?), skremt av en orkan eller innbyggere fjell(hvilke?), bevokst med grantrær. Grammatikkfeil: innbyggere i fjell som er skremt av en orkan eller innbyggere i fjellene, bevokst med grantrær.
Vennligst merk: en av hendelsene som skjedde i fjor sommer(vi er enig i partisippet med ordet EN - vi snakker om om en hendelse). Jeg husker en rekke hendelser som skjedde i fjor sommer (vi stiller spørsmålet fra EVENTS "hvilke?").
3. Partisippet har en presens ( eleven husker en regel), preteritum ( elev som lærte regelen utenat), men det er ingen fremtidig tid ( eleven husker en regel– grammatisk feil).
I oppgaven oppsto en slik feil i setning 5.
Deltakende setning
Huske: Partisippet navngir tilleggshandlingen, og predikatverbet navngir hovedhandlingen. Gerund og predikatverb må referere til samme tegn!
Vi finner subjektet i setningen og sjekker om det utfører en handling som kalles gerund. Da Natasha Rostova gikk til den første ballen, hadde naturlig spenning. Vi begrunner: begeistring oppsto - Natasha Rostova gikk- annerledes tegn. Riktig alternativ: Da hun gikk til det første ballet, opplevde Natasha Rostova naturlig spenning.
I en bestemt personlig setning er det lett å gjenopprette emnet: JEG, VI, DU, DU: Når du gir et tilbud, vurder(Du) grammatisk betydning ord. Vi begrunner: du tar hensyn til Og du gjør opp- det er ingen feil.
Predikatverbet kan uttrykkes infinitiv: Når du skriver en setning, må du ta hensyn til den grammatiske betydningen av ordet.
Vi begrunner: Etter å ha lest setningen ser det ut til at det ikke er noen feil. ME kan ikke være subjektet, siden det ikke er i den opprinnelige formen. Denne setningen har en grammatisk feil.
Den grammatiske sammenhengen mellom subjekt og predikat.
Feilen kan være skjult i komplekse setninger bygget i henhold til modellen “DE SOM …”, “ALLE SOM …”, “ALLE SOM …”, “INGEN AV DE SOM …”, “MANGE AV DE SOM …”, “ EN AV DE SOM..." I hver enkel setning et kompleks vil ha sitt eget emne, du må sjekke om de stemmer overens med predikatene deres. HVEM, ALLE, INGEN, EN, er kombinert med predikater i entall; DE, ALLE, MANGE er kombinert med sine predikater i flertall.
La oss analysere forslaget: Ingen av de som var innom der om sommeren ble skuffet. INGEN VAR – grammatisk feil. HVEM HAR BESØKT – det er ingen feil. De som ikke kom på åpningen av utstillingen angret. DE ANGRET – det var ingen feil. HVEM KOM IKKE - grammatisk feil.
I oppgaven oppsto en slik feil i setning 2.
Brudd på type-temporal korrelasjon av verbformer.
Vennligst betal spesiell oppmerksomhet på predikatverb: feil bruk av verbtid fører til forvirring i handlingsrekkefølgen. Jeg jobber uoppmerksomt, med jevne mellomrom, og som et resultat gjorde jeg mange latterlige feil. La oss fikse feilen: Jeg jobber uoppmerksomt, med jevne mellomrom, og som et resultat gjør jeg mange latterlige feil.(Begge verb Ikke perfekt form er i nåtid.) Jeg jobbet uoppmerksomt, med jevne mellomrom, og som et resultat gjorde jeg mange latterlige feil.(Begge verbene er i preteritum, det første verbet - imperfektivt - indikerer prosessen, det andre - perfektivt - indikerer resultatet.)
I oppgaven oppsto følgende feil i setning 1: Turgenev avslører og avslører...
Homogene medlemmer av setningen
Grammatiske feil i setninger med konjunksjoner OG.
- Union OG kan ikke koble et av medlemmene i en setning med hele setningen. Jeg liker ikke å bli syk og når jeg får dårlig karakter. Moskva er en by som var fødestedet til Pushkin og beskrevet i detalj av ham. Da Onegin kom tilbake til St. Petersburg og etter å ha møtt Tatyana, kjente han henne ikke igjen. Hørte et foredrag om viktigheten av idrett og hvorfor trenger de å gjøre det?. (La oss rette feilen: Hørte på et foredrag om viktigheten av idrett og fordelene med idrettsaktiviteter. Eller: Hørte et foredrag om hva er viktigheten av sport Og hvorfor trenger de å gjøre det? .)
- Union OG kan ikke koble homogene medlemmer uttrykt av komplett og kort form adjektiv og partisipp: Han er høy og tynn. Hun er smart og vakker.
- Union OG kan ikke koble en infinitiv og et substantiv: Jeg elsker å vaske, lage mat og lese bøker. (Høyre: Jeg liker å vaske, lage mat og lese bøker.)
- Det er vanskelig å gjenkjenne en feil i slikt syntaktisk konstruksjon: Decembrists elsket og beundret det russiske folket. I denne setningen refererer tillegget PEOPLE til begge predikatene, men er grammatisk forbundet med bare ett av dem: BEundret (AV HVEM?) FOLKET. Fra verbet LOVED stiller vi spørsmålet HVEM? Sørg for å stille et spørsmål fra hvert predikatverb til objektet. Her typiske feil: foreldre bryr seg og elsker barn; Jeg forstår og sympatiserer med deg; han studerte og brukte regelen; Jeg elsker og er stolt av sønnen min.Å korrigere en slik feil krever å introdusere forskjellige tillegg, hver vil være i samsvar med sitt eget predikatverb: Jeg elsker sønnen min og er stolt av ham.
Bruke sammensatte konjunksjoner.
- Lær å gjenkjenne følgende konjunksjoner i en setning: "IKKE BARE..., MEN OGSÅ"; "SOM ..., SÅ OG." I disse fagforeningene kan du ikke gå glipp av individuelle ord eller erstatte dem med andre: Ikke bare oss, men også gjestene våre ble overrasket. Atmosfæren fra epoken i komedie skapes ikke bare av skuespillerne, men også av karakterer utenfor scenen. Arbeidet er i full gang både på dagtid og natt.
- Deler av en dobbel konjunksjon må være umiddelbart foran hvert av de homogene medlemmene . Feil ordrekkefølge fører til en grammatisk feil: Vi undersøkte ikke bare den eldgamle delen byer, men besøkte også nye områder.(Riktig rekkefølge: Vi så oss ikke bare rundt, men besøkte også...)I essayet trenger du hva med hovedpersonene, fortell meg det O kunstneriske trekk . (Riktig rekkefølge: Essayet må fortelle hva med hovedpersonene, og om kunstneriske trekk. )
Generalisere ord med homogene termer
Det generaliserende ordet og de homogene medlemmene som følger det er i samme tilfelle: Spill to idretter:(hvordan?) ski og svømming.(Grammatikkfeil: Sterke mennesker har to egenskaper: vennlighet og beskjedenhet.)
Preposisjoner med homogene medlemmer
Preposisjoner før homogene medlemmer kan utelates bare hvis disse preposisjonene er de samme: Han besøkte V Hellas, Spania, Italia, på Kypros. Grammatikkfeil: Han besøkte V Hellas, Spania, Italia, Kypros.
Kompleks setning
Feil knyttet til feil bruk av konjunksjoner, allierte ord og demonstrasjonsord er svært vanlige. Det kan være mange mulige feil, la oss se på noen av dem.
Ekstra konjunksjon: Jeg ble plaget av spørsmålet om jeg skulle fortelle faren min alt. Jeg skjønte ikke hvor langt fra sannheten jeg var.
En blanding av kreativ og underordnede konjunksjoner: Da Murka ble lei av å rote med kattungene, og hun gikk et sted for å sove.
Ekstra partikkel VIL: Jeg trenger at han kommer til meg.
Manglende indeksord: Din feil er at du har det for travelt.(Savnet I VOL.)
Konjunktivordet SOM er revet av fra ordet som defineres: Varmt regn fuktet jorda, som plantene så trengte.(Høyre: Varm regn der planter trengte, fuktet jorda.)
I oppgaven ble det gjort en slik feil i setning 9.
Misbruke saksskjema substantiv med preposisjon
1. Preposisjoner TAKK, IFØLGE, MOTTSATT, KONTRAST, I KONTRAST, LIKELY + substantiv i DATIV-KASSEN: takket være dyktighetenyu , i henhold til timeplanenyu , i strid med regleneer .
- Preposisjonen PÅ kan brukes til å bety "ETTER". I dette tilfellet er substantivet i preposisjonell kasus og har en slutt OG: ved eksamen (etter eksamen), ved ankomst til byen (etter ankomst), ved utløp av perioden (etter utløp av semester).
Huske: ved ankomst OG, ved ferdigstillelse OG, ved ferdigstillelse OG, ved utløp OG, ved ankomst E, ved ankomst E.
- Vi husker administrasjonsfunksjonene i følgende setninger:
Bevis (hva?) rett
Beundre (hva?) tålmodighet
Gi et eksempel på (hva?) en feil
Oppsummer (hva?) arbeidet
Tilstå (hva?) for en forbrytelse
Frøken, vær trist (for hvem?) for deg
Vær oppmerksom på (hva?) småting
Påpeke (hvilke?) mangler
Skyld på (hva?) for grådighet
La oss huske parene:
Bekymre deg for sønnen din - bekymre deg for sønnen din
Tro på seier - tillit til seier
Spørsmål om konstruksjon - problemer med konstruksjon
Tjen leieinntekter – motta leieinntekter
Uvitenhet om problemet - ukjenthet med problemet
Å bli fornærmet av mistillit - å bli fornærmet av mistillit
Ta hensyn til helse – ta hensyn til helse
Opptatt av business - bekymre deg for business
Betal for reise - betal for reise
Tilbakemelding på et essay – gjennomgang av et essay
Serviceavgift – betaling for service
Overlegenhet over ham - fordel over ham
Varsle om fare - varsle om fare
Skille mellom venner og fiender - skille venner fra fiender
Overrasket av tålmodighet - overrasket av tålmodighet
Karakteristisk for ham - iboende i ham
Figuren viser en graf av den deriverte av funksjonen f(x), definert på intervallet [–5; 6]. Finn antall punkter på grafen til f(x), hvor tangenten trukket til grafen til funksjonen sammenfaller med eller er parallell med x-aksen
Figuren viser en graf av den deriverte av den differensierbare funksjonen y = f(x).
Finn antall punkter på funksjonsgrafen som tilhører segmentet [–7; 7], der tangenten til grafen til funksjonen er parallell med den rette linjen spesifisert av ligningen y = –3x.

Materialpunkt M begynner å bevege seg fra punkt A og beveger seg i en rett linje i 12 sekunder. Grafen viser hvordan avstanden fra punkt A til punkt M endret seg over tid. Abscisseaksen viser tiden t i sekunder, og ordinataksen viser avstanden s i meter. Bestem hvor mange ganger i løpet av bevegelsen hastigheten til punkt M snudde til null (ikke ta hensyn til begynnelsen og slutten av bevegelsen).

Figuren viser utsnitt av grafen til funksjonen y=f(x) og tangenten til denne i punktet med abscissen x = 0. Det er kjent at denne tangenten er parallell med linjen som går gjennom punktene i grafen med abscissen x = -2 og x = 3. Bruk denne, finn verdien av den deriverte f"(o).

Figuren viser en graf av y = f’(x) - den deriverte av funksjonen f(x), definert på segmentet (−11; 2). Finn abscissen til punktet der tangenten til grafen til funksjonen y = f(x) er parallell med eller sammenfaller med abscissen.

Et materialpunkt beveger seg rettlinjet i henhold til loven x(t)=(1/3)t^3-3t^2-5t+3, der x er avstanden fra referansepunktet i meter, t er tiden i sekunder, målt fra begynnelsen av bevegelsen. På hvilket tidspunkt (i sekunder) var hastigheten lik 2 m/s?
Et materialpunkt beveger seg langs en rett linje fra den opprinnelige til den endelige posisjonen. Figuren viser en graf over bevegelsen. Abscisseaksen viser tid i sekunder, og ordinataksen viser avstanden fra punktets startposisjon (i meter). Finne gjennomsnittlig hastighet punktbevegelse. Gi svaret ditt i meter per sekund.

Funksjonen y = f (x) er definert på intervallet [-4; 4]. Figuren viser en graf av dens deriverte. Finn antall punkter på grafen til funksjonen y = f (x), tangenten som danner en vinkel på 45° med den positive retningen til Ox-aksen.

Funksjonen y = f (x) er definert på intervallet [-2; 4]. Figuren viser en graf av dens deriverte. Finn abscissen til punktet i grafen til funksjonen y = f (x), der den tar minste verdi på segmentet [-2; -0,001].

Figuren viser en graf for funksjonen y = f(x) og en tangent til denne grafen tegnet i punktet x0. Tangenten er gitt av ligningen y = -2x + 15. Finn verdien av den deriverte av funksjonen y = -(1/4)f(x) + 5 i punktet x0.

På grafen til den differensierbare funksjonen y = f (x) er syv punkter markert: x1,.., x7. Finn alle markerte punkter der den deriverte av funksjonen f(x) større enn null. Angi antallet av disse punktene i svaret ditt.

Figuren viser en graf y = f"(x) av den deriverte av funksjonen f(x), definert på intervallet (-10; 2). Finn antall punkter der tangenten til grafen til funksjonen f (x) er parallell med den rette linjen y = -2x-11 eller sammenfaller med den.

Figuren viser en graf av y=f"(x) - den deriverte av funksjonen f(x). Det er ni punkter markert på abscisseaksen: x1, x2, x3, x4, x5, x6, x6, x7, x8, x9.
Hvor mange av disse punktene tilhører intervallene for avtagende funksjon f(x)?

Figuren viser en graf for funksjonen y = f(x) og en tangent til denne grafen tegnet i punktet x0. Tangenten er gitt ved ligningen y = 1,5x + 3,5. Finn verdien av den deriverte av funksjonen y = 2f(x) - 1 i punktet x0.

Figuren viser grafen y=F(x) til en av antiderivative funksjoner f(x). Det er seks punkter markert på grafen med abscisse x1, x2, ..., x6. Ved hvor mange av disse punktene tar funksjonen y=f(x) negative verdier?

Figuren viser en graf over bilen som beveger seg langs ruten. Abscisseaksen viser tid (i timer), og ordinataksen viser tilbakelagt avstand (i kilometer). Finn gjennomsnittshastigheten til bilen på denne ruten. Gi svaret i km/t

Et materialpunkt beveger seg rettlinjet i henhold til loven x(t)=(-1/6)t^3+7t^2+6t+1, der x er avstanden fra referansepunktet (i meter), t er tiden bevegelse (i sekunder). Finn hastigheten (i meter per sekund) til tiden t=6 s
Figuren viser en graf av antideriverten y = F(x) til en funksjon y = f(x), definert på intervallet (-6; 7). Bruk figuren til å bestemme antall nuller for funksjonen f(x) på dette intervallet.

Figuren viser en graf av y = F(x) for en av antiderivatene til en funksjon f(x), definert på intervallet (-7; 5). Bruk figuren til å bestemme antall løsninger til ligningen f(x) = 0 på intervallet [- 5; 2].

Figuren viser grafen til den differensierbare funksjonen y=f(x). Det er ni punkter markert på x-aksen: x1, x2, ... x9. Finn alle markerte punkter der den deriverte av funksjonen f(x) er negativ. Angi antallet av disse punktene i svaret ditt.

Et materialpunkt beveger seg rettlinjet i henhold til loven x(t)=12t^3−3t^2+2t, der x er avstanden fra referansepunktet i meter, t er tiden i sekunder målt fra begynnelsen av bevegelsen. Finn hastigheten (i meter per sekund) til tiden t=6 s.
Figuren viser en graf for funksjonen y=f(x) og en tangent til denne grafen tegnet i punktet x0. Tangentligningen er vist i figuren. finn verdien av den deriverte av funksjonen y=4*f(x)-3 i punktet x0.
Gjennomsnittlig generell utdanning
UMK linje G.K. Muravina. Algebra og begynnelse matematisk analyse(10-11) (dypende)
UMK Merzlyak linje. Algebra og begynnelsen av analyse (10-11) (U)
Matematikk
Forberedelse til Unified State-eksamen i matematikk (profilnivå): oppgaver, løsninger og forklaringer
Vi analyserer oppgaver og løser eksempler sammen med lærerenEksamensoppgave profilnivå varer 3 timer 55 minutter (235 minutter).
Minimum terskel– 27 poeng.
Eksamensoppgaven består av to deler, som er forskjellige i innhold, kompleksitet og antall oppgaver.
Det definerende trekk ved hver del av arbeidet er formen på oppgavene:
- del 1 inneholder 8 oppgaver (oppgave 1-8) med et kort svar i form av et helt tall eller en siste desimalbrøk;
- del 2 inneholder 4 oppgaver (oppgave 9-12) med et kort svar i form av et heltall eller en siste desimalbrøk og 7 oppgaver (oppgave 13–19) med et detaljert svar (en fullstendig oversikt over løsningen med begrunnelse for tiltak iverksatt).
Panova Svetlana Anatolevna, matematikklærer høyeste kategori skoler, arbeidserfaring 20 år:
"For å få skolebevis, må kandidaten bestå to obligatorisk eksamen V Unified State Examination-skjema, hvorav en er matematikk. I samsvar med utviklingskonseptet matematikkundervisning V Den russiske føderasjonen Unified State Examination i matematikk er delt inn i to nivåer: grunnleggende og spesialisert. I dag skal vi se på alternativer på profilnivå."
Oppgave nr. 1- tester Unified State Examination-deltakernes evne til å anvende ferdighetene som er oppnådd i løpet av klasse 5 - 9 i elementær matematikk, i praktiske aktiviteter. Deltakeren må ha datakunnskaper, kunne arbeide med rasjonelle tall, kunne runde desimaler, kunne konvertere en måleenhet til en annen.
Eksempel 1. Det ble installert en strømningsmåler i leiligheten der Peter bor kaldt vann(disk). 1. mai viste måleren et forbruk på 172 kubikkmeter. m vann, og den første juni - 177 kubikkmeter. m. Hvor mye bør Peter betale for kaldt vann i mai, hvis prisen er 1 kubikkmeter? m kaldt vann er 34 rubler 17 kopek? Gi svaret ditt i rubler.
Løsning:
1) Finn mengden vann som brukes per måned:
177 - 172 = 5 (kubikkm)
2) La oss finne ut hvor mye penger de vil betale for bortkastet vann:
34,17 5 = 170,85 (gni)
Svare: 170,85.
Oppgave nr. 2- er en av de enkleste eksamensoppgavene. Flertallet av nyutdannede takler det med hell, noe som indikerer kunnskap om definisjonen av funksjonsbegrepet. Type oppgave nr. 2 i henhold til kravkodifisereren er en oppgave om bruk av tilegnet kunnskap og ferdigheter i praktiske aktiviteter og hverdagen. Oppgave nr. 2 består i å beskrive, bruke funksjoner, ulike reelle sammenhenger mellom størrelser og tolke deres grafer. Oppgave nr. 2 tester evnen til å trekke ut informasjon presentert i tabeller, diagrammer og grafer. Nyutdannede må kunne bestemme verdien av en funksjon fra verdien av argumentet når på ulike måter spesifisere en funksjon og beskrive funksjonen og egenskapene til funksjonen basert på grafen. Du må også kunne finne den største eller minste verdien fra en funksjonsgraf og bygge grafer av de studerte funksjonene. Feilene som er gjort er tilfeldig natur ved å lese betingelsene for problemet, lese diagrammet.
#ADVERTISING_INSERT#
Eksempel 2. Figuren viser endringen i bytteverdien til én aksje i et gruveselskap i første halvdel av april 2017. 7. april kjøpte forretningsmannen 1000 aksjer i dette selskapet. 10. april solgte han tre fjerdedeler av aksjene han kjøpte, og 13. april solgte han alle de resterende aksjene. Hvor mye tapte forretningsmannen som følge av disse operasjonene?

Løsning:
2) 1000 · 3/4 = 750 (aksjer) - utgjør 3/4 av alle kjøpte aksjer.
6) 247500 + 77500 = 325000 (gni) - forretningsmannen mottok 1000 aksjer etter salg.
7) 340 000 – 325 000 = 15 000 (gni) - forretningsmannen tapte som et resultat av alle operasjoner.
Svare: 15000.
Oppgave nr. 3- er en oppgave på grunnleggende nivå i første del, tester evnen til å utføre handlinger med geometriske former om innholdet i kurset «Planimetri». Oppgave 3 tester evnen til å beregne arealet til en figur på rutete papir, evnen til å beregne gradstiltak vinkler, beregne omkrets osv.
Eksempel 3. Finn arealet til et rektangel tegnet på rutepapir med en cellestørrelse på 1 cm x 1 cm (se figur). Gi svaret i kvadratcentimeter.

Løsning: For å beregne arealet til en gitt figur kan du bruke toppformelen:
For å beregne arealet til et gitt rektangel bruker vi Peaks formel:
|
S= B + |
G | |
| 2 |
|
S = 18 + |
6 | |
| 2 |

Les også: Unified State Exam in Physics: løse problemer om svingninger
Oppgave nr. 4- Målet med kurset "Sannsynlighetsteori og statistikk". Evnen til å beregne sannsynligheten for en hendelse i den enkleste situasjonen testes.
Eksempel 4. Det er 5 røde og 1 blå prikker merket på sirkelen. Bestem hvilke polygoner som er større: de med alle toppunktene røde, eller de med en av toppunktene blå. I svaret ditt, angi hvor mange det er flere av noen enn andre.
Løsning: 1) La oss bruke formelen for antall kombinasjoner av n elementer av k:
hvis toppunkter alle er røde.
3) En femkant med alle hjørner røde.
4) 10 + 5 + 1 = 16 polygoner med alle røde hjørner.
som har røde topper eller med én blå topp.
som har røde topper eller med én blå topp.
8) En sekskant med røde topper og en blå topp.
9) 20 + 15 + 6 + 1 = 42 polygoner med alle toppunkter røde eller med ett blått toppunkt.
10) 42 – 16 = 26 polygoner med den blå prikken.
11) 26 – 16 = 10 polygoner – hvor mange flere polygoner der en av toppunktene er en blå prikk er det enn polygoner der alle toppunktene bare er røde.
Svare: 10.
Oppgave nr. 5- det grunnleggende nivået i første del tester evnen til å løse de enkleste ligningene (irrasjonelle, eksponentielle, trigonometriske, logaritmiske).
Eksempel 5. Løs ligning 2 3 + x= 0,4 5 3 + x .
Løsning. La oss skille begge deler gitt ligning med 5 3 + X≠ 0, får vi
| 2 3 + x | = 0,4 eller | 2 | 3 + X | = | 2 | , | ||
| 5 3 + X | 5 | 5 |
hvorfra det følger at 3 + x = 1, x = –2.
Svare: –2.
Oppgave nr. 6 i planimetri for å finne geometriske størrelser (lengder, vinkler, arealer), modellering reelle situasjoner på geometriens språk. Studie av de konstruerte modellene vha geometriske konsepter og teoremer. Kilden til vanskeligheter er som regel uvitenhet eller feilaktig anvendelse av de nødvendige planimetrisetningene.
Arealet av en trekant ABC tilsvarer 129. DE– midtlinje, parallelt med siden AB. Finn arealet av trapesen ABED.

Løsning. Triangel CDE ligner på en trekant CAB i to vinkler, siden vinkelen ved toppunktet C generelt, vinkel СDE lik vinkel CAB som de tilsvarende vinklene ved DE || AB sekant A.C.. Fordi DE– midtlinjen i trekanten etter tilstand, deretter etter egenskap midtlinje | DE = (1/2)AB. Dette betyr at likhetskoeffisienten er 0,5. Arealene med lignende figurer er derfor relatert til kvadratet av likhetskoeffisienten
Derfor, S ABED = S Δ ABC – S Δ CDE = 129 – 32,25 = 96,75.
Oppgave nr. 7- kontrollerer anvendelsen av den deriverte til studiet av en funksjon. Vellykket implementering krever meningsfull, ikke-formell kunnskap om begrepet derivat.
Eksempel 7. Til grafen til funksjonen y = f(x) ved abscissepunktet x 0 tegnes en tangent som er vinkelrett på linjen som går gjennom punktene (4; 3) og (3; –1) i denne grafen. Finne f′( x 0).
Løsning. 1) La oss bruke ligningen til en rett linje som går gjennom to gitt poeng og finn ligningen til den rette linjen som går gjennom punktene (4; 3) og (3; –1).
(y – y 1)(x 2 – x 1) = (x – x 1)(y 2 – y 1)
(y – 3)(3 – 4) = (x – 4)(–1 – 3)
(y – 3)(–1) = (x – 4)(–4)
–y + 3 = –4x+ 16| · (–1)
y – 3 = 4x – 16
y = 4x– 13, hvor k 1 = 4.
2) Finn hellingen til tangenten k 2, som er vinkelrett på linjen y = 4x– 13, hvor k 1 = 4, i henhold til formelen:
3) Helningsfaktor tangent – derivert av funksjonen ved tangenspunktet. Betyr, f′( x 0) = k 2 = –0,25.
Svare: –0,25.
Oppgave nr. 8- tester eksamensdeltakernes kunnskap om elementær stereometri, evnen til å bruke formler for å finne overflatearealer og volumer av figurer, dihedrale vinkler, sammenligne volumene til lignende figurer, kunne utføre handlinger med geometriske figurer, koordinater og vektorer, etc.
Volumet til en terning som er omskrevet rundt en kule er 216. Finn radiusen til kulen.

Løsning. 1) V kube = en 3 (hvor EN– lengden på kanten av kuben), derfor
EN 3 = 216
EN = 3 √216
2) Siden kulen er innskrevet i en kube, betyr det at lengden på kulens diameter er lik lengden på kanten av kuben, derfor d = en, d = 6, d = 2R, R = 6: 2 = 3.
Oppgave nr. 9- krever at kandidaten har ferdigheter til å transformere og forenkle algebraiske uttrykk. Oppgave nr. 9 høyere nivå Vanskeligheter med et kort svar. Oppgavene fra delen "Beregninger og transformasjoner" i Unified State-eksamenen er delt inn i flere typer:
- konvertere numeriske/bokstav trigonometriske uttrykk.
numeriske konverteringer rasjonelle uttrykk;
konvertering av algebraiske uttrykk og brøker;
numeriske/bokstavkonverteringer irrasjonelle uttrykk;
handlinger med grader;
transformasjon logaritmiske uttrykk;
Eksempel 9. Beregn tanα hvis det er kjent at cos2α = 0,6 og
| 3π | < α < π. |
| 4 |
Løsning. 1) La oss bruke dobbeltargumentformelen: cos2α = 2 cos 2 α – 1 og finne
| tan 2 α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos 2 α | 0,8 | 8 | 4 | 4 | 4 |
Dette betyr tan 2 α = ± 0,5.
3) Etter tilstand
| 3π | < α < π, |
| 4 |
dette betyr at α er vinkelen til andre kvartal og tgα< 0, поэтому tgα = –0,5.
Svare: –0,5.
#ADVERTISING_INSERT# Oppgave nr. 10- tester elevenes evne til å bruke tilegnet tidlig kunnskap og ferdigheter i praktiske aktiviteter og hverdagsliv. Vi kan si at dette er problemer i fysikk, og ikke i matematikk, men alle nødvendige formler og verdiene er gitt i tilstanden. Problemene koker ned til å løse en lineær eller andregradsligning, eller lineær eller kvadratisk ulikhet. Derfor er det nødvendig å kunne løse slike likninger og ulikheter og bestemme svaret. Svaret må gis som et helt tall eller en endelig desimalbrøk.
To massekropper m= 2 kg hver, beveger seg med samme hastighet v= 10 m/s i en vinkel på 2α til hverandre. Energien (i joule) som frigjøres under deres absolutt uelastiske kollisjon, bestemmes av uttrykket Q = mv 2 sin 2 α. Ved hvilken minste vinkel 2α (i grader) må kroppene bevege seg slik at minst 50 joule frigjøres som følge av kollisjonen?
Løsning. For å løse problemet må vi løse ulikheten Q ≥ 50, på intervallet 2α ∈ (0°; 180°).
mv 2 sin 2 α ≥ 50
2 10 2 sin 2 α ≥ 50
200 sin 2 α ≥ 50
Siden α ∈ (0°; 90°), vil vi bare løse
La oss representere løsningen på ulikheten grafisk:

Siden betingelse α ∈ (0°; 90°), betyr det 30° ≤ α< 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.
Oppgave nr. 11– er typisk, men viser seg å være vanskelig for elevene. Hovedkilden til vanskeligheter er konstruksjonen av en matematisk modell (tegne opp en ligning). Oppgave nr. 11 tester evnen til å løse ordoppgaver.
Eksempel 11. I løpet av vårpausen måtte 11.-klassingen Vasya løse 560 øvingsproblemer for å forberede seg til Unified State-eksamenen. Den 18. mars, på siste skoledag, løste Vasya 5 problemer. Så hver dag løste han like mange problemer mer enn dagen før. Bestem hvor mange problemer Vasya løste 2. april, den siste dagen i ferien.
Løsning: La oss betegne en 1 = 5 – antall problemer som Vasya løste 18. mars, d– daglig antall oppgaver løst av Vasya, n= 16 – antall dager fra 18. mars til og med 2. april, S 16 = 560 – total mengde oppgaver, en 16 – antall problemer som Vasya løste 2. april. Når vi vet at Vasya hver dag løste samme antall problemer mer enn dagen før, kan vi bruke formler for å finne summen aritmetisk progresjon:560 = (5 + en 16) 8,
5 + en 16 = 560: 8,
5 + en 16 = 70,
en 16 = 70 – 5
en 16 = 65.
Svare: 65.
Oppgave nr. 12- teste elevenes evne til å utføre operasjoner med funksjoner, for å kunne bruke den deriverte til studiet av en funksjon.
Finn maksimumspunktet for funksjonen y= 10ln( x + 9) – 10x + 1.
Løsning: 1) Finn definisjonsdomenet til funksjonen: x + 9 > 0, x> –9, det vil si x ∈ (–9; ∞).
2) Finn den deriverte av funksjonen:
4) Det funnet punktet tilhører intervallet (–9; ∞). La oss bestemme tegnene på den deriverte av funksjonen og skildre funksjonen til funksjonen i figuren:

Ønsket maksimumspunkt x = –8.
Last ned gratis arbeidsprogrammet i matematikk for linjen med undervisningsmateriell G.K. Muravina, K.S. Muravina, O.V. Muravina 10-11 Last ned gratis læremidler i algebraOppgave nr. 13-økt kompleksitetsnivå med et detaljert svar, testing av evnen til å løse ligninger, den mest vellykkede løst blant oppgaver med et detaljert svar av økt kompleksitetsnivå.
a) Løs ligningen 2log 3 2 (2cos x) – 5log 3 (2cos x) + 2 = 0
b) Finn alle røttene til denne ligningen som tilhører segmentet.
Løsning: a) La logg 3 (2cos x) = t, deretter 2 t 2 – 5t + 2 = 0,
|
|
log 3(2cos x) = | 2 | ⇔ |
|
2cos x = 9 | ⇔ |
|
cos x = | 4,5 | ⇔ fordi |cos x| ≤ 1, |
| log 3(2cos x) = | 1 | 2cos x = √3 | cos x = | √3 | ||||||
| 2 | 2 |
| deretter cos x = | √3 |
| 2 |
|
|
x = | π | + 2π k |
| 6 | |||
| x = – | π | + 2π k, k ∈ Z | |
| 6 |
b) Finn røttene som ligger på segmentet .

Av figuren er det tydelig at gitt segment røtter tilhører
| 11π | Og | 13π | . |
| 6 | 6 |
| Svare: EN) | π | + 2π k; – | π | + 2π k, k ∈ Z; b) | 11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Diameteren på sirkelen til sylinderens basis er 20, sylinderens generatrise er 28. Planet skjærer bunnen langs akkorder med lengde 12 og 16. Avstanden mellom akkordene er 2√197.
a) Bevis at sentrene til sylinderens base ligger på den ene siden av dette planet.
b) Finn vinkelen mellom dette planet og planet til bunnen av sylinderen.
Løsning: a) En korde med lengde 12 er i en avstand = 8 fra midten av grunnsirkelen, og en korde med lengde 16 er på samme måte i en avstand på 6. Derfor er avstanden mellom deres projeksjoner på et plan parallelt med basene på sylindrene er enten 8 + 6 = 14, eller 8 - 6 = 2.

Da er avstanden mellom akkordene enten
= = √980 = = 2√245
= = √788 = = 2√197.
I henhold til betingelsen ble det andre tilfellet realisert, der fremspringene til akkordene ligger på den ene siden av sylinderaksen. Dette betyr at aksen ikke skjærer dette planet i sylinderen, det vil si at basene ligger på den ene siden av den. Det som måtte bevises.
b) La oss betegne sentrene til basene som O 1 og O 2. La oss tegne fra midten av basen med en akkord med lengde 12 vinkelrett halveringslinje til denne akkorden (den har lengde 8, som allerede nevnt) og fra midten av den andre basen - til den andre akkorden. De ligger i samme plan β, vinkelrett på disse akkordene. La oss kalle midtpunktet til den mindre akkorden B, den større akkorden A og projeksjonen av A på den andre basen - H (H ∈ β). Da er AB,AH ∈ β og derfor AB,AH vinkelrett på akkorden, det vil si den rette skjæringslinjen mellom basen og det gitte planet.
Dette betyr at den nødvendige vinkelen er lik
| ∠ABH = arktan | A.H. | = arktan | 28 | = arctg14. |
| B.H. | 8 – 6 |
Oppgave nr. 15- økt kompleksitetsnivå med detaljert svar, tester evnen til å løse ulikheter, som mest vellykket løses blant oppgaver med detaljert svar av økt kompleksitetsnivå.
Eksempel 15. Løs ulikhet | x 2 – 3x| logg 2 ( x + 1) ≤ 3x – x 2 .
Løsning: Definisjonsdomenet for denne ulikheten er intervallet (–1; +∞). Vurder tre tilfeller separat:
1) La x 2 – 3x= 0, dvs. X= 0 eller X= 3. I dette tilfellet blir denne ulikheten sann, derfor er disse verdiene inkludert i løsningen.
2) La nå x 2 – 3x> 0, dvs. x∈ (–1; 0) ∪ (3; +∞). Dessuten kan denne ulikheten omskrives som ( x 2 – 3x) logg 2 ( x + 1) ≤ 3x – x 2 og del med et positivt uttrykk x 2 – 3x. Vi får logg 2 ( x + 1) ≤ –1, x + 1 ≤ 2 –1 , x≤ 0,5 –1 eller x≤ –0,5. Med tanke på definisjonsdomenet har vi x ∈ (–1; –0,5].
3) Til slutt, vurder x 2 – 3x < 0, при этом x∈ (0; 3). I dette tilfellet vil den opprinnelige ulikheten skrives om i formen (3 x – x 2) logg 2 ( x + 1) ≤ 3x – x 2. Etter å ha delt på positive 3 x – x 2, vi får logg 2 ( x + 1) ≤ 1, x + 1 ≤ 2, x≤ 1. Med hensyn til regionen har vi x ∈ (0; 1].
Ved å kombinere de oppnådde løsningene får vi x ∈ (–1; –0.5] ∪ ∪ {3}.
Svare: (–1; –0.5] ∪ ∪ {3}.
Oppgave nr. 16- avansert nivå refererer til oppgaver i andre del med et detaljert svar. Oppgaven tester evnen til å utføre handlinger med geometriske former, koordinater og vektorer. Oppgaven inneholder to punkter. I det første punktet skal oppgaven bevises, og i det andre punktet beregnes.
I likebenet trekant ABC med en vinkel på 120° ved toppunkt A tegnes en halveringslinje BD. I trekant ABC rektangel DEFH er innskrevet slik at side FH ligger på segment BC, og toppunkt E ligger på segment AB. a) Bevis at FH = 2DH. b) Finn arealet av rektangelet DEFH hvis AB = 4.
Løsning: EN)

1) ΔBEF – rektangulær, EF⊥BC, ∠B = (180° – 120°): 2 = 30°, så EF = BE ved egenskapen til benet som ligger motsatt vinkelen på 30°.
2) La EF = DH = x, så BE = 2 x, BF = x√3 ifølge Pythagoras teorem.
3) Siden ΔABC er likebenet, betyr det ∠B = ∠C = 30˚.
BD er halveringslinjen til ∠B, som betyr ∠ABD = ∠DBC = 15˚.
4) Tenk på ΔDBH – rektangulær, fordi DH⊥BC.
| 2x | = | 4 – 2x |
| 2x(√3 + 1) | 4 |
| 1 | = | 2 – x |
| √3 + 1 | 2 |
√3 – 1 = 2 – x
x = 3 – √3
EF = 3 – √3
2) S DEFH = ED EF = (3 – √3 ) 2(3 – √3 )
S DEFH = 24 – 12√3.
Svare: 24 – 12√3.
Oppgave nr. 17- en oppgave med et detaljert svar, denne oppgaven tester anvendelsen av kunnskap og ferdigheter i praktiske aktiviteter og hverdagsliv, evnen til å bygge og utforske matematiske modeller. Denne oppgaven er ordproblem med økonomisk innhold.
Eksempel 17. Et depositum på 20 millioner rubler er planlagt åpnet i fire år. Ved utgangen av hvert år øker banken innskuddet med 10 % sammenlignet med størrelsen ved inngangen til året. I tillegg, i begynnelsen av det tredje og fjerde året, fyller investoren årlig på innskuddet med X millioner rubler, hvor X - hel tall. Finn den største verdien X, der banken vil påløpe mindre enn 17 millioner rubler til innskuddet over fire år.
Løsning: På slutten av det første året vil bidraget være 20 + 20 · 0,1 = 22 millioner rubler, og på slutten av det andre - 22 + 22 · 0,1 = 24,2 millioner rubler. Ved begynnelsen av det tredje året vil bidraget (i millioner rubler) være (24,2 + X), og på slutten - (24,2 + X) + (24,2 + X)· 0,1 = (26,62 + 1,1 X). Ved begynnelsen av det fjerde året vil bidraget være (26,62 + 2,1 X), og på slutten - (26.62 + 2.1 X) + (26,62 + 2,1X) · 0,1 = (29,282 + 2,31 X). Etter betingelse må du finne det største heltall x som ulikheten gjelder for
(29,282 + 2,31x) – 20 – 2x < 17
29,282 + 2,31x – 20 – 2x < 17
0,31x < 17 + 20 – 29,282
0,31x < 7,718
| x < | 7718 |
| 310 |
| x < | 3859 |
| 155 |
| x < 24 | 139 |
| 155 |
Den største heltallsløsningen på denne ulikheten er tallet 24.
Svare: 24.
Oppgave nr. 18- en oppgave med økt kompleksitet med et detaljert svar. Denne oppgaven er for konkurransedyktig utvalg til universiteter med økte krav til matematisk forberedelse av søkere. Øvelse høyt nivå kompleksitet - denne oppgaven handler ikke om å bruke én løsningsmetode, men om en kombinasjon ulike metoder. For å fullføre oppgave 18 trenger du i tillegg til solide matematiske kunnskaper også et høyt nivå av matematisk kultur.
På hva en system av ulikheter
| x 2 + y 2 ≤ 2ja – en 2 + 1 | |
| y + en ≤ |x| – en |
har nøyaktig to løsninger?
Løsning: Dette systemet kan skrives om i skjemaet
| x 2 + (y– en) 2 ≤ 1 | |
| y ≤ |x| – en |
Hvis vi tegner på planet settet med løsninger til den første ulikheten, får vi det indre av en sirkel (med en grense) med radius 1 med sentrum i punktet (0, EN). Settet med løsninger til den andre ulikheten er den delen av planet som ligger under grafen til funksjonen y = |
x| –
en,
og sistnevnte er grafen til funksjonen
y = |
x|
, flyttet ned av EN. Løsningen på dette systemet er skjæringspunktet mellom settene med løsninger på hver av ulikhetene.
Derfor to løsninger dette systemet vil bare ha i tilfellet vist i fig. 1.

Kontaktpunktene til sirkelen med linjene vil være de to løsningene til systemet. Hver av de rette linjene er skråstilt til aksene i en vinkel på 45°. Så det er en trekant PQR– rektangulære likebenete. Prikk Q har koordinater (0, EN), og poenget R– koordinater (0, – EN). I tillegg kommer segmentene PR Og PQ lik radiusen til sirkelen lik 1. Dette betyr
| Qr= 2en = √2, en = | √2 | . |
| 2 |
| Svare: en = | √2 | . |
| 2 |
Oppgave nr. 19- en oppgave med økt kompleksitet med et detaljert svar. Denne oppgaven er ment for konkurransedyktig utvelgelse til universiteter med økte krav til matematisk forberedelse av søkere. En oppgave med høy kompleksitet er en oppgave ikke på bruk av én løsningsmetode, men på en kombinasjon av ulike metoder. For å fullføre oppgave 19 må du kunne søke etter en løsning ved å velge ulike tilnærminger blant de kjente, modifisere de studerte metodene.
La Sn sum n termer av en aritmetisk progresjon ( en s). Det er kjent at S n + 1 = 2n 2 – 21n – 23.
a) Oppgi formelen n termin av denne progresjonen.
b) Finn den minste absolutte summen S n.
c) Finn den minste n, hvorpå S n vil være kvadratet av et heltall.
Løsning: a) Det er åpenbart at en n = S n – S n– 1. Bruker denne formelen, vi får:
S n = S (n – 1) + 1 = 2(n – 1) 2 – 21(n – 1) – 23 = 2n 2 – 25n,
S n – 1 = S (n – 2) + 1 = 2(n – 1) 2 – 21(n – 2) – 23 = 2n 2 – 25n+ 27
Betyr, en n = 2n 2 – 25n – (2n 2 – 29n + 27) = 4n – 27.
B) Siden S n = 2n 2 – 25n, og vurder deretter funksjonen S(x) = | 2x 2 – 25x|. Grafen kan sees på figuren.

Det er klart at den minste verdien oppnås ved heltallspunktene som ligger nærmest nullpunktene til funksjonen. Dette er åpenbart poeng X= 1, X= 12 og X= 13. Siden, S(1) = |S 1 | = |2 – 25| = 23, S(12) = |S 12 | = |2 · 144 – 25 · 12| = 12, S(13) = |S 13 | = |2 · 169 – 25 · 13| = 13, så er den minste verdien 12.
c) Av forrige avsnitt følger det at Sn positiv, med utgangspunkt i n= 13. Siden S n = 2n 2 – 25n = n(2n– 25), så blir det åpenbare tilfellet, når dette uttrykket er et perfekt kvadrat, realisert når n = 2n– 25, altså kl n= 25.
Det gjenstår å sjekke verdiene fra 13 til 25:
S 13 = 13 1, S 14 = 14 3, S 15 = 15 5, S 16 = 16 7, S 17 = 17 9, S 18 = 18 11, S 19 = 19 13, S 20 = 20 13, S 21 = 21 17, S 22 = 22 19, S 23 = 23 21, S 24 = 24 23.
Det viser seg at for mindre verdier n perfekt firkant er ikke oppnådd.
Svare: EN) en n = 4n– 27; b) 12; c) 25.
________________
*Siden mai 2017 har den forente forlagsgruppen "DROFA-VENTANA" vært en del av selskapet " Russisk lærebok" Selskapet inkluderte også Astrel forlag og digital pedagogisk plattform"LECTA". Generaldirektør Alexander Brychkin, utdannet ved Finansakademiet under regjeringen i den russiske føderasjonen, kandidat økonomiske vitenskaper, veileder innovative prosjekter forlag «DROFA» på feltet digital utdanning(elektroniske former for lærebøker, "Russian Electronic School", digital utdanningsplattform LECTA). Før han begynte i DROFA forlag, hadde han stillingen som visepresident for strategisk utvikling og investeringer i forlagsselskapet EKSMO-AST. I dag har Russian Textbook Publishing Corporation den største porteføljen av lærebøker inkludert i den føderale listen - 485 titler (omtrent 40 %, unntatt lærebøker for kriminalomsorgsskolen). Selskapets forlag eier de mest populære Russiske skoler sett med lærebøker om fysikk, tegning, biologi, kjemi, teknologi, geografi, astronomi - kunnskapsområder som trengs for utvikling av landets produktive potensial. Selskapets portefølje inkluderer lærebøker og læremidler Til grunnskole, tildelt presidentprisen innen utdanning. Dette er lærebøker og manualer på fagområder, som er nødvendige for utviklingen av Russlands vitenskapelige, tekniske og produksjonspotensiale.
 Logaritmiske ligninger
Logaritmiske ligninger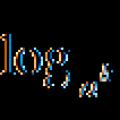 Teknikk for å løse logaritmiske ligninger
Teknikk for å løse logaritmiske ligninger Selvanalyse av logopedlærer
Selvanalyse av logopedlærer