Formel for å finne summen av tall i en aritmetisk progresjon. Aritmetisk progresjon
Hvis for hvert naturlig tall n samsvarer med et reelt tall en n , så sier de at det er gitt nummerrekkefølge :
en 1 , en 2 , en 3 , . . . , en n , . . . .
Så tallsekvensen er en funksjon av det naturlige argumentet.
Tall en 1 ringte første ledd i sekvensen , nummer en 2 — andre ledd i sekvensen , nummer en 3 — tredje og så videre. Tall en n ringte nte medlem av sekvensen , og et naturlig tall n — nummeret hans .
Fra to tilstøtende medlemmer en n Og en n +1 sekvensmedlem en n +1 ringte senere (i forhold til en n ), A en n — tidligere (i forhold til en n +1 ).
For å definere en sekvens, må du spesifisere en metode som lar deg finne et medlem av sekvensen med et hvilket som helst tall.
Ofte er sekvensen spesifisert vha nth term formler , det vil si en formel som lar deg bestemme et medlem av en sekvens etter nummeret.
For eksempel
en sekvens med positive oddetall kan gis av formelen
en n= 2n- 1,
og sekvensen av alternerende 1 Og -1 - formel
b n = (-1)n +1 . ◄
Rekkefølgen kan bestemmes tilbakevendende formel, det vil si en formel som uttrykker et hvilket som helst medlem av sekvensen, starter med noen, gjennom de forrige (ett eller flere) medlemmene.
For eksempel
Hvis en 1 = 1 , A en n +1 = en n + 5
en 1 = 1,
en 2 = en 1 + 5 = 1 + 5 = 6,
en 3 = en 2 + 5 = 6 + 5 = 11,
en 4 = en 3 + 5 = 11 + 5 = 16,
en 5 = en 4 + 5 = 16 + 5 = 21.
Hvis en 1= 1, en 2 = 1, en n +2 = en n + en n +1 , deretter etableres de første syv leddene i den numeriske sekvensen som følger:
en 1 = 1,
en 2 = 1,
en 3 = en 1 + en 2 = 1 + 1 = 2,
en 4 = en 2 + en 3 = 1 + 2 = 3,
en 5 = en 3 + en 4 = 2 + 3 = 5,
en 6 = en 4 + en 5 = 3 + 5 = 8,
en 7 = en 5 + en 6 = 5 + 8 = 13. ◄
Sekvenser kan være endelig Og endeløs .
Sekvensen kalles endelig , hvis den har et begrenset antall medlemmer. Sekvensen kalles endeløs , hvis den har uendelig mange medlemmer.
For eksempel
rekkefølge av tosifrede naturlige tall:
10, 11, 12, 13, . . . , 98, 99
endelig.
Rekkefølge av primtall:
2, 3, 5, 7, 11, 13, . . .
endeløs. ◄
Sekvensen kalles økende , hvis hvert av medlemmene, fra det andre, er større enn det forrige.
Sekvensen kalles avtagende , hvis hvert av medlemmene, fra det andre, er mindre enn det forrige.
For eksempel
2, 4, 6, 8, . . . , 2n, . . . — økende sekvens;
1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 /n, . . . — avtagende sekvens. ◄
En sekvens hvis elementer ikke reduseres når antallet øker, eller omvendt ikke øker, kalles monoton sekvens .
Monotoniske sekvenser, spesielt, er økende sekvenser og avtagende sekvenser.
Aritmetisk progresjon
Aritmetisk progresjon er en sekvens der hvert medlem, fra det andre, er lik det forrige, som det samme tallet er lagt til.
en 1 , en 2 , en 3 , . . . , en n, . . .
er en aritmetisk progresjon hvis for et hvilket som helst naturlig tall n betingelsen er oppfylt:
en n +1 = en n + d,
Hvor d - et visst antall.
Dermed er forskjellen mellom de påfølgende og forrige leddene til en gitt aritmetisk progresjon alltid konstant:
en 2 - en 1 = en 3 - en 2 = . . . = en n +1 - en n = d.
Tall d ringte forskjell i aritmetisk progresjon.
For å definere en aritmetisk progresjon er det nok å indikere dens første ledd og forskjell.
For eksempel
Hvis en 1 = 3, d = 4 , så finner vi de første fem leddene i sekvensen som følger:
en 1 =3,
en 2 = en 1 + d = 3 + 4 = 7,
en 3 = en 2 + d= 7 + 4 = 11,
en 4 = en 3 + d= 11 + 4 = 15,
en 5 = en 4 + d= 15 + 4 = 19. ◄
For en aritmetisk progresjon med første ledd en 1 og forskjellen d henne n
en n = en 1 + (n- 1)d.
For eksempel
finn det trettiende leddet i den aritmetiske progresjonen
1, 4, 7, 10, . . .
en 1 =1, d = 3,
en 30 = en 1 + (30 - 1)d = 1 + 29· 3 = 88. ◄
en n-1 = en 1 + (n- 2)d,
en n= en 1 + (n- 1)d,
en n +1 = en 1 + nd,
da åpenbart
| en n=
| a n-1 + a n+1
|
| 2
|
Hvert medlem av en aritmetisk progresjon, fra den andre, er lik det aritmetiske gjennomsnittet av de foregående og påfølgende medlemmene.
tallene a, b og c er suksessive ledd for en eller annen aritmetisk progresjon hvis og bare hvis en av dem er lik det aritmetiske gjennomsnittet av de to andre.
For eksempel
en n = 2n- 7 , er en aritmetisk progresjon.
La oss bruke uttalelsen ovenfor. Vi har:
en n = 2n- 7,
en n-1 = 2(n- 1) - 7 = 2n- 9,
en n+1 = 2(n+ 1) - 7 = 2n- 5.
Derfor,
| a n+1 + a n-1
| =
| 2n- 5 + 2n- 9
| = 2n- 7 = en n,
|
| 2
| 2
|
◄
Merk at n Det tredje leddet i en aritmetisk progresjon kan ikke bare finnes gjennom en 1 , men også alle tidligere en k
en n = en k + (n- k)d.
For eksempel
Til en 5 kan skrives ned
en 5 = en 1 + 4d,
en 5 = en 2 + 3d,
en 5 = en 3 + 2d,
en 5 = en 4 + d. ◄
en n = en n-k + kd,
en n = a n+k - kd,
da åpenbart
| en n=
| en n-k
+ a n+k
|
| 2
|
ethvert medlem av en aritmetisk progresjon, fra den andre, er lik halvparten av summen av de like fordelte medlemmene av denne aritmetiske progresjonen.
I tillegg, for enhver aritmetisk progresjon gjelder følgende likhet:
a m + a n = a k + a l,
m + n = k + l.
For eksempel
i aritmetisk progresjon
1) en 10 = 28 = (25 + 31)/2 = (en 9 + en 11 )/2;
2) 28 = en 10 = en 3 + 7d= 7 + 7 3 = 7 + 21 = 28;
3) en 10= 28 = (19 + 37)/2 = (en 7 + en 13)/2;
4) a 2 + a 12 = a 5 + a 9, fordi
en 2 + en 12= 4 + 34 = 38,
en 5 + en 9 = 13 + 25 = 38. ◄
S n= a 1 + a 2 + a 3 + . . .+ en n,
først n ledd av en aritmetisk progresjon er lik produktet av halvparten av summen av ekstremleddene og antall ledd:
Herfra, spesielt, følger det at hvis du trenger å summere vilkårene
en k, en k +1 , . . . , en n,
da beholder den forrige formelen sin struktur:
For eksempel
i aritmetisk progresjon 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
S 10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;
10 + 13 + 16 + 19 + 22 + 25 + 28 = S 10 - S 3 = (10 + 28 ) · (10 - 4 + 1)/2 = 133. ◄
Hvis en aritmetisk progresjon er gitt, så mengdene en 1 , en n, d, n OgS n koblet sammen med to formler:
Derfor, hvis verdiene til tre av disse mengdene er gitt, blir de tilsvarende verdiene til de to andre mengdene bestemt fra disse formlene, kombinert til et system med to ligninger med to ukjente.
En aritmetisk progresjon er en monoton sekvens. I dette tilfellet:
- Hvis d > 0 , da øker det;
- Hvis d < 0 , da er det minkende;
- Hvis d = 0 , da vil sekvensen være stasjonær.
Geometrisk progresjon
Geometrisk progresjon er en sekvens der hvert medlem, fra det andre, er lik det forrige multiplisert med det samme tallet.
b 1 , b 2 , b 3 , . . . , b n, . . .
er en geometrisk progresjon hvis for et hvilket som helst naturlig tall n betingelsen er oppfylt:
b n +1 = b n · q,
Hvor q ≠ 0 - et visst antall.
Dermed er forholdet mellom den påfølgende leddet til en gitt geometrisk progresjon og den forrige et konstant tall:
b 2 / b 1 = b 3 / b 2 = . . . = b n +1 / b n = q.
Tall q ringte nevner for geometrisk progresjon.
For å definere en geometrisk progresjon er det nok å indikere dens første ledd og nevner.
For eksempel
Hvis b 1 = 1, q = -3 , så finner vi de første fem leddene i sekvensen som følger:
b 1 = 1,
b 2 = b 1 · q = 1 · (-3) = -3,
b 3 = b 2 · q= -3 · (-3) = 9,
b 4 = b 3 · q= 9 · (-3) = -27,
b 5 = b 4 · q= -27 · (-3) = 81. ◄
b 1 og nevner q henne n Termen kan bli funnet ved å bruke formelen:
b n = b 1 · qn -1 .
For eksempel
finn det syvende leddet i den geometriske progresjonen 1, 2, 4, . . .
b 1 = 1, q = 2,
b 7 = b 1 · q 6 = 1 2 6 = 64. ◄
b n-1 = b 1 · qn -2 ,
b n = b 1 · qn -1 ,
b n +1 = b 1 · qn,
da åpenbart
b n 2 = b n -1 · b n +1 ,
hvert medlem av den geometriske progresjonen, fra den andre, er lik det geometriske gjennomsnittet (proporsjonal) av de foregående og etterfølgende elementene.
Siden det motsatte også er sant, gjelder følgende utsagn:
tallene a, b og c er suksessive ledd av en eller annen geometrisk progresjon hvis og bare hvis kvadratet til en av dem er lik produktet av de to andre, det vil si at ett av tallene er det geometriske gjennomsnittet av de to andre.
For eksempel
La oss bevise at sekvensen gitt av formelen b n= -3 2 n , er en geometrisk progresjon. La oss bruke uttalelsen ovenfor. Vi har:
b n= -3 2 n,
b n -1 = -3 2 n -1 ,
b n +1 = -3 2 n +1 .
Derfor,
b n 2 = (-3 2 n) 2 = (-3 2 n -1 ) · (-3 · 2 n +1 ) = b n -1 · b n +1 ,
som beviser ønsket utsagn. ◄
Merk at n Det tredje leddet i en geometrisk progresjon kan ikke bare finnes gjennom b 1 , men også et hvilket som helst tidligere medlem b k , som det er nok å bruke formelen for
b n = b k · qn - k.
For eksempel
Til b 5 kan skrives ned
b 5 = b 1 · q 4 ,
b 5 = b 2 · q 3,
b 5 = b 3 · q 2,
b 5 = b 4 · q. ◄
b n = b k · qn - k,
b n = b n - k · q k,
da åpenbart
b n 2 = b n - k· b n + k
kvadratet av ethvert ledd i en geometrisk progresjon, fra den andre, er lik produktet av leddene for denne progresjonen like langt fra den.
I tillegg, for enhver geometrisk progresjon er likheten sann:
b m· b n= b k· b l,
m+ n= k+ l.
For eksempel
i geometrisk progresjon
1) b 6 2 = 32 2 = 1024 = 16 · 64 = b 5 · b 7 ;
2) 1024 = b 11 = b 6 · q 5 = 32 · 2 5 = 1024;
3) b 6 2 = 32 2 = 1024 = 8 · 128 = b 4 · b 8 ;
4) b 2 · b 7 = b 4 · b 5 , fordi
b 2 · b 7 = 2 · 64 = 128,
b 4 · b 5 = 8 · 16 = 128. ◄
S n= b 1 + b 2 + b 3 + . . . + b n
først n medlemmer av en geometrisk progresjon med nevner q ≠ 0 beregnet med formelen:
Og når q = 1 - i henhold til formelen
S n= NB 1
Merk at hvis du trenger å summere vilkårene
b k, b k +1 , . . . , b n,
så brukes formelen:
| S n- S k -1 = b k + b k +1 + . . . + b n = b k · | 1 - qn -
k +1
| . |
| 1 - q
|
For eksempel
i geometrisk progresjon 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
S 10 = 1 + 2 + . . . + 512 = 1 · (1 - 2 10) / (1 - 2) = 1023;
64 + 128 + 256 + 512 = S 10 - S 6 = 64 · (1 - 2 10-7+1) / (1 - 2) = 960. ◄
Hvis en geometrisk progresjon er gitt, så mengdene b 1 , b n, q, n Og S n koblet sammen med to formler:
Derfor, hvis verdiene til tre av disse mengdene er gitt, bestemmes de tilsvarende verdiene til de to andre mengdene fra disse formlene, kombinert til et system med to ligninger med to ukjente.
For en geometrisk progresjon med første ledd b 1 og nevner q følgende finner sted egenskapene til monotonisitet :
- progresjonen øker hvis en av følgende betingelser er oppfylt:
b 1 > 0 Og q> 1;
b 1 < 0 Og 0 < q< 1;
- Progresjonen avtar hvis en av følgende betingelser er oppfylt:
b 1 > 0 Og 0 < q< 1;
b 1 < 0 Og q> 1.
Hvis q< 0 , så veksler den geometriske progresjonen: leddene med oddetall har samme fortegn som første ledd, og ledd med partall har motsatt fortegn. Det er klart at en vekslende geometrisk progresjon ikke er monoton.
Produktet av den første n termer for en geometrisk progresjon kan beregnes ved å bruke formelen:
Pn= b 1 · b 2 · b 3 · . . . · b n = (b 1 · b n) n / 2 .
For eksempel
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128) 8/2 = 128 4 = 268 435 456;
3 · 6 · 12 · 24 · 48 = (3 · 48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄
Uendelig avtagende geometrisk progresjon
Uendelig avtagende geometrisk progresjon kalt en uendelig geometrisk progresjon hvis nevnermodul er mindre 1 , altså
|q| < 1 .
Merk at en uendelig avtagende geometrisk progresjon kanskje ikke er en avtagende sekvens. Det passer til anledningen
1 < q< 0 .
Med en slik nevner er sekvensen vekslende. For eksempel
1, - 1 / 2 , 1 / 4 , - 1 / 8 , . . . .
Summen av en uendelig avtagende geometrisk progresjon navngi tallet som summen av de første nærmer seg uten grense n medlemmer av en progresjon med en ubegrenset økning i antall n . Dette tallet er alltid endelig og uttrykkes med formelen
| S= b 1 + b 2 + b 3 + . . . = | b 1
| . |
| 1 - q
|
For eksempel
10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 - 0,1) = 11 1 / 9 ,
10 - 1 + 0,1 - 0,01 + . . . = 10 / (1 + 0,1) = 9 1 / 11 . ◄
Sammenheng mellom aritmetiske og geometriske progresjoner
Aritmetiske og geometriske progresjoner er nært beslektet. La oss se på bare to eksempler.
en 1 , en 2 , en 3 , . . . d , Det
b a 1 , b a 2 , b a 3 , . . . b d .
For eksempel
1, 3, 5, . . . - aritmetisk progresjon med forskjell 2 Og
7 1 , 7 3 , 7 5 , . . . - geometrisk progresjon med nevner 7 2 . ◄
b 1 , b 2 , b 3 , . . . - geometrisk progresjon med nevner q , Det
logg a b 1, logg a b 2, logg a b 3, . . . - aritmetisk progresjon med forskjell logg aq .
For eksempel
2, 12, 72, . . . - geometrisk progresjon med nevner 6 Og
lg 2, lg 12, lg 72, . . . - aritmetisk progresjon med forskjell lg 6 . ◄
Inngangsnivå
Aritmetisk progresjon. Detaljert teori med eksempler (2019)
Nummerrekkefølge
Så la oss sette oss ned og begynne å skrive noen tall. For eksempel:
Du kan skrive alle tall, og det kan være så mange av dem du vil (i vårt tilfelle er det dem). Uansett hvor mange tall vi skriver, kan vi alltid si hvilket som er først, hvilket som er nummer to, og så videre til det siste, det vil si at vi kan nummerere dem. Dette er et eksempel på en tallsekvens:
Nummerrekkefølge
For eksempel for vår sekvens:
Det tildelte nummeret er spesifikt for bare ett nummer i sekvensen. Det er med andre ord ingen tre sekunders tall i sekvensen. Det andre tallet (som det th tallet) er alltid det samme.
Tallet med tall kalles det ste leddet i sekvensen.
Vi kaller vanligvis hele sekvensen med en bokstav (for eksempel), og hvert medlem av denne sekvensen er den samme bokstaven med en indeks som er lik nummeret til dette medlemmet: .
I vårt tilfelle: 
La oss si at vi har en tallrekke der forskjellen mellom tilstøtende tall er den samme og lik.
For eksempel: 
osv.
Denne tallsekvensen kalles en aritmetisk progresjon.
Begrepet "progresjon" ble introdusert av den romerske forfatteren Boethius tilbake på 600-tallet og ble forstått i bredere forstand som en uendelig numerisk rekkefølge. Navnet "aritmetikk" ble overført fra teorien om kontinuerlige proporsjoner, som ble studert av de gamle grekerne.
Dette er en tallsekvens, hvor hvert medlem er lik den forrige lagt til det samme tallet. Dette tallet kalles forskjellen til en aritmetisk progresjon og er utpekt.
Prøv å finne ut hvilke tallsekvenser som er en aritmetisk progresjon og hvilke som ikke er det:
en)
b)
c)
d)
Har du det? La oss sammenligne svarene våre:
Er aritmetisk progresjon - b, c.
er ikke aritmetisk progresjon - a, d.
La oss gå tilbake til den gitte progresjonen () og prøve å finne verdien av dets tredje ledd. Finnes to måte å finne det på.
1. Metode
Vi kan legge til progresjonstallet til den forrige verdien til vi når den tredje ledd av progresjonen. Det er bra at vi ikke har så mye å oppsummere - bare tre verdier:
Så det tredje leddet i den beskrevne aritmetiske progresjonen er lik.
2. Metode
Hva om vi trengte å finne verdien av det tredje leddet i progresjonen? Summeringen ville tatt oss mer enn én time, og det er ikke et faktum at vi ikke ville gjort feil når vi legger til tall.
Selvfølgelig har matematikere kommet opp med en måte der det ikke er nødvendig å legge forskjellen til en aritmetisk progresjon til den forrige verdien. Ta en nærmere titt på det tegnede bildet... Du har sikkert allerede lagt merke til et bestemt mønster, nemlig:
La oss for eksempel se hva verdien av det tredje leddet i denne aritmetiske progresjonen består av: 
Med andre ord:
Prøv å finne verdien av et medlem av en gitt aritmetisk progresjon selv på denne måten.
Har du regnet ut? Sammenlign notatene dine med svaret:
Vær oppmerksom på at du fikk nøyaktig samme tall som i den forrige metoden, da vi sekvensielt la til vilkårene for den aritmetiske progresjonen til den forrige verdien.
La oss prøve å "depersonalisere" denne formelen - la oss sette den i generell form og få:
|
Aritmetisk progresjonsligning. |
Aritmetiske progresjoner kan være økende eller avtagende.
Økende- progresjoner der hver påfølgende verdi av begrepene er større enn den forrige.
For eksempel:
Synkende- progresjoner der hver påfølgende verdi av vilkårene er mindre enn den forrige.
For eksempel:
Den utledede formelen brukes i beregningen av ledd i både økende og avtagende termer for en aritmetisk progresjon.
La oss sjekke dette i praksis.
Vi får en aritmetisk progresjon som består av følgende tall: La oss sjekke hva tallet i denne aritmetiske progresjonen vil være hvis vi bruker formelen vår til å beregne den:

Siden da:
Dermed er vi overbevist om at formelen fungerer i både avtagende og økende aritmetisk progresjon.
Prøv å finne de th og th leddene i denne aritmetiske progresjonen selv.
La oss sammenligne resultatene:
Aritmetisk progresjonsegenskap
La oss komplisere problemet - vi vil utlede egenskapen til aritmetisk progresjon.
La oss si at vi får følgende betingelse:
- aritmetisk progresjon, finn verdien.
Lett, sier du og begynner å telle etter formelen du allerede kjenner:
La, ah, da:
Helt sant. Det viser seg at vi først finner, så legger vi det til det første tallet og får det vi leter etter. Hvis progresjonen er representert av små verdier, så er det ikke noe komplisert med det, men hva om vi får tall i tilstanden? Enig, det er en mulighet for å gjøre feil i beregningene.
Tenk nå på om det er mulig å løse dette problemet i ett trinn ved å bruke en formel? Selvfølgelig ja, og det er det vi skal prøve å få frem nå.
La oss betegne det nødvendige leddet for den aritmetiske progresjonen som formelen for å finne den er kjent for oss - dette er den samme formelen vi avledet i begynnelsen:
, Deretter:
- forrige termin av progresjonen er:
- neste termin i progresjonen er:
La oss oppsummere de forrige og påfølgende betingelsene for progresjonen:
Det viser seg at summen av de forrige og påfølgende leddene i progresjonen er den doble verdien av progresjonsleddet som ligger mellom dem. Med andre ord, for å finne verdien av et progresjonsledd med kjente tidligere og påfølgende verdier, må du legge dem til og dele med.
Det stemmer, vi har samme nummer. La oss sikre materialet. Beregn verdien for progresjonen selv, det er slett ikke vanskelig.
Godt gjort! Du vet nesten alt om progresjon! Det gjenstår å finne ut bare én formel, som ifølge legenden lett ble utledet av en av tidenes største matematikere, "matematikernes konge" - Karl Gauss ...
Da Carl Gauss var 9 år gammel, spurte en lærer, opptatt med å sjekke arbeidet til elevene i andre klasser, følgende oppgave i klassen: "Regn ut summen av alle naturlige tall fra til (ifølge andre kilder til) inklusive." Se for deg lærerens overraskelse da en av elevene hans (dette var Karl Gauss) et minutt senere ga riktig svar på oppgaven, mens de fleste av våghalsens klassekamerater, etter lange utregninger, fikk feil resultat...
Unge Carl Gauss la merke til et bestemt mønster som du også lett kan legge merke til.
La oss si at vi har en aritmetisk progresjon som består av -th ledd: Vi må finne summen av disse leddene av den aritmetiske progresjonen. Selvfølgelig kan vi manuelt summere alle verdiene, men hva om oppgaven krever å finne summen av termene, slik Gauss lette etter?
La oss skildre progresjonen gitt til oss. Ta en nærmere titt på de uthevede tallene og prøv å utføre ulike matematiske operasjoner med dem. 
Har du prøvd det? Hva la du merke til? Høyre! Summene deres er like

Si meg nå, hvor mange slike par er det totalt i progresjonen gitt til oss? Selvfølgelig, nøyaktig halvparten av alle tall, altså.
Basert på det faktum at summen av to ledd i en aritmetisk progresjon er lik, og like par er like, får vi at den totale summen er lik:
.
Dermed vil formelen for summen av de første leddene i enhver aritmetisk progresjon være:
I noen problemer kjenner vi ikke begrepet, men vi vet forskjellen på progresjonen. Prøv å erstatte formelen til det te leddet med sumformelen.
Hva fikk du?
Godt gjort! La oss nå gå tilbake til problemet som ble spurt til Carl Gauss: beregn selv hva summen av tall som starter fra th er lik og summen av tallene som starter fra th.
Hvor mye fikk du?
Gauss fant at summen av leddene er lik, og summen av leddene. Var det det du bestemte deg for?
Faktisk ble formelen for summen av vilkårene for en aritmetisk progresjon bevist av den antikke greske vitenskapsmannen Diophantus tilbake på 300-tallet, og gjennom denne tiden benyttet vittige mennesker egenskapene til den aritmetiske progresjonen til fulle.
Tenk deg for eksempel det gamle Egypt og datidens største byggeprosjekt - byggingen av en pyramide... Bildet viser den ene siden av den. 
Hvor er progresjonen her, sier du? Se nøye og finn et mønster i antall sandblokker i hver rad av pyramideveggen. 
Hvorfor ikke en aritmetisk progresjon? Regn ut hvor mange blokker som trengs for å bygge én vegg hvis blokkklosser er plassert ved basen. Jeg håper du ikke vil telle mens du beveger fingeren over skjermen, husker du den siste formelen og alt vi sa om aritmetisk progresjon?
I dette tilfellet ser progresjonen slik ut: .
Aritmetisk progresjonsforskjell.
Antall ledd i en aritmetisk progresjon.
La oss erstatte dataene våre i de siste formlene (beregn antall blokker på 2 måter).
Metode 1.
Metode 2.
Og nå kan du beregne på skjermen: sammenlign de oppnådde verdiene med antall blokker som er i pyramiden vår. Har du det? Godt gjort, du har mestret summen av de n-te leddene i en aritmetisk progresjon.
Selvfølgelig kan du ikke bygge en pyramide fra blokker ved basen, men fra? Prøv å beregne hvor mange sandklosser som trengs for å bygge en vegg med denne tilstanden.
Klarte du deg?
Riktig svar er blokker:
Opplæring
Oppgaver:
- Masha kommer i form til sommeren. Hver dag øker hun antall knebøy med. Hvor mange ganger vil Masha trene knebøy i løpet av en uke hvis hun gjorde knebøy på den første treningsøkten?
- Hva er summen av alle oddetall som finnes i.
- Ved lagring av tømmerstokker stabler loggere dem på en slik måte at hvert topplag inneholder én tømmerstokk mindre enn den forrige. Hvor mange stokker er det i ett murverk, hvis fundamentet til murverket er stokker?
Svar:
- La oss definere parametrene for den aritmetiske progresjonen. I dette tilfellet
(uker = dager).Svare: Om to uker bør Masha gjøre knebøy en gang om dagen.
- Første oddetall, siste tall.
Aritmetisk progresjonsforskjell.
Antall oddetall i er halvparten, la oss imidlertid sjekke dette faktum ved å bruke formelen for å finne det tredje leddet i en aritmetisk progresjon:Tall inneholder oddetall.
La oss erstatte de tilgjengelige dataene i formelen:Svare: Summen av alle oddetall i er lik.
- La oss huske problemet med pyramider. For vårt tilfelle, en , siden hvert topplag reduseres med en stokk, så er det totalt en haug med lag, altså.
La oss erstatte dataene i formelen:Svare: Det er stokker i murverket.
La oss oppsummere det
- - en tallsekvens der forskjellen mellom tilstøtende tall er lik og lik. Det kan være økende eller avtagende.
- Finne formel Det tredje leddet i en aritmetisk progresjon er skrevet med formelen - , hvor er antall tall i progresjonen.
- Eiendom til medlemmer av en aritmetisk progresjon- - hvor er antall tall i progresjon.
- Summen av leddene til en aritmetisk progresjon kan finnes på to måter:
, hvor er antall verdier.
ARITMETISK PROGRESJON. MIDDELNIVÅ
Nummerrekkefølge
La oss sette oss ned og begynne å skrive noen tall. For eksempel:
Du kan skrive alle tall, og det kan være så mange av dem du vil. Men vi kan alltid si hvilken som er først, hvilken som er nummer to, og så videre, det vil si at vi kan nummerere dem. Dette er et eksempel på en tallrekke.
Nummerrekkefølge er et sett med tall, som hver kan tildeles et unikt nummer.
Med andre ord kan hvert tall assosieres med et visst naturlig tall, og et unikt. Og vi vil ikke tildele dette nummeret til noe annet nummer fra dette settet.
Tallet med nummeret kalles det th medlem av sekvensen.
Vi kaller vanligvis hele sekvensen med en bokstav (for eksempel), og hvert medlem av denne sekvensen er den samme bokstaven med en indeks som er lik nummeret til dette medlemmet: .
Det er veldig praktisk hvis det tredje leddet i sekvensen kan spesifiseres med en formel. For eksempel formelen
setter sekvensen:
Og formelen er følgende sekvens:
For eksempel er en aritmetisk progresjon en sekvens (det første leddet her er likt, og forskjellen er det). Eller (, forskjell).
formel for n. ledd
Vi kaller en formel tilbakevendende der du, for å finne ut begrepet, må kjenne til de forrige eller flere tidligere:
For å finne for eksempel det tredje leddet i progresjonen ved å bruke denne formelen, må vi beregne de ni foregående. For eksempel, la det. Da:
Vel, er det klart nå hva formelen er?
I hver linje legger vi til, multiplisert med et eller annet tall. Hvilken? Veldig enkelt: dette er nummeret på gjeldende medlem minus:
Mye mer praktisk nå, ikke sant? Vi sjekker:
Bestem selv:
I en aritmetisk progresjon, finn formelen for det n'te leddet og finn det hundrede leddet.
Løsning:
Det første leddet er likt. Hva er forskjellen? Her er hva:
(Dette er grunnen til at det kalles forskjell fordi det er lik forskjellen mellom påfølgende ledd i progresjonen).
Så formelen:
Da er det hundrede leddet lik:
Hva er summen av alle naturlige tall fra til?
Ifølge legenden beregnet den store matematikeren Carl Gauss, som en 9 år gammel gutt, dette beløpet på noen få minutter. Han la merke til at summen av første og siste tall er lik, summen av andre og nest siste er den samme, summen av tredje og tredje fra slutten er den samme, og så videre. Hvor mange slike par er det totalt? Det stemmer, nøyaktig halvparten av alle tall, altså. Så,
Den generelle formelen for summen av de første leddene i enhver aritmetisk progresjon vil være:
Eksempel:
Finn summen av alle tosifrede multipler.
Løsning:
Det første slike nummer er dette. Hvert etterfølgende nummer oppnås ved å legge til det forrige nummeret. Dermed danner tallene vi er interessert i en aritmetisk progresjon med det første leddet og differansen.
Formel for begrepet for denne progresjonen:
Hvor mange ledd er det i progresjonen hvis de alle må være tosifrede?
Veldig enkelt:.
Den siste perioden av progresjonen vil være lik. Så summen:
Svar: .
Bestem nå selv:
- Hver dag løper utøveren flere meter enn dagen før. Hvor mange kilometer totalt vil han løpe i løpet av en uke hvis han løper km m den første dagen?
- En syklist reiser flere kilometer hver dag enn dagen før. Den første dagen reiste han km. Hvor mange dager trenger han å reise for å tilbakelegge en kilometer? Hvor mange kilometer vil han reise i løpet av den siste dagen av reisen?
- Prisen på kjøleskap i butikk synker like mye hvert år. Bestem hvor mye prisen på et kjøleskap falt hvert år hvis det ble lagt ut for salg for rubler seks år senere ble solgt for rubler.
Svar:
- Det viktigste her er å gjenkjenne den aritmetiske progresjonen og bestemme dens parametere. I dette tilfellet (uker = dager). Du må bestemme summen av de første leddene i denne progresjonen:
.
Svare: - Her er det gitt: , må finnes.
Selvfølgelig må du bruke samme sumformel som i forrige oppgave:
.
Bytt ut verdiene:Roten passer tydeligvis ikke, så svaret er.
La oss beregne banen som ble reist i løpet av den siste dagen ved å bruke formelen til begrepet:
(km).
Svare: - Gitt:. Finn: .
Det kunne ikke vært enklere:
(gni).
Svare:
ARITMETISK PROGRESJON. KORT OM HOVEDTINGENE
Dette er en tallsekvens der forskjellen mellom tilstøtende tall er den samme og lik.
Aritmetisk progresjon kan være økende () og avtagende ().
For eksempel:
Formel for å finne det n-te leddet i en aritmetisk progresjon
er skrevet av formelen, hvor er antall tall i progresjon.
Eiendom til medlemmer av en aritmetisk progresjon
Den lar deg enkelt finne et ledd i en progresjon hvis naboleddet er kjent - hvor er antallet tall i progresjonen.
Summen av ledd i en aritmetisk progresjon
Det er to måter å finne beløpet på:
Hvor er antall verdier.
Hvor er antall verdier.
Konseptet med en tallsekvens innebærer at hvert naturlig tall tilsvarer en eller annen reell verdi. En slik tallrekke kan enten være vilkårlig eller ha visse egenskaper - en progresjon. I sistnevnte tilfelle kan hvert påfølgende element (medlem) i sekvensen beregnes ved å bruke det forrige.
En aritmetisk progresjon er en sekvens av numeriske verdier der nabomedlemmene skiller seg fra hverandre med samme tall (alle elementer i serien, fra den andre, har en lignende egenskap). Dette tallet - forskjellen mellom forrige og påfølgende ledd - er konstant og kalles progresjonsforskjellen.
Progresjonsforskjell: definisjon
Tenk på en sekvens som består av j-verdier A = a(1), a(2), a(3), a(4) ... a(j), j tilhører settet med naturlige tall N. En aritmetikk progresjon, i henhold til dens definisjon, er en sekvens , der a(3) – a(2) = a(4) – a(3) = a(5) – a(4) = … = a(j) – a(j-1) = d. Verdien d er den ønskede forskjellen for denne progresjonen.
d = a(j) – a(j-1).
Høydepunkt:
- En økende progresjon, i så fall d > 0. Eksempel: 4, 8, 12, 16, 20, ...
- Avtagende progresjon, deretter d< 0. Пример: 18, 13, 8, 3, -2, …
Forskjellsprogresjon og dens vilkårlige elementer
Hvis 2 vilkårlige ledd for progresjonen er kjent (i-th, k-th), kan forskjellen for en gitt sekvens bestemmes basert på forholdet:
a(i) = a(k) + (i – k)*d, som betyr d = (a(i) – a(k))/(i-k).
Forskjell i progresjon og dens første periode
Dette uttrykket vil hjelpe til med å bestemme en ukjent verdi bare i tilfeller der nummeret til sekvenselementet er kjent.
Progresjonsforskjell og summen
Summen av en progresjon er summen av dens termer. For å beregne den totale verdien av de første j-elementene, bruk den riktige formelen:
S(j) =((a(1) + a(j))/2)*j, men siden a(j) = a(1) + d(j – 1), deretter S(j) = ((a(1) + a(1) + d(j – 1))/2)*j=(( 2a(1) + d(– 1))/2)*j.
Når du studerer algebra på en ungdomsskole (9. klasse), er et av de viktige temaene studiet av numeriske sekvenser, som inkluderer progresjoner - geometriske og aritmetiske. I denne artikkelen skal vi se på en aritmetisk progresjon og eksempler med løsninger.
Hva er en aritmetisk progresjon?
For å forstå dette er det nødvendig å definere den aktuelle progresjonen, samt gi de grunnleggende formlene som vil bli brukt senere for å løse problemer.
Aritmetisk eller er et sett med ordnede rasjonelle tall, hvor hvert medlem skiller seg fra det forrige med en konstant verdi. Denne verdien kalles differansen. Det vil si at du kan gjenopprette hele den aritmetiske progresjonen når du kjenner til et hvilket som helst medlem av en ordnet serie med tall og forskjellen.
La oss gi et eksempel. Følgende tallrekke vil være en aritmetisk progresjon: 4, 8, 12, 16, ..., siden forskjellen i dette tilfellet er 4 (8 - 4 = 12 - 8 = 16 - 12). Men settet med tall 3, 5, 8, 12, 17 kan ikke lenger tilskrives typen progresjon som vurderes, siden forskjellen for det ikke er en konstant verdi (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Viktige formler
La oss nå presentere de grunnleggende formlene som vil være nødvendig for å løse problemer ved å bruke aritmetisk progresjon. La oss betegne med symbolet a n det n'te medlem av sekvensen, der n er et heltall. Vi betegner forskjellen med den latinske bokstaven d. Da er følgende uttrykk gyldige:
- For å bestemme verdien av det n-te leddet er følgende formel egnet: a n = (n-1)*d+a 1 .
- For å bestemme summen av de første n leddene: S n = (a n +a 1)*n/2.
For å forstå noen eksempler på aritmetisk progresjon med løsninger i 9. klasse, er det nok å huske disse to formlene, siden eventuelle problemer av typen som vurderes er basert på bruken. Du bør også huske at progresjonsforskjellen bestemmes av formelen: d = a n - a n-1.
Eksempel #1: finne et ukjent medlem

La oss gi et enkelt eksempel på en aritmetisk progresjon og formlene som må brukes for å løse den.
La sekvensen 10, 8, 6, 4, ... gis, du må finne fem ledd i den.
Fra betingelsene for problemet følger det allerede at de første 4 leddene er kjent. Den femte kan defineres på to måter:
- La oss først beregne forskjellen. Vi har: d = 8 - 10 = -2. På samme måte kan du ta to andre medlemmer som står ved siden av hverandre. For eksempel, d = 4 - 6 = -2. Siden det er kjent at d = a n - a n-1, så er d = a 5 - a 4, hvorfra vi får: a 5 = a 4 + d. Vi erstatter de kjente verdiene: a 5 = 4 + (-2) = 2.
- Den andre metoden krever også kunnskap om forskjellen på den aktuelle progresjonen, så du må først bestemme den som vist ovenfor (d = -2). Når vi vet at det første leddet a 1 = 10, bruker vi formelen for n-tallet i sekvensen. Vi har: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2*n. Ved å erstatte n = 5 i det siste uttrykket får vi: a 5 = 12-2 * 5 = 2.
Som du ser førte begge løsningene til samme resultat. Merk at i dette eksemplet er progresjonsforskjellen d en negativ verdi. Slike sekvenser kalles avtagende, siden hvert neste ledd er mindre enn det forrige.
Eksempel #2: progresjonsforskjell
La oss nå komplisere problemet litt, gi et eksempel på hvordan du finner forskjellen på en aritmetisk progresjon.
Det er kjent at i noen algebraisk progresjon er 1. ledd lik 6, og 7. ledd er lik 18. Det er nødvendig å finne forskjellen og gjenopprette denne sekvensen til 7. ledd.
La oss bruke formelen for å bestemme det ukjente leddet: a n = (n - 1) * d + a 1 . La oss erstatte de kjente dataene fra tilstanden inn i den, det vil si tallene a 1 og en 7, vi har: 18 = 6 + 6 * d. Fra dette uttrykket kan du enkelt regne ut differansen: d = (18 - 6) /6 = 2. Dermed har vi besvart første del av oppgaven.
For å gjenopprette sekvensen til det 7. leddet, bør du bruke definisjonen av en algebraisk progresjon, det vil si a 2 = a 1 + d, a 3 = a 2 + d, og så videre. Som et resultat gjenoppretter vi hele sekvensen: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.
Eksempel nr. 3: utarbeide en progresjon

La oss komplisere problemet enda mer. Nå må vi svare på spørsmålet om hvordan finne en aritmetisk progresjon. Følgende eksempel kan gis: to tall er gitt, for eksempel - 4 og 5. Det er nødvendig å lage en algebraisk progresjon slik at ytterligere tre ledd plasseres mellom disse.
Før du begynner å løse dette problemet, må du forstå hvilken plass de gitte tallene vil oppta i den fremtidige progresjonen. Siden det vil være tre ledd til mellom dem, så er en 1 = -4 og en 5 = 5. Etter å ha etablert dette, går vi videre til problemet, som ligner det forrige. Igjen, for det n-te leddet vi bruker formelen, får vi: a 5 = a 1 + 4 * d. Fra: d = (a 5 - a 1)/4 = (5 - (-4)) / 4 = 2,25. Det vi har her er ikke en heltallsverdi av forskjellen, men det er et rasjonelt tall, så formlene for den algebraiske progresjonen forblir de samme.
La oss nå legge den funnet forskjellen til en 1 og gjenopprette de manglende vilkårene i progresjonen. Vi får: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, som falt sammen med betingelsene for problemet.
Eksempel nr. 4: første termin av progresjon

La oss fortsette å gi eksempler på aritmetisk progresjon med løsninger. I alle tidligere problemer var det første tallet i den algebraiske progresjonen kjent. La oss nå vurdere et problem av en annen type: la to tall gis, der en 15 = 50 og en 43 = 37. Det er nødvendig å finne hvilket tall denne sekvensen begynner med.
Formlene som er brukt så langt forutsetter kunnskap om a 1 og d. I problemstillingen er ingenting kjent om disse tallene. Vi vil likevel skrive ned uttrykk for hvert begrep som det finnes informasjon om: a 15 = a 1 + 14 * d og a 43 = a 1 + 42 * d. Vi fikk to likninger der det er 2 ukjente størrelser (a 1 og d). Dette betyr at problemet reduseres til å løse et system med lineære ligninger.
Den enkleste måten å løse dette systemet på er å uttrykke en 1 i hver ligning og deretter sammenligne de resulterende uttrykkene. Første ligning: a 1 = a 15 - 14 * d = 50 - 14 * d; andre ligning: a 1 = a 43 - 42 * d = 37 - 42 * d. Ved å likestille disse uttrykkene får vi: 50 - 14 * d = 37 - 42 * d, hvorav differansen d = (37 - 50) / (42 - 14) = - 0,464 (bare 3 desimaler er gitt).
Når du kjenner d, kan du bruke hvilket som helst av de 2 uttrykkene ovenfor for en 1. For eksempel, først: a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.
Hvis du er i tvil om det oppnådde resultatet, kan du sjekke det, for eksempel bestemme den 43. terminen av progresjonen, som er spesifisert i tilstanden. Vi får: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Den lille feilen skyldes at det ble brukt avrunding til tusendeler i beregningene.
Eksempel nr. 5: beløp
La oss nå se på flere eksempler med løsninger for summen av en aritmetisk progresjon.
La en numerisk progresjon av følgende form gis: 1, 2, 3, 4, ...,. Hvordan beregne summen av 100 av disse tallene?
Takket være utviklingen av datateknologi er det mulig å løse dette problemet, det vil si å legge til alle tallene sekvensielt, som datamaskinen vil gjøre så snart en person trykker på Enter-tasten. Problemet kan imidlertid løses mentalt hvis du legger merke til at den presenterte tallserien er en algebraisk progresjon, og dens forskjell er lik 1. Ved å bruke formelen for summen får vi: S n = n * ( a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.
Det er interessant å merke seg at dette problemet kalles "Gaussian" fordi på begynnelsen av 1700-tallet var den berømte tyskeren, fortsatt bare 10 år gammel, i stand til å løse det i hodet på noen få sekunder. Gutten visste ikke formelen for summen av en algebraisk progresjon, men han la merke til at hvis du legger sammen tallene i enden av sekvensen i par, får du alltid det samme resultatet, det vil si 1 + 100 = 2 + 99 = 3 + 98 = ..., og siden disse summene vil være nøyaktig 50 (100 / 2), er det nok å multiplisere 50 med 101 for å få riktig svar.

Eksempel nr. 6: summen av ledd fra n til m
Et annet typisk eksempel på summen av en aritmetisk progresjon er følgende: gitt en serie med tall: 3, 7, 11, 15, ..., må du finne hva summen av leddene fra 8 til 14 vil være lik .
Problemet løses på to måter. Den første av dem innebærer å finne ukjente termer fra 8 til 14, og deretter summere dem sekvensielt. Siden det er få termer, er ikke denne metoden ganske arbeidskrevende. Ikke desto mindre foreslås det å løse dette problemet ved å bruke en andre metode, som er mer universell.
Tanken er å få en formel for summen av den algebraiske progresjonen mellom leddene m og n, der n > m er heltall. For begge tilfeller skriver vi to uttrykk for summen:
- S m = m * (a m + a 1) / 2.
- S n = n * (a n + a 1) / 2.
Siden n > m er det åpenbart at 2. sum inkluderer den første. Den siste konklusjonen betyr at hvis vi tar differansen mellom disse summene og legger til begrepet a m (i tilfellet vi tar differansen trekkes den fra summen S n), vil vi få det nødvendige svaret på oppgaven. Vi har: S mn = S n - S m + a m =n * (a 1 + a n) / 2 - m *(a 1 + a m)/2 + a m = a 1 * (n - m) / 2 + a n * n/2 + a m * (1- m/2). Det er nødvendig å erstatte formler for en n og en m i dette uttrykket. Da får vi: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1) - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.
Den resulterende formelen er noe tungvint, men summen S mn avhenger bare av n, m, a 1 og d. I vårt tilfelle er a 1 = 3, d = 4, n = 14, m = 8. Ved å erstatte disse tallene får vi: S mn = 301.

Som det fremgår av løsningene ovenfor, er alle problemer basert på kunnskap om uttrykket for det n. leddet og formelen for summen av settet av første ledd. Før du begynner å løse noen av disse problemene, anbefales det at du leser tilstanden nøye, forstår tydelig hva du trenger å finne, og først deretter fortsetter med løsningen.
Et annet tips er å strebe etter enkelhet, det vil si at hvis du kan svare på et spørsmål uten å bruke komplekse matematiske beregninger, må du gjøre nettopp det, siden sannsynligheten for å gjøre en feil i dette tilfellet er mindre. For eksempel, i eksemplet med en aritmetisk progresjon med løsning nr. 6, kan man stoppe ved formelen S mn = n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m, og del opp det overordnede problemet i separate deloppgaver (i dette tilfellet, finn først begrepene a n og a m).
Hvis du er i tvil om det oppnådde resultatet, anbefales det å sjekke det, slik det ble gjort i noen av eksemplene gitt. Vi fant ut hvordan man finner en aritmetisk progresjon. Hvis du finner ut av det, er det ikke så vanskelig.
Mange har hørt om aritmetisk progresjon, men ikke alle har en god ide om hva det er. I denne artikkelen vil vi gi den tilsvarende definisjonen, og også vurdere spørsmålet om hvordan man finner forskjellen på en aritmetisk progresjon, og gi en rekke eksempler.
Matematisk definisjon
Så hvis vi snakker om en aritmetisk eller algebraisk progresjon (disse konseptene definerer det samme), betyr dette at det er en viss tallserie som tilfredsstiller følgende lov: hvert to tilstøtende tall i rekken avviker med samme verdi. Matematisk er det skrevet slik:
Her betyr n antallet element a n i sekvensen, og tallet d er forskjellen på progresjonen (navnet følger av den presenterte formelen).
Hva betyr det å vite forskjellen d? Om hvor "langt" nabonummer er fra hverandre. Kunnskap om d er imidlertid en nødvendig, men ikke tilstrekkelig betingelse for å bestemme (gjenopprette) hele progresjonen. Du må vite ett tall til, som kan være absolutt et hvilket som helst element i den aktuelle serien, for eksempel en 4, a10, men som regel bruker de det første tallet, det vil si en 1.
Formler for å bestemme progresjonselementer
Generelt er informasjonen ovenfor allerede nok til å gå videre til å løse spesifikke problemer. Likevel, før den aritmetiske progresjonen er gitt, og det vil være nødvendig å finne forskjellen, vil vi presentere et par nyttige formler, og dermed lette den påfølgende prosessen med å løse problemer.
Det er lett å vise at ethvert element i sekvensen med nummer n kan finnes som følger:
a n = a 1 + (n - 1) * d
Faktisk kan hvem som helst sjekke denne formelen ved enkelt søk: hvis du erstatter n = 1, får du det første elementet, hvis du erstatter n = 2, så gir uttrykket summen av det første tallet og forskjellen, og så videre.

Betingelsene for mange problemer er sammensatt på en slik måte at gitt et kjent tallpar, hvis tall også er gitt i sekvensen, er det nødvendig å rekonstruere hele tallserien (finn forskjellen og det første elementet). Nå skal vi løse dette problemet i generell form.
Så la to elementer med tallene n og m gis. Ved å bruke formelen ovenfor, kan du lage et system med to ligninger:
a n = a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d
For å finne ukjente størrelser vil vi bruke en kjent enkel teknikk for å løse et slikt system: trekk fra venstre og høyre side i par, likheten vil forbli gyldig. Vi har:
a n = a 1 + (n - 1) * d;
a n - a m = (n - 1) * d - (m - 1) * d = d * (n - m)
Dermed har vi ekskludert en ukjent (a 1). Nå kan vi skrive det endelige uttrykket for å bestemme d:
d = (a n - a m) / (n - m), hvor n > m
Vi mottok en veldig enkel formel: for å beregne forskjellen d i samsvar med betingelsene for problemet, er det bare nødvendig å ta forholdet mellom forskjellene mellom elementene selv og deres serienumre. Et viktig poeng bør tas hensyn til: forskjellene tas mellom "senior" og "junior" medlemmer, det vil si n > m ("senior" betyr å stå lenger fra begynnelsen av sekvensen, dens absolutte verdi kan være enten større eller mindre mer "junior" element).
Uttrykket for forskjellen d-progresjon bør erstattes med en av ligningene i begynnelsen av å løse problemet for å få verdien av det første leddet.

I vår tid med utvikling av datateknologi prøver mange skoleelever å finne løsninger for oppgavene sine på Internett, så spørsmål av denne typen dukker ofte opp: Finn forskjellen på en aritmetisk progresjon på nettet. For en slik forespørsel vil søkemotoren returnere et antall nettsider, ved å gå til som du må angi data kjent fra tilstanden (dette kan enten være to termer av progresjonen eller summen av et visst antall av dem ) og motta et svar umiddelbart. Ikke desto mindre er denne tilnærmingen til å løse problemet uproduktiv når det gjelder studentens utvikling og forståelse av essensen av oppgaven som er tildelt ham.
Løsning uten å bruke formler

La oss løse det første problemet uten å bruke noen av de gitte formlene. La elementene i rekken gis: a6 = 3, a9 = 18. Finn forskjellen på den aritmetiske progresjonen.
Kjente elementer er nær hverandre på rad. Hvor mange ganger må forskjellen d legges til den minste for å få den største? Tre ganger (første gang vi legger til d, får vi det 7. elementet, andre gang - den åttende, til slutt, tredje gang - den niende). Hvilket tall må legges til tre tre ganger for å få 18? Dette er nummer fem. Virkelig:
Dermed er den ukjente forskjellen d = 5.
Selvfølgelig kunne løsningen ha blitt utført ved hjelp av passende formel, men dette ble ikke gjort med vilje. En detaljert forklaring av løsningen på oppgaven skal bli et klart og tydelig eksempel på hva en aritmetisk progresjon er.
En oppgave som ligner den forrige
La oss nå løse et lignende problem, men endre inndataene. Så du bør finne om a3 = 2, a9 = 19.
Selvfølgelig kan du igjen ty til "head-on" løsningsmetoden. Men siden elementene i serien er gitt, som er relativt langt fra hverandre, vil denne metoden ikke være helt praktisk. Men å bruke den resulterende formelen vil raskt føre oss til svaret:
d = (a 9 - a 3) / (9 - 3) = (19 - 2) / (6) = 17 / 6 ≈ 2,83
Her har vi rundet slutttallet. I hvilken grad denne avrundingen førte til en feil kan bedømmes ved å sjekke resultatet:
a 9 = a 3 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 = 18,98
Dette resultatet avviker kun med 0,1 % fra verdien gitt i betingelsen. Derfor kan avrundingen som brukes til nærmeste hundredeler betraktes som et vellykket valg.
Problemer med å bruke formelen for et begrep

La oss vurdere et klassisk eksempel på et problem for å bestemme den ukjente d: finn forskjellen på en aritmetisk progresjon hvis a1 = 12, a5 = 40.
Når to tall av en ukjent algebraisk sekvens er gitt, og ett av dem er elementet a 1, trenger du ikke tenke lenge, men bør umiddelbart bruke formelen for a n-leddet. I dette tilfellet har vi:
a 5 = a 1 + d * (5 - 1) => d = (a 5 - a 1) / 4 = (40 - 12) / 4 = 7
Vi fikk det nøyaktige tallet ved deling, så det er ingen vits i å sjekke nøyaktigheten til det beregnede resultatet, slik det ble gjort i forrige avsnitt.
La oss løse et annet lignende problem: vi må finne forskjellen til en aritmetisk progresjon hvis a1 = 16, a8 = 37.
Vi bruker en tilnærming som ligner den forrige og får:
a 8 = a 1 + d * (8 - 1) => d = (a 8 - a 1) / 7 = (37 - 16) / 7 = 3
Hva annet bør du vite om aritmetisk progresjon?
I tillegg til problemer med å finne en ukjent forskjell eller individuelle elementer, er det ofte nødvendig å løse problemer med summen av de første leddene i en sekvens. Betraktning av disse problemene er utenfor rammen av artikkelen, men for fullstendig informasjon presenterer vi en generell formel for summen av n tall i en serie:
∑ n i = 1 (a i) = n * (a 1 + a n) / 2
 Logaritmiske ligninger
Logaritmiske ligninger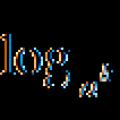 Teknikk for å løse logaritmiske ligninger
Teknikk for å løse logaritmiske ligninger Selvanalyse av logopedlærer
Selvanalyse av logopedlærer