Hvordan finne tyngdepunktet til en uregelmessig formet figur. Posisjonene til tyngdepunktet til noen figurer

Rektangel. Siden rektangelet har to symmetriakser, er dets tyngdepunkt plassert i skjæringspunktet mellom symmetriaksene, dvs. i skjæringspunktet mellom diagonalene til rektangelet.

Triangel. Tyngdepunktet ligger i skjæringspunktet mellom medianene. Det er kjent fra geometrien at medianene til en trekant skjærer hverandre i ett punkt og deler seg i forholdet 1:2 fra basen.

En sirkel. Siden sirkelen har to symmetriakser, er dens tyngdepunkt i skjæringspunktet mellom symmetriaksene.

Halvsirkel. Halvsirkelen har én symmetriakse, så ligger tyngdepunktet på denne aksen. En annen koordinat for tyngdepunktet beregnes med formelen: .

Mange strukturelle elementer er laget av standard rullede produkter - vinkler, I-bjelker, kanaler og andre. Alle dimensjoner, så vel som de geometriske egenskapene til valsede profiler, er tabelldata som kan finnes i referanselitteraturen i standard sortimentstabeller (GOST 8239-89, GOST 8240-89).

Eksempel 1 Bestem posisjonen til tyngdepunktet til figuren vist på figuren.

Løsning:

Vi velger koordinataksene slik at Ox-aksen passerer langs den ekstreme nedre totaldimensjonen, og Oy-aksen - langs den ytterste venstre totaldimensjonen.

Vi deler en kompleks figur inn i minimum antall enkle figurer:

rektangel 20x10;

trekant 15x10;

sirkel R=3 cm.

Vi beregner arealet til hver enkel figur, dens koordinater til tyngdepunktet. Resultatene av beregningene er lagt inn i tabellen

Figur nr.	Området til figur A	Tyngdepunktkoordinater

Svar: C(14,5; 4,5)

Eksempel 2 . Bestem koordinatene til tyngdepunktet til en komposittseksjon som består av et ark og rullede profiler.

Løsning.

Vi velger koordinataksene, som vist på figuren.

Vi betegner tallene med tall og skriver ut de nødvendige dataene fra tabellen:

Figur nr.	Området til figur A	Tyngdepunktkoordinater

Vi beregner koordinatene til figurens tyngdepunkt ved å bruke formlene:

Svar: C(0; 10)

Laboratoriearbeid nr. 1 "Bestemme tyngdepunktet til sammensatte flate figurer"

Mål: Bestem tyngdepunktet til en gitt flat kompleks figur ved eksperimentelle og analytiske metoder og sammenlign resultatene deres.

Arbeidsordre

Tegn i notatbøker din flate figur i størrelse, og angi koordinataksene.

Bestem tyngdepunktet analytisk.

1. Bryt figuren inn i minimum antall figurer, hvis tyngdepunkt vi vet hvordan vi skal bestemme.

   Angi antall områder og koordinatene til tyngdepunktet til hver figur.

   Regn ut koordinatene til tyngdepunktet til hver figur.

   Beregn arealet til hver figur.

   Beregn koordinatene til tyngdepunktet til hele figuren ved å bruke formlene (sett posisjonen til tyngdepunktet på tegningen av figuren):

Installasjon for eksperimentell bestemmelse av koordinatene til tyngdepunktet ved oppheng består av et vertikalt stativ 1 (se fig.) som nålen er festet til 2 . flat figur 3 Laget av papp, som er lett å stikke hull i. hull MEN og PÅ gjennomboret på tilfeldig plasserte punkter (fortrinnsvis i den fjerneste avstanden fra hverandre). En flat figur henges på en nål, først på et punkt MEN , og så på punktet PÅ . Ved hjelp av et lodd 4 , festet på samme nål, tegnes en vertikal linje på figuren med en blyant som tilsvarer loddet. Tyngdepunkt FRA figuren vil være plassert i skjæringspunktet mellom de vertikale linjene som er tegnet når figuren henges på punkter MEN og PÅ .

tyngdepunkt Et stivt legeme er et geometrisk punkt som er stivt forbundet med denne kroppen og er sentrum for parallelle tyngdekraftskrefter som påføres individuelle elementærpartikler i kroppen (Figur 1.6).

Radiusvektor for dette punktet

Figur 1.6

For en homogen kropp er posisjonen til tyngdepunktet til kroppen ikke avhengig av materialet, men bestemmes av kroppens geometriske form.

Hvis egenvekten til en homogen kropp γ , vekten av den elementære partikkelen i kroppen

P k = γΔV k (P = γV ) erstatte i formelen for å bestemme r C , vi har

Fra hvor vi projiserer på aksene og passerer til grensen, får vi koordinatene til tyngdepunktet til et homogent volum

Tilsvarende for koordinatene til tyngdepunktet til en homogen overflate med et areal S (Figur 1.7, a)

Figur 1.7

For koordinatene til tyngdepunktet til en homogen lengdelinje L (Figur 1.7, b)

Metoder for å bestemme koordinatene til tyngdepunktet

Basert på de generelle formlene oppnådd tidligere, er det mulig å indikere metoder for å bestemme koordinatene til tyngdepunktene til faste kropper:

1 Analytisk(ved integrering).

2 Symmetri metode. Hvis kroppen har et plan, en akse eller et symmetrisenter, ligger tyngdepunktet i henholdsvis symmetriplanet, symmetriaksen eller i symmetrisenteret.

3 Eksperimentell(kroppsopphengsmetode).

4 splitting. Kroppen er delt inn i et begrenset antall deler, for hver av disse posisjonen til tyngdepunktet C og område S kjent. For eksempel projeksjonen av en kropp på et plan xOy (Figur 1.8) kan representeres som to flate figurer med arealer S 1 og S 2 (S=S 1 + S 2 ). Tyngdepunktene til disse figurene er på punktene C 1 (x 1 ,y 1 ) og C 2 (x 2 ,y 2 ) . Da er koordinatene til kroppens tyngdepunkt

Figur 1.8

5Addisjon(metode for negative områder eller volumer). Et spesielt tilfelle av partisjoneringsmetoden. Det gjelder kropper med utskjæringer dersom tyngdepunktene til kroppen uten utskjæringen og utskjæringen er kjent. For eksempel må du finne koordinatene til tyngdepunktet til en flat figur (Figur 1.9):

Figur 1.9

Tyngdepunktene til de enkleste figurene

Figur 1.10

1 trekant

Tyngdepunktet til trekantområdet faller sammen med skjæringspunktet mellom dets medianer (Figur 1.10, a).

DM=MB , CM= (1/3)ER .

2 Sirkelbue

Buen har en symmetriakse (Figur 1.10, b). Tyngdepunktet ligger på denne aksen, dvs. y C = 0 .

dl – bueelement, dl = Rdφ , R er radiusen til sirkelen, x = Rcosφ , L= 2aR ,

Følgelig:

x C = R(sinα/α) .

3 Sirkulær sektor

Radiusektor R med midtvinkel 2 α har en symmetriakse Okse , hvor tyngdepunktet er plassert (Figur 1.10, c).

Vi deler sektoren inn i elementære sektorer, som kan betraktes som trekanter. Tyngdepunktene til elementære sektorer er plassert på buen til en sirkel med radius (2/3) R .

Tyngdepunktet til sektoren sammenfaller med tyngdepunktet til buen AB :

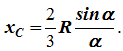
14. Metoder for å spesifisere bevegelsen til et punkt.

Med vektormetoden for å spesifisere bevegelse, bestemmes posisjonen til et punkt av radiusvektoren trukket fra et fast punkt i det valgte referansesystemet.

Med koordinatmetoden for å spesifisere bevegelse, spesifiseres koordinatene til et punkt som en funksjon av tid:

Dette er de parametriske ligningene for banen til et bevegelig punkt, der tiden spiller rollen som en parameter t . For å skrive ned ligningen i en eksplisitt form, er det nødvendig å ekskludere fra dem t .

Med den naturlige metoden for å spesifisere bevegelsen, punktets bane, opprinnelsen på banen med indikasjon på den positive referanseretningen, settes loven for endring av buekoordinaten: s=s(t) . Denne metoden er praktisk å bruke hvis banen til punktet er kjent på forhånd.

15. 1,2 punkts hastighet

Vurder bevegelsen av et punkt over en kort periode Δt :

gjennomsnittshastigheten til et punkt over en tidsperiode Dt . Hastigheten til et punkt på et gitt tidspunkt

Punkthastighet er et kinematisk mål på dens bevegelse, lik den tidsderiverte av radiusvektoren til dette punktet i referanserammen som vurderes. Hastighetsvektoren er rettet tangentielt til punktets bane i bevegelsesretningen.

Forfatter: La oss ta en vilkårlig formkropp. Er det mulig å henge den på en tråd slik at den etter henging beholder sin posisjon (dvs. ikke begynner å snu) når noen innledende orientering (fig. 27.1)?

Med andre ord, er det et slikt punkt, i forhold til hvilket summen av momentene til tyngdekreftene som virker på forskjellige deler av kroppen, vil være lik null ved noen orientering av kroppen i rommet?

Leser: Ja jeg tror det. Et slikt punkt kalles kroppens tyngdepunkt.

Bevis. For enkelhets skyld bør du vurdere en kropp i form av en flat plate med vilkårlig form vilkårlig orientert i rommet (fig. 27.2). Ta koordinatsystemet X 0på med origo i massesenteret - et punkt FRA, deretter x C = 0, på C = 0.

Vi representerer dette organet som en samling av et stort antall punktmasser m jeg, posisjonen til hver av dem er gitt av radiusvektoren .

Per definisjon av massesenteret og koordinaten x C = .

Siden i vårt koordinatsystem x C= 0, så . La oss multiplisere denne ligningen med g og få

Som det fremgår av fig. 27.2, | x i| er styrkens skulder. Og hvis x i> 0, deretter kraftmomentet M i> 0, og hvis x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i kraftmoment vil være M i = m i gx i . Da er likhet (1) ekvivalent med , hvor M i er tyngdemomentet. Og dette betyr at med en vilkårlig orientering av kroppen vil summen av momentene til tyngdekreftene som virker på kroppen være lik null i forhold til dets massesenter.

For at kroppen vi vurderer skal være i likevekt, er det nødvendig å søke på den på et tidspunkt FRA styrke T = mg peker vertikalt oppover. Øyeblikket til denne kraften om punktet FRA er lik null.

Siden resonnementet vårt ikke på noen måte var avhengig av nøyaktig hvordan kroppen er orientert i rommet, beviste vi at tyngdepunktet sammenfaller med massesenteret, som var det som krevdes for å bli bevist.

Oppgave 27.1. Finn tyngdepunktet til en vektløs stang med lengde l, i enden av hvilke to punktmasser er faste t 1 og t 2 .

t 1 t 2 l	Løsning. Vi skal ikke se etter tyngdepunktet, men etter massesenteret (siden de er ett og det samme). La oss introdusere aksen X(Fig. 27.3). Ris. 27.3
x C =?

Svar: borte fra masse t 1 .

STOPPE! Bestem selv: B1-B3.

Uttalelse 1 . Hvis et homogent flatt legeme har en symmetriakse, er tyngdepunktet på denne aksen.

Faktisk for enhver punktmasse m jeg, plassert til høyre for symmetriaksen, er det samme punktmasse plassert symmetrisk i forhold til den første (fig. 27.4). I dette tilfellet er summen av kreftmomentene .

Siden hele kroppen kan representeres som delt inn i like par av punkter, er det totale tyngdemomentet i forhold til ethvert punkt som ligger på symmetriaksen null, noe som betyr at kroppens tyngdepunkt også er plassert på denne aksen. Dette fører til en viktig konklusjon: hvis kroppen har flere symmetriakser, så ligger tyngdepunktet i skjæringspunktet mellom disse aksene(Fig. 27.5).

Ris. 27.5

Uttalelse 2. Hvis to kropper med masser t 1 og t 2 er koblet til ett, så vil tyngdepunktet til et slikt legeme ligge på en rett linje som forbinder tyngdepunktene til det første og andre legeme (fig. 27.6).

Ris. 27.6 Ris. 27.7

Bevis. La oss arrangere komposittlegemet slik at segmentet som forbinder tyngdepunktene til kroppene er vertikalt. Deretter summen av tyngdemomentene til det første legemet i forhold til punktet FRA 1 er lik null, og summen av tyngdemomentene til det andre legemet rundt punktet FRA 2 er null (fig. 27.7).

Legg merke til det skulder tyngdekraften til enhver punktmasse t jeg det samme med hensyn til et hvilket som helst punkt på segmentet FRA 1 FRA 2, og derav tyngdemomentet i forhold til ethvert punkt som ligger på segmentet FRA 1 FRA 2 er like. Derfor er tyngdekraften til hele kroppen null i forhold til et hvilket som helst punkt på segmentet FRA 1 FRA 2. Således ligger tyngdepunktet til komposittlegemet på segmentet FRA 1 FRA 2 .

Påstand 2 innebærer en viktig praktisk konklusjon, som er tydelig formulert i form av instruksjoner.

instruksjon,

hvordan finne tyngdepunktet til en stiv kropp hvis den kan brytes

i deler, posisjonene til tyngdepunktene til hver av dem er kjent

1. Bytt ut hver del med en masse plassert i tyngdepunktet til den delen.

2. Finn tyngdepunkt(og dette er det samme som tyngdepunktet) til det resulterende systemet med punktmasser, ved å velge et praktisk koordinatsystem X 0på, i henhold til formlene:

Faktisk, la oss plassere den sammensatte kroppen på en slik måte at segmentet FRA 1 FRA 2 var horisontal, og vi vil henge den på tråder på punkter FRA 1 og FRA 2 (fig. 27.8, en). Det er klart at kroppen vil være i likevekt. Og denne balansen vil ikke bli forstyrret hvis vi erstatter hver kropp med punktmasser t 1 og t 2 (fig. 27.8, b).

Ris. 27.8

STOPPE! Bestem selv: C3.

Oppgave 27.2. Massekuler er plassert i to hjørner av en likesidet trekant t Hver. Det tredje toppunktet inneholder en kule med masse 2 t(Fig. 27.9, en). Trekantside en. Bestem tyngdepunktet til dette systemet.

t 2t en	Ris. 27.9
x C = ? på C = ?

Løsning. Vi innfører koordinatsystemet X 0på(Fig. 27.9, b). Deretter

,

.

Svar: x C = en/2; ; tyngdepunktet ligger på halve høyden AD.

Evnen til å holde seg i balanse uten å anstrenge seg er svært viktig for effektiv meditasjon, yoga, qigong, og også for magedans. Dette er det første kravet nybegynnere møter i denne typen aktiviteter og en av grunnene til at det er vanskelig å ta de første stegene uten en instruktør. Et spørsmål som antyder at en person ikke kjenner tyngdepunktet sitt kan se noe annerledes ut. I qigong, for eksempel, vil en person spørre hvordan man kan være avslappet og fortsatt utføre bevegelser mens man står, en nybegynner orientalsk danser vil ikke forstå hvordan man skiller og koordinerer bevegelsene til de nedre og øvre delene av kroppen, og i begge tilfeller mennesker vil overanstrenge og ofte miste balansen. Bevegelsene deres vil være usikre, klønete.

Derfor er det viktig å forstå hvordan du finner tyngdepunktet ditt selv, det krever både mentalt arbeid og ferdigheter, men over tid flytter ferdigheten seg til et instinktivt nivå.

Hva må gjøres for ikke å belaste musklene og samtidig ikke bruke eksterne støtter. Svaret er åpenbart, du må flytte støtten innover. Mer presist, stol på en betinget indre akse. Hvor går denne akselen? Begrepet tyngdepunkt er betinget, men det brukes likevel i fysikk. Der er det vanlig å definere det som anvendelsespunktet for de resulterende tyngdekreftene. Den resulterende tyngdekraften er totaliteten av alle tyngdekreftene, tatt i betraktning retningen av deres handling.

Er det vanskelig så langt? Fyll opp med tålmodighet.

Det vil si at vi leter etter et punkt i kroppen vår som vil tillate oss å ikke falle, uten bevisst å kjempe mot tyngdekraften. Dette betyr at jordens tyngdekraft må rettes slik at den konvergerer med resten av de virkende kreftene et sted i midten av kroppen vår.

En slik retning av krefter skaper en betinget akse i midten av kroppen vår, en vertikal overflate, dette er vertikalen til tyngdepunktet. Den delen av kroppen som vi hviler på mot bakken er vårt fotavtrykk (vi hviler mot bakken med føttene) På stedet hvor denne vertikalen hviler mot overflaten vi står på, det vil si at vi hviler mot bakken. dette er tyngdepunktet inne i fotavtrykket. Hvis vertikalen skifter fra dette stedet, vil vi miste balansen og falle. Jo større selve støtteområdet er, jo lettere er det for oss å holde oss nær sentrum, og derfor vil vi alle instinktivt ta et langt skritt mens vi står på et ustabilt underlag. Det vil si at området for støtte ikke bare er føttene selv, men også mellomrommet mellom dem.

Det er også viktig å vite at bredden på området til støtteområdet påvirker mer enn lengden. Når det gjelder et menneske, betyr dette at vi er mer sannsynlig å falle på siden enn bakover, og enda mer fremover. Derfor, når vi løper, er det vanskeligere for oss å opprettholde balansen, det samme kan sies om hæler. Men i brede, stabile sko er det tvert imot lettere å motstå, enda lettere enn helt barbeint. Aktivitetene nevnt i begynnelsen krever imidlertid veldig mykt, lett fottøy eller ingen i det hele tatt. Derfor kan vi ikke hjelpe oss med sko.

Så det er veldig viktig å finne midtpunktet til den vertikale linjen på foten din. Vanligvis er den ikke plassert i midten av foten, som noen automatisk antar, men nærmere hælen, et sted halvveis fra midten av foten, til hælen.
Men det er ikke alt.

I tillegg til den vertikale linjen til tyngdepunktet, er det også en horisontal, samt en separat for lemmene.
Den horisontale linjen for kvinner og menn går litt annerledes.

Fremover, hos kvinner, passerer den lavere, og hos menn høyere. Hos menn går det et sted 4-5 fingre under navlen, og hos kvinner, 10, omtrent. Bak kvinnelinjen går nesten en koopchik, og hannlinjen er omtrent fem fingre høyere enn den. I tillegg, for stabilitet på meditasjonstidspunktet, er det viktig å være oppmerksom på den rene linjen i tyngdepunktet til kneet. Den ligger litt over beinet (underbenet), men to eller tre fingre under brusken.

Under meditasjon, så vel som under magedans, er det ikke veldig bra å spre føttene bredt, den maksimale bredden tilsvarer vanligvis bredden på skuldrene.

Derfor må du hjelpe deg selv litt med knærne, og prøve å bygge den vertikale aksen så rett som mulig. Stå foran speilet, finn alle de beskrevne punktene på deg selv. Sett føttene i skulderbreddes avstand. Slapp av musklene i bena og kroppen. Rett deretter opp ryggen uten å belaste kroppen, slapp av bena med en lett bøyning i knærne. Se for deg tre vertikale linjer som hver løper på et tilsvarende punkt på baksiden av overkroppen, foran den og rundt knærne. Prøv å ordne punktene slik at frontaksen på overkroppen er omtrent halvveis mellom rygg- og kneaksen. I dette tilfellet skal ikke knærne bøyes slik at de går utover tåen, de skal bare være lett bøyd og godt avslappet. Helst over tyngdepunktet innenfor støtteområdet som vi fant på foten. Samtidig kan hendene fritt plasseres på gudene eller legge håndflatene på hoftene.

Hvordan vil du vite at du har funnet tyngdepunktet ditt?

Du vil føle en liten svaiing, men samtidig vil du definitivt vite at du ikke faller.

Forelesning 4. Tyngdepunkt.

Dette foredraget dekker følgende spørsmål

1. Tyngdepunkt for en stiv kropp.

2. Koordinater til tyngdepunktene til inhomogene legemer.

3. Koordinater til tyngdepunktene til homogene legemer.

4. Metoder for å bestemme koordinatene til tyngdepunktene.

5. Tyngdepunkt for noen homogene kropper.

Studiet av disse spørsmålene er nødvendig i fremtiden for å studere dynamikken i bevegelsen av kropper, under hensyntagen til glidende friksjon og rullefriksjon, dynamikken til massesenteret til et mekanisk system, kinetiske momenter, for å løse problemer i disiplinen "Styrke av materialer".

Bringer parallelle krefter.

Etter at vi har vurdert reduksjonen til sentrum av et flatt system og et vilkårlig romlig kraftsystem, går vi igjen tilbake til betraktningen av et spesielt tilfelle av et system med parallelle krefter.

Bringer to parallelle krefter.

I løpet av vurderingen av et slikt styrkesystem er følgende tre tilfeller av reduksjon mulig.

1. System med to kollineære krefter. Betrakt et system med to parallelle og rettet i samme retningskrefter P og Q, brukt på punkter MEN og PÅ. Vi vil anta at kreftene er vinkelrett på dette segmentet (fig. 1, en).

FRA, som tilhører segmentet AB og oppfyller betingelsen:

AC/SW = Q/P.(1)

Hovedsystemvektor RC = P + Q modulo er lik summen av disse kreftene: RC = P + Q.

FRA tatt i betraktning (1) er lik null:MC = P ∙ AC- Q∙ SW = 0.

Derfor, som et resultat av rollebesetningen, fikk vi: RC ≠ 0, MC= 0. Dette betyr at hovedvektoren er ekvivalent med resultanten som går gjennom reduksjonssenteret, det vil si:

Resultanten av kollineære krefter er lik i absolutt verdi med summen, og dens handlingslinje deler segmentet som forbinder punktene for deres påføring, omvendt proporsjonalt med modulene til disse kreftene internt.

Merk at posisjonen til punktet FRA vil ikke endres hvis kreftene R og Q snu et hjørneα . Punktum FRA, som har denne egenskapen kalles sentrum av parallelle krefter.

2. System av to antikollineær og ikke lik i kraftmodul. Måtte kreftene P og Q, brukt på punkter MEN og PÅ, parallell, rettet i motsatte retninger og ulik i modul (fig. 1, b).

La oss velge punktet som referansesenter FRA, som fortsatt tilfredsstiller relasjon (1) og ligger på samme rette linje, men utenfor segmentet AB.

Hovedvektoren til dette systemet RC = P + Q modulo vil nå være lik forskjellen mellom modulene til vektorene: RC = Q - P.

Hovedmoment om senteret FRA er fortsatt null:MC = P ∙ AC- Q∙ SW= 0, altså

Resulterende antikollineær og krefter som ikke er like i absolutt verdi er lik deres forskjell, er rettet mot en større kraft, og dens virkelinje deler segmentet som forbinder punktene for deres påføring, omvendt proporsjonalt med modulene til disse kreftene eksternt.

Figur 1

3. System av to antikollineær og krefter like i modul. La oss ta det forrige tilfellet med reduksjon som det første. La oss fikse strømmen R, og kraft Q la oss prøve modulo å tvinge R.

Så kl Q → R i formel (1) forholdet AC/SW → 1. Dette betyr at AC → SW, altså avstanden AC →∞ .

I dette tilfellet modulen til hovedvektoren RC → 0, og hovedmomentets modul er ikke avhengig av posisjonen til reduksjonssenteret og forblir lik den opprinnelige verdien:

MC = P ∙ AC- Q∙ SW = P ∙ ( AC- SW) =P ∙ MENB.

Dermed har vi i grensen fått et kraftsystem som RC = 0, MC≠ 0, og reduksjonssenteret fjernes til uendelig, som ikke kan erstattes av resultanten. I dette systemet er det ikke vanskelig å finne ut et par krefter, så et par krefter har ingen resultat.

Sentrum av systemet med parallelle krefter.

Vurder systemet n krefter Pi, brukt på punkterA i (x i , y jeg , z i) og parallelt med aksenOv med vektoren l(Fig. 2).

Hvis vi på forhånd utelukker tilfellet med et system som tilsvarer et par krefter, er det ikke vanskelig å bevise, på grunnlag av forrige avsnitt, eksistensen av dets resulterendeR.

Bestem koordinatene til sentrumC(x c, y c, z c) parallelle krefter, det vil si koordinatene til påføringspunktet til resultanten av dette systemet.

Til dette formål bruker vi Varignon-teoremet, på grunnlag av dette:

M0 (R) = Σ M0(Pi).

Fig.2

Vektorkraftmomentet kan representeres som et kryssprodukt, derfor:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r jeg× Pi ).

Gitt at R = Rv ∙ l, a Pi = P vi ∙ l og ved å bruke egenskapene til vektorproduktet får vi:

rc × Rv ∙ l = Σ ( r jeg × P vi ∙ l),

rc ∙ R v × l = Σ ( r jeg ∙ P vi × l) = Σ ( r jeg ∙ P vi ) × l,

eller:

[ r c R v - Σ ( r jeg P vi )] × l= 0.

Det siste uttrykket er bare gyldig hvis uttrykket i hakeparenteser er null. Derfor utelater indeksenvog med tanke på at resultatetR = Σ Pi , herfra får vi:

rc = (Σ Pi r jeg )/(Σ Pi ).

Projiserer den siste vektorlikheten på koordinataksen, får vi ønsket uttrykk for koordinatene til sentrum av parallelle krefter:

x c = (Σ Pi x i)/(Σ Pi );

yc = (Σ Pi y jeg )/(Σ Pi );(2)

z c = (Σ Pi z i )/(Σ Pi ).

Kroppens tyngdepunkt

Koordinater til tyngdepunktene til en homogen kropp.

Vurder en stiv kroppsveiing P og volum V i koordinatsystemet Oxyz, hvor aksene x og y forbundet med jordens overflate, og aksen z rettet mot senit.

Hvis vi bryter kroppen i elementære deler med et volum∆ V Jeg , så vil tiltrekningskraften virke på hver del av den∆ Pirettet mot jordens sentrum. La oss anta at kroppens dimensjoner er mye mindre enn jordens dimensjoner, så kan systemet av krefter som påføres de elementære delene av kroppen betraktes som ikke konvergerende, men parallelt (fig. 3), og alle konklusjonene i forrige kapittel gjelder for det.

Fig.3

Definisjon . Tyngdepunktet til et stivt legeme er sentrum for parallelle tyngdekrefter til de elementære delene av denne kroppen.

Husk det egenvekt elementær del av kroppen kalles forholdet mellom vekten∆ Pi til volum ∆ V Jeg : γ Jeg = ∆ Pi/ ∆ V Jeg . For en homogen kropp er denne verdien konstant:γ Jeg = γ = P/ V.

Bytter inn i (2) ∆ Pi = γ Jeg ∙∆ V Jeg i stedet for Pi, tar hensyn til den siste bemerkningen og reduserer telleren og nevneren medg, vi får uttrykk for koordinatene til tyngdepunktet til en homogen kropp:

x c = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

yc = (Σ ∆ Vi∙ y jeg )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Flere teoremer er nyttige for å bestemme tyngdepunktet.

1) Hvis et homogent legeme har et symmetriplan, er tyngdepunktet i dette planet.

Hvis aksene X og på plassert i dette symmetriplanet, deretter for hvert punkt med koordinater. og koordinere i henhold til (3), vil være lik null, fordi totalt alle termer med motsatte fortegn elimineres i par. Så tyngdepunktet er i symmetriplanet.

2) Hvis et homogent legeme har en symmetriakse, er kroppens tyngdepunkt plassert på denne aksen.

Faktisk, i dette tilfellet, hvis aksenztegne langs symmetriaksen, for hvert punkt med koordinaterdu kan finne et punkt med koordinater og koordinater og beregnet med formler (3) vil være lik null.

Det tredje teoremet er bevist på samme måte.

3) Hvis en homogen kropp har et symmetrisenter, er tyngdepunktet til kroppen lokalisert på dette punktet.

Og noen flere bemerkninger.

Først. Hvis kroppen kan deles inn i deler der vekten og posisjonen til tyngdepunktet er kjent, er det ikke nødvendig å vurdere hvert punkt, men i formler (3) Pi – bestemmes som vekten av den aktuelle delen ogsom koordinatene til tyngdepunktet.

Sekund. Hvis kroppen er homogen, så vekten av en separat del av den, hvor er egenvekten til materialet som kroppen er laget av, og Vi - volumet til denne delen av kroppen. Og formler (3) vil ha en mer praktisk form. For eksempel,

Og på samme måte, hvor - volumet av hele kroppen.

Tredje note. La kroppen se ut som en tynn plate med areal F og tykkelse t ligger i flyet Oxy. Bytter inn i (3)∆ V Jeg =t ∙ ∆F Jeg , vi får koordinatene til tyngdepunktet til en homogen plate:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

yc = (Σ ∆ F i∙ y jeg ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z Jeg ) / (Σ ∆ F i).

hvor - koordinater for tyngdepunktet til individuelle plater;er det totale arealet av kroppen.

Fjerde note. For en kropp i form av en tynn krumlinjet stang med en lengde L med tverrsnittsareal en elementært volum∆ V Jeg = en ∙∆ L Jeg , derfor koordinater for tyngdepunktet til en tynn krumlinjet stav vil være lik:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

yc = (Σ ∆ L i∙ y jeg )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

hvor – koordinater til tyngdepunktetJeg-th seksjon; .

Merk at ifølge definisjonen er tyngdepunktet et geometrisk punkt; den kan også ligge utenfor grensene til en gitt kropp (for eksempel for en ring).

Merk.

I denne delen av kurset skiller vi ikke mellom tyngdekraft, tyngdekraft og kroppsvekt. I virkeligheten er tyngdekraften forskjellen mellom jordens tyngdekraft og sentrifugalkraften forårsaket av rotasjonen.

Koordinater til tyngdepunktene til inhomogene legemer.

Tyngdepunktets koordinater inhomogent fast stoff(Fig. 4) i det valgte referansesystemet er definert som følger:

Fig.4

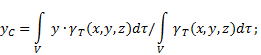
hvor - vekt per enhet kroppsvolum (spesifikk vekt)

- hele kroppsvekten.

ujevn overflate(fig. 5), så bestemmes koordinatene til tyngdepunktet i det valgte referansesystemet som følger:

Fig.5

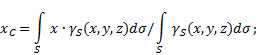
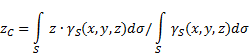
hvor - vekt per kroppsarealenhet

- hele kroppsvekten.

Hvis det faste er heterogen linje(fig. 6), så bestemmes koordinatene til tyngdepunktet i det valgte referansesystemet som følger:

Fig.6

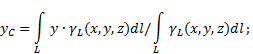
hvor - kroppslengde vektenhet,

Hele kroppsvekten.

Metoder for å bestemme koordinatene til tyngdepunktet.

Basert på de generelle formlene oppnådd ovenfor, er det mulig å indikere spesifikke metoder bestemme koordinatene til legemers tyngdepunkt.

1. Symmetri. Hvis et homogent legeme har et plan, akse eller symmetrisenter (fig. 7), så ligger dets tyngdepunkt henholdsvis i symmetriplanet, symmetriaksen eller i symmetrisenteret.

Fig.7

2. Splitting. Kroppen er delt inn i et begrenset antall deler (fig. 8), for hver av disse er posisjonen til tyngdepunktet og området kjent.

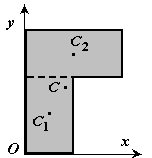
Fig.8

S \u003d S 1 + S 2.

3.Metode for negative områder. Et spesielt tilfelle av partisjoneringsmetoden (fig. 9). Det gjelder kropper med utskjæringer dersom tyngdepunktene til kroppen uten utskjæringen og utskjæringen er kjent. En kropp i form av en plate med en utskjæring er representert ved en kombinasjon av en solid plate (uten utskjæring) med et område S1 og området til den utskårne delen S2.

Fig.9

S \u003d S 1 - S 2.

4.grupperingsmetode. Det er et godt tillegg til de to siste metodene. Etter å ha brutt figuren inn i dens bestanddeler, kan det være praktisk å kombinere noen av dem igjen, for deretter å forenkle løsningen ved å ta hensyn til symmetrien til denne gruppen.

Tyngdepunktene til noen homogene kropper.

1) Tyngdepunktet til en sirkelbue. Tenk på buen AB radiusR med midtvinkel. På grunn av symmetri ligger tyngdepunktet til denne buen på aksenOkse(Fig. 10).

Fig.10

La oss finne koordinaten i henhold til formelen . For å gjøre dette, velg på buen AB element MM ’ lang, hvis posisjon bestemmes av vinkelen. Koordinere X element MM' vil være. Erstatter disse verdiene X og d l og med tanke på at integralet må strekkes over hele lengden av buen, får vi:

der L er lengden på buen AB lik .

Herfra finner vi til slutt at tyngdepunktet til sirkelbuen ligger på symmetriaksen i avstand fra sentrumÅ like

hvor er vinkelen målt i radianer.

2) Tyngdepunktet til området til en trekant. Tenk på en trekant som ligger i flyet Oxy, hvis toppunktkoordinater er kjent: A i (x i,y jeg ), (Jeg= 1,2,3). Bryt trekanten i smale strimler parallelt med siden MEN 1 MEN 2 kommer vi til at trekantens tyngdepunkt må tilhøre medianen MEN 3 M 3 (fig. 11).

Fig.11

Bryt trekanten i strimler parallelt med siden MEN 2 MEN 3 , kan du sørge for at den må ligge på medianen MEN 1 M en . På denne måten, tyngdepunktet til en trekant ligger i skjæringspunktet mellom medianene, som, som du vet, skiller den tredje delen fra hver median, tellende fra den tilsvarende siden.

Spesielt for medianen MEN 1 M 1 får vi, gitt at koordinatene til punktet M 1 - er det aritmetiske gjennomsnittet av koordinatene til toppunktene MEN 2 og MEN 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Dermed er koordinatene til trekantens tyngdepunkt det aritmetiske gjennomsnittet av koordinatene til hjørnene:

x c =(1/3) Σ x i ; y c =(1/3) Σ y jeg .

3) Tyngdepunktet for området til den sirkulære sektoren. Betrakt en sektor av en sirkel med radius R med midtvinkel 2α , plassert symmetrisk om aksen Okse (Fig. 12).

Det er åpenbart det y c = 0, og avstanden fra sentrum av sirkelen som denne sektoren er kuttet fra til tyngdepunktet kan bestemmes av formelen:

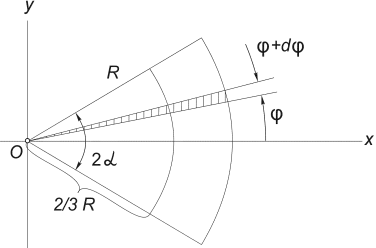
Fig.12

Den enkleste måten å beregne dette integralet på er ved å dele integrasjonsdomenet inn i elementære sektorer med en vinkel dφ . Opp til infinitesimals av første orden kan en slik sektor erstattes av en trekant med en base lik R × dφ og høyde R. Arealet til en slik trekant dF =(1/2)R 2 ∙ dφ , og tyngdepunktet er 2/3 R fra toppen, så i (5) legger vi x = (2/3)R∙ cos. Bytter inn i (5) F= α R 2 får vi:

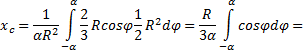
Ved å bruke den siste formelen beregner vi spesielt avstanden til tyngdepunktet halvsirkel.

Ved å erstatte med (2) α = π /2, får vi: x c = (4 R)/(3 π ) ≅ 0,4 R .

Eksempel 1La oss bestemme tyngdepunktet til den homogene kroppen vist i fig. 1. 3.

Fig.13

Løsning.Kroppen er homogen, bestående av to deler som har en symmetrisk form. Koordinatene til deres tyngdepunkt:

Volumene deres:

Derfor er koordinatene til kroppens tyngdepunkt

Eksempel 2 Finn tyngdepunktet til en plate bøyd i rett vinkel. Dimensjoner - på tegningen (fig. 14).

Fig.14

Løsning. Tyngdepunktskoordinater:

0.

Firkanter:

Derfor:

Eksempel 3 På et firkantet ark cm kuttet firkantet hull se (fig. 15). Finn tyngdepunktet til arket. Eksempel 4 Finn posisjonen til tyngdepunktet til platen vist i fig. 16. Mål er oppgitt i centimeter.

Fig.16

Løsning. Vi deler platen inn i figurer (fig. 17), sentre hvis alvorlighetsgrad er kjent.

Arealene til disse figurene og koordinatene til deres tyngdepunkt:

1) et rektangel med sidene 30 og 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; på 1 \u003d 20 cm.

2) en rettvinklet trekant med en base på 50 cm og en høyde på 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; X 2 \u003d 30 + 50 / 3 \u003d 46,7 cm; y 2 =40/3 =13,3 cm;

3) halvsirkel sirkelradius r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; X 3 =4 R /3 π =8,5 cm; på

Løsning. Husk at i fysikk tettheten til en kroppρ og dens egenvektgrelatert av forholdet:γ = ρ g , hvorg - tyngdeakselerasjon. For å finne massen til en slik homogen kropp, må du multiplisere tettheten med volumet.

Fig.19

Begrepet "lineær" eller "lineær" tetthet betyr at for å bestemme massen til fagverksstangen, må den lineære tettheten multipliseres med lengden på denne stangen.

For å løse problemet kan du bruke partisjoneringsmetoden. Ved å representere en gitt fagverk som en sum av 6 individuelle stenger, får vi:

hvorL i lengdeJeg -th stang av gården, ogx i , y jeg - koordinatene til tyngdepunktet.

Løsningen på dette problemet kan forenkles ved å gruppere de siste 5 fagverkstengene. Det er lett å se at de danner en figur med et symmetrisenter plassert i midten av den fjerde staven, der tyngdepunktet til denne gruppen av staver er plassert.

Dermed kan et gitt fagverk representeres av en kombinasjon av bare to grupper av stenger.

Den første gruppen består av den første stangen, for denL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. Den andre gruppen av stenger består av fem stenger, for hvilkeL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

Koordinatene til gårdens tyngdepunkt er funnet ved formelen:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Merk at sentrum FRA ligger på linjen som forbinder FRA 1 og FRA 2 og deler segmentet FRA 1 FRA 2 angående: FRA 1 FRA/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.

Spørsmål til selvransakelse

Hva er sentrum av parallelle krefter?

- Hvordan bestemmes koordinatene til sentrum av parallelle krefter?

- Hvordan bestemme sentrum av parallelle krefter, hvis resultant er null?

Hva er egenskapen til sentrum av parallelle krefter?

- Hvilke formler brukes for å beregne koordinatene til sentrum av parallelle krefter?

Hva er tyngdepunktet til en kropp?

- Hvorfor kan tiltrekningskreftene til Jorden, som virker på et punkt på kroppen, tas som et system av parallelle krefter?

- Skriv ned formelen for å bestemme posisjonen til tyngdepunktet til inhomogene og homogene legemer, formelen for å bestemme posisjonen til tyngdepunktet til flate seksjoner?

- Skriv ned formelen for å bestemme posisjonen til tyngdepunktet til enkle geometriske former: et rektangel, en trekant, en trapes og en halv sirkel?

Hva kalles områdets statiske moment?

- Gi et eksempel på en kropp hvis tyngdepunkt er plassert utenfor kroppen.

- Hvordan brukes symmetriegenskaper for å bestemme tyngdepunktene til legemer?

- Hva er essensen av metoden med negative vekter?

Hvor ligger tyngdepunktet til sirkelbuen?

Hvordan kan du grafisk finne tyngdepunktet til en trekant?

- Skriv ned formelen som bestemmer tyngdepunktet til den sirkulære sektoren.

- Ved å bruke formlene som bestemmer tyngdepunktene til en trekant og en sirkulær sektor, utlede en lignende formel for et sirkulært segment.

- Hvilke formler brukes for å beregne koordinatene til tyngdepunktene til homogene kropper, flate figurer og linjer?

- Hva kalles det statiske momentet til arealet til en flat figur i forhold til aksen, hvordan beregnes det og hvilken dimensjon har det?

- Hvordan bestemme posisjonen til tyngdepunktet i området, hvis posisjonen til tyngdepunktene til de enkelte delene er kjent?

- Hvilke hjelpesetninger brukes for å bestemme posisjonen til tyngdepunktet?