Hvordan finne den deriverte av en funksjon til en potens. Derivert av en logaritmisk funksjon

Bevis og utledning av formlene for den deriverte av eksponentialen (e i potensen av x) og eksponentiell funksjon(a til x-potensen). Eksempler på beregning av derivater av e^2x, e^3x og e^nx. Formler for derivater av høyere orden.

Den deriverte av en eksponent er lik eksponenten selv (den deriverte av e til x-potensen er lik e til x-potensen):
(1) (e x )′ = e x.

Den deriverte av en eksponentiell funksjon med basis av grad a er lik funksjonen selv multiplisert med naturlig logaritme fra en:
(2) .

Avledning av formelen for den deriverte av eksponentialen, e til x potens

En eksponentiell er en eksponentiell funksjon hvis grunntall er lik tallet e, som er følgende grense:
.
Her kan det være både naturlig og reelt tall. Deretter utleder vi formel (1) for den deriverte av eksponentialen.

Avledning av eksponentiell derivatformel

Tenk på eksponentialen, e til x-potensen:
y = e x .
Denne funksjonen er definert for alle.
(3) .

La oss finne dens deriverte med hensyn til variabelen x. Per definisjon er derivatet følgende grense: La oss transformere dette uttrykket for å redusere det til de kjente
matematiske egenskaper og regler. For å gjøre dette trenger vi følgende fakta:
(4) ;
EN) Eksponentegenskap:
(5) ;
B) Egenskapen til logaritmen:
(6) .
I)
Kontinuitet til logaritmen og egenskapen til grenser for en kontinuerlig funksjon: Her er en funksjon som har en grense og denne grensen er positiv.
(7) .

G)
;
.

Betydningen av den andre bemerkelsesverdige grensen:
La oss bruke disse fakta til vår grense (3). Vi bruker eiendom (4):
.
La oss gjøre en erstatning.
.

Så ; .
.

På grunn av kontinuiteten til eksponentialen,
Derfor, når , .
.

Som et resultat får vi:
.
La oss gjøre en erstatning. Så . På , . Og vi har: La oss bruke logaritme-egenskapen (5):
.

.

Da

La oss bruke eiendom (6). Siden det er en positiv grense og logaritmen er kontinuerlig, så:
(8)
Her brukte vi også den andre

bemerkelsesverdig grense (7). Da Dermed fikk vi formel (1) for den deriverte av eksponentialen.
;
.
Derivasjon av formelen for den deriverte av en eksponentiell funksjon
.

Nå utleder vi formel (2) for den deriverte av eksponentialfunksjonen med en base av grad a.

La oss nå finne derivater av høyere ordener. La oss først se på eksponenten:
(14) .
(1) .

Vi ser at den deriverte av funksjon (14) er lik funksjon (14) i seg selv. Ved å differensiere (1), får vi derivater av andre og tredje orden:
;
.

Dette viser at den n-te ordens deriverte også er lik den opprinnelige funksjonen:
.

Høyere ordens deriverte av eksponentialfunksjonen

Tenk nå på en eksponentiell funksjon med basis av grad a:
.
Vi fant dens førsteordens derivat:
(15) .

Ved å differensiere (15), får vi derivater av andre og tredje orden:
;
.

Vi ser at hver differensiering fører til multiplikasjon av den opprinnelige funksjonen med .
.

Derfor har den n-te ordens deriverte følgende form:

Definisjon av potens-eksponentiell funksjon. Utlede en formel for å beregne dens deriverte. Eksempler på beregning av deriverte av potens-eksponentielle funksjoner analyseres i detalj. Power-eksponentiell funksjon er en funksjon som ser ut som
strømfunksjon
y = u v ,
der basen u og eksponenten v er noen funksjoner av variabelen x: u = u(x) u = u.
; v = v Denne funksjonen kalles også

eksponentiell
.
eller . Merk at potens-eksponentialfunksjonen kan representeres i eksponentiell form:.

Derfor kalles det også

kompleks eksponentiell funksjon
(2) ,
Beregning med logaritmisk derivert
La oss finne den deriverte av potens-eksponentialfunksjonen
.
hvor og er funksjoner til variabelen.
(3) .
For å gjøre dette, logaritmer vi ligningen (2), ved å bruke egenskapen til logaritmen: Differensier med hensyn til variabelen x: Vi søker
;
.

regler for å differensiere komplekse funksjoner
.
og fungerer:
.

Vi erstatter i (3):
(1) .
Herfra
.
Så vi fant den deriverte av potens-eksponentialfunksjonen:
.
Hvis eksponenten er konstant, så .

Da er den deriverte lik den deriverte av en kompleks potensfunksjon:

Hvis bunnen av graden er konstant, så .
(2) ,
Da er den deriverte lik den deriverte av en kompleks eksponentiell funksjon:
(4) .

Når og er funksjoner av x, så er den deriverte av potens-eksponentialfunksjonen lik summen av de deriverte av kompleks potens og eksponentialfunksjoner.
.
Beregning av den deriverte ved reduksjon til en kompleks eksponentiell funksjon La oss nå finne den deriverte av potens-eksponentialfunksjonen:

.
presenterer det som en kompleks eksponentiell funksjon:

La oss skille produktet:

Bruk regelen for å finne den deriverte
.

kompleks funksjon

Og vi fikk igjen formel (1).
Eksempel 1 .

Finn den deriverte av følgende funksjon:
;
.
Løsning
.
Vi skiller (A1.1):
.
Fordi
,
At
.

Svare

Eksempel 2

Finn den deriverte av funksjonen
.

kompleks funksjon

La oss logaritme den opprinnelige funksjonen:
(A2.1) .

Operasjonen med å finne den deriverte kalles differensiering.

Som et resultat av å løse problemer med å finne deriverte av de enkleste (og ikke veldig enkle) funksjonene ved å definere den deriverte som grensen for forholdet mellom økningen og økningen av argumentet, dukket det opp en tabell med deriverte og nøyaktig definerte regler for differensiering . De første som arbeidet med å finne derivater var Isaac Newton (1643-1727) og Gottfried Wilhelm Leibniz (1646-1716).

Derfor, i vår tid, for å finne den deriverte av en funksjon, trenger du ikke å beregne den ovennevnte grensen for forholdet mellom økningen av funksjonen og økningen av argumentet, men du trenger bare å bruke tabellen med derivater og differensieringsreglene. Følgende algoritme er egnet for å finne den deriverte.

For å finne den deriverte, trenger du et uttrykk under primtegnet bryte ned enkle funksjoner i komponenter og bestemme hvilke handlinger (produkt, sum, kvotient) disse funksjonene er relatert. Ytterligere derivater elementære funksjoner finner vi i tabellen over deriverte, og formlene for produktets deriverte, sum og kvotient står i differensieringsreglene. Den deriverte tabellen og differensieringsreglene er gitt etter de to første eksemplene.

Eksempel 1. Finn den deriverte av en funksjon

Løsning. Fra reglene for differensiering finner vi ut at den deriverte av en sum av funksjoner er summen av deriverte av funksjoner, dvs.

Fra tabellen over deriverte finner vi ut at den deriverte av "x" er lik en, og den deriverte av sinus er lik cosinus. Vi erstatter disse verdiene i summen av deriverte og finner den deriverte som kreves av tilstanden til problemet:

Eksempel 2. Finn den deriverte av en funksjon

Løsning. Vi differensierer som en derivert av en sum der det andre leddet har en konstant faktor den kan tas ut av tegnet til den deriverte:

Hvis det likevel dukker opp spørsmål om hvor noe kommer fra, blir de vanligvis ryddet opp etter å ha satt seg inn i tabellen over derivater og de enkleste differensieringsreglene. Vi går videre til dem akkurat nå.

Tabell over deriverte av enkle funksjoner

1. Derivert av en konstant (tall). Et hvilket som helst tall (1, 2, 5, 200...) som er i funksjonsuttrykket. Alltid lik null. Dette er veldig viktig å huske, da det kreves veldig ofte
2. Derivert av den uavhengige variabelen. Oftest "X". Alltid lik en. Dette er også viktig å huske lenge
3. Avledet av grad. Når du løser problemer, må du konvertere ikke-kvadratrøtter til potenser.
4. Derivert av en variabel i potensen -1
5. Derivat kvadratrot
6. Derivert av sinus
7. Derivat av cosinus
8. Derivert av tangent
9. Derivat av cotangens
10. Derivat av arcsine
11. Derivat av arccosine
12. Derivat av arctangens
13. Derivat av lysbue cotangens
14. Derivert av den naturlige logaritmen
15. Derivert av en logaritmisk funksjon
16. Derivert av eksponenten
17. Derivert av en eksponentiell funksjon

Regler for differensiering

1. Derivert av en sum eller differanse
2. Derivat av produktet
2a. Derivert av et uttrykk multiplisert med en konstant faktor
3. Derivat av kvotienten
4. Derivat av en kompleks funksjon

Regel 1.Hvis funksjonene

er differensierbare på et tidspunkt, så er funksjonene differensierbare på samme punkt

og

de. den deriverte av den algebraiske summen av funksjoner er lik algebraisk sum derivater av disse funksjonene.

Konsekvens. Hvis to differensierbare funksjoner er forskjellige med et konstant ledd, er deres deriverte like, dvs.

Regel 2.Hvis funksjonene

er differensierbare på et tidspunkt, så er produktet deres differensierbart på samme punkt

og

de. Den deriverte av produktet av to funksjoner er lik summen av produktene til hver av disse funksjonene og den deriverte av den andre.

Konsekvens 1. Konstantfaktoren kan tas ut av tegnet til den deriverte:

Konsekvens 2. Den deriverte av produktet av flere differensierbare funksjoner er lik summen av produktene av den deriverte av hver faktor og alle de andre.

For eksempel for tre multiplikatorer:

Regel 3.Hvis funksjonene

differensierbar på et tidspunkt Og , så på dette punktet er kvotienten deres også differensierbaru/v, og

de. den deriverte av kvotienten av to funksjoner er lik en brøk, hvis teller er forskjellen mellom produktene av nevneren og den deriverte av telleren og telleren og den deriverte av nevneren, og nevneren er kvadratet av den tidligere telleren.

Hvor du kan se etter ting på andre sider

Når man finner den deriverte av et produkt og kvotienten i reelle problemer Det er alltid nødvendig å bruke flere differensieringsregler samtidig, så det er flere eksempler på disse derivatene i artikkelen"Derivat av produktet og kvotient av funksjoner".

Kommentar. Du bør ikke forveksle en konstant (det vil si et tall) som et ledd i en sum og som en konstant faktor! Når det gjelder et ledd, er dets deriverte lik null, og når det gjelder en konstant faktor, er det tatt ut av tegnet til de deriverte. Dette typisk feil, som skjer på innledende fase studere derivater, men ettersom de løser flere en- og todelte eksempler, gjør ikke den gjennomsnittlige eleven lenger denne feilen.

Og hvis du, når du skiller et produkt eller kvotient, har et begrep u"v, hvori u- et tall, for eksempel 2 eller 5, det vil si en konstant, så vil den deriverte av dette tallet være lik null, og derfor vil hele leddet være lik null (dette tilfellet er diskutert i eksempel 10).

En annen vanlig feil er å mekanisk løse den deriverte av en kompleks funksjon som den deriverte av en enkel funksjon. Det er derfor avledet av en kompleks funksjon en egen artikkel er viet. Men først skal vi lære å finne derivater enkle funksjoner.

Underveis kan du ikke gjøre uten å transformere uttrykk. For å gjøre dette må du kanskje åpne manualen i nye vinduer. Handlinger med krefter og røtter Og Operasjoner med brøker .

Hvis du leter etter løsninger på deriverte av brøker med potenser og røtter, det vil si når funksjonen ser ut som , og følg deretter leksjonen "Avledet av summer av brøker med potenser og røtter."

Hvis du har en oppgave som , så vil du ta leksjonen "Derivater av enkle trigonometriske funksjoner".

Steg-for-steg eksempler - hvordan finne den deriverte

Eksempel 3. Finn den deriverte av en funksjon

Løsning. Vi definerer delene av funksjonsuttrykket: hele uttrykket representerer et produkt, og dets faktorer er summer, i det andre inneholder ett av leddene en konstant faktor. Vi bruker produktdifferensieringsregelen: den deriverte av produktet av to funksjoner er lik summen av produktene til hver av disse funksjonene med den deriverte av den andre:

Deretter bruker vi regelen for differensiering av summen: den deriverte av den algebraiske summen av funksjoner er lik den algebraiske summen av de deriverte av disse funksjonene. I vårt tilfelle har det andre leddet et minustegn i hver sum. I hver sum ser vi både en uavhengig variabel, hvis deriverte er lik én, og en konstant (tall), hvis deriverte er lik null. Så, "X" blir til en, og minus 5 blir til null. I det andre uttrykket multipliseres "x" med 2, så vi multipliserer to med samme enhet som den deriverte av "x". Vi får følgende verdier derivater:

Vi erstatter de funnet deriverte i summen av produkter og får den deriverte av hele funksjonen som kreves av tilstanden til problemet:

Eksempel 4. Finn den deriverte av en funksjon

Løsning. Vi er pålagt å finne den deriverte av kvotienten. Vi bruker formelen for å differensiere kvotienten: den deriverte av kvotienten til to funksjoner er lik en brøk, hvis teller er forskjellen mellom produktene til nevneren og den deriverte av telleren og telleren og den deriverte av nevneren, og nevneren er kvadratet til den tidligere telleren. Vi får:

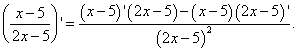
Vi har allerede funnet den deriverte av faktorene i telleren i eksempel 2. La oss heller ikke glemme at produktet, som er den andre faktoren i telleren i gjeldende eksempel, er tatt med et minustegn:

Hvis du leter etter løsninger på problemer der du trenger å finne den deriverte av en funksjon, hvor det er en kontinuerlig haug med røtter og potenser, som f.eks. , så velkommen til timen "Derivat av summer av brøker med potenser og røtter" .

Hvis du trenger å lære mer om derivatene av sinus, cosinus, tangenter og andre trigonometriske funksjoner, det vil si når funksjonen ser ut , så en leksjon for deg "Derivater av enkle trigonometriske funksjoner" .

Eksempel 5. Finn den deriverte av en funksjon

Løsning. I denne funksjonen ser vi et produkt, hvor en av faktorene er kvadratroten av den uavhengige variabelen, den deriverte vi gjorde oss kjent med i tabellen over deriverte. I henhold til regelen om differensiering av produktet og tabellverdi avledet av kvadratroten får vi:

Eksempel 6. Finn den deriverte av en funksjon

Løsning. I denne funksjonen ser vi en kvotient hvis utbytte er kvadratroten av den uavhengige variabelen. Ved å bruke regelen for differensiering av kvotienter, som vi gjentok og brukte i eksempel 4, og den tabulerte verdien av den deriverte av kvadratroten, får vi:

For å bli kvitt en brøk i telleren, multipliser telleren og nevneren med .

På hvilken vi analyserte de enkleste derivatene, og også ble kjent med reglene for differensiering og noen tekniske metoder finne derivater. Derfor, hvis du ikke er veldig god med avledede funksjoner eller noen punkter i denne artikkelen ikke er helt klare, så les først leksjonen ovenfor. Vær så snill å kom i seriøs stemning - materialet er ikke enkelt, men jeg vil likevel prøve å presentere det enkelt og tydelig.

I praksis må du forholde deg til den deriverte av en kompleks funksjon veldig ofte, jeg vil til og med si, nesten alltid, når du får oppgaver med å finne deriverte.

Vi ser på tabellen ved regelen (nr. 5) for å differensiere en kompleks funksjon:

La oss finne ut av det. Først av alt, la oss ta hensyn til oppføringen. Her har vi to funksjoner – og , og funksjonen, billedlig talt, er nestet i funksjonen . En funksjon av denne typen (når en funksjon er nestet i en annen) kalles en kompleks funksjon.

Jeg vil kalle funksjonen ekstern funksjon, og funksjonen – intern (eller nestet) funksjon.

! Disse definisjonene er ikke teoretiske og skal ikke fremkomme i den endelige utformingen av oppgavene. Jeg bruker uformelle uttrykk "ekstern funksjon", "intern" funksjon kun for å gjøre det lettere for deg å forstå stoffet.

For å avklare situasjonen, vurder:

Eksempel 1

Finn den deriverte av en funksjon

Under sinusen har vi ikke bare bokstaven "X", men et helt uttrykk, så det vil ikke fungere å finne den deriverte med en gang fra tabellen. Vi legger også merke til at det er umulig å bruke de fire første reglene her, det ser ut til å være en forskjell, men faktum er at sinusen ikke kan "reves i stykker":

I i dette eksemplet Det er allerede intuitivt klart fra mine forklaringer at en funksjon er en kompleks funksjon, og polynomet er en intern funksjon (embedding), og en ekstern funksjon.

Første steg det du må gjøre når du finner den deriverte av en kompleks funksjon er å forstå hvilken funksjon som er intern og hvilken som er ekstern.

I tilfelle enkle eksempler Det virker klart at et polynom er innebygd under sinusen. Men hva om alt ikke er åpenbart? Hvordan bestemme nøyaktig hvilken funksjon som er ekstern og hvilken som er intern? For å gjøre dette foreslår jeg å bruke følgende teknikk, som kan gjøres mentalt eller i et utkast.

La oss forestille oss at vi må beregne verdien av uttrykket på en kalkulator (i stedet for en kan det være et hvilket som helst tall).

Hva skal vi beregne først? Først av alt du må utføre følgende handling: , derfor vil polynomet være en intern funksjon:

For det andre må finnes, så sinus – vil være en ekstern funksjon:

Etter vi UTSOLGT med interne og eksterne funksjoner er det på tide å bruke regelen om differensiering av komplekse funksjoner .

La oss begynne å bestemme oss. Fra leksjonen Hvordan finne den deriverte? vi husker at utformingen av en løsning til en hvilken som helst derivat alltid begynner slik - vi omslutter uttrykket i parentes og setter et strøk øverst til høyre:

Først vi finner den deriverte av den ytre funksjonen (sinus), ser på tabellen over avledede av elementære funksjoner og legger merke til at . Alle tabellformler kan også brukes hvis "x" erstattes med et komplekst uttrykk, V i dette tilfellet:

Vær oppmerksom på at den indre funksjonen har ikke endret seg, vi rører den ikke.

Vel, det er ganske åpenbart det

Resultatet av å bruke formelen i sin endelige form ser det slik ut:

Konstantfaktoren plasseres vanligvis i begynnelsen av uttrykket:

Hvis det er noen misforståelser, skriv ned løsningen på papir og les forklaringene på nytt.

Eksempel 2

Finn den deriverte av en funksjon

Eksempel 3

Finn den deriverte av en funksjon

Som alltid skriver vi ned:

La oss finne ut hvor vi har en ekstern funksjon og hvor vi har en intern. For å gjøre dette prøver vi (mentalt eller i et utkast) å beregne verdien av uttrykket ved . Hva bør du gjøre først? Først av alt må du beregne hva basen er lik: derfor er polynomet den interne funksjonen:

Og bare da utføres eksponentieringen, derfor er potensfunksjonen en ekstern funksjon:

I henhold til formelen , først må du finne den deriverte av den eksterne funksjonen, i dette tilfellet graden. Leter etter i tabellen den nødvendige formelen: . Vi gjentar igjen: enhver tabellformel er gyldig ikke bare for "X", men også for et komplekst uttrykk. Dermed resultatet av å bruke regelen for å differensiere en kompleks funksjon neste:

Jeg understreker igjen at når vi tar den deriverte av den eksterne funksjonen, endres ikke vår interne funksjon:

Nå gjenstår det bare å finne en veldig enkel avledning av den interne funksjonen og justere resultatet litt:

Eksempel 4

Finn den deriverte av en funksjon

Dette er et eksempel for uavhengig avgjørelse(svar på slutten av timen).

For å konsolidere din forståelse av den deriverte av en kompleks funksjon, vil jeg gi et eksempel uten kommentarer, prøve å finne ut av det på egen hånd, begrunne hvor den eksterne og hvor den interne funksjonen er, hvorfor oppgavene løses på denne måten?

Eksempel 5

a) Finn den deriverte av funksjonen

b) Finn den deriverte av funksjonen

Eksempel 6

Finn den deriverte av en funksjon

Her har vi en rot, og for å skille roten må den representeres som en kraft. Derfor bringer vi først funksjonen til den formen som passer for differensiering:

Ved å analysere funksjonen kommer vi til at summen av de tre leddene er en intern funksjon, og å heve til en potens er en ekstern funksjon. Vi bruker regelen om differensiering av komplekse funksjoner :

Vi representerer igjen graden som en radikal (rot), og for den deriverte av den interne funksjonen bruker vi en enkel regel for å differensiere summen:

Ferdig. Du kan også gi uttrykket i parentes til fellesnevner og skriv alt ned som én brøk. Det er selvfølgelig vakkert, men når du får tungvinte lange derivater, er det bedre å ikke gjøre dette (det er lett å bli forvirret, gjøre en unødvendig feil, og det vil være upraktisk for læreren å sjekke).

Eksempel 7

Finn den deriverte av en funksjon

Dette er et eksempel du kan løse på egen hånd (svar på slutten av leksjonen).

Det er interessant å merke seg at noen ganger i stedet for regelen for å differensiere en kompleks funksjon, kan du bruke regelen for å differensiere en kvotient , men en slik løsning vil se ut som en uvanlig perversjon. Her er et typisk eksempel:

Eksempel 8

Finn den deriverte av en funksjon

Her kan du bruke regelen om differensiering av kvotienten , men det er mye mer lønnsomt å finne den deriverte gjennom regelen for differensiering av en kompleks funksjon:

Vi forbereder funksjonen for differensiering - vi flytter minus ut av det deriverte tegnet, og hever cosinus til telleren:

Cosinus er en intern funksjon, eksponentiering er en ekstern funksjon.
La oss bruke vår regel :

Vi finner den deriverte av den interne funksjonen og tilbakestiller cosinus:

Ferdig. I det betraktede eksemplet er det viktig å ikke bli forvirret i skiltene. Forresten, prøv å løse det ved å bruke regelen , må svarene samsvare.

Eksempel 9

Finn den deriverte av en funksjon

Dette er et eksempel du kan løse på egen hånd (svar på slutten av leksjonen).

Så langt har vi sett på tilfeller der vi kun hadde én hekking i en kompleks funksjon. I praktiske oppgaver kan du ofte finne derivater, der, som hekkende dukker, den ene inne i den andre, 3 eller til og med 4-5 funksjoner er nestet på en gang.

Eksempel 10

Finn den deriverte av en funksjon

La oss forstå vedleggene til denne funksjonen. La oss prøve å beregne uttrykket ved å bruke den eksperimentelle verdien. Hvordan vil vi regne med en kalkulator?

Først må du finne , som betyr at arcsine er den dypeste innebyggingen:

Denne arcsinen til en skal da kvadrateres:

Og til slutt hever vi syv til en makt:

Det vil si at i dette eksemplet har vi tre ulike funksjoner og to embeddings, der den innerste funksjonen er arcsine og den ytterste funksjonen er den eksponentielle funksjonen.

La oss begynne å bestemme oss

I følge regelen Først må du ta den deriverte av den ytre funksjonen. Vi ser på tabellen med deriverte og finner den deriverte av eksponentialfunksjonen: Den eneste forskjellen er at i stedet for "x" har vi komplekst uttrykk, som ikke opphever gyldigheten av denne formelen. Så resultatet av å bruke regelen for å differensiere en kompleks funksjon neste.

Derivasjon av formelen for den deriverte av en potensfunksjon (x i potensen av a). Derivater fra røttene til x vurderes. Formel for den deriverte av en potensfunksjon høyere orden. Eksempler på beregning av derivater.

Den deriverte av x i potensen av a er lik a ganger x i potensen av en minus en:
(1) .

Den deriverte av den n-te roten av x til mte potens er:
(2) .

Avledning av formelen for den deriverte av en potensfunksjon

Sak x > 0

Tenk på en potensfunksjon av variabelen x med eksponent a:
(3) .
Her er a et vilkårlig reelt tall. La oss først vurdere saken.

For å finne den deriverte av funksjon (3), bruker vi egenskapene til en potensfunksjon og transformerer den til følgende form:
.

Nå finner vi den deriverte ved å bruke:
;
.
Her .

Formel (1) er bevist.

Avledning av formelen for den deriverte av en rot av grad n av x til graden av m

Tenk nå på en funksjon som er roten til følgende form:
(4) .

For å finne den deriverte transformerer vi roten til en potensfunksjon:
.
Sammenligner vi med formel (3) ser vi det
.
Da
.

Ved å bruke formel (1) finner vi den deriverte:
(1) ;
;
(2) .

I praksis er det ikke nødvendig å memorere formel (2). Det er mye mer praktisk å først transformere røttene til potensfunksjoner, og deretter finne deres deriverte ved å bruke formel (1) (se eksempler på slutten av siden).

Tilfelle x = 0

Hvis , er potensfunksjonen definert for verdien av variabelen x = 0 . 0 La oss finne den deriverte av funksjon (3) ved x =
.

. 0 :
.
For å gjøre dette bruker vi definisjonen av et derivat:

La oss erstatte x =
.
I dette tilfellet mener vi med avledet den høyre grensen for hvilken .
Så vi fant:
Så vi fant:
Av dette er det klart at for .
(1) .
På , . 0 .

Dette resultatet er også hentet fra formel (1):< 0

Derfor er formel (1) også gyldig for x =
(3) .
Tilfelle x Vurder funksjon (3) igjen: For visse verdier av konstanten a er den også definert for negative verdier variabel x.
,
Nemlig la være rasjonelt tall.

. Da kan det representeres som en irreduserbar brøk: 3 hvor m og n er heltall uten 1 felles deler Hvis n er oddetall, er potensfunksjonen også definert for negative verdier av variabelen x. For eksempel når n =
.
og m =

vi har
.
terningrot
.
fra x:

.
Det er også definert for negative verdier av variabelen x.
.
La oss finne den deriverte av potensfunksjonen (3) for og for rasjonelle verdier av konstanten a som den er definert for. For å gjøre dette, la oss representere x i følgende form:
.
Da
.
Deretter,
(1) .

Vi finner den deriverte ved å plassere konstanten utenfor tegnet til den deriverte og bruke regelen for å differensiere en kompleks funksjon:

Her . Men
(3) .
Siden da
.

Det vil si at formel (1) også er gyldig for:
.
Høyere ordens derivater
;

.

La oss nå finne høyere ordens deriverte av potensfunksjonen Vi har allerede funnet den første ordensderiverten: Ved å ta konstanten a utenfor tegnet til den deriverte, finner vi andreordens deriverte:
.

På samme måte finner vi derivater av tredje og fjerde orden: Av dette er det klart at avledet av vilkårlig n-te orden har følgende form:
.
Merk at
,
hvis a er

naturlig tall

, da er den n-te deriverte konstant:

Da er alle påfølgende derivater lik null:
.

kompleks funksjon

kl.
;
.
Eksempler på beregning av derivater
.

Eksempel
;
.
Finn den deriverte av funksjonen:
.