Hvilken ligning kalles logaritmisk? Logaritmiske ligninger
hovedegenskaper.
- logax + logay = loga(x y);
- logax − logay = loga (x: y).
identiske grunner
Log6 4 + log6 9.
La oss nå komplisere oppgaven litt.
Eksempler på løsning av logaritmer
Hva om basen eller argumentet til en logaritme er en potens? Deretter kan eksponenten for denne graden tas ut av logaritmens fortegn i henhold til følgende regler:
Selvfølgelig gir alle disse reglene mening hvis ODZ til logaritmen blir observert: a > 0, a ≠ 1, x >
Oppgave. Finn betydningen av uttrykket:
Overgang til ny stiftelse
La logaritmen logaks gis. Så for et hvilket som helst tall c slik at c > 0 og c ≠ 1, er likheten sann:
Oppgave. Finn betydningen av uttrykket:
Se også:
Grunnleggende egenskaper for logaritmen
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Eksponenten er 2,718281828…. For å huske eksponenten kan du studere regelen: eksponenten er lik 2,7 og to ganger fødselsåret til Leo Nikolaevich Tolstoy.
Grunnleggende egenskaper ved logaritmer
Når du kjenner denne regelen, vil du vite både eksponentverdien og fødselsdatoen til Leo Tolstoy.
Eksempler på logaritmer
Logaritmeuttrykk
Eksempel 1.
EN). x=10ac^2 (a>0,c>0).
Ved hjelp av egenskaper 3.5 beregner vi
2.
3.
Eksempel 2. Finn x if
Eksempel 3. La verdien av logaritmer gis
Beregn log(x) if
Grunnleggende egenskaper ved logaritmer
Logaritmer, som alle tall, kan legges til, trekkes fra og transformeres på alle måter. Men siden logaritmer ikke er helt vanlige tall, er det regler her, som kalles hovedegenskaper.
Du trenger definitivt å kjenne til disse reglene - uten dem kan ikke et eneste alvorlig logaritmisk problem løses. I tillegg er det svært få av dem – du kan lære alt på en dag. Så la oss komme i gang.
Legge til og subtrahere logaritmer
Tenk på to logaritmer med samme base: logax og logay. Deretter kan de legges til og trekkes fra, og:
- logax + logay = loga(x y);
- logax − logay = loga (x: y).
Så summen av logaritmer er lik logaritmen til produktet, og forskjellen er lik logaritmen til kvotienten. Vennligst merk: nøkkelen her er identiske grunner. Hvis årsakene er forskjellige, fungerer ikke disse reglene!
Disse formlene vil hjelpe deg med å beregne et logaritmisk uttrykk selv når dets individuelle deler ikke vurderes (se leksjonen "Hva er en logaritme"). Ta en titt på eksemplene og se:
Siden logaritmer har samme base, bruker vi sumformelen:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.
Oppgave. Finn verdien av uttrykket: log2 48 − log2 3.
Basene er de samme, vi bruker forskjellsformelen:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.
Oppgave. Finn verdien av uttrykket: log3 135 − log3 5.
Igjen er basene de samme, så vi har:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.
Som du kan se, består de opprinnelige uttrykkene av "dårlige" logaritmer, som ikke beregnes separat. Men etter transformasjonene får man helt normale tall. Mange tester er basert på dette faktum. Ja, testlignende uttrykk tilbys i fullt alvor (noen ganger med praktisk talt ingen endringer) på Unified State Examination.
Trekke ut eksponenten fra logaritmen
Det er lett å se at den siste regelen følger de to første. Men det er bedre å huske det uansett - i noen tilfeller vil det redusere mengden beregninger betydelig.
Selvfølgelig gir alle disse reglene mening hvis ODZ til logaritmen blir observert: a > 0, a ≠ 1, x > 0. Og en ting til: lær å bruke alle formler ikke bare fra venstre til høyre, men også omvendt , dvs. Du kan legge inn tallene før logaritmetegnet i selve logaritmen. Dette er det som oftest kreves.
Oppgave. Finn verdien av uttrykket: log7 496.
La oss bli kvitt graden i argumentet ved å bruke den første formelen:
log7 496 = 6 log7 49 = 6 2 = 12
Oppgave. Finn betydningen av uttrykket:
Legg merke til at nevneren inneholder en logaritme, hvis basis og argument er eksakte potenser: 16 = 24; 49 = 72. Vi har:
Jeg tror det siste eksemplet krever litt avklaring. Hvor har logaritmene blitt av? Helt til siste øyeblikk jobber vi kun med nevneren.
Logaritmeformler. Logaritmer eksempler på løsninger.
Vi presenterte grunnlaget og argumentet for logaritmen som sto der i form av potenser og tok ut eksponentene - vi fikk en "tre-etasjers" brøk.
La oss nå se på hovedbrøken. Telleren og nevneren inneholder samme tall: log2 7. Siden log2 7 ≠ 0, kan vi redusere brøken - 2/4 vil forbli i nevneren. I henhold til reglene for regnestykket kan de fire overføres til telleren, som er det som ble gjort. Resultatet ble svaret: 2.
Overgang til ny stiftelse
Når jeg snakker om reglene for å addere og subtrahere logaritmer, la jeg spesielt vekt på at de bare fungerer med de samme basene. Hva om årsakene er forskjellige? Hva om de ikke er nøyaktige potenser av samme tall?
Formler for overgang til en ny stiftelse kommer til unnsetning. La oss formulere dem i form av et teorem:
La logaritmen logaks gis. Så for et hvilket som helst tall c slik at c > 0 og c ≠ 1, er likheten sann:
Spesielt hvis vi setter c = x, får vi:
Fra den andre formelen følger det at basen og argumentet til logaritmen kan byttes, men i dette tilfellet blir hele uttrykket "snudd", dvs. logaritmen vises i nevneren.
Disse formlene finnes sjelden i vanlige numeriske uttrykk. Det er mulig å vurdere hvor praktiske de er bare når man løser logaritmiske ligninger og ulikheter.
Det er imidlertid problemer som ikke kan løses i det hele tatt bortsett fra å flytte til en ny stiftelse. La oss se på et par av disse:
Oppgave. Finn verdien av uttrykket: log5 16 log2 25.
Merk at argumentene til begge logaritmene inneholder eksakte potenser. La oss ta ut indikatorene: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;
La oss nå "reversere" den andre logaritmen:
Siden produktet ikke endrer seg ved omorganisering av faktorer, multipliserte vi rolig fire og to, og behandlet deretter logaritmer.
Oppgave. Finn verdien av uttrykket: log9 100 lg 3.
Grunnlaget og argumentet til den første logaritmen er eksakte potenser. La oss skrive dette ned og bli kvitt indikatorene:
La oss nå bli kvitt desimallogaritmen ved å flytte til en ny base:
Grunnleggende logaritmisk identitet
Ofte i løsningsprosessen er det nødvendig å representere et tall som en logaritme til en gitt base. I dette tilfellet vil følgende formler hjelpe oss:
I det første tilfellet blir tallet n eksponenten i argumentet. Tallet n kan være absolutt hva som helst, fordi det bare er en logaritmeverdi.
Den andre formelen er faktisk en omskrevet definisjon. Det heter det: .
Faktisk, hva skjer hvis tallet b heves til en slik potens at tallet b i denne potensen gir tallet a? Det stemmer: resultatet er det samme tallet a. Les denne paragrafen nøye igjen - mange setter seg fast på den.
Som formler for å flytte til en ny base, er den grunnleggende logaritmiske identiteten noen ganger den eneste mulige løsningen.
Oppgave. Finn betydningen av uttrykket:
Legg merke til at log25 64 = log5 8 - ganske enkelt tok kvadratet fra basen og argumentet til logaritmen. Når vi tar i betraktning reglene for å multiplisere potenser med samme base, får vi:
Hvis noen ikke vet, var dette en skikkelig oppgave fra Unified State Exam :)
Logaritmisk enhet og logaritmisk null
Avslutningsvis vil jeg gi to identiteter som vanskelig kan kalles egenskaper – snarere er de konsekvenser av definisjonen av logaritmen. De dukker stadig opp i problemer og, overraskende nok, skaper de problemer selv for "avanserte" studenter.
- logaa = 1 er. Husk en gang for alle: logaritmen til en hvilken som helst base a av selve basen er lik én.
- loga 1 = 0 er. Grunnlaget a kan være hva som helst, men hvis argumentet inneholder en, er logaritmen lik null! Fordi a0 = 1 er en direkte konsekvens av definisjonen.
Det er alle egenskapene. Sørg for å trene på å sette dem ut i livet! Last ned juksearket i begynnelsen av leksjonen, skriv det ut og løs oppgavene.
Se også:
Logaritmen av b for å basere a angir uttrykket. Å beregne logaritmen betyr å finne en potens x () der likheten er tilfredsstilt
Grunnleggende egenskaper for logaritmen
Det er nødvendig å kjenne egenskapene ovenfor, siden nesten alle problemer og eksempler relatert til logaritmer løses på grunnlag av dem. Resten av de eksotiske egenskapene kan utledes gjennom matematiske manipulasjoner med disse formlene
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Når man regner ut formelen for sum og forskjell av logaritmer (3.4) kommer man over ganske ofte. Resten er noe sammensatt, men i en rekke oppgaver er de uunnværlige for å forenkle komplekse uttrykk og beregne deres verdier.
Vanlige tilfeller av logaritmer
Noen av de vanlige logaritmene er de der basen til og med er ti, eksponentiell eller to.
Logaritmen til grunntallet ti kalles vanligvis desimallogaritmen og er ganske enkelt betegnet med lg(x).
Det fremgår tydelig av opptaket at det grunnleggende ikke er skrevet i opptaket. For eksempel
En naturlig logaritme er en logaritme hvis base er en eksponent (angitt med ln(x)).
Eksponenten er 2,718281828…. For å huske eksponenten kan du studere regelen: eksponenten er lik 2,7 og to ganger fødselsåret til Leo Nikolaevich Tolstoy. Når du kjenner denne regelen, vil du vite både eksponentverdien og fødselsdatoen til Leo Tolstoy.
Og en annen viktig logaritme til base to er angitt med
Den deriverte av logaritmen til en funksjon er lik en dividert med variabelen
Integral- eller antiderivertelogaritmen bestemmes av forholdet
Det gitte materialet er nok for deg til å løse en bred klasse av problemer knyttet til logaritmer og logaritmer. For å hjelpe deg med å forstå materialet, vil jeg gi bare noen få vanlige eksempler fra skolepensum og universiteter.
Eksempler på logaritmer
Logaritmeuttrykk
Eksempel 1.
EN). x=10ac^2 (a>0,c>0).
Ved hjelp av egenskaper 3.5 beregner vi
2.
Ved egenskapen forskjell av logaritmer har vi
3.
Ved å bruke egenskaper 3.5 finner vi
Et tilsynelatende komplekst uttrykk forenkles til å danne ved hjelp av en rekke regler
Finne logaritmeverdier
Eksempel 2. Finn x if
Løsning. For beregning gjelder vi siste termin 5 og 13 eiendommer
Vi setter det på rekord og sørger
Siden basene er like, setter vi likhetstegn mellom uttrykkene
Logaritmer. Inngangsnivå.
La verdien av logaritmer gis
Beregn log(x) if
Løsning: La oss ta en logaritme av variabelen for å skrive logaritmen gjennom summen av dens ledd
Dette er bare begynnelsen på vårt bekjentskap med logaritmer og deres egenskaper. Øv på beregninger, berik dine praktiske ferdigheter - du vil snart trenge kunnskapen du får for å løse logaritmiske ligninger. Etter å ha studert de grunnleggende metodene for å løse slike ligninger, vil vi utvide kunnskapen din til et annet like viktig emne - logaritmiske ulikheter ...
Grunnleggende egenskaper ved logaritmer
Logaritmer, som alle tall, kan legges til, trekkes fra og transformeres på alle måter. Men siden logaritmer ikke er helt vanlige tall, er det regler her, som kalles hovedegenskaper.
Du trenger definitivt å kjenne til disse reglene - uten dem kan ikke et eneste alvorlig logaritmisk problem løses. I tillegg er det svært få av dem – du kan lære alt på en dag. Så la oss komme i gang.
Legge til og subtrahere logaritmer
Tenk på to logaritmer med samme base: logax og logay. Deretter kan de legges til og trekkes fra, og:
- logax + logay = loga(x y);
- logax − logay = loga (x: y).
Så summen av logaritmer er lik logaritmen til produktet, og forskjellen er lik logaritmen til kvotienten. Vennligst merk: nøkkelen her er identiske grunner. Hvis årsakene er forskjellige, fungerer ikke disse reglene!
Disse formlene vil hjelpe deg med å beregne et logaritmisk uttrykk selv når dets individuelle deler ikke vurderes (se leksjonen "Hva er en logaritme"). Ta en titt på eksemplene og se:
Oppgave. Finn verdien av uttrykket: log6 4 + log6 9.
Siden logaritmer har samme base, bruker vi sumformelen:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.
Oppgave. Finn verdien av uttrykket: log2 48 − log2 3.
Basene er de samme, vi bruker forskjellsformelen:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.
Oppgave. Finn verdien av uttrykket: log3 135 − log3 5.
Igjen er basene de samme, så vi har:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.
Som du kan se, består de opprinnelige uttrykkene av "dårlige" logaritmer, som ikke beregnes separat. Men etter transformasjonene får man helt normale tall. Mange tester er basert på dette faktum. Ja, testlignende uttrykk tilbys i fullt alvor (noen ganger med praktisk talt ingen endringer) på Unified State Examination.
Trekke ut eksponenten fra logaritmen
La oss nå komplisere oppgaven litt. Hva om basen eller argumentet til en logaritme er en potens? Deretter kan eksponenten for denne graden tas ut av logaritmens fortegn i henhold til følgende regler:
Det er lett å se at den siste regelen følger de to første. Men det er bedre å huske det uansett - i noen tilfeller vil det redusere mengden beregninger betydelig.
Selvfølgelig gir alle disse reglene mening hvis ODZ til logaritmen blir observert: a > 0, a ≠ 1, x > 0. Og en ting til: lær å bruke alle formler ikke bare fra venstre til høyre, men også omvendt , dvs. Du kan legge inn tallene før logaritmetegnet i selve logaritmen.
Hvordan løse logaritmer
Dette er det som oftest kreves.
Oppgave. Finn verdien av uttrykket: log7 496.
La oss bli kvitt graden i argumentet ved å bruke den første formelen:
log7 496 = 6 log7 49 = 6 2 = 12
Oppgave. Finn betydningen av uttrykket:
Legg merke til at nevneren inneholder en logaritme, hvis basis og argument er eksakte potenser: 16 = 24; 49 = 72. Vi har:
Jeg tror det siste eksemplet krever litt avklaring. Hvor har logaritmene blitt av? Helt til siste øyeblikk jobber vi kun med nevneren. Vi presenterte grunnlaget og argumentet for logaritmen som sto der i form av potenser og tok ut eksponentene - vi fikk en "tre-etasjers" brøk.
La oss nå se på hovedbrøken. Telleren og nevneren inneholder samme tall: log2 7. Siden log2 7 ≠ 0, kan vi redusere brøken - 2/4 vil forbli i nevneren. I henhold til reglene for regnestykket kan de fire overføres til telleren, som er det som ble gjort. Resultatet ble svaret: 2.
Overgang til ny stiftelse
Når jeg snakker om reglene for å addere og subtrahere logaritmer, la jeg spesielt vekt på at de bare fungerer med de samme basene. Hva om årsakene er forskjellige? Hva om de ikke er nøyaktige potenser av samme tall?
Formler for overgang til en ny stiftelse kommer til unnsetning. La oss formulere dem i form av et teorem:
La logaritmen logaks gis. Så for et hvilket som helst tall c slik at c > 0 og c ≠ 1, er likheten sann:
Spesielt hvis vi setter c = x, får vi:
Fra den andre formelen følger det at basen og argumentet til logaritmen kan byttes, men i dette tilfellet blir hele uttrykket "snudd", dvs. logaritmen vises i nevneren.
Disse formlene finnes sjelden i vanlige numeriske uttrykk. Det er mulig å vurdere hvor praktiske de er bare når man løser logaritmiske ligninger og ulikheter.
Det er imidlertid problemer som ikke kan løses i det hele tatt bortsett fra å flytte til en ny stiftelse. La oss se på et par av disse:
Oppgave. Finn verdien av uttrykket: log5 16 log2 25.
Merk at argumentene til begge logaritmene inneholder eksakte potenser. La oss ta ut indikatorene: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;
La oss nå "reversere" den andre logaritmen:
Siden produktet ikke endrer seg ved omorganisering av faktorer, multipliserte vi rolig fire og to, og behandlet deretter logaritmer.
Oppgave. Finn verdien av uttrykket: log9 100 lg 3.
Grunnlaget og argumentet til den første logaritmen er eksakte potenser. La oss skrive dette ned og bli kvitt indikatorene:
La oss nå bli kvitt desimallogaritmen ved å flytte til en ny base:
Grunnleggende logaritmisk identitet
Ofte i løsningsprosessen er det nødvendig å representere et tall som en logaritme til en gitt base. I dette tilfellet vil følgende formler hjelpe oss:
I det første tilfellet blir tallet n eksponenten i argumentet. Tallet n kan være absolutt hva som helst, fordi det bare er en logaritmeverdi.
Den andre formelen er faktisk en omskrevet definisjon. Det heter det: .
Faktisk, hva skjer hvis tallet b heves til en slik potens at tallet b i denne potensen gir tallet a? Det stemmer: resultatet er det samme tallet a. Les denne paragrafen nøye igjen - mange setter seg fast på den.
Som formler for å flytte til en ny base, er den grunnleggende logaritmiske identiteten noen ganger den eneste mulige løsningen.
Oppgave. Finn betydningen av uttrykket:
Legg merke til at log25 64 = log5 8 - ganske enkelt tok kvadratet fra basen og argumentet til logaritmen. Når vi tar i betraktning reglene for å multiplisere potenser med samme base, får vi:
Hvis noen ikke vet, var dette en skikkelig oppgave fra Unified State Exam :)
Logaritmisk enhet og logaritmisk null
Avslutningsvis vil jeg gi to identiteter som vanskelig kan kalles egenskaper – snarere er de konsekvenser av definisjonen av logaritmen. De dukker stadig opp i problemer og, overraskende nok, skaper de problemer selv for "avanserte" studenter.
- logaa = 1 er. Husk en gang for alle: logaritmen til en hvilken som helst base a av selve basen er lik én.
- loga 1 = 0 er. Grunnlaget a kan være hva som helst, men hvis argumentet inneholder en, er logaritmen lik null! Fordi a0 = 1 er en direkte konsekvens av definisjonen.
Det er alle egenskapene. Sørg for å trene på å sette dem ut i livet! Last ned juksearket i begynnelsen av leksjonen, skriv det ut og løs oppgavene.
Fullt navn | Plotnikova Tatyana Vladimirovna |
Arbeidssted | MBOU "Videregående skole nr. 1 av Suzdal" |
Stillingstittel | Matte lærer |
Punkt | Algebra og prinsipper for matematisk analyse |
Klasse | |
Leksjonens tema | "Metoder for å løse logaritmiske ligninger", 2 timer |
Grunnleggende opplæring | Sh.A. Alimov, Yu.M. Kolyagin og andre / M. Education 2014 |
Mål for leksjonen: gjenta elevenes kunnskap om logaritmen til et tall og dets egenskaper; studere måter å løse logaritmiske ligninger og konsolidere dem når du gjør øvelser.
Oppgaver:
Pedagogisk: gjenta definisjonen og de grunnleggende egenskapene til logaritmer, kunne anvende dem i beregning av logaritmer, i løsning av logaritmiske ligninger;
Utviklingsmessig: utvikle evnen til å løse logaritmiske ligninger;
Pedagogisk: dyrke utholdenhet, uavhengighet; vekke interesse for emnet
Leksjonstype: leksjon med å lære nytt materiale.
Nødvendig teknisk utstyr:datamaskin, projektor, lerret.
Leksjonsstruktur og flyt:
- Organisatorisk øyeblikk.
Lærer .
Hei, sett deg ned! I dag er temaet for leksjonen vår "Løse logaritmiske ligninger", der vi vil lære å løse dem ved å bruke definisjonen og egenskapene til logaritmer.(lysbilde nummer 1)
- Muntlig arbeid.
Forsterker konseptet logaritme, gjentar dets grunnleggende egenskaper og egenskaper til den logaritmiske funksjonen:
1. Oppvarming i henhold til teori:
1. Definer logaritme.(lysbilde nummer 2)
2. Kan du finne en logaritme fra et hvilket som helst tall?
3. Hvilket tall kan stå i bunnen av en logaritme?
4. Funksjon y=log 0,8 Øker eller minker x Hvorfor?
5. Hvilke verdier kan en logaritmisk funksjon ta?
6. Hvilke logaritmer kalles desimal, naturlig?
7. Nevn de grunnleggende egenskapene til logaritmer.(lysbilde nummer 3)
8. Er det mulig å flytte fra en logaritmebase til en annen? Hvordan gjøre dette?(lysbilde nummer 4)
2. Arbeid med kort (3-4 elever):
Kort nr. 1: Beregn: a) logg 6 4 + log 6 9 =
B) log 1/3 36 – log 1/3 12 =
Løs ligning: log 5 x = 4 log 5 3 – 1/3 log 5 27
Kort nr. 2:
Regn ut: a) log211 – log244 =
B) log1/64 + log1/69 =
Løs ligning: log 7 x = 2 log 7 5 + 1/2 log 7 36 – 1/3 log 7 125.
Frontal klasseundersøkelse (muntlige øvelser)
Beregn: (lysbilde nummer 5)
|
|
Sammenlign tall: (lysbilde nummer 6)
- log ½ e og log ½ π;
- log 2 √5/2 og log 2 √3/2.
Finn ut tegnet til uttrykket log 0,8 3 · log 6 2/3.
- (lysbilde nummer 7)
Sjekker lekser:
- Følgende øvelser ble gitt hjemme: nr. 327 (ikke-kap.), 331 (ikke-kap.), 333 (2) og 390 (6). Sjekk svarene på disse oppgavene og svar på elevspørsmål.
Lære nytt materiale: Definisjon:
En ligning som inneholder en variabel under det logaritmiske tegnet kalles logaritmisk.
Det enkleste eksemplet på en logaritmisk ligning er ligningen logg
a x =c (a > 0, a≠ 1) Metoder for å løse logaritmiske ligninger:
- (lysbilde nummer 8) Løse ligninger basert på definisjonen av logaritme.
(lysbilde nummer 9) logg a x = c (a > 0, a≠ 1) har en løsning x = a
Med .
- Basert på definisjonen av logaritmen løses ligninger der:
- ved å bruke de gitte basene og tallet, bestemmes logaritmen,
- ved hjelp av en gitt logaritme og grunntall, bestemmes tallet
Grunnlaget bestemmes ut fra gitt tall og logaritme.
Eksempler:
log 2 128= x, log 16 x = ¾, log x 27= 3,
2 x = 128, x = 16 ¾, x 3 = 27,
2 x = 2 7, x = 2 3, x 3 = 3 3,
x = 7. x = 8. x =3. a) logg 7
(3x-1)=2 (svar: x=3 1/3) b) logg 2
- (7-8x)=2 (svar: x=3/8). Potenseringsmetode.
(lysbilde nummer 10)
Med potensering mener vi overgangen fra en likhet som inneholder logaritmer til en likhet som ikke inneholder dem, dvs. Logg a f(x) = log a
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
Eksempel: =
Løs ligningen
ODZ:
3x-1>0; x>1/3
6x+8>0.
3x-1=6x+8
3x=9
x=-3
3 >1/3 - feil
Svar: det finnes ingen løsninger. lg(x 2
- -2) = log x (svar: x=2) Ligninger løses ved å bruke den grunnleggende logaritmiske identiteten.
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
Eksempel:(lysbilde nr. 11)
Løs ligningen
=logg 2 (6-er)
6x>0;
x>0;
x≠1;
log 2 x 2 >0;
x 2 >0.
Systemløsning: (0;1)Ụ (1;6).
Logg 2 (6-er)
x 2 = 6'er
x 2 + x-6 = 0
x=-3 tilhører ikke ODZ.
x=2 tilhører ODZ.
Svar: x=2:
Løs følgende ligning som en klasse
- = (svar: x=1) En metode for å redusere logaritmer til samme base.
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
(lysbilde nummer 12) Løs log-ligningen
16 x+ log 4 x+ log 2 x=7
ODZ: x>0
¼ log 2 x+½ log 2 x+ log 2 x=7
7/4 log 2 x=7
log 2 x=4
x=16 – tilhører ODZ.
Løs følgende ligning som en klasse:
3 (svar: x=5/3)
- Ligninger løses ved å bruke egenskapene til logaritmen.(lysbilde nummer 13)
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
(lysbilde nummer 12) 2 (x +1) - log 2 (x -2) = 2.
Løs ligningen
x+1>0;
x-2>0. x>1.
La oss bruke formelen for å konvertere forskjellen mellom logaritmer og logaritmen til kvotienten, og vi får log 2 = 2, som følger= 4.
Etter å ha løst den siste ligningen finner vi x = 3, 3>1 - riktig
Svar: x = 3.
Løs følgende ligninger som en klasse:
a)log 5 (x +1) + log 5 (x +5) = 1 (svar: x=0).
b)logg 9 (37-12x) log 7-2x 3 = 1,
37-12x >0, x
7-2x >0, x
7-2х≠ 1; x≠ 3; x≠ 3;
Logg 9 (37-12x) / log 3 (7-2x) = 1,
½ log 3 (37-12x) = log 3 (7-2x) ,
Logg 3 (37-12x) = log 3 (7-2x) 2,
37-12x= 49 -28x +4x 2,
4x 2 -16x +12 =0,
X 2 -4x +3 = 0, D = 19, x 1 = 1, x 2 =3, 3 er en fremmed rot.
Svar: x=1 roten av ligningen.
B) log(x 2 -6x+9) - 2log(x - 7) = log9.
(x 2 -6x+9) >0, x≠ 3,
X-7 >0; x >7; x >7.
Lg ((x-3)/(x-7)) 2 = lg9
((x-3)/(x-7)) 2 = 9,
(x-3)/(x-7) = 3, (x-3)/(x-7)= - 3,
x- 3 = 3x -21, x -3 = - 3x +21,
x = 9. x=6 er en fremmed rot.
Kontroll viser den niende roten av ligningen.
Svar: 9
- Ligninger løses ved å introdusere en ny variabel.(lysbilde nummer 14)
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
Løs lg-ligningen 2 x - 6lgх+5 = 0.
ODZ: x>0.
La logx = p, deretter p 2 -6р+5=0.
p 1 = 1, p 2 = 5.
Tilbake til erstatning:
logx = 1, logx = 5
x=10, 10>0 – sant x=100000, 100000>0 – sant
Svar: 10, 100 000
Løs følgende ligning som en klasse:
Logg 6 2 x + log 6 x +14 = (√16 – x 2 ) 2 + x 2 ,
16 – x 2 ≥0; - 4≤ x ≤ 4;
X >0, x >0, O.D.Z. [0,4).
Logg 6 2 x + log 6 x +14 = 16 – x 2 + x 2,
Logg 6 2 x + log 6 x -2 = 0
Bytt stokk 6 x = t
T2 + t-2=0; D = 9; ti = 1, t2 = -2.
Logg 6 x = 1, x = 6 er en fremmed rot.
Logg 6 x = -2, x = 1/36, kontroll viser at 1/36 er roten.
Svar: 1/36.
- Ligninger løst ved faktorisering.(lysbilde nummer 15)
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
(lysbilde nummer 12) 4 (2x-1)∙ log 4 x=2 log 4 (2x-1)
Løs ligningen
2x-1>0;
X >0. x>½.
log 4 (2x-1)∙ log 4 x - 2 log 4 (2x-1)=0
log 4 (2x-1)∙(log 4 x-2)=0
log 4 (2x-1)=0 eller log 4 x-2=0
2x-1=1 log 4 x = 2
x=1 x=16
1;16 – tilhører ODZ
Svar: 1;16
Løs følgende ligning som en klasse:
logg 3 x ∙logg 3 (3x-2)= logg 3 (3x-2) (svar: x=1)
- Metode for å ta logaritmer på begge sider av en ligning.(lysbilde nummer 16)
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
Løs ligninger
La oss ta logaritmen til begge sider av ligningen til base 3.
Vi får logg 3 = logg 3 (3x)
vi får: log 3 x 2 log 3 x = log 3 (3x),
2log 3 x log 3 x = log 3 3+ log 3 x,
2 log 3 2 x = log 3 x +1,
2 log 3 2 x - log 3 x -1=0,
erstatte log 3 x = p, x >0
2 р2 + р-2 = 0; D = 9; p 1 = 1, p 2 = -1/2
Logg 3 x = 1, x=3,
log 3 x = -1/ 2, x = 1/√3.
Svar: 3; 1/√3
Løs følgende ligning som en klasse:
Logg 2 x - 1
x = 64 (svar: x=8; x=1/4)
- Funksjonell - grafisk metode.(lysbilde nummer 17)
g(x), så f(x) = g(x), forutsatt at f(x)>0, g(x)>0, a> 0, a≠ 1.
Løs ligningene: log 3 x = 12'er.
Siden funksjonen y = log 3 x øker, og funksjonen y = 12 er avtagende på (0; + ∞), så har den gitte ligningen på dette intervallet én rot.
La oss konstruere grafer for to funksjoner i ett koordinatsystem: y= log 3 x og y = 12'er.
Når x=10, blir den gitte ligningen til den riktige numeriske likheten 1=1. Svaret er x=10.
Løs følgende ligning som en klasse:
1-√х =ln x (svar: x=1).
- Oppsummering, refleksjon (del ut sirkler som barna markerer humøret sitt på med en tegning).(lysbilde nr. 18,19)
Bestem metoden for å løse ligningen:
- Lekser: 340(1), 393(1), 395(1,3), 1357(1,2), 337(1), 338(1), 339(1)
Litteratur
- Ryazanovsky, A.R. Matematikk. 5 – 11 karakterer: Tilleggsmateriell til matematikktimen / A.R. – 2. utgave, stereotypi. – M.: Bustard, 2002
- Matematikk. Bilag til avisen «Første september». 1997. nr. 1, 10, 46, 48; 1998. Nr. 8, 16, 17, 20, 21, 47.
- Skorkina, N.M. Ikke-standardiserte former for fritidsaktiviteter. For ungdoms- og videregående skole / N.M. Skorkina. – Volgograd: Lærer, 2004
- Ziv, B.G., Goldich, V.A. Didaktisk materiale om algebra og analyseprinsipper for klasse 10./B.G. Ziv, V.A. – 3. utgave, revidert. – St. Petersburg: «CheRo-on-Neva», 2004
- Algebra og begynnelsen av analyse: matematikk for tekniske skoler / red. G.N.Yakovleva.-M.: Nauka, 1987
Forhåndsvisning:
For å bruke forhåndsvisninger av presentasjoner, opprett en Google-konto og logg på den: https://accounts.google.com
Lysbildetekster:
Metoder for å løse logaritmiske ligninger Matematikklærer: Plotnikova T.V. MBOU "Videregående skole nr. 1 av Suzdal"
Definisjon Logaritmen av et positivt tall b til grunntallet a, hvor a >0, a≠1, er eksponenten c som a må heves til for å få b.
Egenskaper til logaritmer log a 1 = 0 log a a = 1 log a (x y)= log a x + log a y 3
Formler for å flytte til en annen base 4
Regn ut: 5
Sammenlign 6
7 Bestem tegnet på tallet:
Grunnleggende metoder for å løse logaritmiske ligninger
1. Bruk definisjonen av logaritmen l og 2 128= x log x 27= 3 Løs følgende ligninger: a) log 7 (3x-1)=2 b) log 2 (7-8x)=2 9
2. Potenseringsmetode La oss løse følgende ligning: log (x 2 -2) = log x 10 2
11 3. Ligninger løst ved å bruke den grunnleggende logaritmiske identiteten La oss løse følgende likning: 1
12 4. Metode for å redusere logaritmer til samme grunnlog 16 x + log 4 x + log 2 x = 7 Løs følgende ligning:
13 5. Ligninger løst ved å bruke egenskapene til logaritmen log 2 (x +1) - log 2 (x -2) = 2 La oss løse følgende ligninger: a) l og 5 (x +1) + log 5 ( x +5) = 1 b)log 9 (37-12x) log 7-2x 3 = 1 c) log(x 2 -6x+9) - 2log(x - 7) = log9 0 1 9
6. Likninger løst ved å introdusere en ny variabel l g 2 x - 6lgх +5 = 0 La oss løse følgende likninger: log 6 2 x + log 6 x +14 = (√16 – x 2) 2 + x 2 14
15 7. Ligninger løst ved hjelp av faktorisering log 4 (2x-1)∙ log 4 x =2 log 4 (2x-1) La oss løse følgende ligninger: log 3 x ∙ log 3 (3x-2)= log 3 ( 3x- 2) 1
8. Logaritmemetode La oss løse følgende ligning: 16
9. Funksjonell - grafisk metode log 3 x = 12 La oss løse følgende ligning: 17 1
Bestem metoden for å løse ligningen: Ligning: Løsningsmetode for å bestemme logaritmeovergangen til en annen basisfaktorisering potensering innføring av en ny variabelovergang til en annen base ved bruk av egenskapene til logaritmelogaritmegrafikken 18
Ja! Og hvem kom opp med disse logaritmiske ligningene! Alt ordner seg for meg!!! Trenger vi å løse et par eksempler til?! Refleksjon 19
Logaritmiske ligninger. Fra enkelt til komplekst.
Oppmerksomhet!
Det er flere
materialer i spesialseksjon 555.
For de som er veldig "ikke veldig..."
Og for de som "veldig mye...")
Hva er en logaritmisk ligning?
Dette er en ligning med logaritmer. Jeg er overrasket, ikke sant?) Da skal jeg avklare. Dette er en ligning der de ukjente (x-er) og uttrykk med dem finnes inne i logaritmer. Og bare der! Dette er viktig.
Her er noen eksempler logaritmiske ligninger:
log 3 x = log 3 9
log 3 (x 2 -3) = log 3 (2x)
log x+1 (x 2 +3x-7) = 2
lg 2 (x+1)+10 = 11 lg(x+1)
Vel, du forstår... )
Vær oppmerksom! De mest forskjellige uttrykkene med X-er er lokalisert utelukkende innenfor logaritmer. Hvis det plutselig dukker opp en X et sted i ligningen utenfor, For eksempel:
log 2 x = 3+x,
dette vil allerede være en likning av blandet type. Slike ligninger har ikke klare regler for å løse dem. Vi vil ikke vurdere dem foreløpig. Forresten, det er ligninger der inne i logaritmene bare tall. For eksempel:
Hva kan jeg si? Du er heldig hvis du kommer over dette! Logaritme med tall er et eller annet nummer. Det er alt. Det er nok å kjenne egenskapene til logaritmer for å løse en slik likning. Kunnskap om spesielle regler, teknikker tilpasset spesifikt for å løse logaritmiske ligninger, ikke nødvendig her.
Så, hva er en logaritmisk ligning- Vi fant det ut.
Hvordan løse logaritmiske ligninger?
Løsning logaritmiske ligninger– saken er faktisk ikke veldig enkel. Så vår seksjon er en fire... Det kreves en anstendig mengde kunnskap om alle slags relaterte emner. I tillegg er det en spesiell funksjon i disse ligningene. Og denne funksjonen er så viktig at den trygt kan kalles hovedproblemet for å løse logaritmiske ligninger. Vi vil behandle dette problemet i detalj i neste leksjon.
For nå, ikke bekymre deg. Vi går riktig vei fra enkelt til komplekst. Bruker konkrete eksempler. Det viktigste er å fordype seg i enkle ting og ikke være lat til å følge lenkene, jeg legger dem der av en grunn ... Og alt vil ordne seg for deg. Nødvendigvis.
La oss starte med de mest elementære, enkleste ligningene. For å løse dem er det tilrådelig å ha en ide om logaritmen, men ikke noe mer. Bare ingen anelse logaritme, ta en avgjørelse logaritmisk ligninger - på en eller annen måte til og med vanskelig... Veldig dristig, vil jeg si).
De enkleste logaritmiske ligningene.
Dette er ligninger av formen:
1. logg 3 x = logg 3 9
2. stokk 7 (2x-3) = stokk 7 x
3. logg 7 (50x-1) = 2
Løsningsprosess enhver logaritmisk ligning består i overgangen fra en likning med logaritmer til en likning uten dem. I de enkleste ligningene utføres denne overgangen i ett trinn. Det er derfor de er de enkleste.)
Og slike logaritmiske ligninger er overraskende enkle å løse. Se selv.
La oss løse det første eksemplet:
log 3 x = log 3 9
For å løse dette eksempelet trenger du ikke vite nesten noe, ja... Ren intuisjon!) Hva trenger vi særlig liker ikke dette eksemplet? Hva-hva... Jeg liker ikke logaritmer! Høyre. Så la oss bli kvitt dem. Vi ser nøye på eksemplet, og det oppstår et naturlig ønske i oss... Rett og slett uimotståelig! Ta og kast ut logaritmer helt. Og det som er bra er det Kan gjøre! Matematikk tillater. Logaritmer forsvinner svaret er:
Flott, ikke sant? Dette kan (og bør) alltid gjøres. Å eliminere logaritmer på denne måten er en av hovedmåtene for å løse logaritmiske ligninger og ulikheter. I matematikk kalles denne operasjonen potensering. Det finnes selvfølgelig regler for slik avvikling, men de er få. Huske:
Du kan eliminere logaritmer uten frykt hvis de har:
a) de samme numeriske basene
c) logaritmer fra venstre til høyre er rene (uten koeffisienter) og er i utmerket isolasjon.
La meg klargjøre det siste punktet. La oss si i ligningen
log 3 x = 2log 3 (3x-1)
Logaritmer kan ikke fjernes. De to til høyre tillater det ikke. Koeffisienten, du vet... I eksemplet
log 3 x+log 3 (x+1) = log 3 (3+x)
Det er også umulig å potensere ligningen. Det er ingen enslig logaritme på venstre side. Det er to av dem.
Kort sagt, du kan fjerne logaritmer hvis ligningen ser slik ut og bare slik:
log a (.....) = log a (.....)
I parentes, der det er en ellipse, kan det være noen uttrykk. Enkelt, superkomplekst, alle slags. Uansett. Det viktige er at etter å ha eliminert logaritmer sitter vi igjen med enklere ligning. Det antas selvfølgelig at du allerede vet hvordan du løser lineære, kvadratiske, brøk-, eksponentielle og andre ligninger uten logaritmer.)
Nå kan du enkelt løse det andre eksemplet:
stokk 7 (2x-3) = stokk 7 x
Faktisk er det bestemt i tankene. Vi potenserer, vi får:
Vel, er det veldig vanskelig?) Som du kan se, logaritmisk del av løsningen på ligningen er bare ved å eliminere logaritmer... Og så kommer løsningen på den gjenværende ligningen uten dem. En triviell sak.
La oss løse det tredje eksemplet:
log 7 (50x-1) = 2
Vi ser at det er en logaritme til venstre:
La oss huske at denne logaritmen er et tall som basen må heves til (dvs. syv) for å få et sublogaritmisk uttrykk, dvs. (50x-1).
Men dette tallet er to! I følge Eq. Så:
Det er i grunnen alt. Logaritme forsvant, Det som gjenstår er en ufarlig ligning:
Vi løste denne logaritmiske ligningen bare basert på logaritmenes betydning. Er det fortsatt lettere å eliminere logaritmer?) Jeg er enig. Forresten, hvis du lager en logaritme fra to, kan du løse dette eksemplet gjennom eliminering. Ethvert tall kan gjøres til en logaritme. Dessuten slik vi trenger det. En svært nyttig teknikk for å løse logaritmiske ligninger og (spesielt!) ulikheter.
Vet du ikke hvordan du lager en logaritme fra et tall!? Det er greit. Seksjon 555 beskriver denne teknikken i detalj. Du kan mestre det og bruke det til det fulle! Det reduserer antallet feil betraktelig.
Den fjerde ligningen er løst på en helt lignende måte (per definisjon):
Det er det.
La oss oppsummere denne leksjonen. Vi så på løsningen av de enkleste logaritmiske ligningene ved hjelp av eksempler. Dette er veldig viktig. Og ikke bare fordi slike ligninger dukker opp i prøver og eksamener. Faktum er at selv de ondeste og mest kompliserte ligningene nødvendigvis reduseres til de enkleste!
Faktisk er de enkleste ligningene den siste delen av løsningen noen ligninger. Og denne siste delen må forstås strengt! Og en ting til. Sørg for å lese denne siden til slutten. Det er en overraskelse der...)
Nå bestemmer vi selv. La oss bli bedre, for å si det sånn...)
Finn roten (eller summen av røtter, hvis det er flere) av ligningene:
ln(7x+2) = ln(5x+20)
log 2 (x 2 +32) = log 2 (12x)
log 16 (0,5x-1,5) = 0,25
log 0,2 (3x-1) = -3
ln(e 2 +2x-3) = 2
log 2 (14x) = log 2 7 + 2
Svar (i uorden, selvfølgelig): 42; 12; 9; 25; 7; 1,5; 2; 16.
Hva, ikke alt ordner seg? Skjer. Ikke bekymre deg! Seksjon 555 forklarer løsningen på alle disse eksemplene på en klar og detaljert måte. Du vil definitivt finne ut av det der. Du vil også lære nyttige praktiske teknikker.
Alt ordnet seg!? Alle eksempler på «ett igjen»?) Gratulerer!
Det er på tide å avsløre den bitre sannheten for deg. Vellykket løsning av disse eksemplene garanterer ikke suksess i å løse alle andre logaritmiske ligninger. Selv de enkleste som disse. Akk.
Faktum er at løsningen til enhver logaritmisk ligning (selv den mest elementære!) består av to like deler. Løse ligningen og jobbe med ODZ. Vi har mestret én del – å løse selve ligningen. Det er ikke så vanskelig høyre?
Til denne leksjonen har jeg spesielt valgt ut eksempler der DL ikke påvirker svaret på noen måte. Men ikke alle er like snille som meg, ikke sant?...)
Derfor er det viktig å mestre den andre delen. ODZ. Dette er hovedproblemet ved å løse logaritmiske ligninger. Og ikke fordi det er vanskelig - denne delen er enda enklere enn den første. Men fordi de rett og slett glemmer ODZ. Eller de vet ikke. Eller begge deler). Og de faller ut av det blå...
I neste leksjon skal vi ta for oss dette problemet. Da kan du trygt bestemme deg noen enkle logaritmiske ligninger og nærmer seg ganske solide oppgaver.
Hvis du liker denne siden...
Forresten, jeg har et par flere interessante nettsteder for deg.)
Du kan trene på å løse eksempler og finne ut nivået ditt. Testing med umiddelbar verifisering. La oss lære - med interesse!)
Du kan bli kjent med funksjoner og derivater.
Algebra 11. klasse
Emne: "Metoder for å løse logaritmiske ligninger"
Leksjonens mål:
pedagogisk: dannelse av kunnskap om forskjellige måter å løse logaritmiske ligninger på, evnen til å bruke dem i hver spesifikk situasjon og velge hvilken som helst metode for å løse;
utviklingsmessig: utvikling av ferdigheter til å observere, sammenligne, anvende kunnskap i en ny situasjon, identifisere mønstre, generalisere; utvikle ferdigheter for gjensidig kontroll og selvkontroll;
pedagogisk: fremme en ansvarlig holdning til pedagogisk arbeid, oppmerksom oppfatning av materialet i leksjonen og nøye notattaking.
Leksjonstype: leksjon om introduksjon av nytt materiale.
"Oppfinnelsen av logaritmer, mens den reduserte astronomens arbeid, forlenget livet hans."
Den franske matematikeren og astronomen P.S. Laplace
Leksjonsfremgang
I. Sette mål for leksjonen
Den studerte definisjonen av logaritme, egenskapene til logaritmer og logaritmisk funksjon vil tillate oss å løse logaritmiske ligninger. Alle logaritmiske ligninger, uansett hvor komplekse de er, løses ved hjelp av enhetlige algoritmer. Vi skal se på disse algoritmene i dagens leksjon. Det er ikke mange av dem. Hvis du mestrer dem, vil enhver ligning med logaritmer være mulig for hver av dere.
Skriv ned emnet for leksjonen i notatboken din: "Metoder for å løse logaritmiske ligninger." Jeg inviterer alle til å samarbeide.
II. Oppdatering av referansekunnskap
La oss forberede oss på å studere emnet for leksjonen. Du løser hver oppgave og skriver ned svaret du trenger ikke å skrive betingelsen. Arbeid i par.
1) For hvilke verdier av x gir funksjonen mening:
(Svar sjekkes for hvert lysbilde og feil sorteres ut)
2) Sammenfaller grafene til funksjonene?
3) Skriv om likhetene som logaritmiske likheter:
4) Skriv tallene som logaritmer med grunntall 2:
5) Regn ut:
6) Prøv å gjenopprette eller supplere de manglende elementene i disse likhetene.
III. Introduksjon til nytt materiale
Følgende uttalelse vises på skjermen:
"Ligningen er den gyldne nøkkelen som åpner alle matematiske sesamer."
Moderne polsk matematiker S. Kowal
Prøv å formulere definisjonen av en logaritmisk ligning. (En ligning som inneholder en ukjent under logaritmetegnet).
La oss vurdere den enkleste logaritmiske ligningen:Det enkleste eksemplet på en logaritmisk ligning er ligningenENx = b(hvor a>0, a ≠ 1). Siden den logaritmiske funksjonen øker (eller avtar) på settet med positive tall og tar alle reelle verdier, følger det av rotsetningen at for enhver b har denne ligningen, og bare én, løsning og en positiv.
Husk definisjonen av logaritme. (Logaritmen til et tall x til grunntallet a er en indikator på potensen som grunntallet a må heves til for å oppnå tallet x). Fra definisjonen av logaritme følger det umiddelbart at ENV er en slik løsning.
Skriv ned tittelen: Metoder for å løse logaritmiske ligninger
1. Per definisjon av logaritme.
Slik løses formens enkleste likninger.
La oss vurdere nr. 514(a)): Løs ligningen
Hvordan foreslår du å løse det? (Per definisjon av logaritme)
Løsning. , Derfor 2x - 4 = 4; x = 4.
I denne oppgaven, 2x - 4 > 0, siden > 0, så ingen fremmede røtter kan vises, og det er ikke nødvendig å sjekke. Betingelsen 2x - 4 > 0 trenger ikke skrives ut i denne oppgaven.
2. Potensisering(overgang fra logaritmen til et gitt uttrykk til selve uttrykket).
La oss vurdere nr. 519(g): log5(x2+8)-log5(x+1)=3log5 2
Hvilken funksjon la du merke til? (Basene er de samme og logaritmene til de to uttrykkene er like.) Hva kan gjøres? (Potentiser).
Det bør tas i betraktning at enhver løsning finnes blant alle x som de logaritmiske uttrykkene er positive for.
Løsning: ODZ:
X2+8>0 er en unødvendig ulikhet
log5(x2+8) =log5 23+ log5(x+1)
log5(x2+8)= log5 (8 x+8)
La oss potensere den opprinnelige ligningen
vi får ligningen x2+8= 8x+8
La oss løse det: x2-8x=0
Svar: 0; 8
Generelt sett overgang til et tilsvarende system:
Ligning
(Systemet inneholder en redundant tilstand - en av ulikhetene trenger ikke tas i betraktning).
Spørsmål til klassen: Hvilken av disse tre løsningene likte du best? (Drafting av metoder).
Du har rett til å bestemme på alle måter.
3. Innføring av ny variabel.
La oss vurdere nr. 520(g). .
Hva la du merke til? (Dette er en andregradsligning med hensyn til log3x) Noen forslag? (Introduser en ny variabel)
Løsning. ODZ: x > 0.
La , så tar ligningen formen:. Diskriminant D > 0. Røtter i henhold til Vietas teorem:.
La oss gå tilbake til erstatningen: eller.
Etter å ha løst de enkleste logaritmiske ligningene får vi:
Svar: 27;
4. Logaritme begge sider av ligningen.
Løs ligningen:.
Løsning: ODZ: x>0, ta logaritmen til begge sider av ligningen i base 10:
La oss bruke egenskapen til logaritmen til en potens:
(logx + 3) logx = 4
La logx = y, så (y + 3)y = 4
, (D > 0) røtter i henhold til Vietas teorem: y1 = -4 og y2 = 1.
La oss gå tilbake til erstatningen, vi får: lgx = -4,; lgx = 1, .
Svar: 0,0001; 10.
5. Reduksjon til én base.
nr. 523(c). Løs ligningen:
Løsning: ODZ: x>0. La oss gå videre til base 3.
6. Funksjonell-grafisk metode.
№ 509(d). Løs ligningen grafisk: = 3 - x.
Hvordan foreslår du å løse? (Bygg grafer av to funksjoner y = log2x og y = 3 - x ved å bruke punkter og se etter abscissen til grafenes skjæringspunkt).
Se på løsningen din på lysbildet.
Det er en måte å unngå å lage grafer på . Det er som følger : hvis en av funksjonene y = f(x) øker, og den andre y = g(x) avtar på intervallet X, deretter ligningen f(x)= g(x) har høyst én rot på intervallet X.
Hvis det er en rot, kan den gjettes.
I vårt tilfelle øker funksjonen for x>0, og funksjonen y = 3 - x reduseres for alle verdier av x, inkludert for x>0, noe som betyr at ligningen ikke har mer enn én rot. Merk at ved x = 2 blir ligningen til en sann likhet, siden .
«Riktig bruk av metoder kan læres
bare ved å bruke dem på forskjellige eksempler."
Dansk matematikkhistoriker G.G. Zeiten
jegV. Lekser
S. 39 vurdere eksempel 3, løse nr. 514(b), nr. 529(b), nr. 520(b), nr. 523(b)
V. Oppsummering av leksjonen
Hvilke metoder for å løse logaritmiske ligninger så vi på i klassen?
I de neste leksjonene skal vi se på mer komplekse ligninger. For å løse dem vil de studerte metodene være nyttige.
Siste lysbilde vist:
«Hva er mer enn noe annet i verden?
Rom.
Hva er det klokeste?
Tid.
Hva er den beste delen?
Oppnå det du vil."
Thales
Jeg ønsker at alle skal oppnå det de ønsker. Takk for samarbeidet og forståelsen.
Algebra 11. klasse
Emne: "Metoder for å løse logaritmiske ligninger"
Leksjonens mål:
pedagogisk: utvikle kunnskap om ulike måter å løse logaritmiske ligninger på, evnen til å anvende dem i hver spesifikk situasjon og velge hvilken som helst metode for å løse;
utvikle: utvikling av ferdigheter til å observere, sammenligne, anvende kunnskap i en ny situasjon, identifisere mønstre, generalisere; utvikle ferdigheter for gjensidig kontroll og selvkontroll;
pedagogisk: pleie en ansvarlig holdning til pedagogisk arbeid, oppmerksom oppfatning av stoffet i leksjonen og nøye notattaking.
Leksjonstype : leksjon om introduksjon av nytt materiale.
"Oppfinnelsen av logaritmer, mens den reduserte astronomens arbeid, forlenget livet hans."
Den franske matematikeren og astronomen P.S. Laplace
Leksjonsfremgang
I. Sette mål for leksjonen
Den studerte definisjonen av logaritme, egenskapene til logaritmene og logaritmiske funksjoner vil tillate oss å løse logaritmiske ligninger. Alle logaritmiske ligninger, uansett hvor komplekse de er, løses ved hjelp av enhetlige algoritmer. Vi skal se på disse algoritmene i dagens leksjon. Det er ikke mange av dem. Hvis du mestrer dem, vil enhver ligning med logaritmer være mulig for hver av dere.
Skriv ned emnet for leksjonen i notatboken din: "Metoder for å løse logaritmiske ligninger." Jeg inviterer alle til å samarbeide.
II. Oppdatering av referansekunnskap
La oss forberede oss på å studere emnet for leksjonen. Du løser hver oppgave og skriver ned svaret du trenger ikke å skrive betingelsen. Arbeid i par.
1) For hvilke verdier av x gir funksjonen mening:
EN)
b)
V)![]()
d)
(Svar sjekkes for hvert lysbilde og feil sorteres ut)
2) Sammenfaller grafene til funksjonene?
a) y = x og
b)Og![]()
3) Skriv om likhetene som logaritmiske likheter:
4) Skriv tallene som logaritmer med grunntall 2:
4 =
2 =
0,5 =
1 =
5) Regn ut :
6) Prøv å gjenopprette eller supplere de manglende elementene i disse likhetene.

III. Introduksjon til nytt materiale
Følgende uttalelse vises på skjermen:
"Ligningen er den gyldne nøkkelen som åpner alle matematiske sesamer."
Moderne polsk matematiker S. Kowal
Prøv å formulere definisjonen av en logaritmisk ligning. (Ligning som inneholder en ukjent under logaritmetegnet ).
La oss vurdereden enkleste logaritmiske ligningen: Det enkleste eksemplet på en logaritmisk ligning er ligningen EN x = b (hvor a>0, a ≠ 1). Siden den logaritmiske funksjonen øker (eller avtar) på settet med positive tall og tar alle reelle verdier, følger det av rotsetningen at for enhver b har denne ligningen, og bare én, løsning og en positiv.
Husk definisjonen av logaritme. (Logaritmen til et tall x til grunntallet a er en indikator på potensen som grunntallet a må heves til for å oppnå tallet x ). Fra definisjonen av logaritme følger det umiddelbart atEN V er en slik løsning.
Skriv ned tittelen:Metoder for å løse logaritmiske ligninger
1. Per definisjon av logaritme .
Slik løses formens enkleste likninger.
La oss vurderenr. 514(a)
): Løs ligningen![]()
Hvordan foreslår du å løse det? (Per definisjon av logaritme )
Løsning
.
 , Derfor 2x – 4 = 4; x = 4.
, Derfor 2x – 4 = 4; x = 4.
Svar: 4.
I denne oppgaven 2x – 4 > 0, siden> 0, så ingen fremmede røtter kan vises, ogikke nødvendig å sjekke . Det er ikke nødvendig å skrive ut betingelsen 2x – 4 > 0 i denne oppgaven.
2. Potensisering (overgang fra logaritmen til et gitt uttrykk til selve uttrykket).
La oss vurderenr. 519(g): logg 5 ( x 2 +8)- logg 5 ( x+1)=3 logg 5 2
Hvilken funksjon la du merke til?(Basene er like og logaritmene til de to uttrykkene er like) . Hva kan gjøres?(Potentiser).
Det bør tas i betraktning at enhver løsning finnes blant alle x som de logaritmiske uttrykkene er positive for.
Løsning: ODZ:
X 2 +8>0 unødvendig ulikhet
logg 5 ( x 2 +8) = logg 5 2 3 + logg 5 ( x+1)
logg 5 ( x 2 +8)= logg 5 (8 x+8)
La oss potensere den opprinnelige ligningen
x 2 +8= 8 x+8
vi får ligningenx 2 +8= 8 x+8
La oss løse det:x 2 -8 x=0
x=0, x=8
Svar: 0; 8
Generelt settovergang til et tilsvarende system :
Ligning![]()

(Systemet inneholder en redundant tilstand - en av ulikhetene trenger ikke tas i betraktning).
Spørsmål til klassen : Hvilken av disse tre løsningene likte du best? (Drafting av metoder).
Du har rett til å bestemme på alle måter.
3. Innføring av ny variabel .
La oss vurderenr. 520(g) . .
Hva la du merke til? (Dette er en andregradsligning med hensyn til log3x) Hva er dine forslag? (Introduser en ny variabel)
Løsning . ODZ: x > 0.
La, så vil ligningen ha formen:![]() . Diskriminant D > 0. Røtter i henhold til Vietas teorem:
. Diskriminant D > 0. Røtter i henhold til Vietas teorem:![]() .
.
La oss gå tilbake til erstatningen:eller.
Etter å ha løst de enkleste logaritmiske ligningene får vi:
; .
Svare : 27;
4. Logaritme begge sider av ligningen.
Løs ligningen:![]() .
.
Løsning : ODZ: x>0, la oss ta logaritmen til begge sider av ligningen i base 10:
![]() . La oss bruke egenskapen til logaritmen til en potens:
. La oss bruke egenskapen til logaritmen til en potens:
(lgx + 3) lgx =
(logx + 3) logx = 4
La logx = y, så (y + 3)y = 4
![]() , (D > 0) røtter i henhold til Vietas teorem: y1 = -4 og y2 = 1.
, (D > 0) røtter i henhold til Vietas teorem: y1 = -4 og y2 = 1.
La oss gå tilbake til erstatningen, vi får: lgx = -4,![]() ; logx = 1,
; logx = 1,![]() .
.
Det er som følger:
hvis en av funksjonene
y = f(x)
øker, og den andre
y = g(x)
avtar på intervallet X, deretter ligningen
f(x)= g(x)
har høyst én rot på intervallet X
.
.
.
Det er som følger:
hvis en av funksjonene
y = f(x)
øker, og den andre
y = g(x)
avtar på intervallet X, deretter ligningen
f(x)= g(x)
har høyst én rot på intervallet X
.
Hvis det er en rot, kan den gjettes. .
Svare : 2
«Riktig bruk av metoder kan læres
bare ved å bruke dem på forskjellige eksempler."
Dansk matematikkhistoriker G.G. Zeiten
jeg V. Lekser
S. 39 vurdere eksempel 3, løse nr. 514(b), nr. 529(b), nr. 520(b), nr. 523(b)
V. Oppsummering av leksjonen
Hvilke metoder for å løse logaritmiske ligninger så vi på i klassen?
I de neste leksjonene skal vi se på mer komplekse ligninger. For å løse dem vil de studerte metodene være nyttige.
Siste lysbilde vist:
«Hva er mer enn noe annet i verden?
Rom.
Hva er det klokeste?
Tid.
Hva er den beste delen?
Oppnå det du vil."
Thales
Jeg ønsker at alle skal oppnå det de ønsker. Takk for samarbeidet og forståelsen.
 Logaritmiske ligninger
Logaritmiske ligninger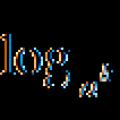 Teknikk for å løse logaritmiske ligninger
Teknikk for å løse logaritmiske ligninger Selvanalyse av logopedlærer
Selvanalyse av logopedlærer