Kinetisk rotasjonsenergi. Kinetisk energi under rotasjonsbevegelse
Tenk først på et stivt legeme som roterer rundt en fast akse OZ med en vinkelhastighet ω (fig.5.6). La oss bryte kroppen i elementære masser. Den lineære hastigheten til en elementær masse er , hvor er avstanden fra rotasjonsaksen. Kinetisk energi Jeg-den elementære massen vil være lik
![]() .
.
Den kinetiske energien til hele kroppen består derfor av de kinetiske energiene til delene
![]() .
.
Tatt i betraktning at summen på høyre side av denne relasjonen representerer treghetsmomentet til kroppen rundt rotasjonsaksen, får vi til slutt
![]() . (5.30)
. (5.30)
Formlene for den kinetiske energien til et roterende legeme (5.30) ligner på de tilsvarende formlene for den kinetiske energien til en kropps translasjonsbevegelse. De oppnås fra sistnevnte ved den formelle substitusjonen ![]() .
.
I generell sak bevegelsen til et stivt legeme kan representeres som en sum av bevegelser - translatorisk med hastighet, lik hastighet kroppens massesenter, og rotasjon med en vinkelhastighet om en momentan akse som går gjennom massesenteret. I dette tilfellet tar uttrykket for den kinetiske energien til kroppen formen
![]() .
.
La oss nå finne arbeidet som er gjort for øyeblikket eksterne krefter, under rotasjon av et stivt legeme. Elementært arbeid av ytre krefter i tid dt vil være lik endringen i den kinetiske energien til kroppen
Ved å ta differensialen fra den kinetiske energien til rotasjonsbevegelse, finner vi dens inkrement
 .
.
I samsvar med den grunnleggende dynamikkligningen for rotasjonsbevegelse
Med hensyn til disse relasjonene reduserer vi uttrykket for elementært arbeid til formen
hvor er projeksjonen av det resulterende øyeblikket av ytre krefter på retningen til rotasjonsaksen OZ, er rotasjonsvinkelen til kroppen for den betraktede tidsperioden.
Ved å integrere (5.31) får vi en formel for arbeidet til ytre krefter som virker på et roterende legeme
Hvis , er formelen forenklet
Dermed blir arbeidet til ytre krefter under rotasjonen av et stivt legeme om en fast akse bestemt av virkningen av projeksjonen av momentet til disse kreftene på en gitt akse.
Gyroskop

Et gyroskop er et raskt roterende symmetrisk legeme, hvis rotasjonsakse kan endre retning i rommet. For at gyroskopets akse skal kunne rotere fritt i rommet, plasseres gyroskopet i det såkalte kardanopphenget (fig. 5.13). Svinghjulet til gyroskopet roterer i det indre ringformede buret rundt C 1 C 2-aksen og passerer gjennom tyngdepunktet. Det indre buret kan på sin side rotere i det ytre buret rundt aksen B 1 B 2 vinkelrett på C 1 C 2. Til slutt kan den ytre ringen fritt rotere i staglagrene rundt aksen A 1 A 2 vinkelrett på aksene C 1 C 2 og B 1 B 2. Alle tre aksene skjærer hverandre i noen fast punkt O, kalt suspensjonssenteret eller gyroskopets omdreiningspunkt. Gyroskopet i gimbalen har tre frihetsgrader og kan derfor foreta enhver rotasjon rundt midten av gimbalen. Hvis gyroskopets opphengssenter faller sammen med tyngdepunktet, er det resulterende tyngdemomentet for alle deler av gyroskopet i forhold til opphengssenteret lik null. Et slikt gyroskop kalles balansert.
La oss nå vurdere det meste viktige egenskaper gyroskop, som har funnet bred anvendelse på forskjellige felt.
1) Bærekraft.
Ved enhver rotasjon av stativet til et balansert gyroskop, beholder rotasjonsaksen den samme retningen mht. laboratoriesystem henvisning. Dette skyldes det faktum at øyeblikket til alle ytre krefter, lik øyeblikket av friksjonskrefter, er veldig lite og praktisk talt ikke forårsaker en endring i gyroskopets vinkelmoment, dvs.
Siden vinkelmomentet er rettet langs rotasjonsaksen til gyroskopet, må dets orientering forbli uendret.
Hvis en ekstern kraft virker i kort tid, vil integralet som bestemmer økningen av vinkelmomentet være lite
![]() . (5.34)
. (5.34)
 Dette betyr at under kortvarig påvirkning av selv store krefter, endres bevegelsen til et balansert gyroskop lite. Gyroskopet motstår som det var alle forsøk på å endre størrelsen og retningen på vinkelmomentet. Forbundet med dette er den bemerkelsesverdige stabiliteten som bevegelsen til et gyroskop oppnår etter å ha brakt det i rask rotasjon. Denne egenskapen til gyroskopet er mye brukt til å automatisk kontrollere bevegelsen til fly, skip, raketter og andre kjøretøy.
Dette betyr at under kortvarig påvirkning av selv store krefter, endres bevegelsen til et balansert gyroskop lite. Gyroskopet motstår som det var alle forsøk på å endre størrelsen og retningen på vinkelmomentet. Forbundet med dette er den bemerkelsesverdige stabiliteten som bevegelsen til et gyroskop oppnår etter å ha brakt det i rask rotasjon. Denne egenskapen til gyroskopet er mye brukt til å automatisk kontrollere bevegelsen til fly, skip, raketter og andre kjøretøy.
Hvis vi handler på gyroskopet lang tid konstant i retning av øyeblikket av ytre krefter, så etableres gyroskopets akse, til slutt, i retning av øyeblikket av ytre krefter. Dette fenomenet brukes i gyrokompasset. Denne enheten er et gyroskop, hvis akse kan roteres fritt inn horisontalt plan. På grunn av daglig rotasjon Jorden og virkningen av sentrifugalkreftene, roteres aksen til gyroskopet slik at vinkelen mellom og blir minimal (fig. 5.14). Dette tilsvarer posisjonen til gyroskopaksen i meridianplanet.
2). Gyroskopisk effekt.
 Hvis et par krefter og påføres et roterende gyroskop, og har en tendens til å rotere det om en akse vinkelrett på rotasjonsaksen, vil det rotere rundt den tredje aksen, vinkelrett på de to første (fig. 5.15). Denne uvanlige oppførselen til gyroskopet kalles den gyroskopiske effekten. Det forklares med at momentet til et par krefter er rettet langs O 1 O 1-aksen og en endring i vektoren med en verdi over tid vil ha samme retning. Som et resultat vil den nye vektoren rotere rundt O 2 O 2-aksen. Dermed samsvarer den tilsynelatende unaturlige oppførselen til gyroskopet fullt ut lovene for dynamikken til rotasjonsbevegelse
Hvis et par krefter og påføres et roterende gyroskop, og har en tendens til å rotere det om en akse vinkelrett på rotasjonsaksen, vil det rotere rundt den tredje aksen, vinkelrett på de to første (fig. 5.15). Denne uvanlige oppførselen til gyroskopet kalles den gyroskopiske effekten. Det forklares med at momentet til et par krefter er rettet langs O 1 O 1-aksen og en endring i vektoren med en verdi over tid vil ha samme retning. Som et resultat vil den nye vektoren rotere rundt O 2 O 2-aksen. Dermed samsvarer den tilsynelatende unaturlige oppførselen til gyroskopet fullt ut lovene for dynamikken til rotasjonsbevegelse
3). Gyropresesjon.
Presesjonen til et gyroskop er den koniske bevegelsen av dets akse. Det oppstår når øyeblikket av ytre krefter, som forblir konstant i størrelse, roterer samtidig med gyroskopets akse, og danner en rett vinkel med det hele tiden. For å demonstrere presesjon kan et sykkelhjul med forlenget aksel, brakt i rask rotasjon (fig. 5.16), tjene.
 Hvis hjulet er opphengt i den forlengede enden av akselen, vil akselen begynne å presse seg rundt den vertikale aksen under påvirkning av sin egen vekt. En raskt roterende topp kan også tjene som en demonstrasjon av presesjon.
Hvis hjulet er opphengt i den forlengede enden av akselen, vil akselen begynne å presse seg rundt den vertikale aksen under påvirkning av sin egen vekt. En raskt roterende topp kan også tjene som en demonstrasjon av presesjon.
Finn ut årsakene til presesjonen til gyroskopet. Tenk på et ubalansert gyroskop hvis akse fritt kan rotere rundt et bestemt punkt O (fig. 5.16). Tyngdemomentet påført gyroskopet er like stort
hvor er massen til gyroskopet, er avstanden fra punktet O til gyroskopets massesenter, er vinkelen som dannes av gyroskopets akse med vertikalen. Vektoren er rettet vinkelrett på det vertikale planet som går gjennom gyroskopets akse.
Under påvirkning av dette øyeblikket vil vinkelmomentet til gyroskopet (begynnelsen er plassert ved punkt O) motta en økning i tid, og det vertikale planet som går gjennom gyroskopets akse vil rotere med en vinkel. Vektoren er alltid vinkelrett på , derfor, uten å endre størrelse, endres vektoren bare i retning. Imidlertid etter en stund gjensidig ordning vektorer og vil være den samme som i første øyeblikk. Som et resultat vil aksen til gyroskopet kontinuerlig rotere rundt vertikalen, og beskrive en kjegle. Denne bevegelsen kalles presesjon.
La oss bestemme presesjonens vinkelhastighet. I følge Fig.5.16 er rotasjonsvinkelen til planet som går gjennom kjeglens akse og gyroskopaksen lik
hvor er vinkelmomentet til gyroskopet, og er dets økning over tid.
Ved å dele med , tar vi i betraktning de ovennevnte relasjonene og transformasjonene, får vi presesjonens vinkelhastighet
![]() . (5.35)
. (5.35)
For gyroskoper som brukes i teknologi, er vinkelhastigheten til presesjon millioner av ganger mindre enn rotasjonshastigheten til gyroskopet.
Avslutningsvis bemerker vi at fenomenet presesjon også observeres i atomer pga. orbital bevegelse elektroner.
Eksempler på anvendelse av dynamikkens lover
 1. Tenk på noen eksempler på loven om bevaring av vinkelmomentum, som kan implementeres ved hjelp av Zhukovsky-benken. I det enkleste tilfellet er Zhukovsky-benken en skiveformet plattform (stol) som fritt kan rotere rundt en vertikal akse på kulelager (fig. 5.17). Demonstranten sitter eller står på benken, hvoretter den bringes i rotasjonsbevegelse. På grunn av at friksjonskreftene på grunn av bruk av lagre er svært små, kan ikke vinkelmomentet til systemet bestående av benken og demonstratoren, i forhold til rotasjonsaksen, endres i tid hvis systemet overlates til seg selv. . Hvis demonstranten holder tunge manualer i hendene og sprer armene til sidene, vil han øke treghetsmomentet til systemet, og derfor må vinkelhastigheten av rotasjonen avta slik at vinkelmomentet forblir uendret.
1. Tenk på noen eksempler på loven om bevaring av vinkelmomentum, som kan implementeres ved hjelp av Zhukovsky-benken. I det enkleste tilfellet er Zhukovsky-benken en skiveformet plattform (stol) som fritt kan rotere rundt en vertikal akse på kulelager (fig. 5.17). Demonstranten sitter eller står på benken, hvoretter den bringes i rotasjonsbevegelse. På grunn av at friksjonskreftene på grunn av bruk av lagre er svært små, kan ikke vinkelmomentet til systemet bestående av benken og demonstratoren, i forhold til rotasjonsaksen, endres i tid hvis systemet overlates til seg selv. . Hvis demonstranten holder tunge manualer i hendene og sprer armene til sidene, vil han øke treghetsmomentet til systemet, og derfor må vinkelhastigheten av rotasjonen avta slik at vinkelmomentet forblir uendret.
I henhold til loven om bevaring av vinkelmomentum lager vi en ligning for denne saken
hvor er treghetsmomentet til personen og benken, og er treghetsmomentet til manualene i første og andre posisjon, og er vinkelhastighetene til systemet.
Vinkelhastighet rotasjon av systemet når avl manualer til siden vil være lik
![]() .
.
arbeid, perfeksjonert av mennesket når du flytter manualer, kan bestemmes gjennom endringen i den kinetiske energien til systemet
 2. La oss gi et eksperiment til med Zhukovskys benk. Demonstranten sitter eller står på en benk og får et raskt roterende hjul med vertikalt rettet akse (Fig. 5.18). Demonstranten dreier så hjulet 180 0 . I dette tilfellet overføres endringen i vinkelmomentet til hjulet fullstendig til benken og demonstratoren. Som et resultat kommer benken, sammen med demonstratoren, i rotasjon med en vinkelhastighet bestemt på grunnlag av loven om bevaring av vinkelmomentum.
2. La oss gi et eksperiment til med Zhukovskys benk. Demonstranten sitter eller står på en benk og får et raskt roterende hjul med vertikalt rettet akse (Fig. 5.18). Demonstranten dreier så hjulet 180 0 . I dette tilfellet overføres endringen i vinkelmomentet til hjulet fullstendig til benken og demonstratoren. Som et resultat kommer benken, sammen med demonstratoren, i rotasjon med en vinkelhastighet bestemt på grunnlag av loven om bevaring av vinkelmomentum.
Vinkelmomentet til systemet i opprinnelige tilstand bestemmes kun av hjulets momentum og er lik
hvor er treghetsmomentet til hjulet, er vinkelhastigheten til dets rotasjon.
Etter å ha dreid hjulet i en vinkel på 180 0, vil systemets momentum allerede være bestemt av summen av momentumet til benken med personen og momentumet til hjulet. Tar i betraktning det faktum at hjulets momentumvektoren har endret retning til motsatt, og projeksjonen til vertikal akse ble negativ, får vi
![]() ,
,
hvor er treghetsmomentet til "mann-plattform"-systemet, er vinkelhastigheten for rotasjon av benken med personen.
I henhold til loven om bevaring av vinkelmomentum
![]() Og
Og ![]() .
.
Som et resultat finner vi benkens rotasjonshastighet
3. Tynn stangmasse m og lengde l roterer med en vinkelhastighet ω=10 s -1 i et horisontalplan rundt en vertikal akse som går gjennom midten av stangen. Fortsetter å rotere i samme plan, beveger stangen seg slik at rotasjonsaksen nå går gjennom enden av stangen. Finn vinkelhastigheten i det andre tilfellet.
I dette problemet, på grunn av det faktum at fordelingen av massen til stangen i forhold til rotasjonsaksen endres, endres også treghetsmomentet til stangen. I samsvar med loven om bevaring av vinkelmomentet til et isolert system, har vi
Her - treghetsmomentet til stangen om aksen som går gjennom midten av stangen; ![]() - treghetsmomentet til staven rundt aksen som går gjennom enden og funnet av Steiners teorem.
- treghetsmomentet til staven rundt aksen som går gjennom enden og funnet av Steiners teorem.
Ved å erstatte disse uttrykkene i loven om bevaring av vinkelmomentum får vi
![]() ,
,
![]() .
.
4. Stanglengde L=1,5 m og vekt m 1=10 kg er hengslet i øvre ende. En kule treffer midten av stangen med en masse m2=10 g, flyr horisontalt med en hastighet på =500 m/s, og setter seg fast i stanga. I hvilken vinkel vil stangen avvike etter støtet?
La oss forestille oss i fig. 5.19. system av samvirkende kropper "stang-kule". Momentene til ytre krefter (tyngdekraft, aksereaksjon) i støtøyeblikket er lik null, så vi kan bruke loven om bevaring av vinkelmomentum
 Vinkelmomentet til systemet før støtet er lik kulens vinkelmoment i forhold til opphengspunktet
Vinkelmomentet til systemet før støtet er lik kulens vinkelmoment i forhold til opphengspunktet
Vinkelmomentet til systemet etter et uelastisk støt bestemmes av formelen
 ,
,
hvor er treghetsmomentet til stangen i forhold til opphengspunktet, er treghetsmomentet til kulen, er vinkelhastigheten til stangen med kulen umiddelbart etter støtet.
Å løse den resulterende ligningen etter substitusjon finner vi
![]() .
.
La oss nå bruke loven om bevaring av mekanisk energi. La oss sette likhetstegn mellom den kinetiske energien til stangen etter at kulen treffer den potensiell energi V høyeste punkt løfting:
![]() ,
,
hvor er høyden på massesenteret til det gitte systemet.
Etter å ha utført de nødvendige transformasjonene får vi
![]()
Avbøyningsvinkelen til stangen er relatert til verdien ved forholdet
![]() .
.
Etter å ha utført beregningene får vi =0,1p=18 0 .
5. Bestem akselerasjonen til kroppene og spenningen til tråden på Atwood-maskinen, forutsatt at (fig. 5.20). Treghetsmomentet til blokken om rotasjonsaksen er Jeg, blokkradius r. Ignorer massen av tråden.
 Vi ordner alle kreftene som virker på lastene og blokken, og komponerer dynamikklikningene for dem
Vi ordner alle kreftene som virker på lastene og blokken, og komponerer dynamikklikningene for dem

Hvis det ikke er noen glidning av tråden langs blokken, så lineær og vinkelakselerasjon knyttet til hverandre av relasjonen
Å løse disse ligningene får vi
![]()
Da finner vi T 1 og T 2 .
 6. En gjenge er festet til remskiven til Oberbeck-korset (fig. 5.21), som en masselast M= 0,5 kg. Bestem hvor lang tid det tar før en last faller fra en høyde h=1 m til bunnposisjon. Remskive radius r\u003d 3 cm. Fire vekter m=250g hver på avstand R= 30 cm fra sin akse. Se bort fra treghetsmomentet til selve korset og remskiven sammenlignet med treghetsmomentet til vektene.
6. En gjenge er festet til remskiven til Oberbeck-korset (fig. 5.21), som en masselast M= 0,5 kg. Bestem hvor lang tid det tar før en last faller fra en høyde h=1 m til bunnposisjon. Remskive radius r\u003d 3 cm. Fire vekter m=250g hver på avstand R= 30 cm fra sin akse. Se bort fra treghetsmomentet til selve korset og remskiven sammenlignet med treghetsmomentet til vektene.
Kinetisk rotasjonsenergi
Forelesning 3. Dynamics of a rigid body
Forelesningsplan
3.1. Kraftens øyeblikk.
3.2. Grunnleggende ligninger for rotasjonsbevegelse. Treghetsmoment.
3.3. Kinetisk rotasjonsenergi.
3.4. øyeblikk av impuls. Loven om bevaring av vinkelmomentum.
3.5. Analogi mellom translasjons- og rotasjonsbevegelse.
Kraftens øyeblikk
Tenk på bevegelsen til en stiv kropp rundt en fast akse. La et stivt legeme ha en fast rotasjonsakse ОО ( fig.3.1) og en vilkårlig kraft påføres den.

Ris. 3.1
Vi dekomponerer kraften i to komponenter av kraften, kraften ligger i rotasjonsplanet, og kraften er parallell med rotasjonsaksen. Deretter dekomponerer vi kraften i to komponenter: – som virker langs radiusvektoren og – vinkelrett på den.
Ingen kraft påført et legeme vil rotere det. Tvinger og skaper trykk på lagrene, men ikke roter det.
Kraften kan eller ikke kan bringe kroppen ut av balanse, avhengig av hvor i radiusvektoren den påføres. Derfor introduseres begrepet kraftmomentet om aksen. Kraftens øyeblikk i forhold til rotasjonsaksen kalles vektorproduktet av radiusvektoren og kraften.
Vektoren er rettet langs rotasjonsaksen og bestemmes av kryssproduktregelen eller høyre skrueregel, eller gimletregelen.
Modulus for kraftmoment
hvor α er vinkelen mellom vektorene og .
Fra Fig.3.1. det er klart det .
r0 – korteste avstand fra rotasjonsaksen til kraftens virkelinje og kalles kraftens arm. Da kan kraftmomentet skrives
M = F r 0 . (3.3)
Fra fig. 3.1.
Hvor F er projeksjonen av vektoren på retningen, vinkelrett på vektoren radius vektor. I dette tilfellet er kraftmomentet
. (3.4)
Hvis flere krefter virker på kroppen, er det resulterende kraftmomentet lik vektorsummen av momentene til individuelle krefter, men siden alle momentene er rettet langs aksen, kan de erstattes algebraisk sum. Øyeblikket vil bli ansett som positivt hvis det roterer kroppen med klokken og negativt hvis det roterer mot klokken. Hvis alle kreftmomenter er lik null (), vil kroppen være i likevekt.
Konseptet med et kraftmoment kan demonstreres ved hjelp av en "snurrig spole". Trådsnellen trekkes av den frie enden av tråden ( ris. 3.2).

Ris. 3.2
Avhengig av trådspenningens retning, ruller spolen i en eller annen retning. Hvis du drar på skrå α , deretter kraftmomentet om aksen OM(vinkelrett på figuren) roterer spolen mot klokken og den ruller tilbake. Ved spenning i vinkel β dreiemomentet er mot klokken og spolen ruller fremover.
Ved å bruke likevektsbetingelsen (), kan du konstruere enkle mekanismer, som er "omformere" av kraft, dvs. Ved å bruke mindre kraft kan du løfte og flytte laster med forskjellige vekter. Leverage, trillebårer, blokker er basert på dette prinsippet. annen type som er mye brukt i konstruksjon. For å overholde likevektstilstanden i byggekraner for å kompensere for kraftmomentet forårsaket av vekten av lasten, er det alltid et system med motvekter som skaper et kraftmoment av motsatt fortegn.
3.2. Grunnleggende rotasjonsligning
bevegelse. Treghetsmoment
Tenk på en absolutt stiv kropp som roterer rundt en fast akse OO(fig.3.3). La oss mentalt dele denne kroppen inn i elementer med massene Δ m 1, Δ m2, …, Δ m n. Under rotasjon vil disse elementene beskrive sirkler med radier r1,r2 , …,rn. Krefter virker på hvert element F1,F2 , …,F n. Rotasjon av et legeme rundt en akse OO skjer under påvirkning av det totale kraftmomentet M.
M \u003d M 1 + M 2 + ... + M n (3.4)
Hvor M 1 = F 1 r 1, M 2 = F 2 r 2, ..., M n = F n r n
I følge Newtons andre lov, hver kraft F, som virker på et element med masse D m, forårsaker akselerasjon av det gitte elementet en, dvs.
F i = D jeg og jeg (3.5)
Ved å erstatte de tilsvarende verdiene i (3.4), får vi

Ris. 3.3
Kjenne til sammenhengen mellom lineær vinkelakselerasjon ε () og at vinkelakselerasjonen er lik for alle elementer, vil formel (3.6) se ut
M = (3.7)
=Jeg (3.8)
Jeg er treghetsmomentet til kroppen om den faste aksen.
Da får vi
M = I ε (3.9)
Eller i vektorform
(3.10)
Denne ligningen er den grunnleggende ligningen for dynamikken i rotasjonsbevegelse. Den ligner i form på ligning II i Newtons lov. Fra (3.10) er treghetsmomentet
Treghetsmomentet til et gitt legeme er altså forholdet mellom kraftmomentet og vinkelakselerasjonen forårsaket av det. Fra (3.11) kan man se at treghetsmomentet er et mål på kroppens treghet med hensyn til rotasjonsbevegelse. Treghetsmomentet spiller samme rolle som masse i translasjonsbevegelse. SI-enhet [ Jeg] = kg m 2. Av formel (3.7) følger det at treghetsmomentet karakteriserer fordelingen av massene til legemets partikler i forhold til rotasjonsaksen.
Så, treghetsmomentet til et element med masse ∆m som beveger seg langs en sirkel med radius r er lik
I = r2 D m (3.12)
jeg= (3.13)
Når kontinuerlig distribusjon massesummen kan erstattes av integralet
I= ∫ r 2 dm (3.14)
hvor integrasjon utføres over hele kroppsmassen.
Dette viser at kroppens treghetsmoment avhenger av massen og dens fordeling i forhold til rotasjonsaksen. Dette kan demonstreres eksperimentelt fig.3.4).

Ris. 3.4
To runde sylindre, en hul (for eksempel metall), den andre solid (tre) med samme lengder, radier og masser begynner å rulle ned samtidig. En hul sylinder med et stort treghetsmoment vil ligge bak en solid.
Du kan beregne treghetsmomentet hvis du kjenner massen m og dens fordeling i forhold til rotasjonsaksen. Det enkleste tilfellet er en ring, når alle elementene i massen er plassert likt fra rotasjonsaksen ( ris. 3.5):
jeg=  (3.15)
(3.15)

Ris. 3.5
La oss gi uttrykk for treghetsmomentene til forskjellige symmetriske legemer med masse m.
1. Treghetsmoment ringer, hul tynnvegget sylinder om rotasjonsaksen som faller sammen med symmetriaksen.
, (3.16)
r er radiusen til ringen eller sylinderen
2. For en solid sylinder og skive, treghetsmomentet om symmetriaksen
(3.17)
3. Treghetsmomentet til ballen rundt aksen som går gjennom midten
(3.18)
r- kuleradius
4. Treghetsmomentet til en tynn stang av lang l i forhold til en akse vinkelrett på stangen og som går gjennom midten
(3.19)
l- lengden på stangen.
Hvis rotasjonsaksen ikke går gjennom massesenteret, bestemmes treghetsmomentet til kroppen rundt denne aksen av Steiners teorem.
![]() (3.20)
(3.20)
I følge denne teoremet, treghetsmomentet om en vilkårlig akse О'O' ( ) er lik treghetsmomentet om en parallell akse som går gjennom kroppens massesenter ( ) pluss produktet av kroppsmasse ganger kvadratet av avstanden EN mellom aksler ( ris. 3.6).

Ris. 3.6
Kinetisk rotasjonsenergi
Tenk på rotasjonen av et absolutt stivt legeme rundt en fast akse OO med en vinkelhastighet ω (ris. 3.7). La oss dele den stive kroppen inn i n elementære masser ∆ m jeg. Hvert element i massen roterer på en sirkel med radius r jeg Med lineær hastighet(). Kinetisk energi er summen av de kinetiske energiene til individuelle elementer.
![]() (3.21)
(3.21)

Ris. 3.7
Husk fra (3.13) det er treghetsmomentet om OO-aksen.
Dermed den kinetiske energien til et roterende legeme
E k \u003d (3.22)
Vi har vurdert den kinetiske energien til rotasjon rundt en fast akse. Hvis kroppen er involvert i to bevegelser: i translasjons- og rotasjonsbevegelser, er den kinetiske energien til kroppen summen av den kinetiske energien til translasjonsbevegelsen og den kinetiske energien til rotasjonen.
For eksempel en massekule m rullende; massesenteret til ballen beveger seg fremover med en hastighet u (ris. 3.8).

Ris. 3.8
Den totale kinetiske energien til ballen vil være lik
![]() (3.23)
(3.23)
3.4. øyeblikk av impuls. fredningsloven
vinkelmomentum
Fysisk mengde lik produktet treghetsmoment Jeg til vinkelhastighet ω , kalles vinkelmomentum (momentum) L om rotasjonsaksen.
– vinkelmomentum er en vektorstørrelse og sammenfaller i retning med retningen til vinkelhastigheten .
Differensieringsligning (3.24) med hensyn til tid får vi
Hvor, M er det totale øyeblikket av ytre krefter. I et isolert system er det ikke noe øyeblikk av ytre krefter ( M=0) og
« Fysikk - klasse 10"
Hvorfor strekker skøyteløperen seg langs rotasjonsaksen for å øke rotasjonsvinkelhastigheten.
Bør et helikopter rotere når propellen roterer?
Spørsmålene som stilles antyder at hvis ytre krefter ikke virker på kroppen eller deres virkning blir kompensert og en del av kroppen begynner å rotere i én retning, så må den andre delen rotere i den andre retningen, akkurat som når drivstoff kastes ut fra en rakett beveger selve raketten seg i motsatt retning.
øyeblikk av impuls.
Hvis vi tar for oss en roterende skive, blir det åpenbart at skivens totale bevegelsesmengde er null, siden enhver partikkel i kroppen tilsvarer en partikkel som beveger seg med lik hastighet i absolutt verdi, men i motsatt retning (fig. 6.9).
Men skiven beveger seg, vinkelhastigheten for rotasjon av alle partikler er den samme. Det er imidlertid klart at jo lenger partikkelen er fra rotasjonsaksen, desto større er momentumet. Derfor, for rotasjonsbevegelse, er det nødvendig å introdusere en mer karakteristikk, som ligner på en impuls, - vinkelmomentet.

Vinkelmomentet til en partikkel som beveger seg i en sirkel er produktet av partikkelens momentum og avstanden fra den til rotasjonsaksen (fig. 6.10):
De lineære og vinkelhastighetene er relatert med v = ωr, da
Alle punkter i en stiv materie beveger seg i forhold til en fast rotasjonsakse med samme vinkelhastighet. En stiv kropp kan representeres som en samling av materielle punkter.
vinkelmomentum solid kropp er lik produktet treghetsmoment per vinkelhastighet:
Vinkelmomentet er en vektorstørrelse, ifølge formel (6.3) er vinkelmomentet rettet på samme måte som vinkelhastigheten.
Den grunnleggende ligningen for dynamikken til rotasjonsbevegelse i impulsiv form.
Vinkelakselerasjonen til et legeme er lik endringen i vinkelhastighet delt på tidsintervallet denne endringen skjedde i: Bytt ut dette uttrykket med den grunnleggende ligningen for dynamikken i rotasjonsbevegelsen ![]() derfor I(ω 2 - ω 1) = MΔt, eller IΔω = MΔt.
derfor I(ω 2 - ω 1) = MΔt, eller IΔω = MΔt.
Dermed,
∆L = M∆t. (6.4)
Endringen i vinkelmomentet er lik produktet av det totale kreftmomentet som virker på kroppen eller systemet og virkningstidspunktet for disse kreftene.
Lov om bevaring av vinkelmomentum:
Hvis det totale kreftmomentet som virker på et legeme eller system av kropper med en fast rotasjonsakse er lik null, så er endringen i vinkelmomentet også lik null, dvs. vinkelmomentet til systemet forblir konstant.
∆L=0, L=konst.
Endringen i systemets bevegelsesmengde er lik den totale bevegelsesmengden til kreftene som virker på systemet.
Den spinnende skateren sprer armene ut til sidene, og øker derved treghetsmomentet for å redusere vinkelhastigheten til rotasjonen.

Loven om bevaring av vinkelmomentum kan demonstreres ved å bruke følgende eksperiment, kalt "eksperimentet med Zhukovsky-benken." En person står på en benk med en vertikal rotasjonsakse som går gjennom midten. Mannen holder manualer i hendene. Hvis benken er laget for å rotere, kan en person endre rotasjonshastigheten ved å trykke manualene til brystet eller senke armene, og deretter spre dem fra hverandre. Ved å spre armene, øker han treghetsmomentet, og vinkelhastigheten av rotasjonen avtar (fig. 6.11, a), senker hendene, han reduserer treghetsmomentet, og benkens vinkelhastighet øker (fig. 6.11, b).
En person kan også få en benk til å rotere ved å gå langs kanten. I dette tilfellet vil benken rotere i motsatt retning, siden det totale vinkelmomentet må forbli lik null.
Prinsippet for drift av enheter kalt gyroskop er basert på loven om bevaring av vinkelmomentum. Hovedegenskapen til et gyroskop er bevaring av retningen til rotasjonsaksen, hvis ytre krefter ikke virker på denne aksen. På 1800-tallet gyroskoper ble brukt av navigatører for å navigere i havet.
Kinetisk energi til et roterende stivt legeme.
Den kinetiske energien til et roterende fast legeme er lik summen av de kinetiske energiene til dets individuelle partikler. La oss dele kroppen inn i små elementer, som hver kan betraktes som et materiell punkt. Da er den kinetiske energien til kroppen lik summen av de kinetiske energiene til de materielle punktene den består av:
Vinkelhastigheten for rotasjon av alle punkter på kroppen er den samme, derfor,
Verdien i parentes, som vi allerede vet, er treghetsmomentet til den stive kroppen. Til slutt har formelen for den kinetiske energien til et stivt legeme med en fast rotasjonsakse formen
I det generelle tilfellet med bevegelse av et stivt legeme, når rotasjonsaksen er fri, er dens kinetiske energi lik summen av energiene til translasjons- og rotasjonsbevegelser. Så den kinetiske energien til et hjul, hvis masse er konsentrert i felgen, ruller langs veien med konstant hastighet, er lik
Tabellen sammenligner formlene for mekanikken til translasjonsbevegelse materiell poeng med lignende formler for rotasjonsbevegelsen til en stiv kropp.

Oppgaver
1. Bestem hvor mange ganger effektiv masse mer enn gravitasjonsmassen til et tog som veier 4000 tonn, hvis massen til hjulene er 15 % av togets masse. Betrakt hjulene som skiver med en diameter på 1,02 m. Hvordan vil svaret endres hvis diameteren på hjulene er halvparten av det?
2. Bestem akselerasjonen som et hjulpar med masse på 1200 kg ruller nedover en bakke med en helning på 0,08. Betrakt hjul som disker. Rullemotstandskoeffisient 0,004. Bestem adhesjonskraften til hjulene til skinnene.
3. Bestem akselerasjonen som et hjulpar med en masse på 1400 kg ruller oppover en bakke med en helning på 0,05. Drakoeffisient 0,002. Hva skal være vedheftskoeffisienten slik at hjulene ikke sklir. Betrakt hjul som disker.
4. Bestem akselerasjonen som en vogn som veier 40 tonn ruller nedover en bakke med en helning på 0,020 hvis den har åtte hjul som veier 1200 kg og en diameter på 1,02 m. Bestem vedheftkraften til hjulene til skinnene. Drakoeffisient 0,003.
5. Bestem trykkkraften til bremseskoene på dekkene, hvis et tog som veier 4000 tonn bremser ned med en akselerasjon på 0,3 m/s 2 . Treghetsmomentet til ett hjulsett er 600 kg m 2, antall aksler er 400, glidefriksjonskoeffisienten til blokken er 0,18, rullemotstandskoeffisienten er 0,004.
6. Bestem bremsekraften som virker på en fireakslet vogn med en masse på 60 tonn på bremseklossen til en rangerbane dersom hastigheten på en 30 m bane gikk ned fra 2 m/s til 1,5 m/s. Treghetsmomentet til ett hjulsett er 500 kg m 2 .
7. Lokomotivets hastighetsmåler viste en økning i togets hastighet innen ett minutt fra 10 m/s til 60 m/s. Sannsynligvis var det en glidning av det fremste hjulsettet. Bestem øyeblikket for krefter som virker på ankeret til den elektriske motoren. Treghetsmoment for hjulsett 600 kg m 2 , ankre 120 kg m 2 . Girforhold gir 4,2. Trykkkraften på skinnene er 200 kN, glidefriksjonskoeffisienten til hjulene langs skinnen er 0,10.
11. ROTATORENS KINETISK ENERGI
BEVEGELSER
Vi utleder formelen for den kinetiske energien til rotasjonsbevegelse. La kroppen rotere med vinkelhastighet ω
om den faste aksen. Enhver liten partikkel i kroppen bevegelse fremover i en sirkel med en hastighet , hvor r jeg - avstand til rotasjonsaksen, radius av banen. Kinetisk energi til en partikkel
masser m jeg er lik  . Den totale kinetiske energien til et system av partikler er lik summen av deres kinetiske energier. La oss summere formlene for den kinetiske energien til partiklene i kroppen og ta ut tegnet på summen av halve kvadratet av vinkelhastigheten, som er lik for alle partiklene,
. Den totale kinetiske energien til et system av partikler er lik summen av deres kinetiske energier. La oss summere formlene for den kinetiske energien til partiklene i kroppen og ta ut tegnet på summen av halve kvadratet av vinkelhastigheten, som er lik for alle partiklene,  . Summen av produktene av massene av partikler og kvadratene av deres avstander til rotasjonsaksen er treghetsmomentet til kroppen rundt rotasjonsaksen
. Summen av produktene av massene av partikler og kvadratene av deres avstander til rotasjonsaksen er treghetsmomentet til kroppen rundt rotasjonsaksen ![]() .
Så, den kinetiske energien til et legeme som roterer om en fast akse er lik halvparten av produktet av treghetsmomentet til legemet om aksen og kvadratet av rotasjonsvinkelhastigheten:
.
Så, den kinetiske energien til et legeme som roterer om en fast akse er lik halvparten av produktet av treghetsmomentet til legemet om aksen og kvadratet av rotasjonsvinkelhastigheten:
Ved hjelp av roterende kropper er det mulig å lagre mekanisk energi. Slike kropper kalles svinghjul. Vanligvis er dette revolusjonsorganer. Bruken av svinghjul i pottemakerhjulet har vært kjent siden antikken. i motorer intern forbrenning under arbeidsslaget gir stempelet mekanisk energi til svinghjulet, som deretter utfører arbeid med rotasjonen av motorakselen i de neste tre syklusene. I dyser og presser drives svinghjulet av en elektrisk motor med relativt lav effekt, akkumulerer mekanisk energi i nesten full sving og i et kort øyeblikk av innvirkning gir det til arbeidet med stempling.
Det er kjent mange forsøk på å bruke roterende svinghjul for å drive Kjøretøy: biler, busser. De kalles mahomobiler, gyrobærere. Mange slike eksperimentelle maskiner ble laget. Det vil være lovende å bruke svinghjul for energilagring under bremsing av elektriske tog for å bruke den akkumulerte energien under påfølgende akselerasjon. Lagring av svinghjulsenergi er kjent for å bli brukt på t-banetog i New York City.
La oss bestemme den kinetiske energien til et stivt legeme som roterer rundt en fast akse. La oss dele denne kroppen inn i n materielle punkter. Hvert punkt beveger seg med en lineær hastighet υ i =ωr i, deretter den kinetiske energien til punktet
eller 
Den totale kinetiske energien til et roterende stivt legeme er lik summen av de kinetiske energiene til alle dets materielle punkter:
 (3.22)
(3.22)
(J - kroppens treghetsmoment om rotasjonsaksen)
Hvis banene til alle punktene ligger i parallelle plan (som en sylinder som ruller ned skråplan, hvert punkt beveger seg i sitt eget plan fig.), dette flat bevegelse. I følge Eulers prinsipp kan planbevegelse alltid dekomponeres på et uendelig antall måter til translasjons- og rotasjonsbevegelse. Hvis ballen faller eller glir langs et skråplan, beveger den seg bare fremover; når ballen ruller, roterer den også.
Hvis en kropp utfører translasjons- og rotasjonsbevegelser samtidig, er dens totale kinetiske energi lik
 (3.23)
(3.23)
Fra en sammenligning av formlene for kinetisk energi for translasjons- og rotasjonsbevegelser, kan man se at treghetsmålet under rotasjonsbevegelse er kroppens treghetsmoment.
§ 3.6 Ytre krefters arbeid under rotasjon av et stivt legeme
Når et stivt legeme roterer, endres ikke dets potensielle energi, derfor er det elementære arbeidet med ytre krefter lik økningen i kroppens kinetiske energi:
dA = dE eller 
Tatt i betraktning at Jβ = M, ωdr = dφ, har vi α av kroppen i en endelig vinkel φ lik
 (3.25)
(3.25)
Når et stivt legeme roterer rundt en fast akse, er arbeidet til ytre krefter bestemt av virkningen av momentet til disse kreftene om en gitt akse. Hvis kreftmomentet rundt aksen er lik null, gir ikke disse kreftene arbeid.
Eksempler på problemløsning
Eksempel 2.1. svinghjulets massem=5kg og radiusr= 0,2 m roterer rundt den horisontale aksen med en frekvensν 0 =720 min -1 og stopper ved bremsingt=20 s. Finn bremsemomentet og antall omdreininger før du stopper.
For å bestemme bremsemomentet bruker vi den grunnleggende ligningen for dynamikken i rotasjonsbevegelse
hvor I=mr 2 er treghetsmomentet til skiven; Δω \u003d ω - ω 0, og ω \u003d 0 er den endelige vinkelhastigheten, ω 0 \u003d 2πν 0 er den første. M er bremsemomentet til kreftene som virker på skiven.
Når du kjenner alle mengdene, er det mulig å bestemme bremsemomentet
Mr 2 2πν 0 = МΔt (1)
 (2)
(2)
Fra kinematikken til rotasjonsbevegelse kan rotasjonsvinkelen under diskrotasjonen til stopp bestemmes av formelen
 (3)
(3)
hvor β er vinkelakselerasjonen.
I henhold til tilstanden til problemet: ω = ω 0 - βΔt, siden ω=0, ω 0 = βΔt
Da kan uttrykk (2) skrives som:

Eksempel 2.2. To svinghjul i form av skiver med samme radier og masse ble spunnet opp til rotasjonshastighetenn= 480 rpm og overlatt til seg selv. Under påvirkning av friksjonskreftene til akslene på lagrene, stoppet den første ettert\u003d 80 s, og den andre gjorde detN= 240 omdreininger for å stoppe. I hvilket svinghjul var momentet for friksjonskreftene til akslene på lagrene større og hvor mange ganger.
Vi vil finne kreftmomentet til tornene M 1 til det første svinghjulet ved å bruke den grunnleggende ligningen for dynamikken til rotasjonsbevegelse
M 1 Δt \u003d Iω 2 - Iω 1
hvor Δt er virkningstidspunktet for friksjonskreftene, I \u003d mr 2 - treghetsmomentet til svinghjulet, ω 1 \u003d 2πν og ω 2 \u003d 0 er de innledende og endelige vinkelhastighetene til svinghjulene
Deretter 
Friksjonskreftene M 2 til det andre svinghjulet uttrykkes gjennom forholdet mellom arbeidet A til friksjonskreftene og endringen i dets kinetiske energi ΔE k:

hvor Δφ = 2πN er rotasjonsvinkelen, N er antall omdreininger til svinghjulet.

 Hvor da
Hvor da
OM  forholdet vil være
forholdet vil være
Friksjonsmomentet til det andre svinghjulet er 1,33 ganger større.
Eksempel 2.3.
Masse av en homogen fast skive m, masse av belastninger m 1
og M 2
(fig.15). Det er ingen slip og friksjon av gjengen i sylinderens akse. Finn akselerasjonen til massene og forholdet mellom trådspenningene i ferd med å bevege seg.
i ferd med å bevege seg.
 Det er ingen glidning av tråden, derfor, når m 1 og m 2 vil gjøre translasjonsbevegelser, vil sylinderen rotere rundt aksen som går gjennom punktet O. La oss anta at m 2 > m 1.
Det er ingen glidning av tråden, derfor, når m 1 og m 2 vil gjøre translasjonsbevegelser, vil sylinderen rotere rundt aksen som går gjennom punktet O. La oss anta at m 2 > m 1.
Deretter senkes lasten m 2 og sylinderen roterer med klokken. La oss skrive ned bevegelseslikningene til kroppene som inngår i systemet

De to første ligningene er skrevet for kropper med masser m 1 og m 2 som utfører translasjonsbevegelse, og den tredje ligningen er for en roterende sylinder. I den tredje ligningen, til venstre er det totale kreftmomentet som virker på sylinderen (kraftmomentet T 1 er tatt med et minustegn, siden kraften T 1 har en tendens til å dreie sylinderen mot klokken). Til høyre er I treghetsmomentet til sylinderen om aksen O, som er lik

hvor R er radiusen til sylinderen; β er vinkelakselerasjonen til sylinderen.
Siden det ikke er noen trådglidning,  . Tar vi i betraktning uttrykkene for I og β, får vi:
. Tar vi i betraktning uttrykkene for I og β, får vi:

Legger vi til likningene til systemet, kommer vi til likningen

Herfra finner vi akselerasjonen en last


Det kan sees av den resulterende ligningen at trådspenningene vil være de samme, dvs.  =1 hvis massen til sylinderen er mye mindre enn massen til vektene.
=1 hvis massen til sylinderen er mye mindre enn massen til vektene.
Eksempel 2.4.
En hul kule med masse m = 0,5 kg har en ytre radius R = 0,08m og en indre radius r = 0,06m. Kulen roterer rundt en akse som går gjennom midten. I et visst øyeblikk begynner en kraft å virke på ballen, som et resultat av at rotasjonsvinkelen til ballen endres i henhold til loven . Bestem øyeblikket for den påførte kraften.
. Bestem øyeblikket for den påførte kraften.
Vi løser problemet ved å bruke den grunnleggende ligningen for dynamikken i rotasjonsbevegelse  . Hovedvanskeligheten er å bestemme treghetsmomentet til den hule kulen, og vinkelakselerasjonen β finnes som
. Hovedvanskeligheten er å bestemme treghetsmomentet til den hule kulen, og vinkelakselerasjonen β finnes som  . Treghetsmomentet I til en hul kule er lik forskjellen mellom treghetsmomentene til en kule med radius R og en kule med radius r:
. Treghetsmomentet I til en hul kule er lik forskjellen mellom treghetsmomentene til en kule med radius R og en kule med radius r:
hvor ρ er tettheten til kulematerialet. Vi finner tettheten ved å vite massen til en hul kule

Herfra bestemmer vi tettheten til materialet til ballen


For kraftmomentet M får vi følgende uttrykk:

Eksempel 2.5. En tynn stang med en masse på 300 g og en lengde på 50 cm roterer med en vinkelhastighet på 10 s -1 i et horisontalt plan rundt en vertikal akse som går gjennom midten av stangen. Finn vinkelhastigheten hvis stangen under rotasjon i samme plan beveger seg slik at rotasjonsaksen går gjennom enden av stangen.
Vi bruker loven om bevaring av vinkelmomentum
 (1)
(1)
(J i - treghetsmomentet til stangen i forhold til rotasjonsaksen).
For et isolert system av kropper forblir vektorsummen av vinkelmomentet konstant. På grunn av det faktum at fordelingen av massen til stangen i forhold til rotasjonsaksen endres, endres treghetsmomentet til stangen også i samsvar med (1):
J 0 ω 1 = J 2 ω 2. (2)
Det er kjent at treghetsmomentet til stangen rundt aksen som går gjennom massesenteret og vinkelrett på stangen er lik
J 0 \u003d mℓ 2/12. (3)
I følge Steiner-teoremet
J = J0 +m EN 2
(J er treghetsmomentet til stangen om en vilkårlig rotasjonsakse; J 0 er treghetsmomentet om en parallell akse som går gjennom massesenteret; EN- avstand fra massesenteret til den valgte rotasjonsaksen).
La oss finne treghetsmomentet rundt aksen som går gjennom enden og vinkelrett på stangen:
J 2 \u003d J 0 +m EN 2, J2 = ml2/12 +m(l/2)2 = ml2/3. (4)
La oss erstatte formlene (3) og (4) med (2):
mℓ 2 ω 1 /12 = mℓ 2 ω 2 /3
ω 2 \u003d ω 1 /4 ω 2 \u003d 10s-1/4 \u003d 2,5s -1
Eksempel 2.6 . masse mannm= 60 kg, stående på kanten av plattformen med masse M = 120 kg, roterende ved treghet rundt en fast vertikal akse med en frekvens ν 1 =12 min -1 , går til sentrum. Betrakt plattformen som en rund homogen skive, og personen som en punktmasse, bestemme med hvilken frekvens ν 2 plattformen vil da rotere.
Gitt: m=60kg, M=120kg, ν 1 =12min -1 = 0,2s -1 .
Finne: v 1
Løsning: I henhold til tilstanden til problemet roterer plattformen med personen ved treghet, dvs. det resulterende momentet av alle krefter påført det roterende systemet er null. Derfor, for "plattform-menneske"-systemet, er loven om bevaring av momentum oppfylt
I 1 ω 1 = I 2 ω 2
Hvor  - treghetsmomentet til systemet når en person står på kanten av plattformen (vi tok hensyn til at treghetsmomentet til plattformen er lik
- treghetsmomentet til systemet når en person står på kanten av plattformen (vi tok hensyn til at treghetsmomentet til plattformen er lik  (R er radius p
(R er radius p  plattform), treghetsmomentet til en person ved kanten av plattformen er mR 2).
plattform), treghetsmomentet til en person ved kanten av plattformen er mR 2).
 - treghetsmomentet til systemet når en person står i midten av plattformen (vi tok hensyn til at øyeblikket til en person som står i midten av plattformen er lik null). Vinkelhastighet ω 1 = 2π ν 1 og ω 1 = 2π ν 2.
- treghetsmomentet til systemet når en person står i midten av plattformen (vi tok hensyn til at øyeblikket til en person som står i midten av plattformen er lik null). Vinkelhastighet ω 1 = 2π ν 1 og ω 1 = 2π ν 2.
Ved å erstatte de skriftlige uttrykkene med formel (1), får vi

hvorfra ønsket rotasjonshastighet

Svar: v2=24 min-1.
 Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler
Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler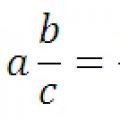 Konvertering av desimaltall til vanlige brøker
Konvertering av desimaltall til vanlige brøker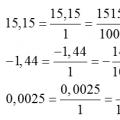 Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler
Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler