Lineær avhengighet og lineær uavhengighet av et system av vektorer. Lineært avhengige og lineært uavhengige vektorer Finn ut om vektorene er lineært uavhengige
Definisjon. Lineær kombinasjon av vektorer a 1 , ..., a n med koeffisientene x 1 , ..., x n kalles en vektor
x 1 a 1 + ... + x n a n .
trivielt, hvis alle koeffisientene x 1, ..., x n er lik null.
Definisjon. Den lineære kombinasjonen x 1 a 1 + ... + x n a n kalles ikke-trivielt, hvis minst én av koeffisientene x 1, ..., x n ikke er lik null.
lineært uavhengig, hvis det ikke er noen ikke-triviell kombinasjon av disse vektorene lik nullvektoren.
Det vil si at vektorene a 1, ..., a n er lineært uavhengige hvis x 1 a 1 + ... + x n a n = 0 hvis og bare hvis x 1 = 0, ..., x n = 0.
Definisjon. Vektorene a 1, ..., a n kalles lineært avhengig, hvis det er en ikke-triviell kombinasjon av disse vektorene lik nullvektoren.
Egenskaper til lineært avhengige vektorer:
For n-dimensjonale vektorer.
n + 1 vektorer er alltid lineært avhengige.
For 2- og 3-dimensjonale vektorer.
To lineært avhengige vektorer er kollineære. (Kolineære vektorer er lineært avhengige.)
For 3-dimensjonale vektorer.
Tre lineært avhengige vektorer er koplanære. (Tre koplanare vektorer er lineært avhengige.)
Eksempler på problemer med lineær avhengighet og lineær uavhengighet av vektorer:
Eksempel 1. Sjekk om vektorene a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) er lineært uavhengige .
Løsning:
Vektorene vil være lineært avhengige, siden dimensjonen til vektorene er mindre enn antall vektorer.
Eksempel 2. Sjekk om vektorene a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) er lineært uavhengige.
Løsning:
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
trekk den andre fra den første linjen; legg til en andre linje til den tredje linjen:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Denne løsningen viser at systemet har mange løsninger, det vil si at det er en ikke-null kombinasjon av verdier av tallene x 1, x 2, x 3 slik at den lineære kombinasjonen av vektorene a, b, c er lik nullvektoren, for eksempel:
A + b + c = 0
og dette betyr at vektorene a, b, c er lineært avhengige.
Svare: vektorene a, b, c er lineært avhengige.
Eksempel 3. Sjekk om vektorene a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) er lineært uavhengige.
Løsning: La oss finne verdiene til koeffisientene der den lineære kombinasjonen av disse vektorene vil være lik nullvektoren.
x 1 a + x 2 b + x 3 c 1 = 0Denne vektorligningen kan skrives som et system av lineære ligninger
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + 2x 3 = 0 |
La oss løse dette systemet ved å bruke Gauss-metoden
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
trekk den første fra den andre linjen; trekk den første fra den tredje linjen:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
trekk den andre fra den første linjen; legg til en andre til den tredje linjen.
I denne artikkelen vil vi dekke:
- hva er kollineære vektorer;
- hva er betingelsene for kollinearitet av vektorer;
- hvilke egenskaper av kollineære vektorer finnes;
- hva er den lineære avhengigheten til kollineære vektorer.
Kollineære vektorer er vektorer som er parallelle med én linje eller ligger på én linje.
Eksempel 1
Betingelser for kollinearitet av vektorer
To vektorer er kollineære hvis noen av følgende forhold er sanne:
- tilstand 1 . Vektorene a og b er kollineære hvis det er et tall λ slik at a = λ b;
- tilstand 2 . Vektorene a og b er kollineære med like koordinatforhold:
a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2
- tilstand 3 . Vektorene a og b er kollineære forutsatt at kryssproduktet og nullvektoren er like:
a ∥ b ⇔ a, b = 0
Merknad 1
Tilstand 2 ikke aktuelt hvis en av vektorkoordinatene er null.
Merknad 2
Tilstand 3 gjelder bare for de vektorene som er spesifisert i rommet.
Eksempler på problemer for å studere kollineariteten til vektorer
Eksempel 1Vi undersøker vektorene a = (1; 3) og b = (2; 1) for kollinearitet.
Hvordan løse?
I dette tilfellet er det nødvendig å bruke den andre kollinearitetsbetingelsen. For gitte vektorer ser det slik ut:
Likheten er falsk. Fra dette kan vi konkludere med at vektorene a og b er ikke-kollineære.
Svare : a | | b
Eksempel 2
Hvilken verdi m av vektoren a = (1; 2) og b = (- 1; m) er nødvendig for at vektorene skal være kollineære?
Hvordan løse?
Ved å bruke den andre kollinearitetsbetingelsen vil vektorer være kollineære hvis koordinatene deres er proporsjonale:
Dette viser at m = - 2.
Svare: m = -2.
Kriterier for lineær avhengighet og lineær uavhengighet av vektorsystemer
TeoremEt system av vektorer i et vektorrom er lineært avhengig bare hvis en av vektorene i systemet kan uttrykkes i form av de gjenværende vektorene i dette systemet.
Bevis
La systemet e 1 , e 2 , . . . , e n er lineært avhengig. La oss skrive en lineær kombinasjon av dette systemet lik nullvektoren:
a 1 e 1 + a 2 e 2 + . . . + a n e n = 0
der minst én av kombinasjonskoeffisientene ikke er lik null.
La a k ≠ 0 k ∈ 1 , 2 , . . . , n.
Vi deler begge sider av likheten med en koeffisient som ikke er null:
a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0
La oss betegne:
A k - 1 a m , hvor m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n
I dette tilfellet:
β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0
eller ek = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 +. . . + (- β n) e n
Det følger at en av vektorene til systemet uttrykkes gjennom alle andre vektorer i systemet. Noe som måtte bevises (osv.).
Tilstrekkelighet
La en av vektorene være lineært uttrykt gjennom alle andre vektorer i systemet:
e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n
Vi flytter vektoren e k til høyre side av denne likheten:
0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n
Siden koeffisienten til vektoren e k er lik - 1 ≠ 0, får vi en ikke-triviell representasjon av null ved et system av vektorer e 1, e 2, . . . , e n , og dette betyr igjen at dette systemet av vektorer er lineært avhengig. Noe som måtte bevises (osv.).
Konsekvens:
- Et system av vektorer er lineært uavhengig når ingen av dets vektorer kan uttrykkes i form av alle andre vektorer i systemet.
- Et system av vektorer som inneholder en nullvektor eller to like vektorer er lineært avhengig.
Egenskaper til lineært avhengige vektorer
- For 2- og 3-dimensjonale vektorer er følgende betingelse oppfylt: to lineært avhengige vektorer er kollineære. To kollineære vektorer er lineært avhengige.
- For 3-dimensjonale vektorer er følgende betingelse oppfylt: tre lineært avhengige vektorer er koplanære. (3 koplanare vektorer er lineært avhengige).
- For n-dimensjonale vektorer er følgende betingelse oppfylt: n + 1 vektorer er alltid lineært avhengige.
Eksempler på å løse problemer som involverer lineær avhengighet eller lineær uavhengighet av vektorer
Eksempel 3La oss sjekke vektorene a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 for lineær uavhengighet.
Løsning. Vektorer er lineært avhengige fordi dimensjonen til vektorer er mindre enn antall vektorer.
Eksempel 4
La oss sjekke vektorene a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 for lineær uavhengighet.
Løsning. Vi finner verdiene til koeffisientene der den lineære kombinasjonen vil være lik nullvektoren:
x 1 a + x 2 b + x 3 c 1 = 0
Vi skriver vektorligningen i lineær form:
x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0
Vi løser dette systemet ved hjelp av Gauss-metoden:
1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~
Fra den andre linjen trekker vi den første, fra den tredje - den første:
~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~
Fra den første linjen trekker vi den andre, til den tredje legger vi til den andre:
~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0
Av løsningen følger det at systemet har mange løsninger. Dette betyr at det er en ikke-null kombinasjon av verdier av slike tall x 1, x 2, x 3 der den lineære kombinasjonen av a, b, c er lik nullvektoren. Derfor er vektorene a, b, c lineært avhengig.
Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter
Lineær avhengighet og vektoruavhengighet
Definisjoner av lineært avhengige og uavhengige vektorsystemer
Definisjon 22
La oss ha et system med n-vektorer og et sett med tall  , Deretter
, Deretter
(11)
kalles en lineær kombinasjon av et gitt system av vektorer med et gitt sett med koeffisienter.
Definisjon 23
Vektorsystem  kalles lineært avhengig hvis det er et slikt sett med koeffisienter
kalles lineært avhengig hvis det er et slikt sett med koeffisienter  , hvorav minst én ikke er lik null, slik at den lineære kombinasjonen av et gitt system av vektorer med dette settet med koeffisienter er lik nullvektoren:
, hvorav minst én ikke er lik null, slik at den lineære kombinasjonen av et gitt system av vektorer med dette settet med koeffisienter er lik nullvektoren:
La  , Deretter
, Deretter

Definisjon 24 ( gjennom representasjonen av en vektor av systemet som en lineær kombinasjon av de andre)
Vektorsystem  kalles lineært avhengig hvis minst én av vektorene i dette systemet kan representeres som en lineær kombinasjon av de gjenværende vektorene i dette systemet.
kalles lineært avhengig hvis minst én av vektorene i dette systemet kan representeres som en lineær kombinasjon av de gjenværende vektorene i dette systemet.
Uttalelse 3
Definisjon 23 og 24 er likeverdige.
Definisjon 25(via null lineær kombinasjon)
Vektorsystem  kalles lineært uavhengig hvis en null lineær kombinasjon av dette systemet bare er mulig for alle
kalles lineært uavhengig hvis en null lineær kombinasjon av dette systemet bare er mulig for alle  lik null.
lik null.
Definisjon 26(på grunn av umuligheten av å representere en vektor av systemet som en lineær kombinasjon av de andre)
Vektorsystem  kalles lineært uavhengig hvis ikke en av vektorene i dette systemet ikke kan representeres som en lineær kombinasjon av andre vektorer i dette systemet.
kalles lineært uavhengig hvis ikke en av vektorene i dette systemet ikke kan representeres som en lineær kombinasjon av andre vektorer i dette systemet.
Egenskaper til lineært avhengige og uavhengige vektorsystemer
Teorem 2 (nullvektor i vektorsystemet)
Hvis et system av vektorer har en nullvektor, er systemet lineært avhengig.
La  , Deretter .
, Deretter .
Vi får  , derfor per definisjon av et lineært avhengig system av vektorer gjennom en lineær nullkombinasjon (12)
systemet er lineært avhengig.
, derfor per definisjon av et lineært avhengig system av vektorer gjennom en lineær nullkombinasjon (12)
systemet er lineært avhengig.
Teorem 3 (avhengig delsystem i et vektorsystem)
Hvis et system av vektorer har et lineært avhengig delsystem, er hele systemet lineært avhengig.
La  - lineært avhengig delsystem
- lineært avhengig delsystem  , hvorav minst én ikke er lik null:
, hvorav minst én ikke er lik null:
Dette betyr, per definisjon 23, at systemet er lineært avhengig.
Teorem 4
Ethvert delsystem av et lineært uavhengig system er lineært uavhengig.
Fra det motsatte. La systemet være lineært uavhengig og ha et lineært avhengig delsystem. Men da, ifølge setning 3, vil hele systemet også være lineært avhengig. Motsigelse. Følgelig kan ikke et delsystem av et lineært uavhengig system være lineært avhengig.
Geometrisk betydning av lineær avhengighet og uavhengighet av et system av vektorer
Teorem 5
To vektorer  Og
Og  er lineært avhengige hvis og bare hvis
er lineært avhengige hvis og bare hvis  .
.
Nødvendighet.
 Og
Og  - lineært avhengig
- lineært avhengig  at betingelsen er oppfylt
at betingelsen er oppfylt  . Da
. Da  , dvs.
, dvs.  .
.
Tilstrekkelighet.
Lineært avhengig.
Konsekvens 5.1
Nullvektoren er kollineær til enhver vektor
Konsekvens 5.2
For at to vektorer skal være lineært uavhengige, er det nødvendig og tilstrekkelig at  var ikke collineær
var ikke collineær  .
.
Teorem 6
For at et system med tre vektorer skal være lineært avhengig, er det nødvendig og tilstrekkelig at disse vektorene er koplanare .
Nødvendighet.
 - er lineært avhengige, derfor kan en vektor representeres som en lineær kombinasjon av de to andre.
- er lineært avhengige, derfor kan en vektor representeres som en lineær kombinasjon av de to andre.
 ,
(13)
,
(13)
Hvor  Og
Og  . Etter parallellogramregelen
. Etter parallellogramregelen  det er en diagonal av et parallellogram med sider
det er en diagonal av et parallellogram med sider  , men et parallellogram er en flat figur
, men et parallellogram er en flat figur  koplanar
koplanar  - er også koplanære.
- er også koplanære.
Tilstrekkelighet.
 - i samme plan. La oss bruke tre vektorer til punkt O:
- i samme plan. La oss bruke tre vektorer til punkt O:


 C
C
 B`
B`

 – lineært avhengig
– lineært avhengig
Konsekvens 6.1
Nullvektoren er koplanar til et hvilket som helst vektorpar.
Konsekvens 6.2
For vektorer  var lineært uavhengige, er det nødvendig og tilstrekkelig at de ikke er koplanære.
var lineært uavhengige, er det nødvendig og tilstrekkelig at de ikke er koplanære.
Konsekvens 6.3
En hvilken som helst vektor i et plan kan representeres som en lineær kombinasjon av to ikke-kollineære vektorer i samme plan.
Teorem 7
Alle fire vektorer i rommet er lineært avhengige .
La oss vurdere 4 tilfeller:
La oss tegne et plan gjennom vektorer, deretter et plan gjennom vektorer og et plan gjennom vektorer. Deretter tegner vi fly som går gjennom punkt D, parallelt med vektorparene ; ; hhv. Vi bygger et parallellepiped langs skjæringslinjene mellom fly 1 O.B. 1 C 1 D.

ABDC ; hhv. Vi bygger et parallellepiped langs skjæringslinjene mellom fly 1
O.B. 1
C 1
La oss vurdere  .
.
– parallellogram ved konstruksjon etter parallellogramregelen  Tenk på OADD 1 - et parallellogram (fra egenskapen til et parallellepiped)
Tenk på OADD 1 - et parallellogram (fra egenskapen til et parallellepiped)
, Deretter
EMBED Equation.3 .  Ved teorem 1
Ved teorem 1  slik at . Da
slik at . Da
, og per definisjon 24 er systemet av vektorer lineært avhengig.
Konsekvens 7.1
Summen av tre ikke-koplanare vektorer i rommet er en vektor som sammenfaller med diagonalen til et parallellepiped bygget på disse tre vektorene påført en felles opprinnelse, og opprinnelsen til sumvektoren sammenfaller med den vanlige opprinnelsen til disse tre vektorene.
Konsekvens 7.2
Hvis vi tar 3 ikke-koplanare vektorer i rommet, kan enhver vektor i dette rommet dekomponeres til en lineær kombinasjon av disse tre vektorene.. En lineær kombinasjon av vektorer er summen av produktene til disse vektorene og skalarene  :
:
Definisjon 2. Vektorsystem  kalles et lineært avhengig system hvis deres lineære kombinasjon (2.8) forsvinner:
kalles et lineært avhengig system hvis deres lineære kombinasjon (2.8) forsvinner:
og blant tallene  det er minst en som er forskjellig fra null.
det er minst en som er forskjellig fra null.
Definisjon 3. Vektorer  kalles lineært uavhengig hvis deres lineære kombinasjon (2.8) forsvinner bare i tilfelle når alle tall.
kalles lineært uavhengig hvis deres lineære kombinasjon (2.8) forsvinner bare i tilfelle når alle tall.
Fra disse definisjonene kan følgende konsekvenser fås.
Konsekvens 1. I et lineært avhengig system av vektorer kan minst én vektor uttrykkes som en lineær kombinasjon av de andre.
Bevis. La (2.9) være tilfreds, og la koeffisienten for bestemthets skyld  . Vi har da:
. Vi har da:  . Merk at det motsatte også er sant.
. Merk at det motsatte også er sant.
Konsekvens 2. Hvis systemet av vektorer  inneholder en nullvektor, så er dette systemet (nødvendigvis) lineært avhengig - beviset er åpenbart.
inneholder en nullvektor, så er dette systemet (nødvendigvis) lineært avhengig - beviset er åpenbart.
Konsekvens 3. Hvis blant n vektorer  noen k(
noen k( ) vektorer er lineært avhengige, så er det alt n vektorer er lineært avhengige (vi vil utelate beviset).
) vektorer er lineært avhengige, så er det alt n vektorer er lineært avhengige (vi vil utelate beviset).
2 0 . Lineære kombinasjoner av to, tre og fire vektorer. La oss vurdere spørsmålene om lineær avhengighet og uavhengighet av vektorer på en rett linje, plan og i rommet. La oss presentere de tilsvarende teoremene.
Teorem 1. For at to vektorer skal være lineært avhengige, er det nødvendig og tilstrekkelig at de er kollineære.
Nødvendighet. La vektorene  Og
Og  lineært avhengig. Dette betyr at deres lineære kombinasjon
lineært avhengig. Dette betyr at deres lineære kombinasjon  =0 og (for ordens skyld)
=0 og (for ordens skyld)  . Dette innebærer likhet
. Dette innebærer likhet  , og (per definisjon av å multiplisere en vektor med et tall) vektorer
, og (per definisjon av å multiplisere en vektor med et tall) vektorer  Og
Og  kollineær.
kollineær.
Tilstrekkelighet. La vektorene  Og
Og  collineær (
collineær (  ║
║ ) (vi antar at de er forskjellige fra nullvektoren; ellers er deres lineære avhengighet åpenbar).
) (vi antar at de er forskjellige fra nullvektoren; ellers er deres lineære avhengighet åpenbar).
Ved teorem (2.7) (se §2.1, punkt 2 0) da  slik at
slik at  , eller
, eller  – den lineære kombinasjonen er lik null, og koeffisienten ved
– den lineære kombinasjonen er lik null, og koeffisienten ved  er lik 1 – vektorer
er lik 1 – vektorer  Og
Og  lineært avhengig.
lineært avhengig.
Følgende konsekvens følger av denne teoremet.
Konsekvens. Hvis vektorene  Og
Og  er ikke kollineære, så er de lineært uavhengige.
er ikke kollineære, så er de lineært uavhengige.
Teorem 2. For at tre vektorer skal være lineært avhengige, er det nødvendig og tilstrekkelig at de er koplanære.
Nødvendighet. La vektorene  ,
, Og
Og  lineært avhengig. La oss vise at de er koplanære.
lineært avhengig. La oss vise at de er koplanære.
Fra definisjonen av lineær avhengighet av vektorer følger det eksistensen av tall  Og
Og  slik at den lineære kombinasjonen
slik at den lineære kombinasjonen  , og samtidig (for å være spesifikk)
, og samtidig (for å være spesifikk)  . Så fra denne likheten kan vi uttrykke vektoren
. Så fra denne likheten kan vi uttrykke vektoren  :
: =
= , det vil si vektoren
, det vil si vektoren  lik diagonalen til et parallellogram konstruert på vektorene på høyre side av denne likheten (fig. 2.6). Dette betyr at vektorene
lik diagonalen til et parallellogram konstruert på vektorene på høyre side av denne likheten (fig. 2.6). Dette betyr at vektorene  ,
, Og
Og  ligge i samme plan.
ligge i samme plan.
Tilstrekkelighet. La vektorene  ,
, Og
Og  koplanar. La oss vise at de er lineært avhengige.
koplanar. La oss vise at de er lineært avhengige.
La oss ekskludere tilfellet med kollinearitet til et hvilket som helst par av vektorer (fordi da dette paret er lineært avhengig og av følge 3 (se avsnitt 1 0) er alle tre vektorene lineært avhengige). Merk at denne antakelsen også utelukker eksistensen av en nullvektor blant disse tre.
La oss flytte tre koplanare vektorer inn i ett plan og bringe dem til et felles opphav. Gjennom slutten av vektoren  tegne linjer parallelt med vektorene
tegne linjer parallelt med vektorene  Og
Og  ; vi får vektorene
; vi får vektorene  Og
Og  (Fig. 2.7) - deres eksistens er sikret ved at vektorene
(Fig. 2.7) - deres eksistens er sikret ved at vektorene  Og
Og  vektorer som ikke er kollineære ved antagelse. Det følger at vektoren
vektorer som ikke er kollineære ved antagelse. Det følger at vektoren  =
= +
+ . Omskriving av denne likheten i formen (–1)
. Omskriving av denne likheten i formen (–1)  +
+ +
+ =0, konkluderer vi med at vektorene
=0, konkluderer vi med at vektorene  ,
, Og
Og  lineært avhengig.
lineært avhengig.
To konsekvenser følger av det påviste teoremet.
Konsekvens 1. La  Og
Og  ikke-kollineære vektorer, vektor
ikke-kollineære vektorer, vektor  – vilkårlig, liggende i planet definert av vektorene
– vilkårlig, liggende i planet definert av vektorene  Og
Og  , vektor. Så er det tall
, vektor. Så er det tall  Og
Og  slik at
slik at
 =
= +
+ .
(2.10)
.
(2.10)
Konsekvens 2. Hvis vektorene  ,
, Og
Og  er ikke koplanære, så er de lineært uavhengige.
er ikke koplanære, så er de lineært uavhengige.
Teorem 3. Alle fire vektorer er lineært avhengige.
Vi vil utelate beviset; med noen modifikasjoner kopierer den beviset for teorem 2. La oss gi en konsekvens av denne teoremet.
Konsekvens. For alle ikke-koplanare vektorer  ,
, ,
, og hvilken som helst vektor
og hvilken som helst vektor  Og
Og  slik at
slik at
 .
(2.11)
.
(2.11)
Kommentar. For vektorer i (tredimensjonalt) rom har begrepene lineær avhengighet og uavhengighet, som følger av teoremene 1-3 ovenfor, en enkel geometrisk betydning.
La det være to lineært avhengige vektorer  Og
Og  . I dette tilfellet er en av dem en lineær kombinasjon av den andre, det vil si at den ganske enkelt skiller seg fra den med en numerisk faktor (for eksempel,
. I dette tilfellet er en av dem en lineær kombinasjon av den andre, det vil si at den ganske enkelt skiller seg fra den med en numerisk faktor (for eksempel,  ). Geometrisk betyr dette at begge vektorene er på en felles linje; de kan ha samme eller motsatte retninger (fig. 2.8 xx).
). Geometrisk betyr dette at begge vektorene er på en felles linje; de kan ha samme eller motsatte retninger (fig. 2.8 xx).
Hvis to vektorer er plassert i en vinkel til hverandre (fig. 2.9 xx), kan i dette tilfellet ikke en av dem oppnås ved å multiplisere den andre med et tall - slike vektorer er lineært uavhengige. Derfor er den lineære uavhengigheten til to vektorer  Og
Og  betyr at disse vektorene ikke kan legges på én rett linje.
betyr at disse vektorene ikke kan legges på én rett linje.
La oss finne ut den geometriske betydningen av lineær avhengighet og uavhengighet av tre vektorer.
La vektorene  ,
, Og
Og  er lineært avhengige og lar (for å være spesifikk) vektoren
er lineært avhengige og lar (for å være spesifikk) vektoren  er en lineær kombinasjon av vektorer
er en lineær kombinasjon av vektorer  Og
Og  , det vil si plassert i planet som inneholder vektorene
, det vil si plassert i planet som inneholder vektorene  Og
Og  . Dette betyr at vektorene
. Dette betyr at vektorene  ,
, Og
Og  ligge i samme plan. Det motsatte er også sant: hvis vektorene
ligge i samme plan. Det motsatte er også sant: hvis vektorene  ,
, Og
Og  ligger i samme plan, da er de lineært avhengige.
ligger i samme plan, da er de lineært avhengige.
Dermed vektorene  ,
, Og
Og  er lineært uavhengige hvis og bare hvis de ikke ligger i samme plan.
er lineært uavhengige hvis og bare hvis de ikke ligger i samme plan.
3 0 . Begrepet grunnlag. Et av de viktigste begrepene i lineær og vektoralgebra er begrepet basis. La oss introdusere noen definisjoner.
Hvis vi tar 3 ikke-koplanare vektorer i rommet, kan enhver vektor i dette rommet dekomponeres til en lineær kombinasjon av disse tre vektorene.. Et vektorpar kalles ordnet hvis det er spesifisert hvilken vektor av dette paret som anses som den første og hvilken den andre.
Definisjon 2. Bestilt par  ,
, ikke-kollineære vektorer kalles en basis på planet definert av de gitte vektorene.
ikke-kollineære vektorer kalles en basis på planet definert av de gitte vektorene.
Teorem 1. Enhver vektor  på planet kan representeres som en lineær kombinasjon av basissystemet av vektorer
på planet kan representeres som en lineær kombinasjon av basissystemet av vektorer  ,
, :
:
 (2.12)
(2.12)
og denne representasjonen er den eneste.
Bevis. La vektorene  Og
Og  danne et grunnlag. Deretter hvilken som helst vektor
danne et grunnlag. Deretter hvilken som helst vektor  kan representeres i skjemaet
kan representeres i skjemaet  .
.
For å bevise unikhet, anta at det er en dekomponering til  . Vi har da = 0, og minst en av forskjellene er forskjellig fra null. Det siste betyr at vektorene
. Vi har da = 0, og minst en av forskjellene er forskjellig fra null. Det siste betyr at vektorene  Og
Og  lineært avhengig, det vil si kollineær; dette strider mot påstanden om at de danner grunnlag.
lineært avhengig, det vil si kollineær; dette strider mot påstanden om at de danner grunnlag.
Men så er det bare nedbrytning.
Definisjon 3. En trippel av vektorer kalles ordnet hvis det er spesifisert hvilken vektor som regnes som den første, hvilken som regnes som den andre, og hvilken som er den tredje.
Definisjon 4. En ordnet trippel av ikke-koplanare vektorer kalles en basis i rommet.
Dekomponerings- og unikhetsteoremet gjelder også her.
Teorem 2. Enhver vektor  kan representeres som en lineær kombinasjon av basisvektorsystemet
kan representeres som en lineær kombinasjon av basisvektorsystemet  ,
, ,
, :
:
 (2.13)
(2.13)
og denne representasjonen er unik (vi vil utelate beviset for teoremet).
I utvidelser (2.12) og (2.13) skal mengdene  kalles vektorkoordinater
kalles vektorkoordinater  på et gitt grunnlag (mer presist, ved affine koordinater).
på et gitt grunnlag (mer presist, ved affine koordinater).
Med fast grunnlag  Og
Og  du kan skrive
du kan skrive  .
.
For eksempel hvis grunnlaget er gitt  og det er gitt det
og det er gitt det  , så betyr dette at det er en representasjon (dekomponering)
, så betyr dette at det er en representasjon (dekomponering)  .
.
4 0 . Lineære operasjoner på vektorer i koordinatform. Innføringen av en basis gjør at lineære operasjoner på vektorer kan erstattes av vanlige lineære operasjoner på tall - koordinatene til disse vektorene.
La det gis noe grunnlag  . Å spesifisere vektorkoordinatene i dette grunnlaget bestemmer selvsagt selve vektoren. Følgende forslag gjelder:
. Å spesifisere vektorkoordinatene i dette grunnlaget bestemmer selvsagt selve vektoren. Følgende forslag gjelder:
a) to vektorer  Og
Og  er like hvis og bare hvis deres korresponderende koordinater er like:
er like hvis og bare hvis deres korresponderende koordinater er like:
b) når du multipliserer en vektor  per nummer
per nummer  dens koordinater multipliseres med dette tallet:
dens koordinater multipliseres med dette tallet:
 ;
(2.15)
;
(2.15)
c) når du legger til vektorer, blir deres tilsvarende koordinater lagt til:
Vi vil utelate bevisene for disse egenskapene; La oss bevise egenskap b) bare som et eksempel. Vi har
 ==
==
Kommentar. I verdensrommet (på flyet) kan du velge uendelig mange baser.
La oss gi et eksempel på en overgang fra en basis til en annen, og etablere relasjoner mellom vektorkoordinatene i forskjellige baser.
Eksempel 1. I grunnsystemet  tre vektorer er gitt:
tre vektorer er gitt:  ,
, Og
Og  . På grunnlag
. På grunnlag  ,
, ,
, vektor
vektor  har nedbrytning. Finn vektorkoordinater
har nedbrytning. Finn vektorkoordinater  i grunnlaget
i grunnlaget  .
.
Løsning. Vi har utvidelser:  ,
, ,
, ; derfor,
; derfor,  =
= +2
+2 +
+ =
=
=
= , altså
, altså  i grunnlaget
i grunnlaget  .
.
Eksempel 2. La inn noe grunnlag  fire vektorer er gitt av deres koordinater:
fire vektorer er gitt av deres koordinater:  ,
, ,
, Og
Og  .
.
Finn ut om vektorene dannes  basis; hvis svaret er positivt, finn nedbrytningen av vektoren
basis; hvis svaret er positivt, finn nedbrytningen av vektoren  på dette grunnlaget.
på dette grunnlaget.
Løsning. 1) vektorer danner grunnlag hvis de er lineært uavhengige. La oss lage en lineær kombinasjon av vektorer  (
( ) og finn ut på hva
) og finn ut på hva  Og
Og  den går til null:
den går til null:  =0. Vi har:
=0. Vi har:
 =
= +
+ +
+ =
=
Ved å definere likheten til vektorer i koordinatform får vi følgende system av (lineære homogene algebraiske) ligninger:  ;
; ;
; , hvis determinant
, hvis determinant  =1
=1 , det vil si at systemet har (bare) en triviell løsning
, det vil si at systemet har (bare) en triviell løsning  . Dette betyr lineær uavhengighet av vektorer
. Dette betyr lineær uavhengighet av vektorer  og derfor danner de et grunnlag.
og derfor danner de et grunnlag.
2) utvide vektoren  på dette grunnlaget. Vi har:
på dette grunnlaget. Vi har:  =
= eller i koordinert form.
eller i koordinert form.
Går vi videre til likheten til vektorer i koordinatform, får vi et system med lineære inhomogene algebraiske ligninger:  ;
; ;
; . Når vi løser det (for eksempel ved å bruke Cramers regel), får vi:
. Når vi løser det (for eksempel ved å bruke Cramers regel), får vi:  ,
, ,
, og (
og (  )
) . Vi har vektordekomponeringen
. Vi har vektordekomponeringen  i grunnlaget
i grunnlaget  :
: =.
=.
5
0
. Projeksjon av en vektor på en akse. Egenskaper til anslag. La det være en akse l, det vil si en rett linje med en retning valgt på og la noen vektor gis  La oss definere konseptet med vektorprojeksjon
La oss definere konseptet med vektorprojeksjon  per akse l.
per akse l.
Definisjon. Vektorprojeksjon  per akse l produktet av modulen til denne vektoren og cosinus til vinkelen mellom aksen kalles l og vektor (fig. 2.10):
per akse l produktet av modulen til denne vektoren og cosinus til vinkelen mellom aksen kalles l og vektor (fig. 2.10):
 .
(2.17)
.
(2.17)
En følge av denne definisjonen er påstanden om at like vektorer har like projeksjoner (på samme akse).
La oss merke oss egenskapene til projeksjoner.
1) projeksjon av summen av vektorer på en akse l lik summen av projeksjonene av termene til vektorene på samme akse:
2) projeksjonen av produktet av en skalar av en vektor er lik produktet av denne skalaren ved projeksjonen av vektoren på samme akse:
 =
= .
(2.19)
.
(2.19)
Konsekvens. Projeksjonen av en lineær kombinasjon av vektorer på aksen er lik den lineære kombinasjonen av deres projeksjoner:
Vi vil utelate bevisene for egenskapene.
6
0
. Rektangulært kartesisk koordinatsystem i rommet.Dekomponering av en vektor i enhetsvektorer av aksene. La tre innbyrdes perpendikulære enhetsvektorer velges som grunnlag; vi introduserer spesielle notasjoner for dem  . Ved å plassere begynnelsen på et punkt O, vil vi lede langs dem (i samsvar med orts
. Ved å plassere begynnelsen på et punkt O, vil vi lede langs dem (i samsvar med orts  ) koordinatakser Okse,Oy ogO z(en akse med positiv retning, origo og lengdeenhet valgt på den kalles en koordinatakse).
) koordinatakser Okse,Oy ogO z(en akse med positiv retning, origo og lengdeenhet valgt på den kalles en koordinatakse).
Definisjon. Et ordnet system med tre innbyrdes perpendikulære koordinatakser med felles opphav og felles lengdeenhet kalles et rektangulært kartesisk koordinatsystem i rommet.
Akser Okse kalt abscisseaksen, Oy– ordinatakse uO z – akse applikator.
La oss ta for oss utvidelsen av en vilkårlig vektor i basis  . Av teoremet (se §2.2, avsnitt 3 0, (2.13)) følger det at
. Av teoremet (se §2.2, avsnitt 3 0, (2.13)) følger det at  kan utvides unikt over grunnlaget
kan utvides unikt over grunnlaget  (her i stedet for å angi koordinater
(her i stedet for å angi koordinater  bruk
bruk  ):
):
 .
(2.21)
.
(2.21)
B (2,21)  essens (kartesisk rektangulære) vektorkoordinater
essens (kartesisk rektangulære) vektorkoordinater  . Betydningen av kartesiske koordinater fastsettes av følgende teorem.
. Betydningen av kartesiske koordinater fastsettes av følgende teorem.
Teorem. Kartesiske rektangulære koordinater  vektor
vektor  er projeksjoner av denne vektoren henholdsvis på aksen Okse,Oy ogO z.
er projeksjoner av denne vektoren henholdsvis på aksen Okse,Oy ogO z.
Bevis. La oss plassere vektoren  til opprinnelsen til koordinatsystemet - punkt O. Da vil dens slutt falle sammen med et punkt
til opprinnelsen til koordinatsystemet - punkt O. Da vil dens slutt falle sammen med et punkt  .
.
La oss trekke gjennom poenget  tre plan parallelt med koordinatplanene Oyz,Oxz Og Oxy(Fig. 2.11 xx). Vi får da:
tre plan parallelt med koordinatplanene Oyz,Oxz Og Oxy(Fig. 2.11 xx). Vi får da:
 .
(2.22)
.
(2.22)
I (2.22) vektorene
 Og
Og
 kalles vektorkomponenter
kalles vektorkomponenter  langs aksene Okse,Oy ogO z.
langs aksene Okse,Oy ogO z.
Slipp gjennom  Og
Og  vinklene som dannes av vektoren er angitt hhv
vinklene som dannes av vektoren er angitt hhv  med orts
med orts  . Så for komponentene får vi følgende formler:
. Så for komponentene får vi følgende formler:
 =
=
 =
= ,
,
 =
=
 =
= ,
,
 =
=
 =
= (2.23)
(2.23)
Fra (2.21), (2.22) (2.23) finner vi:
 =
= =
= ;
; =
= =
= ;
; =
= =
= (2.23)
(2.23)
– koordinater  vektor
vektor  det er projeksjoner av denne vektoren på koordinataksene Okse,Oy ogO z hhv.
det er projeksjoner av denne vektoren på koordinataksene Okse,Oy ogO z hhv.
Kommentar. Tall  kalles retningskosinus til vektoren
kalles retningskosinus til vektoren  .
.
Vektormodul  (diagonal av et rektangulært parallellepiped) beregnes med formelen:
(diagonal av et rektangulært parallellepiped) beregnes med formelen:
 .
(2.24)
.
(2.24)
Fra formlene (2.23) og (2.24) følger det at retningscosinusene kan beregnes ved å bruke formlene:
 =
= ;
; =
= ;
; =
= .
(2.25)
.
(2.25)
Ved å heve begge sider av hver av likhetene i (2.25) og legge til venstre og høyre side av de resulterende likhetene ledd for ledd, kommer vi til formelen:
– ikke hvilke som helst tre vinkler danner en bestemt retning i rommet, men bare de hvis cosinus er relatert ved relasjon (2.26).
7 0 . Radiusvektor og punktkoordinater.Bestemme en vektor ved begynnelsen og slutten. La oss introdusere en definisjon.
Definisjon. Radiusvektoren (betegnet  ) er vektoren som forbinder origo O med dette punktet (fig. 2.12 xx):
) er vektoren som forbinder origo O med dette punktet (fig. 2.12 xx):
 .
(2.27)
.
(2.27)
Ethvert punkt i rommet tilsvarer en viss radiusvektor (og omvendt). Dermed er punkter i rommet representert i vektoralgebra ved deres radiusvektorer.
Tydeligvis koordinatene  poeng M er projeksjoner av dens radiusvektor
poeng M er projeksjoner av dens radiusvektor  på koordinatakser:
på koordinatakser:
 (2.28’)
(2.28’)
og dermed
 (2.28)
(2.28)
– radiusvektoren til et punkt er en vektor hvis projeksjoner på koordinataksene er lik koordinatene til dette punktet. Dette fører til to oppføringer:  Og
Og  .
.
Vi får formler for å beregne vektorprojeksjoner  i henhold til koordinatene til opprinnelsespunktet
i henhold til koordinatene til opprinnelsespunktet  og sluttpunktet
og sluttpunktet  .
.
La oss tegne radiusvektorene  og vektor
og vektor  (Fig. 2.13). Det skjønner vi
(Fig. 2.13). Det skjønner vi
 =
= =(2.29)
=(2.29)
– projeksjonene av vektoren på koordinatenhetsvektorene er lik forskjellene mellom de tilsvarende koordinatene til slutten og begynnelsen av vektoren.
8 0 . Noen problemer som involverer kartesiske koordinater.
1)
betingelser for kollinearitet av vektorer
. Fra teoremet (se §2.1, avsnitt 2 0, formel (2.7)) følger det at for kollinearitet av vektorer  Og
Og  det er nødvendig og tilstrekkelig for at følgende forhold holder:
det er nødvendig og tilstrekkelig for at følgende forhold holder:  =
=
 . Fra denne vektorlikheten får vi tre likheter i koordinatform:, som innebærer betingelsen for kollinearitet av vektorer i koordinatform:
. Fra denne vektorlikheten får vi tre likheter i koordinatform:, som innebærer betingelsen for kollinearitet av vektorer i koordinatform:
 (2.30)
(2.30)
– for kollinearitet av vektorer  Og
Og  det er nødvendig og tilstrekkelig at deres tilsvarende koordinater er proporsjonale.
det er nødvendig og tilstrekkelig at deres tilsvarende koordinater er proporsjonale.
2)
avstand mellom punktene
. Av representasjon (2.29) følger det at avstanden  mellom punktene
mellom punktene  Og
Og  bestemmes av formelen
bestemmes av formelen
 =
= =.
(2.31)
=.
(2.31)
3)
inndeling av et segment i et gitt forhold
. La poeng gis  Og
Og  og holdning
og holdning  . Trenger å finne
. Trenger å finne  – punktkoordinater M
(Fig. 2.14).
– punktkoordinater M
(Fig. 2.14).
Fra tilstanden for kollinearitet til vektorer har vi:  , hvor
, hvor  Og
Og
 .
(2.32)
.
(2.32)
Fra (2.32) får vi i koordinatform:
Fra formler (2.32’) kan vi få formler for å beregne koordinatene til midtpunktet til segmentet  , forutsatt
, forutsatt  :
:
Kommentar. Vi vil telle segmentene  Og
Og  positiv eller negativ avhengig av om retningen deres sammenfaller med retningen fra begynnelsen
positiv eller negativ avhengig av om retningen deres sammenfaller med retningen fra begynnelsen  segment til slutten
segment til slutten  ,
eller stemmer ikke. Deretter, ved å bruke formler (2.32) – (2.32"), kan du finne koordinatene til punktet som deler segmentet
,
eller stemmer ikke. Deretter, ved å bruke formler (2.32) – (2.32"), kan du finne koordinatene til punktet som deler segmentet  eksternt, altså på en slik måte at skillepunktet M er på fortsettelsen av segmentet
eksternt, altså på en slik måte at skillepunktet M er på fortsettelsen av segmentet  , og ikke inne i den. Samtidig, selvfølgelig,
, og ikke inne i den. Samtidig, selvfølgelig,  .
.
4)
sfærisk overflateligning
.
La oss lage en ligning for en sfærisk overflate - det geometriske stedet for punkter  , like langt på avstand
, like langt på avstand  fra et eller annet fast senter - et punkt
fra et eller annet fast senter - et punkt  . Det er åpenbart at i dette tilfellet
. Det er åpenbart at i dette tilfellet  og tar hensyn til formel (2.31)
og tar hensyn til formel (2.31)
Ligning (2.33) er ligningen for den ønskede sfæriske overflaten.
Uttrykk av skjemaet ringte lineær kombinasjon av vektorer A 1 , A 2 ,...,A n med odds λ 1, λ 2 ,..., λ n.
Bestemmelse av lineær avhengighet av et system av vektorer
Vektorsystem A 1 , A 2 ,...,A n ringte lineært avhengig, hvis det er et sett med tall som ikke er null λ 1, λ 2 ,..., λ n, der den lineære kombinasjonen av vektorer λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n lik nullvektoren, det vil si ligningssystemet: har en løsning som ikke er null.
Sett med tall λ 1, λ 2 ,..., λ n er ikke null hvis minst ett av tallene λ 1, λ 2 ,..., λ n forskjellig fra null.
Bestemmelse av lineær uavhengighet av et system av vektorer
Eksempel 29.1Vektorsystem A 1 , A 2 ,...,A n ringte lineært uavhengig, hvis den lineære kombinasjonen av disse vektorene λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n lik nullvektoren bare for et nullsett med tall λ 1, λ 2 ,..., λ n , det vil si ligningssystemet: A 1 x 1 + A 2 x 2 +...+A n x n =Θ har en unik nullløsning.
Sjekk om et system av vektorer er lineært avhengig
Løsning:

1. Vi lager et ligningssystem:
2. Vi løser det ved hjelp av Gauss-metoden. Jordanano-transformasjonene av systemet er gitt i tabell 29.1. Ved beregning skrives ikke høyresiden av systemet ned siden de er lik null og ikke endres under Jordan-transformasjoner.

3. Fra de tre siste radene i tabellen skrive ned et løst system tilsvarende det opprinnelige system:
![]()
4. Vi får den generelle løsningen av systemet:
5. Etter å ha satt verdien til den frie variabelen x 3 =1 etter eget skjønn, vi får en spesiell løsning som ikke er null X=(-3,2,1).
Svar: For et sett med tall som ikke er null (-3,2,1), er den lineære kombinasjonen av vektorer lik nullvektoren -3A 1 +2A 2 +1A 3 =Θ. Derfor, vektorsystem lineært avhengig.
Egenskaper til vektorsystemer
Eiendom (1)
Hvis et system av vektorer er lineært avhengig, utvides minst en av vektorene i forhold til de andre, og omvendt, hvis minst en av vektorene i systemet utvides i forhold til de andre, så utvides systemet av vektorer er lineært avhengig.
Eiendom (2)
Hvis et undersystem av vektorer er lineært avhengig, så er hele systemet lineært avhengig.
Eiendom (3)
Hvis et system av vektorer er lineært uavhengig, så er hvilket som helst av dets undersystemer lineært uavhengig.
Eiendom (4)
Ethvert system av vektorer som inneholder en nullvektor er lineært avhengig.
Eiendom (5)
Et system av m-dimensjonale vektorer er alltid lineært avhengig hvis antallet vektorer n er større enn deres dimensjon (n>m)
Grunnlaget for vektorsystemet
Grunnlaget for vektorsystemet A 1 , A 2 ,..., A n et slikt delsystem B 1 , B 2 ,...,B r kalles(hver av vektorene B 1, B 2,..., B r er en av vektorene A 1, A 2,..., A n), som tilfredsstiller følgende betingelser:
1. B 1 , B 2 ,...,B r lineært uavhengig system av vektorer;
2. hvilken som helst vektor A j system A 1 , A 2 ,..., A n er lineært uttrykt gjennom vektorene B 1 , B 2 ,..., B rr— antall vektorer som er inkludert i grunnlaget.
Teorem 29.1 På enhetsbasis av et system av vektorer.Hvis et system av m-dimensjonale vektorer inneholder m forskjellige enhetsvektorer E 1 E 2 ,..., E m , så danner de grunnlaget for systemet.
Algoritme for å finne grunnlaget for et system av vektorer
For å finne grunnlaget for systemet med vektorer A 1 , A 2 ,..., A n er det nødvendig:
- Lag et homogent ligningssystem som tilsvarer systemet av vektorer A 1 x 1 + A 2 x 2 +...+A n x n =Θ
- Ta med dette systemet
 En kort ordbok over tegnspråk, hvordan ordboken fungerer og hvordan du bruker den Tegnspråktolk på nett
En kort ordbok over tegnspråk, hvordan ordboken fungerer og hvordan du bruker den Tegnspråktolk på nett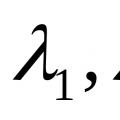 Lineært avhengige og lineært uavhengige vektorer Finn ut om vektorene er lineært uavhengige
Lineært avhengige og lineært uavhengige vektorer Finn ut om vektorene er lineært uavhengige Hva trenger du å vite for å føle deg irsk?
Hva trenger du å vite for å føle deg irsk?