Finn utvidelsen av en vektor i form av basis online kalkulator. Lineær avhengighet og lineær uavhengighet av vektorer. Vektor basis

Basis(gammelgresk βασις, basis) - et sett med slike vektorer i et vektorrom at enhver vektor i dette rommet kan representeres unikt som en lineær kombinasjon av vektorer fra dette settet - basisvektorer

En basis i rommet R n er et hvilket som helst system fra n-lineært uavhengige vektorer. Hver vektor fra R n som ikke er inkludert i basisen kan representeres som en lineær kombinasjon av basisvektorer, dvs. utvide over grunnlaget.
La være et grunnlag for rommet R n og . Så er det tall λ 1 , λ 2 , …, λ n slik at .
Ekspansjonskoeffisientene λ 1, λ 2, ..., λ n, kalles koordinatene til vektoren i basis B. Hvis grunnlaget er gitt, så er koeffisientene til vektoren entydig bestemt.

Kommentar. I hver n-dimensjonalt vektorrom, kan man velge utallige ulike baser. I forskjellige baser har samme vektor ulike koordinater, men unik i det valgte grunnlaget. Eksempel. Utvid vektoren i form av .
Løsning. . Bytt ut koordinatene til alle vektorer og utfør handlinger på dem:

Ved å likestille koordinatene får vi et likningssystem:

La oss løse det: .
Dermed får vi utvidelsen: .
I grunnlaget har vektoren koordinater .

Slutt på arbeidet -

Dette emnet tilhører:

Konseptet med en vektor. Lineære operasjoner på vektorer

En vektor er et rettet segment med en viss lengde i e-segment viss lengde som har ett av sine grensepunkter.. lengden av en vektor kalles dens modul og er betegnet med symbolmodulen til vektoren.. vektoren kalles null angis hvis begynnelsen og slutten sammenfaller. nullvektoren har ingen bestemt ..

Hvis du trenger tilleggsmateriale om dette emnet, eller du ikke fant det du lette etter, anbefaler vi å bruke søket i vår database over verk:

Hva skal vi gjøre med det mottatte materialet:

Hvis dette materialet viste seg å være nyttig for deg, kan du lagre det på siden din i i sosiale nettverk:

Grunnlaget for plass kall et slikt system av vektorer der alle andre vektorer i rommet kan representeres som en lineær kombinasjon av vektorer inkludert i basisen.
I praksis er alt dette ganske enkelt. Grunnlaget kontrolleres som regel på et plan eller i rommet, og for dette må du finne determinanten til en matrise av andre, tredje orden, sammensatt av koordinatene til vektorene. Skjematisk skrevet nedenfor forhold som vektorene danner et grunnlag under

Til utvide vektoren b i form av basisvektorer
e,e...,e[n] det er nødvendig å finne koeffisientene x, ..., x[n] som den lineære kombinasjonen av vektorene e,e...,e[n] er lik for vektoren b:
x1*e+ ... + x[n]*e[n] = b.
For å gjøre dette, bør vektorligningen konverteres til systemet lineære ligninger og finne løsninger. Det er også ganske enkelt å implementere.
De funnet koeffisientene x, ..., x[n] kalles koordinatene til vektoren b i basisen e,e...,e[n].
La oss gå videre til den praktiske siden av emnet.

Dekomponering av en vektor i basisvektorer

Oppgave 1. Sjekk om vektorene a1, a2 danner et grunnlag på planet

1) a1 (3; 5), a2 (4; 2)
Løsning: Komponer determinanten fra koordinatene til vektorene og beregn den

Determinanten er ikke lik null, derfor vektorer er lineært uavhengige, noe som betyr at de danner en basis.

2) a1 (2; -3), a2 (5; -1)
Løsning: Vi beregner determinanten sammensatt av vektorer

Determinanten er lik 13 (ikke lik null) - av dette følger det at vektorene a1, a2 er en basis på planet.

---=================---

Ta i betraktning typiske eksempler fra IAPM-programmet i faget "Høyre matematikk".

Oppgave 2. Vis at vektorene a1, a2, a3 danner grunnlaget for en tredimensjonal vektorrom, og utvide vektoren b i dette grunnlaget (når du løser et system med lineær algebraiske ligninger bruke Cramers metode).
1) a1 (3; 1; 5), a2 (3; 2; 8), a3 (0; 1; 2), b (−3; 1; 2).
Løsning: Vurder først systemet med vektorer a1, a2, a3 og kontroller determinanten til matrisen A

bygget på andre vektorer enn null. Matrisen inneholder ett nullelement, så det er mer hensiktsmessig å beregne determinanten som en tidsplan for den første kolonnen eller tredje raden.

Som et resultat av beregningene fant vi at determinanten er forskjellig fra null, derfor vektorene a1, a2, a3 er lineært uavhengige.
Per definisjon danner vektorer et grunnlag i R3. La oss skrive ned planen til vektoren b i form av grunnlaget

Vektorer er like når deres respektive koordinater er like.
Derfor får vi fra vektorligningen et system med lineære ligninger

Løs SLAE Cramers metode. For å gjøre dette skriver vi ligningssystemet i skjemaet

Hoveddeterminanten til SLAE er alltid lik determinanten sammensatt av basisvektorer

Derfor beregnes det i praksis ikke to ganger. For å finne hjelpedeterminanter setter vi en kolonne med frie termer i stedet for hver kolonne i hoveddeterminanten. Determinantene beregnes i henhold til regelen om trekanter



Bytt de funne determinantene inn i Cramers formel



Så utvidelsen av vektoren b når det gjelder basis har formen b=-4a1+3a2-a3. Koordinatene til vektoren b i basisen a1, a2, a3 vil være (-4,3, 1).

2)a1 (1; -5; 2), a2 (2; 3; 0), a3 (1; -1; 1), b (3; 5; 1).
Løsning: Vi sjekker vektorene for grunnlaget - vi komponerer determinanten fra koordinatene til vektorene og beregner den

Determinanten er derfor ikke lik null vektorer danner et grunnlag i rommet. Det gjenstår å finne tidsplanen til vektoren b i form av det gitte grunnlaget. For å gjøre dette skriver vi vektorligningen

og transformere til et system av lineære ligninger

Vi skriver ned matriseligning

Deretter finner vi hjelpedeterminanter for Cramer-formlene



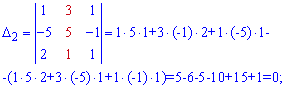
Bruk av Cramers formler



Så den gitte vektoren b har et skjema gjennom to basisvektorer b=-2a1+5a3, og dens koordinater i basisen er lik b(-2,0, 5).

L. 2-1 Grunnleggende begreper i vektoralgebra. Lineære operasjoner på vektorer.

Dekomponering av en vektor i form av en basis.

Grunnleggende konsepter for vektoralgebra

En vektor er settet av alle rettede segmenter som har samme lengde og retning
.

Egenskaper:

Lineære operasjoner over vektorer

1.

Parallelogramregel:

MED ummah to vektorer Og kalt vektor , som kommer ut av deres felles opprinnelse og er diagonalen til et parallellogram bygget på vektorer Og som på sidene.

Polygonregel:

For å konstruere summen av et hvilket som helst antall vektorer, må du plassere begynnelsen av den andre vektoren på slutten av første ledd, begynnelsen av den tredje på slutten av den andre, og så videre. Vektoren som lukker resultatet brutt linje, er summen. Begynnelsen faller sammen med begynnelsen av den første, og slutten med slutten av den siste.

Egenskaper:

2.

Vektor produkt per nummer , kalles en vektor som tilfredsstiller betingelsene:
.

Egenskaper:

3.

forskjell vektorer Og kalle vektor lik summen av vektoren og en vektor motsatt vektoren , dvs.
.

- loven til det motsatte elementet (vektor).

Dekomponering av en vektor i form av en basis

Summen av vektorer bestemmes på en unik måte
(men bare ). Den omvendte operasjonen, dekomponeringen av en vektor i flere komponenter, er tvetydig: For å gjøre det entydig, er det nødvendig å indikere retningene der utvidelsen av den betraktede vektoren skjer, eller, som de sier, det er nødvendig å indikere basis.

Ved bestemmelse av grunnlaget er kravet om ikke-koplanaritet og ikke-kollinearitet av vektorer vesentlig. For å forstå betydningen av dette kravet, er det nødvendig å vurdere konseptet lineær avhengighet og lineær uavhengighet av vektorer.

Vilkårlig uttrykk for formen: , kalt lineær kombinasjon vektorer
.

En lineær kombinasjon av flere vektorer kalles triviell hvis alle koeffisientene er lik null.

Vektorer
kalt lineært avhengig, hvis det er en ikke-triviell lineær kombinasjon av disse vektorene lik null:
(1), gitt
. Hvis likhet (1) bare gjelder for alle
samtidig lik null, deretter vektorer som ikke er null
vil lineært uavhengig.

Det er lett å bevise: alle to kollineære vektorer er lineært avhengige, og to ikke-kollineære vektorer er lineært uavhengige.

Vi starter beviset med den første påstanden.

La vektorene Og kollineær. La oss vise at de er lineært avhengige. Faktisk, hvis de er kollineære, skiller de seg fra hverandre bare med en numerisk faktor, dvs.
, derfor
. Siden den resulterende lineære kombinasjonen er tydelig ikke-triviell og er lik "0", så er vektorene Og lineært avhengig.

Tenk nå på to ikke-kollineære vektorer Og . La oss bevise at de er lineært uavhengige. Vi konstruerer beviset ved selvmotsigelse.

Vi antar at de er lineært avhengige. Da må det eksistere en ikke-triviell lineær kombinasjon
. La oss late som det
, Deretter
. Den resulterende likheten betyr at vektorene Og er kollineære, i motsetning til vår opprinnelige antagelse.

På samme måte kan man bevise: alle tre koplanare vektorer er lineært avhengige, og to ikke-koplanare vektorer er lineært uavhengige.

For å gå tilbake til begrepet et grunnlag og til problemet med å utvide en vektor i et bestemt grunnlag, kan vi si det grunnlaget på planet og i rommet er dannet av et sett med lineært uavhengige vektorer. Et slikt begrep om grunnlag er generelt, siden den gjelder for et rom med et hvilket som helst antall dimensjoner.

Uttrykk som:
, kalles dekomponering av vektoren av vektorer ,…,.

Hvis vi vurderer en basis i tredimensjonalt rom, så nedbrytningen av vektoren basis
vil
, Hvor
-vektorkoordinater.

I problemet med å utvide en vilkårlig vektor på et eller annet grunnlag, er følgende utsagn veldig viktig: hvilken som helst vektorkan dekomponeres på en unik måte i det gitte grunnlaget
. Med andre ord, koordinatene
for enhver vektor i forhold til grunnlaget
er definert entydig.

Innføringen av en basis i rommet og på et plan gjør det mulig å tilordne hver vektor ordnet trippel (par) av tall - dens koordinater. Dette svært viktige resultatet, som gjør det mulig å etablere en sammenheng mellom geometriske objekter og tall, gjør det mulig å analytisk beskrive og studere posisjonen og bevegelsen til fysiske objekter.

Kombinasjonen av et punkt og et grunnlag kalles koordinatsystem.

Hvis vektorene som danner grunnlaget er enhet og parvis perpendikulære, kalles koordinatsystemet rektangulær, og grunnlaget ortonormal.

L. 2-2 Produkt av vektorer

Dekomponering av en vektor i form av en basis

Tenk på vektoren
, gitt av koordinatene:
.

- vektorkomponenter i retninger av basisvektorer
.

Uttrykk av skjemaet
kalles dekomponering av vektoren basis
.

På lignende måte kan man dekomponere basis
vektor
:

.

Cosinus av vinklene dannet av den betraktede vektoren med basisvektorer
kalt retning cosinus

;
;
.

Skalært produkt av vektorer.

Skalarproduktet av to vektorer Og kalles tallet som er lik produktet av modulene til disse vektorene ved cosinus til vinkelen mellom dem

Skalarproduktet av to vektorer kan betraktes som produktet av modulen til en av disse vektorene og den ortogonale projeksjonen av den andre vektoren i retningen til den første
.

Egenskaper:

Hvis koordinatene til vektorene er kjent
Og
, da etter å ha utvidet vektorene når det gjelder grunnlaget
:
Og
, finne

, fordi
,
, Det

.

.

Betingelse for vinkelrett til vektorer:
.

Kolinearitetsbetingelse for rektorer:
.

Kryssprodukt av vektorer

eller

vektor kunst per vektor en slik vektor kalles
, som tilfredsstiller vilkårene:

Egenskaper:

De betraktede algebraiske egenskapene gjør det mulig å finne et analytisk uttrykk for kryssproduktet i form av koordinatene til de konstituerende vektorene på ortonormal basis.

Gitt:
Og
.

fordi ,
,
,
,
,
,
, Det

. Denne formelen kan skrives kortere, i form av en tredjeordens determinant:

.

Blandet produkt av vektorer

Blandet produkt av tre vektorer ,Og kalt et tall som er lik vektorproduktet
, multiplisert skalært med vektoren .

Følgende likhet er sann:
, så det blandede produktet er skrevet
.

Som følger av definisjonen, resultatet av en blandet produkter av tre vektorer er et tall. Dette tallet har en klar geometrisk betydning:

Blandet produktmodul
er lik volumet av parallellepipedet bygget på redusert til felles begynnelse vektorer ,Og .

Blandede produktegenskaper:

Hvis vektorene ,,er gitt i ortonormalt grunnlag
deres koordinater, blir beregningen av det blandede produktet utført i henhold til formelen

.

Faktisk, hvis
, Det

;
;
, Deretter
.

Hvis vektorene ,,er koplanære, deretter vektorproduktet
vinkelrett på vektoren . Og omvendt, hvis
, da er volumet av parallellepipedet null, og dette er bare mulig hvis vektorene er koplanære (lineært avhengige).

Dermed er tre vektorer koplanære hvis og bare hvis deres blandede produkt er null.

I vektorkalkulus og dens anvendelser veldig viktig har et dekomponeringsproblem, som består i å representere en gitt vektor som en sum av flere vektorer, kalt komponenter av en gitt

vektor. Denne oppgaven, som har generell sak et uendelig antall løsninger, blir ganske bestemt hvis noen elementer i de konstituerende vektorene er gitt.

2. Eksempler på dekomponering.

La oss vurdere flere svært vanlige tilfeller av dekomponering.

1. Dekomponer den gitte vektoren c i to komponentvektorer hvorav en, for eksempel a, er gitt i størrelse og retning.

Problemet er redusert til å bestemme forskjellen mellom to vektorer. Faktisk, hvis vektorene er komponenter av vektoren c, så er likheten

Herfra bestemmes den andre komponentvektoren

2. Dekomponer den gitte vektoren c i to komponenter, hvorav den ene må ligge i gitt fly og den andre må ligge på den gitte linjen a.

For å bestemme komponentvektorene flytter vi vektoren c slik at dens begynnelse faller sammen med skjæringspunktet for den gitte rette linjen med planet (punkt O - se fig. 18). Tegn en rett linje fra enden av vektoren c (punkt C) til

skjæringspunktet med planet (B er skjæringspunktet), og deretter fra punktet C trekker vi en rett linje parallelt

Vektorene og vil bli søkt, dvs. naturlig nok er ekspansjonen ovenfor mulig hvis den rette linjen a og planet ikke er parallelle.

3. Tre koplanare vektorer a, b og c er gitt, og vektorene er ikke kollineære. Det er nødvendig å dekomponere vektoren c til vektorer

La oss ta alle tre gitte vektorer til ett punkt O. Da vil de, på grunn av deres koplanaritet, være plassert i samme plan. På gitt vektor med som på diagonalen konstruerer vi et parallellogram, hvis sider er parallelle med vektorenes handlingslinjer (fig. 19). Denne konstruksjonen er alltid mulig (med mindre vektorene er kollineære) og unik. Fra fig. 19 viser det