Generaliserte homogene differensialligninger av første orden. Generalisert homogen likning Generaliserte homogene likninger av andre orden
Differensialligninger i generaliserte funksjoner
La det være en ligning. Hvis er en vanlig funksjon, så er løsningen dens et antiderivat, det vil si. La nå være en generalisert funksjon.
Definisjon. En generalisert funksjon kalles en primitiv generalisert funksjon if. Hvis er en entall generalisert funksjon, er det mulige tilfeller der antiderivativet er en vanlig generalisert funksjon. For eksempel er et antiderivat; antideriverten er en funksjon, og løsningen til ligningen kan skrives på formen: , hvor.
Det er en lineær ligning av th orden med konstante koeffisienter
hvor er en generalisert funksjon. La være et differensialpolynom av th orden.
Definisjon. En generalisert løsning av differensialligningen (8) er en generalisert funksjon som følgende relasjon gjelder:
Hvis er en kontinuerlig funksjon, så er den eneste løsningen til ligning (8) den klassiske løsningen.
Definisjon. En grunnleggende løsning på ligning (8) er enhver generalisert funksjon slik at.
Greens funksjon er en grunnleggende løsning som tilfredsstiller en grense-, initial- eller asymptotisk tilstand.
Teorem. En løsning til ligning (8) eksisterer og har formen:
med mindre konvolusjon er definert.
Bevis. Virkelig,. I henhold til konvolusjonsegenskapen følger det: .
Det er lett å se at den grunnleggende løsningen på denne ligningen er siden
Egenskaper til generaliserte derivater
Driften av differensiering er lineær og kontinuerlig fra til:
i, hvis i;

Hver generalisert funksjon er uendelig differensierbar. Faktisk, hvis, da; i sin tur osv.;
Resultatet av differensiering avhenger ikke av rekkefølgen av differensiering. For eksempel, ;
Hvis og, så er Leibniz sin formel for differensiering av et produkt gyldig. For eksempel, ;
Hvis det er en generalisert funksjon, så;
Hvis en serie sammensatt av lokalt integrerbare funksjoner konvergerer jevnt på hvert kompakt sett, kan den differensieres termin-for-term et antall ganger (som en generalisert funksjon), og den resulterende serien vil konvergere inn.
Eksempel. La
Funksjonen kalles Heaviside-funksjonen eller enhetsfunksjonen. Den er lokalt integrerbar og kan derfor betraktes som en generalisert funksjon. Du kan finne dens derivater. Etter definisjonen, dvs. .
Generaliserte funksjoner som tilsvarer kvadratiske former med komplekse koeffisienter
Foreløpig har kun kvadratiske former med reelle koeffisienter blitt vurdert. I denne delen studerer vi rommet til alle kvadratiske former med komplekse koeffisienter.
Oppgaven er å bestemme den generaliserte funksjonen, hvor er et komplekst tall. Men i det generelle tilfellet vil det ikke være en unik analytisk funksjon av. Derfor, i rommet for alle kvadratiske former, er det "øvre halvplanet" av kvadratiske former med en positiv bestemt imaginær del isolert og en funksjon bestemmes for dem. Nemlig, hvis en kvadratisk form tilhører dette "halvplanet", så antas det at hvor. En slik funksjon er en unik analytisk funksjon av.
Vi kan nå assosiere funksjonen med en generalisert funksjon:
hvor integrering utføres over hele rommet. Integral (13) konvergerer ved og er en analytisk funksjon av i dette halvplanet. Hvis du fortsetter denne funksjonen analytisk, bestemmes funksjonen for andre verdier.
For kvadratiske former med en positiv bestemt imaginær del, blir entallspunktene til funksjonene funnet og restene av disse funksjonene ved entallspunktene beregnet.
Den generaliserte funksjonen avhenger analytisk ikke bare av, men også av koeffisientene til den kvadratiske formen. Dermed er det en analytisk funksjon i det øvre "halvplanet" av alle kvadratiske former av formen der det er en positiv bestemt form. Følgelig er det unikt bestemt av verdiene på den "imaginære halvaksen", det vil si på settet med kvadratiske former for formen, hvor er en positiv bestemt form.
.
Differensialligninger.
§ 1. Grunnleggende begreper om ordinære differensialligninger.
Definisjon 1. Vanlig differensialligning n– rekkefølge for funksjonen y argument x kalles en relasjon av formen
Hvor F– en gitt funksjon av argumentene. I navnet til denne klassen av matematiske ligninger, understreker begrepet "differensial" at de inkluderer derivater  (funksjoner dannet som et resultat av differensiering); begrepet "vanlig" indikerer at ønsket funksjon avhenger av bare ett reelt argument.
(funksjoner dannet som et resultat av differensiering); begrepet "vanlig" indikerer at ønsket funksjon avhenger av bare ett reelt argument.
En vanlig differensialligning inneholder kanskje ikke et eksplisitt argument x,
den nødvendige funksjonen  og hvilken som helst av dens derivater, men den høyeste derivater
og hvilken som helst av dens derivater, men den høyeste derivater  må inkluderes i ligningen n-
bestilling. For eksempel
må inkluderes i ligningen n-
bestilling. For eksempel
EN)  – første ordens ligning;
– første ordens ligning;
b)  – tredjeordens ligning.
– tredjeordens ligning.
Når du skriver vanlige differensialligninger, brukes ofte notasjonen for derivater i form av differensialer:
V)  – andreordens ligning;
– andreordens ligning;
G)  - første ordens ligning,
- første ordens ligning,
generator etter divisjon etter dx ekvivalent form for å spesifisere ligningen:  .
.
Funksjon  kalles en løsning på en ordinær differensialligning hvis den, ved substitusjon i den, blir til en identitet.
kalles en løsning på en ordinær differensialligning hvis den, ved substitusjon i den, blir til en identitet.
For eksempel en 3. ordens ligning
Har en løsning  .
.
Å finne ved en eller annen metode, for eksempel seleksjon, en funksjon som tilfredsstiller ligningen betyr ikke å løse den. Å løse en vanlig differensialligning betyr å finne Alle funksjoner som danner en identitet når de erstattes i en ligning. For ligning (1.1) dannes en familie av slike funksjoner ved hjelp av vilkårlige konstanter og kalles den generelle løsningen av en ordinær differensialligning n-te orden, og antall konstanter faller sammen med rekkefølgen av ligningen: Den generelle løsningen kan være, men er ikke eksplisitt løst mht. y(x) : I dette tilfellet kalles løsningen vanligvis det generelle integralet av ligning (1.1).
For eksempel den generelle løsningen av differensialligningen  er følgende uttrykk: , og det andre leddet kan også skrives som
er følgende uttrykk: , og det andre leddet kan også skrives som  , siden en vilkårlig konstant
, siden en vilkårlig konstant  , delt på 2, kan erstattes av en ny vilkårlig konstant
, delt på 2, kan erstattes av en ny vilkårlig konstant  .
.
Ved å tilordne noen tillatte verdier til alle vilkårlige konstanter i den generelle løsningen eller i det generelle integralet, får vi en viss funksjon som ikke lenger inneholder vilkårlige konstanter. Denne funksjonen kalles en partiell løsning eller partiell integral av ligning (1.1). For å finne verdiene til vilkårlige konstanter, og derfor en spesiell løsning, brukes forskjellige tilleggsbetingelser til ligning (1.1). For eksempel kan de såkalte startbetingelsene spesifiseres ved (1.2)
På høyre side av startbetingelsene (1.2) er de numeriske verdiene til funksjonen og deriverte spesifisert, og det totale antallet startbetingelser er lik antallet definerte vilkårlige konstanter.
Problemet med å finne en bestemt løsning på ligning (1.1) basert på startbetingelsene kalles Cauchy-problemet.
§ 2. Ordinære differensialligninger av 1. orden - grunnleggende begreper.
Ordinær differensialligning av 1. orden ( n=1) har formen:  eller, hvis det kan løses med hensyn til derivatet:
eller, hvis det kan løses med hensyn til derivatet:  . Generell løsning y=
y(x,MED) eller generell integral
. Generell løsning y=
y(x,MED) eller generell integral  1. ordens ligninger inneholder én vilkårlig konstant. Den eneste startbetingelsen for en 1. ordens ligning
1. ordens ligninger inneholder én vilkårlig konstant. Den eneste startbetingelsen for en 1. ordens ligning  lar deg bestemme verdien av en konstant fra en generell løsning eller fra et generelt integral. Dermed vil en bestemt løsning bli funnet eller, som er den samme, Cauchy-problemet vil bli løst. Spørsmålet om eksistensen og det unike ved en løsning på Cauchy-problemet er et av de sentrale i den generelle teorien om vanlige differensialligninger. Spesielt for en 1. ordens ligning er teoremet gyldig, som godtas her uten bevis.
lar deg bestemme verdien av en konstant fra en generell løsning eller fra et generelt integral. Dermed vil en bestemt løsning bli funnet eller, som er den samme, Cauchy-problemet vil bli løst. Spørsmålet om eksistensen og det unike ved en løsning på Cauchy-problemet er et av de sentrale i den generelle teorien om vanlige differensialligninger. Spesielt for en 1. ordens ligning er teoremet gyldig, som godtas her uten bevis.
Teorem 2.1. Hvis i ligningen funksjonen  og dens partielle derivater
og dens partielle derivater  kontinuerlig i enkelte regioner D flyet XOY, og i dette området er det spesifisert et punkt
kontinuerlig i enkelte regioner D flyet XOY, og i dette området er det spesifisert et punkt  , så er det en unik løsning som tilfredsstiller både ligningen og startbetingelsen
, så er det en unik løsning som tilfredsstiller både ligningen og startbetingelsen  .
.
Geometrisk er den generelle løsningen av en 1. ordens ligning en familie av kurver på planet XOY, uten felles punkter og skiller seg fra hverandre i en parameter - verdien av konstanten C. Disse kurvene kalles integralkurver for en gitt ligning. Integrerte ligningskurver har en åpenbar geometrisk egenskap: ved hvert punkt er tangenten til tangenten til kurven lik verdien til høyre side av ligningen på dette punktet:  . Med andre ord er ligningen gitt i planet XOY retningsfelt for tangenter til integralkurver. Kommentar: Det skal bemerkes at til lign.
. Med andre ord er ligningen gitt i planet XOY retningsfelt for tangenter til integralkurver. Kommentar: Det skal bemerkes at til lign.  ligningen og den såkalte ligningen er gitt i symmetrisk form
ligningen og den såkalte ligningen er gitt i symmetrisk form  .
.
§ 3. Differensialligninger av 1. orden med separerbare variabler.
Definisjon. En differensialligning med separerbare variabler er en formlikning  (3.1)
(3.1)
eller en ligning av formen (3.2)
For å skille variablene i likning (3.1), dvs. reduser denne ligningen til den såkalte separerte variabelligningen, utfør følgende handlinger:
 ;
;
Nå må vi løse ligningen g(y)= 0 . Hvis det har en reell løsning y= en, At y= en vil også være en løsning på ligning (3.1).
Ligning (3.2) reduseres til en adskilt variabel ligning ved å dele på produktet  :
:
 , som lar oss få det generelle integralet av ligning (3.2):
, som lar oss få det generelle integralet av ligning (3.2):  . (3.3)
. (3.3)
Integralkurver (3.3) vil bli supplert med løsninger  , hvis slike løsninger finnes.
, hvis slike løsninger finnes.
Løs ligningen:.
Vi skiller variablene:

 .
.
Integrering, får vi 
Videre fra ligningene  Og
Og  finner vi x=1,
y=-1.
Disse løsningene er private løsninger.
finner vi x=1,
y=-1.
Disse løsningene er private løsninger.
§ 4. Homogene differensialligninger av 1. orden.
Definisjon 1. En 1. ordens ligning kalles homogen hvis for sin høyre side for noen  forholdet er gyldig
forholdet er gyldig  , kalt tilstanden for homogenitet til en funksjon av to variabler med null dimensjon.
, kalt tilstanden for homogenitet til en funksjon av to variabler med null dimensjon.
Eksempel 1. Vis den funksjonen  - homogen nulldimensjon.
- homogen nulldimensjon.
Løsning.
 ,
,
Q.E.D.
Teorem. Enhver funksjon  - homogen og omvendt enhver homogen funksjon
- homogen og omvendt enhver homogen funksjon  nulldimensjon reduseres til formen
nulldimensjon reduseres til formen  .
.
Bevis.
Den første setningen i teoremet er åpenbar, fordi  . La oss bevise det andre utsagnet. La oss sette
. La oss bevise det andre utsagnet. La oss sette  , deretter for en homogen funksjon
, deretter for en homogen funksjon  , som var det som måtte bevises.
, som var det som måtte bevises.
Definisjon 2. Ligning (4.1)
i hvilken M Og N– homogene funksjoner av samme grad, dvs. har eiendommen til alle  , kalles homogen.
, kalles homogen.
Selvfølgelig kan denne ligningen alltid reduseres til formen  (4.2), selv om du ikke trenger å gjøre dette for å løse det.
(4.2), selv om du ikke trenger å gjøre dette for å løse det.
En homogen ligning reduseres til en ligning med separerbare variabler ved å erstatte ønsket funksjon y i henhold til formelen y=
zx,
Hvor z(x)
– ny nødvendig funksjon. Etter å ha utført denne substitusjonen i ligning (4.2), får vi:  eller
eller  eller
eller  .
.
Ved å integrere får vi det generelle integralet til ligningen med hensyn til funksjonen z(x)
 , som etter gjentatt utskifting
, som etter gjentatt utskifting  gir det generelle integralet til den opprinnelige ligningen. Dessuten, hvis
gir det generelle integralet til den opprinnelige ligningen. Dessuten, hvis  - røttene til ligningen
- røttene til ligningen  , deretter funksjonene
, deretter funksjonene  - løse en homogen gitt ligning. Hvis
- løse en homogen gitt ligning. Hvis  , så tar ligning (4.2) formen
, så tar ligning (4.2) formen
 og blir en ligning med separerbare variabler. Løsningene er semi-direkte:
og blir en ligning med separerbare variabler. Løsningene er semi-direkte:  .
.
Kommentar. Noen ganger er det tilrådelig å bruke substitusjonen i stedet for substitusjonen ovenfor x= zy.
§ 5. Differensialligninger redusert til homogene.
Tenk på en formlikning  . (5.1)
. (5.1)
Hvis  , så er dette ligningen som bruker substitusjon, hvor
, så er dette ligningen som bruker substitusjon, hvor  Og
Og  - nye variabler, og
- nye variabler, og  - noen konstante tall bestemt fra systemet
- noen konstante tall bestemt fra systemet 
Redusert til en homogen ligning 
Hvis  , så tar ligning (5.1) formen
, så tar ligning (5.1) formen
 .
.
Troende z= øks+ ved, vi kommer til en ligning som ikke inneholder en uavhengig variabel.
La oss se på eksempler.
Eksempel 1.
Integrer ligning
og marker integralkurven som går gjennom punktene: a) (2;2); b) (1;-1).
Løsning.
La oss sette y= zx. Da dy= xdz+ zdx Og
La oss forkorte det med  og samle medlemmer kl dx Og dz:
og samle medlemmer kl dx Og dz:
La oss skille variablene: 
 .
.
Integrering får vi ;
eller  ,
,  .
.
Bytter ut her z på  , får vi det generelle integralet til den gitte ligningen i formen (5.2)
, får vi det generelle integralet til den gitte ligningen i formen (5.2)  eller
eller 
 .
.
Dette er en familie av sirkler  , hvis sentre ligger på den rette linjen y =
x og som ved origo er tangent til linjen y +
x = 0.
Denne linjeny
= -
x
i sin tur en spesiell løsning av ligningen.
, hvis sentre ligger på den rette linjen y =
x og som ved origo er tangent til linjen y +
x = 0.
Denne linjeny
= -
x
i sin tur en spesiell løsning av ligningen.
Nå er Cauchy-problemmodusen:
A) å sette inn den generelle integralen x=2,
y=2,
finner vi C=2, derfor vil den nødvendige løsningen være  .
.
B) ingen av sirklene (5.2) går gjennom punktet (1;-1). Men det er semi-rett y = -
x,  går gjennom punktet og gir ønsket løsning.
går gjennom punktet og gir ønsket løsning.
Eksempel 2. Løs ligningen:.
Løsning.
Ligningen er et spesialtilfelle av ligning (5.1).
Determinant  i dette eksemplet
i dette eksemplet  , så vi må løse følgende system
, så vi må løse følgende system 
Løsning, det skjønner vi  . Ved å utføre en substitusjon i en gitt ligning
. Ved å utføre en substitusjon i en gitt ligning  , får vi en homogen ligning. Integrering ved hjelp av substitusjon
, får vi en homogen ligning. Integrering ved hjelp av substitusjon  , finner vi
, finner vi  .
.
Gå tilbake til gamle variabler x Og y i henhold til formler  , vi har.
, vi har.
§ 6. Generalisert homogen likning.
Ligning M(x,
y)
dx+
N(x,
y)
dy=0
kalles en generalisert homogen hvis det er mulig å velge et slikt tall k, at venstre side av denne ligningen blir en homogen funksjon av en viss grad m relativt x,
y,
dx Og dy forutsatt at x regnes som verdien av den første dimensjonen, y – k målinger ,
dx Og dy –
henholdsvis null og (k-1)
målinger. For eksempel vil dette være ligningen  . (6.1)
. (6.1)
Gyldig under de forutsetninger som er gjort angående målinger
x,
y,
dx Og dy medlemmer av venstre side  Og dy vil ha dimensjonene -2, 2 hhv k Og k-1. Ved å likestille dem får vi en betingelse som det nødvendige antallet må tilfredsstille k: -2 = 2k=k-1. Denne betingelsen er oppfylt når k= -1 (med dette k alle ledd på venstre side av ligningen under vurdering vil ha en dimensjon på -2). Følgelig er likning (6.1) generalisert homogen.
Og dy vil ha dimensjonene -2, 2 hhv k Og k-1. Ved å likestille dem får vi en betingelse som det nødvendige antallet må tilfredsstille k: -2 = 2k=k-1. Denne betingelsen er oppfylt når k= -1 (med dette k alle ledd på venstre side av ligningen under vurdering vil ha en dimensjon på -2). Følgelig er likning (6.1) generalisert homogen.
En generalisert homogen ligning reduseres til en ligning med separerbare variabler ved bruk av substitusjon  , Hvor z– ny ukjent funksjon. La oss integrere likning (6.1) ved å bruke den angitte metoden. Fordi k= -1, da
, Hvor z– ny ukjent funksjon. La oss integrere likning (6.1) ved å bruke den angitte metoden. Fordi k= -1, da  , hvoretter vi får ligningen .
, hvoretter vi får ligningen .
Å integrere det, finner vi  , hvor
, hvor  . Dette er en generell løsning på ligning (6.1).
. Dette er en generell løsning på ligning (6.1).
§ 7. Lineære differensiallikninger av 1. orden.
En 1. ordens lineær ligning er en ligning som er lineær med hensyn til ønsket funksjon og dens deriverte. Det ser ut som:
 , (7.1)
, (7.1)
Hvor P(x)
Og Q(x)
– gitt kontinuerlige funksjoner av x.
Hvis funksjonen  ,
så har ligning (7.1) formen:
,
så har ligning (7.1) formen:  (7.2)
(7.2)
og kalles en lineær homogen ligning, ellers  det kalles en lineær inhomogen ligning.
det kalles en lineær inhomogen ligning.
Den lineære homogene differensialligningen (7.2) er en ligning med separerbare variabler:

 (7.3)
(7.3)
Uttrykk (7.3) er den generelle løsningen av ligning (7.2). For å finne en generell løsning på ligning (7.1), hvor funksjonen P(x) betegner samme funksjon som i ligning (7.2), bruker vi en teknikk som kalles metoden for variasjon av en vilkårlig konstant og består av følgende: vi vil prøve å velge funksjonen C=C(x) slik at den generelle løsningen til den lineære homogene ligningen (7.2) ville være en løsning på den inhomogene lineære ligningen (7.1). Så for den deriverte av funksjon (7.3) får vi:
 .
.
Ved å erstatte den funnet deriverte i ligning (7.1), vil vi ha:
eller  .
.
Hvor  , hvor er en vilkårlig konstant. Som et resultat vil den generelle løsningen til den inhomogene lineære ligningen (7.1) være (7.4)
, hvor er en vilkårlig konstant. Som et resultat vil den generelle løsningen til den inhomogene lineære ligningen (7.1) være (7.4) 
Det første leddet i denne formelen representerer den generelle løsningen (7.3) av den lineære homogene differensialligningen (7.2), og det andre leddet i formelen (7.4) er en spesiell løsning av den lineære inhomogene ligningen (7.1), hentet fra den generelle (7.1). 7.4) med  . Vi fremhever denne viktige konklusjonen i form av et teorem.
. Vi fremhever denne viktige konklusjonen i form av et teorem.
Teorem. Hvis en spesiell løsning av en lineær inhomogen differensialligning er kjent  , så har alle andre løsninger formen
, så har alle andre løsninger formen  , Hvor
, Hvor  - generell løsning av den tilsvarende lineære homogene differensialligningen.
- generell løsning av den tilsvarende lineære homogene differensialligningen.
Det skal imidlertid bemerkes at for å løse den lineære inhomogene differensialligningen av 1. orden (7.1), brukes en annen metode oftere, noen ganger kalt Bernoulli-metoden. Vi skal se etter en løsning til ligning (7.1) i skjemaet  . Da
. Da  . La oss erstatte den funnet deriverte i den opprinnelige ligningen:
. La oss erstatte den funnet deriverte i den opprinnelige ligningen:  .
.
La oss kombinere for eksempel andre og tredje ledd i det siste uttrykket og trekke ut funksjonen u(x)
bak braketten:  (7.5)
(7.5)
Vi krever at parentesen annulleres:  .
.
La oss løse denne ligningen ved å sette en vilkårlig konstant C lik null:  . Med funnfunksjonen v(x)
La oss gå tilbake til ligning (7.5):
. Med funnfunksjonen v(x)
La oss gå tilbake til ligning (7.5):  .
.
Når vi løser det, får vi:  .
.
Derfor har den generelle løsningen til ligning (7.1) formen:
§ 8. Bernoullis ligning.
Definisjon.
Formens differensialligning  , Hvor
, Hvor  , kalles Bernoullis ligning.
, kalles Bernoullis ligning.
Forutsatt at  , del begge sider av Bernoulli-ligningen med
, del begge sider av Bernoulli-ligningen med  . Som et resultat får vi:
. Som et resultat får vi:  (8.1)
(8.1)
La oss introdusere en ny funksjon  . Da
. Da  . La oss multiplisere ligning (8.1) med
. La oss multiplisere ligning (8.1) med  og la oss gå til funksjonen z(x)
:
og la oss gå til funksjonen z(x)
:  , dvs. for funksjon z(x)
oppnådde en lineær inhomogen ligning av 1. orden. Denne ligningen løses ved å bruke metodene diskutert i forrige avsnitt. La oss bytte inn i den generelle løsningen i stedet z(x)
uttrykk
, dvs. for funksjon z(x)
oppnådde en lineær inhomogen ligning av 1. orden. Denne ligningen løses ved å bruke metodene diskutert i forrige avsnitt. La oss bytte inn i den generelle løsningen i stedet z(x)
uttrykk  , får vi det generelle integralet til Bernoulli-ligningen, som lett løses mht. y. På
, får vi det generelle integralet til Bernoulli-ligningen, som lett løses mht. y. På  løsning tilsettes y(x)=0
. Bernoullis ligning kan også løses uten å gjøre overgangen til en lineær ligning ved substitusjon
løsning tilsettes y(x)=0
. Bernoullis ligning kan også løses uten å gjøre overgangen til en lineær ligning ved substitusjon  , og ved å bruke Bernoulli-metoden, diskutert i detalj i § 7. La oss vurdere bruken av denne metoden for å løse Bernoulli-ligningen ved å bruke et spesifikt eksempel.
, og ved å bruke Bernoulli-metoden, diskutert i detalj i § 7. La oss vurdere bruken av denne metoden for å løse Bernoulli-ligningen ved å bruke et spesifikt eksempel.
Eksempel. Finn den generelle løsningen på ligningen:  (8.2)
(8.2)
Løsning.
Derfor har den generelle løsningen på denne ligningen formen:  , y(x)=0.
, y(x)=0.
§ 9. Differensialligninger i totale differensialer.
Definisjon. Hvis i Eq. M(x, y) dx+ N(x, y) dy=0 (9.1) venstre side er den totale differensialen til en funksjon U(x, y) , da kalles det en total differensialligning. Denne ligningen kan skrives om som du(x, y)=0 , derfor er dens generelle integral u(x, y)= c.
For eksempel ligningen xdy+
ydx=0
det er en ligning i totale differensialer, siden den kan skrives om i formen d(xy)=0.
Den generelle integralen vil være xy=
c- vilkårlig differensierbar funksjon. La oss skille (9.3) med hensyn til u
§ 10. Integrerende faktor.
Hvis ligningen M(x, y) dx + N(x, y) dy = 0 er ikke en total differensialligning og det er en funksjon µ = µ(x, y) , slik at etter å ha multiplisert begge sider av ligningen med den, får vi ligningen
µ(Mdx + Ndy) = 0 i totale differensialer, dvs. µ(Mdx + Ndy)du, deretter funksjonen µ(x, y) kalles integreringsfaktoren til ligningen. I tilfellet der ligningen allerede er en ligning i totale differensialer, antar vi µ = 1.
Hvis integreringsfaktoren er funnet µ , så reduseres integrasjonen av denne ligningen til å multiplisere begge sidene med µ og finne det generelle integralet til den resulterende ligningen i totale differensialer.
Hvis µ
er en kontinuerlig differensierbar funksjon av x Og y, Det  .
.
Det følger at den integrerende faktoren µ tilfredsstiller følgende 1. ordens partielle differensialligning:
 (10.1).
(10.1).
Hvis det er kjent på forhånd µ= µ(ω) , Hvor ω – gitt funksjon fra x Og y, så reduseres ligning (10.1) til en ordinær (og dessuten lineær) ligning med en ukjent funksjon µ på uavhengig variabel ω :
 (10.2),
(10.2),
Hvor  , dvs. brøken er kun en funksjon av ω
.
, dvs. brøken er kun en funksjon av ω
.
Løser vi ligning (10.2), finner vi den integrerende faktoren
 , Med = 1.
, Med = 1.
Spesielt ligningen M(x, y) dx + N(x, y) dy = 0 har en integrerende faktor som kun avhenger av x(ω = x) eller bare fra y(ω = y), hvis følgende vilkår er oppfylt i samsvar med dette:
 ,
, 
 ,
,  .
.
Ved å klikke på "Last ned arkiv"-knappen vil du laste ned filen du trenger helt gratis.
Før du laster ned denne filen, tenk på de gode abstraktene, testene, semesteroppgavene, avhandlingene, artiklene og andre dokumenter som ikke er gjort krav på på datamaskinen din. Dette er ditt arbeid, det skal delta i samfunnsutviklingen og komme mennesker til gode. Finn disse verkene og send dem til kunnskapsbasen.
Vi og alle studenter, hovedfagsstudenter, unge forskere som bruker kunnskapsbasen i studiene og arbeidet vil være dere veldig takknemlige.
For å laste ned et arkiv med et dokument, skriv inn et femsifret nummer i feltet nedenfor og klikk på knappen "Last ned arkiv"
Lignende dokumenter
Cauchy-problemer for differensialligninger. Graf av løsningen til en førsteordens differensialligning. Ligninger med separerbare variabler og reduserer til en homogen ligning. Homogene og inhomogene lineære ligninger av første orden. Bernoullis ligning.
foredrag, lagt til 18.08.2012
Grunnleggende begreper i teorien om vanlige differensialligninger. Tegn på en likning i totale differensialer, konstruksjon av et generelt integral. De enkleste tilfellene for å finne den integrerende faktoren. Tilfellet av en multiplikator som bare avhenger av X og kun av Y.
kursarbeid, lagt til 24.12.2014
Egenskaper ved differensialligninger som forhold mellom funksjoner og deres deriverte. Bevis på teoremet om eksistens og løsningens unikhet. Eksempler og algoritme for å løse likninger i totale differensialer. Integrerende faktor i eksempler.
kursarbeid, lagt til 02.11.2014
Riccati differensialligninger. Generell løsning av en lineær ligning. Finne alle mulige løsninger på Bernoullis differensialligning. Løse ligninger med separerbare variabler. Generelle og spesielle løsninger av Clairaut-differensialligningen.
kursarbeid, lagt til 26.01.2015
Ligning med separerbare variabler. Homogene og lineære differensialligninger. Geometriske egenskaper til integralkurver. Fullstendig differensial av en funksjon av to variabler. Bestemmelse av integralet ved Bernoulli-metoder og variasjoner av en vilkårlig konstant.
sammendrag, lagt til 24.08.2015
Konsepter og løsninger av de enkleste differensialligninger og differensialligninger av vilkårlig rekkefølge, inkludert de med konstante analytiske koeffisienter. Systemer av lineære ligninger. Asymptotisk oppførsel av løsninger av noen lineære systemer.
avhandling, lagt til 06.10.2010
Generell integral av ligningen, anvendelse av Lagrange-metoden for å løse en inhomogen lineær ligning med en ukjent funksjon. Løse en differensialligning i parametrisk form. Eulers tilstand, første ordens ligning i totale differensialer.
test, lagt til 11.02.2011
def 1 DU type
ringte homogen differensialligning av første orden(ODU).
Th 1 La følgende betingelser være oppfylt for funksjonen:
1) kontinuerlig kl
Da har ODE (1) et generelt integral, som er gitt av formelen:
hvor er et antiderivat av funksjonen Med er en vilkårlig konstant.
Merknad 1 Hvis betingelsen er oppfylt for noen, kan løsninger av skjemaet gå tapt i prosessen med å løse ODE (1), og slike tilfeller må behandles mer nøye, og hver av dem må kontrolleres separat.
Altså fra teoremet Th1 burde generell algoritme for å løse ODE (1):
1) Gjør en erstatning:
2) Dermed vil det fås en differensialligning med separerbare variabler, som bør integreres;
3) Gå tilbake til gamle gvariabler;
4) Sjekk verdiene for deres involvering i løsningen original fjernkontroll, der betingelsen vil være oppfylt
5) Skriv ned svaret.
Eksempel 1 Løs DE (4).
Løsning: DE (4) er en homogen differensialligning, siden den har formen (1). La oss gjøre en endring (3), dette vil bringe ligning (4) til skjemaet:
Ligning (5) er det generelle integralet til DE (4).
Merk at når man skiller variabler og deler med, kan løsninger gå tapt, men dette er ikke en løsning på DE (4), som lett kan verifiseres ved direkte substitusjon til likhet (4), siden denne verdien ikke er inkludert i definisjonsdomenet av den opprinnelige DE.
Svare:
Merknad 2 Noen ganger kan du skrive ODE-er i form av differensialer av variabler X Og u. Det anbefales å gå fra denne notasjonen til fjernkontrollen til uttrykket gjennom den deriverte og først deretter utføre erstatningen (3).
Differensialligninger redusert til homogene.
def 2 Funksjonen kalles homogen funksjon av grad k i området, som likestillingen vil være oppfylt for:
Her er de vanligste typene differensialligninger som kan reduseres til form (1) etter ulike transformasjoner.
1) hvor er funksjonen er homogen, nullgrad, det vil si at likheten er gyldig: DE (6) reduseres lett til formen (1), hvis vi setter , som integreres videre ved hjelp av erstatning (3).
2) (7), hvor funksjonene er homogene i samme grad k . DE av formen (7) er også integrert ved bruk av substitusjon (3).
Eksempel 2 Løs DE (8).
Løsning: La oss vise at DE (8) er homogen. La oss dele på det som er mulig, siden det ikke er en løsning på DE (8).
La oss gjøre en endring (3), dette vil bringe ligning (9) til skjemaet:
Ligning (10) er det generelle integralet til DE (8).
Merk at når du skiller variabler og deler med, kan løsninger som tilsvarer verdiene til og gå tapt. La oss sjekke disse uttrykkene. La oss erstatte dem med DE (8):
Svare:
Det er interessant å merke seg at når du løser dette eksemplet, vises en funksjon kalt "tegnet" til tallet X(leser" signum x"), definert av uttrykket:
Merknad 3Å redusere DE (6) eller (7) til formen (1) er ikke nødvendig hvis det er åpenbart at DE er homogen, kan du umiddelbart gjøre erstatningen
3) En DE av formen (11) er integrert som en ODE hvis , og substitusjonen utføres først:
(12), hvor er løsningen av systemet: (13), og deretter bruke erstatning (3) for funksjonen Etter å ha mottatt den generelle integralen, går de tilbake til variablene X Og på.
Hvis , da, forutsatt i ligning (11), får vi en differensialligning med separerbare variabler.
Eksempel 3 Løs Cauchy-problemet (14).
Løsning: La oss vise at DE (14) er redusert til en homogen DE og integrert i henhold til skjemaet ovenfor:
La oss løse det inhomogene systemet med lineære algebraiske ligninger (15) ved å bruke Cramer-metoden:
La oss gjøre en endring av variabler og integrere den resulterende ligningen:
(16) – Generell integral av DE (14). Ved separering av variabler kan løsninger gå tapt ved divisjon med et uttrykk, som kan oppnås eksplisitt etter å ha løst den kvadratiske ligningen. De er imidlertid tatt hensyn til i den generelle integralen (16) kl
La oss finne en løsning på Cauchy-problemet: bytt inn verdiene og inn i det generelle integralet (16) og finn Med.
Dermed vil det partielle integralet bli gitt av formelen:
Svare:
4) Det er mulig å redusere noen differensialligninger til homogene for en ny, ennå ukjent funksjon hvis vi bruker en substitusjon av formen:
I dette tilfellet nummeret m velges fra betingelsen at den resulterende ligningen, hvis mulig, blir homogen til en viss grad. Men hvis dette ikke lar seg gjøre, kan den aktuelle DE ikke reduseres til en homogen på denne måten.
Eksempel 4 Løs DE. (18)
Løsning: La oss vise at DE (18) reduseres til en homogen DE ved bruk av substitusjon (17) og er videre integrert ved bruk av substitusjon (3):
La oss finne Med:
Således har en spesiell løsning av DE (24) formen
Det vises hvordan man gjenkjenner en generalisert homogen differensialligning. En metode for å løse en generalisert homogen differensialligning av første orden vurderes. Et eksempel på en detaljert løsning av en slik ligning er gitt.
InnholdDefinisjon
En generalisert homogen differensialligning av første orden er en ligning av formen:, hvor α ≠ 0 , α ≠ 1 , f - funksjon.
Hvordan bestemme om en differensialligning er generalisert homogen
For å bestemme om en differensialligning er generalisert homogen, må du introdusere en konstant t og gjøre substitusjonen:
y → t α · y , x → t · x .
Hvis det er mulig å velge en verdi α der konstanten t avtar, så er dette - generalisert homogen differensialligning. Endringen i den deriverte y′ med denne erstatningen har formen:
.
Eksempel
Bestem om den gitte ligningen er generalisert homogen:
.
Vi gjør erstatningen y → t α y, x → t x, y′ → t α- 1 år:
;
.
Del på t α+ 5
:
;
.
Ligningen vil ikke inneholde t if
4 α - 6 = 0,
α = 3/2
.
Siden da α = 3/2
, t har gått ned, da dette er en generalisert homogen ligning.
Løsningsmetode
Tenk på den generaliserte homogene differensialligningen av første orden:
(1)
.
La oss vise at det er redusert til en homogen ligning ved bruk av substitusjon:
t = xα.
Virkelig,
.
Herfra
;
.
(1)
:
;
.
Dette er en homogen ligning. Det kan løses ved substitusjon:
y = z t,
der z er en funksjon av t.
Når du løser problemer, er det lettere å umiddelbart bruke substitusjon:
y = z x α,
der z er en funksjon av x.
Et eksempel på løsning av en generalisert homogen differensialligning av første orden
Løs differensialligning
(S.1) .
La oss sjekke om denne ligningen er generalisert homogen. For å gjøre dette i (S.1) gjør en erstatning:
y → t α y , x → t x , y′ → t α- 1 år.
.
Del på t α:
.
t vil bli kansellert hvis vi setter α = - 1
.
Dette betyr at dette er en generalisert homogen ligning.
La oss gjøre en erstatning: 1
,
der z er en funksjon av x.
.
y = z x α = z x - (S.1):
(S.1) ;
;
.
Bytt inn i den opprinnelige ligningen
;
;
.
Multipliser med x og åpne parentesene: 2
Vi skiller variablene - multipliserer med dx og deler på x z 0
.
.
Når z ≠
;
;
;
.
vi har:
.
Vi integrerer ved å bruke tabellen over integraler:
.
La oss potensere:
.
La oss erstatte konstanten e C → C og fjerne modultegnet, siden valget av det ønskede tegnet bestemmes av valget av tegnet til konstanten C:
La oss gå tilbake til variabelen y. .
Erstatter z = xy: 2
Del på x: 0
(S.2) 0
Når vi deler på z 0
.
, vi antok at z ≠ 0
. La oss gå tilbake til variabelen y. Tenk nå på løsningen z = xy = 0
.
;
.
, eller y =
Siden da y =
 ikke er definert, legger vi til det resulterende generelle integralet løsningen y =
ikke er definert, legger vi til det resulterende generelle integralet løsningen y =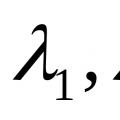 Lineært avhengige og lineært uavhengige vektorer Finn ut om vektorene er lineært uavhengige
Lineært avhengige og lineært uavhengige vektorer Finn ut om vektorene er lineært uavhengige Brukt litteratur:
Brukt litteratur: