Invers matrise og dens egenskaper. invers matrise

Finne den inverse matrisen- et problem som oftest løses på to måter:

metoden for algebraiske tillegg, der det er nødvendig å finne determinanter og transponere matriser;
eliminasjonsmetode ukjent gauss, der det er nødvendig å utføre elementære transformasjoner av matriser (legge til rader, multiplisere rader med samme tall, etc.).

For de som er spesielt nysgjerrige, finnes det andre metoder, for eksempel metoden for lineære transformasjoner. I denne leksjonen vil vi analysere de tre nevnte metodene og algoritmer for å finne den inverse matrisen ved hjelp av disse metodene.

invers matrise MEN, en slik matrise kalles

MEN
. (1)

invers matrise , som kreves for å bli funnet for en gitt kvadratisk matrise MEN, en slik matrise kalles

produktet som matrisene bygger på MEN til høyre er identitetsmatrisen, dvs.
. (1)

En identitetsmatrise er en diagonal matrise der alle diagonale oppføringer er lik én.

Teorem.For hver ikke-entall (ikke-entall, ikke-entall) kvadratisk matrise kan man finne en invers matrise, og dessuten bare en. For en spesiell (degenerert, entall) kvadratisk matrise eksisterer ikke den inverse matrisen.

Den kvadratiske matrisen kalles ikke-spesiell(eller ikke-degenerert, ikke-entall) hvis determinanten ikke er lik null, og spesiell(eller degenerert, entall) hvis determinanten er null.

invers matrise kan bare finnes for en kvadratisk matrise. Naturligvis vil den inverse matrisen også være kvadratisk og av samme rekkefølge som den gitte matrisen. En matrise som en invers matrise kan bli funnet for, kalles en inverterbar matrise.

Til invers matrise det er en passende analogi med det gjensidige til et tall. For hvert tall en, som ikke er lik null, finnes det et tall b at arbeidet en og b lik en: ab= 1 . Antall b kalles den gjensidige av et tall b. For eksempel, for tallet 7, er det inverse tallet 1/7, siden 7*1/7=1.

Finne den inverse matrisen ved hjelp av metoden for algebraiske addisjoner (unionsmatrise)

For en ikke-entall kvadratisk matrise MEN den inverse er matrisen

hvor er matrisedeterminanten MEN, а er matrisen assosiert med matrisen MEN.

Alliert med en kvadratisk matrise EN er en matrise av samme orden hvis elementer er algebraiske tillegg tilsvarende elementer av determinanten til matrisen transponert med hensyn til matrisen A. Således, hvis

deretter

Algoritme for å finne den inverse matrisen ved hjelp av metoden for algebraiske addisjoner

1. Finn determinanten til denne matrisen EN. Hvis determinanten er lik null, stopper det å finne den inverse matrisen, siden matrisen er degenerert og det ikke er invers for den.

2. Finn en matrise transponert mht EN.

3. Beregn elementene i unionsmatrisen som de algebraiske komplementene til maritaen funnet i trinn 2.

4. Bruk formel (2): gang tallet, invers determinant matriser EN, til unionsmatrisen funnet i trinn 4.

5. Sjekk resultatet oppnådd i trinn 4 ved å multiplisere gitt matrise EN til den inverse matrisen. Hvis produktet av disse matrisene er lik identitetsmatrisen, ble den inverse matrisen funnet riktig. Start ellers løsningsprosessen på nytt.

Eksempel 1 For matrise

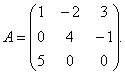
finn den inverse matrisen.

Løsning. For å finne den inverse matrisen er det nødvendig å finne determinanten til matrisen MEN. Vi finner etter regelen for trekanter:

Derfor matrisen MEN er ikke-entall (ikke-degenerert, ikke-entall) og det er en invers for det.

La oss finne matrisen knyttet til den gitte matrisen MEN.

La oss finne matrisen transponert i forhold til matrisen EN:

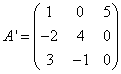
Vi beregner elementene i unionsmatrisen som algebraiske komplementer til matrisen transponert i forhold til matrisen EN:

Derfor ble matrisen konjugert med matrisen EN, har formen

Kommentar. Rekkefølgen for beregning av elementer og transponering av matrisen kan være forskjellig. Man kan først beregne de algebraiske komplementene til matrisen EN, og transponer deretter matrisen av algebraiske komplementer. Resultatet bør være de samme elementene i fagforeningsmatrisen.

Ved å bruke formel (2), finner vi matrisen invers til matrisen MEN:

Finne den inverse matrisen ved Gaussisk eliminering av ukjente

Det første trinnet for å finne den inverse matrisen ved gaussisk eliminering er å tilordne til matrisen EN identitetsmatrise av samme rekkefølge, og skille dem med en vertikal stang. Vi får en dobbel matrise. Multipliser begge deler av denne matrisen med , så får vi

Algoritme for å finne den inverse matrisen ved gaussisk eliminering av ukjente

1. Til matrisen EN tilordne en identitetsmatrise av samme rekkefølge.

2. Transformer den resulterende doble matrisen slik at identitetsmatrisen oppnås i dens venstre del, så vil den inverse matrisen automatisk fås i den høyre delen i stedet for identitetsmatrisen. Matrise EN på venstre side konverteres til identitetsmatrisen ved elementære transformasjoner matriser.

2. Hvis i ferd med matrisetransformasjon EN inn i identitetsmatrisen i en hvilken som helst rad eller i hvilken som helst kolonne vil det bare være nuller, da er determinanten til matrisen lik null, og derfor matrisen EN vil være degenerert, og den har ingen invers matrise. I dette tilfellet stopper videre funn av den inverse matrisen.

Eksempel 2 For matrise

finn den inverse matrisen.

og vi vil transformere den slik at identitetsmatrisen oppnås på venstre side. La oss starte transformasjonen.

Multipliser den første raden i venstre og høyre matrise med (-3) og legg den til den andre raden, og multipliser deretter den første raden med (-4) og legg den til den tredje raden, så får vi

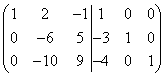For å unngå, hvis mulig brøktall i påfølgende transformasjoner vil vi først lage en enhet i den andre raden på venstre side av den doble matrisen. For å gjøre dette, multipliser den andre raden med 2 og trekk den tredje raden fra den, så får vi

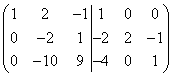La oss legge den første raden til den andre, og deretter multiplisere den andre raden med (-9) og legge den til den tredje raden. Så får vi

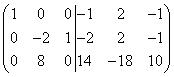Del den tredje raden med 8, da

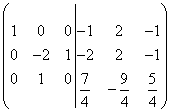Multipliser den tredje raden med 2 og legg den til i den andre raden. Det viser seg:

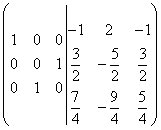Ved å bytte plass på andre og tredje linje, så får vi endelig:

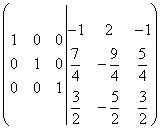Vi ser at identitetsmatrisen er oppnådd på venstre side, derfor er den inverse matrisen oppnådd på høyre side. På denne måten:

Du kan kontrollere riktigheten av beregningene ved å multiplisere den opprinnelige matrisen med den funnet inverse matrisen:

Resultatet skal være en invers matrise.

Eksempel 3 For matrise

finn den inverse matrisen.

Løsning. Kompilere en dobbel matrise

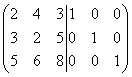
og vi vil forvandle det.

Vi multipliserer den første raden med 3, og den andre med 2, og trekker fra den andre, og deretter multipliserer vi den første raden med 5, og den tredje med 2 og trekker fra den tredje raden, så får vi

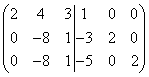Vi multipliserer den første raden med 2 og legger den til den andre, og trekker deretter den andre fra den tredje raden, så får vi

Vi ser at i den tredje linjen på venstre side viste alle elementene seg å være lik null. Derfor er matrisen degenerert og har ingen invers matrise. Vi stopper ytterligere funn av omvendt maria.

Dette emnet er et av de mest hatede blant studenter. Verre, sannsynligvis, bare determinanter.

Trikset er at selve konseptet med det inverse elementet (og jeg snakker ikke bare om matriser nå) refererer oss til operasjonen av multiplikasjon. Selv i skolepensum multiplikasjon vurderes komplisert operasjon, og multiplikasjon av matriser er generelt et eget emne, som jeg har et helt avsnitt og en videoopplæring viet til det.

I dag vil vi ikke gå inn på detaljene i matriseberegninger. Bare husk: hvordan matriser betegnes, hvordan de multipliseres og hva som følger av dette.

Gjennomgang: Matrisemultiplikasjon

Først av alt, la oss bli enige om notasjon. En matrise $A$ av størrelsen $\left[ m\times n \right]$ er ganske enkelt en talltabell med nøyaktig $m$ rader og $n$ kolonner:

\=\underbrace(\venstre[ \begin(matrise) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrise) \right])_(n)\]

For ikke å forveksle rader og kolonner ved et uhell på steder (tro meg, i eksamen kan du forveksle en med en toer - hva kan vi si om noen linjer der), bare ta en titt på bildet:

Bestemmelse av indekser for matriseceller

Hva skjer? Hvis vi plasserer standard koordinatsystemet $OXY$ til venstre øvre hjørne og rett aksene slik at de dekker hele matrisen, så kan hver celle i denne matrisen assosieres unikt med koordinatene $\left(x;y \right)$ - dette vil være radnummer og kolonnenummer.

Hvorfor er koordinatsystemet plassert nøyaktig i øvre venstre hjørne? Ja, for det er derfra vi begynner å lese tekster. Det er veldig lett å huske.

Hvorfor peker $x$-aksen ned og ikke til høyre? Igjen, det er enkelt: ta standard koordinatsystemet ($x$-aksen går til høyre, $y$-aksen går opp) og roter den slik at den omslutter matrisen. Dette er en 90 graders rotasjon med klokken - vi ser resultatet på bildet.

Generelt fant vi ut hvordan vi skulle bestemme indeksene til matriseelementene. La oss nå ta for oss multiplikasjon.

Definisjon. Matrisene $A=\venstre[ m\ ganger n \right]$ og $B=\left[ n\ ganger k \right]$, når antall kolonner i den første samsvarer med antall rader i den andre, er kalt konsekvent.

Det er i den rekkefølgen. Man kan være tvetydig og si at matrisene $A$ og $B$ danner et ordnet par $\left(A;B \right)$: hvis de er konsistente i denne rekkefølgen, så er det slett ikke nødvendig at $B $ og $A$, de. paret $\left(B;A \right)$ er også konsistent.

Bare konsistente matriser kan multipliseres.

Definisjon. Produktet av konsistente matriser $A=\venstre[ m\ ganger n \høyre]$ og $B=\venstre[ n\ ganger k \høyre]$ er den nye matrisen $C=\venstre[ m\ ganger k \høyre ]$ , hvis elementer $((c)_(ij))$ beregnes med formelen:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Med andre ord: for å få elementet $((c)_(ij))$ i matrisen $C=A\cdot B$, må du ta $i$-raden til den første matrisen, $j$ -th kolonne i den andre matrisen, og multipliser deretter i par elementer fra denne raden og kolonnen. Legg sammen resultatene.

Ja, det er en hard definisjon. Flere fakta følger umiddelbart av det:

Matrisemultiplikasjon er generelt sett ikke-kommutativ: $A\cdot B\ne B\cdot A$;
Imidlertid er multiplikasjon assosiativ: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
Og til og med distributiv: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
Og distributivt igjen: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Distributiviteten til multiplikasjon måtte beskrives separat for venstre og høyre multiplikasjonssum bare på grunn av ikke-kommutativiteten til multiplikasjonsoperasjonen.

Hvis det likevel viser seg at $A\cdot B=B\cdot A$, kalles slike matriser permutable.

Blant alle matrisene som multipliseres med noe der, er det spesielle - de som, når de multipliseres med en hvilken som helst matrise $A$, igjen gir $A$:

Definisjon. En matrise $E$ kalles identitet hvis $A\cdot E=A$ eller $E\cdot A=A$. I tilfellet med en kvadratisk matrise $A$ kan vi skrive:

Identitetsmatrisen er en hyppig gjest i løsningen matriseligninger. Og generelt, en hyppig gjest i matrisens verden. :)

Og på grunn av denne $E$, kom noen opp med alt spillet som skal skrives neste gang.

Hva er en invers matrise

Siden matrisemultiplikasjon er en veldig tidkrevende operasjon (du må multiplisere en haug med rader og kolonner), er konseptet med en invers matrise heller ikke det mest trivielle. Og det trenger litt forklaring.

Nøkkeldefinisjon

Vel, det er på tide å vite sannheten.

Definisjon. Matrisen $B$ kalles den inverse av matrisen $A$ if

Den inverse matrisen er betegnet med $((A)^(-1))$ (ikke å forveksle med graden!), så definisjonen kan skrives om slik:

Det ser ut til at alt er ekstremt enkelt og klart. Men når man analyserer en slik definisjon, oppstår det umiddelbart flere spørsmål:

Finnes det alltid en invers matrise? Og hvis ikke alltid, hvordan bestemme: når det eksisterer og når det ikke finnes?
Og hvem sa at en slik matrise er nøyaktig en? Hva om det for en original matrise $A$ er en hel mengde inverser?
Hvordan ser alle disse "reversene" ut? Og hvordan teller du dem egentlig?

Når det gjelder beregningsalgoritmene - vi vil snakke om dette litt senere. Men vi vil svare på resten av spørsmålene nå. La oss ordne dem i form av separate påstandslemmaer.

Grunnleggende egenskaper

La oss starte med hvordan matrisen $A$ skal se ut for at den skal ha $((A)^(-1))$. Nå skal vi sørge for at begge disse matrisene må være kvadratiske og av samme størrelse: $\left[ n\ ganger n \right]$.

Lemma 1. Gitt en matrise $A$ og dens inverse $((A)^(-1))$. Da er begge disse matrisene kvadratiske og har samme rekkefølge $n$.

Bevis. Alt er enkelt. La matrisen $A=\venstre[ m\ ganger n \høyre]$, $((A)^(-1))=\venstre[ a\ ganger b \høyre]$. Siden produktet $A\cdot ((A)^(-1))=E$ eksisterer per definisjon, er matrisene $A$ og $((A)^(-1))$ konsistente i den rekkefølgen:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( tilpasse)\]

Dette er en direkte konsekvens av: koeffisientene $n$ og $a$ er "transit" og må være like.

Samtidig er den inverse multiplikasjonen også definert: $((A)^(-1))\cdot A=E$, så matrisene $((A)^(-1))$ og $A$ er også konsekvent i denne rekkefølgen:

\[\begin(align) & \venstre[ a\ ganger b \høyre]\cdot \venstre[ m\ ganger n \høyre]=\venstre[ a\ganger n \høyre] \\ & b=m \end( tilpasse)\]

Dermed, uten tap av generalitet, kan vi anta at $A=\venstre[ m\ ganger n \høyre]$, $((A)^(-1))=\venstre[ n\ ganger m \høyre]$. Imidlertid, i henhold til definisjonen av $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, så er dimensjonene til matrisene nøyaktig de samme:

\[\begin(align) & \venstre[ m\ ganger n \høyre]=\venstre[ n\ ganger m \høyre] \\ & m=n \end(align)\]

Så det viser seg at alle tre matrisene - $A$, $((A)^(-1))$ og $E$ - er kvadratisk størrelse$\venstre[ n\ ganger n \høyre]$. Lemmaet er bevist.

Vel, det er allerede bra. Vi ser at bare kvadratiske matriser er inverterbare. La oss nå sørge for at den inverse matrisen alltid er den samme.

Lemma 2. Gitt en matrise $A$ og dens inverse $((A)^(-1))$. Da er denne inverse matrisen unik.

Bevis. La oss starte fra det motsatte: la matrisen $A$ ha minst to forekomster av inverser - $B$ og $C$. Da, i henhold til definisjonen, er følgende likheter sanne:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(align)\]

Fra Lemma 1 konkluderer vi med at alle fire matrisene $A$, $B$, $C$ og $E$ er kvadratiske av samme rekkefølge: $\venstre[ n\ ganger n \right]$. Derfor er produktet definert:

Siden matrisemultiplikasjon er assosiativ (men ikke kommutativ!), kan vi skrive:

\[\begin(align) & B\cdot A\cdot C=\venstre(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \venstre(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Høyrepil B=C. \\ \end(align)\]

Kun mottatt mulig variant: to forekomster av den inverse matrisen er like. Lemmaet er bevist.

Resonnementet ovenfor gjentar nesten ordrett beviset på det unike med det omvendte elementet for alle reelle tall$b\ne 0$. Det eneste signifikante tillegget er å ta hensyn til dimensjonen til matriser.

Vi vet imidlertid fortsatt ikke noe om noen kvadratisk matrise er reversibel. Her kommer determinanten til hjelp - dette er en nøkkelegenskap for alle kvadratiske matriser.

Lemma 3. Gitt en matrise $A$. Hvis matrisen $((A)^(-1))$ invers til den eksisterer, så er determinanten til den opprinnelige matrisen ikke null:

\[\venstre| En \right|\ne 0\]

Bevis. Vi vet allerede at $A$ og $((A)^(-1))$ er kvadratiske matriser av størrelsen $\left[ n\ ganger n \right]$. Derfor er det mulig for hver av dem å beregne determinanten: $\left| A \right|$ og $\left| ((A)^(-1)) \right|$. Imidlertid er produktdeterminanten er lik produktet determinanter:

\[\venstre| A\cdot B \right|=\venstre| En \høyre|\cdot \venstre| B \høyre|\Høyrepil \venstre| A\cdot ((A)^(-1)) \right|=\venstre| En \høyre|\cdot \venstre| ((A)^(-1)) \right|\]

Men i henhold til definisjonen av $A\cdot ((A)^(-1))=E$, og determinanten til $E$ er alltid lik 1, så

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \venstre| A\cdot ((A)^(-1)) \right|=\venstre| E\høyre|; \\ & \venstre| En \høyre|\cdot \venstre| ((A)^(-1)) \right|=1. \\ \end(align)\]

Produktet av to tall er lik én bare hvis hvert av disse tallene er forskjellig fra null:

\[\venstre| En \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Så det viser seg at $\venstre| En \right|\ne 0$. Lemmaet er bevist.

Faktisk er dette kravet ganske logisk. Nå skal vi analysere algoritmen for å finne den inverse matrisen - og det vil bli helt klart hvorfor det i prinsippet ikke kan eksistere noen invers matrise med null determinant.

Men først, la oss formulere en "hjelpe" definisjon:

Definisjon. En degenerert matrise er en kvadratisk matrise med størrelsen $\venstre[ n\ ganger n \høyre]$ hvis determinant er null.

Dermed kan vi hevde at enhver inverterbar matrise er ikke degenerert.

Hvordan finne den inverse matrisen

Nå skal vi vurdere en universell algoritme for å finne inverse matriser. Generelt er det to allment aksepterte algoritmer, og vi vil også vurdere den andre i dag.

Den som vil bli vurdert nå er svært effektiv for matriser med størrelse $\venstre[ 2\ ganger 2 \høyre]$ og - delvis - av størrelse $\venstre[ 3\ ganger 3 \høyre]$. Men fra størrelsen $\left[ 4\times 4 \right]$ er det bedre å ikke bruke det. Hvorfor - nå vil du forstå alt.

Algebraiske tillegg

Gjør deg klar. Nå blir det smerte. Nei, ikke bekymre deg: en vakker sykepleier i et skjørt, strømper med blonder kommer ikke til deg og vil ikke gi deg en injeksjon i baken. Alt er mye mer prosaisk: algebraiske tillegg og Hennes Majestet "Union Matrix" kommer til deg.

La oss starte med den viktigste. La det være en kvadratisk matrise med størrelsen $A=\venstre[ n\ ganger n \høyre]$ hvis elementer heter $((a)_(ij))$. Så, for hvert slikt element, kan man definere et algebraisk komplement:

Definisjon. Algebraisk komplement $((A)_(ij))$ til elementet $((a)_(ij))$ i $i$-th rad og $j$-th kolonne i matrisen $A=\venstre [ n \times n \right]$ er en konstruksjon av formen

\[((A)_(ij))=((\venstre(-1 \høyre))^(i+j))\cdot M_(ij)^(*)\]

Hvor $M_(ij)^(*)$ er determinanten for matrisen hentet fra den opprinnelige $A$ ved å slette den samme $i$-th rad og $j$-th kolonne.

En gang til. Det algebraiske komplementet til matriseelementet med koordinatene $\left(i;j \right)$ er betegnet som $((A)_(ij))$ og beregnes i henhold til skjemaet:

Først sletter vi $i$-raden og $j$-th-kolonnen fra den opprinnelige matrisen. Vi får en ny kvadratisk matrise, og vi betegner dens determinant som $M_(ij)^(*)$.
Så multipliserer vi denne determinanten med $((\left(-1 \right))^(i+j))$ - til å begynne med kan dette uttrykket virke overveldende, men faktisk finner vi bare ut tegnet foran $ M_(ij)^(*) $.
Vi teller – vi får spesifikt nummer. De. det algebraiske tillegget er bare et tall, ikke en ny matrise, og så videre.

Selve matrisen $M_(ij)^(*)$ kalles den komplementære moll til elementet $((a)_(ij))$. Og i denne forstand er definisjonen ovenfor av et algebraisk komplement et spesielt tilfelle av et mer kompleks definisjon- hva vi vurderte i leksjonen om determinanten.

Viktig notat. Faktisk, i "voksen" matematikk, er algebraiske tillegg definert som følger:

Vi tar $k$ rader og $k$ kolonner i en kvadratisk matrise. I skjæringspunktet deres får vi en matrise med størrelsen $\venstre[ k\ ganger k \right]$ — dens determinant kalles en minor av orden $k$ og er betegnet med $((M)_(k))$.

Så krysser vi ut disse "utvalgte" $k$-radene og $k$-kolonnene. Igjen får vi en kvadratisk matrise - dens determinant kalles den komplementære moll og er betegnet med $M_(k)^(*)$.

Multipliser $M_(k)^(*)$ med $((\left(-1 \right))^(t))$, der $t$ er (merk nå!) summen av tallene for alle valgte rader og kolonner. Dette vil være det algebraiske tillegget.

Ta en titt på det tredje trinnet: det er faktisk en sum på $2k$ vilkår! En annen ting er at for $k=1$ får vi bare 2 ledd - disse vil være de samme $i+j$ - "koordinatene" til elementet $((a)_(ij))$, som vi er for ser etter et algebraisk komplement.

Så i dag bruker vi en litt forenklet definisjon. Men som vi skal se senere, blir det mer enn nok. Mye viktigere er følgende:

Definisjon. Unionsmatrisen $S$ til kvadratmatrisen $A=\venstre[ n\ ganger n \right]$ er en ny matrise med størrelsen $\left[ n\ ganger n \right]$, som er hentet fra $A$ ved å erstatte $(( a)_(ij))$ med algebraiske komplementer $((A)_(ij))$:

\\Høyrepil S=\venstre[ \begin(matrise) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrise) \right]\]

Den første tanken som dukker opp i øyeblikket av å realisere denne definisjonen er "dette er hvor mye du må telle totalt!" Slapp av: du må telle, men ikke så mye. :)

Vel, alt dette er veldig hyggelig, men hvorfor er det nødvendig? Men hvorfor.

Hovedteorem

La oss gå litt tilbake. Husk, Lemma 3 uttalte at en inverterbar matrise $A$ alltid er ikke-singular (det vil si at dens determinant er ikke-null: $\left| A \right|\ne 0$).

Så det motsatte er også sant: hvis matrisen $A$ ikke er degenerert, så er den alltid inverterbar. Og det er til og med et søkeskjema $((A)^(-1))$. Sjekk det ut:

Invers matriseteorem. La en kvadratisk matrise $A=\venstre[ n\ ganger n \right]$ gis, og dens determinant er ikke null: $\left| En \right|\ne 0$. Da eksisterer den inverse matrisen $((A)^(-1))$ og beregnes med formelen:

\[((A)^(-1))=\frac(1)(\venstre| A \høyre|)\cdot ((S)^(T))\]

Og nå - likevel, men med lesbar håndskrift. For å finne den inverse matrisen trenger du:

Beregn determinanten $\left| A \right|$ og sørg for at den ikke er null.
Kompiler unionsmatrisen $S$, dvs. tell 100500 algebraiske tillegg $((A)_(ij))$ og sett dem på plass $((a)_(ij))$.
Transponer denne matrisen $S$ og multipliser den med et tall $q=(1)/(\left| A \right|)\;$.

Og det er det! Den inverse matrisen $((A)^(-1))$ er funnet. La oss se på eksempler:

\[\venstre[ \begin(matrise) 3 & 1 \\ 5 & 2 \\\end(matrise) \right]\]

Løsning. La oss sjekke reversibiliteten. La oss beregne determinanten:

\[\venstre| En \høyre|=\venstre| \begin(matrise) 3 & 1 \\ 5 & 2 \\\end(matrise) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinanten er forskjellig fra null. Så matrisen er inverterbar. La oss lage en fagforeningsmatrise:

La oss beregne de algebraiske addisjonene:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\høyre|=2; \\ & ((A)_(12))=((\venstre(-1 \høyre))^(1+2))\cdot \venstre| 5\høyre|=-5; \\ & ((A)_(21))=((\venstre(-1 \høyre))^(2+1))\cdot \venstre| 1 \right|=-1; \\ & ((A)_(22))=((\venstre(-1 \høyre))^(2+2))\cdot \venstre| 3\høyre|=3. \\ \end(align)\]

Vær oppmerksom: determinanter |2|, |5|, |1| og |3| er determinantene for matriser med størrelse $\venstre[ 1\ ganger 1 \høyre]$, ikke moduler. De. hvis determinantene var negative tall, er det ikke nødvendig å fjerne "minus".

Totalt ser fagforeningsmatrisen vår slik ut:

\[((A)^(-1))=\frac(1)(\venstre| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\venstre[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\venstre[ \begin (matrise)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(matrise) \right]\]

OK, det er over nå. Problem løst.

Svar. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

En oppgave. Finn den inverse matrisen:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Løsning. Igjen tar vi for oss determinanten:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matrise) ) \venstre(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\venstre (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrise)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Determinanten er forskjellig fra null - matrisen er inverterbar. Men nå blir det mest blikk: du må telle så mange som 9 (ni, for helvete!) algebraiske tillegg. Og hver av dem vil inneholde $\left[ 2\times 2 \right]$-kvalifiseringen. Fløy:

\[\begin(matrise) ((A)_(11))=((\venstre(-1 \høyre))^(1+1))\cdot \venstre| \begin(matrise) 2 & -1 \\ 0 & 1 \\\end(matrise) \right|=2; \\ ((A)_(12))=((\venstre(-1 \høyre))^(1+2))\cdot \venstre| \begin(matrise) 0 & -1 \\ 1 & 1 \\\end(matrise) \right|=-1; \\ ((A)_(13))=((\venstre(-1 \høyre))^(1+3))\cdot \venstre| \begin(matrise) 0 & 2 \\ 1 & 0 \\\end(matrise) \right|=-2; \\ ... \\ ((A)_(33))=((\venstre(-1 \høyre))^(3+3))\cdot \venstre| \begin(matrise) 1 & -1 \\ 0 & 2 \\\end(matrise) \right|=2; \\ \end(matrise)\]

Kort fortalt vil fagforeningsmatrisen se slik ut:

Derfor vil den inverse matrisen være:

\[((A)^(-1))=\frac(1)(-1)\cdot \venstre[ \begin(matrise) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrise) \right]=\venstre[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(array) \right]\]

Vel, det er alt. Her er svaret.

Svar. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Som du kan se, utførte vi en sjekk på slutten av hvert eksempel. I denne forbindelse, en viktig merknad:

Ikke vær lat med å sjekke. Multipliser den opprinnelige matrisen med den funnet inverse - du bør få $E$.

Det er mye enklere og raskere å utføre denne kontrollen enn å se etter en feil i videre beregninger, når du for eksempel løser en matriseligning.

Alternativ måte

Som jeg sa, den inverse matriseteoremet fungerer fint for størrelsene $\venstre[ 2\ ganger 2 \høyre]$ og $\venstre[ 3\ ganger 3 \høyre]$ (i siste tilfelle- det er ikke så "perfekt" lenger), men for store matriser begynner tristhet.

Men ikke bekymre deg: det finnes en alternativ algoritme som kan brukes til å finne inversen rolig selv for $\venstre[ 10\ ganger 10 \right]$ matrisen. Men som ofte er tilfellet, for å vurdere denne algoritmen, trenger vi litt teoretisk bakgrunn.

Elementære transformasjoner

Blant de forskjellige transformasjonene av matrisen er det flere spesielle - de kalles elementære. Det er nøyaktig tre slike transformasjoner:

Multiplikasjon. Du kan ta $i$-th rad (kolonne) og multiplisere den med et hvilket som helst tall $k\ne 0$;
Addisjon. Legg til $i$-th rad (kolonne) en hvilken som helst annen $j$-th rad (kolonne) multiplisert med et hvilket som helst tall $k\ne 0$ (selvfølgelig er $k=0$ også mulig, men hva er vitsen av det? Ingenting vil imidlertid endre seg).
Permutasjon. Ta $i$-th og $j$-th radene (kolonner) og bytt dem.

Hvorfor disse transformasjonene kalles elementære (for store matriser ser de ikke så elementære ut) og hvorfor det bare er tre av dem - disse spørsmålene er utenfor rammen av dagens leksjon. Derfor vil vi ikke gå i detaljer.

En annen ting er viktig: vi må utføre alle disse perversjonene på den tilhørende matrisen. Ja, ja, du hørte riktig. Nå blir det en definisjon til - den siste i dagens leksjon.

Vedlagt matrise

Sikkert på skolen løste du likningssystemer ved hjelp av addisjonsmetoden. Vel, der, trekk en annen fra en linje, multipliser en linje med et tall - det er alt.

Så: nå vil alt være det samme, men allerede "på en voksen måte". Klar?

Definisjon. La matrisen $A=\venstre[ n\ ganger n \right]$ og identitetsmatrisen $E$ av samme størrelse $n$ gis. Deretter den tilknyttede matrisen $\left[ A\left| E\rett. \right]$ er en ny $\left[ n\ ganger 2n \right]$ matrise som ser slik ut:

\[\venstre[ A\venstre| E\rett. \right]=\venstre[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Kort sagt, vi tar matrisen $A$, til høyre tilordner vi den identitetsmatrisen $E$ av ønsket størrelse, vi skiller dem med en vertikal strek for skjønnhet - her er den vedlagte. :)

Hva er fangsten? Og her er hva:

Teorem. La matrisen $A$ være inverterbar. Tenk på den tilstøtende matrisen $\left[ A\left| E\rett. \right]$. Hvis du bruker elementære strengtransformasjoner ta den til formen $\left[ E\left| Lys. \right]$, dvs. ved å multiplisere, subtrahere og omorganisere rader for å få fra $A$ matrisen $E$ til høyre, så er matrisen $B$ oppnådd til venstre den inverse av $A$:

\[\venstre[ A\venstre| E\rett. \høyre]\til \venstre[ E\venstre| Lys. \right]\Høyrepil B=((A)^(-1))\]

Så enkelt er det! Kort sagt, algoritmen for å finne den inverse matrisen ser slik ut:

Skriv den tilknyttede matrisen $\left[ A\left| E\rett. \right]$;
Utfør elementære strengkonverteringer til høyre i stedet for $A$ vises $E$;
Selvfølgelig vil det også dukke opp noe til venstre - en viss matrise $B$. Dette vil være omvendt;
FORTJENESTE! :)

Selvfølgelig mye lettere sagt enn gjort. Så la oss se på et par eksempler: for størrelsene $\venstre[ 3\ ganger 3 \høyre]$ og $\venstre[ 4\ ganger 4 \høyre]$.

En oppgave. Finn den inverse matrisen:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Løsning. Vi komponerer den vedlagte matrisen:

\[\venstre[ \begin(matrise)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Siden den siste kolonnen i den opprinnelige matrisen er fylt med enere, trekker du den første raden fra resten:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \right]\begin(matrise) \downarrow \\ -1 \\ -1 \\\end(matrise)\to \\ & \to \venstre [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Det er ingen flere enheter, bortsett fra den første linjen. Men vi rører den ikke, ellers vil de nylig fjernede enhetene begynne å "multipiseres" i den tredje kolonnen.

Men vi kan trekke den andre linjen to ganger fra den siste - vi får en enhet i nedre venstre hjørne:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right]\begin(matrise) \ \\ \nedoverpil \\ -2 \\\end(matrise)\to \\ & \venstre [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Nå kan vi trekke den siste raden fra den første og to ganger fra den andre - på denne måten vil vi "nulle ut" den første kolonnen:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrise) -1 \\ -2 \\ \uparrow \\\end(matrise)\to \\ & \ til \venstre[ \begin(matrise)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Multipliser den andre raden med −1 og trekk den 6 ganger fra den første og legg til 1 gang til den siste:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrise) \ \\ \venstre| \cdot \left(-1 \right) \right. \\ \ \\\end(matrise)\to \\ & \to \venstre[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrise) -6 \\ \updownarrow \\ +1 \\\end (matrise)\to \\ & \to \venstre[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(align)\]

Det gjenstår bare å bytte linje 1 og 3:

\[\venstre[ \begin(matrise)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(array) \right]\]

Klar! Til høyre er den nødvendige inverse matrisen.

Svar. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

En oppgave. Finn den inverse matrisen:

\[\venstre[ \begin(matrise) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matrise) \right]\]

Løsning. Igjen komponerer vi den vedlagte:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

La oss låne litt, bekymre oss for hvor mye vi må telle nå ... og begynne å telle. Til å begynne med "nuller" vi den første kolonnen ved å trekke rad 1 fra rad 2 og 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\begin(matrise) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrise)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Vi observerer for mange "minus" i linje 2-4. Multipliser alle tre radene med −1, og brenn deretter ut den tredje kolonnen ved å trekke rad 3 fra resten:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(matrise) \right]\begin(matrise) \ \\ \venstre| \cdot \left(-1 \right) \right. \\ \venstre| \cdot \left(-1 \right) \right. \\ \venstre| \cdot \left(-1 \right) \right. \\\end(matrise)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (matrise) \right]\begin(matrise) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrise)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Nå er det på tide å "steke" den siste kolonnen i den opprinnelige matrisen: trekk rad 4 fra resten:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array ) \right]\begin(matrise) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrise)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Siste kast: "brenn ut" den andre kolonnen ved å trekke fra rad 2 fra rad 1 og 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matrise) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrise)\to \\ & \to \venstre[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Og igjen, identitetsmatrisen til venstre, så den omvendte til høyre. :)

Svar. $\left[ \begin(matrise) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrise) \right]$

Definisjon 1: En matrise kalles degenerert hvis determinanten er null.

Definisjon 2: En matrise kalles ikke-singular hvis determinanten ikke er lik null.

Matrise "A" kalles invers matrise, hvis betingelsen A*A-1 = A-1 *A = E (identitetsmatrise) er oppfylt.

En kvadratisk matrise er inverterbar bare hvis den er ikke-singular.

Skjema for å beregne den inverse matrisen:

1) Beregn determinanten til matrisen "A" if ∆ A = 0, da eksisterer ikke den inverse matrisen.

2) Finn alle algebraiske komplementer til matrisen "A".

3) Lag en matrise av algebraiske addisjoner (Aij )

4) Transponer matrisen av algebraiske komplementer (Aij )T

5) Multipliser den transponerte matrisen med den resiproke av determinanten til denne matrisen.

6) Kjør en sjekk:

Ved første øyekast kan det virke som om det er vanskelig, men faktisk er alt veldig enkelt. Alle løsninger er basert på enkle aritmetiske operasjoner, det viktigste når du løser er ikke å bli forvirret med tegnene "-" og "+", og ikke miste dem.

La oss nå bestemme sammen praktisk oppgave, beregner den inverse matrisen.

Oppgave: finn den inverse matrisen "A", vist på bildet nedenfor:

Vi løser alt nøyaktig som angitt i planen for beregning av den inverse matrisen.

1. Det første du må gjøre er å finne determinanten til matrisen "A":

Forklaring:

Vi har forenklet vår determinant ved å bruke hovedfunksjonene. Først la vi til 2. og 3. rad elementene i den første raden, multiplisert med ett tall.

For det andre endret vi 2. og 3. kolonne av determinanten, og i henhold til egenskapene endret vi tegnet foran den.

For det tredje tok vi ut fellesfaktoren (-1) på den andre raden, og endret dermed tegnet igjen, og det ble positivt. Vi forenklet også linje 3 på samme måte som helt i begynnelsen av eksemplet.

Vi har en trekantet determinant, der elementene under diagonalen er lik null, og ved egenskap 7 er den lik produktet av elementene i diagonalen. Som et resultat fikk vi ∆ A = 26, derfor eksisterer den inverse matrisen.

A11 = 1*(3+1) = 4

A12 \u003d -1 * (9 + 2) \u003d -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Neste trinn er å kompilere en matrise fra de resulterende tilleggene:

5. Vi multipliserer denne matrisen med den resiproke av determinanten, det vil si med 1/26:

6. Vel, nå trenger vi bare å sjekke:

Under verifiseringen mottok vi en identitetsmatrise, derfor ble avgjørelsen tatt helt riktig.

2 måter å beregne den inverse matrisen på.

1. Elementær transformasjon av matriser

2. Invers matrise gjennom en elementær omformer.

Elementær matrisetransformasjon inkluderer:

1. Multiplisere en streng med et tall som ikke er null.

2. Legge til en linje på en annen linje, multiplisert med et tall.

3. Bytte radene i matrisen.

4. Ved å bruke en kjede av elementære transformasjoner får vi en annen matrise.

MEN -1 = ?

1. (A|E) ~ (E|A -1 )

2. A -1*A=E

Tenk på det praktisk eksempel med reelle tall.

Trening: Finn den inverse matrisen.

Løsning:

La oss sjekke:

En liten avklaring på løsningen:

Vi byttet først rad 1 og 2 i matrisen, deretter multipliserte vi den første raden med (-1).

Etter det ble den første raden multiplisert med (-2) og lagt til den andre raden i matrisen. Så multipliserte vi den andre raden med 1/4.

siste trinn transformasjoner var multiplikasjonen av den andre raden med 2 og addisjonen fra den første. Som et resultat har vi en identitetsmatrise til venstre, derfor er den inverse matrisen matrisen til høyre.

Etter å ha sjekket, var vi overbevist om riktigheten av løsningen.

Som du kan se, er det veldig enkelt å beregne den inverse matrisen.

Som avslutning på dette foredraget vil jeg også vie litt tid til egenskapene til en slik matrise.

Metoder for å finne den inverse matrisen, . Tenk på en kvadratisk matrise

Angi Δ = det A.

Kvadratmatrisen A kalles ikke-degenerert, eller ikke-spesiell hvis determinanten er ikke-null, og degenerert, eller spesiell, hvisΔ = 0.

En kvadratisk matrise B eksisterer for en kvadratisk matrise A av samme rekkefølge hvis produktet deres A B = B A = E, der E er identitetsmatrisen av samme rekkefølge som matrisene A og B.

Teorem . For at matrisen A skal ha en invers matrise, er det nødvendig og tilstrekkelig at dens determinant ikke er null.

Invers matrise til matrise A, betegnet med A- 1 så B = A - 1 og beregnes med formelen

, (1)

hvor А i j - algebraiske komplementer av elementer a i j av matrise A..

Beregning A -1 ved formel (1) for matriser høy orden veldig arbeidskrevende, så i praksis er det praktisk å finne A -1 ved å bruke metoden for elementære transformasjoner (EP). Enhver ikke-singular matrise A kan reduseres med EP av bare kolonner (eller bare rader) til identitetsmatrisen E. Hvis EP-ene utført på matrisen A brukes i samme rekkefølge på identitetsmatrisen E, blir resultatet en invers matrise. Det er praktisk å utføre en EP på matrisene A og E samtidig, og skrive begge matrisene side om side gjennom linjen. Vi bemerker nok en gang at når man søker etter den kanoniske formen til en matrise, for å finne den, kan man bruke transformasjoner av rader og kolonner. Hvis du trenger å finne den inverse matrisen, bør du bare bruke rader eller bare kolonner i transformasjonsprosessen.

Eksempel 2.10. For matrise finn A -1.

Løsning.Vi finner først determinanten til matrisen A
så den inverse matrisen eksisterer, og vi kan finne den ved formelen: , hvor A i j (i,j=1,2,3) - algebraiske komplementer av elementene a i j av den opprinnelige matrisen.

Hvor .

Eksempel 2.11. Bruk metoden for elementære transformasjoner, finn A -1 for matrisen: A=.

Løsning.Vi tildeler en identitetsmatrise av samme rekkefølge til den opprinnelige matrisen til høyre: . Ved hjelp av elementære kolonnetransformasjoner reduserer vi venstre "halvdel" til identiteten, og utfører samtidig nøyaktig slike transformasjoner på høyre matrise.
For å gjøre dette, bytt den første og andre kolonnen: ~ . Vi legger den første til den tredje kolonnen, og den første multiplisert med -2 til den andre: . Fra den første kolonnen trekker vi den doble andre, og fra den tredje - den andre multiplisert med 6; . La oss legge til den tredje kolonnen til den første og andre: . Multipliser den siste kolonnen med -1: . Den kvadratiske matrisen til høyre for den vertikale stolpen er den inverse matrisen til den gitte matrisen A. Så,
.

For enhver ikke degenerert matrise Og det eksisterer og dessuten en unik matrise A -1 slik at

A*A -1 =A -1 *A = E,

hvor E er identitetsmatrisen av samme rekkefølge som A. Matrisen A -1 kalles den inverse av matrise A.

Hvis noen har glemt, i identitetsmatrisen, bortsett fra diagonalen fylt med enere, er alle andre posisjoner fylt med nuller, et eksempel på en identitetsmatrise:

Finne den inverse matrisen ved hjelp av adjoint matrise-metoden

Den inverse matrisen er definert av formelen:

hvor A ij - elementer a ij .

De. For å beregne inversen til en matrise, må du beregne determinanten til denne matrisen. Finn deretter algebraiske tillegg for alle elementene og lag en ny matrise fra dem. Deretter må du transportere denne matrisen. Og del hvert element i den nye matrisen med determinanten til den opprinnelige matrisen.

La oss se på noen få eksempler.

Finn A -1 for matrise

Løsning Finn A -1 ved hjelp av adjoint matrise-metoden. Vi har det A = 2. Finn de algebraiske komplementene til elementene i matrisen A. I denne saken de algebraiske komplementene til matriseelementene vil være de tilsvarende elementene i selve matrisen, tatt med et tegn i samsvar med formelen

Vi har A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Vi danner den adjunkte matrisen

Vi transporterer matrisen A*:

Vi finner den inverse matrisen ved formelen:

Vi får:

Bruk adjoint matrise-metoden for å finne A -1 if

Løsning: Først og fremst beregner vi den gitte matrisen for å sikre at den inverse matrisen eksisterer. Vi har

Her har vi lagt til elementene i den andre raden elementene i den tredje raden, multiplisert tidligere med (-1), og deretter utvidet determinanten med den andre raden. Siden definisjonen av denne matrisen er forskjellig fra null, eksisterer matrisen invers til den. For å konstruere den tilstøtende matrisen finner vi de algebraiske komplementene til elementene i denne matrisen. Vi har

I henhold til formelen

vi transporterer matrisen A*:

Deretter i henhold til formelen

Finne den inverse matrisen ved hjelp av metoden for elementære transformasjoner

I tillegg til metoden for å finne den inverse matrisen, som følger av formelen (metoden til den tilhørende matrisen), finnes det en metode for å finne den inverse matrisen, kalt metoden for elementære transformasjoner.

Elementære matrisetransformasjoner

Følgende transformasjoner kalles elementære matrisetransformasjoner:

1) permutasjon av rader (kolonner);

2) multiplisere en rad (kolonne) med et tall som ikke er null;

3) legge til elementene i en rad (kolonne) de tilsvarende elementene i en annen rad (kolonne), tidligere multiplisert med et visst tall.

For å finne matrisen A -1 konstruerer vi rektangulær matrise B = (A|E) av ordrer (n; 2n), som tildeler til matrisen A til høyre identitetsmatrisen E gjennom delelinjen:

Tenk på et eksempel.

Bruk metoden for elementære transformasjoner, finn A -1 if

Løsning. Vi danner matrisen B:

Angi radene i matrisen B til α 1 , α 2 , α 3 . La oss utføre følgende transformasjoner på radene i matrisen B.