Regelen sier at hvis funksjonene f(x) og g(x) har følgende sett med betingelser:

så er det . Dessuten er teoremet også sant for andre baser (beviset vil bli gitt for den angitte).

Historie

En metode for å avsløre denne typen usikkerhet ble publisert av Lopital i hans arbeid "Analysis of infinitesimals", publisert i året. I forordet til dette verket påpeker Lopital at han brukte oppdagelsene til Leibniz og Bernoulli-brødrene uten å nøle og «har ingenting imot at de viser opphavsretten til hva de måtte ønske». Johann Bernoulli gjorde krav på hele L'Hospitals arbeid, og spesielt etter L'Hospitals død publiserte han et verk under den bemerkelsesverdige tittelen "Forbedring av metoden min publisert i Infinitesimal Analysis for å bestemme verdien av en brøk, telleren og nevneren hvorav noen ganger forsvinner", .

Bevis

Forholdet mellom infinitesimals

La oss bevise teoremet for tilfellet når grensene for funksjonene er lik null (den såkalte usikkerheten til formen ).

Siden vi ser på funksjoner f og g bare i det høyre punkterte semine-området til punktet en, kan vi kontinuerlig redefinere dem på dette punktet: la f(en) = g(en) = 0 . La oss ta noen x fra semine-kvarteret under vurdering og bruk Cauchy-teoremet på segmentet. Ved dette teoremet får vi:

,

men f(en) = g(en) = 0 , derfor .

src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> for endegrense og src="/pictures/wiki/files/101/e8b2f2b88619474c81400 for border"6740d">p3d3d4c81400d"6740d"6d3d3d" ,

som er definisjonen av grensen for forholdet mellom funksjoner.

Forholdet mellom uendelig stor

La oss bevise teoremet for usikkerheter i formen.

La, for det første, grensen for forholdet mellom derivater være begrenset og lik EN. Så, mens du strever x til en til høyre kan denne relasjonen skrives som EN+ a, hvor a - (1). La oss skrive denne tilstanden:

.

La oss fikse t fra segmentet og bruk Cauchy-teoremet på alle x fra segmentet:

, som kan føre til neste type: .

Til x, nær nok til en, uttrykket gir mening; grensen for den første faktoren på høyre side lik en(fordi f(t) og g(t) er konstanter, og f(x) og g(x) har en tendens til uendelig). Derfor er denne faktoren lik 1 + β, hvor β er en uendelig liten funksjon som x til en til høyre. Vi skriver ut definisjonen av dette faktum ved å bruke samme verdi som i definisjonen for α :

.

Vi har funnet ut at forholdet mellom funksjoner kan representeres på formen (1 + β)( EN+ α), og . For enhver gitt kan man finne slik at modulen til differansen mellom forholdene mellom funksjonene og EN var mindre, noe som betyr at grensen for forholdet mellom funksjoner egentlig er lik EN .

Hvis grensen EN er uendelig (la oss si det er lik pluss uendelig), da

(x))(g"(x))>2M)" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">.

I definisjonen av β vil vi ta ; den første faktoren på høyre side vil være større enn 1/2 når x, nær nok til en, og deretter src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">.

For andre baser er bevisene lik de som er gitt.

Eksempler

(Bare hvis telleren og nevneren BEGGE har en tendens til enten 0 ; eller ; eller .)

Wikimedia Foundation. 2010 .

Se hva "L'Hopital-regelen" er i andre ordbøker:

Historisk ukorrekt navn på en av de grunnleggende reglene for avsløring av usikkerheter. L. p. ble funnet av I. Bernoulli og rapportert av ham til G. L'Hopital (Se L'Hopital), som publiserte denne regelen i 1696. Se Ubestemte uttrykk ... Stor sovjetisk leksikon

Avsløring av usikkerheter i formen ved å redusere grensen for forholdet mellom funksjoner til grensen for forholdet mellom derivatene av funksjonene som vurderes. Så, for tilfelle når reelle funksjoner f og g er definert i et punktert høyreområde til et numerisk punkt ... ... Matematisk leksikon

Bernoulli L'Hospitals regel er en metode for å finne grensene for funksjoner, og avsløre usikkerheter i formen u. Teoremet som begrunner metoden sier at under visse forhold er grensen for forholdet mellom funksjoner lik grensen for forholdet mellom deres deriverte. ... ... Wikipedia

I matematisk analyse er L'Hopitals regel en metode for å finne grensene for funksjoner, avsløre usikkerheter i formen 0 / 0 og. Teoremet som begrunner metoden sier at under visse forhold er grensen for forholdet mellom funksjoner lik grensen ... ... Wikipedia

I matematisk analyse er L'Hopitals regel en metode for å finne grensene for funksjoner, avsløre usikkerheter i formen 0 / 0 og. Teoremet som begrunner metoden sier at under visse forhold er grensen for forholdet mellom funksjoner lik grensen ... ... Wikipedia

Avhengighet av koordinater på tid ved flytting materiell poeng i fly

Bestem modulhastighet (

A. Modulen til hastigheten til et materialpunkt fra tid uttrykkes med formelen:

B. . Modulen for akselerasjon av et materialpunkt fra tid uttrykkes med formelen:

Disse ligningene beskriver bevegelsen til et materialpunkt med konstant akselerasjon

Satellitten roterer rundt jorden i en sirkulær bane i en høyde

En satellitt som beveger seg i en sirkulær bane er utsatt for tyngdekraften

Denne formelen kan forenkles som følger. På en kroppsvekt

På denne måten, linjehastighet satellitt er

og vinkelhastigheten

Begge ballene som vurderes i oppgaven danner et lukket system og i etuiet elastisk støt både systemets momentum og den mekaniske (kinetiske) energien er bevart. La oss skrive ned begge bevaringslovene (ta hensyn til immobiliteten til den andre ballen før støtet):

Dermed reduserte den innfallende (første) ballen som et resultat av støtet sin hastighet fra 1,05 m/s til 0,45 m/s, selv om den fortsatte å bevege seg i samme retning, og den tidligere stasjonære (andre) ballen oppnådde en hastighet som var lik. til 1,5 m/s og nå beveger begge kulene seg i samme rette linje og i samme retning.

Siden massen til gassen i sylinderen endres, kan ikke start- og slutttilstanden til gassen i sylinderen relateres verken av Boyle-Mariotte-loven eller Charles-loven. Hvis gassen i sylinderen endres ved utjevning, vil start- og slutttilstander for gassen i sylinderen kan ikke relateres av Boyle-Mariotte-loven. Hver stat skriver Mendeleev-Clapeyron-ligningen

Hvordan finne grensen for en funksjon uten å bruke lopitalregelen

Systemversjon:
7.47 (16.04.2018)

Generelle nyheter:
13.04.2018, 10:33

Siste spørsmål:
26.07.2018, 15:23

Siste svar:
27.07.2018, 13:48

SEKSJON Matematikk

Konsultasjoner og problemløsning innen algebra, geometri, analyse, diskret matematikk.

De beste ekspertene i denne delen

Hallo! Jeg har problemer med dette spørsmålet:

Finn grensen for en funksjon uten å bruke L'Hopitals regel

lim (2x+3) [ ln (x+2) - ln x ] (under lim står det "x har en tendens til uendelig")

Det var flere eksempler på begrensninger i oppgaven, men denne forvirret. Jeg vet ikke hvordan jeg skal løse det. Kanskje på en eller annen måte bruke den andre fantastiske grensen, men hvordan (bare denne tanken kommer til hodet)?

La meg bare spørre i det samme spørsmålet om en slik uttalelse av problemet finner sted (hvis den gjør det, vil jeg legge det ut senere som et betalt spørsmål): Bruk Taylor-formelen med en restledd i Lagrange-formen på funksjonen, beregn verdien med en nøyaktighet på 0,001; a = 0,29.
Her skjønner jeg ikke hvilken funksjon? Den er ikke satt (?), oppgaven høres akkurat slik jeg skrev den ned. Kanskje du kan ta funksjonen selv, men hvilken?

Status: Høring avsluttet

Hei Aleksandrkib!
Det er den andre du må bruke! For å starte, la oss forenkle:
lim (2x+3) [ ln (x+2) - ln x ] = lim (2x+3) ln ((x+2)/x) = lim (2x+3) ln (1+2/x) = lim ln ((1+2/x)^(2x+3)) = lim ln ((1+2/x)^2x)+lim ln ((1+2/x)^3) [den andre grensen er null , siden 2/x har en tendens til null og ln 1 = 0]
La oss gjøre endringen y = x/2, så lim ln ((1+2/x)^2x) = 4 lim ln ((1+1/y)^y) = 4 * ln e =4. Svar: 4.

Det må være en funksjon.

Send meldinger
moderatorer kan
kun medlemmer av portalen.
LOGG PÅ PORTALEN »
registrering "

L'Hopitals regel: teori og eksempler på løsninger

L'Hopitals regel og avsløring av usikkerheter

Avsløringen av usikkerheter av formen 0/0 eller ∞/∞ og noen andre usikkerheter som oppstår når man beregner grensen for forholdet mellom to uendelig store eller uendelig store funksjoner er sterkt forenklet ved å bruke L'Hopitals regel (faktisk to regler og kommentarer til dem ).

essens regler for L'Hospital er at i det tilfellet når beregningen av grensen for forholdet mellom to uendelig små eller uendelig store funksjoner gir usikkerheter på formen 0/0 eller ∞/∞, kan grensen for forholdet mellom to funksjoner erstattes med grensen for forholdet mellom deres derivater og dermed et visst resultat kan oppnås.

La oss gå videre til formuleringen av L'Hopitals regler.

L'Hopitals regel for tilfellet av grensen for to uendelig små verdier. Hvis funksjoner f(x) og g(x en en, og i dette nabolaget g‘(x en lik hverandre og lik null

(),

da er grensen for forholdet mellom disse funksjonene lik grensen for forholdet til deres deriverte

().

L'Hôpitals regel for tilfellet med grensen på to uendelig store mengder. Hvis funksjoner f(x) og g(x) er differensierbare i noen områder av punktet en, med mulig unntak av punktet en, og i dette nabolaget g‘(x)≠0 og hvis og hvis grensene for disse funksjonene som x har en tendens til verdien av funksjonen i punktet en lik hverandre og lik uendelig

(),

Med andre ord, for usikkerheter av formen 0/0 eller ∞/∞, er grensen for forholdet mellom to funksjoner lik grensen for forholdet mellom deres deriverte, hvis sistnevnte eksisterer (endelig eller uendelig).

Merknader.

1. L'Hopitals regler gjelder også når funksjonene f(x) og g(x) er ikke definert på x = en.

2. Hvis, når du beregner grensen for forholdet mellom derivater av funksjoner f(x) og g(x) kommer vi igjen til en usikkerhet på formen 0/0 eller ∞/∞, da bør L'Hopitals regler brukes gjentatte ganger (minst to ganger).

3. L'Hopitals regler gjelder også når argumentet for funksjoner (x) har en tendens til ikke å endelig nummer en, og til det uendelige ( x → ∞).

Usikkerheter av andre typer kan også reduseres til usikkerheter av typen 0/0 og ∞/∞.

Avsløring av usikkerheter av typene "null delt på null" og "uendelig delt på uendelig"

Eksempel 1

x=2 fører til en ubestemthet på formen 0/0. Derfor, den deriverte av hver funksjon og vi får

I telleren ble den deriverte av polynomet beregnet, og i nevneren den deriverte av komplekset logaritmisk funksjon. Før det siste likhetstegnet ble den vanlige grensen beregnet, og erstattet en toer i stedet for en x.

Eksempel 2 Beregn grensen for forholdet mellom to funksjoner ved å bruke L'Hospitals regel:

Eksempel 3 Beregn grensen for forholdet mellom to funksjoner ved å bruke L'Hospitals regel:

Løsning. Bytte inn gitt funksjon verdier x=0 fører til en ubestemthet på formen 0/0. Derfor beregner vi de deriverte av funksjonene i telleren og nevneren og får:

Eksempel 4 Regne ut

Løsning. Å erstatte verdien av x lik pluss uendelig i en gitt funksjon fører til en ubestemthet av formen ∞/∞. Derfor bruker vi L'Hopitals regel:

Kommentar. La oss gå videre til eksempler der L'Hopital-regelen må brukes to ganger, det vil si for å komme til grensen for forholdet mellom de andre derivertene, siden grensen for forholdet til de første derivertene er en formusikkerhet 0/0 eller ∞/∞.

Eksempel 5 Beregn grensen for forholdet mellom to funksjoner ved å bruke L'Hospitals regel:

Her brukes L'Hospitals regel to ganger, siden både grensen for forholdet mellom funksjoner og grensen for forholdet mellom derivater gir en usikkerhet på formen ∞/∞.

Eksempel 6 Regne ut

Her brukes L'Hospitals regel to ganger, siden både grensen for forholdet mellom funksjoner og grensen for forholdet mellom derivater gir en usikkerhet på formen 0/0.

Eksempel 7 Regne ut

Her brukes L'Hopitals regel to ganger, siden både grensen for forholdet mellom funksjoner og grensen for forholdet mellom deriverte først gir en usikkerhet på formen - ∞/∞, og deretter en usikkerhet på formen 0/0.

Eksempel 8 Regne ut

Her brukes L'Hospitals regel to ganger, siden både grensen for forholdet mellom funksjoner og grensen for forholdet mellom derivater først gir en usikkerhet på formen ∞/∞, og deretter en usikkerhet på formen 0/0.

Bruk L'Hopitals regel selv og se deretter løsningen

Eksempel 9 Regne ut

Clue. Her må du puste litt mer enn vanlig på forvandlingen av uttrykk under grensetegnet.

Eksempel 10 Regne ut

.

Clue. Her vil L'Hopitals regel måtte brukes tre ganger.

Avsløring av usikkerheter i formen "null multiplisert med uendelig"

Eksempel 11. Regne ut

(her har vi transformert usikkerheten til formen 0∙∞ til formen ∞/∞, siden

og deretter brukt L'Hopitals regler).

Eksempel 12. Regne ut

.

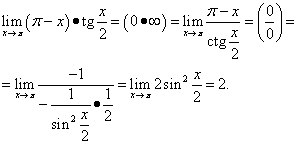
Dette eksemplet bruker den trigonometriske identiteten.

Avsløring av usikkerheter av typene "null til null", "uendelig til null potens" og "en til uendelig potens"

Usikkerheter i formen, eller reduseres vanligvis til formen 0/0 eller ∞/∞ ved å bruke logaritmen til en funksjon av formen

For å beregne grensen for et uttrykk bør man bruke logaritmisk identitet, et spesialtilfelle som også er egenskapen til logaritmen .

Ved å bruke den logaritmiske identiteten og kontinuitetsegenskapen til funksjonen (for å gå utover fortegnet på grensen), bør grensen beregnes som følger:

Hver for seg skal man finne grensen for uttrykket i eksponenten og bygge e i funnet grad.

Eksempel 13

.

.

Eksempel 14 Regn ut ved å bruke L'Hopitals regel

.

.

Eksempel 15 Regn ut ved å bruke L'Hopitals regel

Regn ut grensen for uttrykket i eksponenten

.

Avsløring av usikkerheter i formen "uendelig minus uendelig"

Dette er tilfeller der beregningen av grensen for forskjellen av funksjoner fører til usikkerheten "uendelig minus uendelig": .

Beregningen av en slik grense etter L'Hopitals regel i generelt syn følgende:

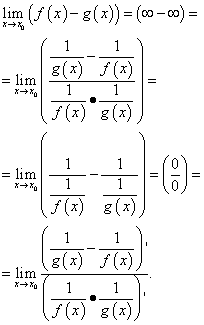
Disse transformasjonene resulterer ofte i komplekse uttrykk, derfor er det tilrådelig å bruke slike transformasjoner av forskjellen av funksjoner som reduksjon til fellesnevner, multiplikasjon og divisjon med samme tall, bruk trigonometriske identiteter etc.

Eksempel 16 Regn ut ved å bruke L'Hopitals regel

.

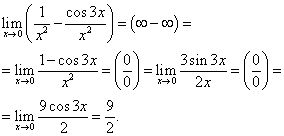
Eksempel 17. Regn ut ved å bruke L'Hopitals regel

.

Beregn grenser ved å bruke lopitalregelen

Usikkerhet motstår heller ikke å bli til eller:

Regler for L'Hospital

Vi fortsetter å utvikle emnet, som ble kastet til oss av medlemmet av Paris Academy of Sciences, Marquis Guillaume Francois de Lopital. Artikkelen får en uttalt praktisk fargelegging og i en ganske vanlig oppgave kreves det:

For ikke å krympe, beregner vi grensen for indikatoren separat:

En annen papuan gir også opp før formelen. I dette tilfellet:

L'Hopitals regler er en veldig kraftig metode som lar deg raskt og effektivt eliminere disse usikkerhetene, det er ingen tilfeldighet at i samlinger av problemer, i tester, tester, blir det ofte funnet et stabilt stempel: "beregn grensen, uten å bruke L'Hopitals regel". Dedikert med fet skrift krav er mulig med god samvittighet tilordne og til enhver leksjonsgrense Grenser. Løsningseksempler, Bemerkelsesverdige grenser. Begrens løsningsmetoder, Bemerkelsesverdige ekvivalenser, hvor usikkerheten "null til null" eller "uendelig til uendelig" oppstår. Selv om oppgaven er formulert kort - "beregn grensene", så er det implisitt forstått at du vil bruke alt du liker, men ikke reglene til L'Hospital.

Metamorfosene fortsetter, nå har usikkerheten «null til null» kommet ut. I prinsippet kan du bli kvitt cosinus ved å indikere at den har en tendens til enhet. Men en klok strategi er å sikre at ingen kommer til bunns i noe. Derfor bruker vi umiddelbart L'Hopital-regelen, som kreves av tilstanden til problemet:

En lignende oppgave for en uavhengig løsning:

Som du kan se, førte differensieringen av telleren og nevneren oss til svaret med en halv omgang: vi fant to enkle derivater, erstattet "to" i dem, og det viste seg at usikkerheten forsvant sporløst!

Beregn grensen for en funksjon ved å bruke L'Hopitals regel

På sin side trekkes drikkekamerater og mer eksotiske kamerater opp til lyset. Transformasjonsmetoden er enkel og standard:

Det betraktede eksemplet er ødelagt og gjennom fantastiske grenser , en lignende sak diskuteres på slutten av artikkelen Complex limits.

Jeg tar umiddelbart forbehold om at reglene vil bli gitt i en kortfattet "praktisk" form, og hvis du må bestå teorien, anbefaler jeg at du slår til læreboken for mer strenge beregninger.

6) Gjelder siste regel informasjon til den andre fantastiske grensen

Opplysningene om usikkerhet er redusert til de tidligere omtalte usikkerhetene. Hvis, og ved, bruk transformasjonen

uendelig eller null med null er anvendelsen av L'Hopitals regel: grensen for forholdet mellom to

Ved de tre siste usikkerhetene må transformasjoner benyttes

5) Det er en ubestemthet av formen uendelig til uendelig.

uendelig små eller to uendelig store funksjoner er lik grensen for forholdet mellom deres deriverte,

3) Gitt usikkerheten, bruk den forrige regelen

Beregning av grenser etter L'Hopitals regel

En effektiv måte å beregne grensene for funksjoner som har singulariteter av typen infinity på

Løsning. 1) Ved substitusjon fastslår vi at vi har en usikkerhet av formen null med null. Å bli kvitt

Igjen fikk vi usikkerheten til skjemaet og bruker L'Hospitals regel på nytt

2) Som i forrige eksempel har vi usikkerhet. Etter L'Hopitals regel finner vi

Anvendelsen av L'Hopitals regel viste alle mulighetene for å avsløre usikkerheter.

Tallet er valgt på en slik måte at likhet (1) er oppfylt og derfor . Altså for en funksjon på intervallet

I nærheten av punktet x 0, dvs. på (x 0 ,x), er betingelsene til Cauchy-setningen oppfylt for funksjonene f(x) og g(x). Derfor er det et punkt сО(x 0 , x) slik at

L'Hopitals regel

En situasjon er imidlertid mulig når funksjonen vil ha et ekstremum ved punktet x 0 i tilfellet der den deriverte ikke eksisterer.

La funksjonen være n ganger differensierbar i et nabolag til punktet x 0. La oss finne et polynom med grad som ikke er høyere enn n-1, slik at

La funksjonene f(x) og g(x) være kontinuerlige og differensierbare i et eller annet område av punktet x 0 , bortsett fra selve punktet x 0. La,. Så hvis det er en grense for forholdet mellom derivater av funksjoner, så er det en grense for forholdet til funksjonene selv, og de er like med hverandre, dvs. .

Konklusjon: eksponentiell funksjon(y=a n) vokser alltid raskere enn potensloven (y=x n).

Som et eksempel på anvendelsen av Maclaurin-formelen, bestemmer vi antall ledd i utvidelsen av en funksjon i form av formelå beregne verdien med en nøyaktighet på 0,001 for enhver x fra intervallet [-1,1].

Definisjon: Funksjonen kalles ikke-avtagende (ikke-økende) til (a;b) hvis for noen x 1 Skrevet i Nyttige artikler

Finne grensen for en funksjon ved et punkt i henhold til L'Hopitals regel

Å finne grensen for en funksjon, i henhold til L'Hopitals regel, avslører usikkerheter på formen 0/0 og ∞/∞.

Kalkulatoren nedenfor finner grensen for funksjonen i henhold til L'Hospital-regelen (gjennom de deriverte av telleren og nevneren). Se regelbeskrivelse nedenfor.

Begrensning av en funksjon ved et punkt - L'Hopitals regel

Gyldige operasjoner: + - / * ^ Konstanter: pi Funksjoner: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

L'Hopitals regel

Hvis følgende betingelser er oppfylt:

• grensene for funksjonene f(x) og g(x) er lik hverandre og lik null eller uendelig:
  eller;
• funksjonene g(x) og f(x) er differensierbare i det punkterte nabolaget a;
• den deriverte av funksjonen g(x) er ikke lik null i det punkterte nabolaget a
• og det er en grense for forholdet mellom den deriverte f(x) og den deriverte g(x):

Da er det en grense for forholdet mellom funksjonene f(x) og g(x):
,

Og det er lik grensen for forholdet mellom den deriverte av funksjonen f(x) og den deriverte av funksjonen g(x):

Formelen tillater bruk av tallet pi (pi), eksponenten (e), følgende matematiske operatorer:

+ - tillegg
— - subtraksjon
* - multiplikasjon
/ - divisjon
^ - eksponentiering

og følgende funksjoner:

sqrt - kvadratrot

rot s- graders rot s, for eksempel rot3(x) er kuberoten

exp - e til spesifisert effekt

lb - base 2 logaritme

lg - base 10 logaritme

ln- naturlig logaritme(basert på e)

Logg s- grunnlogaritme s, for eksempel log7(x) - base 7 logaritme

sin - sinus

cos - kosinus

tg - tangent

ctg - cotangens

sek - sekant

cosec - cosecant

arcsin - arcsine

arccos - arc cosinus

arctg - buetangens

arcctg - buetangens

arcsec - arcsecant

arccosec - arccosecant

versin - versinus

vercos - coversine

haversin - haversinus

exsec - exsecant

excsc - excosecant

sh - hyperbolsk sinus

ch - hyperbolsk cosinus

th - hyperbolsk tangent

cth - hyperbolsk kotangens

sech - hyperbolsk sekant

csch - hyperbolsk cosecant

abs- absolutt verdi(modul)

sgn - signum (tegn)

• Lei en Gazelle eller Sable Van uten sjåfør Gazelle-Business, 1 sjåfør + 2 passasjerer. Kropp: 3 m. lengde, 2 m. høyde, butka. Volumet av kuben 10.5. Motor: UMZ-4216 (bensin), euro-4, 106,8 […]
• Opplysninger om innbetaling av skatter og avgifter i 2017-2018 Opplysninger om innbetaling av skatt i 2017-2018 er en integrert del av enhver betaling. Fyll ut betalingsordren riktig [...]
• Prosedyren for behandling av forbundsrådet av den vedtatte Statsdumaen føderal lov(Artikkel 103–110) Artikkel 103. Vedtakelse av en føderal lov for behandling av […]
• Strafferett. Generell del Strafferettsregel En strafferettsregel er en atferdsregel fastsatt av staten som stiller med deltakere PR […]
• Størrelsen på straffen for forsinkelse på et boliglån er begrenset 24. juli trer en lov i kraft som begrenser straffens størrelse for manglende oppfyllelse eller utilbørlig oppfyllelse av […]
• Drap med skjerpede omstendigheter straff I samsvar med gjeldende straffelov, er enkelt drap (del 1 av artikkel 105 i den russiske føderasjonens straffelov) «straffes med fengsel for en […]

Opplysninger om usikkerheter av formen 0/0 eller ∞/∞ og noen andre usikkerheter som oppstår i beregningen grense forholdet mellom to uendelig store eller uendelig store funksjoner er sterkt forenklet ved hjelp av L'Hospitals regel (egentlig to regler og bemerkninger om dem).

essens regler for L'Hospital er at i tilfellet når beregningen av grensen for forholdet mellom to uendelig små eller uendelig store funksjoner gir usikkerheter på formen 0/0 eller ∞/∞, kan grensen for forholdet mellom to funksjoner erstattes med grensen for forholdet mellom deres derivater og dermed få et visst resultat.

La oss gå videre til formuleringen av L'Hopitals regler.

L'Hopitals regel for tilfellet av grensen for to uendelig små verdier. Hvis funksjoner f(x) og g(x enen, og i dette nabolaget g"(x en lik hverandre og lik null

().

L'Hôpitals regel for tilfellet med grensen på to uendelig store mengder. Hvis funksjoner f(x) og g(x) er differensierbare i noen områder av punktet en, med mulig unntak av punktet en, og i dette nabolaget g"(x)≠0 og hvis og hvis grensene for disse funksjonene som x har en tendens til verdien av funksjonen i punktet en lik hverandre og lik uendelig

(),

da er grensen for forholdet mellom disse funksjonene lik grensen for forholdet til deres deriverte

().

Med andre ord, for usikkerheter av formen 0/0 eller ∞/∞, er grensen for forholdet mellom to funksjoner lik grensen for forholdet mellom deres deriverte, hvis sistnevnte eksisterer (endelig eller uendelig).

Merknader.

1. L'Hopitals regler gjelder også når funksjonene f(x) og g(x) er ikke definert på x = en.

2. Hvis, når du beregner grensen for forholdet mellom derivater av funksjoner f(x) og g(x) kommer vi igjen til en usikkerhet på formen 0/0 eller ∞/∞, da bør L'Hopitals regler brukes gjentatte ganger (minst to ganger).

3. L'Hopitals regler gjelder også når argumentet til funksjonene (x) har en tendens til et ikke-endelig tall en, og til det uendelige ( x → ∞).

Usikkerheter av andre typer kan også reduseres til usikkerheter av typen 0/0 og ∞/∞.

Avsløring av usikkerheter av typene "null delt på null" og "uendelig delt på uendelig"

Eksempel 1

x=2 fører til en ubestemthet på formen 0/0. Derfor, den deriverte av hver funksjon og vi får

I telleren ble den deriverte av polynomet beregnet, og i nevneren - avledet av en kompleks logaritmisk funksjon. Før siste likhetstegnet, det vanlige grense, erstatte en toer i stedet for x.

Eksempel 2 Beregn grensen for forholdet mellom to funksjoner ved å bruke L'Hospitals regel:

Løsning. Substitusjon i en gitt verdifunksjon x

Eksempel 3 Beregn grensen for forholdet mellom to funksjoner ved å bruke L'Hospitals regel:

Løsning. Substitusjon i en gitt verdifunksjon x=0 fører til en ubestemthet på formen 0/0. Derfor beregner vi de deriverte av funksjonene i telleren og nevneren og får:

Eksempel 4 Regne ut

Løsning. Å erstatte verdien av x lik pluss uendelig i en gitt funksjon fører til en ubestemthet av formen ∞/∞. Derfor bruker vi L'Hopitals regel:

Kommentar. La oss gå videre til eksempler der L'Hopital-regelen må brukes to ganger, det vil si for å komme til grensen for forholdet mellom de andre derivertene, siden grensen for forholdet til de første derivertene er en usikkerhet i formen 0/0 eller ∞/∞.

Bruk L'Hopitals regel selv og se deretter løsningen

Avsløring av usikkerheter i formen "null multiplisert med uendelig"

Eksempel 12. Regne ut

.

Løsning. Vi får

Dette eksemplet bruker den trigonometriske identiteten.

Avsløring av usikkerheter av typene "null til null", "uendelig til null potens" og "en til uendelig potens"

Usikkerheter i formen, eller reduseres vanligvis til formen 0/0 eller ∞/∞ ved å bruke logaritmen til en funksjon av formen

For å beregne grensen for uttrykket, bør man bruke den logaritmiske identiteten, et spesialtilfelle som er egenskapen til logaritmen .

Ved å bruke den logaritmiske identiteten og kontinuitetsegenskapen til funksjonen (for å gå utover fortegnet på grensen), bør grensen beregnes som følger:

Hver for seg skal man finne grensen for uttrykket i eksponenten og bygge e i funnet grad.

Eksempel 13

Løsning. Vi får

.

.

Eksempel 14 Regn ut ved å bruke L'Hopitals regel

Løsning. Vi får

Regn ut grensen for uttrykket i eksponenten

.

.

Eksempel 15 Regn ut ved å bruke L'Hopitals regel

Dette matematisk kalkulator online vil hjelpe deg om nødvendig beregne funksjonsgrense. Program begrense løsninger gir ikke bare svaret på problemet, det leder detaljert løsning med forklaringer, dvs. viser fremdriften til grenseberegningen.

Dette programmet kan være nyttig for elever på videregående skole allmennpedagogiske skoler som forberedelse til kontrollarbeid og eksamener, når du tester kunnskap før eksamen, foreldre til å kontrollere løsningen av mange problemer i matematikk og algebra. Eller kanskje det er for dyrt for deg å ansette en veileder eller kjøpe nye lærebøker? Eller vil du bare få det gjort så fort som mulig? hjemmelekser matte eller algebra? I dette tilfellet kan du også bruke våre programmer med en detaljert løsning.

Dermed kan du gjennomføre din egen trening og/eller trene deres yngre brødre eller søstre, mens utdanningsnivået på oppgavefeltet som løses øker.

Skriv inn et funksjonsuttrykk

Beregn grense

Det ble funnet at noen skript som trengs for å løse denne oppgaven ikke ble lastet inn, og det kan hende at programmet ikke fungerer.
Du kan ha AdBlock aktivert.
I dette tilfellet, deaktiver den og oppdater siden.

Du har deaktivert JavaScript i nettleseren din.
JavaScript må være aktivert for at løsningen skal vises.
Her er instruksjoner for hvordan du aktiverer JavaScript i nettleseren din.

Fordi Det er mange mennesker som ønsker å løse problemet, forespørselen din står i kø.
Etter noen sekunder vil løsningen vises nedenfor.
Vennligst vent sek...

Hvis du oppdaget en feil i løsningen, så kan du skrive om det i tilbakemeldingsskjemaet .
Ikke glem angi hvilken oppgave du bestemmer hva skriv inn i feltene.

Våre spill, puslespill, emulatorer:

Litt teori.

Grensen for funksjonen ved x-> x 0

La funksjonen f(x) være definert på et sett X og la punktet \(x_0 \i X \) eller \(x_0 \notin X \)

Ta fra X en sekvens av andre punkter enn x 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
konvergerer til x*. Funksjonsverdiene i punktene i denne sekvensen danner også en numerisk sekvens
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
og man kan stille spørsmålet om eksistensen av dens grense.

Definisjon. Tallet A kalles grensen for funksjonen f (x) ved punktet x \u003d x 0 (eller ved x -> x 0), hvis for en hvilken som helst sekvens (1) av verdier av argumentet x som konvergerer til x 0, forskjellig fra x 0, konvergerer den tilsvarende sekvensen (2) av verdifunksjonen til tallet A.

$$ \lim_(x\to x_0)( f(x)) = A $$

Funksjonen f(x) kan bare ha én grense ved punktet x 0. Dette følger av at sekvensen
(f(x n)) har bare én grense.

Det er en annen definisjon av grensen for en funksjon.

Definisjon Tallet A kalles grensen for funksjonen f(x) i punktet x = x 0 hvis det for et hvilket som helst tall \(\varepsilon > 0 \) eksisterer et tall \(\delta > 0 \) slik at for alle \ (x \i X, \; x \neq x_0 \) som tilfredsstiller ulikheten \(|x-x_0| Ved å bruke logiske symboler kan denne definisjonen skrives som
\((\forall \varepsilon > 0) (\eksisterer \delta > 0) (\forall x \i X, \; x \neq x_0, \; |x-x_0| Merk at ulikhetene \(x \neq x_0 , \; |x-x_0| Den første definisjonen er basert på forestillingen om en grense nummerrekkefølge, og det er derfor det ofte refereres til som "sekvensspråk"-definisjonen. Den andre definisjonen kalles "språk \(\varepsilon - \delta \)"-definisjonen.
Disse to definisjonene av grensen for en funksjon er ekvivalente, og du kan bruke en av dem, avhengig av hva som passer best for å løse et bestemt problem.

Merk at definisjonen av grensen til en funksjon "på sekvensspråket" også kalles definisjonen av grensen for en funksjon i følge Heine, og definisjonen av grensen for en funksjon "i språket \(\varepsilon - \delta \)" kalles også definisjonen av grensen for en funksjon i henhold til Cauchy.

Funksjonsgrense ved x->x 0 - og ved x->x 0 +

I det følgende vil vi bruke begrepene ensidige grenser for en funksjon, som er definert som følger.

Definisjon Tallet A kalles høyre (venstre) grense for funksjonen f (x) i punktet x 0 hvis for en hvilken som helst sekvens (1) som konvergerer til x 0, hvis elementer x n er større (mindre) enn x 0 , den tilsvarende sekvensen (2) konvergerer til A.

Symbolsk er det skrevet slik:
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$

Man kan gi en ekvivalent definisjon av ensidige grenser for en funksjon "på språket \(\varepsilon - \delta \)":

Definisjon tallet A kalles høyre (venstre) grense for funksjonen f(x) i punktet x 0 hvis det for noen \(\varepsilon > 0 \) eksisterer \(\delta > 0 \) slik at for alle x som tilfredsstiller ulikhetene \(x_0 symbolske oppføringer:

\((\forall \varepsilon > 0) (\eksisterer \delta > 0) (\forall x, \; x_0

Vi har allerede begynt å forholde oss til grensene og løsningen på dem. La oss fortsette i jakten og takle løsningen av grenser i henhold til L'Hopitals regel. Dette enkel regel i stand til å hjelpe deg med å komme deg ut av de lumske og vanskelige fellene som lærere så elsker å bruke i eksemplene på kontrollprogramvaren høyere matematikk og matematisk analyse. Løsningen etter L'Hopitals regel er enkel og rask. Hovedsaken er å kunne skille.

L'Hopitals regel: historie og definisjon

Dette er faktisk ikke akkurat L'Hopitals regel, men regelen L'Hospital-Bernoulli. Formulert av en sveitsisk matematiker Johann Bernoulli, og franskmennene Guillaume Lopital først publisert i sin lærebok infinitesimals in the glorious 1696 år. Kan du forestille deg hvordan folk måtte løse grensene med avsløring av usikkerhetsfaktorer før dette skjedde? Det er vi ikke.

Før du fortsetter med analysen av L'Hopital-regelen, anbefaler vi å lese den innledende artikkelen om og metoder for å løse dem. Ofte i oppgaver er det en formulering: finn grensen uten å bruke L'Hopital-regelen. Du kan også lese om teknikkene som vil hjelpe deg med dette i artikkelen vår.

Hvis du har å gjøre med grensene for en brøkdel av to funksjoner, vær forberedt: du vil snart møte en usikkerhet av formen 0/0 eller uendelig/uendelig. Hva betyr det? I telleren og nevneren har uttrykkene en tendens til null eller uendelig. Hva man skal gjøre med en slik grense, ved første øyekast, er helt uforståelig. Men hvis du bruker L'Hopitals regel og tenker deg litt om, faller alt på plass.

Men la oss formulere L'Hospital-Bernoulli-regelen. For å være helt presis, er det uttrykt ved et teorem. L'Hopitals regel, definisjon:

Hvis to funksjoner er differensierbare i et nabolag til et punkt x=a forsvinne på dette punktet, og det er en grense for forholdet mellom de deriverte av disse funksjonene, da for X streber etter en det er en grense for forholdet mellom funksjonene i seg selv, som er lik grensen for forholdet mellom de deriverte.

La oss skrive ned formelen, og alt vil umiddelbart bli lettere. L'Hopitals regel, formel:

Siden vi er interessert i den praktiske siden av saken, vil vi ikke presentere beviset for dette teoremet her. Du må enten ta ordet vårt for det, eller finne det i en lærebok for kalkulus og forsikre deg om at teoremet er riktig.

Forresten! For våre lesere er det nå 10% rabatt på

Avsløring av usikkerheter i henhold til L'Hopitals regel

Hvilke usikkerheter kan L'Hospitals regel bidra til å avdekke? Tidligere snakket vi hovedsakelig om usikkerhet 0/0 . Dette er imidlertid langt fra den eneste usikkerheten man kan møte. Her er andre typer usikkerheter:

La oss vurdere transformasjonene som kan brukes til å bringe disse usikkerhetene til formen 0/0 eller uendelig/uendelig. Etter transformasjonen vil det være mulig å bruke L'Hospital-Bernoulli-regelen og klikke eksempler som nøtter.

Artsusikkerhet uendelig/uendelig reduserer til en ubestemthet av formen 0/0 enkel transformasjon:

La det være et produkt av to funksjoner, hvorav den første har en tendens til null, og den andre - til uendelig. Vi bruker transformasjonen, og produktet av null og uendelighet blir til ubestemthet 0/0 :

For å finne grenser med usikkerhet av typen uendelig minus uendelig vi bruker følgende transformasjon som fører til usikkerhet 0/0 :

For å bruke L'Hopitals regel må du kunne ta derivater. Nedenfor er en tabell over derivater elementære funksjoner, som du kan bruke når du løser eksempler, samt reglene for beregning av deriverte av komplekse funksjoner:

La oss nå gå videre til eksempler.

Eksempel 1

Finn grensen etter L'Hospitals regel:

Eksempel 2

Regn ut ved å bruke L'Hopitals regel:

Viktig poeng! Hvis grensen for den andre og påfølgende deriverte av funksjoner eksisterer for X streber etter en , så kan L'Hopitals regel brukes flere ganger.

La oss finne grensen ( n – naturlig tall). For å gjøre dette, bruk L'Hospitals regel n en gang:

Vi ønsker deg lykke til med læringen matematisk analyse. Og hvis du trenger å finne grensen ved å bruke L'Hopital-regelen, skriv et sammendrag i henhold til L'Hopital-regelen, beregn røttene differensial ligning eller til og med beregne treghetstensoren til en kropp, vennligst kontakt våre forfattere. De hjelper deg gjerne med å finne ut av løsningens vanskeligheter.