Anvendelse av avgrensningsegenskapen til en funksjon. anvendelse av egenskapene til funksjoner for å løse likninger og ulikheter, arbeidet er viet til en av de ikke-standardiserte metodene

Utarbeidet og gjennomført av en matematikklærer

MCOU "Secondary School No. 1" Povorino

Voronezh-regionen

Kartashova S.A.

2014

Leksjonsemne:"Løse ligninger ved å bruke ikke-standardmetoder ved å bruke egenskapene til funksjoner"

Leksjonsformen er en forelesning etterfulgt av forsterkning. Designet for 2 leksjoner

(lysbilde nr. 1)

Leksjonens mål:

Gjenta og generalisere kunnskap om emnet: "Funksjoners egenskaper"

Lær å bruke den funksjonelle metoden for å løse likninger

Utvikle logisk tenkning, observasjon

Fremme aktivitet og kreativt initiativ.

(lysbilde nr. 2)

Utstyr: interaktiv tavle, datamaskin med presentasjon.

Leksjonsplan:

Organisatorisk øyeblikk.

Motivasjon pedagogiske aktiviteter(budskap om emnet, leksjonsmål).

Oppdatering av grunnleggende kunnskap (repetisjon av egenskaper ved grunnleggende funksjoner).

Studere nytt materiale (funksjonell metode for å løse ligninger).

Konsolidering av kunnskap (løsningsøvelser).

Oppsummering. Vurderinger.

Fremdrift av leksjonen.

Lærer:

For å løse de fleste ligningene man møter på eksamen, er det nok å vite skolekurs matematikk, men samtidig er det nødvendig å kunne løse ikke bare ved hjelp av standardteknikker beregnet på svært spesifikke typer ligninger, men også "ikke-standard" metoder, som vi skal snakke om i dag i klassen. En av disse metodene for å løse ligninger er funksjonell, basert på bruk av egenskapene til funksjoner. I motsetning til grafisk metode, kunnskap om egenskapene til funksjoner lar deg finne de eksakte røttene til ligningen, uten å måtte konstruere grafer av funksjoner. Å bruke egenskapene til funksjoner bidrar til å rasjonalisere løsningen av ligninger.

(lysbilde nr. 3)

La oss svare på spørsmålene:

Hva heter ligningen?

Hva er roten til en ligning?

Hva vil det si å løse en ligning?

Hva kalles en funksjon?

Hva er domenet til en funksjon?

Hva er rekkevidden til en funksjon?

(lysbilde nr. 4)

La oss vurdere(lysbilde nr. 5)

EKSEMPEL 1. Løs ligningen:

Løsning: ODZ:

Svar: det finnes ingen løsninger.

(lysbilde nr. 6)

EKSEMPEL 2. Løs ligningen:

Løsning: ODZ:

ODZ består av ett punkt x=1. Det gjenstår å sjekke om x=1 er en rot av ligningen. Ved å erstatte, ser vi at x=1 er roten til ligningen.

Svar: x=1.

Lærer:

Noen ganger viser det seg å være tilstrekkelig å vurdere ikke hele definisjonsdomenet til en funksjon, men bare dens undergruppe, der funksjonen tar verdier som tilfredsstiller visse betingelser (for eksempel bare ikke-negative verdier)

(lysbilde nr. 7 )

EKSEMPEL 3.

Løsning. La oss finne skjæringspunktet mellom domenene for definisjon av funksjoner på høyre og venstre side av ligningen:

D 1

La oss begrense settetD, tatt i betraktning at venstre side av ligningen er ikke-negativ, og derfor bør den være den samme høyre side For å gjøre dette må vi vurdere skjæringspunktet mellom settetDmed mange løsninger på ulikheten , altså med mange . Derfor er det nok å vurdere ligningen på settet .

Ved substitusjon sørger vi for at begge elementene fungerer som en løsning på ligningen.

Svar: -3; 2.

(lysbilde nr. 8 )

EKSEMPEL 4.

Løsning.

Med tanke på det roten av ligningen er x=4.

Svar: 4.

Lærer:

La oss gå videre til å løse ligninger ved å bruke konseptet med en funksjons verdiområde.

(lysbilde nr. 9-nr. 10)

(lysbilde nr. 11)

EKSEMPEL 1.

Løsning. Fordi , så har ligningen ingen løsning.

Svar: ingen løsninger.

EKSEMPEL 2.

Løsning. ODZ:

Svar: ingen løsninger.

Lærer:

Hvis funksjonen f ( x ) på intervallet X er avgrenset ovenfra, og funksjonen g ( x ) er avgrenset nedenfor, deretter ligningen f ( x ) = g ( x ) tilsvarer systemet

(lysbilde nr. 12)

EKSEMPEL 3.

Løsning. Per definisjon,

Likhet oppnås hvis

La oss løse den første ligningen i systemet:

arccos (x-1) =π, x-1 = -1, x=0.

Når x=0, blir den andre ligningen til en sann numerisk likhet.

Derfor er løsningen til systemet og denne ligningen x=0.

Svar: 0.

(lysbilde nr. 13-14)

EKSEMPEL 4.

Løsning.

La oss finne maksimum av denne funksjonen på intervallet (2;4) ved å bruke den deriverte.

= 0,

g’ + -

g 2 3 4 x

Maks

g(3)=2.Vi har

Da gitt ligning tilsvarende systemet

Etter å ha løst den første likningen til systemet, får vi x=3, ved å krysse av, erstatte den med den andre likningen, vil vi forsikre oss om at x=3 er løsningen til systemet og denne likningen.

Svar: 3.

(lysbilde nr. 15)

Lærer:

Denne metoden finnes ofte på Unified State Exam i matematikk. Denne metoden ligger i at den ene delen av ligningen er begrenset ovenfra av et visst tall M, og den andre delen av ligningen begrenses nedenfra av det samme tallet M. Tallet M kalles vanligvismajorante , og denne metoden erhovedmetoden . I majorant-metoden, som du kanskje har gjettet, må du ha god forståelse for hva en funksjon er og kunne studere egenskapene til funksjoner.

(lysbilde nr. 16)

Øvelser for konsolidering, utvikling av ferdigheter.

Klassen er delt inn i 2 grupper etter valg.

Alternativ 1.

Bevis at ligningen ikke har noen røtter.

Løs ligninger: Svar: 2.6.

Svar: 2.

Lærer:

I dag har vi sett på en ikke-standard metode for å løse ligninger ved å bruke egenskapene til funksjoner, som også kan brukes for å løse ulikheter, men vi vil snakke om dette i flere påfølgende leksjoner.

Oppsummering, vurderinger.

(lysbilde nr. 17)

Lekser:

Seksjon I. Matematikk og fysikk

UDC 372.8 BBK 74.262.21

IKKE. Lyakhova, A.I. Grishina, I.V. Yakovenko

BRUKE BEGRENSEDE FUNKSJONER I ET SKOLEMATEMATIKKURS

Merknad. Artikkelen presenterer en metodikk for å studere en metode for å løse "ikke-standard" ligninger av elementær matematikk ved å bruke avgrensede funksjoner.

Nøkkelord: løse likninger ved å bruke avgrensningen til en funksjon.

N.E. Lyakhova, A.I. Grishina, I.V. Yakovenko

BRUK AV BEGRENSNING AV FUNKSJONER I SKOLEKURS MATEMATIKK

Abstrakt. Oppgaven presenterer en metodikk for å studere metoden for å løse de "ikke-standardiserte" ligningene til elementær matematikk med begrensede funksjoner. Stikkord: løsning av ligninger, ved bruk av en begrenset funksjon.

Begrensede funksjoner gjør det mulig å løse mange ikke-standardiserte ligninger og ulikheter som samtidig inneholder ulike funksjoner, som ikke tillater bruk av standardmetoder for å løse problemet på dem bestemt type. Ved å bruke funksjoner avgrenset, bygges slike metoder for å løse likninger og ulikheter som mini-maks-metoden og dens konsekvenser. Navnet på metoden - mini-max-metoden - kan være kontroversielt, men det lar deg raskt huske essensen av metoden og fungerer som et referansepunkt for studenten. Merk at å studere denne metoden er nyttig for en skoleutdannet både med tanke på å utvide evnene hans til å løse "ikke-standard" problemer, og fra synspunktet om å utvikle ferdigheter i å studere funksjoner (spesielt ved å bruke metodene for elementær matematikk ). Begge er viktige for å forberede en kandidat til Unified State Exam i matematikk, siden testen målematerialer tradisjonelt inneholder slike oppgaver, mens de i skolebøkene er klart utilstrekkelig representert eller ikke presentert i det hele tatt.

Essensen av mini-max-metoden er følgende uttalelse.

Utsagn 1. Hvis på definisjonsdomenet X ligningene

og funksjonen

da er denne ligningen ekvivalent med systemet

f (*) = a g(*) = a "

Faktisk, under de angitte forholdene likhet

er mulig hvis og bare hvis funksjonene f (*) og g (*) tar verdien a for samme verdi *. I dette tilfellet vil tallet a være for funksjonene f (*) og g (*), henholdsvis den største og minste verdien på settet X. Merk at hvis minst en av funksjonene f (*) eller g (*) på settet X tar ikke verdien a, deretter ligningen

har ingen røtter. Men i dette tilfellet har systemet heller ingen løsninger, og derfor blir ikke ekvivalensen til ligningen og systemet krenket. Derfor, når man innhenter de nødvendige estimatene, er det ikke nødvendig å fastslå at a er på settet X høyeste verdi funksjonene f(*) og laveste verdi funksjoner g(*) .

Bruke erklæring 1 og egenskaper numeriske ulikheter, er det ikke vanskelig å bevise ytterligere to utsagn, som er konsekvenser av mini-maks-metoden.

Utsagn 2. La mengden X være skjæringspunktet mellom definisjonsdomenene til funksjonene f (x) og g (x), og ulikhetene gjelder for denne mengden

deretter ulikhet

f (x) + g (x) > a + b,

er ekvivalent med ligningen

f (x) + g (x) = a + b, som igjen er ekvivalent med systemet:

/ (x) = a, e (x) = b.

Utsagn 3. La mengden X være skjæringspunktet mellom definisjonsdomenene til funksjonene f (x) og е (x), og ulikhetene gjelder for denne mengden

0 < f (х) < а

e (x)< Ь, где а >0, b > 0

deretter ulikhet

f (x) e (x) > a b

vil være ekvivalent med ligningen

f (x) e (x) = a b, som igjen er ekvivalent med systemet

/ (x) = a, e(x) = b.

Som det fremgår av ordlyden av utsagnene, for å implementere mini-maks-metoden (eller dens konsekvenser), er det nødvendig å estimere funksjonene som er inkludert i likningene eller ulikhetene. Faktisk er funksjonsevaluering hovedaktiviteten i metodeimplementering. Derfor må undervisning i metoden bygge på å utvikle ferdigheter for å vurdere ulike funksjoner. Etter vår mening vil følgende metoder for slik vurdering være de mest relevante for skoleelever.

1. Den enkleste teknikken- evaluering av en funksjon av formen f (x) = A ± a(x), hvor a(x) er en ikke-negativ funksjon.

5. Evaluering av en kompleks funksjon.

La oss dvele mer detaljert på hver teknikk, illustrere den med eksempler og gi et sett treningsøvelserå utvikle ferdigheter i å løse ligninger ved hjelp av denne teknikken.

1. Den enkleste metoden for å estimere en funksjon. La a(x) være en ikke-negativ funksjon, da:

Hvis f (x) = A + a (x), så f (x) > A;

Hvis f (x) = A - a (x), så f (x)< А.

Vi kalte den første metoden den enkleste, siden estimatet i dette tilfellet er praktisk talt åpenbart forutsatt at studenten kjenner settet med ikke-negative funksjoner: 24x, x2", x~2", xa (hvor-), |x|, |x| -x, arccosx, arc^x, ax, osv. I tillegg vil ikke-negative verdier ta komplekse funksjoner, som er resultatet av en sammensetning av funksjoner hvis den siste funksjonen til sammensetningen er ikke-negativ. Dermed kan en liste over ikke-negative funksjoner være

generaliser: 2^u(x), (u(x))2", (m(x))-2i, ageo8u(x), agccyoi(x), |u(x)|, |u(x) - u(x), a"(x), (u(x))a (hvor k).

La oss gi eksempler på bruk av mini-maks-metoden, i løsningen som den vurderte estimeringsteknikken brukes.

Eksempel 1. Løs ligning 2 + |x(x -1)| = 2 - ^(x -1)(x + 2) . Løsning. Funksjoner

/ (x) = |x(x -1)|, I (x) = 7 (x -1)(x + 2)

ikke-negativ. Derfor har vi følgende estimat for venstre og høyre side av ligningen

2 + | x(x -1)| > 2,

2-y/(x-1)(x + 2)< 2 "

Da, ifølge utsagn 1, er den opprinnelige ligningen ekvivalent med systemet

Da:

Hvis funksjonen f (u) øker på et intervall, gjelder ulikheten

f(a)< f (u(x)) < f (b);

Hvis funksjonen f (u) avtar på intervallet, så holder ulikheten

f(b)< f (u(x)) < f (a) .

Eksempel 7. Løs ligningen log2 (x2 - 6x+11) = cos((x - 3) sin x).

Løsning. Utheving perfekt firkant i et kvadratisk trinomium under logaritmetegnet får vi ligningen

log2 (2+(x - 3)2) = cos((x - 3) sin x). La oss evaluere funksjonene til venstre og riktige deler denne ligningen.

f (x) = log2 (2+(x - 3)2) > 1. Faktisk, 2 + (x - 3)2 > 2, funksjonen log2 u øker, derfor,

log2 (2+(x - 3)2) > log2 2 = 1. Funksjonen u2 øker monotont.

"Anvendelse av kontinuitet" - Betydning av uttrykk. Geometrisk betydning derivat. Intervall metode. Skriv en ligning for tangenten til grafen til funksjonen. Tangent til grafen til en funksjon. Grafen er nær en tangent. Formel. La oss beregne ved å bruke formelen. Tangenten til kurven i et gitt punkt M er grenseposisjonen til sekant NM. Hyperbel.

"Ekstrem funksjon" - Avhengighet av gasstrykk på temperatur. Leksjonsemne: «Tegn på økende og minkende funksjoner. Test. Endring i strømstyrke når kretsen åpnes. Undersøkelse av en funksjon til et ekstremum". Endre AC. Plan: Strømavhengighet av spenning. Avhengighet av gasstrykk på volum. Tema: «Tegn på økende og minkende funksjoner.

"Funksjoner og deres egenskaper" - Den uavhengige variabelen kalles et argument. Økende funksjon. Definisjon av en funksjon. Selv og rare funksjoner. Monotonicitet av funksjonen. Verdiene til den avhengige variabelen kalles funksjonens verdier. Alle verdier av den uavhengige variabelen danner definisjonsdomenet til funksjonen -D (f). 1. Funksjonsverdiene er positive.

Det er totalt 23 presentasjoner i temaet

Emne: Metoder for bruk av begrensede funksjoner.
Livet er bra på grunn av det som er i det du kan gjøre matematikk. (Leonard Euler)Mål: utvikling av ny, ukonvensjonell tenkning som med hell kan brukes på andre områder menneskelig aktivitet(kybernetikk, datateknologi, økonomi, radiofysikk, kjemi osv.).
Oppgaver: - opplæring i å vurdere den objektive og subjektive vanskeligheten til oppgaver og klokt velge disse oppgavene i eksamen;

Å lage en "sparegrise" av ukonvensjonelle og uvanlige resonnementer.

Leksjonsfremgang:

Org. øyeblikk. Studentene formulerer emnet for leksjonen ved å fullføre Unified State Exam-oppgavene del A og B og dechiffrere emnet i synkende rekkefølge etter svarene som mottas. (Krypter 12 kort nummerert fra -2 til 10 som antatte ord) (vedlegg 1 og 2)

begrensninger

2. Del elevene inn i 2 grupper, gi dem settet «Teori + 10 oppgaver» (vedlegg 3 og 4), be dem velge de oppgavene som kan gjennomføres for denne teoretiske delen, og begrunn valget.3. Vis fremdriften til disse oppgavene på tavlen av elevene: Noskova K., Dedevshin I., Veselov I.4. Del oppgavene fra kortet i 2 grupper for å løse dem, etterfulgt av selvtest på arket ferdige løsninger. (Vedlegg 5)5. Del ark til grupper som beskriver nye ikke-standardmetoder for å løse likninger og ulikheter for seleksjon neste emne(som hjemmeoppgaver, finn dem i samlinger Unified State Exam-oppgaver, som kan løses med denne metoden (vedlegg 6)6. Elevrefleksjon (fyller ut tabellen) F.I. student

Vedlegg 1.
Løs disse oppgavene og ordne svarene i synkende rekkefølge, samle emnet for leksjonen vår basert på svarene.

Finn abscissen til punktet i grafen til funksjonen y=3x 2 -7x+7, der tangenten til tangentvinkelen er lik -1.

Vedlegg 2.
9 2 0 7Studium av funksjoner ved bruk av deriverte. 10 5 1 -1 Metode for bruk av begrensede funksjoner. 4 -2 8 12Løse ulikheter grafisk.
3 11 6Løsninger av funksjonelle ligninger.
Studere

Vedlegg 3.

En av effektive metoderå løse likninger eller ulikheter er en metode basert på bruk av avgrensede funksjoner. Til de mest kjente begrensede funksjoner inkludere, for eksempel, noen trigonometriske; omvendt trigonometriske funksjoner; funksjoner som inneholder modul, grad, rot c jevn grad og andre.

De vanligste ulikhetene er følgende:

│f(x) │≥ 0, -1 ≤ sinx ≤ 1, -1 ≤ cosx ≤ 1, -

-

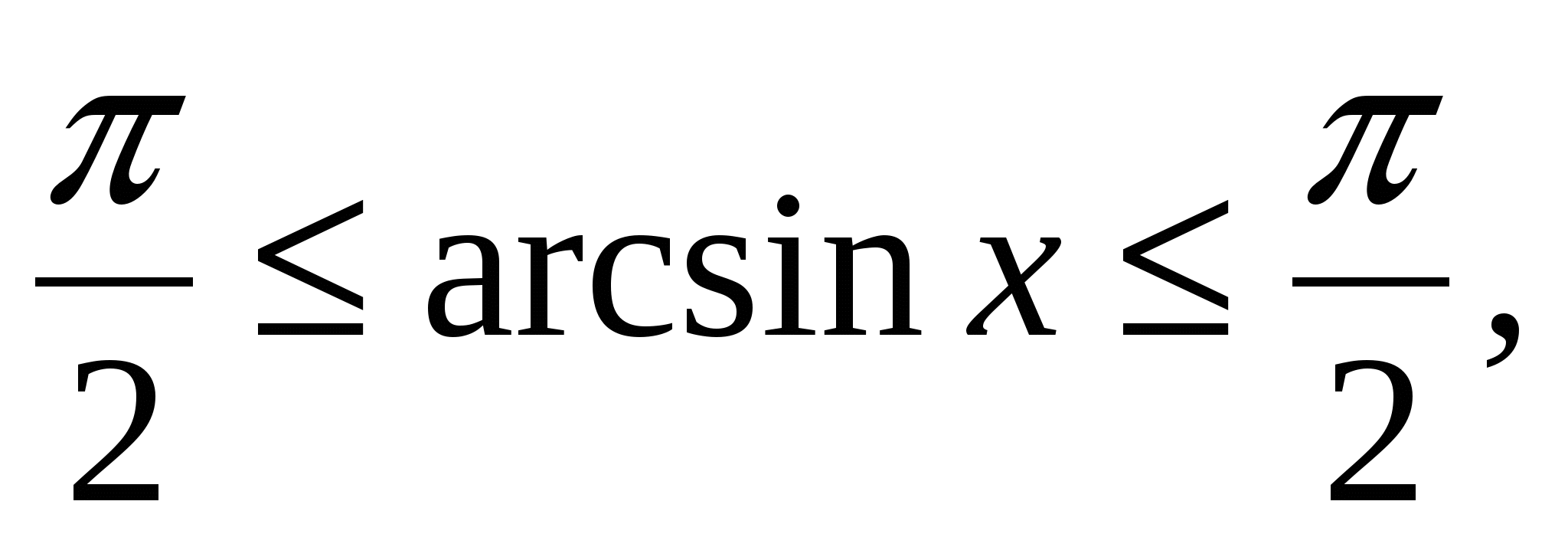
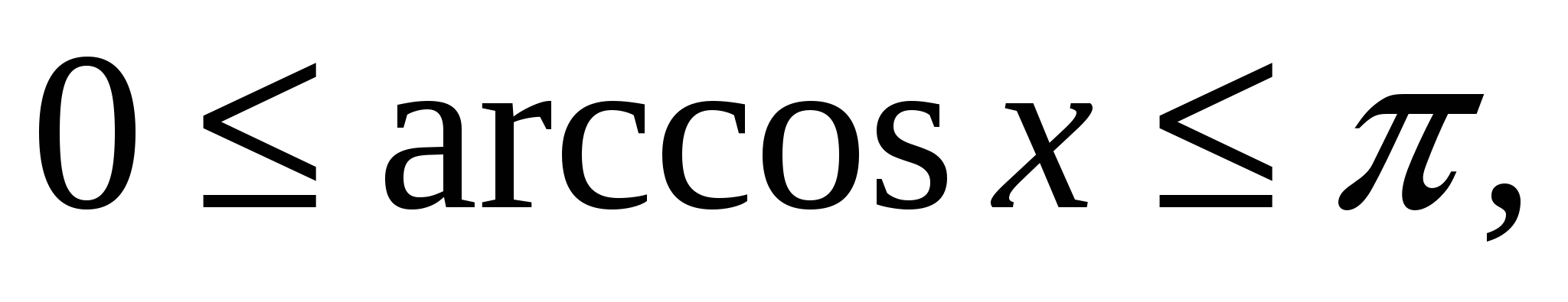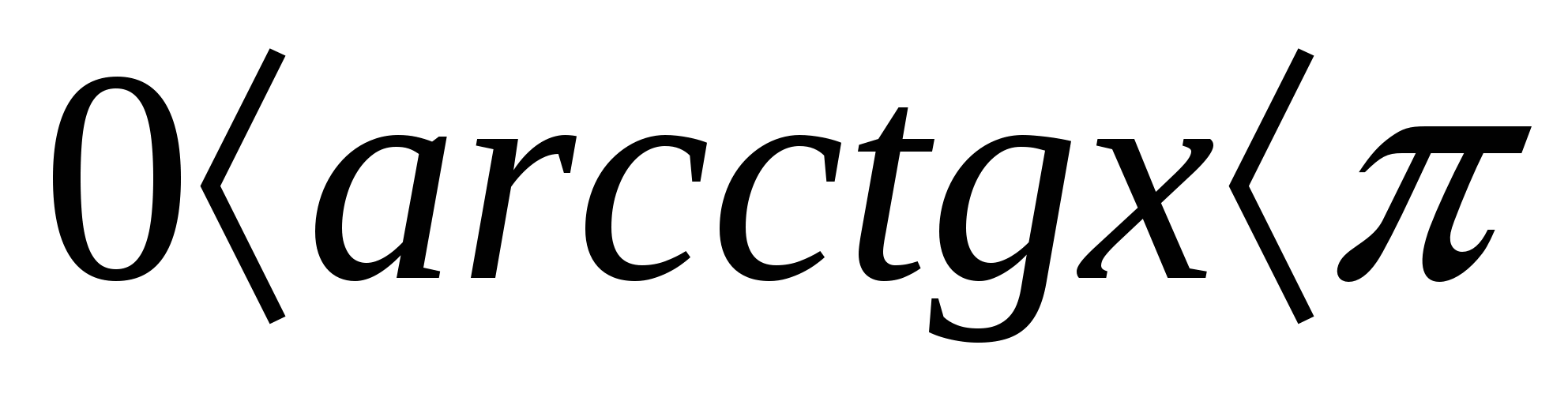, en f ( x ) >0, (f(x) ± g(x)) 2 n ≥ 0,
, en+ ≥ 2, b+ ≤ -2 og mange andre. Her n - naturlig tall, h(x) ≥ 0, en>0, b 0.

I tillegg til de enkleste ulikhetene gitt ovenfor, er det også mer komplekse, spesielt, trigonometriske ulikheter -,

,

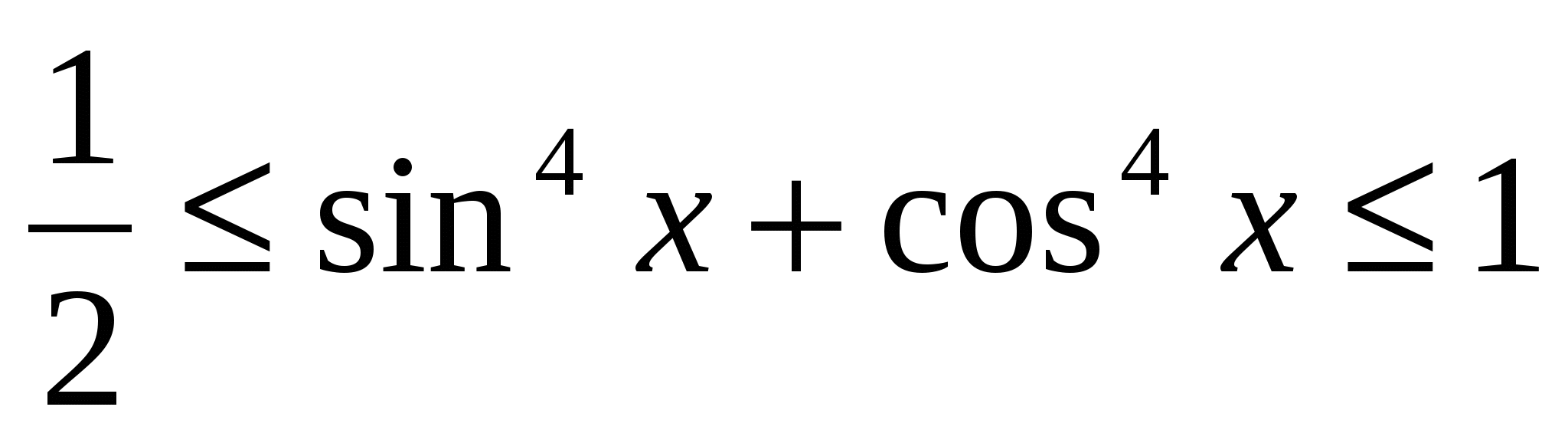og ulikheter med moduler av skjemaet
.

Eksempel 1.Løs ligningen:

Løsning: La oss velge et komplett kvadrat på høyre side av ligningen, dvs. . Det følger av det
. Siden i dette tilfellet sinπ x ≤ 1, så får vi et ligningssystem

Løser vi den andre ligningen i systemet, får vi at x=. Ved å substituere inn i den første ligningen sikrer vi at den funnet verdien av x er en løsning på systemet, og derfor er en løsning på den opprinnelige ligningen.

Svare: x=.

Eksempel 2.Løs ligningen:

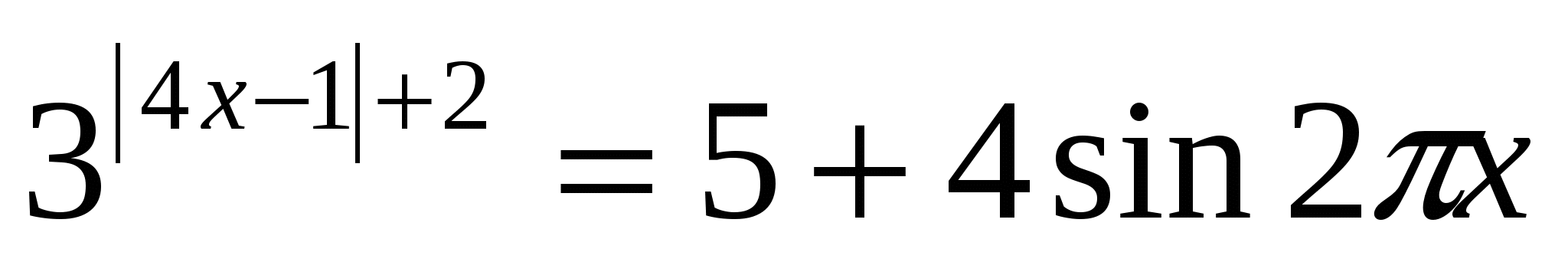
Løsning: siden Imidlertid sin2 π x ≤ 1. Derfor, 5+4 sin2 π x ≤ 9. Dermed får vi et ligningssystem:

Herfra får vi et ligningssystem
, fra den første ligningen finner vi x=. La oss erstatte det i den andre ligningen i systemet og sørge for at x = er en løsning på systemet, og derfor er en løsning på den opprinnelige ligningen.

Svare: x=

Vedlegg 4. Fra den foreslåtte listen over oppgaver velger du de som kan løses ved hjelp av metoden med begrenset funksjon. 1. Løs ligningen x 2 -4 x=(2-cos
2. Finn mengden heltallsløsninger ulikheter x 2 ctg 2
3. Løs ligningen
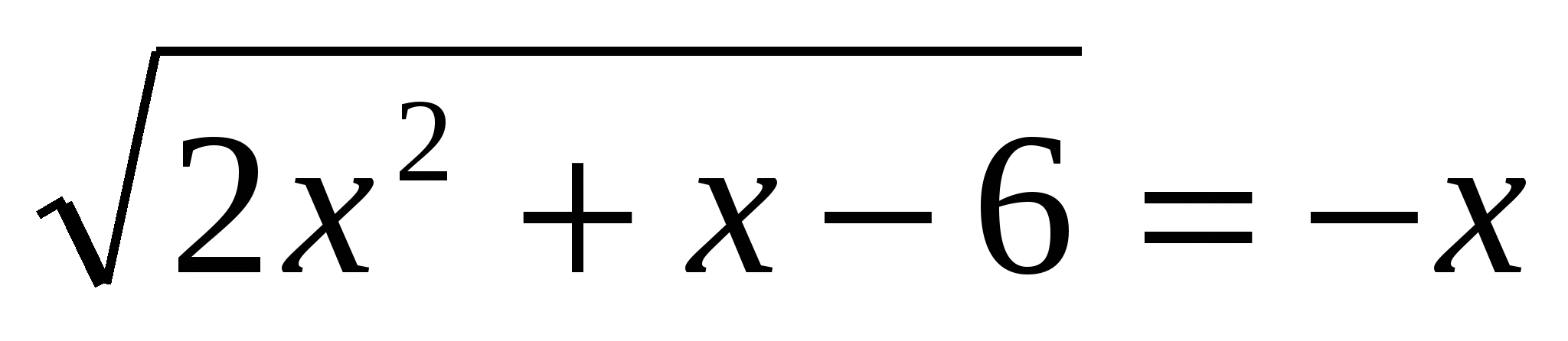4. Løs ligning 3-(5. Finn antall heltallsløsninger til ulikheten 16s 2 ≥0 som tilfredsstiller betingelse 3 tg 2
6. Løs ligningen
7. Løs ligningen -25x 2 +40x-23=( cos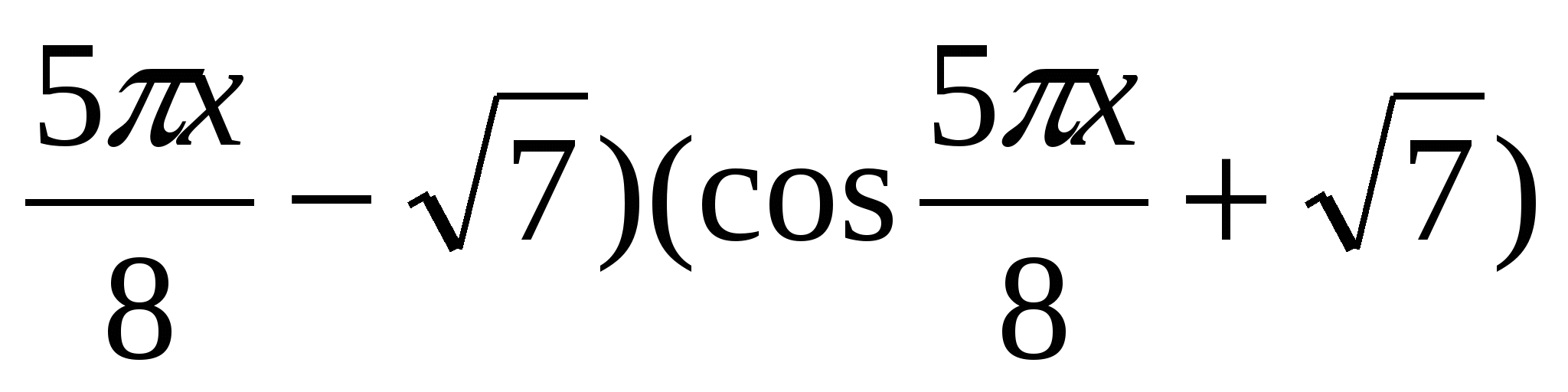
8. Finn produktet av røttene til ligningen x
9. Løs ligningen
10. Løs ligning 3- cos 2

Selvtestark. Vedlegg 5. 1. Løs ligningen Løsning: fordi , da fordi og deretter
vi får et ligningssystem

løs den første ligningen, få x=, bytt denne verdien inn i den andre ligningen

2 . Løs ligningen 3- cos 2 Løsning: fordi , da fordi og deretter
vi får et ligningssystem

løs den andre ligningen, få x=, bytt denne verdien inn i den første ligningen

dette betyr at x= er en løsning på den opprinnelige ligningen. Svar: x=
3. Finn antall heltallsløsninger til ulikheten x 2 +7x-8≤0, tilfredsstiller betingelsen ctg 2 Løsning: fordi og for alle tillatte verdier av x vil vi finne nuller kvadratisk trinomium, ifølge Vietas teorem, løser vi ulikheten ved å bruke intervallmetoden
At. det vet vi
heltallsverdier av x er tall eliminert Svar: 8 heltallsløsninger 4. Finn antall heltallsløsninger til ulikheten 16s 2 ≥0 som tilfredsstiller betingelse 3 tg 2 Løsning: fordi og deretter for alle tillatte verdier av x, finner vi nullpunktene til uttrykket, x = og x = Løs ulikheten ved å bruke intervallmetoden
At. det vet vi

heltallsverdier av x er tall eliminert Svar: 7 heltallsløsninger
Vedlegg 6.

Metode for å bruke monotoni av funksjoner. Når du løser en ligning som f(x)=g(x) i noen tilfeller er en effektiv metode som bruker monotoniteten til funksjonene y= f(x) og y= g(x) Hvis funksjonen y= f(x) er kontinuerlig og øker (minker) på segmentet en≤ x ≤ b, og funksjonen у= g(x) er kontinuerlig og avtar (øker) på samme segment, deretter ligningen f(x)=g(x) på segmentet en≤ x ≤ b kan ikke ha mer enn én rot, noe som betyr at det er nødvendig å enten prøve å finne den eneste roten av ligningen ved å velge, eller vise at en slik rot ikke eksisterer. Denne metoden er spesielt effektiv i tilfellet når begge sider av ligningen f(x) = g(x) er "ubeleilige" funksjoner for felles studier. Kommentar: Hvis funksjonen y= f(x) øker, og funksjonen y= g(x) reduseres for en≤ x ≤ b Og samtidig f(a)>g(EN), da er røttene til ligningen blant en≤ x ≤ b Ingen.

Eksempel: Løs ligningenLøsning: Region akseptable verdier ligningene er x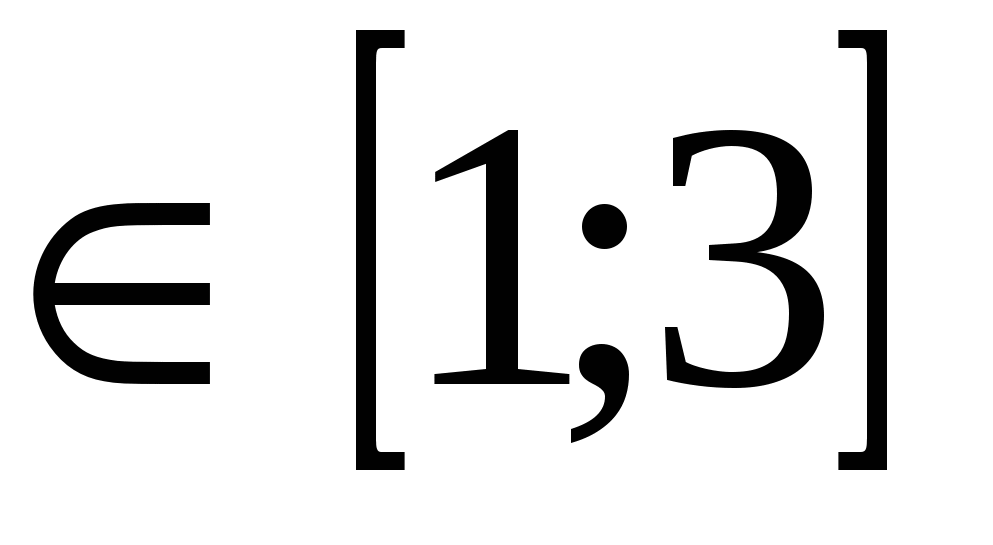
. Det er lett å se at i dette området øker venstre side av ligningen, og høyre side avtar, dvs. funksjonf(x)=
øker, og funksjoneng(x)=
- avtagende. I denne forbindelse kan den opprinnelige ligningen bare ha én rot (hvis noen). Ved seleksjon finner vi denne roten av ligningen x = 2.Svare: x=2
Metode for å løse funksjonelle ligninger. Blant de fleste komplekse oppgaver Unified State Examination inkluderer problemer hvis løsning koker ned til vurdering av funksjonelle ligninger av formen f(f(….f(x)…))=x eller f(g(x))=f(h(x)), der f(x),g(x),h(x) er noen funksjoner og n≥ 2
Metoder for å løse disse funksjonelle ligningene er basert på anvendelsen av mange teoremer, la oss vurdere en av dem.
Teorem 1. Røttene til ligningen f(x)=0 er røttene til ligningen f(f(….f(x)…))=x
Eksempel: Løs ligningen x=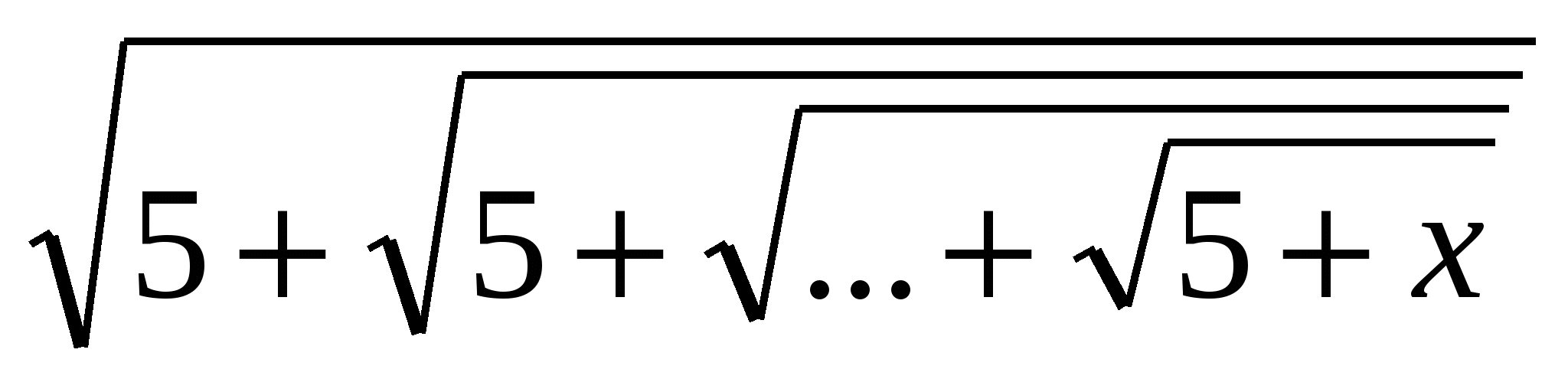
, Hvor kvadratrot tattnen gang ogn≥ 1 Løsning: Fra problemforholdene følger det at x> 0. Laf(x)=
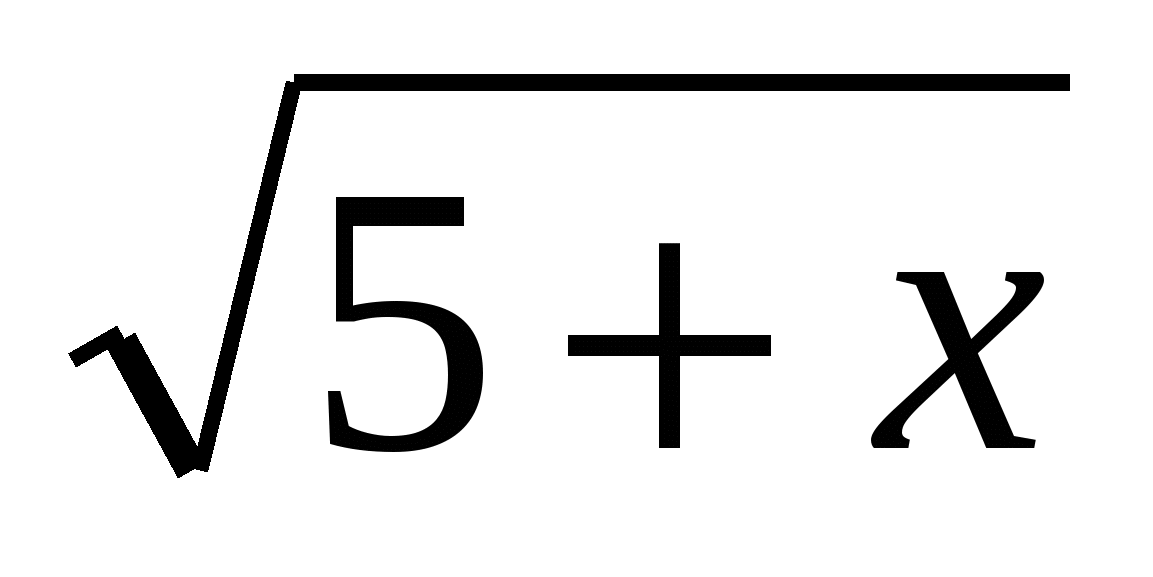, så kan ligningen vår representeres som en funksjonell f( f(…. f( x)…))= x. Siden ved x> 0 funksjonf(x)= øker ogf(x) > 0, da er ligningen x= ekvivalent med ligningenf(x)= x, dvs. =x, hvis positive løsning er x=
Svare: x=