Eksempler på integrasjon av rasjonelle funksjoner av brøker. Integrasjon av rasjonelle funksjoner Brøk - rasjonell funksjon Den enkleste

Tidligere har vi diskutert generelle metoder for integrering. I dette og de følgende avsnittene vil vi snakke om integrering av spesifikke funksjonsklasser ved å bruke teknikkene som er diskutert.

Integrasjon av de enkleste rasjonelle funksjonene

La oss vurdere en integral av formen \tekststil(\int R(x)\,dx), hvor y=R(x) er en rasjonell funksjon. Ethvert rasjonelt uttrykk R(x) kan representeres i formen \frac(P(x))(Q(x)), hvor P(x) og Q(x) er polynomer. Hvis denne brøken er uekte, det vil si hvis graden av telleren er større enn eller lik graden av nevneren, kan den representeres som summen av et polynom (heltallsdel) og en egenbrøk. Derfor er det nok å vurdere integrasjonen av riktige fraksjoner.

La oss vise at integrasjonen av slike brøker reduseres til integrasjonen enkle brøker, dvs. uttrykk for formen:

\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).

Hvor A,\,B,\,a,\,p,\,q er reelle tall, og kvadrattrinomialet x^2+px+q har ingen reelle røtter. Uttrykk av type 1) og 2) kalles brøker av 1. slag, og uttrykk av type 3) og 4) kalles brøker av 2. slag.

Integraler av brøker av 1. type beregnes direkte

\begin(aligned)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\ldots). \end(justert)

La oss vurdere beregningen av integraler av brøker av den andre typen: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.

Først merker vi det

\int\frac(dt)(t^2+a^2)= \frac(1)(a)\operatørnavn(arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.

For å redusere beregningen av integral 3) til disse to integralene, transformerer vi kvadrattrinomialet x^2+px+q ved å skille hele kvadratet fra det:

x^2+px+q= (\venstre(x+\frac(p)(2)\høyre)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}

Siden ved antagelsen har dette trinomialet ingen reelle røtter, altså q-\frac(p^2)(4)>0 og vi kan sette q-\frac(p^2)(4)=a^2. Substitusjon x+\frac(p)(2)=t,~ dx=dt transformerer integral 3) til en lineær kombinasjon av de indikerte to integralene:

\begin(aligned)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\right )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2) )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\venstre(B-\frac(Ap)(2)\høyre)\!\ \operatørnavn(arctg)\frac(t)(a)+C. \end(justert)

I det endelige svaret trenger du bare å erstatte (t) med x+\frac(p)(2) og (a) med \sqrt(q-\frac(p^2)(4)). Siden t^2+a^2=x^2+px+q, altså

\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \operatørnavn(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac (p^2)(4)))+C.

Vurder saken \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.

Som i forrige tilfelle, la oss sette x+\frac(p)(2)=t. Vi får:

\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \venstre(B-\frac(Ap)(2)\høyre)\! \int\frac(dt)((t^2+a^2)^n)\,.

Den første termen beregnes som følger:

A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.

Det andre integralet beregnes ved hjelp av en gjentakelsesformel.

Eksempel 1. La oss beregne \int\frac(3x+2)(x^2+2x+3)\,dx.

Løsning. Vi har: x^2+2x+3=(x+1)^2+2. La oss sette x+1=t. Så dx=dt og 3x+2=3(t-1)+2=3t-1 og derfor

\begin(justert)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\operatørnavn(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\operatørnavn(arctg)\frac(x+1)(\ sqrt(2))+C. \end(justert)

Eksempel 2. La oss beregne \int\frac(x+2)((x^2+6x+10)^2)\,dx.

Løsning. Vi har: x^2+6x+10=(x+3)^2+1. La oss introdusere en ny variabel ved å sette x+3=t. Så dt=dx og x+2=t-1. Ved å erstatte variabelen under integrertegnet får vi:

\begin(justert)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \end(justert))

La oss sette I_2=\int\frac(dt)((t^2+1)^2). Vi har:

I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Men I_1=\int\frac(dt)(t^2+1)= \operatørnavn(arctg)t Dermed, I_2= \frac(1)(2)\operatørnavn(arctg)t+ \frac(t)(2(t^2+1)).

Til slutt får vi:

\begin(justert)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\operatørnavn(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\operatørnavn(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\operatørnavn(arctg)(x+3)+C \end(justert)

Integrering av egenbrøker

Tenk på en skikkelig brøkdel R(x)=\frac(P(x))(Q(x)), hvor Q(x) er et polynom av grad n. Uten tap av generalitet kan vi anta at ledende koeffisient i Q(x) er lik 1. I et algebrakurs er det bevist at et slikt polynom med reelle koeffisienter kan faktoriseres til faktorer av første og andre grad med reelle koeffisienter :

Q(x)= (x-x_1)^(\alpha)\ldots (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\ldots (x^2) +r\,x+s)^(\delta).

hvor x_1,\ldots,x_k er de reelle røttene til polynomet Q(x) og kvadrattrinomer har ingen reelle røtter. Det kan bevises at da er R(x) representert som summen av enkle brøker av formen 1) -4):

\begin(justert)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta) ))(x^2+rx+s)\, \end(justert)

hvor eksponentene for nevnerne reduseres suksessivt fra \alfa til 1, ..., fra \beta til 1, fra \gamma til 1, ..., fra \delta til 1, og A_1,\ldots,F_(\delta)- usikre koeffisienter. For å finne disse koeffisientene er det nødvendig å kvitte seg med nevnerne og, etter å ha oppnådd likheten til to polynomer, bruke metoden med ubestemte koeffisienter.

En annen måte å bestemme odds på A_1,\ldots, A_(\alpha), \ldots, F_(\delta) er basert på substitusjon av verdiene til variabelen x. Ved å erstatte et hvilket som helst tall i stedet for x i likheten oppnådd fra likhet (1) etter å ha fjernet nevnerne, kommer vi til en lineær ligning for de nødvendige koeffisientene. Ved å erstatte det nødvendige antallet slike partielle verdier av variabelen, får vi et system av ligninger for å finne koeffisientene. Det er mest praktisk å velge røttene til nevneren (både reelle og komplekse) som private verdier av variabelen. I dette tilfellet forsvinner nesten alle ledd på høyre side av likheten (som betyr likheten til to polynomer), noe som gjør det enkelt å finne de gjenværende koeffisientene. Når du erstatter komplekse verdier, husk at to komplekse tall er like hvis og bare hvis deres reelle og imaginære deler er like, henholdsvis. Derfor, fra hver likhet som inneholder komplekse tall, oppnås to ligninger.

Etter å ha funnet de ubestemte koeffisientene, gjenstår det å beregne integralene til de enkleste fraksjonene som er oppnådd. Siden ved integrering av de enkleste brøkene, som vi har sett, oppnås bare rasjonelle funksjoner, arctangens og logaritmer, da integralet til enhver rasjonell funksjon uttrykkes gjennom den rasjonelle funksjonen, arctangenter og logaritmer.

Eksempel 3. La oss beregne integralet til en riktig rasjonell brøk \int\frac(6x+1)(x^2+2x-3)\,dx.

Løsning. La oss faktorisere nevneren til integranden:

x^2+2x-3=(x-1)(x+3).

La oss skrive ut integranden og presentere den som en sum av enkle brøker:

\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.

Når vi frigjør oss fra nevnerne i denne likheten, får vi:

6x+1=A\cdot (x+3)+B\cdot (x-1)\,.

For å finne koeffisientene vil vi bruke metoden for substitusjon av partielle verdier. For å finne koeffisienten A, la oss sette x=1. Så fra likhet (2) får vi 7=4A, hvorav A=7/4. For å finne koeffisienten B, la oss sette x=-3. Så fra likhet (2) får vi -17=-4B, hvorav B=17/4.

Så, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1)(x+3). Midler,

\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4) )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.

Eksempel 4. La oss beregne \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.

Løsning. La oss skrive ut integranden og presentere den som en sum av enkle brøker. Nevneren inneholder en faktor x^2+2, som ikke har noen reelle røtter; den tilsvarer en brøkdel av den andre typen: \frac(Ax+B)(x^2+2) multiplikatoren (x-1)^2 tilsvarer summen av to brøker av den første typen: \frac(C)((x-1)^2)+ \frac(D)(x-1); til slutt tilsvarer faktoren x+2 en brøkdel av den første typen \frac(E)(x+2) . Dermed representerer vi integrandfunksjonen som en sum av fire brøker:

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.

La oss frigjøre oss fra nevnere i denne likestillingen. Vi får:

\begin(justert) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\phantom(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(justert)

Nevneren til integranden har to reelle røtter: x=1 og x=-2. Når verdien x=1 erstattes med likhet (4), får vi 16=9C, hvorfra vi finner C=16/9. Når vi erstatter x=-2 får vi 13=54E og definerer følgelig E=13/54. Ved å erstatte verdien x=i\,\sqrt(2) (roten av polynomet x^2+2 ) kan vi gå til likheten

4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).

Den forvandles til formen:

(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, hvorfra 10A+2B=5, og (2A-5B)\sqrt(2)=8\sqrt(2).

Løse et system med to ligninger med to variabler \begin(cases)10A+2B=5,\\ 2A-5B=8,\end(cases) Vi finner: A=\frac(41)(54),~ B=-\frac(35)(27).

Det gjenstår å bestemme verdien av koeffisienten D. For å gjøre dette, la oss åpne parentesene i likhet (4), presentere lignende termer, og deretter sammenligne koeffisientene for x^4. Vi får:

A+D+E=1, det vil si D=0.

La oss erstatte de funnet verdiene til koeffisientene med likhet (3):

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,

og gå videre til integrering:

\begin(justert)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16) )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41) )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\operatørnavn(arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(justert)

Integrering av uekte brøker

Anta at vi må integrere funksjonen y=\frac(f(x))(g(x)), hvor f(x) og g(x) er polynomer, og graden av polynomet f(x) er større enn eller lik graden av polynomet g(x) . I dette tilfellet må du først og fremst velge hele delen av den upassende brøkdelen \frac(f(x))(g(x)), dvs. representere det i formen

\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,

hvor s(x) er et polynom av grad lik forskjellen mellom gradene til polynomene f(x) og g(x), og \frac(r(x))(g(x))- riktig brøk.

Da har vi \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..

Eksempel 5. La oss beregne integralet til den uekte brøken \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.

Løsning. Vi har:

\begin(justert)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \end(justert)

For å isolere hele delen, del f(x) med g(x): \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.

Midler, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx

Vi har: \int(x-2)dx=\frac(x^2)(2)-2x+C.

For å beregne integralet \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx Metoden med ubestemte koeffisienter brukes, som ovenfor. Etter utregningene, som vi overlater til leseren, får vi.

Integrasjon av rasjonelle funksjoner Brøk - rasjonell funksjon De enkleste rasjonelle brøker Dekomponering av en rasjonell brøk til enkle brøker Integrasjon av enkle brøker Generell regel for integrasjon av rasjonelle brøker

polynom av grad n. Brøk - rasjonell funksjon En brøk - rasjonell funksjon er en funksjon lik forholdet mellom to polynomer: En rasjonell brøk kalles egen hvis graden av telleren er mindre enn graden av nevneren, det vil si m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P

Brøk - rasjonell funksjon Reduser en uekte brøk til riktig form: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 63 x 3 15 2 95 4 x xx 342 23 xxx 2 15 x

Enkleste rasjonelle brøker Egne rasjonelle brøker av formen: De kalles enkleste rasjonelle brøker av typer. øks A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,

Dekomponering av en rasjonell brøk til enkle brøker Teorem: Enhver egen rasjonell brøk, hvis nevner er faktorisert: kan dessuten representeres på en unik måte i form av en sum av enkle brøker: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx. M)(

Dekomponering av en rasjonell brøk til enkle brøker La oss forklare formuleringen av teoremet ved å bruke følgende eksempler: For å finne de usikre koeffisientene A, B, C, D... brukes to metoder: metoden for å sammenligne koeffisienter og metoden av partielle verdier av en variabel. La oss se på den første metoden ved å bruke et eksempel. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x

Dekomponering av en rasjonell brøk til enkle brøker Presenter brøken som en sum av enkle brøker: La oss bringe de enkleste brøkene til en fellesnevner Lik tellerne til de resulterende og opprinnelige brøkene Lik koeffisientene med samme potenser x)52)(1( 332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x

Integrasjon av de enkleste brøkene La oss finne integralene til de enkleste rasjonelle brøkene: La oss se på integrasjonen av type 3-brøkene ved å bruke et eksempel. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k

Integrasjon av enkle brøker dx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 dtt 3 9 2 3 2 2 t td 33 2 t arctg.C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln

Integrasjon av enkle brøker Et integral av denne typen ved bruk av substitusjon: reduseres til summen av to integraler: Det første integralet beregnes ved å introdusere t under differensialtegnet. Det andre integralet beregnes ved å bruke gjentaksformelen: dx qpxx NMx k 2 V t p x 2 kk ved dt N ved dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Integrasjon av enkle brøker a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 322 t) t 2t (4)1(

Generell regel for integrering av rasjonelle brøker Hvis brøken er uekte, representer den som summen av et polynom og en egenbrøk. Etter å ha faktorisert nevneren til en riktig rasjonell brøk, representer den som en sum av enkle brøker med ubestemte koeffisienter. Finn ubestemte koeffisienter ved hjelp av metoden for å sammenligne koeffisienter eller ved metoden for partielle verdier av en variabel. Integrer polynomet og den resulterende summen av enkle brøker.

Eksempel La oss sette brøken i riktig form. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 225 5 5 2348 5 2 xx

Eksempel La oss faktorisere nevneren til en egenbrøk La oss representere brøken som en sum av enkle brøker La oss finne de ubestemte koeffisientene ved å bruke metoden for partielle verdier av variabelen xxx xx 23 2 2 48 2 2)1(48 xx xx 2 )1(1 x C x B x A 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx

Eksempel dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln

En rasjonell funksjon er en brøkdel av formen , hvis teller og nevner er polynomer eller produkter av polynomer.

Eksempel 1. Steg 2.

.

Vi multipliserer de ubestemte koeffisientene med polynomer som ikke er i denne individuelle brøken, men som er i andre resulterende brøker:

Vi åpner parentesene og setter likhetstegn mellom telleren til den opprinnelige integranden til det resulterende uttrykket:

På begge sider av likheten ser vi etter termer med samme potenser av x og komponerer et ligningssystem fra dem:

.

Vi kansellerer alle x-ene og får et ekvivalent system av ligninger:

.

Dermed er den endelige utvidelsen av integranden til en sum av enkle brøker:

.

Eksempel 2. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

.

Nå begynner vi å lete etter usikre koeffisienter. For å gjøre dette, setter vi likhetstegn mellom telleren til den opprinnelige brøken i funksjonsuttrykket til telleren til uttrykket oppnådd etter å ha redusert summen av brøkene til en fellesnevner:

Nå må du lage og løse et likningssystem. For å gjøre dette, setter vi likhetstegn mellom koeffisientene til variabelen i tilsvarende grad i telleren til det opprinnelige uttrykket for funksjonen og lignende koeffisienter i uttrykket oppnådd i forrige trinn:

Vi løser det resulterende systemet:

Så herfra

.

Eksempel 3. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

Vi begynner å lete etter usikre koeffisienter. For å gjøre dette, setter vi likhetstegn mellom telleren til den opprinnelige brøken i funksjonsuttrykket til telleren til uttrykket oppnådd etter å ha redusert summen av brøkene til en fellesnevner:

Som i tidligere eksempler, komponerer vi et ligningssystem:

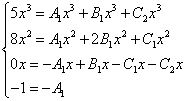
Vi reduserer x-ene og får et ekvivalent system av ligninger:

Ved å løse systemet får vi følgende verdier av de usikre koeffisientene:

Vi får den endelige dekomponeringen av integranden til summen av enkle brøker:

.

Eksempel 4. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

.

Vi vet allerede fra tidligere eksempler hvordan man kan likestille telleren til den opprinnelige brøken med uttrykket i telleren oppnådd etter å ha dekomponert brøken til summen av enkle brøker og bringe denne summen til en fellesnevner. Derfor, bare for kontrollformål, presenterer vi det resulterende likningssystemet:

Ved å løse systemet får vi følgende verdier av de usikre koeffisientene:

Vi får den endelige dekomponeringen av integranden til summen av enkle brøker:

Eksempel 5. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

.

Vi reduserer uavhengig denne summen til en fellesnevner, og likestiller telleren til dette uttrykket med telleren til den opprinnelige brøken. Resultatet skal være følgende ligningssystem:

Ved å løse systemet får vi følgende verdier av de usikre koeffisientene:

.

Vi får den endelige dekomponeringen av integranden til summen av enkle brøker:

.

Eksempel 6. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

Vi utfører de samme handlingene med dette beløpet som i de foregående eksemplene. Resultatet skal være følgende ligningssystem:

Ved å løse systemet får vi følgende verdier av de usikre koeffisientene:

.

Vi får den endelige dekomponeringen av integranden til summen av enkle brøker:

.

Eksempel 7. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

.

Etter visse handlinger med den resulterende mengden, bør følgende ligningssystem oppnås:

Ved å løse systemet får vi følgende verdier av de usikre koeffisientene:

Vi får den endelige dekomponeringen av integranden til summen av enkle brøker:

.

Eksempel 8. Steg 2. På trinn 1 oppnådde vi følgende dekomponering av den opprinnelige brøken til summen av enkle brøker med ubestemte koeffisienter i tellerne:

.

La oss gjøre noen endringer i handlingene som allerede har blitt brakt til automatikk for å få et system av ligninger. Det er en kunstig teknikk som i noen tilfeller bidrar til å unngå unødvendige beregninger. Ved å bringe summen av brøker til en fellesnevner, får vi og likestiller telleren til dette uttrykket med telleren til den opprinnelige brøken vi får.

«En matematiker, akkurat som en kunstner eller poet, skaper mønstre. Og hvis mønstrene hans er mer stabile, er det bare fordi de er sammensatt av ideer... Mønstrene til en matematiker, akkurat som mønstrene til en kunstner eller en poet, må være vakre; Ideer, akkurat som farger eller ord, må samsvare med hverandre. Skjønnhet er det første kravet: det er ingen plass i verden for stygg matematikk».

G.H.Hardy

I det første kapittelet ble det lagt merke til at det er antiderivater av ganske enkle funksjoner som ikke lenger kan uttrykkes gjennom elementære funksjoner. I denne forbindelse får de klassene av funksjoner som vi nøyaktig kan si at deres antiderivater er elementære funksjoner enorm praktisk betydning. Denne klassen av funksjoner inkluderer rasjonelle funksjoner, som representerer forholdet mellom to algebraiske polynomer. Mange problemer fører til integrering av rasjonelle brøker. Derfor er det svært viktig å kunne integrere slike funksjoner.

2.1.1. Fraksjonelle rasjonelle funksjoner

Rasjonell brøk(eller rasjonell brøkfunksjon) kalles relasjonen mellom to algebraiske polynomer:

hvor og er polynomer.

La oss minne deg på det polynom (polynom, hele rasjonelle funksjon) ngrad kalt en funksjon av formen

Hvor – reelle tall. For eksempel,

– polynom av første grad;

– polynom av fjerde grad, etc.

Den rasjonelle brøken (2.1.1) kalles riktig, hvis graden er lavere enn graden , dvs. n<m, ellers kalles brøken feil.

Enhver uekte brøk kan representeres som summen av et polynom (hele delen) og en egenbrøk (brøkdelen). Separasjonen av hele og brøkdelen av en uekte brøk kan gjøres i henhold til regelen for å dele polynomer med et "hjørne".

Eksempel 2.1.1. Identifiser hele og brøkdeler av følgende upassende rasjonelle brøker:

EN) , b) .

Løsning . a) Ved å bruke "hjørne"-divisjonsalgoritmen får vi

Dermed får vi

.

b) Her bruker vi også «hjørne»-divisjonsalgoritmen:

Som et resultat får vi

.

La oss oppsummere. I det generelle tilfellet kan det ubestemte integralet til en rasjonell brøk representeres som summen av integralene til polynomet og den riktige rasjonelle brøken. Å finne antiderivater av polynomer er ikke vanskelig. Derfor vil vi i det følgende hovedsakelig vurdere riktige rasjonelle brøker.

2.1.2. De enkleste rasjonelle brøkene og deres integrasjon

Blant riktige rasjonelle brøker er det fire typer, som er klassifisert som de enkleste (elementære) rasjonelle brøkene:

3) ,

4) ,

hvor er et heltall, , dvs. kvadratisk trinomium har ingen reelle røtter.

Integrering av enkle brøker av 1. og 2. type gir ingen store vanskeligheter:

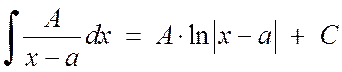, (2.1.3)

. (2.1.4)

La oss nå vurdere integrasjonen av enkle brøker av 3. type, men vi vil ikke vurdere brøker av 4. type.

La oss starte med integraler av skjemaet

.

Dette integralet beregnes vanligvis ved å isolere det perfekte kvadratet av nevneren. Resultatet er en tabellintegral av følgende form

eller .

Eksempel 2.1.2. Finn integralene:

EN) , b) .

Løsning . a) Velg et komplett kvadrat fra et kvadratisk trinomium:

Herfra finner vi

b) Ved å isolere et komplett kvadrat fra et kvadratisk trinomium får vi:

Dermed,

.

For å finne integralet

du kan isolere den deriverte av nevneren i telleren og utvide integralet til summen av to integraler: den første av dem ved substitusjon kommer ned til utseende

,

og den andre - til den som er diskutert ovenfor.

Eksempel 2.1.3. Finn integralene:

.

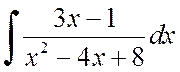Løsning . Legg merke til det . La oss isolere den deriverte av nevneren i telleren:

Den første integralen beregnes ved hjelp av substitusjonen :

I det andre integralet velger vi det perfekte kvadratet i nevneren

Endelig får vi

2.1.3. Riktig rasjonell brøkekspansjon
for summen av enkle brøker

Enhver riktig rasjonell brøk kan representeres på en unik måte som en sum av enkle brøker. For å gjøre dette må nevneren faktoriseres. Fra høyere algebra er det kjent at hvert polynom med reelle koeffisienter

TEMA: Integrasjon av rasjonelle brøker.

Merk følgende! Når du studerer en av de grunnleggende metodene for integrasjon: integrering av rasjonelle brøker, er det nødvendig å vurdere polynomer i det komplekse domenet for å utføre strenge bevis. Derfor er det nødvendig studere på forhånd noen egenskaper ved komplekse tall og operasjoner på dem.

Integrasjon av enkle rasjonelle brøker.

Hvis P(z) Og Q(z) er polynomer i det komplekse domenet, så er de rasjonelle brøker. Det kalles riktig, hvis grad P(z) mindre grad Q(z) , Og feil, hvis grad R ikke mindre enn en grad Q.

Enhver uekte brøk kan representeres som: ,

P(z) = Q(z) S(z) + R(z),

en R(z) – polynom hvis grad er mindre enn graden Q(z).

Dermed kommer integrasjonen av rasjonelle brøker ned til integrasjonen av polynomer, det vil si potensfunksjoner, og egenbrøker, siden det er en egenbrøk.

Definisjon 5. De enkleste (eller elementære) brøkene er følgende typer brøker:

1) , 2) , 3) , 4) .

La oss finne ut hvordan de integreres.

3) (studert tidligere).

Teorem 5. Hver egenbrøk kan representeres som en sum av enkle brøker (uten bevis).

Konsekvens 1. Hvis er en riktig rasjonell brøk, og hvis det blant røttene til polynomet bare er enkle reelle røtter, vil det i dekomponeringen av brøken til summen av enkle brøker bare være enkle brøker av 1. type:

Eksempel 1.

Konsekvens 2. Hvis er en egen rasjonell brøk, og hvis det blant røttene til polynomet bare er flere reelle røtter, vil det i dekomponeringen av brøken til summen av enkle brøker bare være enkle brøker av 1. og 2. type :

Eksempel 2.

Konsekvens 3. Hvis er en riktig rasjonell brøk, og hvis det blant røttene til polynomet bare er enkle komplekse konjugerte røtter, vil det i dekomponeringen av brøken til summen av enkle brøker bare være enkle brøker av den 3. typen:

Eksempel 3.

Konsekvens 4. Hvis er en egen rasjonell brøk, og hvis det blant røttene til polynomet bare er flere komplekse konjugerte røtter, vil det i dekomponeringen av brøken til summen av enkle brøker bare være enkle brøker av 3. og 4. typer:

For å bestemme de ukjente koeffisientene i de gitte utvidelsene, fortsett som følger. Venstre og høyre side av utvidelsen som inneholder ukjente koeffisienter multipliseres med Likheten til to polynomer oppnås. Fra den oppnås ligninger for de nødvendige koeffisientene ved å bruke:

1. likhet er sant for alle verdier av X (delverdimetoden). I dette tilfellet oppnås et hvilket som helst antall ligninger, hvorav enhver m lar en finne de ukjente koeffisientene.

2. koeffisientene faller sammen for de samme gradene av X (metode for ubestemte koeffisienter). I dette tilfellet oppnås et system av m - ligninger med m - ukjente, hvorfra de ukjente koeffisientene er funnet.

3. kombinert metode.

Eksempel 5. Utvid en brøk til det enkleste.

Løsning:

La oss finne koeffisientene A og B.

Metode 1 – metode for privat verdi:

Metode 2 – metode for ubestemte koeffisienter:

Svar:

Integrering av rasjonelle brøker.

Teorem 6. Det ubestemte integralet av enhver rasjonell brøk på ethvert intervall der dens nevner ikke er lik null, eksisterer og uttrykkes gjennom elementære funksjoner, nemlig rasjonelle brøker, logaritmer og arctangents.

Bevis.

La oss forestille oss en rasjonell brøk i formen: . I dette tilfellet er siste ledd en egenbrøk, og ifølge setning 5 kan den representeres som en lineær kombinasjon av enkle brøker. Dermed reduseres integrasjonen av en rasjonell brøk til integrasjonen av et polynom S(x) og enkle brøker, hvis antiderivater, som det er vist, har den formen som er angitt i teoremet.

Kommentar. Hovedvanskeligheten i dette tilfellet er dekomponeringen av nevneren i faktorer, det vil si søket etter alle dens røtter.

Eksempel 1. Finn integralet