Formel for gjennomsnittlig varians. Variasjonsindikatorer: konsept, typer, formler for beregninger

De viktigste generaliserende indikatorene på variasjon i statistikk er varianser og gjennomsnitt standardavvik.

Spredning det aritmetisk gjennomsnitt kvadrerte avvik for hver funksjonsverdi fra det totale gjennomsnittet. Variansen kalles vanligvis middelkvadrat av avvikene og betegnes  2 . Avhengig av de første dataene, kan variansen beregnes fra det aritmetiske gjennomsnittet, enkelt eller vektet:

 uvektet (enkel) dispersjon;

 vektet varians.

Standardavvik er en generaliserende karakteristikk av absolutte dimensjoner variasjoner egenskap til sammen. Det uttrykkes i samme enheter som tegnet (i meter, tonn, prosent, hektar osv.).

Standardavviket er kvadratroten av variansen og er betegnet med :

 uvektet standardavvik;

 vektet standardavvik.

Standardavviket er et mål på påliteligheten til gjennomsnittet. Jo mindre standardavviket er, jo bedre gjenspeiler det aritmetiske gjennomsnittet hele den representerte populasjonen.

Beregningen av standardavviket innledes med beregningen av variansen.

Prosedyren for å beregne den vektede variansen er som følger:

1) Bestem det aritmetiske vektede gjennomsnittet:

2) beregn avvikene til opsjonene fra gjennomsnittet:

3) kvadrat avviket for hvert alternativ fra gjennomsnittet:

4) multipliser kvadrerte avvik med vekter (frekvenser):

5) oppsummer de mottatte verkene:

6) den resulterende mengden er delt på summen av vektene:

Eksempel 2.1

Beregn det aritmetiske vektede gjennomsnittet:

Verdiene av avvik fra gjennomsnittet og deres kvadrater er presentert i tabellen. La oss definere variansen:

Standardavviket vil være lik:

Hvis kildedataene presenteres som et intervall distribusjonsserie , så må du først bestemme den diskrete verdien av funksjonen, og deretter bruke metoden beskrevet.

Eksempel 2.2

La oss vise beregningen av variansen for intervallserien på dataene om fordelingen av det sådde arealet til kollektivbruket etter hveteutbytte.

Det aritmetiske gjennomsnittet er:

La oss beregne variansen:

6.3. Beregning av dispersjonen i henhold til formelen for individuelle data

Regneteknikk spredning komplisert, og store verdier alternativer og frekvenser kan være tungvint. Beregninger kan forenkles ved hjelp av dispersjonsegenskapene.

Dispersjonen har følgende egenskaper.

1. En reduksjon eller økning i vektene (frekvensene) til en variabel funksjon med et visst antall ganger endrer ikke spredningen.

2. Redusere eller øke hver funksjonsverdi med samme konstante verdi EN spredning endres ikke.

3. Redusere eller øke hver funksjonsverdi med et visst antall ganger k henholdsvis reduserer eller øker variansen i k 2 ganger standardavvik  inn k en gang.

4. Variansen til et trekk i forhold til en vilkårlig verdi er alltid større enn variansen i forhold til det aritmetiske gjennomsnittet med kvadratet av forskjellen mellom gjennomsnittsverdien og vilkårlig verdi:

Hvis EN 0, så kommer vi til følgende likhet:

dvs. variansen til et trekk er lik differansen mellom middelkvadraten til funksjonsverdiene og kvadratet av gjennomsnittet.

Hver egenskap kan brukes alene eller i kombinasjon med andre ved beregning av variansen.

Prosedyren for å beregne variansen er enkel:

1) bestemme aritmetisk gjennomsnitt :

2) kvadrat det aritmetiske gjennomsnittet:

3) kvadrat avviket for hver variant av serien:

X Jeg 2 .

4) finn summen av kvadrater av alternativer:

5) del summen av kvadratene til alternativene med antallet, dvs. bestem midtre firkant:

6) bestem forskjellen mellom middelkvadraten til funksjonen og kvadratet av gjennomsnittet:

Eksempel 3.1 Vi har følgende data om produktiviteten til arbeidere:

La oss gjøre følgende beregninger:

Denne siden beskriver standard eksempel finne variansen, kan du også se på andre oppgaver for å finne den

Eksempel 1. Bestemmelse av gruppe, gjennomsnitt av gruppe, mellom-gruppe og total varians

Eksempel 2. Finne variansen og variasjonskoeffisienten i en grupperingstabell

Eksempel 3. Finne variansen i diskrete serier

Eksempel 4. Vi har følgende data for en gruppe på 20 elever korrespondanseavdelingen. Trenger å bygge intervallserie fordeling av funksjonen, beregne middelverdien av funksjonen og studere variansen

La oss bygge intervallgruppering. La oss bestemme rekkevidden til intervallet med formelen:

hvor X maks– maksimal verdi gruppering tegn;
X min er minimumsverdien for grupperingsfunksjonen;
n er antall intervaller:

Vi aksepterer n=5. Trinnet er: h \u003d (192 - 159) / 5 \u003d 6.6

La oss lage en intervallgruppering

For ytterligere beregninger vil vi bygge en hjelpetabell:

X "i - midten av intervallet. (for eksempel midten av intervallet 159 - 165,6 \u003d 162,3)

gjennomsnittlig verdi veksten til elever bestemmes av formelen til det aritmetiske vektede gjennomsnittet:

Vi bestemmer spredningen med formelen:

Formelen kan konverteres slik:

Av denne formelen følger det at variansen er forskjellen mellom gjennomsnittet av kvadratene til alternativene og kvadratet og gjennomsnittet.

Varians i variasjonsserier Med med like intervaller ved metoden for momenter kan beregnes på følgende måte når du bruker den andre egenskapen til variansen (deler alle alternativer med verdien av intervallet). Definisjon av varians, beregnet ved metoden for øyeblikk, i henhold til følgende formel er mindre tidkrevende:

hvor i er verdien av intervallet;
A er en betinget null, som det er praktisk å bruke midten av et intervall som har høyeste frekvens;
m1 er kvadratet av momentet av første orden;
m2 - moment av andre orden

Funksjonsvariasjon (hvis i den statistiske populasjonen attributtet endres på en slik måte at det bare er to gjensidig utelukkende alternativer, så kalles en slik variabilitet alternativ) kan beregnes med formelen:

Bytter inn denne formelen dispersjon q \u003d 1- p, får vi:

Typer spredning

Total varians måler variasjonen av en egenskap over hele befolkningen som helhet under påvirkning av alle faktorene som forårsaker denne variasjonen. Det er lik middelkvadrat for avvikene individuelle verdier egenskap x av den totale gjennomsnittsverdien av x og kan defineres som enkel varians eller vektet varians.

Intragruppe varians karakteriserer tilfeldig variasjon, dvs. en del av variasjonen, som skyldes påvirkning av uregnskapsmessige faktorer og ikke er avhengig av tegn-faktoren som ligger til grunn for grupperingen. Denne variansen er lik middelkvadraten av avvikene til de individuelle verdiene til attributtet innenfor X-gruppen fra det aritmetiske gjennomsnittet av gruppen og kan beregnes som en enkel varians eller som en vektet varians.

Dermed, variasjonsmål innen gruppe variasjon av en egenskap i en gruppe og bestemmes av formelen:

hvor xi - gruppegjennomsnitt;
ni er antall enheter i gruppen.

For eksempel viser intragruppeavvik som må bestemmes i oppgaven med å studere effekten av arbeidernes kvalifikasjoner på nivået av arbeidsproduktivitet i en butikk, variasjoner i produksjon i hver gruppe forårsaket av alle mulige faktorer (teknisk tilstand av utstyr, tilgjengelighet av verktøy og materialer, arbeidernes alder, arbeidsintensitet osv. .), bortsett fra forskjeller i kvalifikasjonskategorien (innen gruppen har alle arbeidere samme kvalifikasjoner).

La oss regne innMSUTMERKEspredning og standardavvik prøver. Vi beregner også variansen til en tilfeldig variabel hvis fordelingen er kjent.

Vurder først spredning, deretter standardavvik.

Prøveavvik

Prøveavvik (prøveavvik,prøveforskjell) karakteriserer spredningen av verdier i matrisen i forhold til .

Alle 3 formlene er matematisk likeverdige.

Det kan sees fra den første formelen at prøveavvik er summen av kvadrerte avvik for hver verdi i matrisen fra gjennomsnittet delt på prøvestørrelsen minus 1.

spredning prøver funksjonen DISP() brukes, eng. navnet på VAR, dvs. Forskjell. Siden MS EXCEL 2010, anbefales det å bruke dens analoge DISP.V() , eng. navnet VARS, dvs. Eksempelvarians. I tillegg, fra og med versjonen av MS EXCEL 2010, er det en DISP.G () funksjon, eng. VARP-navn, dvs. BefolkningsVARIanse som beregner spredning Til befolkning . Hele forskjellen kommer ned til nevneren: i stedet for n-1 som DISP.V() , har DISP.G() bare n i nevneren. Før MS EXCEL 2010 ble VARP()-funksjonen brukt til å beregne populasjonsvariansen.

Prøveavvik
=FIRKANT(Sample)/(ANTALL(Sample)-1)
=(SUMSQ(Sample)-COUNT(Sample)*AVERAGE(Sample)^2)/ (COUNT(Sample)-1)- den vanlige formelen
=SUM((Sample -AVERAGE(Sample))^2)/ (ANTALL(Sample)-1) –

Prøveavvik er lik 0 bare hvis alle verdier er like med hverandre og følgelig er like middelverdi. Vanligvis, jo høyere verdi spredning, jo større spredning av verdier i matrisen.

Prøveavvik er punktestimat spredning fordeling av den tilfeldige variabelen som prøve. Om bygging konfidensintervaller ved evaluering spredning kan leses i artikkelen.

Varians av en tilfeldig variabel

Å beregne spredning tilfeldig variabel, du må vite det.

Til spredning tilfeldig variabel X bruker ofte notasjonen Var(X). Spredning er lik kvadratet av avviket fra gjennomsnittet E(X): Var(X)=E[(X-E(X)) 2 ]

spredning beregnet med formelen:

hvor x i er verdien som den tilfeldige variabelen kan ta, og μ er gjennomsnittsverdien (), p(x) er sannsynligheten for at den tilfeldige variabelen vil ta verdien x.

Hvis den tilfeldige variabelen har , da spredning beregnet med formelen:

Dimensjon spredning tilsvarer kvadratet på måleenheten til de opprinnelige verdiene. For eksempel, hvis verdiene i prøven er målinger av vekten til delen (i kg), vil dimensjonen på variansen være kg 2 . Dette kan derfor være vanskelig å tolke for å karakterisere spredningen av verdier, en verdi lik kvadratrot fra spredning – standardavvik.

Noen eiendommer spredning:

Var(X+a)=Var(X), der X er en tilfeldig variabel og a er en konstant.

Var(aХ)=a 2 Var(X)

Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2=E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2

Denne spredningsegenskapen brukes i artikkel om lineær regresjon.

Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), hvor X og Y er tilfeldige variabler, Cov(Х;Y) - kovarians av disse tilfeldige variablene.

Hvis tilfeldige variabler er uavhengige, så deres kovarians er 0, og derfor Var(X+Y)=Var(X)+Var(Y). Denne egenskapen til variansen brukes i utdataene.

La oss vise det for uavhengige mengder Var(X-Y)=Var(X+Y). Faktisk, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Denne egenskapen til variansen brukes til å plotte .

Eksempel på standardavvik

Eksempel på standardavvik er et mål på hvor vidt spredt verdiene i prøven er i forhold til deres .

A-priory, standardavvik er lik kvadratroten av spredning:

Standardavvik tar ikke hensyn til størrelsen på verdiene i prøvetaking, men bare graden av spredning av verdier rundt dem midten. La oss ta et eksempel for å illustrere dette.

La oss beregne standardavviket for 2 prøver: (1; 5; 9) og (1001; 1005; 1009). I begge tilfeller er s=4. Det er åpenbart at forholdet mellom standardavviket og verdiene til matrisen er betydelig forskjellig for prøvene. For slike tilfeller, bruk Variasjonskoeffisienten(Variasjonskoeffisient, CV) - forhold standardavvik til gjennomsnittet aritmetikk, uttrykt i prosent.

I MS EXCEL 2007 og nyere tidlige versjonerå beregne Eksempel på standardavvik funksjonen =STDEV() brukes, eng. navnet STDEV, dvs. standardavvik. Siden MS EXCEL 2010 anbefales det å bruke dens analoge = STDEV.B () , eng. navn STDEV.S, dvs. Eksempel på standardavvik.

I tillegg, fra og med versjonen av MS EXCEL 2010, er det en funksjon STDEV.G () , eng. navn STDEV.P, dvs. Populasjonsstandard DEViation som beregner standardavvik Til befolkning. Hele forskjellen kommer ned til nevneren: i stedet for n-1 som STDEV.V() , har STDEV.G() bare n i nevneren.

Standardavvik kan også beregnes direkte fra formlene nedenfor (se eksempelfil)
=SQRT(SQUADROTIV(Sample)/(COUNT(Sample)-1))
=SQRT((SUMSQ(Sample)-COUNT(Sample)*AVERAGE(Sample)^2)/(COUNT(Sample)-1))

Andre spredningstiltak

SQUADRIVE()-funksjonen beregner med umm av kvadrerte avvik av verdier fra deres midten. Denne funksjonen vil returnere det samme resultatet som formelen =VAR.G( Prøve)*KRYSS AV( Prøve) , Hvor Prøve- en referanse til et område som inneholder en rekke prøveverdier (). Beregninger i QUADROTIV()-funksjonen gjøres i henhold til formelen:

SROOT()-funksjonen er også et mål på spredningen til et sett med data. AVERAGE()-funksjonen beregner gjennomsnittet absolutte verdier avvik fra midten. Denne funksjonen vil returnere samme resultat som formelen =SUMPRODUKT(ABS(Sample-AVERAGE(Sample)))/ANTALL(Sample), Hvor Prøve- en referanse til et område som inneholder en rekke utvalgsverdier.

Beregninger i funksjonen SROOTKL () gjøres i henhold til formelen:

For grupperte data restdispersjon - gjennomsnitt på intra-gruppe avvik:

Hvor σ 2 j er variansen i gruppen til den j-te gruppen.

For ugrupperte data restdispersjon er et mål på tilnærmingsnøyaktigheten, dvs. tilnærming av regresjonslinjen til de opprinnelige dataene:
hvor y(t) er prognosen i henhold til trendligningen; y t - innledende serie med dynamikk; n er antall poeng; p er antall koeffisienter til regresjonsligningen (antall forklaringsvariabler).
I dette eksemplet heter det objektivt estimat av varians.

Eksempel #1. Fordelingen av arbeidere i tre foretak i en forening etter tariffkategorier er preget av følgende data:

Arbeiderlønnskategori	Antall arbeidere ved bedriften
	bedrift 1	bedrift 2	bedrift 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definere:
1. spredning for hver virksomhet (interngruppespredning);
2. gjennomsnitt av intragruppedispersjoner;
3. spredning mellom grupper;
4. total varians.

Løsning.
Før du fortsetter med å løse problemet, er det nødvendig å finne ut hvilken funksjon som er effektiv og hvilken som er faktoriell. I eksemplet under vurdering er den effektive funksjonen "Tariffkategori", og faktorfunksjonen er "Nummer (navn) på foretaket".
Så har vi tre grupper (bedrifter) som det er nødvendig å beregne gruppegjennomsnittet og intragruppeavvikene for:

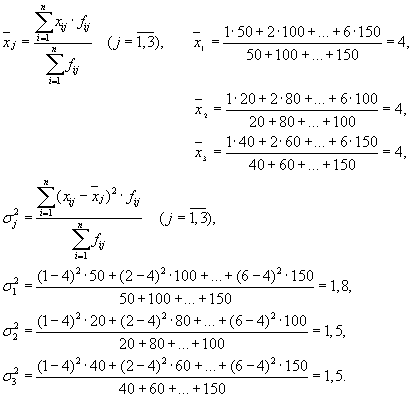
Selskap	gruppegjennomsnitt,	variasjon innen gruppe,
1	4	1,8

Gjennomsnittet av intragruppe-variansene ( restdispersjon) beregnet med formelen:

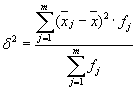
hvor du kan regne ut:
eller:

Deretter:
Den totale spredningen vil være lik: s 2 \u003d 1,6 + 0 \u003d 1,6.
Den totale variansen kan også beregnes ved å bruke en av følgende to formler:

Når man skal løse praktiske problemer, må man ofte forholde seg til et skilt som kun tar to alternative verdier. I dette tilfellet snakker de ikke om vekten til en bestemt verdi av en funksjon, men om dens andel i aggregatet. Hvis andelen populasjonsenheter som har egenskapen som studeres, er angitt med " R", og ikke eie - gjennom" q”, så kan spredningen beregnes med formelen:
s 2 = p×q

Eksempel #2. I følge dataene om utviklingen av seks arbeidere i brigaden, bestemme intergruppevariasjonen og evaluer virkningen av arbeidsskiftet på deres arbeidsproduktivitet hvis den totale variansen er 12,2.

nr. til arbeidsbrigaden	Arbeidseffekt, stk.
	i første skift	i 2. skift
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Løsning. Innledende data

X	f1	f2	f 3	f4	f5	f6	Total
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Total	31	33	37	37	40	38

Da har vi 6 grupper som det er nødvendig å beregne gruppemiddel og intragruppevarianser for.
1. Finn gjennomsnittsverdiene for hver gruppe.







2. Finn middelkvadrat for hver gruppe.







Vi oppsummerer resultatene av beregningen i en tabell:

Gruppenummer	Gruppegjennomsnitt	Intragruppe varians
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Intragruppe varians karakteriserer endringen (variasjonen) av den studerte (resulterende) egenskapen i gruppen under påvirkning av alle faktorer, bortsett fra faktoren som ligger til grunn for grupperingen:
Vi beregner gjennomsnittet av intragruppedispersjonene ved å bruke formelen:


4. Intergruppevarians karakteriserer endringen (variasjonen) av den studerte (resulterende) egenskapen under påvirkning av en faktor (faktortrekk) som ligger til grunn for grupperingen.
Intergruppespredning er definert som:

Hvor


Deretter

Total varians karakteriserer endringen (variasjonen) av den studerte (resulterende) egenskapen under påvirkning av alle faktorer (faktortrekk) uten unntak. Ved tilstanden til problemet er det lik 12,2.
Empirisk korrelasjonsrelasjon måler hvor mye av den totale fluktuasjonen av den resulterende attributten som er forårsaket av den studerte faktoren. Dette er forholdet mellom den faktorielle variansen og den totale variansen:

Vi bestemmer den empiriske korrelasjonsrelasjonen:

Relasjoner mellom funksjoner kan være svake eller sterke (nære). Kriteriene deres er evaluert på Chaddock-skalaen:
0,1 0,3 0,5 0,7 0,9 I vårt eksempel er forholdet mellom egenskap Y-faktor X svak
Bestemmelseskoeffisient.

La oss definere bestemmelseskoeffisienten:

Dermed skyldes 0,67 % av variasjonen forskjeller mellom egenskaper, og 99,37 % skyldes andre faktorer.
Konklusjon: V denne saken utviklingen av arbeidere er ikke avhengig av arbeid på et bestemt skift, dvs. påvirkningen av arbeidsskiftet på deres arbeidsproduktivitet er ikke signifikant og skyldes andre faktorer.

Eksempel #3. Basert på gjennomsnitt lønn og kvadreret avvik fra verdien for to grupper av arbeidere, finn den totale variansen ved å bruke regelen for å legge til avvik:

Løsning:
Gjennomsnitt av avvik innen gruppe

Intergruppespredning er definert som:


Den totale variansen vil være: 480 + 13824 = 14304

Blant de mange indikatorene som brukes i statistikk, er det nødvendig å fremheve variansberegningen. Det skal bemerkes at å utføre denne beregningen manuelt er en ganske kjedelig oppgave. Heldigvis finnes det funksjoner i Excel som lar deg automatisere beregningsprosedyren. La oss finne ut algoritmen for å jobbe med disse verktøyene.

Varians er et mål på variasjon, som er middelkvadraten av avvikene fra matematisk forventning. Dermed uttrykker det spredningen av tall om gjennomsnittet. Beregningen av spredningen kan utføres både for den generelle befolkningen og for utvalget.

Metode 1: beregning på den generelle befolkningen

For å beregne denne indikatoren i Excel for den generelle befolkningen, brukes funksjonen DISP.G. Syntaksen for dette uttrykket er som følger:

DISP.G(Nummer1;Nummer2;…)

Totalt kan fra 1 til 255 argumenter brukes. Argumenter kan være numeriske verdier, samt referanser til cellene de er inneholdt i.

La oss se hvordan du beregner denne verdien for en rekke numeriske data.

Metode 2: prøveberegning

I motsetning til beregningen av verdien for den generelle befolkningen, er ikke nevneren angitt i beregningen for utvalget Total tall, men ett mindre. Dette gjøres for å rette feilen. Excel tar hensyn til denne nyansen i en spesiell funksjon som er designet for denne typen beregninger - DISP.V. Syntaksen er representert av følgende formel:

VAR.B(Tall1;Tall2;...)

Antall argumenter, som i forrige funksjon, kan også variere fra 1 til 255.

Som du kan se, er Excel-programmet i stand til i stor grad å lette beregningen av variansen. Dette statistikk kan beregnes av søknaden, både for befolkningen generelt og for utvalget. I dette tilfellet reduseres faktisk alle brukerhandlinger bare til å spesifisere rekkevidden av tall som skal behandles, og Excel gjør hovedarbeidet selv. Selvfølgelig vil dette spare en betydelig mengde tid for brukerne.