Kontinuitet av elementære funksjoner

Kontinuitetssetningene for funksjoner følger direkte av de tilsvarende grensesetningene.

Teorem. Summen, produktet og kvotienten av to kontinuerlige funksjoner er en kontinuerlig funksjon (for kvotienten, bortsett fra de verdiene til argumentet der divisor er null).

Teorem. La funksjonene u= φ (x) er kontinuerlig på punktet X 0 , og funksjonen y = f(u) er kontinuerlig på punktet u 0 = φ (X 0). Deretter den komplekse funksjonen f(φ (x)) som består av kontinuerlige funksjoner er kontinuerlig på punktet x 0 .

Teorem. Hvis funksjonen på = f(X) er kontinuerlig og strengt monoton på [ en; b] aksen Åh, deretter den inverse funksjonen på = φ (X) er også kontinuerlig og monoton på det tilsvarende intervallet [ c;d] aksen OU(ingen bevis).

Funksjoner kontinuerlig på et intervall har en rekke viktige egenskaper. Vi formulerer dem i form av teoremer uten å gi bevis.

Teorem (Weierstrass). Hvis en funksjon er kontinuerlig på et segment, når den sine maksimums- og minimumsverdier på dette segmentet.

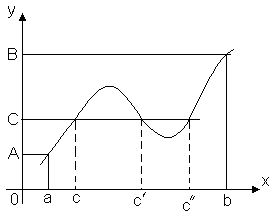
Funksjonen vist i figur 5 på = f(x) er kontinuerlig i intervallet [ en; b], tar sin maksimale verdi M på punktet x 1, og den minste m- på punktet X 2. For alle X [en; b] m ≤ f(x) ≤ M.

Konsekvens. Hvis en funksjon er kontinuerlig på et intervall, er den avgrenset på dette intervallet.

Teorem (Bolzano - Cauchy). Hvis funksjonen på= f(x) er kontinuerlig i intervallet [ en; b] og tar ulik verdi i endene f(en) = EN og f(b) = =PÅ, så på dette segmentet tar det også på seg alle mellomverdier mellom OG og PÅ.

Geometrisk er teoremet åpenbart (se fig. 6).

For et hvilket som helst nummer FRA konkludert mellom OG og PÅ, det er et poeng Med inne i dette segmentet slik at f(Med) = FRA. Rett på = FRA skjærer grafen til funksjonen i minst ett punkt.

Konsekvens. Hvis funksjonen på = f(x) er kontinuerlig i intervallet [ en; b] og tar på seg verdier av forskjellige tegn i endene, deretter inne i segmentet [ en; b] det er minst ett poeng Med, der denne funksjonen f(x) forsvinner: f(Med) = 0.

Den geometriske betydningen av teoremet: hvis grafen til en kontinuerlig funksjon går fra den ene siden av aksen Åh til en annen, så krysser den aksen Okse(Se fig. 7).

Ris. 7.

Definisjon 4. En funksjon kalles kontinuerlig på et segment hvis den er kontinuerlig i hvert punkt i dette segmentet (i punkt a er den kontinuerlig til høyre, dvs. og ved punkt b er den kontinuerlig til venstre, dvs.).

Alle grunnleggende elementære funksjoner er kontinuerlige i sitt definisjonsdomene.

Egenskaper til funksjoner som er kontinuerlige på et segment:

• 1) Hvis en funksjon er kontinuerlig på et segment, så er den avgrenset på dette segmentet (det første Weierstrass-teoremet).
• 2) Hvis en funksjon er kontinuerlig på et segment, så når den på dette segmentet sin minimumsverdi og sin maksimumsverdi (det andre Weierstrass-teoremet) (se fig. 2).
• 3) Hvis en funksjon er kontinuerlig på et segment og tar verdier av forskjellige fortegn i endene, så er det minst ett punkt inne i segmentet slik at (Bolzano-Cauchy-teoremet).

Funksjonsbruddpunkter og deres klassifisering

funksjon kontinuitet punkt segment

Punktene der kontinuitetsbetingelsen ikke er oppfylt kalles diskontinuitetspunkter for denne funksjonen. Hvis er et diskontinuitetspunkt for en funksjon, er minst en av de tre betingelsene for kontinuiteten til funksjonen spesifisert i definisjon 1, 2 ikke oppfylt i den, nemlig:

1) Funksjonen er definert i nærheten av punktet, men ikke definert i selve punktet. Så funksjonen vurdert i eksempel 2 a) har et brudd på et punkt, siden den ikke er definert på dette punktet.

2) Funksjonen er definert ved et punkt og dets nabolag, det er ensidige grenser og, men de er ikke like med hverandre: . For eksempel er funksjonen fra eksempel 2 b) definert ved et punkt og dets nabolag, men siden a.

3) Funksjonen er definert ved punktet og dets omgivelser, det er ensidige grenser og, de er lik hverandre, men ikke lik verdien av funksjonen i punktet: . For eksempel funksjon. Her er bruddpunktet: på dette punktet er funksjonen definert, det er ensidige grenser og lik hverandre, men, dvs.

Funksjonsbruddpunkter er klassifisert som følger.

Definisjon 5. Et punkt kalles et diskontinuitetspunkt av den første typen av en funksjon hvis det er endelige grenser og på dette punktet, men de er ikke like med hverandre: . Mengden kalles da funksjonens hopp i punktet.

Definisjon 6. Et punkt kalles et punkt for en fjernbar diskontinuitet til en funksjon hvis det på dette punktet er endelige grenser og de er like med hverandre: , men funksjonen i seg selv er ikke definert ved punktet, eller er definert, men.

Definisjon 7. Et punkt kalles et diskontinuitetspunkt av den andre typen funksjon hvis på dette tidspunktet minst en av de ensidige grensene (eller) ikke eksisterer eller er lik uendelig.

Eksempel 3. Finn bruddpunkter for følgende funksjoner og bestem deres type: a) b)

Beslutning. a) Funksjonen er definert og kontinuerlig på intervallene u, siden den på hvert av disse intervallene er gitt av kontinuerlige elementære funksjoner. Derfor kan bruddpunktene til en gitt funksjon bare være de punktene der funksjonen endrer sin analytiske tilordning, dvs. poeng i. La oss finne de ensidige grensene for funksjonen på punktet:

Siden ensidige grenser eksisterer og er endelige, men ikke like hverandre, er punktet et diskontinuitetspunkt av den første typen. Funksjonshopp:

For et poeng finner vi.

EGENSKAPER TIL FUNKSJONER KONTINUERLIG PÅ ET INTERVALL

La oss vurdere noen egenskaper til funksjoner som er kontinuerlige i et intervall. Vi presenterer disse egenskapene uten bevis.

Funksjon y = f(x) kalt kontinuerlig på segmentet [en, b], hvis den er kontinuerlig ved alle interne punkter i dette segmentet, og i endene, dvs. på poeng en og b, er kontinuerlig på henholdsvis høyre og venstre side.

Teorem 1. En funksjon kontinuerlig på segmentet [ en, b], minst på ett punkt av dette segmentet tar den største verdien og minst på ett punkt - den minste.

Teoremet sier at hvis funksjonen y = f(x) kontinuerlig på intervallet [ en, b], så er det minst ett poeng x 1 Î [ en, b] slik at verdien av funksjonen f(x) på dette tidspunktet vil være den største av alle verdiene på dette segmentet: f(x1) ≥ f(x). På samme måte er det et slikt poeng x2, der verdien av funksjonen vil være den minste av alle verdiene på segmentet: f(x 1) ≤ f(x).

Det er tydelig at det kan være flere slike punkter, for eksempel viser figuren at funksjonen f(x) tar den minste verdien ved to punkter x2 og x 2 ".

Kommentar. Utsagnet til teoremet kan bli usant hvis vi vurderer verdien av funksjonen på intervallet ( en, b). Faktisk, hvis vi vurderer funksjonen y=x på (0, 2), så er den kontinuerlig på dette intervallet, men når ikke sine maksimums- eller minimumsverdier i det: den når disse verdiene på slutten av intervallet, men endene tilhører ikke vår region.

Dessuten slutter teoremet å være sant for diskontinuerlige funksjoner. Gi et eksempel.

Konsekvens. Hvis funksjonen f(x) kontinuerlig på [ en, b], så er det avgrenset på dette segmentet.

Teorem 2. La funksjonen y = f(x) kontinuerlig på segmentet [ en, b] og tar på seg verdier av forskjellige tegn i enden av dette segmentet, så er det minst ett punkt inne i segmentet x=C, hvor funksjonen forsvinner: f(C)= 0, hvor a< C< b

Denne teoremet har en enkel geometrisk betydning: hvis punktene til grafen til en kontinuerlig funksjon y = f(x), tilsvarende endene av segmentet [ en, b] ligge på motsatte sider av aksen Okse, så skjærer denne grafen minst ett punkt av segmentet aksen Okse. Det kan hende at diskontinuerlige funksjoner ikke har denne egenskapen.

Denne teoremet innrømmer følgende generalisering.

Teorem 3 (setning om mellomverdier). La funksjonen y = f(x) kontinuerlig på segmentet [ en, b] og f(a) = A, f(b) = B. Deretter for et hvilket som helst tall C mellom EN og B, det er et slikt punkt inne i dette segmentet CÎ [ en, b], hva f(c) = C.

Denne teoremet er geometrisk tydelig. Tenk på grafen til funksjonen y = f(x). La f(a) = A, f(b) = B. Deretter hvilken som helst linje y=C, hvor C- et hvilket som helst tall mellom EN og B, skjærer grafen til funksjonen i minst ett punkt. Abscissen til skjæringspunktet vil være den verdien x=C, ved hvilken f(c) = C.

Dermed passerer en kontinuerlig funksjon, som går fra en av verdiene til en annen, nødvendigvis gjennom alle mellomverdier. Spesielt:

Konsekvens. Hvis funksjonen y = f(x) er kontinuerlig på et eller annet intervall og tar på seg den største og minste verdien, så tar den på dette intervallet, minst én gang, en hvilken som helst verdi mellom dens minste og største verdi.

DERIVAT OG DETS APPLIKASJONER. DERIVATIV DEFINISJON

La oss ha en funksjon y=f(x), definert på et eller annet intervall. For hver argumentverdi x fra dette intervallet funksjonen y=f(x) har en viss betydning.

Tenk på to argumentverdier: initial x 0 og ny x.

Forskjell x–x 0 kalles økning av argument x på punktet x 0 og betegnet Δx. På denne måten, ∆x = x – x 0 (argumentøkning kan være enten positiv eller negativ). Av denne likestillingen følger det at x=x 0 +Δx, dvs. startverdien til variabelen har fått en viss økning. Så, hvis det er på punktet x 0 funksjonsverdi var f(x 0 ), så på det nye punktet x funksjonen vil ta verdien f(x) = f(x 0 +∆x).

Forskjell å-å 0 = f(x) – f(x 0 ) kalt funksjonsøkning y = f(x) på punktet x 0 og er merket med symbolet Δy. På denne måten,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Vanligvis startverdien til argumentet x 0 regnes som fast og den nye verdien x- variabel. Deretter y 0 = f(x 0 ) viser seg å være konstant og y = f(x)- variabel. trinn Δy og Δx vil også være variabler og formel (1) viser det Dy er en funksjon av variabelen Δx.

Komponer forholdet mellom økningen av funksjonen og økningen av argumentet

La oss finne grensen for dette forholdet ved Δx→0. Hvis denne grensen eksisterer, kalles den den deriverte av denne funksjonen. f(x) på punktet x 0 og angir f "(x 0). Så,

derivat denne funksjonen y = f(x) på punktet x 0 kalles grensen for inkrementforholdet til funksjonen Δ y til økningen av argumentet Δ x når sistnevnte vilkårlig har en tendens til null.

Merk at for samme funksjon er den deriverte på forskjellige punkter x kan anta ulike verdier, dvs. den deriverte kan tenkes som en funksjon av argumentet x. Denne funksjonen er angitt f "(x)

Den deriverte er merket med symbolene f "(x),y", . Den spesifikke verdien av derivatet på x = a angitt f "(en) eller y "| x=a.

Operasjonen med å finne den deriverte av en funksjon f(x) kalles differensiering av denne funksjonen.

For å finne den deriverte direkte per definisjon, kan du bruke følgende tommelfingerregel:

Eksempler.

MEKANISK BETYDNING AV DERIVATET

Det er kjent fra fysikken at loven om jevn bevegelse har formen s = v t, hvor s- sti reist frem til tidspunktet t, v er hastigheten til jevn bevegelse.

Imidlertid siden de fleste bevegelsene som forekommer i naturen er ujevne, da i det generelle tilfellet, hastigheten, og følgelig avstanden s vil avhenge av tid t, dvs. vil være en funksjon av tid.

Så la materialpunktet bevege seg i en rett linje i én retning i henhold til loven s=s(t).

Legg merke til et øyeblikk t 0 . På dette tidspunktet har punktet passert stien s=s(t 0 ). La oss bestemme hastigheten v materielle tidspunkt t 0 .

For å gjøre dette, tenk på et annet øyeblikk t 0 + Δ t. Det tilsvarer den tilbakelagte avstanden s =s(t 0 + Δ t). Deretter for tidsintervallet Δ t punktet har gått veien Δs =s(t 0 + Δ t)–s(t).

La oss vurdere forholdet. Det kalles gjennomsnittshastigheten i tidsintervallet Δ t. Gjennomsnittshastigheten kan ikke nøyaktig karakterisere bevegelseshastigheten til et punkt for øyeblikket t 0 (fordi bevegelsen er ujevn). For å uttrykke denne sanne hastigheten mer nøyaktig ved bruk av gjennomsnittshastigheten, må du ta et mindre tidsintervall Δ t.

Altså bevegelseshastigheten på et gitt tidspunkt t 0 (øyeblikkelig hastighet) er grensen for gjennomsnittshastigheten i intervallet fra t 0 til t 0 +Δ t når Δ t→0:

,

de. hastighet på ujevn bevegelse er den deriverte av tilbakelagt avstand i forhold til tid.

GEOMETRISK BETYDNING AV DERIVATET

La oss først introdusere definisjonen av en tangent til en kurve i et gitt punkt.

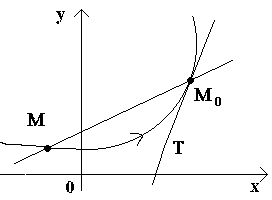
La oss ha en kurve og et fast punkt på den M 0(se figur) Tenk på et annet punkt M denne kurven og tegne en sekant M 0 M. Hvis punkt M begynner å bevege seg langs kurven, og punktet M 0 forblir stasjonær, endrer sekanten sin posisjon. Hvis, med ubegrenset tilnærming av punktet M kurve til punkt M 0 på hvilken som helst side har sekanten en tendens til å innta posisjonen til en viss rett linje M 0 T, deretter den rette linjen M 0 T kalles tangenten til kurven i det gitte punktet M 0.

At., tangent til kurven på et gitt punkt M 0 kalt grenseposisjonen til sekanten M 0 M når poenget M tenderer langs kurven til et punkt M 0.

Tenk nå på den kontinuerlige funksjonen y=f(x) og kurven som tilsvarer denne funksjonen. For en viss verdi X 0-funksjonen tar en verdi y0=f(x0). Disse verdiene x 0 og y 0 på kurven tilsvarer et punkt M 0 (x 0; y 0). La oss argumentere x0øke Δ X. Den nye verdien av argumentet tilsvarer den økte verdien til funksjonen y 0 +Δ y=f(x 0 –Δ x). Vi får et poeng M(x 0+Δ x; y 0+Δ y). La oss tegne en sekant M 0 M og angi med φ vinkelen som dannes av sekanten med den positive retningen til aksen Okse. La oss lage en relasjon og legge merke til det.

Hvis nå Δ x→0, da, på grunn av kontinuiteten til funksjonen Δ på→0, og derfor poenget M, beveger seg langs kurven, nærmer seg punktet på ubestemt tid M 0. Deretter sekanten M 0 M vil ha en tendens til å ta posisjonen til en tangent til kurven ved punktet M 0, og vinkelen φ→α ved Δ x→0, hvor α angir vinkelen mellom tangenten og den positive retningen til aksen Okse. Siden funksjonen tg φ kontinuerlig avhenger av φ ved φ≠π/2, vil ved φ→α tg φ → tg α og derfor stigningstallet til tangenten være:

de. f"(x)= tgα.

Altså geometrisk y "(x 0) representerer stigningstallet til tangenten til grafen til denne funksjonen ved punktet x0, dvs. for en gitt verdi av argumentet x, er den deriverte lik tangenten til vinkelen som dannes av tangenten til grafen til funksjonen f(x) på tilsvarende punkt M 0 (x; y) med positiv akseretning Okse.

Eksempel. Finn hellingen til tangenten til kurven y = x 2 på punktet M(-1; 1).

Det har vi allerede sett ( x 2)" = 2X. Men helningen til tangenten til kurven er tg α = y"| x=-1 = - 2.

DIFFERENSIERBARHET AV FUNKSJONER. KONTINUITET AV EN DIFFERENSIERBAR FUNKSJON

Funksjon y=f(x) kalt differensierbar på et tidspunkt x 0 hvis den har en viss derivert på dette tidspunktet, dvs. hvis grensen for relasjonen eksisterer og er endelig.

Hvis en funksjon er differensierbar på hvert punkt i et segment [ en; b] eller intervall ( en; b), så sier de at det differensierbar på segmentet [ en; b] eller, henholdsvis, i intervallet ( en; b).

Følgende teorem er gyldig, som etablerer en sammenheng mellom differensierbare og kontinuerlige funksjoner.

Teorem. Hvis funksjonen y=f(x) differensierbar på et tidspunkt x0, så er den kontinuerlig på dette punktet.

Dermed innebærer differensierbarheten til en funksjon dens kontinuitet.

Bevis. Hvis , deretter

,

hvor α er en uendelig verdi, dvs. mengde som tenderer til null ved Δ x→0. Men da

Δ y=f "(x0) Δ x+αΔ x=> Δ y→0 ved Δ x→0, dvs. f(x) – f(x0)→0 kl x→x 0 , som betyr at funksjonen f(x) kontinuerlig på punktet x 0 . Q.E.D.

På diskontinuitetspunkter kan funksjonen således ikke ha en derivert. Det motsatte utsagnet er ikke sant: det er kontinuerlige funksjoner som ikke er differensierbare på noen punkter (det vil si at de ikke har en derivert på disse punktene).

Tenk på punktene i figuren a, b, c.

På punktet en ved Δ x→0 forholdet har ingen grense (fordi de ensidige grensene er forskjellige for Δ x→0–0 og Δ x→0+0). På punktet EN grafen har ingen definert tangent, men det er to forskjellige ensidige tangenter med helninger til 1 og til 2. Denne typen punkt kalles et hjørnepunkt.

På punktet b ved Δ x→0 forholdet har konstant fortegn uendelig stor verdi. Funksjonen har en uendelig derivert. På dette tidspunktet har grafen en vertikal tangent. Punkttype - "bøyningspunkt" med vertikal tangent.

På punktet c ensidige derivater er uendelig store mengder forskjellige tegn. På dette tidspunktet har grafen to sammenslåtte vertikale tangenter. Type - "cusp" med en vertikal tangent - et spesialtilfelle av et hjørnepunkt.

Fra et praktisk synspunkt er det mest interessante bruken av den deriverte for å finne den største og minste verdien av en funksjon. Hva henger det sammen med? Maksimere profitt, minimere kostnader, bestemme optimal belastning av utstyr... Med andre ord, på mange områder av livet må man løse problemet med å optimalisere noen parametere. Og dette er problemet med å finne de største og minste verdiene av funksjonen.

Det skal bemerkes at den største og minste verdien av en funksjon vanligvis søkes på et eller annet intervall X , som enten er hele domenet til funksjonen eller en del av domenet. Selve intervallet X kan være et linjestykke, et åpent intervall , et uendelig intervall .

I denne artikkelen vil vi snakke om å finne de største og minste verdiene av en eksplisitt gitt funksjon av en variabel y=f(x) .

Sidenavigering.

Den største og minste verdien av en funksjon - definisjoner, illustrasjoner.

La oss kort dvele ved hoveddefinisjonene.

Den største verdien av funksjonen , som for evt ulikheten er sann.

Den minste verdien av funksjonen y=f(x) på intervallet X kalles en slik verdi , som for evt ulikheten er sann.

Disse definisjonene er intuitive: den største (minste) verdien av en funksjon er den største (minste) verdien akseptert på intervallet som vurderes med abscissen.

Stasjonære punkter er verdiene til argumentet der den deriverte av funksjonen forsvinner.

Hvorfor trenger vi stasjonære punkter når vi skal finne de største og minste verdiene? Svaret på dette spørsmålet er gitt av Fermats teorem. Det følger av denne teoremet at hvis en differensierbar funksjon har et ekstremum (lokalt minimum eller lokalt maksimum) på et tidspunkt, så er dette punktet stasjonært. Dermed tar funksjonen ofte sin maksimale (minste) verdi på intervallet X i et av de stasjonære punktene fra dette intervallet.

Dessuten kan en funksjon ofte ta på seg de største og minste verdiene på punkter der den første deriverte av denne funksjonen ikke eksisterer, og selve funksjonen er definert.

La oss umiddelbart svare på et av de vanligste spørsmålene om dette emnet: "Er det alltid mulig å bestemme den største (minste) verdien av en funksjon"? Nei ikke alltid. Noen ganger faller grensene til intervallet X sammen med grensene for funksjonens domene, eller intervallet X er uendelig. Og noen funksjoner i det uendelige og på grensene til definisjonsdomenet kan ha både uendelig store og uendelig små verdier. I disse tilfellene kan det ikke sies noe om den største og minste verdien av funksjonen.

For klarhet gir vi en grafisk illustrasjon. Se på bildene – så vil mye bli klart.

På segmentet

I den første figuren tar funksjonen de største (max y ) og minste (min y ) verdiene ved stasjonære punkter inne i segmentet [-6;6] .

Vurder saken vist i den andre figuren. Endre segmentet til . I dette eksemplet oppnås den minste verdien av funksjonen ved et stasjonært punkt, og den største - ved et punkt med en abscisse som tilsvarer den høyre grensen til intervallet.

I figur nr. 3 er grensepunktene til segmentet [-3; 2] abscissen til punktene som tilsvarer funksjonens største og minste verdi.

I det åpne området

I den fjerde figuren tar funksjonen de største (max y ) og minste (min y ) verdiene ved stasjonære punkter innenfor det åpne intervallet (-6;6).

På intervallet kan det ikke trekkes konklusjoner om den største verdien.

I det uendelige

I eksemplet vist i den syvende figuren tar funksjonen den største verdien (max y ) i et stasjonært punkt med x=1 abscisse, og den minste verdien (min y ) nås ved høyre grense av intervallet. Ved minus uendelig nærmer funksjonens verdier seg asymptotisk y=3.

På intervallet når ikke funksjonen verken den minste eller største verdien. Ettersom x=2 har en tendens til høyre, tenderer funksjonsverdiene til minus uendelig (den rette linjen x=2 er en vertikal asymptote), og ettersom abscissen har en tendens til pluss uendelig, nærmer funksjonsverdiene seg asymptotisk y=3 . En grafisk illustrasjon av dette eksemplet er vist i figur 8.

Algoritme for å finne de største og minste verdiene av en kontinuerlig funksjon på segmentet.

Vi skriver en algoritme som lar oss finne den største og minste verdien av en funksjon på et segment.

1. Vi finner domenet til funksjonen og sjekker om den inneholder hele segmentet.
2. Vi finner alle punkter der den førstederiverte ikke eksisterer og som finnes i segmentet (vanligvis forekommer slike punkter i funksjoner med et argument under modultegnet og i potensfunksjoner med en brøk-rasjonell eksponent). Hvis det ikke er slike punkter, gå til neste punkt.
3. Vi bestemmer alle stasjonære punkter som faller inn i segmentet. For å gjøre dette likestiller vi den til null, løser den resulterende ligningen og velger de riktige røttene. Hvis det ikke er noen stasjonære punkter eller ingen av dem faller inn i segmentet, gå til neste trinn.
4. Vi beregner verdiene til funksjonen ved de valgte stasjonære punktene (hvis noen), på punkter der den første deriverte ikke eksisterer (hvis noen), og også ved x=a og x=b .
5. Fra de oppnådde verdiene for funksjonen velger vi den største og minste - de vil være henholdsvis de ønskede maksimale og minste verdiene for funksjonen.

La oss analysere algoritmen når vi løser et eksempel for å finne de største og minste verdiene til en funksjon på et segment.

Eksempel.

Finn den største og minste verdien av en funksjon

• på segmentet;
• på intervallet [-4;-1] .

Beslutning.

Domenet til funksjonen er hele settet med reelle tall, bortsett fra null, det vil si . Begge segmentene faller innenfor definisjonsdomenet.

Vi finner den deriverte av funksjonen med hensyn til:

Det er klart at den deriverte av funksjonen eksisterer på alle punkter i segmentene og [-4;-1] .

Stasjonære punkter bestemmes fra ligningen. Den eneste reelle roten er x=2. Dette stasjonære punktet faller inn i det første segmentet.

For det første tilfellet beregner vi verdiene til funksjonen i enden av segmentet og på et stasjonært punkt, det vil si for x=1 , x=2 og x=4 :

Derfor er den største verdien av funksjonen nås ved x=1, og den minste verdien – ved x=2.

For det andre tilfellet beregner vi verdiene til funksjonen bare i endene av segmentet [-4;-1] (siden det ikke inneholder et enkelt stasjonært punkt):

Beslutning.

La oss starte med omfanget av funksjonen. Det kvadratiske trinomium i nevneren til en brøk må ikke forsvinne:

Det er enkelt å kontrollere at alle intervaller fra tilstanden til problemet tilhører funksjonens domene.

La oss skille funksjonen:

Det er klart at den deriverte eksisterer på hele domenet til funksjonen.

La oss finne stasjonære punkter. Den deriverte forsvinner kl. Dette stasjonære punktet faller innenfor intervallene (-3;1] og (-3;2) .

Og nå kan du sammenligne resultatene oppnådd på hvert punkt med grafen til funksjonen. De blå stiplede linjene indikerer asymptotene.

Dette kan ende med å finne den største og minste verdien av funksjonen. Algoritmene som er omtalt i denne artikkelen lar deg få resultater med et minimum av handlinger. Det kan imidlertid være nyttig å først bestemme intervallene for økning og reduksjon av funksjonen og først etter det trekke konklusjoner om den største og minste verdien av funksjonen på ethvert intervall. Dette gir et klarere bilde og en streng begrunnelse av resultatene.

Kontinuitet til en funksjon på et segment.

Sammen med kontinuiteten til en funksjon i et punkt, vurderer man dens kontinuitet på forskjellige intervaller.

En funksjon f (x) kalles kontinuerlig på et intervall (a, b) hvis den er kontinuerlig i hvert punkt i dette intervallet.

En funksjon f(x) kalles kontinuerlig på intervallet [a, b] hvis den er kontinuerlig på intervallet (a, b), kontinuerlig til høyre i punkt a, og kontinuerlig til venstre i punkt b.

Funksjonen kalles kontinuerlig på segmentethvis den er kontinuerlig i intervallet, kontinuerlig til høyre på punktet, det er og kontinuerlig til venstre ved punktet, det er .

Kommentar. En funksjon som er kontinuerlig på segmentet [ a , b ] kan være diskontinuerlig i punktene a og b (fig. 1)

Settet med funksjoner som er kontinuerlige på segmentet [a, b] er merket med symbolet C[a, b].

Grunnleggende teoremer om funksjoner kontinuerlig på et intervall.

Teorem 1(om avgrensningen av en kontinuerlig funksjon). Hvis funksjonen f (x) er kontinuerlig på segmentet [a, b], så er den avgrenset på dette segmentet, dvs. det er et tall C > 0 slik at " x 0 [ a , b ] ulikheten | f (x)| ≤ C .

Teorem 2(Weierstrass). Hvis funksjonen f (x) er kontinuerlig på segmentet [a, b], så når den sin maksimale verdi M og sin minimumsverdi m på dette intervallet, dvs. det er punkter α , β О [ a , b ] slik at m = f (α) ≤ f (x) ≤ f (β) = M for alle x О [ a , b ] (fig. 2).

Den største verdien av M er merket med symbolet maks x Om [a, b] f (x), og den minste verdien av m er symbolet min x Om [a, b] f(x).
Teorem 3(om eksistensen av null). Hvis funksjonen f (x) er kontinuerlig på segmentet [ a , b ] og tar ikke-null-verdier av forskjellige fortegn ved enden av segmentet, så er det på intervallet (a , b) minst ett punkt ξ hvor f (ξ) = 0.
Den geometriske betydningen av teoremet er at grafen til en funksjon som tilfredsstiller betingelsene for teoremet, nødvendigvis vil skjære aksen OKSE(Fig. 3).

Kommentar. Denne teoremet er grunnlaget for metoden for omtrentlig løsning av ligningen

f(x) = 0,

(1)

kalt halveringsmetoden (dikotomi), eller halveringsmetoden.

Teorem 4(Bolzano-Cauchy). Hvis funksjonen f (x) er kontinuerlig i intervallet [a, b], tar den på seg (a, b) alle mellomverdier mellom f (a) og f (b).
Eksistensen av en kontinuerlig invers funksjon
La funksjonen y = f (x) være definert, strengt monoton og kontinuerlig på segmentet [a, b]. Så på intervallet [ α , β ] (α = f (a), β = f (b)) eksisterer det en invers funksjon x = g (y), som også er strengt monotonisk og kontinuerlig på intervallet (α , β ).