Trigonometri tabell. Vel, la oss prøve disse formlene for en smak, og øve på å finne punkter på en sirkel? Det foreslåtte matematiske apparatet er en komplett analog av den komplekse beregningen for n-dimensjonale hyperkomplekse tall med et hvilket som helst antall grader med
Merk følgende!
Det er flere
materiale i spesialseksjon 555.
For de som sterkt "ikke veldig..."
Og for de som "veldig mye...")
Først av alt, la meg minne deg om en enkel, men veldig nyttig konklusjon fra leksjonen "Hva er sinus og cosinus? Hva er tangent og cotangens?"
Her er utgangen:
Sinus, cosinus, tangens og cotangens er tett forbundet med vinklene deres. Vi vet én ting, så vi vet noe annet.
Med andre ord har hver vinkel sin egen faste sinus og cosinus. Og nesten alle har sin egen tangent og cotangens. Hvorfor nesten? Mer om det nedenfor.
Denne kunnskapen vil hjelpe deg mye! Det er mange oppgaver hvor du skal gå fra sinus til vinkler og omvendt. For dette er det sinustabell. Tilsvarende, for jobber med cosinus - kosinusbord. Og, du gjettet riktig, det er det tangenttabell Og cotangenstabell.)
Tabeller er forskjellige. Lange, hvor du kan se hva, si, sin37 ° 6 'er lik. Vi åpner Bradis-tabellene, ser etter en vinkel på trettisju grader seks minutter og ser verdien på 0,6032. Selvfølgelig å huske dette nummeret (og tusenvis av andre tabellverdier) er ikke nødvendig i det hele tatt.
I vår tid er det faktisk ikke behov for lange tabeller med cosinus, sinus, tangenter og cotangenter. En god kalkulator erstatter dem fullstendig. Men det skader ikke å vite om eksistensen av slike tabeller. For generell lærdom.)
Hvorfor da denne leksjonen? - du spør.
Men hvorfor. Blant det uendelige antallet vinkler som finnes spesiell, som du bør vite om Alle. All skolegeometri og trigonometri er bygget på disse vinklene. Dette er en slags "multiplikasjonstabell" av trigonometri. Hvis du ikke vet hva sin50° er lik, for eksempel, vil ingen dømme deg.) Men hvis du ikke vet hva sin30° er lik, gjør deg klar til å få en velfortjent toer...
Slik spesiell hjørner er også anstendig skrevet. Skolebøker tilbys vanligvis for memorering. sinustabell og cosinustabell for sytten hjørner. Og selvfølgelig, tangenttabell og kotangenstabell for de samme sytten hjørnene... Altså. det foreslås å huske 68 verdier. Som forresten er veldig like hverandre, gjentar og bytter tegn nå og da. For en person uten et ideelt visuelt minne - det er en annen oppgave ...)
Vi vil gå den andre veien. La oss erstatte mekanisk memorering med logikk og oppfinnsomhet. Da må vi huske 3 (tre!) verdier for sinustabellen og cosinustabellen. Og 3 (tre!) verdier for tabellen over tangenter og tabellen over kotangenter. Og det er det. Seks verdier er lettere å huske enn 68, tror jeg...)
Annen nødvendige verdier vi kommer ut av disse seks med et kraftig juridisk jukseark - trigonometrisk sirkel. Hvis du ikke har studert dette emnet, gå til lenken, ikke vær lat. Denne sirkelen er ikke bare for denne leksjonen. Han er uerstattelig for all trigonometri på en gang. Å ikke bruke et slikt verktøy er rett og slett synd! Vil du ikke? Det er din sak. huske sinustabell. kosinusbord. Tangentbord. Cotangens bord. Alle 68 verdier for forskjellige vinkler.)
Så la oss begynne. Til å begynne med, la oss dele alle disse spesielle vinklene inn i tre grupper.
Den første gruppen av hjørner.
Tenk på den første gruppen hjørner av sytten spesiell. Dette er 5 vinkler: 0°, 90°, 180°, 270°, 360°.
Slik ser tabellen over sinus, cosinus, tangenter og cotangens for disse vinklene ut:
Vinkel x
|
0 |
90 |
180 |
270 |
360 |
Vinkel x
|
0 |
||||
synd x |
0 |
1 |
0 |
-1 |
0 |
fordi x |
1 |
0 |
-1 |
0 |
1 |
tg x |
0 |
ikke substantiv |
0 |
ikke substantiv |
0 |
ctg x |
ikke substantiv |
0 |
ikke substantiv |
0 |
ikke substantiv |
De som vil huske – husk. Men jeg må si med en gang at alle disse enerne og nullene er veldig forvirret i hodet mitt. Mye sterkere enn du ønsker.) Derfor slår vi på logikken og den trigonometriske sirkelen.
Vi tegner en sirkel og markerer de samme vinklene på den: 0°, 90°, 180°, 270°, 360°. Jeg merket disse hjørnene med røde prikker:

Du kan umiddelbart se hva det særegne ved disse hjørnene er. Ja! Dette er hjørnene som faller nøyaktig på koordinataksen! Det er faktisk derfor folk blir forvirret ... Men vi vil ikke bli forvirret. La oss finne ut hvordan du finner de trigonometriske funksjonene til disse vinklene uten mye memorering.
Forresten, posisjonen til vinkelen er 0 grader helt sammenfallende med 360 graders vinkel. Dette betyr at sinus, cosinus, tangentene til disse vinklene er nøyaktig de samme. Jeg markerte 360 graders vinkel for å fullføre sirkelen.
Anta, i et vanskelig stressende miljø under Unified State Examination, tvilte du på en eller annen måte ... Hva er lik sinus 0 grader? Det virker som null ... Hva om det er en enhet?! Mekanisk minne er en slik ting. Under tøffe forhold begynner tvilen å gnage ...)
Rolig, bare rolig!) Jeg skal fortelle deg det praktisk teknikk, som vil gi et 100 % riktig svar og fullstendig fjerne all tvil.
Som et eksempel, la oss finne ut hvordan du tydelig og pålitelig bestemmer for eksempel en sinus på 0 grader. Og samtidig cosinus 0. Det er i disse verdiene, merkelig nok, at folk ofte blir forvirret.
For å gjøre dette, tegn på en sirkel vilkårlig hjørne X. I første kvarter, slik at det ikke var langt unna 0 grader. Merk på aksene sinus og cosinus for denne vinkelen X, alt er kinar. Som dette:
Og nå - oppmerksomhet! Reduser vinkelen X, før den bevegelige siden til aksen ÅH. Hold markøren over bildet (eller trykk på bildet på nettbrettet) og se alt.
Slå nå på den elementære logikken!. Se og tenk: Hvordan oppfører sinx seg når vinkelen x minker? Når vinkelen nærmer seg null? Det krymper! Og cosx - øker! Det gjenstår å finne ut hva som vil skje med sinusen når vinkelen kollapser helt? Når vil den bevegelige siden av vinkelen (punkt A) legge seg på OX-aksen og vinkelen blir lik null? Selvfølgelig vil sinusen til vinkelen også gå til null. Og cosinus vil øke til ... til ... Hva er lengden på den bevegelige siden av vinkelen (radiusen til den trigonometriske sirkelen)? Enhet!
Her er svaret. Sinusen til 0 grader er 0. Cosinusen til 0 grader er 1. Absolutt jernbelagt og uten tvil!) Rett og slett fordi ellers det kan ikke være.
På nøyaktig samme måte kan du for eksempel finne ut (eller tydeliggjøre) sinusen til 270 grader. Eller cosinus 180. Tegn en sirkel, vilkårlig en vinkel i et kvarter ved siden av koordinataksen som er av interesse for oss, beveger siden av vinkelen mentalt og fanger opp hva sinus og cosinus blir når siden av vinkelen legger seg på aksen. Det er alt.
Som du kan se, er det ikke nødvendig å huske noe for denne gruppen av vinkler. ikke nødvendig her sinustabell... Ja og kosinusbord- også.) Forresten, etter flere anvendelser av den trigonometriske sirkelen, huskes alle disse verdiene av seg selv. Og hvis de er glemt, tegnet jeg en sirkel på 5 sekunder og klargjorde den. Mye enklere enn å ringe en venn fra toalettet med risiko for sertifikat, ikke sant?)
Når det gjelder tangenten og cotangensen, er alt det samme. Vi tegner en tangentlinje (cotangens) på sirkelen - og alt er umiddelbart synlig. Hvor de er lik null, og hvor de ikke eksisterer. Hva, vet du ikke om linjene for tangent og cotangens? Dette er trist, men kan fikses.) Besøkte seksjon 555 Tangent og cotangens på en trigonometrisk sirkel - og ikke noe problem!
Hvis du forstår hvordan du klart definerer sinus, cosinus, tangens og cotangens for disse fem vinklene - gratulerer! Bare i tilfelle informerer jeg deg om at du nå kan definere funksjoner eventuelle vinkler som faller på aksen. Og dette er 450°, og 540°, og 1800°, og til og med et uendelig antall ...) Jeg telte (riktig!) Vinkelen på sirkelen - og det er ingen problemer med funksjonene.
Men, bare med telling av vinkler, oppstår problemer og feil ... Hvordan unngå dem er skrevet i leksjonen: Hvordan tegne (telle) en hvilken som helst vinkel på en trigonometrisk sirkel i grader. Elementært, men veldig nyttig i kampen mot feil.)
Og her er leksjonen: Hvordan tegne (telle) en hvilken som helst vinkel på en trigonometrisk sirkel i radianer - det vil være mer brå. Når det gjelder muligheter. La oss si, bestemme hvilken av de fire halvaksene vinkelen faller på
du kan på et par sekunder. Jeg tuller ikke! Bare om et par sekunder. Vel, selvfølgelig, ikke bare 345 "pi" ...) Og 121, og 16, og -1345. Enhver heltallskoeffisient er bra for et øyeblikkelig svar.
Hva om vinkelen
Synes at! Riktig svar fås på 10 sekunder For evt brøkverdi radianer med en nevner på to.
Egentlig er dette bra trigonometrisk sirkel. Det faktum at evnen til å jobbe med noen hjørner den utvides automatisk til uendelig sett hjørner.
Så, med fem hjørner av sytten - fant det ut.
Den andre gruppen av vinkler.
Neste gruppe vinklene er 30°, 45° og 60°. Hvorfor disse, og ikke for eksempel 20, 50 og 80? Ja, det skjedde liksom slik... Historisk sett.) Videre vil det ses hvor gode disse vinklene er.
Tabellen over sinus, cosinus, tangenter, cotangenter for disse vinklene ser slik ut:
Vinkel x
|
0 |
30 |
45 |
60 |
90 |
Vinkel x
|
0 |
||||
synd x |
0 |
1 |
|||
fordi x |
1 |
0 |
|||
tg x |
0 |
1 |
ikke substantiv |
||
ctg x |
ikke substantiv |
1 |
0 |
Jeg forlot verdiene for 0° og 90° fra forrige tabell for fullstendighet.) For å gjøre det klart at disse vinklene ligger i første kvartal og øker. Fra 0 til 90. Dette vil være nyttig for oss videre.
Tabellverdiene for vinklene 30°, 45° og 60° må huskes. Skrap hvis du vil. Men også her er det en mulighet til å gjøre livet enklere for deg selv.) Vær oppmerksom på sinustabellverdier disse hjørnene. Og sammenligne med cosinustabellverdier...
Ja! De samme! Kun plassert i omvendt rekkefølge. Vinklene øker (0, 30, 45, 60, 90) - og sinusverdiene øke fra 0 til 1. Du kan verifisere med en kalkulator. Og cosinusverdiene - avta fra 1 til null. Dessuten verdiene seg selv samme. For vinkler på 20, 50, 80 ville dette ikke ha skjedd...
Derfor en nyttig konklusjon. Nok å lære tre verdier for vinkler 30, 45, 60 grader. Og husk at de øker i sinus, og minker i cosinus. Mot sinus.) Halvveis (45°) møtes de, dvs. sinus på 45 grader er lik cosinus på 45 grader. Og så divergerer de igjen ... Tre betydninger kan læres, ikke sant?
Med tangenter - cotangenter er bildet utelukkende det samme. En til en. Bare verdiene er forskjellige. Disse verdiene (tre til!) må også læres.
Vel, nesten all memorering er over. Du forsto (forhåpentligvis) hvordan du bestemmer verdiene for de fem vinklene som faller på aksen og lærte verdiene for vinklene på 30, 45, 60 grader. Totalt 8.
Det gjenstår å håndtere den siste gruppen på 9 hjørner.
Dette er hjørnene:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. For disse vinklene må du kjenne sinustabellen, cosinustabellen osv.
Mareritt, ikke sant?)
Og hvis du legger til vinkler her, som: 405 °, 600 ° eller 3000 ° og mange, mange av de samme vakre?)
Eller vinkler i radianer? For eksempel om hjørner:

og mange flere du bør vite Alle.
Det morsomste er å vite Alle - umulig i prinsippet. Hvis du bruker mekanisk minne.
Og det er veldig enkelt, faktisk elementært - hvis du bruker en trigonometrisk sirkel. Hvis du blir praktisk med den trigonometriske sirkelen, kan alle de forferdelige vinklene i grader enkelt og elegant reduseres til de gode gamle:
Forresten, jeg har et par flere interessante nettsteder for deg.)
Du kan trene på å løse eksempler og finne ut nivået ditt. Testing med umiddelbar verifisering. Læring - med interesse!)
du kan bli kjent med funksjoner og deriverte.
Vi begynner studiet av trigonometri med en rettvinklet trekant. La oss definere hva sinus og cosinus er, samt tangenten og cotangensen til en spiss vinkel. Dette er det grunnleggende om trigonometri.
Husk det rett vinkel er en vinkel lik 90 grader. Med andre ord halvparten av det utfoldede hjørnet.
Skarpt hjørne- mindre enn 90 grader.
Stump vinkel- større enn 90 grader. I forhold til en slik vinkling er ikke "stump" en fornærmelse, men et matematisk begrep :-)
La oss tegne en rettvinklet trekant. En rett vinkel er vanligvis betegnet . Merk at siden motsatt hjørnet er merket med samme bokstav, bare liten. Så siden som ligger motsatt vinkelen A er angitt.
En vinkel er angitt med den tilsvarende greske bokstaven.

Hypotenus En rettvinklet trekant er siden motsatt den rette vinkelen.
Ben- sider motsatt skarpe hjørner.
Benet motsatt hjørnet kalles motsatte(i forhold til vinkel). Det andre benet, som ligger på den ene siden av hjørnet, kalles ved siden av.
Sinus spiss vinkel i en rettvinklet trekant er forholdet mellom det motsatte benet og hypotenusen:
Cosinus spiss vinkel i en rettvinklet trekant - forholdet mellom det tilstøtende benet og hypotenusen:
Tangent spiss vinkel i en rettvinklet trekant - forholdet mellom det motsatte benet og det tilstøtende:
En annen (tilsvarende) definisjon: tangenten til en spiss vinkel er forholdet mellom sinusen til en vinkel og dens cosinus:
Cotangens spiss vinkel i en rettvinklet trekant - forholdet mellom det tilstøtende benet og det motsatte (eller tilsvarende forholdet mellom cosinus og sinus):
Vær oppmerksom på de grunnleggende forholdene for sinus, cosinus, tangens og cotangens, som er gitt nedenfor. De vil være nyttige for oss for å løse problemer.

La oss bevise noen av dem.
Ok, vi har gitt definisjoner og skrevet formler. Men hvorfor trenger vi sinus, cosinus, tangens og cotangens?
Vi vet det summen av vinklene til en hvilken som helst trekant er.
Vi kjenner forholdet mellom fester høyre trekant. Dette er Pythagoras teorem: .
Det viser seg at når du kjenner to vinkler i en trekant, kan du finne den tredje. Når du kjenner to sider i en rettvinklet trekant, kan du finne den tredje. Så for vinkler - deres forhold, for sider - deres egne. Men hva skal jeg gjøre hvis en vinkel (bortsett fra en rett) og en side i en rettvinklet trekant er kjent, men du må finne andre sider?

Dette er hva folk møtte tidligere, og laget kart over området og stjernehimmelen. Det er tross alt ikke alltid mulig å måle alle sidene i en trekant direkte.
Sinus, cosinus og tangens – de kalles også trigonometriske funksjoner til vinkelen- gi forholdet mellom fester Og hjørner triangel. Når du kjenner vinkelen, kan du finne alle trigonometriske funksjoner ved hjelp av spesielle tabeller. Og når du kjenner sinus, cosinus og tangens til vinklene til en trekant og en av sidene, kan du finne resten.
Vi vil også tegne en tabell med sinus-, cosinus-, tangens- og cotangensverdier for "gode" vinkler fra til.
Legg merke til de to røde strekene i tabellen. For de tilsvarende verdiene til vinklene eksisterer ikke tangens og cotangens.
La oss analysere flere problemer i trigonometri fra Bank of FIPI-oppgaver.
1. I en trekant er vinkelen , . Finn .
Problemet er løst på fire sekunder.
Fordi det , .
2. I en trekant er vinkelen , , . Finn .

La oss finne ved Pythagoras teorem.
Problem løst.
Ofte i oppgaver er det trekanter med vinkler og eller med vinkler og . Lær de grunnleggende forholdstallene for dem utenat!

For en trekant med vinkler og benet motsatt vinkelen på er lik halvparten av hypotenusen.
En trekant med vinkler og er likebenet. I den er hypotenusen ganger større enn benet.
Vi vurderte problemer for å løse rettvinklede trekanter - altså for å finne ukjente parter eller hjørner. Men det er ikke alt! I BRUK alternativer i matematikk er det mange problemer hvor sinus, cosinus, tangens eller cotangens til trekantens ytre vinkel vises. Mer om dette i neste artikkel.
Hovedbord trigonometriske funksjoner for vinkler 0, 30, 45, 60, 90, … grader
Fra de trigonometriske definisjonene av funksjonene $\sin$, $\cos$, $\tan$ og $\cot$ kan man finne verdiene deres for vinkler $0$ og $90$ grader:
$\sin0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ ikke definert;
$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ er ikke definert.
I skolekurs geometrier i studiet av rette trekanter finner de trigonometriske funksjonene til vinklene $0°$, $30°$, $45°$, $60°$ og $90°$.
De funnet verdiene av trigonometriske funksjoner for de spesifiserte vinklene i henholdsvis grader og radianer ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) for enkel memorering og bruk legges inn i en tabell kalt trigonometrisk tabell, Tabell over grunnleggende verdier for trigonometriske funksjoner og så videre.
Når du bruker reduksjonsformler, trigonometrisk tabell kan utvides til henholdsvis $360°$ og $2\pi$ radianer:
Ved å bruke periodisitetsegenskapene til trigonometriske funksjoner, kan hver vinkel som skiller seg fra den allerede kjente med $360°$ beregnes og registreres i en tabell. For eksempel vil den trigonometriske funksjonen for vinkelen $0°$ ha samme verdi for vinkelen $0°+360°$, og for vinkelen $0°+2 \cdot 360°$, og for vinkelen $0°+3 \ cdot 360°$ og etc.
Ved å bruke en trigonometrisk tabell kan du bestemme verdiene for alle vinkler i en enhetssirkel.
I skolekurset i geometri er det ment å huske de grunnleggende verdiene til trigonometriske funksjoner samlet i en trigonometrisk tabell, for enkelhets skyld å løse trigonometriske problemer.
Ved hjelp av et bord
I tabellen er det nok å finne den nødvendige trigonometriske funksjonen og verdien av vinkelen eller radianen som denne funksjonen må beregnes for. I skjæringspunktet mellom raden med funksjonen og kolonnen med verdien, får vi ønsket verdi av den trigonometriske funksjonen til det gitte argumentet.
På figuren kan du se hvordan du finner verdien $\cos60°$ som er lik $\frac(1)(2)$.
Den utvidede trigonometriske tabellen brukes på samme måte. Fordelen med å bruke den er, som allerede nevnt, beregningen av den trigonometriske funksjonen til nesten hvilken som helst vinkel. For eksempel kan du enkelt finne verdien $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$:
Bradis-tabeller over grunnleggende trigonometriske funksjoner
Evnen til å beregne den trigonometriske funksjonen til absolutt hvilken som helst vinkelverdi for en heltallsverdi på grader og en heltallsverdi på minutter gir bruk av Bradis-tabeller. Finn for eksempel verdien $\cos34°7"$. Tabellene er delt inn i 2 deler: tabellen med $\sin$ og $\cos$ verdier og tabellen med $\tan$ og $\ cot$-verdier.
Bradis-tabeller gjør det mulig å oppnå en omtrentlig verdi av trigonometriske funksjoner med en nøyaktighet på opptil 4 desimaler.
Bruke Bradis-tabeller
Ved å bruke tabellene til Bradys for sinus finner vi $\sin17°42"$. For å gjøre dette finner vi i kolonnen til venstre for tabellen over sinus og cosinus verdien av grader - $17°$, og i den øverste linjen finner vi verdien av minutter - $42"$. I skjæringspunktet deres får vi ønsket verdi:
$\sin17°42"=0,304$.
For å finne verdien av $\sin17°44"$, må du bruke korreksjonen på høyre side av tabellen. I denne saken til verdien av $42"$, som er i tabellen, må du legge til en korreksjon for $2"$, som er lik $0,0006$. Vi får:
$\sin17°44"=0,304+0,0006=0,3046$.
For å finne verdien av $\sin17°47"$ bruker vi også korreksjonen på høyre side av tabellen, bare i dette tilfellet tar vi verdien av $\sin17°48"$ som grunnlag og trekker fra korreksjonen for $1"$:
$\sin17°47"=0,3057-0,0003=0,3054$.
Når vi beregner cosinusene, utfører vi lignende handlinger, men vi ser på gradene i høyre kolonne, og minuttene i den nederste kolonnen i tabellen. For eksempel $\cos20°=0,9397$.
Det er ingen korrigeringer for tangentverdier opp til $90°$ og liten vinkelkontangens. La oss for eksempel finne $\tan 78°37"$, som ifølge tabellen er $4,967$.
1. Trigonometriske funksjoner representere elementære funksjoner, hvis argument er hjørne. Ved hjelp av trigonometriske funksjoner kan relasjonene mellom sidene og skarpe hjørner i en rettvinklet trekant. Bruksområdene for trigonometriske funksjoner er ekstremt forskjellige. Så for eksempel kan alle periodiske prosesser representeres som en sum av trigonometriske funksjoner (Fourier-serien). Disse funksjonene dukker ofte opp når man løser differensial- og funksjonelle ligninger.
2. Trigonometriske funksjoner inkluderer følgende 6 funksjoner: sinus, kosinus, tangent,cotangens, sekant Og cosecant. For hver av spesifiserte funksjoner det er en invers trigonometrisk funksjon.
3. Geometrisk definisjon trigonometriske funksjoner er praktisk introdusert ved hjelp av enhetssirkel. Figuren under viser en sirkel med radius r=1. Punktet M(x,y) er markert på sirkelen. Vinkelen mellom radiusvektoren OM og den positive retningen til Ox-aksen er α.
4. sinus vinkelen α er forholdet mellom ordinaten y til punktet M(x,y) og radius r:
sinα=y/r.
Siden r=1, så er sinus lik ordinaten til punktet M(x,y).
5. kosinus vinkelen α er forholdet mellom abscissen x til punktet M(x,y) og radius r:
cosα=x/r
6. tangent vinkelen α er forholdet mellom ordinaten y til punktet M(x,y) og abscissen x:
tanα=y/x,x≠0
7. Cotangens vinkelen α er forholdet mellom abscissen x til punktet M(x,y) og ordinaten y:
cotα=x/y,y≠0
8. Sekant vinkel α er forholdet mellom radius r og abscissen x til punktet M(x,y):
sekα=r/x=1/x,x≠0
9. Cosecant vinkel α er forholdet mellom radius r og ordinaten y til punktet M(x,y):
csca=r/y=1/y,y≠0
10. I enhetssirkel projeksjonene x, y av punktet M(x,y) og radius r danner en rettvinklet trekant der x,y er bena og r er hypotenusen. Derfor er definisjonene ovenfor av trigonometriske funksjoner brukt på høyre trekant er formulert på denne måten:
sinus vinkel α er forholdet mellom det motsatte benet og hypotenusen.
kosinus vinkel α er forholdet mellom det tilstøtende benet og hypotenusen.
tangent vinkel α kalles det motsatte benet til det tilstøtende.
Cotangens vinkel α kalles det tilstøtende benet til det motsatte.
Sekant vinkel α er forholdet mellom hypotenusen og det tilstøtende benet.
Cosecant vinkel α er forholdet mellom hypotenusen og motsatt ben.
11. sinusfunksjonsgraf
y=sinx, domene: x∈R, domene: −1≤sinx≤1
12. Graf over cosinusfunksjonen
y=cosx, domene: x∈R, område: −1≤cosx≤1
13. tangentfunksjonsgraf 14. Graf over cotangensfunksjonen 15. Graf over sekantfunksjonen
y=tanx, domene: x∈R,x≠(2k+1)π/2, domene: −∞ 
y=cotx, domene: x∈R,x≠kπ, domene: −∞ 
y=secx, domene: x∈R,x≠(2k+1)π/2, domene: secx∈(−∞,−1]∪∪)
 Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler
Konvertering av en desimalbrøk til en vanlig brøk og omvendt: en regel, eksempler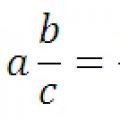 Konvertering av desimaltall til vanlige brøker
Konvertering av desimaltall til vanlige brøker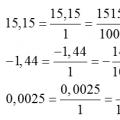 Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler
Konvertering av en vanlig brøk til en desimalbrøk og omvendt, regler, eksempler